Cenno alle serie di Fourier
|
|
|
- Francesca Ricciardi
- 6 anni fa
- Visualizzazioni
Transcript
1 Luciao Battaia 7 settembre 00 Idice Queste pagie cotegoo solo u itroduzioe iformale e seza alcua pretesa di completezza e sistematicità alle serie di Fourier. I particolare o soo proposte dimostrazioi dei teoremi euciati. Alcui richiami di Algebra lieare Relazioi di ortogoalità e base i R ],π] 3 Sviluppo di Fourier 5 Periodo arbitrario 5 Forma complessa 7 Qualche esercizio Alcui richiami di Algebra lieare Se ello spazio V dei vettori geometrici itroduciamo ua base ortoormale qualuque e, e, e 3, si può stabilire ua corrispodeza biuivoca tra l isieme dei vettori e l isieme delle tere di umeri reali, R 3 : se () u = u e + u e + u 3 e 3, si può idetificare u co (u, u, u 3 ) : () u = (u, u, u 3 ). I questo modo le operazioi lieari sui vettori si traducoo i operazioi sulle tere: alla somma di due vettori corrispode la somma termie a termie delle tere corrispodeti, ecc. Qui ci iteressa il fatto che ache il prodotto scalare tra vettori può essere eseguito usado le tere rappresetative: se u = (u, u, u 3 ) e v = (v, v, v 3 ), si ha (3) u v = u v cos uc v = u v + u v + u 3 v 3 = 3 u i v i, i=
2 e () u = u u = u + u + u 3. Le compoeti di u vettore u rispetto alla tera ortoormale e, e, e 3 si possoo trovare co il prodotto scalare (5) u = u e, u = u e, u 3 = u e 3. Se la tera fosse solo ortogoale, a, a, a 3, si potrebbe passare a ua tera ortoormale dividedo ciascuo dei suoi elemeti per la lughezza, e si avrebbe a () u = u a = a u a, a u = u a = a u a, a 3 u 3 = u a 3 = a 3 u a 3. Dalle () e () si deduce che il vettore u si può scrivere rispetto alla tera ortogoale come segue: (7) u = u a a a a + u a a a a + u a 3 a 3 a 3 a 3 = u a a a + u a a a + u a 3 a 3 a 3 Ricordiamo ifie che due vettori o ulli soo ortogoali se e solo il loro prodotto scalare è ullo. Relazioi di ortogoalità e base i R ],π] Cosideriamo l isieme, B, delle fuzioi () x cos x x si x, = 0,,..., Osserviamo esplicitamete che per = 0 si ha cos x e si x 0. Ua qualuque combiazioe lieare di fuzioi di B produce ua fuzioe periodica di periodo π. La teoria delle serie di Fourier si occupa sostazialmete del problema iverso: data ua fuzioe periodica di periodo π, ci si chiede se essa può essere espressa come combiazioe lieare di fuzioi di B. La risposta, come vedremo, è sostazialmete affermativa per ua vasta classe di fuzioi, pur di sostituire le combiazioi lieari ordiarie, cioè costituite da u umero fiito di addedi, co combiazioi lieari ifiite, cioè costituite da serie di fuzioi. Per arrivare a questo risultato servoo alcue defiizioi e osservazioi prelimiari. Lemma (Relazioi di ortogoalità). Se m ed soo due aturali qualuque, si ha π, se m = = 0 (9) cos mx cos x dx = π, se m = 0, 0, se m (0) 0, se m = = 0 si mx si x dx = π, se m = 0 0, se m, () cos mx si x dx = 0. Luciao Battaia
3 Dimostrazioe. La dimostrazioe è u semplice (ma utile!) esercizio sugli itegrali. Facciamo esplicitamete tutti i calcoli per la terza delle (9). Si ha cos mx cos x dx = = = = ( cos(mx x) + cos(mx + x) ) dx = ( cos(m )x + cos(m + )x ) dx = (m ) ( cos(m )x dx+ (m ) π + (m + ) ( cos(m + )x dx = (m + ) ] π [ si(m )x (m ) + [ ] π si(m + )x = 0 (m + ) Queste relazioi si chiamao relazioi di ortogoalità perché, i aalogia co la formula (), possiamo pesare a ua fuzioe u: ] π, π] R come a u vettore ifiito-dimesioale, le cui compoeti soo i valori di u(x) al variare di x i ] π, π]: () u R ],π], u = ( u(x) ) x [0,π], dove abbiamo idicato co R ]π,π] l isieme delle fuzioi da ] π, π] i R. I aalogia alla formula (3), se le fuzioi soo opportuamete regolari, potremo pesare alle formule (9), (0) e () come a prodotti scalari () tra queste fuzioi, e leggere le formule stesse dicedo che cos 0x = ha orma π; cos mx e si mx hao orma π se m > 0; cos mx e cos x, oppure si mx e si x, soo ortogoali tra di loro se m ; cos mx e si x so ortogoali tra di loro. Sempre i aalogia co quato succede egli spazi vettoriali, possiamo chiederci se le fuzioi di B costituiscoo ua base per lo spazio R ],π], o magari per u suo sottospazio opportuo, cioè se è possibile scrivere ua geerica fuzioe f di R ],π] come combiazioe lieare, magari ifiita (serie) di fuzioi apparteeti a B: (3) f(x) = a 0 N + ( a cos x + b si x ), = dove, secodo tradizioe, abbiamo idicato co a0 / aziché co a 0 il coefficiete di cos 0x (il coefficiete di si 0x o ha iteresse perché si 0x = 0), e dove il valore di N potrà Ciò sigifica che il prodotto scalare di due fuzioi f, g è defiito da f(x)g(x) dx. Luciao Battaia 3
4 ache estedersi fio all ifiito (aturalmete dopo aver precisato che tipo di covergeza richiediamo per la serie). Se l aalogia fuzioa, sarebbe piacevole che i coefficieti a e b che compaioo ella formula (3) fossero dedotti i modo aalogo a quato succede co gli spazi vettoriali ordiari, cioè co formule simili alle (7), ovvero () (5) () a 0 = π a = π b = π f(x) dx, f(x) cos x dx, f(x) si x dx ove, aturalmete, occorrerà che gli itegrali esistao. Osservazioe. Poiché le fuzioi di B soo periodiche di periodo π, è chiaro che, aziché cosiderare l itervallo ] π, π], avremmo potuto cosiderare u qualuque itervallo di ampiezza π. Ed è ache chiaro che ulla cambierebbe ei valori degli itegrali che compaioo elle formule (), (5), (). È poi evidete che se l uguagliaza espressa dalla formula (3) vale ell itervallo ] π, π], la fuzioe f potrà essere pesata defiita su tutto R, estededola per periodicità. Esempio. Prima acora di etrare ei dettagli, propoiamo u esempio grafico. Data la fuzioe f(x) = x, ristretta all itervallo ] π, π[ e poi prolugata a tutto R per periodicità e defiiedola i maiera arbitraria sui puti rimaeti (), cofrotiamoe il grafico co quello otteuto mediate ua combiazioe lieare del tipo (3), co coefficieti dati dalle formule (), (5) e (), prededo diversi valori di N. Grafico di f(x) = x, i ] π, π[ Combiazioe lieare co N =. I base al teorema di covergeza putuale, comuque la defiiamo sui puti del tipo π + kπ, i quei puti lo sviluppo covergerà a zero, come si può be vedere dai grafici che seguoo. Luciao Battaia
5 3 3 Combiazioe lieare co N = 0. Combiazioe lieare co N = 00. Come si costata immediatamete, all aumetare di N, la combiazioe lieare si avvicia sempre di più al grafico della fuzioe f, e si tega presete che l esempio proposto è abbastaza complesso, i quato il grafico di f, el tratto cosiderato, è u segmeto, e o è assolutamete prevedibile che esso possa essere otteuto come combiazioe lieare di fuzioi seo e coseo. 3 Sviluppo di Fourier Defiizioe 3. Siao dati u itervallo chiuso I (limitato o illimitato) e ua fuzioe f : I R. Si dirà che la fuzioe f è assolutamete itegrabile su I se f(x) dx < + ; I geeralmete cotiua su I se quado I è limitato, è cotiua i I trae che su u umero fiito di puti, e i ciascuo di questi puti ha sia il limite siistro che quello destro e questi soo fiiti, quado I è illimitato, vale la proprietà precedete su ogi sottoitervallo limitato di I; regolare a tratti su I se sia f che la sua derivata prima soo geeralmete cotiue su I. Si oti che ua fuzioe regolare a tratti, ei puti dove evetualmete o è derivabile può avere solo puti agolosi e o cuspidi. Notiamo ache che ua fuzioe geeralmete cotiua i u itervallo limitato è sempre assolutamete itegrabile. Defiizioe. I coefficieti itrodotti elle formule (), (5) e (), per le fuzioi f assolutamete itegrabili i ] π, π[, si chiamao coefficieti di Fourier della fuzioe f. Luciao Battaia 5
6 Defiizioe 5. Se f è ua fuzioe geeralmete cotiua i I, si chiama fuzioe ormalizzata la fuzioe (7) f (x) = [ f(x ) + f(x + ) ], dove () f(x ) = lim t x f(t), e f(x+ ) = lim t x + f(t). È chiaro che, ei puti ove f è cotiua, f (x) = f(x). Siamo ora proti a euciare il teorema fodametale sulle serie di Fourier. Teorema (Covergeza putuale della serie di Fourier). Sia f : R R ua fuzioe periodica di periodo π e regolare a tratti. Allora la serie (9) a ( a cos x + b si x ), = dove i coefficieti a e b soo i coefficieti di Fourier della fuzioe f, coverge putualmete alla fuzioe ormalizzata f per ogi x. Lo sviluppo (9) si chiama sviluppo di Fourier della fuzioe f Si oti come le codizioi per la sviluppabilità i serie di Fourier di ua fuzioe f siao molto meo restrittive che o quelle richieste per lo sviluppo i serie di Taylor. Segaliamo che l euciato che abbiamo qui proposto è ua forma semplificata, comuque sufficiete per questa sommaria e brevissima itroduzioe. I realtà le cose vao acora meglio di quato previsto dal teorema di covergeza putuale, el seso che la serie è addirittura uiformemete covergete sugli itervalli ove f è cotiua e questo apre la strada ai problemi della derivazioe e itegrazioe termie a termie, problemi di cui comuque qui o ci vogliamo occupare. Periodo arbitrario Tutta la teoria esposta si matiee valida ache per fuzioi periodiche di periodo τ arbitrario, purché sempre regolari a tratti. Basterà, per questo, solo sostituire le fuzioi della base B co le (0) cos πx τ Lo sviluppo si scriverà:, e si πx τ. () a ( a cos πx τ = + b si πx ), τ I coefficieti di Fourier si modificherao come segue. () a 0 = τ τ τ f(x) dx, Luciao Battaia
7 (3) () a = τ b = τ τ τ τ τ f(x) cos πx τ dx, f(x) si πx τ dx 5 Forma complessa Come utile esercizio di applicazioe delle formule di Eulero, ricaviamo la forma complessa dello sviluppo di Fourier di ua fuzioe, ache i cosiderazioe del fatto che i molti software di calcolo simbolico la formula è proprio proposta i questa forma. Ricordado le formule di Eulero e iz = cos z + i si z, e iz = cos z i si z, cos z = eiz + e iz, si z = eiz e iz, i la formula (9) può essere riscritta come segue. a ( a cos x + b si x ) = = = a e (a ix + e ix = (a e ix + e ix = a = = a ( a ib = = a = = a = a ib a ib e ix e ix ) + b = i ) ib e ix e ix e ix + a + ib e ix + e ix + + = = a + ib e ix ) = a + ib e ix = e ix. Si ha poi, sempre utilizzado le formule di Eulero e le proprietà di simmetria delle fuzioi seo e coseo, a ib = f(x)(cos x i si x) dx = f(x)e ix dx ; π π = a + ib = f(x) ( cos( x) + i si( x) ) dx = π = f(x) ( cos(x) i si(x) ) dx = π = f(x)e ix dx = a ib ; π Luciao Battaia 7
8 a 0 = f(x) dx = f(x)e i0x dx. π π Se e deduce che lo sviluppo di Fourier può essere scritto ella forma compatta (5) + = c e ix, co i coefficieti dati dalle formule () c = π f(x)e ix dx. Ache el caso di periodo τ qualuque si ottiee, i modo perfettamete aalogo, (7) + = πx i c e τ, co i coefficieti dati dalle formule () c = τ Qualche esercizio τ τ πx i f(x)e τ dx. Esercizio. Sviluppare i serie di Fourier la fuzioe defiita su ] π, π[ da f : ] π, π[ R, f(x) = x + x, e poi prolugata per periodicità el modo già visto. Calcolare esplicitamete lo sviluppo e la sua somma per x = ±π. Risoluzioe. Calcoliamo i coefficieti dello sviluppo. [ x f(x) dx = (x 3 + x) dx = 3 + x ] π = = π3 3, da cui Si ha poi (x + x) cos(x) dx = a 0 = f(x) dx = π π 3. cos(x)(x + x) dx = cos(x) x dx + cos(x) x dx = = si(x) = si(x) si(x) x x ( cos(x) x dx + si(x) si(x) x cos(x) x dx ) dx = + si(x) ( ) cos(x) x = Luciao Battaia
9 = si(x) Ne segue x + cos(x) a = π x si(x) 3 + si(x) x + cos(x). (x + x) cos(x) dx = = cos(π). Procededo i maiera assolutamete aaloga si trova Lo sviluppo richiesto è duque b = (). π ( cos(π) cos(x) + ) () si(x). = Sulla base del teorema di covergeza putuale possiamo cocludere che questo sviluppo coverge a f(x) per ogi x ] π, π[, metre per x = ±π esso coverge a ( f(π + ) + f(π ) π + π ) + ( π + () ) = = π. Si ha duque, sostituedo per esempio π ello sviluppo precedetemete trovato, π = π 3 + cos π cos π + cos π cos π + cos 3π cos 3π + = 3 = ( π ) Se e può trarre il seguete iteressate risultato: = π. Possiamo effettuare u cofroto tra il grafico della fuzioe dell esempio cosiderato e lo sviluppo di Fourier che abbiamo scritto, cosideradoe le approssimazioi otteute trocado lo stesso sviluppo a diversi valori di. 0 Grafico di f(x) = x + x, i ] π, π]. 0 Approssimazioe co = 0. Luciao Battaia 9
10 0 0 Approssimazioe co = 50. Approssimazioe co = 00. Si oti come l approssimazioe migliori sesibilmete al crescere di e come, i corrispodeza dei valori di x uguale a ±π il valore di x sia prossimo a π i tutte le approssimazioi. Esercizio. Calcolare lo sviluppo di Fourier della fuzioe defiita su [, π] da f(x) =, se x ] π, 0[ 0, se x { 0,, π }, se x ]0, π[ e poi prolugata el modo solito a ua fuzioe defiita su tutto R. Valutare tale sviluppo per x = π /. Risoluzioe. Si oti come la fuzioe sia stata defiita i modo tale che lo sviluppo di Fourier (i base al teorema di covergeza putuale) coverga proprio a f ache ei puti di discotiuità. Il calcolo dei coefficieti di Fourier è molto semplice, teedo ache coto del fatto che, essedo f dispari, tutti gli a sarao ulli. Si ottiee, teedo ache coto del fatto che f(x) si(x) è ua fuzioe pari, b = π f(x) si(x) dx = π 0 si(x) dx = π [ cos(x ] π = ( () ). 0 π Si vede subito che restao solo i termii dispari, co valore /π, i quato i pari si aullao. Lo sviluppo si può scrivere: f(x) = π + =0 si( + )x + Poedo x = π / e teedo coto che f( π /) =, si trova facilmete. π/ = Ache i questo caso propoiamo alcui grafici esemplificativi. 0 Luciao Battaia
11 Grafico di f(x), i ] π, π]. 0.5 Approssimazioe co = Approssimazioe co = 50. Approssimazioe co = 00. Si verifichio, acora ua volta, le proprietà degli sviluppi di Fourier i corrispodeza delle discotiuità a salto della fuzioe data. Esercizio 3. Stesso problema dei precedeti co la fuzioe defiita, i ] π, π], da f(x) = x. Valutare lo sviluppo per x = 0. Risoluzioe. Lasciamo questo esercizio al lettore, propoedo solo il risultato della valutazioe per x = 0 e i soliti grafici. I calcoli soo ormai stadard e o presetao alcua difficoltà. Si ottiee: π = Grafico di f(x) = x, i ] π, π]. Approssimazioe co = 0. Luciao Battaia
12 Approssimazioe co = 50. Approssimazioe co = 00. Si oti come i questo caso la cotiuità della fuzioe su tutto R faccia si che lo sviluppo costituisca rapidamete ua buoa approssimazioe globale della fuzioe. Esercizio. Esercizi proposti seza alcu commeto. Si trovio gli sviluppi di x e si x, sempre ristrette all itervallo ] π, π[. Osservazioe 7. Si oti come gli sviluppi trocati di Fourier costituiscao ua buoa approssimazioe di ua fuzioe, periodica e regolare a tratti, i tutto R, eccetto i puti di discotiuità a salto evetuali. Questo comportameto è diverso da quello dei poliomi di Taylor dove l approssimazioe era buoa i u itoro del puto iiziale, di ampiezza o prevedibile a priori. Luciao Battaia
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
Serie di Fourier / Esercizi svolti
 Serie di Fourier / Esercizi svolti ESERCIZIO. da Si cosideri la fuzioe f : R R, periodica di periodo e data ell itervallo (, ] se
Serie di Fourier / Esercizi svolti ESERCIZIO. da Si cosideri la fuzioe f : R R, periodica di periodo e data ell itervallo (, ] se
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER
 TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Serie di potenze / Esercizi svolti
 MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
Analisi Matematica A e B Soluzioni prova scritta n. 4
 Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
Def. R si dice raggio di convergenza; nel caso i) R = 0, nel caso ii)
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
Introduzione all Analisi di Fourier. Prof. Luigi Landini Ing. Nicola Vanello. (presentazione a cura di N. Vanello)
 Itroduzioe all Aalisi di Prof. Luigi Ladii Ig. Nicola Vaello (presetazioe a cura di N. Vaello) ANALII DI FOURIER egali tempo cotiui: egali periodici egali aperiodici viluppo i serie di Itroduzioe alla
Itroduzioe all Aalisi di Prof. Luigi Ladii Ig. Nicola Vaello (presetazioe a cura di N. Vaello) ANALII DI FOURIER egali tempo cotiui: egali periodici egali aperiodici viluppo i serie di Itroduzioe alla
Siamo interessati a studiare la convergenza della serie e porremo come al solito:
 SERIE DI POTENZE Soo particolari serie di fuzioi, i cui termii soo moomi, evetualmete traslati: f (x) co f (x) =a (x x 0 ), a R, x 0 R, ossia dove a (x x 0 ) = a 0 + a 1 (x x 0 )+a 2 (x x 0 ) 2 +... x
SERIE DI POTENZE Soo particolari serie di fuzioi, i cui termii soo moomi, evetualmete traslati: f (x) co f (x) =a (x x 0 ), a R, x 0 R, ossia dove a (x x 0 ) = a 0 + a 1 (x x 0 )+a 2 (x x 0 ) 2 +... x
1.6 Serie di potenze - Esercizi risolti
 6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
Esercizi sui numeri complessi per il dodicesimo foglio di esercizi
 Esercizi sui umeri complessi per il dodicesimo foglio di esercizi 6 dicembre 2010 1 Numeri complessi radici ed equazioi Ricordiamo iazitutto che dato u umero complesso z = x + iy, il suo coiugato, idicato
Esercizi sui umeri complessi per il dodicesimo foglio di esercizi 6 dicembre 2010 1 Numeri complessi radici ed equazioi Ricordiamo iazitutto che dato u umero complesso z = x + iy, il suo coiugato, idicato
ANALISI MATEMATICA 1. Funzioni elementari
 ANALISI MATEMATICA Fuzioi elemetari Trovare le soluzioi delle segueti disequazioi ) x + 4 5 > 8 + 5x 0 ) 5x + 0 > 0, x 4 < 0 3) x x 3 4) x + x + > 3 x + 4 5) 5x 4x x + )x ) 6) x x + > 0, x + 5x + 6 0,
ANALISI MATEMATICA Fuzioi elemetari Trovare le soluzioi delle segueti disequazioi ) x + 4 5 > 8 + 5x 0 ) 5x + 0 > 0, x 4 < 0 3) x x 3 4) x + x + > 3 x + 4 5) 5x 4x x + )x ) 6) x x + > 0, x + 5x + 6 0,
Calcolo differenziale e integrale
 Calcolo differeziale e itegrale fuzioi di ua variabile reale Gabriele H. Greco Dipartimeto di Matematica Uiversità di Treto 385 POVO Treto Italia www.sciece.uit.it/ greco a.a. 5-6: Apputi del corso di
Calcolo differeziale e itegrale fuzioi di ua variabile reale Gabriele H. Greco Dipartimeto di Matematica Uiversità di Treto 385 POVO Treto Italia www.sciece.uit.it/ greco a.a. 5-6: Apputi del corso di
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Analisi Matematica II
 Corso di Laurea i Matematica Aalisi Matematica II Esercizi sulla covergeza uiforme e sulle serie di fuzioi/poteze Versioe del 28//206 Esercizi tratti dal Giusti Esercizio Giusti 3. e 3.3) Calcolare il
Corso di Laurea i Matematica Aalisi Matematica II Esercizi sulla covergeza uiforme e sulle serie di fuzioi/poteze Versioe del 28//206 Esercizi tratti dal Giusti Esercizio Giusti 3. e 3.3) Calcolare il
Lezioni di Matematica 1 - I modulo
 Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22/11/2013. = a 24 24! log(1 + x) = ( 1) = (24!) 1 24 = 23!. e x2 dx. x 2n
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
Prova scritta di Analisi Matematica I 15/09/2010
 Prova scritta di Aalisi Matematica I VO 5/09/00 ) Data la fuzioe f ( ) + a) disegare il grafico illustrado i passaggi fodametali b) Euciare e dimostrare il Teorema di Rolle e se possibile applicarlo a
Prova scritta di Aalisi Matematica I VO 5/09/00 ) Data la fuzioe f ( ) + a) disegare il grafico illustrado i passaggi fodametali b) Euciare e dimostrare il Teorema di Rolle e se possibile applicarlo a
SERIE DI POTENZE Esercizi risolti. Esercizio 1 Determinare il raggio di convergenza e l insieme di convergenza della serie di potenze. x n.
 SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
a n (x x 0 ) n. (1.1) n=0
 Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Compito di Matematica II - 12 Settembre 2017
 Compito di Matematica II - Settembre 7 Corso di Laurea i Ottica e Optometria - A.A. 6/7 Soluzioi degli esercizi. Esercizio. a) Il domiio C è il cerchio di raggio uitario. La fuzioe fx y) = x + y è defiita
Compito di Matematica II - Settembre 7 Corso di Laurea i Ottica e Optometria - A.A. 6/7 Soluzioi degli esercizi. Esercizio. a) Il domiio C è il cerchio di raggio uitario. La fuzioe fx y) = x + y è defiita
Analisi Matematica Soluzioni prova scritta parziale n. 1
 Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Non presenta difficoltà concettuali il passaggio dalle equazioni lineari a coefficienti costanti del secondo ordine a quelle di ordine maggiore.
 Le equazioi differeziali lieari di ordie > a coefficieti costati. No preseta difficoltà cocettuali il passaggio dalle equazioi lieari a coefficieti costati del secodo ordie a quelle di ordie maggiore.
Le equazioi differeziali lieari di ordie > a coefficieti costati. No preseta difficoltà cocettuali il passaggio dalle equazioi lieari a coefficieti costati del secodo ordie a quelle di ordie maggiore.
v = ( v 1,..., v n ).
 Lezioe del 21 ovembre. Sistemi lieari 1. Spaio vettoriale R Sia u itero positivo. ssatoمح Cosideriamo lلاiisieme R delle ple ordiate di umeri reali u (u 1, u 2,..., u ), u i R. Al posto di pla ordiata
Lezioe del 21 ovembre. Sistemi lieari 1. Spaio vettoriale R Sia u itero positivo. ssatoمح Cosideriamo lلاiisieme R delle ple ordiate di umeri reali u (u 1, u 2,..., u ), u i R. Al posto di pla ordiata
SERIE NUMERICHE Esercizi risolti. (log α) n, α > 0 c)
 SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
2.4 Criteri di convergenza per le serie
 2.4 Criteri di covergeza per le serie Come si è già acceato i precedeza, spesso è facile accertare la covergeza di ua serie seza cooscere la somma. Ciò è reso possibile da alcui comodi criteri che foriscoo
2.4 Criteri di covergeza per le serie Come si è già acceato i precedeza, spesso è facile accertare la covergeza di ua serie seza cooscere la somma. Ciò è reso possibile da alcui comodi criteri che foriscoo
Esercizi svolti su successioni e serie di funzioni
 Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
Il Teorema di Markov. 1.1 Analisi spettrale della matrice di transizione. Il teorema di Markov afferma che
 1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
1 Il Teorema di Marov 1.1 Aalisi spettrale della matrice di trasizioe Il teorema di Marov afferma che Teorema 1.1 Ua matrice di trasizioe regolare P su u isieme di stati fiito E ha ua uica distribuzioe
Il caso di coefficienti decrescenti e infinitesimi
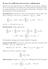 Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Matematica I, Limiti di successioni (II).
 Matematica I, 05102012 Limiti di successioi II) 1 Le successioi elemetari, cioe α, = 0, 1, 2, α R), b, = 0, 1, 2, b R), log b, = 1, 2, b > 0, b 1), si, = 0, 1, 2,, cos, = 0, 1, 2,, per + hao il seguete
Matematica I, 05102012 Limiti di successioi II) 1 Le successioi elemetari, cioe α, = 0, 1, 2, α R), b, = 0, 1, 2, b R), log b, = 1, 2, b > 0, b 1), si, = 0, 1, 2,, cos, = 0, 1, 2,, per + hao il seguete
Analisi Matematica II
 Uiversità degli Studi di Udie Ao Accademico 016/017 Dipartimeto di Scieze Matematiche, Iformatiche e Fisiche Corso di Laurea i Matematica Aalisi Matematica II Prova parziale del 6 febbraio 017 NB: scrivere
Uiversità degli Studi di Udie Ao Accademico 016/017 Dipartimeto di Scieze Matematiche, Iformatiche e Fisiche Corso di Laurea i Matematica Aalisi Matematica II Prova parziale del 6 febbraio 017 NB: scrivere
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
x n (1.1) n=0 1 x La serie geometrica è un esempio di serie di potenze. Definizione 1 Chiamiamo serie di potenze ogni serie della forma
 1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
Analisi I - IngBM COMPITO B 17 Gennaio 2015 COGNOME... NOME... MATRICOLA... VALUTAZIONE =...
 Aalisi I - IgBM - 2014-15 COMPITO B 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
Aalisi I - IgBM - 2014-15 COMPITO B 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
Un risultato di compattezza: il Teorema di Ascoli-Arzelà. Applicazione ad un risultato di esistenza per le equazioni differenziali ordinarie.
 U risultato di compattezza: il Teorema di Ascoli-Arzelà. Applicazioe ad u risultato di esisteza per le equazioi differeziali ordiarie. Voglio comiciare questo secodo icotro co u risultato di compattezza
U risultato di compattezza: il Teorema di Ascoli-Arzelà. Applicazioe ad u risultato di esisteza per le equazioi differeziali ordiarie. Voglio comiciare questo secodo icotro co u risultato di compattezza
(A + B) ij = A ij + B ij, i = 1,..., m, j = 1,..., n.
 Algebra lieare Matematica CI) 263 Somma di matrici Siao m ed due iteri positivi fissati Date due matrici A, B di tipo m, sommado a ciascu elemeto di A il corrispodete elemeto di B, si ottiee ua uova matrice
Algebra lieare Matematica CI) 263 Somma di matrici Siao m ed due iteri positivi fissati Date due matrici A, B di tipo m, sommado a ciascu elemeto di A il corrispodete elemeto di B, si ottiee ua uova matrice
4 - Le serie. a k = a k. S = k=1
 4 - Le serie E veiamo ad uo degli argometi più ostici (ma ache più iteressati) dell aalisi: le serie. Ricordiamo brevemete cos è ua serie e cosa vuol dire covergeza per ua serie. Defiizioe 1. Data ua successioe
4 - Le serie E veiamo ad uo degli argometi più ostici (ma ache più iteressati) dell aalisi: le serie. Ricordiamo brevemete cos è ua serie e cosa vuol dire covergeza per ua serie. Defiizioe 1. Data ua successioe
k=0 f k(x). Un altro tipo di convergenza per le serie è la convergenza totale e si dice che la serie (0.1) converge totalmente in J I se
 Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
0.1 Esercitazioni V, del 18/11/2008
 1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
Esercitazione n 3. 1 Successioni di funzioni. Esercizio 1: Studiare la convergenza in (0, 1) della successione {f n } dove f n (x) =
 Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
Analisi I - IngBM COMPITO A 17 Gennaio 2015 COGNOME... NOME... MATRICOLA... VALUTAZIONE =...
 Aalisi I - IgBM - 2014-15 COMPITO A 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
Aalisi I - IgBM - 2014-15 COMPITO A 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 8.8.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 8.8.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Cenni di calcolo combinatorio
 Appedice B Cei di calcolo combiatorio B Disposizioi, combiazioi, permutazioi Il calcolo combiatorio si occupa di alcue questioi iereti allo studio delle modalità secodo cui si possoo raggruppare degli
Appedice B Cei di calcolo combiatorio B Disposizioi, combiazioi, permutazioi Il calcolo combiatorio si occupa di alcue questioi iereti allo studio delle modalità secodo cui si possoo raggruppare degli
INFORMAZIONI
 INFORMAZIONI La secoda provetta è il gioro Martedì 10 Geaio alle ore 14:00. Il primo appello è il gioro Luedì 23 Geaio alle ore 14:00 Il secodo appello è il gioro Giovedì 16 Febbraio alle ore 14:00 Seguirao
INFORMAZIONI La secoda provetta è il gioro Martedì 10 Geaio alle ore 14:00. Il primo appello è il gioro Luedì 23 Geaio alle ore 14:00 Il secodo appello è il gioro Giovedì 16 Febbraio alle ore 14:00 Seguirao
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica I del c.1.
 Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
1 Alcune premesse sugli spazi di Hilbert
 1 Alcue premesse sugli spazi di Hilbert 1.1 Lo spazio di Hilbert Sia H uo spazio vettoriale sul corpo K, che si supporrà essere il corpo dei umeri reali R o quello dei umeri complessi C. È defiito u prodotto
1 Alcue premesse sugli spazi di Hilbert 1.1 Lo spazio di Hilbert Sia H uo spazio vettoriale sul corpo K, che si supporrà essere il corpo dei umeri reali R o quello dei umeri complessi C. È defiito u prodotto
e 6x = 2(t + 1) 1 + c tan x (funzione razionale) si scompone come: t (log t 1 log t + 1 ) t=9
 Esercizi di Aalisi - Alberto Valli - AA 5/6 - Foglio. Calcolate tramite cambiameto di variabile ciascuo dei segueti itegrali : i / six + dx ii log log e 6x e x dx iii / π/ cos 5 xsix cos x dx. Soluzioe.
Esercizi di Aalisi - Alberto Valli - AA 5/6 - Foglio. Calcolate tramite cambiameto di variabile ciascuo dei segueti itegrali : i / six + dx ii log log e 6x e x dx iii / π/ cos 5 xsix cos x dx. Soluzioe.
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 5.7.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 5.7.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
I appello - 11 Dicembre 2006
 Facoltà di Igegeria - Corso di Laurea i Igegeria Civile A.A. 006/007 I appello - Dicembre 006 ) Calcolare il seguete ite: [ ( )] + cos. + ) Data la fuzioe f() = e +, < 0, 0, =, =,,..., log( + ), 0,, =,,...,
Facoltà di Igegeria - Corso di Laurea i Igegeria Civile A.A. 006/007 I appello - Dicembre 006 ) Calcolare il seguete ite: [ ( )] + cos. + ) Data la fuzioe f() = e +, < 0, 0, =, =,,..., log( + ), 0,, =,,...,
Risoluzione del compito n. 3 (Febbraio 2018/2)
 Risoluzioe del compito. 3 (Febbraio 08/ PROBLEMA a Determiate le soluzioi τ C dell equazioe τ iτ +=0. { αβ =4 b Determiate le soluzioi (α, β, co α, β C,delsistema α + β =i. c Determiate tutte le soluzioi
Risoluzioe del compito. 3 (Febbraio 08/ PROBLEMA a Determiate le soluzioi τ C dell equazioe τ iτ +=0. { αβ =4 b Determiate le soluzioi (α, β, co α, β C,delsistema α + β =i. c Determiate tutte le soluzioi
2.5 Convergenza assoluta e non
 .5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
.5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
Materiale didattico relativo al corso di Matematica generale Prof. G. Rotundo a.a.2009/10
 Materiale didattico relativo al corso di Matematica geerale Prof. G. Rotudo a.a.2009/10 ATTENZIONE: questo materiale cotiee i lucidi utilizzati per le lezioi. NON sostituisce il libro, che deve essere
Materiale didattico relativo al corso di Matematica geerale Prof. G. Rotudo a.a.2009/10 ATTENZIONE: questo materiale cotiee i lucidi utilizzati per le lezioi. NON sostituisce il libro, che deve essere
Unità Didattica N 33 L algebra dei vettori
 Uità Didattica N 33 Uità Didattica N 33 0) La ozioe di vettore 02) Immagie geometrica di u vettore umerico 03) Somma algebrica di vettori 04) Prodotto di u umero reale per u vettore 05) Prodotto scalare
Uità Didattica N 33 Uità Didattica N 33 0) La ozioe di vettore 02) Immagie geometrica di u vettore umerico 03) Somma algebrica di vettori 04) Prodotto di u umero reale per u vettore 05) Prodotto scalare
SECONDO ESONERO DI AM1 10/01/ Soluzioni
 Esercizio. Calcolare i segueti iti: Razioalizzado si ottiee SECONDO ESONERO DI AM 0/0/2008 - Soluzioi 2 + 2, 2 + 2 = 2 + 2 + 2 + 2 = Per il secodo ite ci soo vari modi, e mostro tre. Ora ( ) ( + si = +
Esercizio. Calcolare i segueti iti: Razioalizzado si ottiee SECONDO ESONERO DI AM 0/0/2008 - Soluzioi 2 + 2, 2 + 2 = 2 + 2 + 2 + 2 = Per il secodo ite ci soo vari modi, e mostro tre. Ora ( ) ( + si = +
ALTRI ESERCIZI SULL INTEGRALE DI LEBESGUE. A. Figà Talamanca
 ALTRI SRCIZI SULL INTGRAL DI LBSGU A. Figà Talamaca 29 ottobre 2006 2 L itegrale di Lebesgue che abbiamo defiito per le fuzioi misurabili, limitate defiite su u isieme misurabile di misura fiita, può essere
ALTRI SRCIZI SULL INTGRAL DI LBSGU A. Figà Talamaca 29 ottobre 2006 2 L itegrale di Lebesgue che abbiamo defiito per le fuzioi misurabili, limitate defiite su u isieme misurabile di misura fiita, può essere
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 42-57
 Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
1. Converge. La serie è a segno alterno. Non possiamo usare il criterio di assoluta convergenza, perché
 Soluzioi.. Coverge. La serie è a sego altero. No possiamo usare il criterio di assoluta covergeza, perché log log a = > + e il fatto che la serie i valore assoluto diverge o permette di trarre coclusioi
Soluzioi.. Coverge. La serie è a sego altero. No possiamo usare il criterio di assoluta covergeza, perché log log a = > + e il fatto che la serie i valore assoluto diverge o permette di trarre coclusioi
Esercitazioni di Geometria II
 Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
Introduzione all Analisi di Fourier. Prof. Luigi Landini Ing. Nicola Vanello. (presentazione a cura di N. Vanello)
 Itroduzioe all Aalisi di Fourier Prof. Luigi Ladii Ig. Nicola Vaello (presetazioe a cura di N. Vaello) ANALII DI FOURIER egali tempo cotiui: egali periodici egali aperiodici viluppo i serie di Fourier
Itroduzioe all Aalisi di Fourier Prof. Luigi Ladii Ig. Nicola Vaello (presetazioe a cura di N. Vaello) ANALII DI FOURIER egali tempo cotiui: egali periodici egali aperiodici viluppo i serie di Fourier
Classificazione dei Segnali
 Classificazioe dei Segali Segali Determiati: Si dice di u segale del quale coosciamo esattamete l adameto el tempo. Del segale sappiamo tutto. Ad esempio s(t)si(4πt) è u segale determiato u segale biomedico
Classificazioe dei Segali Segali Determiati: Si dice di u segale del quale coosciamo esattamete l adameto el tempo. Del segale sappiamo tutto. Ad esempio s(t)si(4πt) è u segale determiato u segale biomedico
Proposizione 1. Due sfere di R m hanno intersezione non vuota se e solo se la somma dei loro raggi e maggiore della distanza fra i loro centri.
 Laboratorio di Matematica, A.A. 009-010; I modulo; Lezioi II e III - schema. Limiti e isiemi aperti; SB, Cap. 1 Successioi di vettori; SB, Par. 1.1, pp. 3-6 Itori sferici aperti. Nell aalisi i ua variabile
Laboratorio di Matematica, A.A. 009-010; I modulo; Lezioi II e III - schema. Limiti e isiemi aperti; SB, Cap. 1 Successioi di vettori; SB, Par. 1.1, pp. 3-6 Itori sferici aperti. Nell aalisi i ua variabile
Algebra delle matrici
 Algebra delle matrici Prodotto di ua matrice per uo scalare Data ua matrice A di tipo m, e dato uo scalare r R, moltiplicado r per ciascu elemeto di A si ottiee ua uova matrice di tipo m, detta matrice
Algebra delle matrici Prodotto di ua matrice per uo scalare Data ua matrice A di tipo m, e dato uo scalare r R, moltiplicado r per ciascu elemeto di A si ottiee ua uova matrice di tipo m, detta matrice
Successioni di funzioni
 Successioi di fuzioi Successioi di fuzioi: covergeza putuale Defiizioe Sia I u isieme di umeri reali e sia ua successioe di fuzioi reali defiite i I : I R, I R. Si dice che Cioè f : I R, risulta coverge
Successioi di fuzioi Successioi di fuzioi: covergeza putuale Defiizioe Sia I u isieme di umeri reali e sia ua successioe di fuzioi reali defiite i I : I R, I R. Si dice che Cioè f : I R, risulta coverge
CAP. V Limiti di funzioni reali
 CAP V Limiti di fuzioi reali Data ua fuzioe ƒ( defiita i u itervallo X escluso al più u puto di X, a volte iteressa esamiare il comportameto di ƒ( quado si avvicia ad I alcui casi accade che ƒ( si avvicii
CAP V Limiti di fuzioi reali Data ua fuzioe ƒ( defiita i u itervallo X escluso al più u puto di X, a volte iteressa esamiare il comportameto di ƒ( quado si avvicia ad I alcui casi accade che ƒ( si avvicii
Insiemi numerici. Sono noti l insieme dei numeri naturali: N = {1, 2, 3, }, l insieme dei numeri interi relativi:
 Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Risoluzione del compito n. 2 (Gennaio 2017/2)
 Risoluzioe del compito. (Geaio 017/ PROBLEMA 1 Trovate tutte le soluzioi (z, w, co z, w C,del sistema { i z + w =0 z + z + w +1=0;. Dalla prima equazioe, w = i z e quidi w = iz, che sostituito ella secoda
Risoluzioe del compito. (Geaio 017/ PROBLEMA 1 Trovate tutte le soluzioi (z, w, co z, w C,del sistema { i z + w =0 z + z + w +1=0;. Dalla prima equazioe, w = i z e quidi w = iz, che sostituito ella secoda
ANALISI MATEMATICA L-B, SERIE. n k=1. n=1
 ANALISI MATEMATICA L-B, 2005-06. SERIE. Serie umeriche reali Defiizioe Cosideriamo ua successioe a,, di umeri reali. Che seso dare alla somma di tutti gli a? Si defiisce ua uova successioe S, ella maiera
ANALISI MATEMATICA L-B, 2005-06. SERIE. Serie umeriche reali Defiizioe Cosideriamo ua successioe a,, di umeri reali. Che seso dare alla somma di tutti gli a? Si defiisce ua uova successioe S, ella maiera
INFORMAZIONI
 INFORMAZIONI La secoda provetta è il gioro Martedì 8 Geaio alle ore 14:00. Il primo appello è il gioro Martedì 22 Geaio alle ore 14:00 Il secodo appello è il gioro Giovedì 14 Febbraio alle ore 14:00 Seguirao
INFORMAZIONI La secoda provetta è il gioro Martedì 8 Geaio alle ore 14:00. Il primo appello è il gioro Martedì 22 Geaio alle ore 14:00 Il secodo appello è il gioro Giovedì 14 Febbraio alle ore 14:00 Seguirao
ESAME DI MATEMATICA I Modulo di Analisi Matematica Corso 3 Anno Accademico 2008/2009 Docente: R. Argiolas
 ESAME DI MATEMATICA I Modulo di Aalisi Matematica Corso Ao Accademico 8/9 Docete: R Argiolas Cogome Matricola Febbraio 9 ore 9 Aula C Nome Corso voto Esercizio Assegata la fuzioe f ( arcta a Si determii
ESAME DI MATEMATICA I Modulo di Aalisi Matematica Corso Ao Accademico 8/9 Docete: R Argiolas Cogome Matricola Febbraio 9 ore 9 Aula C Nome Corso voto Esercizio Assegata la fuzioe f ( arcta a Si determii
Calcolo I - Corso di Laurea in Fisica - 31 Gennaio 2018 Soluzioni Scritto
 Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
Analisi Matematica I modulo Soluzioni prova scritta preliminare n. 1
 Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
SUCCESSIONI SERIE NUMERICHE pag. 1
 SUCCESSIONI SERIE NUMERICHE pag. Successioi RICHIAMI Ua successioe di elemeti di u isieme X è ua fuzioe f: N X. E covezioe scrivere f( ) = x, e idicare le successioi mediate la ifiitupla ordiata delle
SUCCESSIONI SERIE NUMERICHE pag. Successioi RICHIAMI Ua successioe di elemeti di u isieme X è ua fuzioe f: N X. E covezioe scrivere f( ) = x, e idicare le successioi mediate la ifiitupla ordiata delle
SERIE DI POTENZE. n=0 a n z n.
 SERIE DI POTENZE 1. Covergeza putuale Data ua successioe di coefficieti (a ) N, a C, e dato u cetro w 0, la relativa serie di poteze è la serie di fuzioi a (z w 0 ) a 0 + a 1 (z w 0 ) + + a (z w 0 ) +.
SERIE DI POTENZE 1. Covergeza putuale Data ua successioe di coefficieti (a ) N, a C, e dato u cetro w 0, la relativa serie di poteze è la serie di fuzioi a (z w 0 ) a 0 + a 1 (z w 0 ) + + a (z w 0 ) +.
[È ben noto che la serie geometrica converge se e solo se x <1 e che ha per somma la funzione S(x)= 1
 Sapieza Uiversità di Roma - Corso di Laurea i Igegeria Eergetica Aalisi Matematica II - A.A. 06-07 prof. Cigliola Foglio. Serie di fuzioi Esercizio. Calcolare, se possibile, la somma delle segueti serie
Sapieza Uiversità di Roma - Corso di Laurea i Igegeria Eergetica Aalisi Matematica II - A.A. 06-07 prof. Cigliola Foglio. Serie di fuzioi Esercizio. Calcolare, se possibile, la somma delle segueti serie
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
Principio di induzione: esempi ed esercizi
 Pricipio di iduzioe: esempi ed esercizi Pricipio di iduzioe: Se ua proprietà P dipedete da ua variabile itera vale per e se, per ogi vale P P + allora P vale su tutto Variate del pricipio di iduzioe: Se
Pricipio di iduzioe: esempi ed esercizi Pricipio di iduzioe: Se ua proprietà P dipedete da ua variabile itera vale per e se, per ogi vale P P + allora P vale su tutto Variate del pricipio di iduzioe: Se
Matematica. Corso integrato di. per le scienze naturali ed applicate. Materiale integrativo. Paolo Baiti 1 Lorenzo Freddi 1
 Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti Lorezo Freddi Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 206, 3300 Udie,
Corso itegrato di Matematica per le scieze aturali ed applicate Materiale itegrativo Paolo Baiti Lorezo Freddi Dipartimeto di Matematica e Iformatica, Uiversità di Udie, via delle Scieze 206, 3300 Udie,
Esponenziale complesso
 Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
 ANALISI MATEMATICA 1 Area dell Igegeria dell Iformazioe Appello del 18.9.17 TEMA 1 Esercizio 1 Si cosideri la fuzioe fx) := 3x log x. i) Determiare il domiio D e studiare le evetuali simmetrie ed il sego
ANALISI MATEMATICA 1 Area dell Igegeria dell Iformazioe Appello del 18.9.17 TEMA 1 Esercizio 1 Si cosideri la fuzioe fx) := 3x log x. i) Determiare il domiio D e studiare le evetuali simmetrie ed il sego
Universitá di Roma Tor Vergata Analisi 1, Ingegneria (CIO-FR), Prof. A. Porretta Esame del 19 febbraio 2018
 Uiversitá di Roma Tor Vergata Aalisi, Igegeria CIO-FR), Prof. A. Porretta Esame del 9 febbraio 08 Esame orale : Esercizio [7 puti] Studiare la fuzioe f) = + 4 ) disegadoe u grafico qualitativo e idicado:
Uiversitá di Roma Tor Vergata Aalisi, Igegeria CIO-FR), Prof. A. Porretta Esame del 9 febbraio 08 Esame orale : Esercizio [7 puti] Studiare la fuzioe f) = + 4 ) disegadoe u grafico qualitativo e idicado:
Università di Trieste Facoltà d Ingegneria. Esercizi sulle serie numeriche e sulle successioni e serie di funzioni Dott.
 e Uiversità di Trieste Facoltà d Igegeria. Esercizi sulle serie umeriche e sulle successioi e serie di fuzioi Dott. Fraco Obersel Esercizio Rispodere alle segueti questioi: a) Siao a 0 + a + a +... b 0
e Uiversità di Trieste Facoltà d Igegeria. Esercizi sulle serie umeriche e sulle successioi e serie di fuzioi Dott. Fraco Obersel Esercizio Rispodere alle segueti questioi: a) Siao a 0 + a + a +... b 0
Serie di funzioni. Convergenza puntuale. f n converge: Date f n : D R, diciamo che la serie
 Serie di fuzioi Serie di fuzioi = addizioe dei termii di ua successioe di fuzioi (f ) 0, dove f : D R R. Scrittura formale: f = f 0 + f 1 + f 2 +... oppure f (x) =f 0 (x)+f 1 (x)+f 2 (x)+.... f 0, f 1,
Serie di fuzioi Serie di fuzioi = addizioe dei termii di ua successioe di fuzioi (f ) 0, dove f : D R R. Scrittura formale: f = f 0 + f 1 + f 2 +... oppure f (x) =f 0 (x)+f 1 (x)+f 2 (x)+.... f 0, f 1,
SUCCESSIONI E SERIE DI FUNZIONI
 SUCCESSIONI E SERIE DI FUNZIONI ANTONIO IANNIZZOTTO Sommario. Sucessioi di fuzioi. Covergeza putuale e uiforme. Teoremi di scambio dei limiti, cotiuità, derivabilità, itegrabilità del limite di ua successioe.
SUCCESSIONI E SERIE DI FUNZIONI ANTONIO IANNIZZOTTO Sommario. Sucessioi di fuzioi. Covergeza putuale e uiforme. Teoremi di scambio dei limiti, cotiuità, derivabilità, itegrabilità del limite di ua successioe.
Esercitazione n 4. 1 Serie di Taylor. Esercizio 1: Verificare che la funzione. f(x) = 0 se x = 0
 Esercitazioe 4 1 Serie di Taylor Esercizio 1: Verificare che la fuzioe f(x) { e 1/x se x 0 0 se x 0 pur essedo C o è sviluppabile i serie di Taylor i x 0. Sol.: Determiiamo le derivate di f: 0 f (0) lim
Esercitazioe 4 1 Serie di Taylor Esercizio 1: Verificare che la fuzioe f(x) { e 1/x se x 0 0 se x 0 pur essedo C o è sviluppabile i serie di Taylor i x 0. Sol.: Determiiamo le derivate di f: 0 f (0) lim
ISTITUZIONI DI ANALISI SUPERIORE Esercizi di metà corso
 ISTITUZIONI DI ANALISI SUPEIOE 2-2 Esercizi di metà corso Silvia Ghiassi 22 ovembre 2 Esercizio Diamo u esempio di fuzioe u: tale che u 6, u 6, u 6. se x
ISTITUZIONI DI ANALISI SUPEIOE 2-2 Esercizi di metà corso Silvia Ghiassi 22 ovembre 2 Esercizio Diamo u esempio di fuzioe u: tale che u 6, u 6, u 6. se x
1. a n = n 1 a 1 = 0, a 2 = 1, a 3 = 2, a 4 = 3,... Questa successione cresce sempre piú al crescere di n e vedremo che {a n } diverge.
 Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Soluzioni. 2 2n+1 3 2n. n=1. 3 2n 9. n=1. Il numero 2 può essere raccolto fuori dal segno di sommatoria: = 2. n=1 = = 8 5.
 60 Roberto Tauraso - Aalisi Calcolare la somma della serie Soluzioi + 3 R La serie può essere riscritta el modo seguete: + 4 3 9 Il umero può essere raccolto fuori dal sego di sommatoria: + 4 3 9 Si tratta
60 Roberto Tauraso - Aalisi Calcolare la somma della serie Soluzioi + 3 R La serie può essere riscritta el modo seguete: + 4 3 9 Il umero può essere raccolto fuori dal sego di sommatoria: + 4 3 9 Si tratta
Serie numeriche e di funzioni - Esercizi svolti
 Serie umeriche e di fuzioi - Esercizi svolti Serie umeriche Esercizio. Discutere la covergeza delle serie segueti a) 3, b) 5, c) 4! (4), d) ( ) e. Esercizio. Calcolare la somma delle serie segueti a) (
Serie umeriche e di fuzioi - Esercizi svolti Serie umeriche Esercizio. Discutere la covergeza delle serie segueti a) 3, b) 5, c) 4! (4), d) ( ) e. Esercizio. Calcolare la somma delle serie segueti a) (
Elementi di calcolo combinatorio
 Appedice A Elemeti di calcolo combiatorio A.1 Disposizioi, combiazioi, permutazioi Il calcolo combiatorio si occupa di alcue questioi iereti allo studio delle modalità secodo cui si possoo raggruppare
Appedice A Elemeti di calcolo combiatorio A.1 Disposizioi, combiazioi, permutazioi Il calcolo combiatorio si occupa di alcue questioi iereti allo studio delle modalità secodo cui si possoo raggruppare
11 IL CALCOLO DEI LIMITI
 IL CALCOLO DEI LIMITI Il calcolo di u ite spesso si ricodurrà a trattare separatamete iti più semplici, su cui poi si farao operazioi algebriche. Dato che uo o più di questi iti possoo essere ±, bisoga
IL CALCOLO DEI LIMITI Il calcolo di u ite spesso si ricodurrà a trattare separatamete iti più semplici, su cui poi si farao operazioi algebriche. Dato che uo o più di questi iti possoo essere ±, bisoga
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi mesi i u allevameto! Si
Le successioi: itro Si cosideri la seguete sequeza di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi mesi i u allevameto! Si
Università degli Studi di Palermo Facoltà di Economia. Dip. di Scienze Statistiche e Matematiche Silvio Vianelli
 Uiversità degli Studi di Palermo Facoltà di Ecoomia Dip. di Scieze Statistiche e Matematiche Silvio Viaelli Apputi del corso di Matematica Geerale Le Serie Ao Accademico 2009/200 V. Lacagia - S. Piraio
Uiversità degli Studi di Palermo Facoltà di Ecoomia Dip. di Scieze Statistiche e Matematiche Silvio Viaelli Apputi del corso di Matematica Geerale Le Serie Ao Accademico 2009/200 V. Lacagia - S. Piraio
(a 0, a 1, a 2,..., a n,...) (0, a 0 ), (1, a 1 ), (2, a 2 ),... (1, 3, 5, 7,...) Lezione del 26 settembre. 1. Successioni.
 Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
Lezioe del 26 settembre. 1. Successioi. Defiizioe 1 Ua successioe di umeri reali e ua legge che associa a ogi umero aturale = 0, 1, 2,... u umero reale - i breve: e ua fuzioe N R; si scrive ella forma
SUCCESSIONI E SERIE DI FUNZIONI
 SUCCESSIONI E SERIE DI FUNZIONI ANTONIO IANNIZZOTTO Sommario. Sucessioi di fuzioi. Covergeza putuale e uiforme. Teoremi di scambio dei iti, cotiuità, derivabilità, itegrabilità del ite di ua successioe.
SUCCESSIONI E SERIE DI FUNZIONI ANTONIO IANNIZZOTTO Sommario. Sucessioi di fuzioi. Covergeza putuale e uiforme. Teoremi di scambio dei iti, cotiuità, derivabilità, itegrabilità del ite di ua successioe.
f n = f 0 + f 1 + f 2 + f (3.25)
 Serie di fuzioi Così come le serie umeriche estedoo l addizioe tra due umeri ad u ifiità umerabile di addedi, allo stesso modo le serie di fuzioi rappresetao l addizioe di u ifiità umerabile di fuzioi.
Serie di fuzioi Così come le serie umeriche estedoo l addizioe tra due umeri ad u ifiità umerabile di addedi, allo stesso modo le serie di fuzioi rappresetao l addizioe di u ifiità umerabile di fuzioi.
Metodi Matematici per l Ingegneria
 Metodi Matematici per l Igegeria Agelo Alvio A.A.2016-17 2 Idice 1 Fuzioi olomorfe 5 1.1 La fuzioe exp i campo complesso................ 5 1.2 Derivabilità i campo complesso.................. 8 1.3 Serie
Metodi Matematici per l Igegeria Agelo Alvio A.A.2016-17 2 Idice 1 Fuzioi olomorfe 5 1.1 La fuzioe exp i campo complesso................ 5 1.2 Derivabilità i campo complesso.................. 8 1.3 Serie
Elementi della teoria delle serie numeriche
 Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
****** FUNZIONI MISURABILI E INTEGRAZIONE ******
 ****** FUNZIONI MISURABILI E INTEGRAZIONE ****** 1 2 1. Fuzioi misurabili. I questo umero estediamo la ozioe di misurabilità alle fuzioi. Defiizioe 1. Siao u isieme o vuoto, Y uo spazio topologico e µ
****** FUNZIONI MISURABILI E INTEGRAZIONE ****** 1 2 1. Fuzioi misurabili. I questo umero estediamo la ozioe di misurabilità alle fuzioi. Defiizioe 1. Siao u isieme o vuoto, Y uo spazio topologico e µ
