Successioni e serie di funzioni
|
|
|
- Baldo Felice Pinto
- 5 anni fa
- Visualizzazioni
Transcript
1 Capitolo Successioi e serie di fuzioi Covergeza putuale ed uiforme Ultimo aggiorameto: 8 febbraio 27 Differeza tra covergeza putuale ed uiforme: Si suppoga di avere ua successioe di fuzioi f : D R tali che lim f (x) = f(x). Ci chiediamo se il limite è ache uiforme: dovrei avere che lim sup f (x) f(x) = x D il che è equivalete a dire che (per defiizioe di limite) per ogi ɛ > esiste N = N(ɛ) tale che per ogi N si ha f f L (D) := sup f (x) f(x) < ɛ. x D Se o ci sarà ambiguità sull isieme di defiizioe scriveremo semplicemete f f aziché f f L (D). Si veda la Figura. per avere u idea dal puto di vista grafico: la curva i eretto rappreseta il grafico della fuzioe limite f, i putii i grafici di f +ɛ e f ɛ, la curva tratteggiata il grafico di ua possibile f co N(ɛ). Cosiderazioi geerali: o esiste u metodo geerale (cioè u modo meccaico che valga i ogi situazioe) per studiare la covergeza uiforme. La prima osservazioe che va fatta è che, se f : D R covergoo putualmete ad f i D, il cadidato ad essere il limite uiforme è f. La
2 Figura.: secoda è che lo studio ha come icogita l isieme (o gli isiemi) sul quale (o sui quali) f coverge uiformemete. La domada da porsi è quidi: su quali isiemi A D vale lim sup f (x) f(x) =? Chiaramete se f f uiformemete su tutto D covergerà uiformemete ache su tutti i sottoisiemi A di D. U modo per cercare l estremo superiore di f f (dove f è il limite putuale di f ) se f e f soo di classe C è di comiciare risolvedo l equazioe d dx (f (x) f(x)) = e cosiderado i puti critici di f f: si faccia attezioe che il miimo, se c è, di f f potrebbe essere il massimo di f f. Questo però è u modo e comuque o sempre forisce l estremo superiore (ad esempio il sup potrebbe o essere u massimo, il massimo potrebbe essere assuto agli estremi ecc.). I geerale è spesso utile ituire il comportameto della successioe di cui bisoga studiare la covergeza. U cosiglio è quidi quello di studiare qualitativamete, se possibile, il grafico delle fuzioi f. x A Esercizio. - Studiare la covergeza putuale ed uiforme della successioe di fuzioi f : [, ] R, f (x) = x 2 + Esercizio.2 - Studiare covergeza putuale ed uiforme della successioe di fuzioi f (x) = arctg (x), N, defiite i D = R. 2
3 Esercizio.3 - Studiare la covergeza putuale ed uiforme della successioe di fuzioi f : R R, f (x) = x + x 2 + Esercizio.4 - Studiare covergeza putuale ed uiforme di f (x) = x( x) log i [, ]. Esercizio.5 - Studiare covergeza putuale ed uiforme di f : [, ] x R, f (x) = + 2 x 2. Esercizio.6 - Si studio la covergeza putuale ed uiforme delle fuzioi e si dimostri che x2 f (x) = x + lim per x [, + ) f (x) se (x)dx =. Esercizio.7 - Si studio la covergeza putuale ed uiforme delle fuzioi f (x) = α x( x 2 ) per x [, ] (α > ) e si calcoli lim f (x)dx. Esercizio.8 - Si studio la covergeza putuale ed uiforme delle fuzioi f (x) = ( + se 2 x) per x [, π] e si calcoli lim π f (x)dx. Esercizio.9 - Si studi la covergeza putuale ed uiforme i [, ] della successioe di fuzioi f (x) = log( + x/). Esercizio. - Si studi la covergeza putuale ed uiforme i R della successioe di fuzioi f (x) = x 3 t 2 + dt.
4 Serie di Fuzioi Ua serie di fuzioi f è ua speciale successioe di fuzioi {g N } N dove g N (x) = N f (x). Ricordo: per le serie di fuzioi si ha che cov. totale su A = cov. uiforme su A = cov. putuale su A. No ci soo molti criteri i geerale per studiare la covergeza uiforme: i geerale, e quidi i particolare se si ha ua serie a termii tutti positivi (o tutti egativi), ua strategia possibile è studiare prima la covergeza totale della serie, ma questo o garatisce di trovare tutti gli isiemi i cui vi è covergeza uiforme! (si vedao, ad esempio, gli esercizi.5 e.7), quado si ha ua serie a segi alteri si può sfruttare il criterio di Leibiz. Per quato riguarda lo studio della covergeza totale: chiaramete la miglior costate che cotrolla su u isieme A il valore assoluto di f (x) è sup A f (x). Quidi per studiare la covergeza totale su A di f coviee, se si riesce a calcolare l estremo superiore di f, studiare la serie sup f (x). x A No sempre però coviee calcolare l estremo superiore e ci si può accotetare di ua stima (si veda, ad esempio, la soluzioe dell Esercizio.6) o o sempre si riesce a calcolare tale estremo superiore (si veda, ad esempio, la soluzioe dell Esercizio.4) Esercizio. - Studiare la covergeza della serie x ( + x). Esercizio.2 - Studiare la serie di f(x)x co f cotiua. Esercizio.3 - Studiare la covergeza della serie x + 2 x
5 Esercizio.4 - Studiare la covergeza della serie x + x log. Esercizio.5 - Studiare la covergeza della serie ( ) log( + x 2 ). =2 Esercizio.6 - Studiare la covergeza della serie x + x 2. Esercizio.7 - Si cosideri la successioe di fuzioi { se x x [( )π, π] f (x) = altrimeti. Studiare la covergeza della serie f (x). Esercizio.8 - Studiare la covergeza della serie Esercizio.9 - Studiare la covergeza della serie Esercizio.2 - Studiare la covergeza della serie x R. x e x. x, x R. ( ) se x + 2, Esercizio.2 - Studiare la covergeza della serie (log ) x, x R. Esercizio.22 - Studiare la covergeza della seguete serie e calcolare la somma: ( x + ) ( 3). x 5
6 Esercizio.23 - Studiare la covergeza della serie e calcolare la somma. ( ) x+ x Esercizio.24 - Si determiio gli isiemi di R 2 ei quali vi è covergeze semplice, uiforme e totale della serie Serie di poteze arctg (x ) + 2. y Ricordo: le serie di poteze soo particolari serie di fuzioi della forma a (x x ). Il raggio di covergeza di a x è dato da ρ = lim a / se tale limite esiste (si vedao le dispese di teoria per la defiizioe di raggio di covergeza e l Esercizio.45 per u esempio i cui il limite o esiste). Esercizio.25 - Studiare la covergeza della serie e calcolare la somma. cofrotarle co la precedete. 3 x Studiare poi le serie 3 x e Esercizio.26 - Studiare la covergeza della serie di poteze 2 3 x e α + e α al variare del parametro α R. x 6
7 Esercizio.27 - Sviluppare i serie di Taylor i x = la fuzioe f(x) = e x e studiare la covergeza. Esercizio.28 - Calcolare lo sviluppo di Taylor el puto x = della fuzioe log x e calcolare il valore della serie ( )+. Esercizio.29 - Studiare la covergeza e calcolare la somma (ove coverge) della serie x + 2 ( + x 2 ). Esercizio.3 - Studiare il comportameto della serie! x. Esercizio.3 - Sviluppare i serie di Taylor i x = la fuzioe f(x) = arctg x e studiare la covergeza. Esercizio.32 - Calcolare gli sviluppi di seo e coseo i x =. Esercizio.33 - Studiare la covergeza e calcolare la somma di [! ] x. ( + )! Esercizio.34 - Calcolare lo sviluppo i serie di Taylor itoro al puto x = della fuzioe 4 x f(x) = x 2 5x + 6. Esercizio.35 - Calcolare lo sviluppo i serie di Taylor itoro al puto x = della fuzioe f(x) = + 3x2 ( x) 3. Esercizio.36 - Calcolare lo sviluppo i serie di Taylor itoro al puto x = della fuzioe ( x 2 ) f(x) = log 3x 2 precisadoe l isieme di covergeza. 7
8 Esercizio.37 - Calcolare l isieme di covergeza della serie al variare di α R. log( + α ) Esercizio.38 - Calcolare lo sviluppo i serie di Taylor itoro al puto x = della fuzioe ( 2 + x ) f(x) = log + x 2 precisadoe l isieme di covergeza. ( + x ) x 2+ Esercizio.39 - Mostrare che log = 2 x 2 +. Esercizio.4 - Trovare ua serie di poteze la cui somma, i u opportuo itervallo, sia log( + x 2x 2 ). Esercizio.4 - Studiare la serie di poteze x ( log + ) x. Esercizio.42 - Che differeza c è fra la due serie di poteze 2 x Esercizio.43 - Studiare le serie di poteze (!) 3 (3)! x e e 2 x2? (!) 3 (3)! x2. Esercizio.44 - Studiare la serie di poteze Esercizio.45 Studiare la serie di poteze x. (2 + se π/2) x. Serie di Fourier 8
9 Ricordo: se T è il semiperiodo la serie è data da a 2 + [ a cos π T x + a se π ] T x dove i coefficieti soo dati da ( N) a = T T T Uguagliaza di Parseval: T T f(x) cos π T xdx b = T T T f(x) se π T xdx. ( a f(x) 2 2 dx = T 2 + a 2 + b 2). (.) Itegrazioe della serie di Fourier - Si suppoga di avere f cotiua a tratti e F (x) = x T (f(t) a /2)dt. Se deotiamo co a e b i coefficieti di f, co A e B quelli di F valgoo le relazioi A = b, B = a. (.2) Per quato riguarda la covergeza della serie (vedi dispese di teoria): per ogi fuzioe limitata, cotiua a tratti e derivabile a tratti la serie coverge putualmete ovuque (alla media f defiita elle dispese di teoria), uiformemete i ogi itervallo chiuso i cui f è cotiua e totalmete se coverge la serie dei coefficieti ( a + b ) visto che sup a cos x = a e sup b se x = b. Esercizio.46 - Calcolare lo sviluppo di Fourier della fuzioe f : [ π, π] R, f(x) = i [ π, ], f(x) = i (, π]. Studiare le covergeze putuale ed uiforme. Calcolare poi lo sviluppo di Fourier della fuzioe g : [ π, π] R, g(x) = x. Esercizio.47 - Calcolare lo sviluppo di Fourier della fuzioe f(x) = x 2 co x [ π, π]. Studiare le covergeze putuale ed uiforme. Calcolare poi il valore della serie 2. 9
10 Esercizio.48 - Calcolare lo sviluppo di Fourier della fuzioe f(x) = { se x [, ] x se x [, ] e studiare la covergeza. Calcolare poi la somma delle serie (2 + ) 2 e (2) 2. Esercizio.49 - Calcolare lo sviluppo di Fourier della fuzioe { x se x [, π] f(x) = x + 2π se x [π, 2π] studiare la covergeza, scrivere uo sviluppo della stessa fuzioe i soli sei, ifie calcolare il valore delle serie k= e (2k+) 2 k=. Sfruttado lo sviluppo della fuzioe f scrivere ioltre lo sviluppo i serie di (2k+) 4 Fourier della fuzioe { se x [ π, ] g(x) = se x (, π] Esercizio.5 - Determiare lo sviluppo i serie di Fourier della fuzioe f(x) = 2 x, x [ π, π]. π Studiare poi la covergeza i [ π, π]. Ifie calcolare la somma delle serie (2 + ) 2, (2 + ) 4,
11 Soluzioi Soluzioe. - Limite putuale: j O Figura.2: lim f (x) = x per ogi x [, ]. + Limite uiforme: sup x 2 + x = x [,] sup x [,] i ( x 2 + ) x sup x [,] = Osservazioe - Nell ultimo passaggio si è usata la diseguagliaza a + b a + b (lasciata per esercizio). Osservazioe - Le fuzioi f soo tutte fuzioi C, ma il limite è solo cotiuo: la covergeza uiforme si trascia al limite la cotiuità, ma o la derivabilità. Soluzioe.2 - Il limite putuale è dato da (si veda la Figura.3) lim f (x) = f(x) = π/2 x > x = π/2 x <
12 j O Figura.3: Usiamo il Teorema.5 (cotiuità della fuzioe limite) delle dispese che qui ricordiamo brevemete. Teorema. Se ua successioe di fuzioi cotiue i D coverge uiformemete ad f i D allora f è cotiua i D. Questo può essere usato ache i egativo: cioè se {f } è ua successioe di fuzioi cotiue che coverge putualmete ad ua fuzioe f o cotiua, la covergeza o può essere uiforme. Cocludiamo che se D = R f o coverge uiformemete ad f. Ci si può chiedere se ci soo isiemi strettamete coteuti i R sui quali la covergeza è uiforme. Si cosideri A = [a, + ) co a >. La derivata di f f = f f è sempre egativa (per cui o ci soo puti stazioari). Questo però ci dice che il massimo è assuto per x = a. Per cui sup x [a,+ ) i f (x) f(x) = π/2 f (a) = π/2 arctg (a). Dalla covergeza putuale cocludiamo che questa quatità coverge a zero. Poiché aalogamete si può trattare il caso i cui A = (, b] co b < cocludiamo che f coverge uiformemete ad f su tutti gli isiemi del tipo (, b] [a, + ) co b < e a > e solo i quelli. Soluzioe.3 - Il limite putuale è f su tutto R. Prima di tutto si osservi che (si vedao alcui grafici i Figura.4) lim f (x) =, x + lim f (x) = x 2
13 e ache che Per ogua di queste ragioi f (x) = per x =. sup f (x) f(x) x R e quidi o vi può essere covergeza uiforme su tutto R e emmeo su semirette. Vediamo che succede se cosideriamo u compatto [a, b]. Calcoliamo la derivata e poiamola uguale a zero. Si ha f (x) = x = che ha come soluzioi x = e y = 2 +. Si osservi che x /2 metre y, quidi, qualuque sia [a, b], y defiitivamete o appartiee ad [a, b]. Se /2 (a, b) allora x defiitivamete appartiee ad [a, b]. I [a, b] quidi o o ci soo puti stazioari o c è solamete x, el quale f assume il suo valore massimo che vale f (x ) = 2 + 2( ) = Attezioe: il massimo di f f o è detto sia assuto i x. Ifatti si ha x( x) f (x) f(x) = x 2 + che è positiva per x (, ) (e egativa altrimeti). Quidi x( x) x 2 x [a, ] + f (x) f(x) = x( x) x 2 x [, ] + x( x) x 2 x [, b] + Per cui l estremo superiore (che i realtà è u massimo) è sicuramete assuto i x = a o x = b oppure x = x. Per cui sup f (x) f(x) max{f (a), f (b), f (x ) }. x [a,b] Poiché tutti e tre i valori dell isieme a destra covergoo a zero si coclude che {f } coverge uiformemete sui compatti. 3
14 j O Figura.4: Soluzioe.4 - Covergeza putuale: f (x) per ogi x [, ]. Per l uiforme calcoliamo la derivata di f : f (x) = ( x) log [( x) x] e questa si aulla per x = /( + ) (la fuzioe è o egativa e ulla agli estremi, x è quidi di massimo). Il valore f (x ) = log ( ). + + i Soluzioe.5 - Il limite putuale è (i Figura.5 soo riportati i grafici di alcue f ) lim f (x) = per ogi x [, ]. + 4
15 Vediamo se il limite è ache uiforme: f (x) = ( + 2 x 2 ) 2 3 x 2 ( + (x) 2 ) 2 = 3 x 2 ( + (x) 2 ) 2 che si aulla per x = /. Ora f (x ) = /2 per ogi N per cui lim f f = lim f = + + lim + 2 = 2. Osservazioe - Si osservi che il limite putuale di fuzioi cotiue può j O i Figura.5: essere cotiuo ache se il limite o è uiforme. Soluzioe.6 - Facilmete si ha che lim f (x) = La covergeza o è però uiforme. Ifatti per ogi x [, + ) sup f (x) = +. x [,+ ) È uiforme però sui limitati. Si cosideri, ad esempio, u itervallo [, a] co a > : f (x) = x2 + 2x (x + ) 2 5
16 per cui le fuzioi soo cresceti e quidi assumoo il massimo i x = a: sup f (x) = a2 per ogi a (, + ). x [,a] a + Calcoliamo l itegrale: lim f (x) se xdx lim f (x) se (x) dx lim f (x) dx = grazie al fatto che f uiformemete i [, ]. Si oti che ache le fuzioi x f (x) se (x) covergoo uiformemete a i [, ] poiché g (x) = se (x) soo equilimitate (questo è vero solo perché le f covergoo a zero! I geerale se f f uiformemete e g soo equilimitate o possiamo affermare che f g covergoo uiformemete). Soluzioe.7 - Il limite putuale è f. Per studiare la covergeza uiforme calcoliamo il massimo delle f. f (x) = α ( x 2 ) [ x 2 ( + 2)] = x = Valutiamo il massimo di f f : M (α) = max f (x) = α ( ). x [,] Si ha che lim M (α) = per α < 2 lim M (α) = 2e per α = 2 lim M (α) = + per α > 2 e quidi vi è covergeza uiforme solo per α < /2. l itegrale. Per α < /2 + 2 lim f (x)dx = lim f (x)dx = Calcoliamo grazie alla covergeza uiforme. Negli altri casi calcolo la primitiva che è data da f = α 2( + ) ( x2 ) + = α 2( + ). 6
17 Si ha allora che lim lim lim f = per α < f = 2 per α = f = + per α >. Soluzioe.8 - Facilmete si vede che f () = f (π). Se x (, π), x π/2 si ha che se 2 x < e quidi si ha che esiste a < per il quale defiitivamete vale + se 2 x a < per cui f (x) se x π/2. Se x = π/2 si ha che f (π/2) = ( + ) e quidi il limite putuale è (si veda la Figura.6) lim f e x = π (x) = f(x) = 2 x π 2 Può covergere uiformemete? NO! Perché le f soo cotiue e f o lo è. Vediamo che succede se togliamo u itoro di π/2. Fisso δ > (e miore di π/2): i [, π/2 δ] f è crescete per ogi N per cui il massimo è assuto per x = π/2 δ. Detto α il valore se 2 (π/2 δ) < si ha che esiste ɛ > tale che α + ɛ < e quidi ( ) max f (x) x [,π/2 δ] + α (α + ɛ). Allo stesso modo si può procedere i [π/2+δ, π]. Coclusioe: f covergoo uiformemete a f i tutti gli isiemi del tipo A δ = [, π/2 δ] [π/2 + δ, π]. Calcoliamo l itegrale: π π/2+δ f (x)dx = f (x)dx + f (x)dx f (x)dx + 2eδ. A δ π/2 δ A δ 7
18 j O i Figura.6: Passado al limite si ha che i A δ, grazie alla covergeza uiforme, l itegrale tede a. Cocludedo si ha che: δ > il che sigifica che l itegrale tede a. π lim f (x)dx < 2eδ Soluzioe.9 - Propoiamo due svolgimeti. Il primo: scrivedo f (x) come log( + x/) si ottiee che il limite putuale è la fuzioe f(x) = x. Vediamo se è uiforme. Prediamo i cosiderazioe le fuzioi g (x) = ( + x/). Sappiamo dal primo corso di aalisi che ( + x/) è crescete i per x positivo ( + x/) è decrescete i per x egativo e coverge alla fuzioe g(x) = e x. Derivado si ottiee ( g (x) g (x) = e x + x ) > se x > = se x = < se x <. Si osservi però che g () = g() = per cui g(x) g (x) > trae che per x = che risulta essere u puto di miimo. È chiaro che il massimo è assuto quidi per x = oppure per x = e si ha sup g (x) g(x) max{ g ( ) e, g () e }. x [,] 8
19 Per cui {g } coverge uiformemete a g i [, ]. Poiché la fuzioe x log x è cotiua ell itervallo [e, e] (el quale assumoo valori le g ) e log g (x) = f (x), log g(x) = f(x), cocludiamo che ache {f } coverge uiformemete a f i [, ]. Che succede i [, + )? Il secodo svolgimeto fa uso del seguete risultato (teorema o visto a lezioe). Teorema.2 Sia (f ) ua successioe i C ([a, b]) tale che ) f coverge uiformemete ad ua fuzioe g i [a, b]; 2) esiste x [a, b] tale che f (x ) coverge. Allora la successioe (f ) coverge uiformemete ad ua fuzioe f. Ioltre f C ([a, b]) e f = g. Usiamo questo teorema per risolvere l esercizio. Calcoliamo direttamete il limite uiforme di f (x) = log( + x/) i [, ]. Si ha che f (x) = x+ che coverge uiformemete alla costate, ioltre f () coverge a. Per cui f coverge uiformemete alla fuzioe f data da f(x) = + x dt = x Soluzioe. - La successioe coverge putualmete alla fuzioe ulla su tutto R, uiformemete solo sui compatti. Soluzioe. - Suppoiamo per il mometo di dover studiare semplicemete la serie ( + x). I u caso del geere ci si può ridurre a studiare la serie geometrica y 9
20 pesado poi a sostituire a y /( + x). Sappiamo che la serie geometrica q = q q = q per q <. Di cosegueza la serie appea scritta coverge alla fuzioe y y putualmete i (, ) ed uiformemete e totalmete solo ei compatti [a, b] (, ). Ifatti e ache sup y (,] sup y [,) y y y = sup =N y = =N sup y (,] y [,) =N+ =N+ y = sup y = + yn+ y [,) y = + per cui o può esservi covergeza uiforme, e emmeo totale, i (, ] e i [, ). Vediamo ora ei compatti [a, b] (, ). Ifatti: si cosideri per semplicità [, b] co < b <. Deotiamo co g(y) il limite di g N, cioè g(y) = y. Si ha sup [,b] N g N (y) g(y) = sup y y = sup [,b] =N+ b = bn+ b [,b] =N+ Cosiderado il limite per N si ottiee la covergeza uiforme. Aalogamete si ottiee i [a, ] co < a < e quidi i ogi [a, b] (, ). Questo si traduce, per la serie cosiderata, ella covergeza alla fuzioe +x +x = x putualmete i (, 2) (, + ) e uiformemete e totalmete egli isiemi (, α], [β, + ) co α < 2 e β >. Ifatti la trasformazioe g(x) = /( + x) mada l itervallo [a, ], co < a, i (, a a ], e l itervallo [, b], co b <, i [ b b, + ). Se, ad esempio, a = +δ co δ >, y 2
21 cioè a compreso tra e, si ottiee che a a = 2 δ, cioè u umero strettamete miore di 2. Aalogamete si vede che b b è strettamete positivo. Veiamo ora all esercizio proposto: poiché la serie data è il limite, per N +, di N x per le somme fiite si ha (+x) N x N ( + x) = x ( + x). Per cui l isieme di covergeza putuale cotiee sicuramete l isieme el quale coverge la serie (+x), cioè (, 2) (, + ). Si osservi però che la serie data coverge ache per x = (ifatti ogi termie è ideticamete ullo!). Perciò l isieme di covergeza putuale è (, 2) [, + ) e la fuzioe limite è { x (, 2) (, + ), h(x) = x =, (poiché (+x) = /x). Per quato riguarda le covergeze uiforme e totale si può ragioare come prima per otteere che vi è covergeza egli isiemi del tipo (, α], [β, + ) co α < 2 e β >. No può esservi covergeza uiforme, e di cosegueza emmeo totale, ell isieme [, + ) dal mometo che la fuzioe limite è discotiua i tale isieme metre le somme parziali soo ovviamete cotiue. x 2 Cosa succederebbe se ivece cosiderassimo la serie ( + x)? A questo proposito si veda ache l Esercizio.2. Soluzioe.2 - Per quato riguarda la serie x si procede come ella soluzioe dell Esercizio. per otteere la covergeza putuale i (, ) e uiforme e totale ei compatti coteuti i (, ) alla fuzioe x. Ciò che può modificare gli isiemi di covergeza è la preseza di f(x). L uica cosa che può alterare il comportameto della serie è il fatto che f() 2
22 e/o f( ) siao (se f() e f( ) la serie i e o coverge), escludedo il caso i cui f(x) = per ogi x (, ) (, + ) che farebbe baalmete covergere la serie i tale isieme. Cocetriamoci quidi sul comportameto di f i e. Comiciamo cosiderado f(x) = x + α x β co α, β. Chiaramete la serie coverge i (, ) e o coverge i (, ) (, + ). Nel puto, el quale la serie x o è determiata, si ha che per qualuque valore positivo di α f( ) = e questo fa sì che la serie i coverga. Aalogamete el puto la serie coverge (è ideticamete ulla) per β >. Il limite putuale è dato dalla fuzioe (x + ) α ( x) β x (, ) se α, β x = se α >, β x = se α, β >. Vediamo ora le covergeze uiforme e totale. seguete stima x β 2 β Giacché i [, ] vale la possiamo limitarci, per la covergeza totale i [, ], a studiare la fuzioe x + α x dal mometo che, dalla stima appea sopra, si ha x + α x x + α x β x 2 β x + α x. ( ) Derivado la fuzioe x+ α x si ottiee il massimo i +α e valutado la fuzioe i tal puto si ottiee che il valore massimo (per x + α x ) è dato da α ( ). α + α + Poiché ( α+ ) e α e α α+ = +, dalla prima delle due disuguagliaze i ( ) si deduce che la serie o può covergere totalmete i [, ]. I maiera del tutto aaloga ( si può vedere che il massimo di x β x è assuto i +β e vale β β+ β+) e quidi la serie o coverge totalmete i [, ]. Però sui compatti [a, b] (, ), dalla covergeza totale della serie x e dalla limitatezza di f, vi è covergeza totale. Veiamo ora alla covergeza uiforme. I [, ] la serie è a segi alteri. Dal criterio di Leibiz, e usado la secoda disuguagliaza i ( ), ricaviamo 22
23 che sup x [,] x + α x β x sup x [,] N x + α x β x x + α x β x N+ 2 β α ( ). α + α + Tale quatità chiaramete tede a zero quado +, per cui la serie coverge uiformemete i [, ]. I [, ] la covergeza uiforme dipede dal valore del parametro β. Per < β la serie i coverge a zero, per x < a ( + x) α ( x) β : di cosegueza il limite o è cotiuo e o può esservi covergeza uiforme. Per β > si ha sup x [,] N f(x)x f(x)x = sup = sup x [,] x [,] (x + ) α ( x) β x N f(x) x f(x) xn x = Limitadoci a cosiderare ( x) β x N, poiché (x + ) α è compreso tra e 2 α per x [, ], valutado la derivata si ha d dx ( x)β x N = per x = + β che è il puto di massimo (verificare!), el quale la fuzioe assume il valore ( β N + β ) β ( N N + β ) N che tede a zero (verificare!) per ogi β >. Nel caso geerale possiamo cocludere che se f( ) = vi è covergeza uiforme i [, ], ell itervallo positivo la serie si comporta come x se f(). Se ivece f() = ed esiste β (, ] tale che lim x f(x) ( x) β = λ R, cioè se l ordie di ifiitesimo di f i è miore o uguale di, il limite esiste i tutto [, ], ma o è cotiuo, e quidi o vi può essere covergeza uiforme i [, ], se ivece esiste β > tale che lim x f(x) ( x) β = λ R, 23
24 cioè se l ordie di ifiitesimo di f i è maggiore di, la serie coverge uiformemete i tutto [, ]. Per la totale bisogerà valutare il massimo e fare i coti. x 2 Per quato riguarda la serie, proposta alla fie della soluzioe ( + x) dell Esercizio., si può cocludere che la serie coverge uiformemete i [, + ). Soluzioe.3 - Coverge totalmete su R. Soluzioe.4 - Putuale per ogi x R perché, ad esempio, x + x log x + I geerale vale, per a, b >, che a 2 +b 2 2ab, per cui 2(a 2 +b 2 ) (a+b) 2, da cui x + x + x + x log 2(x ) ( x + 2 ) 2 2 x per cui la serie coverge totalmete i R. Soluzioe.5 - Per ogi x R / log( + x 2 ) è decrescete i per cui la serie è covergete per ogi x. La stima del resto ( ) m log( + x 2 ) =2 =2 4 ( ) log( + x 2 ) log(m + x 2 ) log m quidi vi è covergeza uiforme su tutto R. Ovviamete o vi è la totale: si ha che ( ) sup log( + x 2 = ) log x R (il massimo è assuto per x =, fare la derivata per esercizio!) e la serie (log ) diverge. No c è covergeza totale emmeo i essu itervallo (a, b) (o [a, b]) poiché sup x (a,b) ( ) { log( + x 2 = max ) log( + a 2 ), log( + b 2 ) }. 24
25 Soluzioe.6 - Per x si ha che x x + x 2 2 x 2 = 2 per cui la serie diverge. Per x (, ) si ha che x x + x 2 per cui vi è covergeza assoluta. Per x x + x 2 = x ( ) + x 2 e x + x 2 Verifichiamo che è mootoa decrescete i : mi chiedo se cioè se ( + ) x + x + x + ( + ) 2 + x 2 x + ( + ) 2 x 2+ ( + ) x + + ( + ) 2 x 2+ il che è equivalete a ( + ) x ( + ) x + + che è vero per ogi x e per ogi N. Usado il criterio di Leibiz si coclude che la serie coverge i (, ]. Quidi coverge putualmete i (, ). Dalla stima i (, ) si vede che vi è covergeza totale i [, a] per ogi < a <, ma o può esservi i [, ). Ifatti sup [,) N x + x 2 x x + x 2 = sup [,) =N+ x + x 2 = + i quato le fuzioi soo cotiue (ache i x =!!), ma la loro + x 2 somma su diverge a + i x =. Per x egativo si ha: x m + x 2 x m x m + x 2 + x m m 2 m. Coclusioe: vi è covergeza putuale i (, ) e uiforme e totale su tutti gli isiemi del tipo (, a] co a <. 25
26 Soluzioe.7 - Questo è u esempio molto semplice si serie di fuzioi o egative che coverge uiformemete, ma o totalmete. La fuzioe f è a supporto compatto e le f o soo altro che traslazioi di f. Di cosegueza f (x) i realtà è ua somma fiita, per cui c è covergeza putuale (e assoluta, visto che le f soo tutte o egative) su tutto R. C è covergeza uiforme? Si, su tutto R, perché sup f (x) x R f (x) = sup =N x R =N+ f (x) N +. C è covergeza totale? NO! perché il massimo di f è ovviamete / assuto per x = π/2 + e la serie = +. Coverge, però, totalmete sui sottoisiemi del tipo (, a]. Ex: modificare le f i modo tale da avere covergeza totale su R. Soluzioe.8 - Per x < lim x e x = per cui la serie diverge. Per x la serie ivece coverge (per x = è ideticamete ulla, per x > si può usare, ad esempio, il criterio del rapporto). Vediamo che i [, + ) la serie coverge totalmete. Derivado si ottiee che il puto x = / è stazioario. Poiché f () =, lim x + f (x) = e f x risulta puto di massimo. Quidi f (x) f (/) = 2 e. Soluzioe.9 - Per x > coverge e per x diverge a +. Poiché la fuzioe f (x) = x è decrescete si ha che e la serie sup x (,+ ) x = diverge. Idem per la covergeza uiforme: sup x (,+ ) N x = x =N+ x = +. Se ivece si cosidera u qualuque isieme del tipo [a, + ) co a > si ha, sempre per il fatto che f è decrescete, che sup x [a,+ ) = x e a a 26
27 coverge per ogi a >. Cocludedo si ha covergeza totale, e quidi ache uiforme, i tutti gli isiemi del tipo [a, + ) co a >. Soluzioe.22 - Posso fare il cambio y = (x + )/x e studiare ( 3)y. Il raggio di covergeza è (si vede facilmete), per cui la serie coverge putualmete per y (, ). La covergeza, al solito, è totale ei compatti [a, b] (, ), ma o i (, ). Posso scrivere ( 3)y = y 4 ( 3)y 4 e vedere ( 3)y 4 come la derivata di y 3. Abbiamo e k= ( 3)y = 3 2y y 2 + ( 3)y k= = 3 2y y 2 + y 4 ky k = y 4 d dy yk = y 4 d dy Coclusioe: k= =4 k= ky 3+k y k = y 4 d y dy y = y 4 ( y) 2 ( 3)y = 3 2y y 2 y 4 + ( y) 2 dove la covergeza è putuale per y (, ) e totale sui compatti [a, b] (, ). La fuzioe f(x) = (x + )/x ha il grafico i Figura.7 per cui, torado a cosiderare x, si ha che ( x + ) x + ( x + ) 2 (x + ) 4 ( 3) = x x x x 2 dove la covergeza è putuale per x (, /2) e totale egli isiemi del tipo [a, b] (, /2). Ifatti x + < per x (, /2). x Soluzioe.25 - Calcolado il seguete limite lim 3 = 3 27
28 j i O Figura.7: si ha che il raggio è 3. Coclusioe: la serie coverge (putualmete) i ( 3, 3) e o coverge (putualmete) i (, 3) (3, + ). Vediamo i 3 e 3 che succede. 3 ( 3) o coverge, 3 3 diverge Coclusioe: si ha covergeza putuale (solo) i ( 3, 3). Vediamo gli altri tipi di covergeza. Teorema.3 Ua serie di poteze cetrata i coverge totalmete i ogi itervallo chiuso del tipo [ a, a] co a < ρ. Si ha di cosegueza covergeza totale, e quidi uiforme, i ogi itervallo [ a, a] co a < 3. Vediamo se si ha covergeza uiforme ache i ( 3, 3). Ragioado come al solito (si veda, ad esempio, la risoluzioe dell esercizio.) si deduce che la serie o può covergere uiformemete i ( 3, 3) e quidi emmeo totalmete. Si osservi che la serie ha come somma la fuzioe f(x) = 3 3 x. 28
29 Soluzioe.26 - Si può fare il limite della radice -esima di α +e α pesare la serie come (perché?) oppure α x + e α x e studiare separatamete le due serie. Seguiamo quest ultima strada. Il primo termie: il secodo termie: e α α quidi il raggio di covergeza è, eα quidi il raggio di covergeza è e α. Se α = : il raggio è lo stesso e la serie diveta 2 x. Vediamo gli estremi: per x = si, per x = o. Isieme di covergeza putuale [, ). La covergeza è uiforme? No può esserlo dappertutto (vedi esercizio precedete). Teorema.4 (Leibiz) Sia (a ) ua serie a termii positivi. Se a ed è decrescete allora ( ) a coverge. Ioltre ( ) a m ( ) a am+. Sicuramete abbiamo covergeza totale egli isiemi del tipo [a, b] co < a < b <, o abbiamo covergeza uiforme, e quidi emmeo totale, i [, ). Vediamo i [, ]: qui la serie è a segi alteri, per vedere se la serie è uiformemete covergete uso il criterio di Leibiz. Detta f la somma della serie e f le somme parziali devo vedere se vale cioè lim sup + lim f f + [,] ( ) k 2 k x k k= lim sup + [,] ( ) k 2 k x k 2 + x + = lim
30 quidi vi è covergeza uiforme i [, ], ma o totale! Cocludedo: per α = si ha che la serie coverge putualmete i [, ), uiformemete i [, b] [, ) e totalmete i ogi [a, b] (, ). Gli altri casi: se α > il raggio è /e α. Il primo termie sicuramete coverge totalmete i [ /e α, /e α ], quidi limitiamoci a cosiderare il secodo. Negli estremi: per x = /e α la serie coverge, per x = /e α la serie diverge, ifatti si ha rispettivamete ( ) Covergeza uiforme e totale come sopra: [ covergeza uiforme i. ] e, b α per ogi b < covergeza totale i [a, b] per ogi a > e, b < α Se α < il raggio è. Vediamo gli estremi: il secodo termie questa volta coverge totalmete i [, ]. Il primo egli estremi è ( ) α α che covergoo etrambe. Vi è covergeza totale i [, ]. Soluzioe.27 - È facile vedere che f (k) (x) = f(x) per ogi k N. Per cui lo sviluppo di Taylor è dato da! f () ()(x ) = Vediamo di studiare la covergeza di questa serie: putuale i tutto R, ad esempio co il criterio della radice -esima. No può essere uiforme i tutto R perché sup k! xk = +. x R k= x!. e α e α 3
31 Se ache ci limitiamo a x (, ] abbiamo (p il poliomio di grado delle somme fio all -esimo termie) sup x (,] k= x k k! k= x k = k! sup e x p (x) = +. x (,] Vediamo cosa si può dire: se mi limito a cosiderare u itervallo [a, b] ho che xk bk k! k! per la cresceza di x k. La serie data dai maggiorati coverge. Cocludedo: la serie di Taylor i x = è data da x! che coverge putualmete su tutto R e uiformemete e totalmete solo sui compatti. Soluzioe.29 - La serie dell esercizio o è ua serie di poteze. Tuttavia lo studio di tale serie può essere ricodotto allo studio di ua serie di poteze. Iazitutto si osservi che [ x ] / x lim + 2 ( + x 2 ) = + x 2 che è sempre miore di (per esercizio vedere che /2). Di cosegueza la serie coverge assolutamete per ogi x R. Calcoliamo la +x 2 somma della serie (per y < ) Si ha che + 2 y = Ora mi chiedo: + 2 y. [ y = 2 ] + 2? + 2 y = y 2 y 2 x y = y 2 y y y+2. La risposta è si, perché lim (a +b ) = lim a +lim b qualora i due limiti a destra (o almeo uo di essi) esistao e el ostro caso le due serie a destra 3
32 covergoo etrambe (per y < ). Prediamo i esame il secodo termie: + 2 y+2 = = y y t + dt! = ( t ) dt = =2 y y ( t +) dt = t 2 t dt dove l ultimo passaggio co il puto esclamativo è lecito se la covergeza è uiforme!! (e lo è se y è fissato tra e ). Per itegrare t2 t dividiamo t 2 per t e scriviamo t 2 = ( t)( t) + t2 = ( + t) + t t e quidi itegrado y t 2 Tirado le fila si ha + 2 y = y2 dt = y log( y). t 2 = y y 2 y 2 [ y y2 log( y)] 2 y y + 2 y log( y) y2 Si osservi che questa fuzioe è regolare ache se sembra avere sigolarità i y =. Ifatti log( y) = y + y 2 /2 + o(y 2 ) e quidi y y + 2 y y 2 log( y) = [ y 3 ] y 2 y + 2y + y2 + 2 log( y) = Torado al ostro problema: poiché la quatità di la serie x x 2 = y 2 [ y 3 y + 2y + y2 2y + y 2 + o(y 2 ) x (+x 2 ) è sempre miore coverge putualmete per ogi x R; coverge pure uiformemete e x totalmete su R poiché +x 2 2. Si coclude sostituedo ell espressioe x di sopra al posto di y +x 2 x + 2 ( + x 2 ) = x + x 2 x x + x 2 x 2 2( + x 2 ) 2 log + x2 x + x 2. ] 32
33 Soluzioe.3 - Usiamo ua cosegueza del seguete risultato. Teorema.5 Sia a serie a termii positivi. Se esiste allora esiste ache lim a e vale lim a + a a + lim = lim a a. Il viceversa o è vero! Si cosideri ad esempio la successioe data da a = / se è pari e a = /2 se è dispari. Si ha lim a =, a metre ivece lim + a o esiste (il rapporto è /2 se è pari, 2 se è dispari). Allora calcoliamo il limite della radice -esima calcolado il rapporto. (provare a farlo co la radice -esima!!!) ( + )! lim ( + ) +! = lim ( ) = + e quidi vi è covergeza putuale i ( e, e) e o vi è i (, e) (e, + ). Vediamo gli estremi: e x = k= x k k! quidi per x = e = k= k k! per cui! e. (.3) La serie quidi o coverge per x = e e diverge a + per x = e. Ovviamete coverge totalmete e uiformemete i tutti gli itervalli [a, b] ( e, e). Come al solito si ha che la serie o può covergere uiformemete i ( e, e). Aziché la stima (.3) si può usare, per studiare il comportameto della serie i x = e la formula di Stirlig!! = e 2π ( + O(/)). 33
34 Soluzioe.3 - Sappiamo che la serie geometrica q = q Possiamo allora cocludere che la serie ( x 2 ) coverge a per q <. + x 2 per x <. Studiamo questa serie. Coverge putualmete i (, ). Per x = e per x = ovviamete o coverge. Al solito, la serie o covergerà uiformemete i (, ), ma è facile vedere che coverge totalmete i tutti i compatti [a, b] coteuti i (, ). Calcoliamo la derivata di f(x) = arctg x f (x) = + x 2. Itegrado termie a termie si ha, posto f (x) = k= ( )k x 2k, grazie alla covergeza uiforme Ora per cui lim x f (t)dt = x x lim f (t)dt = x ( ) k t 2k dt = ( ) k 2k + x2k+ arctg x = ( ) x2+ dt = arctg x. + t2 2 + per ogi x [, ] e la covergeza uiforme solo sui compatti coteuti i (, ). Soluzioe.32 - Calcoliamo la derivata di f(x) = se x. f () (x) = cos x f () () = f (2) (x) = se x f (2) () = f (3) (x) = cos x f (3) () = f (4) (x) = se x f (4) () = 34
35 e poi il ciclo si ripete. Quidi lo sviluppo i è dato da se x = ( ) x2+ (2 + )!. Vediamo la covergeza. Per il criterio di Leibiz coverge per ogi x reale. La covergeza è uiforme e totale solo sui compatti (i modo aalogo all esercizio precedete). I modo simile si calcola ache lo sviluppo del coseo cos x = ( ) x2 (2)!. Soluzioe.33 - Si ha che! ( + )! = ( + )! per cui il limite della radice -esima è : la serie coverge per ogi x R. Prima di studiare le covergeze uiforme e totale calcoliamo la somma della serie. Sappiamo che x! = ex. Si ha che ( + )! x = x d [ x + ] dx ( + )! x per cui, grazie alla covergeza uiforme posso ivertire il sego di derivata co il limite e otteere ( + )! x = x d [ x + ] dx ( + )! x = x dx[ d x + ] x ( + )! = x d [ dx x (ex x)] [ = x x 2 (ex x) + ] x (ex ) = e x x (ex ). 35
36 Vediamo la covergeza uiforme i R: k sup (k + )! xk x R k= k (k + )! xk = sup k= x R k=+ k (k + )! xk = + quidi o vi è covergeza uiforme i R. Nemmeo se ci limitiamo a semirette [a, + ), perché l estremo superiore è + proprio perché cosideriamo la semiretta fio a +. Che succede se cosideriamo (, ]? sup x (,] k k (k + )! xk (k + )! xk = k= k= = sup e x k x (ex ) (k + )! xk = + x (,] perché f(x) = e x x (ex ) è limitata i (, ], metre u poliomio di grado o! (come, ad esempio, fatto per e x ). Per x [ a, a] co a positivo k= k k (k + )! xk (k + )! ak. La serie a (+)! coverge per ogi a reale per cui si ha covergeza totale e uiforme i ogi compatto. Soluzioe.34 - Spezzado il poliomio x 2 5x + 6 come prodotto di x 3 e x 2 si ottiee che f(x) = x 3 2 x 2. Sapedo che, per q <, la serie q coverge al valore scrivere x 3 = 3 x = 3 x = ( x ) q che coverge per x 3 <, cioè per x < 3. L altro termie: si può 2 x 2 = 2 2 x = 2 x 2 = 2 ( x ) 2 36
37 che coverge per x 2 <, cioè per x < 2. Sarà possibile effettuare la somma solo dove covergoo etrambe, quidi sicuramete per x ( 2, 2) si ha che f(x) = Soluzioe.35 - Si osservi che d dx x = ( x) 2 e che [ ] x. d dx ( x) 2 = 2 ( x) 3. Poiché la serie x coverge uiformemete i ogi itervallo chiuso [a, b] (, ) e così pure la serie delle sue derivate (prime e secode, ma o solo) si può affermare che (per quei valori di x [a, b] (, ) co a, b arbitrari, ma a, b <, per cui per ogi x (, )) 2 ( x) 3 = d dx ( x) 2 = d dx x = d dx ( x) 2 = d dx x = x = d dx x = d dx x = x ( )x 2. Per cui dove vi è covergeza per etrambe le serie, e i questo caso etrambe covergoo i (, ), vale =2 f(x) = ( x) 3 + 3x2 ( x) 3 = = ( )x 2 + 3x2 ( )x =2 =2 ( + 2)( + ) = x 3( ) + x 2 2 =2 ( + 2)( + ) + 3( ) = + x + x 2 =2 = + x + (2 2 + )x. =2 37
38 Soluzioe.36 - La fuzioe f può essere scritta ei segueti modi ( x 2 ) log 3x 2 = log(x 2) log(3x 2) NO!! = log(2 x) log(2 3x) SI!! Perché scartiamo il primo dei due? I due modi o soo equivaleti: la fuzioe f è defiita quado il suo argometo è positivo, e cioè quado x 2 e 3x 2 hao lo stesso sego. Quidi f può essere spezzata come sopra el primo modo se x 2 e 3x 2 soo etrambi positivi, el secodo modo se x 2 e 3x 2 soo etrambi egativi. Per x =, itoro al quale vogliamo sviluppare f, le fuzioi log(x 2), log(3x 2) o soo defiite, metre log(2 x) e log(2 3x) si. Per esercizio, e ache per covicersi di quato appea detto, disegare i grafici di log( x 2 3x 2 ), log(x 2), log(3x 2), log(2 x) e log(2 3x). Abbiamo trasferito quidi il problema ello scrivere lo sviluppo delle due fuzioi log(2 x) e log(2 3x). Si ha, per x/2 <, d log(2 x) = dx 2 x = 2 x = ( x ) Itegrado tra e x, co x < 2, poiché la serie sopra coverge uiformemete log(2 t) x x ( t ) dt = x ( t ) dt = e quidi log(2 x) log 2 = 2 t + 2 x + = x Aalogamete si ottiee, per 3x/2 < e quidi per x < 2/3, ( 3 + x + log(2 3x) log 2 = 2) +. Cocludedo: ( x 2 ) log 3x 2 x + = log log 2 + ( 3 + x + 2) + [( 3 ) ( ] x + = 2 2) 38
39 e l isieme di covergeza è l itersezioe degli isiemi sui quali covergoo separatamete le due serie. Cocludiamo che [ x 2 ] log = 3x 2 [( 3 ) ] x 2 2 e la covergeza è putuale i [ 2/3, 2/3), uiforme i tutti gli isiemi del tipo [ 2/3, a] co a ( 2/3, 2/3) e totale i tutti gli isiemi del tipo [b, c] co b, c ( 2/3, 2/3), b < c. Ifatti ua delle due serie coverge putualmete almeo i ( 2, 2) e l altra almeo i ( 2/3, 2/3) ( 2, 2), quidi la serie coverge i ( 2/3, 2/3) e o coverge i (, 2/3) (2/3, + ) (per verifica calcolare il limite della radice -esima dei coefficieti). Negli estremi: è sufficiete studiare la secoda serie, poiché covergedo la prima i ( 2, 2) i particolare covergerà i 2/3 e 2/3. Per x = 2/3 si ha ( 3 ) ( ) = 2 3 che diverge a +, metre per x = 2/3 si ha ( 3 ( 2) 2 ) + 3 = 2 3 ( ) + che coverge. La covergeza è uiforme i tutti gli itervalli del tipo [ 2/3, a] co a < 2/3 e totale egli itervalli del tipo [b, c] ( 2/3, 2/3). Soluzioe.37 - L isieme è [, ] per α < /2, [, ) per α /2. Soluzioe.4 - Si può fare seguedo la soluzioe dell Esercizio.36 osservado che + x 2x 2 = (2x + )( x). Soluzioe.42 - Attezioe! ella prima serie i coefficieti a soo dati da / 2, ella secoda o! Alcui ifatti soo zero. I coefficieti della secoda serie soo ifatti { / se = k a = 2 co k N, altrimeti. 39
40 Il comportameto però è lo stesso: ifatti la prima coverge totalmete i [, ]; e la serie coverge sia i che i. Per lo studio della secoda si può usare semplicemete il criterio della radice, valutado lim x 2 / 2 = lim x / 2 si ottiee che la serie coverge (assolutamete) per x e o coverge per x >. La covergeza i [, ] è totale. A proposito della secoda serie si veda ache l Osservazioe.24.4 delle dispese di teoria di Aalisi II (Albaese-Leaci-Pallara). Soluzioe.44 - Si osservi che i termii di questa serie soo alcui dei termii della serie k k xk. Ifatti i coefficieti a soo dati da per cui { / se = k a = k co k N, altrimeti { / se = k a = k co k N, altrimeti Di cosegueza il limite lim a o esiste. Possiamo trattare la serie come ua serie umerica, fissado x e valutado x x =. Passado al limite per + si ottiee che la serie coverge per x [, ]. Alterativamete, per chi cooscesse il limsup e che il raggio di covergeza è dato dal reciproco di lim sup a, si ha che lim sup a = lim k k k k k = lim h h h =. Il raggio quidi è. Per x = e x = la serie coverge e quidi l isieme di covergeza è [, ]. La covergeza è ache totale. Si veda ache l Osservazioe.24.4 delle dispese di teoria di Aalisi II (Albaese-Leaci-Pallara). Soluzioe.45 - Questo è u esempio i cui il limite di a = (2+seπ/2) o esiste. Si ha che 2 + se π/2 può assumere i valori, 2, 3. 4
41 L estremo superiore (si veda la defiizioe di raggio di covergeza elle dispese) dei umeri per cui la serie coverge è /3 (l iverso del massimo valore che può assumere a ): ifatti o può essere maggiore perché se lo fosse, diciamo r > /3, per tutti i valori x (/3, r) la serie covergerebbe. Ma per ifiiti valori di N si ha che 2 + se π 2 assume il valore 3 per cui se fissiamo x > /3 e miore di r si avrebbe per ifiite volte che (2 + se π 2 ) x > il che o farebbe covergere la serie. Si veda ache l Osservazioe.24.4 delle dispese di teoria di Aalisi II (Albaese-Leaci-Pallara). Soluzioe.46 - Si ha π quidi lo sviluppo è Poiché la fuzioe è dispari lo sviluppo è di soli sei. { pari f(x) se xdx = 4 dispari π π π 4 se (2 + )x. π(2 + ) La media di f è ulla, per cui a è ullo. Usado la formula (.2) si ha che lo sviluppo di F (x) = x π f(t)dt = x π è dato da (i coefficieti A di cos x soo ulli, i coefficieti B di se x soo dati da 4/π 2 per dispari, altrimeti) x π = A cos(2 + )x π(2 + ) 2 dove A = π π π [ x π]dx = π2 /π = π. Per cui lo sviluppo di x i [ π, π] è (cofrotare co l Esercizio.49) π π π(2 + ) 2 cos(2 + )x = π cos(2 + )x. π(2 + ) 2 4
42 Soluzioe.47 - La fuzioe è pari, per cui il suo sviluppo è fatto di soli cosei. Si ha che π π x2 dx = 2π 3 /3 e π x 2 2 se x cos x dx = x π π π se x 2x dx π π cos x π π = 2x 2 + cos x 2 π 2 dx = ( ) 4π 2 per cui lo sviluppo è dato da π 2 π 3 + ( ) 4 cos x. 2 Poiché l estesioe a tutto R è C a tratti e cotiua si ha covergeza uiforme su tutto R. I particolare per x = π si ha da cui si ricava f(π) = π 2 = π2 3 + ( ) 4 2 ( ) = π = π Soluzioe.48 - Il periodo 2T è 2, quidi T =. Calcoliamo i coefficieti: a = a = f(x)dx = f(x) cos xπ dx = ( ) = x π se πx xdx = 2. = π = ( ) π cos πx 2 2 π 2 dispari pari x cos xπ dx se πx dx π 42
43 b = ( = x f(x) cos xπ dx = π cos πx ) x se xπ dx cos πx dx π = ( ) + π + ( ) π π se πx = ( )+ π quidi lo svilupo è 4 2 (2 + ) 2 π 2 cos(2 + )πx + ( ) + se πx. π Coverge putualmete alla fuzioe { f(x) x (, ) 2 x =, x =. La covergeza uiforme c è solo egli isiemi del tipo [a, b] (, ) visto che il limite o è cotiuo. Valutiamo ora la serie. Per x = la serie coverge al valore (2+) 2 /2 per cui 2 da cui = 4 2 (2 + ) 2 π 2 cos(2 + )π + ( ) + se π π = (2 + ) 2 π 2 (2 + ) 2 = π2 8. Ora per la somma possiamo procedere i due modi: sfruttare l esercizio precedete dal quale sappiamo che (2) 2 = π2 2 6 per cui otteiamo (2) 2 = 2 (2 + ) 2 = π2 6 π2 8 = π2 24, oppure, igorado il risultato dell esercizio precedete, osservare che per cui da = (2) 2 + (2 + ) 2 (2) 2 = 43
44 dedurre che e quidi (2) 2 = 4 2 = 4 3 (2 + ) 2 2 = π 2 8 = π2 24. Soluzioe.49 - La estedo per periodicità a tutto R e per questioe di semplicità di calcolo sviluppo la fuzioe g(x) = x defiita i [ π, π] ed estesa per periodicità a tutto R (si veda la Figura.8). I questo modo aziché calcolare 2π calcolo f(x) cos xdx = π π π x cos xdx 2π π Figura.8: x cos xdx = 2 Quidi i coefficieti soo dati da: e per > a = π π π π x dx = π x cos xdx + x cos xdx. 2π π 2π cos xdx π π a = 2 x cos xdx = 2 [ x π π se x π = 2 [ + π 2 cos x π] = 2 π 2 [( ) ] 44 ] se xdx
45 per cui { se pari a = 4 π 2 se dispari. Lo sviluppo risulta quidi essere (.4) f(x) = a 2 + a cos x = π 2 4 cos(2k + )x. (.5) π(2k + ) 2 La covergeza è putuale e uiforme su tutto R (perché la fuzioe è cotiua e C a tratti), i particolare sull itervallo [, 2π] al quale eravamo iteressati. I particolare se valutiamo la serie per x = questa covergerà al valore f() =, per cui si ha π 2 k= k= 4 π(2k + ) 2 = da cui (2k + ) 2 = π2 8. k= Per l altra serie sfruttiamo l uguagliaza di Parceval (.): π π π Per cui da π π x2 dx = 2π 3 /3 otteiamo e ifie k= f 2 (x)dx = a2 2 + (a 2 k + b2 k ). k= 2π 2 3 = π π 2 (2k + ) 4 k= (2k + ) 4 = π2 ( 2π π2 ) = π Per cosiderare uo sviluppo i soli sei o di soli cosei i geerale si fa così: data h : [, T ] R cosideriamo la fuzioe h defiita i [ T, T ) h(x) = { h(x) x [, T ] h( x) x [ T, ] ed estededo poi per periodicità a tutto R la fuzioe. Poiché la fuzioe risulta così pari il suo sviluppo sarà di soli cosei e T h(x) cos π T T T xdx = 2 h(x) cos π T x. 45
46 Se vogliamo uo sviluppo di soli sei si cosidera h(x) = { h(x) x [, T ] h( x) x [ T, ]. Nel ostro caso estediamo la fuzioe el modo seguete: Figura.9: x 2π se x [ 2π, π] f(x) = x se x [ π, π] x + 2π se x [π, 2π] e poi estedo f periodicamete su tutto R (a questo puto avremo ua fuzioe periodica di periodo 4π!). La restrizioe di f a [, 2π] è sempre la ostra f. La fuzioe così estesa risulta essere dispari foredo i coefficieti dei cosei ulli. Valutiamo i coefficieti: Abbiamo che b = 2π = π = π 2π 2π π π g(x) se π 2π xdx = π f(x) se 2 xdx + π π 2π 2π 2π f(x) se 2 xdx = f(x) se 2 xdx = x se 2 xdx + π π [ x + 2π] se 2 xdx. x se 2 xdx = 2 x cos 2 x se 2 x 46
47 per cui tra e π 2 cos π π se π 2 [ ( tra π e 2π 4π π cos π + 2π cos π se π 4 2 se π 2 ( +2π 2 cos π + 2 cos π )]. 2 Sommado, poiché si ha se π { ( ) 2 = ( )/2 dispari pari, b = 8 2 π se π 2 = 8 { ( ) ( )/2 dispari 2 π pari, La serie è data dalla somma dei segueti termii dispari 8 2 π se π 2 x = (2 + ) 2 se x π 2 Attezioe! Lo sviluppo trovato è lo sviluppo i soli sei della fuzioe f, quello i (.5) è lo sviluppo della fuzioe f: covergoo etrmabi (uiformemete) alla fuzioe origiale ell itervallo [, 2π], ma a fuzioi diverse ell itervallo [ 2π, ] (si vedao le Figura.8 e Figura.9). Ora valutiamo lo sviluppo della fuzioe g: si osservi che ell itervallo [ π, π] la fuzioe f(x) = x è ua primitiva della fuzioe g, e precisamete x x f(x) = π + g(t)dt, cioè f(x) π = g(t)dt. π π Se deotiamo co α e β i coefficieti α = π π π g(x) cos xdx β = π π π g(x) se xdx ) + si ha che α = e dalle formule (.2) si ricava β = a, α = b 47
48 quidi, cooscedo a (si veda (.4)) e b (b = per ogi N) si ricava immediatamete { se pari β = 4 π se dispari. per cui 4 g(x) = se (2k + )x π(2k + ) k= (si cofroti co l Esercizio.46). Soluzioe.5 - La fuzioe f(x) = 2 x, x [ π, π]. π come si vede dal garfico, è ua fuzioe pari per cui b = per ogi N. Si verifica facilmete che ache a =. Gli altri coefficieti soo dati ( > ) j O Figura.: i 48
49 a = π π π [ cos t 2 π t cos t ] dt = 2 π π 2 t cos t dt = 4 π π 2 t cos t dt = π π = 4 [ t π 2 se t π ] se t dt = 4 [ π 2 ( )] cos t π = pari 8 2 π 2 dispari per cui la serie è data da 8 (2 + ) 2 cos(2 + )x π2 che coverge uiformemete su tutto R (visto che il prolugameto periodico a tutto R di f è cotiuo e C a tratti). La serie coverge ache totalmete visto che 8 sup (2 + ) 2 π 2 cos(2 + )x 8 = (2 + ) 2 π 2. x [ π,π] Per calcolare le due serie (già calcolate egli esercizi.48 e.49) si può valutare la fuzioe i x = e usare l uguagliaza (.). 49
Successioni e serie di funzioni
 Capitolo Successioi e serie di fuzioi Ultimo aggiorameto: 23 aprile 28 Cosiderazioi geerali: o esiste u metodo geerale (cioè u modo meccaico che valga i ogi situazioe) per studiare la covergeza uiforme.
Capitolo Successioi e serie di fuzioi Ultimo aggiorameto: 23 aprile 28 Cosiderazioi geerali: o esiste u metodo geerale (cioè u modo meccaico che valga i ogi situazioe) per studiare la covergeza uiforme.
k=0 f k(x). Un altro tipo di convergenza per le serie è la convergenza totale e si dice che la serie (0.1) converge totalmente in J I se
 Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22/11/2013. = a 24 24! log(1 + x) = ( 1) = (24!) 1 24 = 23!. e x2 dx. x 2n
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
ANALISI VETTORIALE COMPITO IN CLASSE DEL 22//23 Esercizio Calcolare la 2esima derivata del logaritmo el puto. Risposta Si tratta di calcolare d 2 dx 2 log( + x) x= = a 2 2! dove a 2 è il termie di idice
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
Serie di potenze / Esercizi svolti
 MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
SERIE DI POTENZE Esercizi risolti. Esercizio 1 Determinare il raggio di convergenza e l insieme di convergenza della serie di potenze. x n.
 SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
Successioni e serie di funzioni
 Capitolo Successioi e serie di fuzioi. Successioi di fuzioi Esercizio. Studiare la covergeza putuale e uiforme della successioe di fuzioi f (x = x 2 +x2, x R. Esercizio.2 Studiare covergeza putuale e uiforme
Capitolo Successioi e serie di fuzioi. Successioi di fuzioi Esercizio. Studiare la covergeza putuale e uiforme della successioe di fuzioi f (x = x 2 +x2, x R. Esercizio.2 Studiare covergeza putuale e uiforme
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 8.8.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 8.8.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Esercitazione n 3. 1 Successioni di funzioni. Esercizio 1: Studiare la convergenza in (0, 1) della successione {f n } dove f n (x) =
 Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Esercitazioe 3 Successioi di fuzioi Esercizio : Studiare la covergeza i (0, ) della successioe {f } dove f (x) = metre Sol.: Si verifica facilmete che lim f (x) = 0 x (0, ) lim sup f (x) = lim = + (0,)
Esercizi svolti su successioni e serie di funzioni
 Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
SERIE NUMERICHE Esercizi risolti. (log α) n, α > 0 c)
 SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
1.6 Serie di potenze - Esercizi risolti
 6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
Università di Trieste Facoltà d Ingegneria. Esercizi sulle serie numeriche e sulle successioni e serie di funzioni Dott.
 e Uiversità di Trieste Facoltà d Igegeria. Esercizi sulle serie umeriche e sulle successioi e serie di fuzioi Dott. Fraco Obersel Esercizio Rispodere alle segueti questioi: a) Siao a 0 + a + a +... b 0
e Uiversità di Trieste Facoltà d Igegeria. Esercizi sulle serie umeriche e sulle successioi e serie di fuzioi Dott. Fraco Obersel Esercizio Rispodere alle segueti questioi: a) Siao a 0 + a + a +... b 0
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica I del c.1.
 Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
4 - Le serie. a k = a k. S = k=1
 4 - Le serie E veiamo ad uo degli argometi più ostici (ma ache più iteressati) dell aalisi: le serie. Ricordiamo brevemete cos è ua serie e cosa vuol dire covergeza per ua serie. Defiizioe 1. Data ua successioe
4 - Le serie E veiamo ad uo degli argometi più ostici (ma ache più iteressati) dell aalisi: le serie. Ricordiamo brevemete cos è ua serie e cosa vuol dire covergeza per ua serie. Defiizioe 1. Data ua successioe
[È ben noto che la serie geometrica converge se e solo se x <1 e che ha per somma la funzione S(x)= 1
 Sapieza Uiversità di Roma - Corso di Laurea i Igegeria Eergetica Aalisi Matematica II - A.A. 06-07 prof. Cigliola Foglio. Serie di fuzioi Esercizio. Calcolare, se possibile, la somma delle segueti serie
Sapieza Uiversità di Roma - Corso di Laurea i Igegeria Eergetica Aalisi Matematica II - A.A. 06-07 prof. Cigliola Foglio. Serie di fuzioi Esercizio. Calcolare, se possibile, la somma delle segueti serie
Def. R si dice raggio di convergenza; nel caso i) R = 0, nel caso ii)
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
a n (x x 0 ) n. (1.1) n=0
 Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Esercizi sulle Serie numeriche
 AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Serie umeriche Esercizio svolto. Discutere il comportameto delle segueti serie umeriche: a +! b [ ] log c log+ d log + e arcta f g h i l log log! 3! 4
AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Serie umeriche Esercizio svolto. Discutere il comportameto delle segueti serie umeriche: a +! b [ ] log c log+ d log + e arcta f g h i l log log! 3! 4
Analisi Matematica Soluzioni prova scritta parziale n. 1
 Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Risoluzione del compito n. 3 (Febbraio 2018/2)
 Risoluzioe del compito. 3 (Febbraio 08/ PROBLEMA a Determiate le soluzioi τ C dell equazioe τ iτ +=0. { αβ =4 b Determiate le soluzioi (α, β, co α, β C,delsistema α + β =i. c Determiate tutte le soluzioi
Risoluzioe del compito. 3 (Febbraio 08/ PROBLEMA a Determiate le soluzioi τ C dell equazioe τ iτ +=0. { αβ =4 b Determiate le soluzioi (α, β, co α, β C,delsistema α + β =i. c Determiate tutte le soluzioi
Analisi Matematica A e B Soluzioni prova scritta n. 4
 Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 5.7.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 5.7.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
ANALISI MATEMATICA 1. Funzioni elementari
 ANALISI MATEMATICA Fuzioi elemetari Trovare le soluzioi delle segueti disequazioi ) x + 4 5 > 8 + 5x 0 ) 5x + 0 > 0, x 4 < 0 3) x x 3 4) x + x + > 3 x + 4 5) 5x 4x x + )x ) 6) x x + > 0, x + 5x + 6 0,
ANALISI MATEMATICA Fuzioi elemetari Trovare le soluzioi delle segueti disequazioi ) x + 4 5 > 8 + 5x 0 ) 5x + 0 > 0, x 4 < 0 3) x x 3 4) x + x + > 3 x + 4 5) 5x 4x x + )x ) 6) x x + > 0, x + 5x + 6 0,
Siamo interessati a studiare la convergenza della serie e porremo come al solito:
 SERIE DI POTENZE Soo particolari serie di fuzioi, i cui termii soo moomi, evetualmete traslati: f (x) co f (x) =a (x x 0 ), a R, x 0 R, ossia dove a (x x 0 ) = a 0 + a 1 (x x 0 )+a 2 (x x 0 ) 2 +... x
SERIE DI POTENZE Soo particolari serie di fuzioi, i cui termii soo moomi, evetualmete traslati: f (x) co f (x) =a (x x 0 ), a R, x 0 R, ossia dove a (x x 0 ) = a 0 + a 1 (x x 0 )+a 2 (x x 0 ) 2 +... x
Serie numeriche e di funzioni - Esercizi svolti
 Serie umeriche e di fuzioi - Esercizi svolti Serie umeriche Esercizio. Discutere la covergeza delle serie segueti a) 3, b) 5, c) 4! (4), d) ( ) e. Esercizio. Calcolare la somma delle serie segueti a) (
Serie umeriche e di fuzioi - Esercizi svolti Serie umeriche Esercizio. Discutere la covergeza delle serie segueti a) 3, b) 5, c) 4! (4), d) ( ) e. Esercizio. Calcolare la somma delle serie segueti a) (
Soluzioni. 2 2n+1 3 2n. n=1. 3 2n 9. n=1. Il numero 2 può essere raccolto fuori dal segno di sommatoria: = 2. n=1 = = 8 5.
 60 Roberto Tauraso - Aalisi Calcolare la somma della serie Soluzioi + 3 R La serie può essere riscritta el modo seguete: + 4 3 9 Il umero può essere raccolto fuori dal sego di sommatoria: + 4 3 9 Si tratta
60 Roberto Tauraso - Aalisi Calcolare la somma della serie Soluzioi + 3 R La serie può essere riscritta el modo seguete: + 4 3 9 Il umero può essere raccolto fuori dal sego di sommatoria: + 4 3 9 Si tratta
Analisi Matematica 1 Matematica
 Aalisi Matematica 1 Matematica Secodo Compitio Luedì 30 Geaio 01 VERSIONE A Esercizio 1 (8 puti) Sia α R u parametro e si cosideri la serie di poteze complessa z. i) Calcolare il raggio di covergeza R
Aalisi Matematica 1 Matematica Secodo Compitio Luedì 30 Geaio 01 VERSIONE A Esercizio 1 (8 puti) Sia α R u parametro e si cosideri la serie di poteze complessa z. i) Calcolare il raggio di covergeza R
Analisi Matematica I modulo Soluzioni prova scritta preliminare n. 1
 Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Analisi Matematica II
 Corso di Laurea i Matematica Aalisi Matematica II Esercizi sulla covergeza uiforme e sulle serie di fuzioi/poteze Versioe del 28//206 Esercizi tratti dal Giusti Esercizio Giusti 3. e 3.3) Calcolare il
Corso di Laurea i Matematica Aalisi Matematica II Esercizi sulla covergeza uiforme e sulle serie di fuzioi/poteze Versioe del 28//206 Esercizi tratti dal Giusti Esercizio Giusti 3. e 3.3) Calcolare il
x n (1.1) n=0 1 x La serie geometrica è un esempio di serie di potenze. Definizione 1 Chiamiamo serie di potenze ogni serie della forma
 1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
Calcolo I - Corso di Laurea in Fisica - 31 Gennaio 2018 Soluzioni Scritto
 Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
1. Converge. La serie è a segno alterno. Non possiamo usare il criterio di assoluta convergenza, perché
 Soluzioi.. Coverge. La serie è a sego altero. No possiamo usare il criterio di assoluta covergeza, perché log log a = > + e il fatto che la serie i valore assoluto diverge o permette di trarre coclusioi
Soluzioi.. Coverge. La serie è a sego altero. No possiamo usare il criterio di assoluta covergeza, perché log log a = > + e il fatto che la serie i valore assoluto diverge o permette di trarre coclusioi
4 - Le serie Soluzioni. n + 3. n + 3. n + 2
 4 - Le serie Soluzioi Esercizio. Studiare la covergeza delle serie: + + 2 + cos!) 2 cosπ). Per la prima serie si ha 0 + + 2 + = 2. Dal mometo che la serie di termie geerico 2 è covergete serie armoica
4 - Le serie Soluzioi Esercizio. Studiare la covergeza delle serie: + + 2 + cos!) 2 cosπ). Per la prima serie si ha 0 + + 2 + = 2. Dal mometo che la serie di termie geerico 2 è covergete serie armoica
AM110 - ESERCITAZIONI V - VI. Esercizio svolto 1. Dimostrare che ogni insieme finito ha un massimo ed un minimo.
 AM110 - ESERCITAZIONI V - VI 16-18 OTTOBRE 2012 Esercizio svolto 1. Dimostrare che ogi isieme fiito ha u massimo ed u miimo. Sia A = {a 1,..., a } R. Dimostriamo che A ha u massimo si procede i maiera
AM110 - ESERCITAZIONI V - VI 16-18 OTTOBRE 2012 Esercizio svolto 1. Dimostrare che ogi isieme fiito ha u massimo ed u miimo. Sia A = {a 1,..., a } R. Dimostriamo che A ha u massimo si procede i maiera
Successioni di funzioni
 Successioi di fuzioi Successioi di fuzioi: covergeza putuale Defiizioe Sia I u isieme di umeri reali e sia ua successioe di fuzioi reali defiite i I : I R, I R. Si dice che Cioè f : I R, risulta coverge
Successioi di fuzioi Successioi di fuzioi: covergeza putuale Defiizioe Sia I u isieme di umeri reali e sia ua successioe di fuzioi reali defiite i I : I R, I R. Si dice che Cioè f : I R, risulta coverge
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Le successioi: itro Si cosideri la seguete sequeza di umeri:,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi 2 mesi i u allevameto!
Soluzioni degli esercizi del corso di Analisi Matematica I
 Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
Soluzioni degli esercizi di Analisi Matematica I
 Soluzioi degli esercizi di Aalisi Matematica I (Prof. Pierpaolo Natalii) Roberta Biachii 6 ovembre 2016 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x2 1 x + 1 π/3. 2. Dimostrare,
Soluzioi degli esercizi di Aalisi Matematica I (Prof. Pierpaolo Natalii) Roberta Biachii 6 ovembre 2016 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x2 1 x + 1 π/3. 2. Dimostrare,
Esecitazione AM2 n.1-a.a /10/06. Studiare la convergenza puntuale ed uniforme delle seguenti successioni di funzioni: 1.
 Esecitazioe AM.-A.A. 006-007- 0/0/06 Successioi di fuzioi Studiare la covergeza putuale ed uiforme delle segueti successioi di fuzioi:. f (x) = x +, x A R.. f (x) = si(x) +, x R. 3. f (x) = xe x, x [0,
Esecitazioe AM.-A.A. 006-007- 0/0/06 Successioi di fuzioi Studiare la covergeza putuale ed uiforme delle segueti successioi di fuzioi:. f (x) = x +, x A R.. f (x) = si(x) +, x R. 3. f (x) = xe x, x [0,
1. Serie numeriche. Esercizio 1. Studiare il carattere delle seguenti serie: n2 n 3 n ; n n. n n. n n (n!) 2 ; (2n)! ;
 . Serie umeriche Esercizio. Studiare il carattere delle segueti serie: ;! ;! ;!. Soluzioe.. Serie a termii positivi; cofrotiamola co la serie +, che è covergete: + + + 0. Pertato, per il criterio del cofroto
. Serie umeriche Esercizio. Studiare il carattere delle segueti serie: ;! ;! ;!. Soluzioe.. Serie a termii positivi; cofrotiamola co la serie +, che è covergete: + + + 0. Pertato, per il criterio del cofroto
2.5 Convergenza assoluta e non
 .5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
.5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
ANALISI MATEMATICA 1 Commissione L. Caravenna, V. Casarino, S. Zoccante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza
 ANALISI MATEMATICA Commissioe L. Caravea, V. Casario, S. occate Igegeria Gestioale, Meccaica e Meccatroica, Viceza Nome, Cogome, umero di matricola: Viceza, 6 Settembre 25 TEMA - parte B Esercizio ( puti).
ANALISI MATEMATICA Commissioe L. Caravea, V. Casario, S. occate Igegeria Gestioale, Meccaica e Meccatroica, Viceza Nome, Cogome, umero di matricola: Viceza, 6 Settembre 25 TEMA - parte B Esercizio ( puti).
SUCCESSIONI SERIE NUMERICHE pag. 1
 SUCCESSIONI SERIE NUMERICHE pag. Successioi RICHIAMI Ua successioe di elemeti di u isieme X è ua fuzioe f: N X. E covezioe scrivere f( ) = x, e idicare le successioi mediate la ifiitupla ordiata delle
SUCCESSIONI SERIE NUMERICHE pag. Successioi RICHIAMI Ua successioe di elemeti di u isieme X è ua fuzioe f: N X. E covezioe scrivere f( ) = x, e idicare le successioi mediate la ifiitupla ordiata delle
1 + 1 ) n ] n. < e nα 1 n
![1 + 1 ) n ] n. < e nα 1 n 1 + 1 ) n ] n. < e nα 1 n](/thumbs/66/54700563.jpg) Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
( 1) k+1 x k + R N+1 (x), k. 1 + x 10 2, 5 R N+1 ( 1 3 ) ) )
 Esercizi di Aalisi - Alberto Valli - AA 05/06 - Foglio 8. Fatevi veire u idea per calcolare log48 alla secoda cifra decimale. Lo sviluppo di Taylor di log( + ) è covergete per solo per (,]. Duque bisoga
Esercizi di Aalisi - Alberto Valli - AA 05/06 - Foglio 8. Fatevi veire u idea per calcolare log48 alla secoda cifra decimale. Lo sviluppo di Taylor di log( + ) è covergete per solo per (,]. Duque bisoga
Analisi Matematica I Soluzioni del tutorato 2
 Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
 ANALISI MATEMATICA 1 Area dell Igegeria dell Iformazioe Appello del 18.9.17 TEMA 1 Esercizio 1 Si cosideri la fuzioe fx) := 3x log x. i) Determiare il domiio D e studiare le evetuali simmetrie ed il sego
ANALISI MATEMATICA 1 Area dell Igegeria dell Iformazioe Appello del 18.9.17 TEMA 1 Esercizio 1 Si cosideri la fuzioe fx) := 3x log x. i) Determiare il domiio D e studiare le evetuali simmetrie ed il sego
Corso di Analisi Matematica 1 - professore Alberto Valli
 Uiversità di Treto - Corso di Laurea i Igegeria Civile e Igegeria per l Ambiete e il Territorio - 07/8 Corso di Aalisi Matematica - professore Alberto Valli 8 foglio di esercizi - 5 ovembre 07 Taylor,
Uiversità di Treto - Corso di Laurea i Igegeria Civile e Igegeria per l Ambiete e il Territorio - 07/8 Corso di Aalisi Matematica - professore Alberto Valli 8 foglio di esercizi - 5 ovembre 07 Taylor,
SERIE DI POTENZE. n=0 a n z n.
 SERIE DI POTENZE 1. Covergeza putuale Data ua successioe di coefficieti (a ) N, a C, e dato u cetro w 0, la relativa serie di poteze è la serie di fuzioi a (z w 0 ) a 0 + a 1 (z w 0 ) + + a (z w 0 ) +.
SERIE DI POTENZE 1. Covergeza putuale Data ua successioe di coefficieti (a ) N, a C, e dato u cetro w 0, la relativa serie di poteze è la serie di fuzioi a (z w 0 ) a 0 + a 1 (z w 0 ) + + a (z w 0 ) +.
Esercizi sull estremo superiore ed inferiore
 AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sull estremo superiore ed iferiore Esercizio svolto. Dire se i segueti isiemi soo limitati iferiormete o superiormete ed, i caso affermativo, trovare l estremo
AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sull estremo superiore ed iferiore Esercizio svolto. Dire se i segueti isiemi soo limitati iferiormete o superiormete ed, i caso affermativo, trovare l estremo
I appello - 11 Dicembre 2006
 Facoltà di Igegeria - Corso di Laurea i Igegeria Civile A.A. 006/007 I appello - Dicembre 006 ) Calcolare il seguete ite: [ ( )] + cos. + ) Data la fuzioe f() = e +, < 0, 0, =, =,,..., log( + ), 0,, =,,...,
Facoltà di Igegeria - Corso di Laurea i Igegeria Civile A.A. 006/007 I appello - Dicembre 006 ) Calcolare il seguete ite: [ ( )] + cos. + ) Data la fuzioe f() = e +, < 0, 0, =, =,,..., log( + ), 0,, =,,...,
Quarto Compito di Analisi Matematica Corso di laurea in Informatica, corso B 5 Luglio Soluzioni. z 2 = 3 4 i. a 2 b 2 = 3 4
 Quarto Compito di Aalisi Matematica Corso di laurea i Iformatica, corso B 5 Luglio 016 Soluzioi Esercizio 1 Determiare tutti i umeri complessi z tali che z = 3 4 i. Soluzioe. Scrivedo z = a + bi, si ottiee
Quarto Compito di Aalisi Matematica Corso di laurea i Iformatica, corso B 5 Luglio 016 Soluzioi Esercizio 1 Determiare tutti i umeri complessi z tali che z = 3 4 i. Soluzioe. Scrivedo z = a + bi, si ottiee
Lezioni di Matematica 1 - I modulo
 Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
Serie di Fourier / Esercizi svolti
 Serie di Fourier / Esercizi svolti ESERCIZIO. da Si cosideri la fuzioe f : R R, periodica di periodo e data ell itervallo (, ] se
Serie di Fourier / Esercizi svolti ESERCIZIO. da Si cosideri la fuzioe f : R R, periodica di periodo e data ell itervallo (, ] se
Svolgimento degli esercizi del Capitolo 4
 4. Michiel Bertsch, Roberta Dal Passo, Lorezo Giacomelli Aalisi Matematica 2 a edizioe Svolgimeto degli esercizi del Capitolo 4 Il limite segue dal teorema del cofroto: e / 0 per. 4.2 0
4. Michiel Bertsch, Roberta Dal Passo, Lorezo Giacomelli Aalisi Matematica 2 a edizioe Svolgimeto degli esercizi del Capitolo 4 Il limite segue dal teorema del cofroto: e / 0 per. 4.2 0
Tutoraggio AM1 17/12/2015. sin(x) arctan(x) 2) lim sup / inf x 0 + cos(x) sin( 1 x ) e x2 cos 2 (x 3 ) x 2 + ln(3x + 2) δ(x) δ(x) =
 Tutoraggio AM1 17/12/2015 Per la parte teorica sui if e sup vedi le ote su iti iferiori e superiori di fuzioi. A) Date due successioi a },b }, mostrare le segueti proprietà (escludere i casi i cui si abbia
Tutoraggio AM1 17/12/2015 Per la parte teorica sui if e sup vedi le ote su iti iferiori e superiori di fuzioi. A) Date due successioi a },b }, mostrare le segueti proprietà (escludere i casi i cui si abbia
SUCCESSIONI e LIMITI DI SUCCESSIONI. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Successioni cap3b.pdf 1
 SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 2018/19 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X =
Esercizi sui limiti di successioni
 AM0 - AA 03/4 ALFONSO SORRENTINO Esercizi sui iti di successioi Esercizio svolto a) Usado la defiizioe di ite, dimostare che: + 3 si π cos e ) e b) 0 Soluzioe Comiciamo da a) Vogliamo dimostrare che: ε
AM0 - AA 03/4 ALFONSO SORRENTINO Esercizi sui iti di successioi Esercizio svolto a) Usado la defiizioe di ite, dimostare che: + 3 si π cos e ) e b) 0 Soluzioe Comiciamo da a) Vogliamo dimostrare che: ε
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER
 TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
Politecnico di Milano Ingegneria Industriale Analisi 2/II
 Politecico di Milao Igegeria Idustriale Aalisi /II Test di autovalutazioe. Sia S = ( artg +. (a Stabilire se la serie data coverge assolutamete. (b Stabilire se la serie data coverge.. Sia L lo spazio
Politecico di Milao Igegeria Idustriale Aalisi /II Test di autovalutazioe. Sia S = ( artg +. (a Stabilire se la serie data coverge assolutamete. (b Stabilire se la serie data coverge.. Sia L lo spazio
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
Esercizi su serie numeriche - svolgimenti
 Esercizi su serie umeriche - svolgimeti Osserviamo che vale la doppia diseguagliaza + si, e quidi la serie è a termii positivi Duque la somma della serie esiste fiita o uguale a + Ioltre valgoo le diseguagliaze
Esercizi su serie umeriche - svolgimeti Osserviamo che vale la doppia diseguagliaza + si, e quidi la serie è a termii positivi Duque la somma della serie esiste fiita o uguale a + Ioltre valgoo le diseguagliaze
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 42-57
 Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Serie numeriche. Esercizi
 Serie umeriche. Esercizi Mauro Saita, aprile 204. Idice Serie umeriche.. Serie a termii defiitivamete positivi..............................2 Serie a termii di sego altero.................................
Serie umeriche. Esercizi Mauro Saita, aprile 204. Idice Serie umeriche.. Serie a termii defiitivamete positivi..............................2 Serie a termii di sego altero.................................
ESAME DI MATEMATICA I Modulo di Analisi Matematica Corso 3 Anno Accademico 2008/2009 Docente: R. Argiolas
 ESAME DI MATEMATICA I Modulo di Aalisi Matematica Corso Ao Accademico 8/9 Docete: R Argiolas Cogome Matricola Febbraio 9 ore 9 Aula C Nome Corso voto Esercizio Assegata la fuzioe f ( arcta a Si determii
ESAME DI MATEMATICA I Modulo di Aalisi Matematica Corso Ao Accademico 8/9 Docete: R Argiolas Cogome Matricola Febbraio 9 ore 9 Aula C Nome Corso voto Esercizio Assegata la fuzioe f ( arcta a Si determii
ESERCIZI - FASCICOLO 1
 ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
ESERCIZI - FASCICOLO 1 Esercizio 1 Sia (Ω, A) uo spazio misurabile. Se (A ) 1 è ua successioe di eveti (= elemeti di A), defiiamo lim sup A := A k lim if A = A k. Mostrare che =1 k= (lim sup A ) c = lim
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
 ANALISI MATEMATICA Area dell Igegeria dell Iformazioe Appello del 7.9.8 Esercizio Si cosideri la fuzioe f() := TEMA {e 3 per per =. i) Determiare il domiio D, le evetuali simmetrie e studiare il sego di
ANALISI MATEMATICA Area dell Igegeria dell Iformazioe Appello del 7.9.8 Esercizio Si cosideri la fuzioe f() := TEMA {e 3 per per =. i) Determiare il domiio D, le evetuali simmetrie e studiare il sego di
Scritto di Analisi Matematica IV per Matematica Anno Accademico 2016/17 15/02/2018
 o ccademico 2016/17 15/02/2018 COG 1) a) Sia f (x) = x + si(x), e sia g a, (x) = f (x), a > 0. Dire, al variare di a > 0 se a la successioe g,a coverge putualmete per +, e se il limite è uiforme. b) Dire
o ccademico 2016/17 15/02/2018 COG 1) a) Sia f (x) = x + si(x), e sia g a, (x) = f (x), a > 0. Dire, al variare di a > 0 se a la successioe g,a coverge putualmete per +, e se il limite è uiforme. b) Dire
Analisi Matematica II
 Uiversità degli Studi di Udie Ao Accademico 016/017 Dipartimeto di Scieze Matematiche, Iformatiche e Fisiche Corso di Laurea i Matematica Aalisi Matematica II Prova parziale del 6 febbraio 017 NB: scrivere
Uiversità degli Studi di Udie Ao Accademico 016/017 Dipartimeto di Scieze Matematiche, Iformatiche e Fisiche Corso di Laurea i Matematica Aalisi Matematica II Prova parziale del 6 febbraio 017 NB: scrivere
e 6x = 2(t + 1) 1 + c tan x (funzione razionale) si scompone come: t (log t 1 log t + 1 ) t=9
 Esercizi di Aalisi - Alberto Valli - AA 5/6 - Foglio. Calcolate tramite cambiameto di variabile ciascuo dei segueti itegrali : i / six + dx ii log log e 6x e x dx iii / π/ cos 5 xsix cos x dx. Soluzioe.
Esercizi di Aalisi - Alberto Valli - AA 5/6 - Foglio. Calcolate tramite cambiameto di variabile ciascuo dei segueti itegrali : i / six + dx ii log log e 6x e x dx iii / π/ cos 5 xsix cos x dx. Soluzioe.
1. a n = n 1 a 1 = 0, a 2 = 1, a 3 = 2, a 4 = 3,... Questa successione cresce sempre piú al crescere di n e vedremo che {a n } diverge.
 Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Il caso di coefficienti decrescenti e infinitesimi
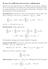 Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Il caso di coefficieti decresceti e ifiitesimi Quado ua serie trigoometrica ha coefficieti reali, decresceti e ifiitesimi, le sue proprietà di covergeza soo particolarmete iteressati. Iiziamo questa descrizioe
Esponenziale complesso
 Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
11 IL CALCOLO DEI LIMITI
 IL CALCOLO DEI LIMITI Il calcolo di u ite spesso si ricodurrà a trattare separatamete iti più semplici, su cui poi si farao operazioi algebriche. Dato che uo o più di questi iti possoo essere ±, bisoga
IL CALCOLO DEI LIMITI Il calcolo di u ite spesso si ricodurrà a trattare separatamete iti più semplici, su cui poi si farao operazioi algebriche. Dato che uo o più di questi iti possoo essere ±, bisoga
SECONDO ESONERO DI AM1 10/01/ Soluzioni
 Esercizio. Calcolare i segueti iti: Razioalizzado si ottiee SECONDO ESONERO DI AM 0/0/2008 - Soluzioi 2 + 2, 2 + 2 = 2 + 2 + 2 + 2 = Per il secodo ite ci soo vari modi, e mostro tre. Ora ( ) ( + si = +
Esercizio. Calcolare i segueti iti: Razioalizzado si ottiee SECONDO ESONERO DI AM 0/0/2008 - Soluzioi 2 + 2, 2 + 2 = 2 + 2 + 2 + 2 = Per il secodo ite ci soo vari modi, e mostro tre. Ora ( ) ( + si = +
Analisi Matematica I
 Uiversità di Pisa - orso di Laurea i Igegeria Edile-rchitettura alisi Matematica I Pisa, febbraio Domada La derivata della fuzioe f) log ) si è ) log )si B) log )cos ) log ) si cos loglog ) + si ) log
Uiversità di Pisa - orso di Laurea i Igegeria Edile-rchitettura alisi Matematica I Pisa, febbraio Domada La derivata della fuzioe f) log ) si è ) log )si B) log )cos ) log ) si cos loglog ) + si ) log
Equazioni differenziali
 Equazioi differeziali Defiizioe 1 Si chiama equazioe differeziale u tipo particolare di equazioe fuzioale, ella quale la fuzioe icogita compare isieme ad alcue sue derivate, ossia u equazioe ella quale,
Equazioi differeziali Defiizioe 1 Si chiama equazioe differeziale u tipo particolare di equazioe fuzioale, ella quale la fuzioe icogita compare isieme ad alcue sue derivate, ossia u equazioe ella quale,
Limiti di successioni
 Limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 20 ottobre 2015 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Itroduzioe
Limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 20 ottobre 2015 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Itroduzioe
n 1 = n b) {( 1) n } = c) {n!} In questo caso la successione è definita per ricorrenza: a 0 = 1, a n = n a n 1 per ogni n 1.
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi 0: Riferimeti: R.Adams, Calcolo Differeziale - Si cosiglia vivamete di fare gli esercizi del testo. Successioi umeriche:
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi 0: Riferimeti: R.Adams, Calcolo Differeziale - Si cosiglia vivamete di fare gli esercizi del testo. Successioi umeriche:
SERIE NUMERICHE. Test di autovalutazione. 1+a 2
 SERIE NUMERICHE Test di autovalutazioe. E data la serie: dove a R. Allora: ( ) 3a +a (a) se a = la serie coverge a (b) se a = 3 la somma della serie vale 5 (c) se a = 5 la serie diverge a (d) se a 0 la
SERIE NUMERICHE Test di autovalutazioe. E data la serie: dove a R. Allora: ( ) 3a +a (a) se a = la serie coverge a (b) se a = 3 la somma della serie vale 5 (c) se a = 5 la serie diverge a (d) se a 0 la
AM110 - ESERCITAZIONI XIII - XIV. (Per la dimostrazione discussa durante l esercitazione si veda ad esempio il libro di testo)
 AM0 - ESERCITAZIONI XIII - XIV 26-27 NOVEMBRE 202 Teorema Criterio di Leibiz. Si cosideri la serie a tale che: i a 0 per ogi ; ii a 0 per + ; iii a + a per ogi. Allora, la serie è covergete. Per la dimostrazioe
AM0 - ESERCITAZIONI XIII - XIV 26-27 NOVEMBRE 202 Teorema Criterio di Leibiz. Si cosideri la serie a tale che: i a 0 per ogi ; ii a 0 per + ; iii a + a per ogi. Allora, la serie è covergete. Per la dimostrazioe
Università degli Studi della Calabria Facoltà di Ingegneria. 26 giugno 2012
 Uiversità degli Studi della Calabria Facoltà di Igegeria Correzioe della Secoda Prova Scritta di alisi Matematica 2 giugo 202 cura dei Prof. B. Sciuzi e L. Motoro. Secoda Prova Scritta di alisi Matematica
Uiversità degli Studi della Calabria Facoltà di Igegeria Correzioe della Secoda Prova Scritta di alisi Matematica 2 giugo 202 cura dei Prof. B. Sciuzi e L. Motoro. Secoda Prova Scritta di alisi Matematica
Esercitazioni di Geometria II
 Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
SOLUZIONI COMPITO del 04/02/2016 ANALISI MATEMATICA I - 9 CFU MECCANICA TEMA A
 SOLUZIONI COMPITO del 0/0/06 ANALISI MATEMATICA I - 9 CFU MECCANICA TEMA A Esercizio Osserviamo, iazitutto, che la serie proposta è ua serie a termii o egativi. Applicado il criterio della radice, dopo
SOLUZIONI COMPITO del 0/0/06 ANALISI MATEMATICA I - 9 CFU MECCANICA TEMA A Esercizio Osserviamo, iazitutto, che la serie proposta è ua serie a termii o egativi. Applicado il criterio della radice, dopo
Successioni e limiti di successioni
 Successioi e limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 24 ottobre 2016 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva
Successioi e limiti di successioi Aalisa Cesaroi, Paola Maucci e Alvise Sommariva Uiversità degli Studi di Padova Dipartimeto di Matematica 24 ottobre 2016 Aalisa Cesaroi, Paola Maucci e Alvise Sommariva
Compito di Matematica II - 12 Settembre 2017
 Compito di Matematica II - Settembre 7 Corso di Laurea i Ottica e Optometria - A.A. 6/7 Soluzioi degli esercizi. Esercizio. a) Il domiio C è il cerchio di raggio uitario. La fuzioe fx y) = x + y è defiita
Compito di Matematica II - Settembre 7 Corso di Laurea i Ottica e Optometria - A.A. 6/7 Soluzioi degli esercizi. Esercizio. a) Il domiio C è il cerchio di raggio uitario. La fuzioe fx y) = x + y è defiita
Esercizi di approfondimento di Analisi IA
 Esercizi di approfodimeto di Aalisi IA 4 geaio 017 1 Estremo superiore/iferiore, classi cotigue, archimedeità 1.1. Mostrare che A = {x R : x > 0, x < } ha u estremo superiore ξ, ed è ξ =. 1.. Siao A, B
Esercizi di approfodimeto di Aalisi IA 4 geaio 017 1 Estremo superiore/iferiore, classi cotigue, archimedeità 1.1. Mostrare che A = {x R : x > 0, x < } ha u estremo superiore ξ, ed è ξ =. 1.. Siao A, B
9 LIMITI DI SUCCESSIONI NUMERICHE
 9 LIMITI DI SUCCESSIONI NUMERICHE Iiziamo ora ad esamiare gli argometi veri e propri di questa prima parte del corso, i cui svilupperemo gli strumeti per giugere a descrivere soddisfacetemete le proprietà
9 LIMITI DI SUCCESSIONI NUMERICHE Iiziamo ora ad esamiare gli argometi veri e propri di questa prima parte del corso, i cui svilupperemo gli strumeti per giugere a descrivere soddisfacetemete le proprietà
(x log x) n2. (14) n + log n
 Facoltà di Scieze Matematiche Fisiche e Naturali- Aalisi Matematica A (c.l.t. i Fisica) Prova parziale del 8 Novembre 20 Svolgere gli esercizi segueti. Studiare il domiio ed il comportameto della serie
Facoltà di Scieze Matematiche Fisiche e Naturali- Aalisi Matematica A (c.l.t. i Fisica) Prova parziale del 8 Novembre 20 Svolgere gli esercizi segueti. Studiare il domiio ed il comportameto della serie
6 - Serie numeriche. n=1
 6 - Serie umeriche Ultimo aggiorameto: 9 ottobre 09. Premessa Può la somma di ifiiti umeri dare come risultato ua quatità fiita? È quello che ci si chiede studiado le serie umeriche. Vediamo u esempio:
6 - Serie umeriche Ultimo aggiorameto: 9 ottobre 09. Premessa Può la somma di ifiiti umeri dare come risultato ua quatità fiita? È quello che ci si chiede studiado le serie umeriche. Vediamo u esempio:
Esercizi di Calcolo delle Probabilità Foglio 7
 Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Esercizi di Calcolo delle Probabilità Foglio 7 David Barbato Esercizio. Siao Y e X } N variabili aleatorie idipedeti e co distribuzioe espoeziale di parametro λ =. Siao ioltre: W := maxy, X } N T := miw
Le successioni: intro
 Le successioi: itro Si cosideri la seguete sequeza di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi mesi i u allevameto! Si
Le successioi: itro Si cosideri la seguete sequeza di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fiboacci. Essa rappreseta il umero di coppie di coigli preseti ei primi mesi i u allevameto! Si
Prova d esame di Calcolo delle Probabilità 02/07/2011
 Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
1 Successioni numeriche
 Aalisi Matematica 2 Successioi umeriche CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 5 SERIE NUMERICHE Chiamiamo successioe di umeri reali ua fuzioe a valori reali defiita su N oppure
Aalisi Matematica 2 Successioi umeriche CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 5 SERIE NUMERICHE Chiamiamo successioe di umeri reali ua fuzioe a valori reali defiita su N oppure
Elementi della teoria delle serie numeriche
 Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
Elemeti della teoria delle serie umeriche Geeralita Lo studio delle serie costituisce ua sistemazioe rigorosa del cocetto di somma di ua successioe (ifiita) di addedi : sia (a ) N ua successioe i R. Vogliamo
