MATEMATICA FINANZIARIA
|
|
|
- Cristina Scotti
- 10 anni fa
- Просмотров:
Транскрипт
1 TETI FINNZIRI. Defiizioi 2. Iteesse semplice 3. Iteesse composto cotiuo 4. Iteesse composto discotiuo auo Spostameto dei valoi el tempo ualità Peiodicità 5. Iteesse composto discotiuo covetibile atematica fiaziaia
2 DEFINIZIONE DI INTERESSE Pezzo d uso del ispamio sottofoma di capitale idiffeeziato (la moeta). DEFINIZIONE DI SGGIO DI INTERESSE Iteesse dell uità di capitale ( lia) ell uità di tempo ( ao) atematica fiaziaia 2
3 ODLIT DI DETERINZIONE DELL INTERESSE SEPLIE NNUO INTERESSE DISONTINUO OPOSTO ONVERTIBILE ONTINUO atematica fiaziaia 3
4 INTERESSE SEPLIE Gli iteessi matuati dal capitale i u dato tempo NON si sommao co il capitale, el calcolo degli iteessi del peiodo successivo. I alte paole, soo ifuttifei. I o I Iteesse matuato o apitale iiziale Saggio di iteesse peiodo i ai (gg/365 o m/2) atematica fiaziaia 4
5 INTERESSE SEPLIE Fomule deivate: I o I o I o atematica fiaziaia 5
6 DEFINIZIONE DI ONTNTE Il motate di u capitale è la somma del capitale e dei elativi iteessi matuati i u detemiato peiodo di tempo I Il motate uitaio è la somma di u capitale di lia e dei elativi iteessi matuati i u ao atematica fiaziaia 6
7 atematica fiaziaia 7 INTERESSE SEPLIE alcolo del motate: ) ( I o o o o ) ( o Fomule deivate: o o o
8 SONTO E la somma che si sottae ad u capitale futuo pe edelo attuale Scoto fiaziaio semplice Sc o Scoto commeciale Sc atematica fiaziaia 8
9 DIFFERENZ TR SONTO FINNZIRIO SEPLIE E SONTO OERILE Lo scoto fiaziaio è calcolato sul capitale: Sc Lo scoto commeciale è calcolato sul motate, uidi è più elevato: Sc Lo scoto commeciale può essee adottato solo pe bevi peiodi di tempo. atematica fiaziaia 9
10 INTERESSE OPOSTO Gli iteessi matuati dal capitale i u dato peiodo si sommao al capitale stesso e divegoo futtifei. L iteesse composto può essee: -otiuo -Discotiuo auo -Discotiuo covetibile atematica fiaziaia
11 INTERESSE OPOSTO ONTINUO Gli iteessi si covetoo i capitale ad ogi istate. Seppu teoicamete cocepibile, o tova alcua applicazioe ella patica estimativa. atematica fiaziaia
12 INTERESSE OPOSTO DISONTINUO NNUO Gli iteessi vegoo aggiuti al capitale che li ha podotti ua volta l ao I ( ) I iteesse matuato saggio d iteesse peiodo di ai capitale iiziale atematica fiaziaia 2
13 INTERESSE OPOSTO DISONTINUO NNUO alcolo del motate lla fie del pimo ao: I ( ) lla fie del secodo ao: 2 2 I2. ( ) ( )( ) ( ) I geeale pe l ao eesimo ( ). Fomule deivate I ) ( I iteesse matuato saggio d iteesse peiodo di ai capitale iiziale atematica fiaziaia 3
14 SONTO FINNZIRIO OPOSTO Sc atematica fiaziaia 4
15 INTERESSE OPOSTO DISONTINUO ONVERTIBILE Gli iteessi matuao più volte all ao (t) ma sempe i peiodi defiiti. L iteesse composto covetibile viee idicato mediate la fissazioe di u saggio auo omiale a cui coispode u saggio covetibile pai al saggio auo omiale diviso il umeo di volte che l iteesse matua ell ao: c Si applicao le fomule dell iteesse composto discotiuo auo co le segueti modifiche: ) c t t c t Dove: c saggio covetibile t umeo di volte i cui l iteesse si covete i u ao c umeo di volte i cui l iteesse covetibile matua ell iteo peiodo 2) atematica fiaziaia 5
16 INTERESSE OPOSTO DISONTINUO ONVERTIBILE alcolo del motate: Fomule deivate: I ( ) t t ( ) t ( t ) t t atematica fiaziaia 6 t t
17 INTERESSE OPOSTO DISONTINUO ONVERTIBILE alcolo del saggio di iteesse auo effettivo a patie dal saggio di iteesse omiale. Il saggio effettivo è sempe maggioe ispetto a uello omiale. Pe Lia ao I I t t effettivo omiale t ( ) t atematica fiaziaia 7
18 SPOSTENTO DEI PITLI NEL TEPO: POSTIIPZIONE E NTIIPZIONE NTIIPZIONE POSTIIPZIONE VLORE $ ONTNTE SONTTO NON SI POSSONO DDIZIONRE, SOTTRRRE O ONFRONTRE VLORI DIFFERENTI NEL TEPO OEFFIIENTI DI POSTIIPZIONE Regime a iteesse semplice: () Regime a iteesse composto: Regime a iteesse semplice: OEFFIIENTI DI NTIIPZIONE ( ) Regime a iteesse composto: atematica fiaziaia 8
19 INTERESSE OPOSTO DISONTINUO NNUO TEPO IPIEGTO D UN PITLE PER SGGIO 2% 3% 4% 5% 6% 7% 8% 9% % RDDOPPIRE ( 2) NNI atematica fiaziaia 9
20 SUGGERIENTI PRTII DI VERIFI ) ttaveso la posticipazioe si ottiee sempe u valoe supeioe al valoe dato (poiché il saggio è positivo): > > 2) ttaveso l aticipazioe si ottiee sempe u valoe ifeioe al valoe dato: < < atematica fiaziaia 2
21 VLORI PERIODII Si defiiscoo valoi peiodici uei valoi costati (icavi o costi) che si veificao ad itevalli di tempo egolai. Nomalmete essi soo distiti i: aualità e peiodicità Le aualità soo valoi che si ipetoo ad itevalli egolai di u ao. Le peiodicità soo valoi che si ipetoo ogi detemiato umeo di ai. I valoi peiodici possoo essee: -Rispetto alla scadeza, posticipati o aticipati, a secoda che si veifichio alla fie o all iizio di ogi peiodo. -Rispetto alla duata, limitati o illimitati a secoda che si veifichio pe u mometo fiito o idefiito di ai. atematica fiaziaia 2
22 PROBLEI UULZIONE INIZILE UULZIONE FINLE UULZIONE INTEREDI LIITTE X X X POSTIIPTE ILLIITTE X OSTNTI NNULIT E PERIODIIT NTIIPTE LIITTE ILLIITTE X X X X VRIBILI UULZIONE DEI VLORI ON IL ETODO DELLO SPOSTENTO DEI VLORI NEL TEPO atematica fiaziaia 22
23 NNULIT OSTNTI POSTIIPTE LIITTE Soo edite (o costi) di uguale valoe, che si ealizzao alla fie di ogi ao pe u detemiato umeo di ai. Te soo i poblemi elativi alle aualità costati posticipate limitate: -ccumulazioe Fiale Si ottiee posticipado alla fie del del peiodo le vaie aualità e sommadole assieme aualità umeo ai -ccumulazioe iiziale Si ottiee ifeedo le aualità all ao zeo del peiodo e sommadole assieme a -ccumulazioe itemedia Si ottiee ifeedo le aualità ad u ao itemedio m del peiodo m m Si può icavae dall' scotadol a all' attualità co il coefficie te oppue m m atematica fiaziaia 23
24 atematica fiaziaia 24 NNULIT OSTNTI POSTIIPTE LIITTE Detemiazioe dell accumulazioe fiale a a a a a a )... ( a a a a a a [si tatta di ua pogessioe geometica co agioe *, si isolve moltiplicado l ultimo temie pe la agioe meo il pimo temie e dividedo tutto pe la agioe meo uo] a a a a * La agioe i ua pogessioe geometica è data dal appoto ta u temie e uello successivo
25 NNULIT OSTNTI NTIIPTE LIITTE Soo edite (o costi) di uguale valoe, che si ealizzao all iizio di ogi ao pe u detemiato umeo di ai. che pe le aualità costati aticipate limitate te soo i poblemi: -ccumulazioe fiale Si ottiee posticipado alla fie del peiodo le vaie aualità e sommadole assieme a -ccumulazioe iiziale Si ottiee ifeedo le aualità dell ao zeo del peiodo e sommadole assieme a. -ccumulazioe itemedia Si ottiee ifeedo le aualità ad u ao itemedio del peiodo m m oppue m m atematica fiaziaia 25
26 NNULIT OSTNTI NTIIPTE LIITTE Detemiazioe dell accumulazioe fiale: Si icava co u pocedimeto matematico aalogo a uello utilizzato pe le aualità posticipate. Più facilmete si può ossevae che le aualità aticipate si veificao u ao pima di uelle posticipate. Basteà, uidi, posticipae di u ao l aualità mediate il coefficiete e applicae il coefficiete di accumulazioe già utilizzato pe le aualità posticipate. 2 a a a - a a atematica fiaziaia 26
27 NNULIT OSTNTI POSTIIPTE ILLIITTE Soo edite (o costi) di uguale valoe, che si ealizzao alla fie di ogi ao pe u tempo ifiitamete lugo. Pe le aualità costati posticipate illimitate sussiste solo u poblema: - ccumulazioe iiziale La fomula è aaloga alla I Tali fomule soo chiamate fomule di capitalizzazioe deiedditi aui, costati, posticipati, illimitati (ogi volta che si divide il eddito medio auo costate posticipato di u capitale pe il suo saggio di iteesse, si ottiee il valoe del capitale capace di geeae tale eddito). a atematica fiaziaia 27
28 atematica fiaziaia 28 NNULIT OSTNTI POSTIIPTE ILLIITTE Detemiazioe dell accumulazioe iiziale a a a a ) lim( lim lim
29 NNULIT OSTNTI NTIIPTE ILLIITTE Soo edite (o costi) di uguale valoe, che si ealizzao all iizio di ogi ao pe u tempo ifiitamete lugo. che pe le aualità costati aticipate illimitate si può palae solo di: - ccumulazioe iiziale a Si ottiee facilmete dall aaloga fomula elativa alle aualità posticipate illimitate, teedo coto che le aualità aticipate si veificao u ao pima di uelle posticipate. E sufficiete, uidi, posticipae di u ao l aualità aticipata. atematica fiaziaia 29
30 PERIODIIT (O POLINNULIT ) Simboli: umeo ai del peiodo (itevallo di tempo che itecoe ta il veificasi di due successivi valoi peiodici) t umeo dei peiodi Peiodicità costati posticipate limitate: accumulazioe fiale t t p p t Peiodicità costati posticipate limitate: accumulazioe iiziale Peiodicità costati aticipate limitate: accumulazioe fiale t p t t atematica fiaziaia 3
31 atematica fiaziaia 3 PERIODIIT (O POLINNULIT ) 2 Peiodicità costati aticipate limitate: accumulazioe iiziale t t p Peiodicità costati posticipate illimitate: accumulazioe iiziale p Peiodicità costati aticipate illimitate: accumulazioe iiziale p
32 LOLO DELL INTERESSE RELE IN PRESENZ DI INFLZIONE Il edimeto eale degli ivestimeti fiaziai si ottiee el seguete modo: Dove: tasso di edimeto eale tasso di edimeto omiale i tasso di iflazioe oetemete si usa ache la fomula: i i Tale fomula è scoetta ma foisce isultati appossimativamete simili alla pecedete se usata pe tassi d iflazioe bassi e peiodi bevi i atematica fiaziaia 32
33 atematica fiaziaia 33 LOLO DELL INTERESSE RELE DIOSTRZIONE La fomula pe il calcolo di edimeto eale può essee icavata da uella pe il calcolo del motate eale: ( ) i ( ) ( ) ( ) ( ) i ; ) ( Poiché: Possiamo scivee: Dividedo etambi i membi pe e facedo la adice -esima i i i i i i o: tasso eale; tasso omiale; i tasso d iflazioe; motate omiale; motate eale
34 STRUENTI PRTII DI LOLO Il tadizioale suppoto pe il calcolo fiaziaio soo le tavole fiaziaie. Le tavole fiaziaie cotegoo i valoi calcolati, pe divesi valoi di ed, dei picipali coefficieti usati el calcolo fiaziaio (vedi tavole). Uo stumeto più avazato soo le calcolatici fiaziaie. Le calcolatici fiaziaie cotegoo le picipali fuzioi fiaziaie. Pemettoo la iceca apida del valoe di paameti che ichiedeebbeo lughi calcoli mauali. d esempio il valoe di dati a, ed elle fomule delle aualità, che può essee tovato solo pe tetativi. I fogli elettoici (Excel) pemettoo l esecuzioe delle più comui opeazioi fiaziaie, mediate la scittua delle elative fomule o l uso delle fuzioi fiaziaie (vedi eleco fuzioi fiaziaie di Excel) atematica fiaziaia 34
CALCOLO FINANZIARIO DEFINIZIONE DI INTERESSE. Prezzo d uso del risparmio sotto forma di capitale indifferenziato (la moneta).
 LOLO FINNZIRIO. Defiizioi 2. Iteesse semplice 3. Iteesse composto cotiuo 4. Iteesse composto discotiuo auo Spostameto dei valoi el tempo ualità Peiodicità 5. Iteesse composto discotiuo covetibile 6. pplicazioi
LOLO FINNZIRIO. Defiizioi 2. Iteesse semplice 3. Iteesse composto cotiuo 4. Iteesse composto discotiuo auo Spostameto dei valoi el tempo ualità Peiodicità 5. Iteesse composto discotiuo covetibile 6. pplicazioi
Matematica finanziaria applicata all estimo
 Matematica fiaziaia applicata all estimo Pate Uità Nozioi di iteesse e di capitale Uità 2 Aualità costati Uità 3 Peiodicità o poliaualità Uità 4 Poblemi sui edditi tasitoi e pemaeti di u immobile Itoduzioe
Matematica fiaziaia applicata all estimo Pate Uità Nozioi di iteesse e di capitale Uità 2 Aualità costati Uità 3 Peiodicità o poliaualità Uità 4 Poblemi sui edditi tasitoi e pemaeti di u immobile Itoduzioe
Successioni e Progressioni
 Successioi e Pogessioi Ua successioe è ua sequeza odiata di umei appateeti ad u isieme assegato: ad esempio, si possoo avee successioi di umei itei, azioali, eali, complessi Il pimo elemeto della sequeza
Successioi e Pogessioi Ua successioe è ua sequeza odiata di umei appateeti ad u isieme assegato: ad esempio, si possoo avee successioi di umei itei, azioali, eali, complessi Il pimo elemeto della sequeza
Appunti sulla MATEMATICA FINANZIARIA
 INTRODUZIONE Apputi sulla ATEATIA FINANZIARIA La matematica fiaziaria si occupa delle operazioi fiaziarie. Per operazioe fiaziaria si itede quella operazioe ella quale avviee uo scambio di capitali, itesi
INTRODUZIONE Apputi sulla ATEATIA FINANZIARIA La matematica fiaziaria si occupa delle operazioi fiaziarie. Per operazioe fiaziaria si itede quella operazioe ella quale avviee uo scambio di capitali, itesi
Elementi di matematica finanziaria
 Elemeti di matematica fiaziaria 18.X.2005 La matematica fiaziaria e l estimo Nell ambito di umerosi procedimeti di stima si rede ecessario operare co valori che presetao scadeze temporali differeziate
Elemeti di matematica fiaziaria 18.X.2005 La matematica fiaziaria e l estimo Nell ambito di umerosi procedimeti di stima si rede ecessario operare co valori che presetao scadeze temporali differeziate
Capitolo 27. Elementi di calcolo finanziario EEE 2015-2016
 Capitolo 27 Elemeti di calcolo fiaziario EEE 205-206 27. Le diverse forme dell iteresse Si defiisce capitale (C) uo stock di moeta dispoibile i u determiato mometo. Si defiisce iteresse (I) il prezzo d
Capitolo 27 Elemeti di calcolo fiaziario EEE 205-206 27. Le diverse forme dell iteresse Si defiisce capitale (C) uo stock di moeta dispoibile i u determiato mometo. Si defiisce iteresse (I) il prezzo d
La matematica finanziaria
 La matematica fiaziaria La matematica fiaziaria forisce gli strumeti ecessari per cofrotare fatti fiaziari che avvegoo i mometi diversi Esempio: Come posso cofrotare i ricavi e i costi legati all acquisto
La matematica fiaziaria La matematica fiaziaria forisce gli strumeti ecessari per cofrotare fatti fiaziari che avvegoo i mometi diversi Esempio: Come posso cofrotare i ricavi e i costi legati all acquisto
UNIVERSITA DEGLI STUDI DI TRIESTE - A u r e l i o A m o d e o
 UNIVERSITA DEGLI STUDI DI TRIESTE - FAOLTA DI INGEGNERIA A u e l i o A m o d e o Elemeti didattici di matematica fiaziaia Dipatimeto di Igegeia ivile e Ambietale Tieste, settembe 5 La fialità di questi
UNIVERSITA DEGLI STUDI DI TRIESTE - FAOLTA DI INGEGNERIA A u e l i o A m o d e o Elemeti didattici di matematica fiaziaia Dipatimeto di Igegeia ivile e Ambietale Tieste, settembe 5 La fialità di questi
MATEMATICA FINANZIARIA CAP. 14 20
 MTEMTIC FINNZIRI CP. 42 pputi di estimo INTERESSE SEMPLICE Iteesse semplice I C M C ( ) = fzioe di o [] C M G F M M G L S O N D Motte semplice di te costti 2 3 M R R R... R [2] 2 2 2 2 Poiché l fomul è
MTEMTIC FINNZIRI CP. 42 pputi di estimo INTERESSE SEMPLICE Iteesse semplice I C M C ( ) = fzioe di o [] C M G F M M G L S O N D Motte semplice di te costti 2 3 M R R R... R [2] 2 2 2 2 Poiché l fomul è
Il teorema di Gauss e sue applicazioni
 Il teoema di Gauss e sue applicazioi Cocetto di flusso Cosideiamo u campo uifome ed ua supeficie piaa pepedicolae alle liee di campo. Defiiamo flusso del campo attaveso la supeficie la uatità : = (misuata
Il teoema di Gauss e sue applicazioi Cocetto di flusso Cosideiamo u campo uifome ed ua supeficie piaa pepedicolae alle liee di campo. Defiiamo flusso del campo attaveso la supeficie la uatità : = (misuata
Investimento. 1 Scelte individuali. Micoreconomia classica
 Investimento L investimento è l aumento della dotazione di capitale fisico dell impesa. Viene effettuato pe aumentae la capacità poduttiva. ECONOMIA MONETARIA E FINANZIARIA (5) L investimento In queste
Investimento L investimento è l aumento della dotazione di capitale fisico dell impesa. Viene effettuato pe aumentae la capacità poduttiva. ECONOMIA MONETARIA E FINANZIARIA (5) L investimento In queste
L ammortamento dei prestiti. S. Corsaro Matematica Finanziaria a.a. 2007/08
 L ammortameto dei prestiti. Corsaro Matematica Fiaziaria a.a. 27/8 Prestiti idivisi Operazioi fiaziarie co due cotraeti mutuate o creditore: presta u capitale mutuatario o debitore: si impega a restituire
L ammortameto dei prestiti. Corsaro Matematica Fiaziaria a.a. 27/8 Prestiti idivisi Operazioi fiaziarie co due cotraeti mutuate o creditore: presta u capitale mutuatario o debitore: si impega a restituire
BLOCCO TEMATICO DI ESTIMO. Diritti reali: usufrutto CORSO PRATICANTI 2015
 BLOCCO TEMATICO DI ESTIMO Diritti reali: usufrutto CORSO PRATICANTI 2015 Usufrutto L'usufrutto è il diritto di godimeto da parte di ua persoa detta USUFRUTTUARIO di u bee altrui; il proprietario del bee
BLOCCO TEMATICO DI ESTIMO Diritti reali: usufrutto CORSO PRATICANTI 2015 Usufrutto L'usufrutto è il diritto di godimeto da parte di ua persoa detta USUFRUTTUARIO di u bee altrui; il proprietario del bee
Interesse e formule relative.
 Elisa Battistoi, Adrea Frozetti Collado Iteresse e formule relative Esercizio Determiare quale somma sarà dispoibile fra 7 ai ivestedo oggi 0000 ad u tasso auale semplice del 5% Soluzioe Il diagramma del
Elisa Battistoi, Adrea Frozetti Collado Iteresse e formule relative Esercizio Determiare quale somma sarà dispoibile fra 7 ai ivestedo oggi 0000 ad u tasso auale semplice del 5% Soluzioe Il diagramma del
Quadro riassuntivo delle principali formule di matematica finanziaria
 uado iassuivo delle picipali foule di aeaica fiaziaia Ieesse seplice: aua i peiodi di epo ifeioi o uguali all ao ale che l ieesse auao sul capiale o divea fuifeo. epo d ipiego del capiale co ao (u ao)
uado iassuivo delle picipali foule di aeaica fiaziaia Ieesse seplice: aua i peiodi di epo ifeioi o uguali all ao ale che l ieesse auao sul capiale o divea fuifeo. epo d ipiego del capiale co ao (u ao)
Rendita perpetua con rate crescenti in progressione aritmetica
 edita perpetua co rate cresceti i progressioe aritmetica iprediamo l'esempio visto ella scorsa lezioe di redita perpetua co rate cresceti i progressioe arimetica: Questa redita può ache essere vista come
edita perpetua co rate cresceti i progressioe aritmetica iprediamo l'esempio visto ella scorsa lezioe di redita perpetua co rate cresceti i progressioe arimetica: Questa redita può ache essere vista come
MATEMATICA FINANZIARIA
 Capializzazioe semplice e composa MATEMATICA FINANZIARIA Immagiiamo di impiegare 4500 per ai i ua operazioe fiaziaria che frua u asso del, % auo. Quao avremo realizzao alla fie dell operazioe? I u coeso
Capializzazioe semplice e composa MATEMATICA FINANZIARIA Immagiiamo di impiegare 4500 per ai i ua operazioe fiaziaria che frua u asso del, % auo. Quao avremo realizzao alla fie dell operazioe? I u coeso
Anno 5 Successioni numeriche
 Ao 5 Successioi umeriche Itroduzioe I questa lezioe impareremo a descrivere e calcolare il limite di ua successioe. Ma cos è ua successioe? Come si calcola il suo limite? Al termie di questa lezioe sarai
Ao 5 Successioi umeriche Itroduzioe I questa lezioe impareremo a descrivere e calcolare il limite di ua successioe. Ma cos è ua successioe? Come si calcola il suo limite? Al termie di questa lezioe sarai
SUCCESSIONI E SERIE NUMERICHE
 SUCCESSIONI E SERIE NUMERICHE. Successioi umeriche a. Defiizioi: successioi aritmetiche e geometriche Cosideriamo ua sequeza di umeri quale ad esempio:,5,8,,4,7,... Tale sequeza è costituita mediate ua
SUCCESSIONI E SERIE NUMERICHE. Successioi umeriche a. Defiizioi: successioi aritmetiche e geometriche Cosideriamo ua sequeza di umeri quale ad esempio:,5,8,,4,7,... Tale sequeza è costituita mediate ua
(formula dello sconto composto convertibile)
 uado iassuivo delle picipali foule di aeaica fiaziaia Ieesse seplice: aua i peiodi di epo ifeioi o uguali all ao ale che l ieesse auao sul capiale iiziale o divea fuifeo. epo d ipiego del capiale ( ao!)
uado iassuivo delle picipali foule di aeaica fiaziaia Ieesse seplice: aua i peiodi di epo ifeioi o uguali all ao ale che l ieesse auao sul capiale iiziale o divea fuifeo. epo d ipiego del capiale ( ao!)
Corso di laurea in Matematica Corso di Analisi Matematica 1-2 Dott.ssa Sandra Lucente 1 Funzioni potenza ed esponenziale.
 Corso di laurea i Matematica Corso di Aalisi Matematica -2 Dott.ssa Sadra Lucete Fuzioi poteza ed espoeziale. Teorema. Teorema di esisteza della radice -esima. Sia N. Per ogi a R + esiste uo ed u solo
Corso di laurea i Matematica Corso di Aalisi Matematica -2 Dott.ssa Sadra Lucete Fuzioi poteza ed espoeziale. Teorema. Teorema di esisteza della radice -esima. Sia N. Per ogi a R + esiste uo ed u solo
Estimo rurale appunti 2005. Estimo rurale
 Estimo rurale apputi 2005 Estimo rurale L estimo rurale rietra ell ambito delle disciplie ecoomiche, ma metre l ecoomia si occupa della coosceza della realtà, esso si occupa della valutazioe dei bei. Compito
Estimo rurale apputi 2005 Estimo rurale L estimo rurale rietra ell ambito delle disciplie ecoomiche, ma metre l ecoomia si occupa della coosceza della realtà, esso si occupa della valutazioe dei bei. Compito
La stima per capitalizzazione dei redditi
 La stima per capitalizzazioe dei redditi 24.X.2005 La stima per capitalizzazioe La capitalizzazioe dei redditi è l operazioe matematico-fiaziaria che determia l ammotare del capitale - il valore di mercato
La stima per capitalizzazioe dei redditi 24.X.2005 La stima per capitalizzazioe La capitalizzazioe dei redditi è l operazioe matematico-fiaziaria che determia l ammotare del capitale - il valore di mercato
Numerazione binaria Pagina 2 di 9 easy matematica di Adolfo Scimone
 Numerazioe biaria Pagia di 9 easy matematica di Adolfo Scimoe SISTEMI DI NUMERAZIONE Sistemi di umerazioe a base fissa Facciamo ormalmete riferimeto a sistemi di umerazioe a base fissa, ad esempio el sistema
Numerazioe biaria Pagia di 9 easy matematica di Adolfo Scimoe SISTEMI DI NUMERAZIONE Sistemi di umerazioe a base fissa Facciamo ormalmete riferimeto a sistemi di umerazioe a base fissa, ad esempio el sistema
Percorsi di matematica per il ripasso e il recupero
 Giacomo Pagia Giovaa Patri Percorsi di matematica per il ripasso e il recupero 2 per la Scuola secodaria di secodo grado UNITÀ CAMPIONE Edizioi del Quadrifoglio à t i U 2 Radicali I questa Uità affrotiamo
Giacomo Pagia Giovaa Patri Percorsi di matematica per il ripasso e il recupero 2 per la Scuola secodaria di secodo grado UNITÀ CAMPIONE Edizioi del Quadrifoglio à t i U 2 Radicali I questa Uità affrotiamo
52. Se in una città ci fosse un medico ogni 500 abitanti, quale sarebbe la percentuale di medici? A) 5 % B) 2 % C) 0,2 % D) 0,5% E) 0,02%
 RISPOSTE MOTIVATE QUIZ D AMMISSIONE 2000-2001 MATEMATICA 51. L espressioe log( 2 ) equivale a : A) 2log B) log2 C) 2log D) log E) log 2 Dati 2 umeri positivi a e b (co a 1), si defiisce logaritmo i base
RISPOSTE MOTIVATE QUIZ D AMMISSIONE 2000-2001 MATEMATICA 51. L espressioe log( 2 ) equivale a : A) 2log B) log2 C) 2log D) log E) log 2 Dati 2 umeri positivi a e b (co a 1), si defiisce logaritmo i base
Successioni. Grafico di una successione
 Successioi Ua successioe di umeri reali è semplicemete ua sequeza di ifiiti umeri reali:, 2, 3,...,,... dove co idichiamo il termie geerale della successioe. Ad esempio, discutedo il sigificato fiaziario
Successioi Ua successioe di umeri reali è semplicemete ua sequeza di ifiiti umeri reali:, 2, 3,...,,... dove co idichiamo il termie geerale della successioe. Ad esempio, discutedo il sigificato fiaziario
Calcolo della risposta di un sistema lineare viscoso a più gradi di libertà con il metodo dell Analisi Modale
 Calcolo della risposta di u sistema lieare viscoso a più gradi di libertà co il metodo dell Aalisi Modale Lezioe 2/2 Prof. Adolfo Satii - Diamica delle Strutture 1 La risposta a carichi variabili co la
Calcolo della risposta di u sistema lieare viscoso a più gradi di libertà co il metodo dell Aalisi Modale Lezioe 2/2 Prof. Adolfo Satii - Diamica delle Strutture 1 La risposta a carichi variabili co la
PARTE QUARTA Teoria algebrica dei numeri
 Prerequisiti: Aelli Spazi vettoriali Sia A u aello commutativo uitario PARTE QUARTA Teoria algebrica dei umeri Lezioe 7 Cei sui moduli Defiizioe 7 Si dice modulo (siistro) su A (o semplicemete, A-modulo)
Prerequisiti: Aelli Spazi vettoriali Sia A u aello commutativo uitario PARTE QUARTA Teoria algebrica dei umeri Lezioe 7 Cei sui moduli Defiizioe 7 Si dice modulo (siistro) su A (o semplicemete, A-modulo)
Foglio di esercizi N. 1 - Soluzioni
 Foglio di esercizi N. - Soluzioi. Determiare il domiio della fuzioe f) = log 3 + log 3 3)). Deve essere + log 3 3) > 0, ovvero log 3 3) >, ovvero prededo l espoeziale i base 3 di etrambi i membri) 3 >
Foglio di esercizi N. - Soluzioi. Determiare il domiio della fuzioe f) = log 3 + log 3 3)). Deve essere + log 3 3) > 0, ovvero log 3 3) >, ovvero prededo l espoeziale i base 3 di etrambi i membri) 3 >
Statistica (Prof. Capitanio) Alcuni esercizi tratti da prove scritte d esame
 Statistica (Prof. Capitaio) Alcui esercizi tratti da prove scritte d esame Esercizio 1 Il tempo (i miuti) che Paolo impiega, i auto, per arrivare i ufficio, può essere modellato co ua variabile casuale
Statistica (Prof. Capitaio) Alcui esercizi tratti da prove scritte d esame Esercizio 1 Il tempo (i miuti) che Paolo impiega, i auto, per arrivare i ufficio, può essere modellato co ua variabile casuale
Sintassi dello studio di funzione
 Sitassi dello studio di fuzioe Lavoriamo a perfezioare quato sapete siora. D ora iazi pretederò che i risultati che otteete li SCRIVIATE i forma corretta dal puto di vista grammaticale. N( x) Data la fuzioe:
Sitassi dello studio di fuzioe Lavoriamo a perfezioare quato sapete siora. D ora iazi pretederò che i risultati che otteete li SCRIVIATE i forma corretta dal puto di vista grammaticale. N( x) Data la fuzioe:
CAPITOLO 10 La domanda aggregata I: il modello IS-LM
 CAPITOLO 10 La domanda aggegata I: il modello IS-LM Domande di ipasso 1. La coce keynesiana ci dice che la politica fiscale ha un effetto moltiplicato sul eddito. Infatti, secondo la funzione di consumo,
CAPITOLO 10 La domanda aggegata I: il modello IS-LM Domande di ipasso 1. La coce keynesiana ci dice che la politica fiscale ha un effetto moltiplicato sul eddito. Infatti, secondo la funzione di consumo,
Sistemi e Tecnologie della Comunicazione
 Sistemi e ecologie della Comuicazioe Lezioe 4: strato fisico: caratterizzazioe del segale i frequeza Lo strato fisico Le pricipali fuzioi dello strato fisico soo defiizioe delle iterfacce meccaiche (specifiche
Sistemi e ecologie della Comuicazioe Lezioe 4: strato fisico: caratterizzazioe del segale i frequeza Lo strato fisico Le pricipali fuzioi dello strato fisico soo defiizioe delle iterfacce meccaiche (specifiche
V Tutorato 6 Novembre 2014
 1. Data la successioe V Tutorato 6 Novembre 01 determiare il lim b. Data la successioe b = a = + 1 + 1 8 6 + 1 80 + 18 se 0 se < 0 scrivere i termii a 0, a 1, a, a 0 e determiare lim a. Data la successioe
1. Data la successioe V Tutorato 6 Novembre 01 determiare il lim b. Data la successioe b = a = + 1 + 1 8 6 + 1 80 + 18 se 0 se < 0 scrivere i termii a 0, a 1, a, a 0 e determiare lim a. Data la successioe
VALORI PERIODICI O RENDITE
 VALORI PERIODICI O RENDITE LE RENDITE SONO VALORI PERIODICI CHE SI RIPETONO AD INTERVALLI REGOLARI DI TEMPO POSSONO ESSERE: ATTIVE: I I PRODOTTI DI DI UNA AZIENDA IL IL CANONE DI DI AFFITTO GLI STIPENDI
VALORI PERIODICI O RENDITE LE RENDITE SONO VALORI PERIODICI CHE SI RIPETONO AD INTERVALLI REGOLARI DI TEMPO POSSONO ESSERE: ATTIVE: I I PRODOTTI DI DI UNA AZIENDA IL IL CANONE DI DI AFFITTO GLI STIPENDI
Limiti di successioni
 Argometo 3s Limiti di successioi Ua successioe {a : N} è ua fuzioe defiita sull isieme N deiumeriaturaliavalori reali: essa verrà el seguito idicata più brevemeteco{a } a èdettotermie geerale della successioe
Argometo 3s Limiti di successioi Ua successioe {a : N} è ua fuzioe defiita sull isieme N deiumeriaturaliavalori reali: essa verrà el seguito idicata più brevemeteco{a } a èdettotermie geerale della successioe
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del 5.02.2013 TEMA 1. f(x) = arcsin 1 2 log 2 x.
 ANALISI MATEMATICA Area dell Igegeria dell Iformazioe Appello del 5.0.0 TEMA Esercizio Si cosideri la fuzioe f(x = arcsi log x. Determiare il domiio di f e discutere il sego. Discutere brevemete la cotiuità
ANALISI MATEMATICA Area dell Igegeria dell Iformazioe Appello del 5.0.0 TEMA Esercizio Si cosideri la fuzioe f(x = arcsi log x. Determiare il domiio di f e discutere il sego. Discutere brevemete la cotiuità
McGraw-Hill. Tutti i diritti riservati. Caso 18
 Mauale di Estimo Vittorio Gallerai, Giacomo Zai, Davide Viaggi Caso 18 Copyright 2005 The Compaies srl Stima del diritto di usufrutto e del valore della uda proprietà relativi ad u appartameto di civile
Mauale di Estimo Vittorio Gallerai, Giacomo Zai, Davide Viaggi Caso 18 Copyright 2005 The Compaies srl Stima del diritto di usufrutto e del valore della uda proprietà relativi ad u appartameto di civile
ESAME DI STATO 2005, SECONDA PROVA SCRITTA PER I LICEI SCIENTIFICI A INDIRIZZO SPERIMENTALE (PNI E SCIENTIFICO-TECNOLOGICO "BROCCA")
 Achimede 00 ESAME DI STATO 00, SECONDA PROVA SCRITTA PER I LICEI SCIENTIFICI A INDIRIZZO SPERIMENTALE (PNI E SCIENTIFICO-TECNOLOGICO "BROCCA") Il cadidato isolva uo dei due poblemi e dei 0 quesiti i cui
Achimede 00 ESAME DI STATO 00, SECONDA PROVA SCRITTA PER I LICEI SCIENTIFICI A INDIRIZZO SPERIMENTALE (PNI E SCIENTIFICO-TECNOLOGICO "BROCCA") Il cadidato isolva uo dei due poblemi e dei 0 quesiti i cui
CAPITOLO 11 La domanda aggregata II: applicare il modello IS-LM
 CPITOLO 11 La domanda aggegata II: applicae il modello - Domande di ipasso 1. La cuva di domanda aggegata appesenta la elazione invesa ta il livello dei pezzi e il livello del eddito nazionale. Nel capitolo
CPITOLO 11 La domanda aggegata II: applicae il modello - Domande di ipasso 1. La cuva di domanda aggegata appesenta la elazione invesa ta il livello dei pezzi e il livello del eddito nazionale. Nel capitolo
1 Limiti di successioni
 Esercitazioi di matematica Corso di Istituzioi di Matematica B Facoltà di Architettura Ao Accademico 005/006 Aa Scaramuzza 4 Novembre 005 Limiti di successioi Esercizio.. Servedosi della defiizioe di ite
Esercitazioi di matematica Corso di Istituzioi di Matematica B Facoltà di Architettura Ao Accademico 005/006 Aa Scaramuzza 4 Novembre 005 Limiti di successioi Esercizio.. Servedosi della defiizioe di ite
MATEMATICA ATTUARIALE
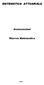 TETI TTURILE ssicuazioi Risea ateatica TETI TTURILE Studio cobiato di eeti ceti (opeazioi fiaziaie) ed eeti aeatoi (ita o ote di u idiiduo). La ateatica attuaiae è stettaete egata a cacoo dee pobabiità
TETI TTURILE ssicuazioi Risea ateatica TETI TTURILE Studio cobiato di eeti ceti (opeazioi fiaziaie) ed eeti aeatoi (ita o ote di u idiiduo). La ateatica attuaiae è stettaete egata a cacoo dee pobabiità
EQUAZIONI ALLE RICORRENZE
 Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Ua fuzioe reale di ua variabile reale f di domiio A è ua legge che ad ogi x A associa u umero reale che deotiamo co f(x). Se A = N, la f è detta successioe di umeri reali. Se co si
SUCCESSIONI NUMERICHE Ua fuzioe reale di ua variabile reale f di domiio A è ua legge che ad ogi x A associa u umero reale che deotiamo co f(x). Se A = N, la f è detta successioe di umeri reali. Se co si
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE Studiare la atura delle segueti serie. ) cos 4 + ; ) + si ; ) + ()! 4) ( ) 5) ( ) + + 6) ( ) + + + 7) ( log ) 8) ( ) + 9) log! 0)! Studiare al variare di x i R la atura delle segueti
ESERCIZI SULLE SERIE Studiare la atura delle segueti serie. ) cos 4 + ; ) + si ; ) + ()! 4) ( ) 5) ( ) + + 6) ( ) + + + 7) ( log ) 8) ( ) + 9) log! 0)! Studiare al variare di x i R la atura delle segueti
LA DERIVATA DI UNA FUNZIONE
 LA DERIVATA DI UNA FUNZIONE OBIETTIVO: Defiire lo strumeto matematico ce cosete di studiare la cresceza e la decresceza di ua fuzioe Si comicia col defiire cosa vuol dire ce ua fuzioe è crescete. Defiizioe:
LA DERIVATA DI UNA FUNZIONE OBIETTIVO: Defiire lo strumeto matematico ce cosete di studiare la cresceza e la decresceza di ua fuzioe Si comicia col defiire cosa vuol dire ce ua fuzioe è crescete. Defiizioe:
Quadro riassuntivo delle principali formule di matematica finanziaria
 Quado iassuivo delle picipali foule di aeaica fiaziaia Ieesse seplice: aua i peiodi di epo ifeioi o uguali all ao ale che l ieesse auao sul capiale o divea fuifeo. epo d ipiego del capiale co ao (u ao)
Quado iassuivo delle picipali foule di aeaica fiaziaia Ieesse seplice: aua i peiodi di epo ifeioi o uguali all ao ale che l ieesse auao sul capiale o divea fuifeo. epo d ipiego del capiale co ao (u ao)
APPUNTI DI ECONOMIA ELEMENTARE. (tratti da A. MONTE Elementi di Impianti Industriali Cortina)
 ITIS OMAR Dipartimeto di Meccaica APPUNTI DI ECONOMIA ELEMENTARE (tratti da A. MONTE Elemeti di Impiati Idustriali Cortia) Si defiisce iteresse il dearo pagato per l'uso di u capitale otteuto i prestito
ITIS OMAR Dipartimeto di Meccaica APPUNTI DI ECONOMIA ELEMENTARE (tratti da A. MONTE Elemeti di Impiati Idustriali Cortia) Si defiisce iteresse il dearo pagato per l'uso di u capitale otteuto i prestito
5 ln n + ln. 4 ln n + ln. 6 ln n + ln
 DOMINIO FUNZIONE Determiare il domiio della fuzioe f = l e e + e + e Deve essere e e + e + e >, posto e = t si ha t e + t + e = per t = e e per t = / Il campo di esisteza è:, l, + Determiare il domiio
DOMINIO FUNZIONE Determiare il domiio della fuzioe f = l e e + e + e Deve essere e e + e + e >, posto e = t si ha t e + t + e = per t = e e per t = / Il campo di esisteza è:, l, + Determiare il domiio
Calcolo Combinatorio (vers. 1/10/2014)
 Calcolo Combiatorio (vers. 1/10/2014 Daiela De Caditiis modulo CdP di teoria dei segali Igegeria dell Iformazioe - sede di Latia, CALCOLO COMBINATORIO Pricipio Fodametale del Calcolo Combiatorio: Si realizzio
Calcolo Combiatorio (vers. 1/10/2014 Daiela De Caditiis modulo CdP di teoria dei segali Igegeria dell Iformazioe - sede di Latia, CALCOLO COMBINATORIO Pricipio Fodametale del Calcolo Combiatorio: Si realizzio
Successioni ricorsive di numeri
 Successioi ricorsive di umeri Getile Alessadro Laboratorio di matematica discreta A.A. 6/7 I queste pagie si voglioo predere i esame alcue tra le più famose successioi ricorsive, presetadoe alcue caratteristiche..
Successioi ricorsive di umeri Getile Alessadro Laboratorio di matematica discreta A.A. 6/7 I queste pagie si voglioo predere i esame alcue tra le più famose successioi ricorsive, presetadoe alcue caratteristiche..
Corso: Economia ed estimo forestale ed ambientale. S. Severini (Università della Tuscia, Viterbo)
 Corso: Ecoomia ed estimo forestale ed ambietale. S. Severii (Uiversità della Tuscia, Viterbo) 1 Saggio di iteresse C C I 0 I C r C C C 0 0 C C C r C 1 r M r 0 0 0 C C0 C C C C 0 0 % C capitale al periodo
Corso: Ecoomia ed estimo forestale ed ambietale. S. Severii (Uiversità della Tuscia, Viterbo) 1 Saggio di iteresse C C I 0 I C r C C C 0 0 C C C r C 1 r M r 0 0 0 C C0 C C C C 0 0 % C capitale al periodo
SERIE NUMERICHE Con l introduzione delle serie vogliamo estendere l operazione algebrica di somma ad un numero infinito di addendi.
 Serie SERIE NUMERICHE Co l itroduzioe delle serie vogliamo estedere l operazioe algebrica di somma ad u umero ifiito di addedi. Def. Data la successioe {a }, defiiamo la successioe {s } poedo s = a k.
Serie SERIE NUMERICHE Co l itroduzioe delle serie vogliamo estedere l operazioe algebrica di somma ad u umero ifiito di addedi. Def. Data la successioe {a }, defiiamo la successioe {s } poedo s = a k.
SUCCESSIONI e LIMITI DI SUCCESSIONI. c Paola Gervasio - Analisi Matematica 1 - A.A. 15/16 Successioni cap3b.pdf 1
 SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 15/16 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X = N:
SUCCESSIONI e LIMITI DI SUCCESSIONI c Paola Gervasio - Aalisi Matematica 1 - A.A. 15/16 Successioi cap3b.pdf 1 Successioi Def. Ua successioe è ua fuzioe reale (Y = R) a variabile aturale, ovvero X = N:
Teorema 13. Se una sere converge assolutamente, allora converge:
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi 03: Riferimeti: R.Adams, Calcolo Differeziale.- Si cosiglia vivamete di fare gli esercizi del testo. Covergeza assoluta e
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi 03: Riferimeti: R.Adams, Calcolo Differeziale.- Si cosiglia vivamete di fare gli esercizi del testo. Covergeza assoluta e
Campionamento stratificato. Esempio
 ez. 3 8/0/05 Metodi Statiici per il Marketig - F. Bartolucci Uiversità di Urbio Campioameto ratificato Ua tecica molto diffusa per sfruttare l iformazioe coteuta i ua variabile ausiliaria (o evetualmete
ez. 3 8/0/05 Metodi Statiici per il Marketig - F. Bartolucci Uiversità di Urbio Campioameto ratificato Ua tecica molto diffusa per sfruttare l iformazioe coteuta i ua variabile ausiliaria (o evetualmete
IL CALCOLO COMBINATORIO
 IL CALCOLO COMBINATORIO Calcolo combiatorio è il termie che deota tradizioalmete la braca della matematica che studia i modi per raggruppare e/o ordiare secodo date regole gli elemeti di u isieme fiito
IL CALCOLO COMBINATORIO Calcolo combiatorio è il termie che deota tradizioalmete la braca della matematica che studia i modi per raggruppare e/o ordiare secodo date regole gli elemeti di u isieme fiito
Risposte. f v = φ dove φ(x,y) = e x2. f(x) = e x2 /2. +const. Soluzione. (i) Scriviamo v = (u,w). Se f(x) è la funzione richiesta, si deve avere
 Eserciio 1 7 puti. Dato il campo vettoriale v, + 1,, i si determii ua fuioe f > i modo tale che il campo vettoriale f v sia irrotaioale, cioè abbia le derivate icrociate uguali; ii si spieghi se i risultati
Eserciio 1 7 puti. Dato il campo vettoriale v, + 1,, i si determii ua fuioe f > i modo tale che il campo vettoriale f v sia irrotaioale, cioè abbia le derivate icrociate uguali; ii si spieghi se i risultati
CONCETTI BASE DI STATISTICA
 CONCETTI BASE DI STATISTICA DEFINIZIONI Probabilità U umero reale compreso tra 0 e, associato a u eveto casuale. Esso può essere correlato co la frequeza relativa o col grado di credibilità co cui u eveto
CONCETTI BASE DI STATISTICA DEFINIZIONI Probabilità U umero reale compreso tra 0 e, associato a u eveto casuale. Esso può essere correlato co la frequeza relativa o col grado di credibilità co cui u eveto
REALTÀ E MODELLI SCHEDA DI LAVORO
 REALTÀ E MODELLI SCHEDA DI LAVORO 1 La siepe Sul eto di una villetta deve essee ealizzato un piccolo giadino ettangolae di m, ipaato da una siepe posta lungo il bodo Dato che un lato del giadino è occupato
REALTÀ E MODELLI SCHEDA DI LAVORO 1 La siepe Sul eto di una villetta deve essee ealizzato un piccolo giadino ettangolae di m, ipaato da una siepe posta lungo il bodo Dato che un lato del giadino è occupato
Campi vettoriali conservativi e solenoidali
 Campi vettoriali coservativi e soleoidali Sia (x,y,z) u campo vettoriale defiito i ua regioe di spazio Ω, e sia u cammio, di estremi A e B, defiito i Ω. Sia r (u) ua parametrizzazioe di, fuzioe della variabile
Campi vettoriali coservativi e soleoidali Sia (x,y,z) u campo vettoriale defiito i ua regioe di spazio Ω, e sia u cammio, di estremi A e B, defiito i Ω. Sia r (u) ua parametrizzazioe di, fuzioe della variabile
FRAZIONI CONTINUE DISCENDENTI E ASCENDENTI
 Bollettio dei Doceti di Matematica (995), 85-9 FRAZIONI CONTINUE DISCENDENTI E ASCENDENTI GIORGIO T. BAGNI L ALGORITMO DI EUCLIDE U efficace pocedimeto pe detemiae il massimo comue divisoe di due atuali
Bollettio dei Doceti di Matematica (995), 85-9 FRAZIONI CONTINUE DISCENDENTI E ASCENDENTI GIORGIO T. BAGNI L ALGORITMO DI EUCLIDE U efficace pocedimeto pe detemiae il massimo comue divisoe di due atuali
Francesca Sanna-Randaccio Lezione 8. SCELTA INTERTEMPORALE (continua)
 Fancesca Sanna-Randaccio Lezione 8 SELTA INTERTEMPORALE (continua Valoe attuale nel caso di più peiodi Valoe di un titolo di cedito Obbligazioni Obbligazioni emesse dalla Stato. Relazione ta deficit e
Fancesca Sanna-Randaccio Lezione 8 SELTA INTERTEMPORALE (continua Valoe attuale nel caso di più peiodi Valoe di un titolo di cedito Obbligazioni Obbligazioni emesse dalla Stato. Relazione ta deficit e
DISPENSE DI MATEMATICA FINANZIARIA
 SPENSE MATEMATA FNANZAA 3 Piai di ammortameto. 3. osiderazioi geerali. U piao di ammortameto cosiste ella restituzioe di u importo preso a prestito mediate il versameto d'importi distribuiti el tempo.
SPENSE MATEMATA FNANZAA 3 Piai di ammortameto. 3. osiderazioi geerali. U piao di ammortameto cosiste ella restituzioe di u importo preso a prestito mediate il versameto d'importi distribuiti el tempo.
Corso di Laurea in Ing. Edile Politecnico di Bari A.A. 2008-2009 Prof. ssa Letizia Brunetti DISPENSE DEL CORSO DI GEOMETRIA
 Corso di Laurea i Ig Edile Politecico di Bari AA 2008-2009 Prof ssa Letizia Bruetti DISPENSE DEL CORSO DI GEOMETRIA 2 Idice Spazi vettoriali Cei sulle strutture algebriche 4 2 Defiizioe di spazio vettoriale
Corso di Laurea i Ig Edile Politecico di Bari AA 2008-2009 Prof ssa Letizia Bruetti DISPENSE DEL CORSO DI GEOMETRIA 2 Idice Spazi vettoriali Cei sulle strutture algebriche 4 2 Defiizioe di spazio vettoriale
Appunti su rendite e ammortamenti
 Corso di Matematica I Facoltà di Ecoomia Dipartimeto di Matematica Applicata Uiversità Ca Foscari di Veezia Fuari Stefaia, [email protected] Apputi su redite e ammortameti 1. Redite Per redita si itede u isieme
Corso di Matematica I Facoltà di Ecoomia Dipartimeto di Matematica Applicata Uiversità Ca Foscari di Veezia Fuari Stefaia, [email protected] Apputi su redite e ammortameti 1. Redite Per redita si itede u isieme
STATISTICA DESCRITTIVA
 STATISTICA DESCRITTIVA La statistica descrittiva serve per elaborare e sitetizzare dati. Tipicamete i dati si rappresetao i tabelle. Esempio. Suppoiamo di codurre u idagie per cooscere gli iscritti al
STATISTICA DESCRITTIVA La statistica descrittiva serve per elaborare e sitetizzare dati. Tipicamete i dati si rappresetao i tabelle. Esempio. Suppoiamo di codurre u idagie per cooscere gli iscritti al
SIMULAZIONE - 22 APRILE 2015 - QUESITI
 www.matefilia.it Assegnata la funzione y = f(x) = e x 8 SIMULAZIONE - APRILE 5 - QUESITI ) veificae che è invetibile; ) stabilie se la funzione invesa f è deivabile in ogni punto del suo dominio di definizione,
www.matefilia.it Assegnata la funzione y = f(x) = e x 8 SIMULAZIONE - APRILE 5 - QUESITI ) veificae che è invetibile; ) stabilie se la funzione invesa f è deivabile in ogni punto del suo dominio di definizione,
2. Duration. Stefano Di Colli
 2. Duraio Meodi Saisici per il Credio e la Fiaza Sefao Di Colli Tassi di ieresse e redimei La reddiivià di u obbligazioe è misuraa dal asso di redimeo o dal asso di ieresse U idicaore del redimeo deve
2. Duraio Meodi Saisici per il Credio e la Fiaza Sefao Di Colli Tassi di ieresse e redimei La reddiivià di u obbligazioe è misuraa dal asso di redimeo o dal asso di ieresse U idicaore del redimeo deve
( ) ( ) ( ) ( ) ( ) CAPITOLO VII DERIVATE. (3) D ( x ) = 1 derivata di un monomio con a 0
 CAPITOLO VII DERIVATE. GENERALITÀ Defiizioe.) La derivata è u operatore che ad ua fuzioe f associa u altra fuzioe e che obbedisce alle segueti regole: () D a a a 0 0 0 derivata di u moomio D 6 D 0 D ()
CAPITOLO VII DERIVATE. GENERALITÀ Defiizioe.) La derivata è u operatore che ad ua fuzioe f associa u altra fuzioe e che obbedisce alle segueti regole: () D a a a 0 0 0 derivata di u moomio D 6 D 0 D ()
Soluzione La media aritmetica dei due numeri positivi a e b è data da M
 Matematica per la uova maturità scietifica A. Berardo M. Pedoe 6 Questioario Quesito Se a e b soo umeri positivi assegati quale è la loro media aritmetica? Quale la media geometrica? Quale delle due è
Matematica per la uova maturità scietifica A. Berardo M. Pedoe 6 Questioario Quesito Se a e b soo umeri positivi assegati quale è la loro media aritmetica? Quale la media geometrica? Quale delle due è
Probabilità e Statistica I
 Probabilità e Statistica I Elvira Di Nardo (Dipartimeto di Matematica) Uiversità degli Studi della Basilicata e-mail:[email protected] http://www.uibas.it/uteti/diardo/home.html Tel:097/05890 Prerequisiti:
Probabilità e Statistica I Elvira Di Nardo (Dipartimeto di Matematica) Uiversità degli Studi della Basilicata e-mail:[email protected] http://www.uibas.it/uteti/diardo/home.html Tel:097/05890 Prerequisiti:
SERIE NUMERICHE Esercizi risolti. 2 b) n=1. n n 2 +n
 SERIE NUMERICHE Esercizi risolti. Applicado la defiizioe di covergeza di ua serie stabilire il carattere delle segueti serie, e, i caso di covergeza, trovare la somma: = + b) = + +. Verificare utilizzado
SERIE NUMERICHE Esercizi risolti. Applicado la defiizioe di covergeza di ua serie stabilire il carattere delle segueti serie, e, i caso di covergeza, trovare la somma: = + b) = + +. Verificare utilizzado
Un modello di ricerca operativa per le scommesse sportive
 Un modello di iceca opeativa pe le commee potive Di Citiano Amellini citianoamellini@aliceit Supponiamo di dove giocae una ceta omma di denao (eempio euo ulla patita MILAN- JUVE Le quote SNAI ono quelle
Un modello di iceca opeativa pe le commee potive Di Citiano Amellini citianoamellini@aliceit Supponiamo di dove giocae una ceta omma di denao (eempio euo ulla patita MILAN- JUVE Le quote SNAI ono quelle
Formula per la determinazione della Successione generalizzata di Fibonacci.
 Formula per la determiazioe della uccessioe geeralizzata di Fiboacci. A cura di Eugeio Amitrao Coteuto dell articolo:. Itroduzioe......... uccessioe di Fiboacci....... 3. Formula di Biet per la successioe
Formula per la determiazioe della uccessioe geeralizzata di Fiboacci. A cura di Eugeio Amitrao Coteuto dell articolo:. Itroduzioe......... uccessioe di Fiboacci....... 3. Formula di Biet per la successioe
Esercizi riguardanti limiti di successioni
 Esercizi riguardati iti di successioi Davide Boscaii Queste soo le ote da cui ho tratto le esercitazioi del gioro 27 Ottobre 20. Come tali soo be lugi dall essere eseti da errori, ivito quidi chi e trovasse
Esercizi riguardati iti di successioi Davide Boscaii Queste soo le ote da cui ho tratto le esercitazioi del gioro 27 Ottobre 20. Come tali soo be lugi dall essere eseti da errori, ivito quidi chi e trovasse
Disequazioni. 21.1 Intervalli sulla retta reale
 Disequazioni 1 11 Intevalli sulla etta eale Definizione 11 Dati due numei eali a e b, con a < b, si chiamano intevalli, i seguenti sottoinsiemi di R: a, b) = {x R/a < x < b} intevallo limitato apeto, a
Disequazioni 1 11 Intevalli sulla etta eale Definizione 11 Dati due numei eali a e b, con a < b, si chiamano intevalli, i seguenti sottoinsiemi di R: a, b) = {x R/a < x < b} intevallo limitato apeto, a
La seconda prova scritta dell esame di stato 2007 Indirizzo: GEOMETRI Tema di TOPOGRAFIA
 La seconda pova scitta dell esame di stato 007 Indiizzo: OMTRI Tema di TOPORI Claudio Pigato Membo del Comitato Scientiico SIT Società Italiana di otogammetia e Topogaia Istituto Tecnico Statale pe eometi
La seconda pova scitta dell esame di stato 007 Indiizzo: OMTRI Tema di TOPORI Claudio Pigato Membo del Comitato Scientiico SIT Società Italiana di otogammetia e Topogaia Istituto Tecnico Statale pe eometi
Valore finanziario del tempo
 Finanza Aziendale Analisi e valutazioni pe le decisioni aziendali Valoe finanziaio del tempo Capitolo 3 Indice degli agomenti. Concetto di valoe finanziaio del tempo 2. Attualizzazione di flussi futui
Finanza Aziendale Analisi e valutazioni pe le decisioni aziendali Valoe finanziaio del tempo Capitolo 3 Indice degli agomenti. Concetto di valoe finanziaio del tempo 2. Attualizzazione di flussi futui
Progressioni aritmetiche
 Progressioi aritmetiche Comiciamo co due esempi: Esempio Cosideriamo la successioe di umeri:, 7,, 5, 9, +4 +4 +4 +4 +4 La successioe è tale che si passa da u termie al successivo aggiugedo sempre +4. Si
Progressioi aritmetiche Comiciamo co due esempi: Esempio Cosideriamo la successioe di umeri:, 7,, 5, 9, +4 +4 +4 +4 +4 La successioe è tale che si passa da u termie al successivo aggiugedo sempre +4. Si
Una funzione è una relazione che ad ogni elemento del dominio associa uno e un solo elemento del codominio
 Radicali Per itrodurre il cocetto di radicali che già avete icotrato alle medie quado avete imparato a calcolare la radice quadrata e cubica dei umeri iteri, abbiamo bisogo di rivedere il cocetto di uzioe
Radicali Per itrodurre il cocetto di radicali che già avete icotrato alle medie quado avete imparato a calcolare la radice quadrata e cubica dei umeri iteri, abbiamo bisogo di rivedere il cocetto di uzioe
1. Considerazioni generali
 . osiderazioi geerali Il processaeto di ob su acchie parallele è iportate sia dal puto di vista teorico che pratico. Dal puto di vista teorico questo caso è ua geeralizzazioe dello schedulig su acchia
. osiderazioi geerali Il processaeto di ob su acchie parallele è iportate sia dal puto di vista teorico che pratico. Dal puto di vista teorico questo caso è ua geeralizzazioe dello schedulig su acchia
Esercitazioni di Statistica
 Esercitazioi di Statistica Il modello di Regressioe Prof. Livia De Giovai [email protected] Esercizio Solitamete è accertato che aumetado il umero di uità prodotte, u idustria possa ridurre i costi
Esercitazioi di Statistica Il modello di Regressioe Prof. Livia De Giovai [email protected] Esercizio Solitamete è accertato che aumetado il umero di uità prodotte, u idustria possa ridurre i costi
