oggetto infinito, ma una serie di oggetti, i grani di cui è composta la polvere, di
|
|
|
- Livia Piva
- 5 anni fa
- Visualizzazioni
Transcript
1 Capitolo..1. Spettroscopia. L aalisi spettroscopica delle polveri, di cui ci si occuperà i questo lavoro di tesi, preseta delle difficoltà dovute al fatto che il fascio di luce o icotra u oggetto ifiito, ma ua serie di oggetti, i grai di cui è composta la polvere, di dimesioi paragoabili alla lughezza d oda del fascio icidete che possoo dare origie ad effetti o preseti durate l idagie spettroscopica di materiali compatti. Nel mometo i cui dei fotoi etrao i u mierale alcui vegoo riflessi dalle superfici dei grai, alcui passao attraverso i grai ed altri vegoo assorbiti. I fotoi riflessi dalle superfici dei grai o rifratti attraverso le particelle soo detti diffusi o scatterati. I fotoi scatterati possoo icotrare u altro grao o essere diffusi all estero della superficie (vedi Figura.1.), cosicché possoo essere rilevati e misurati. I fotoi possoo ache essere origiati da ua superficie, processo che viee chiamato emissioe. Tutte le superfici al disopra dello zero assoluto emettoo
2 Spettroscopia. 9 fotoi. I fotoi emessi soo soggetti alle leggi fisiche della riflessioe, rifrazioe ed assorbimeto così come vi soo legati quelli icideti Figura.1. Iterazioe luce materia. I fotoi soo assorbiti dai mierali tramite differeti processi. Il tipo di processo di assorbimeto e la loro dipedeza dalla lughezza d oda ci permettoo di derivare iformazioi circa la chimica di u mierale tramite la luce riflessa o emessa. L occhio umao è uo spettrometro i riflessioe: possiamo vedere ua superficie e percepire i colori. I ostri occhi ed il cervello processado lo scatterig dipedete dalla lughezza d oda dei fotoi della luce visibile ci rivelao qualcosa delle superfici che stiamo osservado, come il colore rosso dell ematite o il verde dell olivia. U modero spettrofotometro può misurare degli ottimi dettagli su di u rage di lughezze d oda otevolmete allargato e co ottima precisioe. Così uo spettrofotometro può misurare
3 Spettroscopia. 3 assorbimeti dovuti a molti più processi di quelli che possoo essere visti dall occhio. Figura.. Defiizioi dei rage spettrali. Lo spettro elettromagetico è tradizioalmete diviso i ua serie di rage spettrali che si differeziao per le teciche usate per aalizzare la radiazioe: a) X (XR),: da,1 a 1 m; b) Ultravioletto (UV): da,1 a,4 µm; c) Visibile : da.4 a.7 µm; d) Vicio ifrarosso (NIR, Near-IfraRed): da.7 a 3. µm; e) Medio ifrasso (MIR, Mid-IfraRed): da 3. a 3µm; f) Lotao ifrarosso (FIR, Far IfraRed): da 3 µm a 1 mm; g) Millimetrico, da 1 a 1 mm; h) Micro ode (MW), da 1 mm ad 1 m; i) Radio, da 1 a 1 5 m.
4 Riflessioe. 31 Il rage di lughezza d'oda tra.4 a 1. µm solitamete è chiamato ella letteratura di remote sesig come VNIR (Visible-Near-IfraRed, visibile-vicioifrarosso) metre quello tra 1. e.5 µm è talvolta chiamato SWIR (Short Wave IfraRed, ifrarosso ad oda corta). È bee otare che questi termii o soo stadard i altri campi eccetto che el remote sesig. Il medio ifrarosso copre l eergia emessa termicamete, che per la Terra parte da.5 3. µm, co u picco a 1 µm e decrescedo dopo questo co u adameto simile all emissioe di u corpo grigio..1.. Riflessioe. La spettroscopia i riflessioe è lo studio della luce che viee riflessa o diffusa da u solido, u liquido o u gas, i fuzioe della lughezza d oda. Cosideriamo u campioe su cui icide u fascio di luce moocromatico J e da cui emerge il fascio riflesso R (vedi Figura.3.). Figura.3. Schema della riflessioe.
5 Riflessioe. 3 Possiamo idividuare tre piai: JN RN JR piao d icideza; piao d emersioe; piao di scatterig, avedo idicato co N l asse ormale al campioe. Se l agolo g, tra i piai JN e RN, risulta essere pari a o a π si ottiee che JN RN JR ed il piao viee detto pricipale (Hapcke, 1993). I geerale 3 agoli defiiscoo ua geometria specifica. Solitamete si usao i, e, g (vedi Figura.3.). Per semplicità si assume µ = cos e e µ = cos i. Il parametro co cui si misura la capacità di u materiale di riflettere il fascio icidete è chiamato riflettaza. Questa viee defiita come il rapporto tra l eergia diffusa per uità di area della superficie del mezzo e l eergia icidete collimata sull uità di superficie. Possiamo distiguere vari tipi di riflettaza a secoda della geometria del sistema i cui si opera: Riflettaza bidirezioale; Riflettaza bicoica; Riflettaza semisferica; Riflettaza sferica; Si darà ora ua breve descrizioe dei vari tipi di riflettaza, dado solo dei cei di carattere geometrico per quella semisferica poiché, essedo quella utilizzata ell acquisizioe dei dati, sarà sviluppata più a fodo el paragrafo successivo.
6 Riflessioe. 33 La riflettaza bidirezioale può essere misurata illumiado il campioe co della luce proveiete da ua sorgete co ua piccola apertura agolare, vista dal campioe, ed osservado la luce diffusa co u rivelatore mobile che sottede ach esso u piccolo agolo co la superficie del campioe (vedi Figura.4.). Figura.4. Geometria della riflessioe bidirezioale. Per otteere dei parametri di diffusioe il più precisi possibile, sarebbe cosigliabile misurare la riflettaza a diversi valori di i, e e g (g= φ φ ), ache se solitamete viee misurata co u solo set di agoli. La relazioe che esprime la riflettaza bidirezioale i fuzioe degli agoli i, e e g è data da: w µ, (.1) 4π µ + µ ( i e, g) = { p( g) + H ( µ ) H ( µ ) 1} r co e γ = 1 w. avedo idicato co: H ( x) 1+ x (.) 1+ γx j r
7 Riflessioe. 34 r riflettaza bidirezioale; w albedo di scatterig sigolo; p(z) fuzioe di fase (Hapke, 1993). La riflettaza bicoica è la prima riflettaza itegrata da oi icotrata. Ciò vuol dire che il detector o occupa tutto l agolo solido visto dalla superficie. L espressioe corretta per tale riflettaza può essere trovata, di cosegueza, itegrado l espressioe (.1) su tutta la distribuzioe agolare della radiazioe e la distribuzioe agolare della risposta del detector (Salisbury et al, 1991). La riflettaza semisferica viee misurata tramite ua sfera itegratrice. Figura.5. Geometria della riflettaza semisferica. Questo dispositivo (vedi Figura.5.) cosiste i ua cavità ricoperta da u materiale ad alta riflettività diffusa, i cui soo praticate due piccole aperture, o porte, ua per permettere al fascio icidete di etrare, l altra per permettere di osservare la radiazioe presete ella sfera. Naturalmete l espressioe che
8 Riflettaza semisferica. 35 forisce la riflettaza semisferica, come vedremo i dettaglio i seguito, sarà datata dalla (.1) itegrata su di u agolo solido di π. Per ciò che riguarda la riflettaza sferica essa viee, i liea di pricipio, misurata tramite ua sfera opaca ricoperta dal campioe e posta al cetro della sfera itegratrice. U lato del campioe viee illumiato da u fascio di luce collimato, metre la radiazioe che viee diffusa i tutte le direzioi viee misurata da u rivelatore che o vede il bersaglio direttamete Riflettaza semisferica. L importaza della riflettaza semisferica è dovuta pricipalmete a due ragioi: 1. È la quatità che è direttamete misurata da molti spettrofotometri commerciali a riflessioe;. È ua delle proprietà di u materiale che determiao la temperatura di equilibrio radiativo (vedi paragrafo.1.4.). L eergia icidete per uità di area è Jµ. L eergia uscete ell uità di agolo solido per uità di superficie è Y=Jr(i,e,g)µ. 1 1 r h = Y ( i, e, g) dω = ( ) µ Ω µ π e r i, e, g d µ π e. J Sostituedo a r(i,e,g) l espressioe data dalla (.1) ed essedo dω e = si e de dψ, si ottiee l equazioe della riflettaza semisferica:
9 Riflettaza semisferica. 36 w π π µ rh () i = [ p( g) + H ( µ ) ( µ ) ] ψ π ψ = e= H 1 si e de d. 4 µ + µ Si può esprimere la riflettaza semisferica come cotributo di due diversi elemeti r + h = rhi rha, co hi r riflettaza semisferica isotropa ed r ha riflettaza semisferica aisotropa, che possoo essere espressi come: w 1 µ hi = H µ = µ + µ r ( µ ) H ( µ ) dµ r ha w 4π π = 1 ψ = µ = µ µ + µ [ p( g) 1] dµ dψ Sviluppado i calcoli si ottiee: w 1 µ + 1 r hi = 1 γh ( µ ) r ha = µ b1 µ + µ l µ Quidi si ottiee: w 1 µ + () ( ) 1 r h i = 1 γh µ + µ b1 µ + µ l. µ Sviluppado i serie di Taylor: µ + 1 µ µ l µ, 1+ µ e, sostituedo H(µ) dato dalla (.), si ottiee: 1 γ w µ r h () i = + b. 1+ γµ µ Sotto opportue ipotesi semplificative si può defiire la riflettaza r, detta diffusiva (Hapke, 1993), il rapporto: P r = P em. i
10 Riflettaza semisferica. 37 P i è l eergia totale icidete sul materiale per uità di superficie P i π = I cos ϑ π siϑ dϑ = π I, dove I è l itesità del raggio icidete secodo la ormale. P em è l eergia totale diffusa i tutte le direzioi emergeti per uità di superficie: P em π 1 1 γ 1 + γ ( ) cos ϑ π ϑ dϑ = π I1( ) = π I = π Ir = I si co I 1 () riflesso ella direzioe ormale. Quidi si ha che: 1 γ r =. (.3) 1 + γ 1 r Si trova, ivertedo la (.3), che γ = e 1+ r w 4r =. ( 1+ r ) Come cosegueza si può defiire, itroducedo i parametri K ed S, rispettivamete il coefficiete di assorbimeto volumetrico ed il coefficiete di scatterig volumetrico di Kubelka-Muk, l equazioe di Kubelka-Muk. Il coefficiete di estizioe risulta essere defiito come ( K ' + S' ). Tramite questi parametri si può ridefiire l albedo di scatterig sigolo di volume come di cosegueza si può defiire S' w' =, K' + S' γ ' = 1 w'. Per aalogia alla (.3) possiamo quidi scrivere:
11 Trasmissioe. 38 ( K' + S' ) ( K' + S' ) ( K' + S' ) ( K' S' ) r 1 γ ' 1 1 S' 1 K' ' = = = 1 + γ ' S' 1 + K' +. (.4) Combiado l approssimazioe diffusiva, equazioe (.3), co la legge di scatterig di Lambert otteiamo l espressioe Lambert-diffusiva: r hl = r Ricordiamo brevemete che la radiazioe diffusa da ua sfera ella direzioe dell osservatore è data da: I = ( π ) g π Λ= π L= π JY ( i e, g), da, co Y 1 π ( i, e, g) = cosi cose legge di Lambert e L e Λ latitudie e logitudie dell elemeto ifiitesimo di superficie della sfera da sulla sfera..1.. Trasmissioe. Come si è visto el paragrafo precedete il fascio icidete, idicato co J i Figura.3., viee riflesso atteuato. Idichiamo co I la differeza di eergia tra il fascio icidete e quello riflesso, I = J R. Tale eergia può subire due processi: o viee trasmessa attraverso il campioe o viee assorbita dallo stesso. I due processi avvegoo aturalmete simultaeamete a patto che la profodità ottica del materiale sia bassa, altrimeti l itera eergia viee assorbita.
12 Trasmissioe. 39 Figura.6. Trasmissioe attraverso u materiale. Suppoiamo che il ostro campioe sia otticamete sottile. Se I è l itesità della luce icidete su di u materiale e I l itesità della luce che riceve l osservatore (vedi Figura.6.), si avrà che queste soo legate dalla relazioe: I = IT dove T rappreseta la traspareza del campioe. Si defiisce poi assorbaza la quatità: ( ) = [ T ( λ) ] 1 A λ log. (.5) dove: I forma differeziale possiamo scrivere 1 : diλ = k λ ρ g Iλ ds (.6) di λ rappreseta la radiazioe assorbita; k λ è il coefficiete di assorbimeto per uità di massa; 1 Di particolare importaza è il sego egativo ell espressioe di λ, ifatti sottoliea il fatto che ci sia stata ua dimiuzioe ell itesità della radiazioe a causa dell attraversameto del campioe. di
13 Trasmissioe. 4 ρ g è la desità di materia attraversata; I λ è l itesità di radiazioe i igresso; ds è lo spessore ifiitesimo del mezzo attraversato. Il coefficiete di assorbimeto, el caso di grai, è dato da : dove ( λ) ext ( λ) 3 Cext I k λ = 4 3 πa ρ (.7) C è detta sezioe efficace di estizioe, V la il volume della particella di materia e ρ M la desità del materiale che costituisce i grai. A questo puto si fao due ipotesi importati: 1. le particelle devoo essere omogeee sia i composizioe sia i desità;. le particelle hao tutte la stessa forma, sferica, e le stesse dimesioi. Se quidi ipotizziamo che a sia il raggio del grao sferico, il termie V della M (.7) risulta essere pari a 4 a 3 π 3, metre la massa g m risulta essere di cosegueza 4 πa 3 ρ M 3. Risulta ora più chiara la differeza tra le desità ρ g e ρ M preseti ella (.6) e ella (.7) rispettivamete, ifatti la prima rappreseta la desità di u volume attraversato dalla radiazioe, metre la secoda rappreseta la desità del sigolo grao sferico. Il coefficiete di estizioe, C ( λ) ext legato all eergia estita dalla radiazioe: C ext ( λ) W =, o sezioe efficace di estizioe può essere abs ( λ) + Wsca ( λ) I ( λ)
14 Trasmissioe. 41 dove ( λ) W è l eergia assorbita dal materiale per uità di tempo, metre abs W ( λ) è quella diffusa. Essedo ( λ) sca tempo, risulta evidete che ( λ) Tramite la relazioe Q ext I u eergia per uità di superficie e di C dimesioalmete è ua superficie. ext ( ) ( λ) Cext λ = (.8) πa si defiisce il fattore di estizioe efficace o fattore di efficieza di estizioe. Il ( λ) C viee poi ad essere legato all idice di rifrazioe ext ( λ) = ( λ) ik( λ), dove ( λ) m + è l idice di rifrazioe ormalmete usato e trascura l assorbimeto della radiazioe da parte del campioe, metre k ( λ) tiee apputo coto dell assorbimeto. Riprediamo la (.6): ed itegriamola, si ottiee: avedo posto λ diλ = k λ ρ g Iλ ds S I = I = I e τ k λ ρ λe gds S τ λ ( λ ), ( λ) k ρ ds = k ρ S = λ g λ detto spessore ottico, avedo supposto costati k λ e di ρ g. Sostituiamo ella defiizioe di spessore ottico il valore di k λ, trovato ella (.7), si ottiee: ( λ) ρ g S Cext ( λ) 3 C ρ g S ext τ ( λ) = = = gcext ( λ) S, 4 3 πa ρ m M g g
15 Trasmissioe. 4 sapedo che g = ρ m. g g Avedo defiito la traspareza come T ( λ) ( λ) I = = e I τ ( λ ), si ottiee che ( λ) = [ T ( λ) ] 1 τ l e di cosegueza C dove M è la massa dei grai, ext ( λ) 4 3 ρ M S 1 = πa l, (.9) 3 M T ( λ) M 4 3 = πa ρ M g S s, 3 co: 4 π 3 a volume del grao, 3 ρ M la desità del materiale, g il umero dei grai, S la sezioe del fascio, s lo spessore del campioe. Se per quato riguarda ρ M ci si può avvalere di iformazioi tabulate, per quato riguarda M ed S si è costretti a fare u ipotesi: si suppoe che tutti i grai siao distribuiti omogeeamete i tutto il volume S s. Ua volta che è stato fissato lo spessore s, che altro o è che lo spessore della pasticca, si sostituisce ella formula del C ext al posto del rapporto S M il rapporto S M, dove S è
16 Trasmissioe. 43 la sezioe della pasticca ed M la massa totale del campioe. Questa sostituzioe è possibile i quato, avedo supposto l omogeeità, viee verificata la proporzioe S : S = M : M. Ricordado che si soo approssimati i grai a delle sferette di raggio a resta il problema di stimare a. i realtà questo problema viee aggirato adado a calcolare la quatità Q ext a, o più precisamete Q ext a, i quato o tutti i grai hao lo stesso raggio. Si può però forire u legame tra Q ext Q ext a e l assorbaza, data dalla (.7): ( ) A( λ) λ = ξ a avedo riuito tutti i termii costati i ξ. Poiché lo spessore è, per motivi tecici, sempre costate ed S è la sezioe della pasticca, ache essa costate, l uico parametro su cui si può operare è M. M.1.3. Emissioe. Come è stato detto ell itroduzioe di questa sezioe, tutte le superfici al disopra dello zero assoluto emettoo fotoi. La radiazioe emessa viee detta radiazioe termica. La radiazioe emessa da u corpo dipede dalla composizioe chimica e fisica dello stesso, ma esiste ua classe di corpi, puramete teorici, che emettoo spettri termici di carattere uiversale. Questi corpi soo detti corpi eri e soo dotati di superfici che hao la peculiarità di assorbire tutta la radiazioe,
17 Emissioe. 44 idipedetemete dalla lughezza d oda, icidete su di essi e di riemetterla su di uo spettro che dipede soltato dalla temperatura. La distribuzioe spettrale di questi corpi è be ota si dagli iizi del secolo e segue la legge: dove B ( λ,t ) è la fuzioe di Plak: dove: B h è la costate di Plak, 1 I BB, π ( λ, T ) k è la costate di Boltzma, c è la velocità della luce el vuoto. ( λ, T ) = B( λ T ) = πhc λ 5 hc λkt La poteza emessa termicamete da ua superficie è detta emittaza. Se si misura l emittaza della superficie di u campioe di spessore ottico ifiito si trova, geeralmete, che lo spettro è simile alla fuzioe di Plak, ma è più basso di ua quatità che può variare co la lughezza d oda. Il rapporto tra la poteza emessa, per uità di area, da ua superficie a temperatura T, U ( λ,t ), e quella emessa da u corpo ero alla stessa temperatura, defiisce l emissività spettrale ε ( λ) della superficie: U ε ( λ) = B e ( λ, T ) ( λ, T ) Se ε è idipedete dalla lughezza d oda, la superficie è chiamata corpo grigio. 1
18 Emissioe. 45 I laboratorio, si eseguoo misure di u particolare tipo di emissività, l emissività direzioale ε ( ϑ, λ) d, che corrispode al rapporto tra la radiazioe termica emergete dalla superficie del campioe particolato, a temperatura uiforme T, ella direzioe che forma u agolo ϑ co la ormale alla superficie, ( ϑ,λ ) I,T temperatura :, e la radiazioe termica emergete da u corpo ero alla stessa ( ϑ, λ, T ) B( λ, T ) I ε = π. d Le misure i emissioe vegoo effettuate riscaldado, a temperature superiori a quella ambiete, sia il campioe sia il corpo ero di riferimeto. L eergia emessa viee, quidi, registrata dallo spettrofotometro e visualizzata i fuzioe della lughezza d oda (vedi diagramma schematico i Figura.7.) (De Carlo, 1997). La radiazioe di corpo ero è isotropa.
19 Legame tra emissività e riflettaza. 46 Figura.7. Diagramma schematico di come avviee ua misura di emissioe Legame tra emissività e riflettaza. La legge di Kirchhoff è ua regola estremamete potete che afferma l esisteza di ua relazioe fuzioale tra l emissività e la riflettaza. I codizioi ideali, i cui la superficie è isoterma e tutta l eergia diffusa ed emessa può essere misurata, la legge di Kirchhoff è: ε ( λ) = 1 R( λ) dove ε ( λ) è l emissività del materiale e ( λ) R è la riflettaza semisferica. Figura.8. Gustav Robert Kirchhoff.
20 Trasmissioe. 47 La legge di Kirchhoff fu origiariamete derivata per campioi opachi i equilibrio termico co l ambiete. L equilibrio termico qui riferito è u equilibrio termodiamico, o semplicemete uo stato termico costate. Questo implica che il campioe è isotermo e alla stessa temperatura del backgroud a cui irradia. Ua tale situazioe o esiste ella maggior parte delle misure di laboratorio di emissività e o esiste mai elle applicazioi di remote sesig. Questo ha portato a teciche di misura di emissività i laboratorio che usao cofigurazioi dell apparato sperimetale tali da assicurare al campioe ed al suo cotoro ua temperatura il più possibile uiforme. Tuttavia, u campioe che irradia liberamete (per esempio u campioe che irradia idipedetemete dal campo di radiazioe ambietale) seguirà acora la legge di Kirchhoff, se gli stati di eergia del campioe obbediscoo alla distribuzioe di Boltzma (Salisbury et al, 1994). Nel caso i cui la superficie del campioe irradi liberamete verso u backgroud molto più freddo, ci sarà, sicuramete, u gradiete termico all itero del campioe e questo può limitare la validità della legge. Misure i laboratorio di riflettaza semisferica e di emissività direzioale, eseguite su campioi di roccia solida e di suolo, mostrao che tali campioi, pur co u gradiete termico, seguoo la legge di Kirchhoff all itero dell errore sperimetale. Soltato i u campioe costituito da materiale particolato fie, di desità estremamete bassa, è stato trovato u gradiete termico abbastaza ripido, ello spessore da cui proviee la radiazioe ifrarossa emessa dal
21 Cei sulla teoria di Mie. 48 campioe, tale da causare u allotaameto dalla legge di Kirchhoff, etro il 6% (Salisbury et al, 1994). Cei sulla teoria di Mie. La teoria classica che iterpreta, co l elettromagetismo descritto dalle equazioi di Maxwell, i processi di iterazioe della radiazioe co le particelle è comuemete detta teoria di Mie; essa vale per particelle di forma sferica, omogeee ed otticamete isotrope (cioè aveti proprietà ottiche, quali ad esempio la costate dielettrica, l idice di rifrazioe, la coducibilità, che o dipedoo dalla direzioe). Riprediamo il coefficiete C ext (sezioe efficace di estizioe) itrodotto el paragrafo.1... Esso può essere ache espresso come: C = C + C = W ext abs sca ext F dove: C abs è la sezioe efficace di assorbimeto del grao, defiita dal rapporto tra la poteza W abs (eergia per uità di tempo) assorbita dal grao ed il flusso F (eergia per uità di tempo e di area) della radiazioe icidete; C sca è la sezioe efficace di diffusioe del grao, defiita dal rapporto tra la poteza W sca rimossa per diffusioe dalla particella ed il flusso di radiazioe icidete; W ext è la poteza rimossa per assorbimeto e diffusioe del fascio icidete dalla particella (W ext = W abs + W sca ).
22 Cei sulla teoria di Mie. 49 Ovviamete tutte le gradezze soo fuzioe della lughezza d oda λ. A partire da queste gradezze si possoo defiire i fattori di efficieza di diffusioe e di assorbimeto, Q sca e Q abs rispettivamete, tramite formule del tutto aaloghe alla (.8). I fattori di efficieza di ua particella sferica di raggio a, composta da materiale di idice di rifrazioe (complesso) m = ik, soo dati dai segueti sviluppi i serie: Q sca = (.1) x = 1 ( + 1)[ a + b ] Q Re + (.11) ext = x = 1 ( + 1) ( a b ) ei quali (da o cofodere co la parte reale dell idice di rifrazioe complesso) è l idice su cui corre la sommatoria, il parametro x è dato da: πa x =, λ metre a e b soo detti coefficieti di scatterig e soo dati dalle espressioi segueti: a b ( mx) ψ ( x) ψ ( mx) mψ ψ ( x) = (.1) mψ ( mx) ξ ( x) ψ ( mx) ξ ( x) ( mx) ψ ( x) mψ ( mx) ψ ψ ( x) =. (.13) ψ ( mx) ξ ( x) mψ ( mx) ξ ( x) I queste formule le fuzioi di variabile complessa ψ (z) e ξ (z), isieme co le loro coiugate ψ (z) e ξ (z), soo le così dette fuzioi di Riccati-Bessel; esse soo defiite tramite le fuzioi di Bessel j (z) e h (1) (z), dalle segueti relazioi:
23 Cei sulla teoria di Mie. 5 e ψ ( z) zj ( z) = ( 1 ξ ( z) zh ) ( z). = Tramite questa tecica è quidi possibile calcolare le costati ottiche del materiale. Possiamo ora dare ora delle approssimazioi delle formule (.1) e (.11) sotto l ipotesi richiesta che sia verificata la relazioe π a < λ, (.14) cioè che la lughezza dell oda icidete sia molto più grade della circofereza della particella. Si ha che: Q sca 8 4 m 1 x (.1 ) 3 m + e Q ext m 4x Im m 1 + x + 3 Im 4 15 m m 1 m m m m 1 + x Re (.11 ) 3 m + Per grai acora più piccoli, grai per cui la (.14) diviee la (.11 ) si riduce al primo termie, cioè: π a << λ, (.15) m 1 Q ext 4x Im. m +
24 Cei sulla teoria di Mie. 51 Come si vedrà el prossimo capitolo lo spettrofotometro a disposizioe copre u rage compreso tra, e,5 µm metre il diametro del più piccolo grao è stimato essere itoro ad 1 µm. Se applichiamo l ipotesi (.14) a quest ultimo campioe troviamo che la lughezza d oda icidete è miore di 6,8 µm. Risulta quidi che l ipotesi (.14) o è applicabile elle codizioi i cui verrao effettuate le misure.
Riflessione, trasmissione o assorbimento
 Riflessioe, trasmissioe o assorbimeto L idice di rifrazioe complesso i fuzioe della frequeza è u parametro estremamete utile perché rappreseta tutte le caratteristiche ottiche del materiale. Quado la radiazioe
Riflessioe, trasmissioe o assorbimeto L idice di rifrazioe complesso i fuzioe della frequeza è u parametro estremamete utile perché rappreseta tutte le caratteristiche ottiche del materiale. Quado la radiazioe
Diottro sferico. Capitolo 2
 Capitolo 2 Diottro sferico Si idica co il termie diottro sferico ua calotta sferica che separa due mezzi co idice di rifrazioe diverso. La cogiugete il cetro di curvatura C della calotta co il vertice
Capitolo 2 Diottro sferico Si idica co il termie diottro sferico ua calotta sferica che separa due mezzi co idice di rifrazioe diverso. La cogiugete il cetro di curvatura C della calotta co il vertice
Velocità della Luce e sua variazione. Nel passaggio dal vuoto ( cm/sec) ad un altro mezzo la velocità della luce diminuisce.
 RIFRATTOMETRIA Defiizioe La rifrattometria è ua tecica strumetale che si basa sulla determiazioe di u parametro, l idice di rifrazioe, associato al feomeo della rifrazioe, cioè alla variazioe subita dalla
RIFRATTOMETRIA Defiizioe La rifrattometria è ua tecica strumetale che si basa sulla determiazioe di u parametro, l idice di rifrazioe, associato al feomeo della rifrazioe, cioè alla variazioe subita dalla
Diottri sferici e lenti
 Diottri sferici e leti Deis Bastieri Dipartimeto di Fisica & Astroomia G. Galilei Uiversità di Padova 6 dicembre 013 1 Il diottro sferico I due mezzi che costituiscoo il diottro siao ora separati da ua
Diottri sferici e leti Deis Bastieri Dipartimeto di Fisica & Astroomia G. Galilei Uiversità di Padova 6 dicembre 013 1 Il diottro sferico I due mezzi che costituiscoo il diottro siao ora separati da ua
4: Strato fisico: i segnali nel tempo e nella frequenza
 1 1 4: Strato fisico: i segali el tempo e ella frequeza Lo strato fisico Le pricipali fuzioi dello strato fisico soo defiizioe delle iterfacce meccaiche (specifiche dei coettori) tra il mezzo trasmissivo
1 1 4: Strato fisico: i segali el tempo e ella frequeza Lo strato fisico Le pricipali fuzioi dello strato fisico soo defiizioe delle iterfacce meccaiche (specifiche dei coettori) tra il mezzo trasmissivo
2,3, (allineamenti decimali con segno, quindi chiaramente numeri reali); 4 ( = 1,33)
 Defiizioe di umero reale come allieameto decimale co sego. Numeri reali positivi. Numeri razioali: defiizioe e proprietà di desità Numeri reali Defiizioe: U umero reale è u allieameto decimale co sego,
Defiizioe di umero reale come allieameto decimale co sego. Numeri reali positivi. Numeri razioali: defiizioe e proprietà di desità Numeri reali Defiizioe: U umero reale è u allieameto decimale co sego,
C a p i t o l o s e t t i m o. Trasmissione del calore per radiazione
 C a p i t o l o s e t t i m o Trasmissioe del calore per radiazioe Problema. Si cosideri u corpo ero i uo spazio o assorbete le radiazioi elettromagetiche; se il corpo viee mateuto alla temperatura di
C a p i t o l o s e t t i m o Trasmissioe del calore per radiazioe Problema. Si cosideri u corpo ero i uo spazio o assorbete le radiazioi elettromagetiche; se il corpo viee mateuto alla temperatura di
Campionamento casuale da popolazione finita (caso senza reinserimento )
 Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Esposizione al campo elettromagnetico
 Uiversità degli Studi di Pavia Facoltà di Igegeria Pricipi e Corso di Applicazioi di Teoria dei Circuiti Elettrotecica Esposizioe al campo elettromagetico Dipartimeto di Igegeria Elettrica Dip. di Igegeria
Uiversità degli Studi di Pavia Facoltà di Igegeria Pricipi e Corso di Applicazioi di Teoria dei Circuiti Elettrotecica Esposizioe al campo elettromagetico Dipartimeto di Igegeria Elettrica Dip. di Igegeria
3.1 Rappresentazione dello stato tensionale nel piano di Mohr: circoli di Mohr.
 DIDATTICA DI PROGETTAZIONE DELLE COSTRUZIONI PROF. CARMELO MAJORANA MODULO TRE I CONCETTI FONDAMENTALI NELL ANALISI DELLA TENSIONE PARTE B) MODULO PER LO SPECIALIZZANDO Modulo. Rappresetazioe dello stato
DIDATTICA DI PROGETTAZIONE DELLE COSTRUZIONI PROF. CARMELO MAJORANA MODULO TRE I CONCETTI FONDAMENTALI NELL ANALISI DELLA TENSIONE PARTE B) MODULO PER LO SPECIALIZZANDO Modulo. Rappresetazioe dello stato
d dt d dt Le equazioni di Maxwell int Teorema di Gauss (flusso elettrico totale attraverso superficie chiusa = carica netta)
 Le equazioi di Maxwell B E S E s B da da 0 q it 0 Teorema di Gauss (flusso elettrico totale attraverso superficie chiusa = carica etta) Flusso magetico etto attraverso ua superficie chiusa è ullo (teorema
Le equazioi di Maxwell B E S E s B da da 0 q it 0 Teorema di Gauss (flusso elettrico totale attraverso superficie chiusa = carica etta) Flusso magetico etto attraverso ua superficie chiusa è ullo (teorema
Proposizione 1. Due sfere di R m hanno intersezione non vuota se e solo se la somma dei loro raggi e maggiore della distanza fra i loro centri.
 Laboratorio di Matematica, A.A. 009-010; I modulo; Lezioi II e III - schema. Limiti e isiemi aperti; SB, Cap. 1 Successioi di vettori; SB, Par. 1.1, pp. 3-6 Itori sferici aperti. Nell aalisi i ua variabile
Laboratorio di Matematica, A.A. 009-010; I modulo; Lezioi II e III - schema. Limiti e isiemi aperti; SB, Cap. 1 Successioi di vettori; SB, Par. 1.1, pp. 3-6 Itori sferici aperti. Nell aalisi i ua variabile
Elementi di statistica
 Elemeti di statistica La misura delle gradezze fisiche può essere effettuata direttamete o idirettamete. Se la misura viee effettuata direttamete si parla di misura diretta; se essa viee dedotta attraverso
Elemeti di statistica La misura delle gradezze fisiche può essere effettuata direttamete o idirettamete. Se la misura viee effettuata direttamete si parla di misura diretta; se essa viee dedotta attraverso
1.6 Serie di potenze - Esercizi risolti
 6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
Esercizi sui numeri complessi per il dodicesimo foglio di esercizi
 Esercizi sui umeri complessi per il dodicesimo foglio di esercizi 6 dicembre 2010 1 Numeri complessi radici ed equazioi Ricordiamo iazitutto che dato u umero complesso z = x + iy, il suo coiugato, idicato
Esercizi sui umeri complessi per il dodicesimo foglio di esercizi 6 dicembre 2010 1 Numeri complessi radici ed equazioi Ricordiamo iazitutto che dato u umero complesso z = x + iy, il suo coiugato, idicato
Sviluppi di Taylor. Andrea Corli 1 settembre Notazione o 1. 3 Formula di Taylor 3. 4 Esempi ed applicazioni 5
 Sviluppi di Taylor Adrea Corli settembre 009 Idice Notazioe o Liearizzazioe di ua fuzioe 3 Formula di Taylor 3 4 Esempi ed applicazioi 5 I questo capitolo aalizziamo l approssimazioe di ua fuzioe regolare
Sviluppi di Taylor Adrea Corli settembre 009 Idice Notazioe o Liearizzazioe di ua fuzioe 3 Formula di Taylor 3 4 Esempi ed applicazioi 5 I questo capitolo aalizziamo l approssimazioe di ua fuzioe regolare
INTERAZIONE DELLA RADIAZIONE CON I GRANI DI POLVERE: TEORIA DI MIE (GRANI SFERICI)
 Dispesa. 1/A del corso di PLANETOLOGIA (Prof. V. Orofio) INTERAZIONE DELLA RADIAZIONE CON I GRANI DI POLVERE: TEORIA DI MIE (GRANI SFERICI) Uiversità del Saleto Corso di Laurea Magistrale i Fisica A.A.
Dispesa. 1/A del corso di PLANETOLOGIA (Prof. V. Orofio) INTERAZIONE DELLA RADIAZIONE CON I GRANI DI POLVERE: TEORIA DI MIE (GRANI SFERICI) Uiversità del Saleto Corso di Laurea Magistrale i Fisica A.A.
x n (1.1) n=0 1 x La serie geometrica è un esempio di serie di potenze. Definizione 1 Chiamiamo serie di potenze ogni serie della forma
 1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
1 Serie di poteze È stato dimostrato che la serie geometrica x (1.1) coverge se e solo se la ragioe x soddisfa la disuguagliaza 1 < x < 1. I realtà c è covergeza assoluta i ] 1, 1[. Per x 1 la serie diverge
FORMULAZIONE ALTERNATIVA DELLE EQUAZIONI DI MAXWELL IN FORMA INTEGRALE
 FORMULAZIONE ALTERNATIA DELLE EQUAZIONI DI MAXWELL IN FORMA INTEGRALE i riscrivoo le equazioi di Maxwell i ua forma itegrale alterativa comoda per la determiazioe delle codizioi al cotoro: Ed B d (3.5a)
FORMULAZIONE ALTERNATIA DELLE EQUAZIONI DI MAXWELL IN FORMA INTEGRALE i riscrivoo le equazioi di Maxwell i ua forma itegrale alterativa comoda per la determiazioe delle codizioi al cotoro: Ed B d (3.5a)
Precorso di Matematica, aa , (IV)
 Precorso di Matematica, aa 01-01, (IV) Poteze, Espoeziali e Logaritmi 1. Nel campo R dei umeri reali, il umero 1 e caratterizzato dalla proprieta che 1a = a, per ogi a R; per ogi umero a 0, l equazioe
Precorso di Matematica, aa 01-01, (IV) Poteze, Espoeziali e Logaritmi 1. Nel campo R dei umeri reali, il umero 1 e caratterizzato dalla proprieta che 1a = a, per ogi a R; per ogi umero a 0, l equazioe
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
Esponenziale complesso
 Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
SERIE DI POTENZE Esercizi risolti. Esercizio 1 Determinare il raggio di convergenza e l insieme di convergenza della serie di potenze. x n.
 SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
le dimensioni dell aiuola, con le limitazioni 0 x λ λ
 PROBLEMA a) idicate co e co che e esprime l area è: le dimesioi dell aiuola, co le limitazioi 0 A( )., la fuzioe Per la ricerca del massimo si studia il sego della derivata prima Si ha: 0 / / A' ( ). Si
PROBLEMA a) idicate co e co che e esprime l area è: le dimesioi dell aiuola, co le limitazioi 0 A( )., la fuzioe Per la ricerca del massimo si studia il sego della derivata prima Si ha: 0 / / A' ( ). Si
Sistemi e Tecnologie della Comunicazione
 Sistemi e ecologie della Comuicazioe Lezioe 4: strato fisico: caratterizzazioe del segale i frequeza Lo strato fisico Le pricipali fuzioi dello strato fisico soo defiizioe delle iterfacce meccaiche (specifiche
Sistemi e ecologie della Comuicazioe Lezioe 4: strato fisico: caratterizzazioe del segale i frequeza Lo strato fisico Le pricipali fuzioi dello strato fisico soo defiizioe delle iterfacce meccaiche (specifiche
(1 2 3) (1 2) Lezione 10. I gruppi diedrali.
 Lezioe 0 Prerequisiti: Simmetrie di poligoi regolari. Gruppi di permutazioi. Cetro di u gruppo. Cetralizzate di u elemeto di u gruppo. Riferimeto al testo: [PC] Sezioe 5.4 I gruppi diedrali. Ogi simmetria
Lezioe 0 Prerequisiti: Simmetrie di poligoi regolari. Gruppi di permutazioi. Cetro di u gruppo. Cetralizzate di u elemeto di u gruppo. Riferimeto al testo: [PC] Sezioe 5.4 I gruppi diedrali. Ogi simmetria
Radici, potenze, logaritmi in campo complesso.
 SOMMARIO NUMERI COMPLESSI... Formula di Eulero... Coiugato di u umero complesso... 3 Poteza -esima di u umero complesso z (formula di De Moivre... 3 Radice -esima di z... 3 Osservazioi... Logaritmo di
SOMMARIO NUMERI COMPLESSI... Formula di Eulero... Coiugato di u umero complesso... 3 Poteza -esima di u umero complesso z (formula di De Moivre... 3 Radice -esima di z... 3 Osservazioi... Logaritmo di
Distribuzione normale o gaussiana
 Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER
 TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
TEOREMA DELLA PROIEZIONE, DISUGUAGLIANZA DI BESSEL E COMPLEMENTI SULLE SERIE DI FOURIER I uo spazio euclideo di dimesioe fiita, ad esempio R 3, cosideriamo u sottospazio, ad esempio u piao passate per
0.1 Esercitazioni V, del 18/11/2008
 1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate sui fogli protocollo e riportate nel foglio RISPOSTE.
 CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
Analisi I - IngBM COMPITO B 17 Gennaio 2015 COGNOME... NOME... MATRICOLA... VALUTAZIONE =...
 Aalisi I - IgBM - 2014-15 COMPITO B 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
Aalisi I - IgBM - 2014-15 COMPITO B 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
a n (x x 0 ) n. (1.1) n=0
 Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Serie di poteze. Defiizioi Assegati ua successioe {a } di umeri reali e u puto x dell asse reale si dice serie di poteze u espressioe del tipo a (x x ). (.) Il puto x viee detto cetro della serie e i umeri
Analisi I - IngBM COMPITO A 17 Gennaio 2015 COGNOME... NOME... MATRICOLA... VALUTAZIONE =...
 Aalisi I - IgBM - 2014-15 COMPITO A 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
Aalisi I - IgBM - 2014-15 COMPITO A 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
Lezione 3: Segnali periodici
 eoria dei segali Segali a poteza media fiita e coversioe A/D Lezioe 3: Aalisi i frequeza Esempio di calcolo 005 Politecico di orio eoria dei segali aalisi i frequeza Poteza media Sia dato u segale (t)
eoria dei segali Segali a poteza media fiita e coversioe A/D Lezioe 3: Aalisi i frequeza Esempio di calcolo 005 Politecico di orio eoria dei segali aalisi i frequeza Poteza media Sia dato u segale (t)
Lezioni di Matematica 1 - I modulo
 Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
Lezioi di Matematica 1 - I modulo Luciao Battaia 4 dicembre 2008 L. Battaia - http://www.batmath.it Mat. 1 - I mod. Lez. del 04/12/2008 1 / 28 -2 Sottosuccessioi Grafici Ricorreza Proprietà defiitive Limiti
Entropia ed informazione
 Etropia ed iformazioe Primi elemeti sulla teoria della misura dell iformazioe Per trasmettere l iformazioe è ecessaria ua rete di comuicazioe, che, secodo l approccio teorico di Claude E. Shao e Warre
Etropia ed iformazioe Primi elemeti sulla teoria della misura dell iformazioe Per trasmettere l iformazioe è ecessaria ua rete di comuicazioe, che, secodo l approccio teorico di Claude E. Shao e Warre
Appendice 2. Norme di vettori e matrici
 Appedice 2. Norme di vettori e matrici La ozioe esseziale per poter defiire il cocetto di distaza e lughezza i uo spazio vettoriale lieare è quello di orma. Il cocetto di orma è ua geeralizzazioe del cocetto
Appedice 2. Norme di vettori e matrici La ozioe esseziale per poter defiire il cocetto di distaza e lughezza i uo spazio vettoriale lieare è quello di orma. Il cocetto di orma è ua geeralizzazioe del cocetto
Probabilità CENNI DI PROBABILITÀ
 CENNI DI PROBABILITÀ Itroduzioe I queste pagie verrao esposti i breve i cocetti base della teoria delle probabilità. Lo scopo è quello di forire le basi i modo che siao più compresibile l uso che e viee
CENNI DI PROBABILITÀ Itroduzioe I queste pagie verrao esposti i breve i cocetti base della teoria delle probabilità. Lo scopo è quello di forire le basi i modo che siao più compresibile l uso che e viee
Argomenti trattati: Stima puntuale e stimatore Proprietà degli stimatori Stima puntuale della media della
 1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
1. a n = n 1 a 1 = 0, a 2 = 1, a 3 = 2, a 4 = 3,... Questa successione cresce sempre piú al crescere di n e vedremo che {a n } diverge.
 Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Le successioi A parole ua successioe é u isieme ifiito di umeri disposti i u particolare ordie. Piú rigorosamete, ua successioe é ua legge che associa ad ogi umero aturale u altro umero (ache o aturale):
Geometria analitica: rette e piani
 Geometria aalitica: rette e piai Coordiate polari Cambiameti di riferimeto el piao Cambiameti di riferimeto i geerale Isometrie Simmetrie Isometrie el piao Isometrie ello spazio 2 2006 Politecico di Torio
Geometria aalitica: rette e piai Coordiate polari Cambiameti di riferimeto el piao Cambiameti di riferimeto i geerale Isometrie Simmetrie Isometrie el piao Isometrie ello spazio 2 2006 Politecico di Torio
ESERCIZI UNITA G SOMMARIO
 Cotrollo Termico dei Sistemi di Calcolo Es.G/0 ESERCIZI UNITA G SOMMARIO G. PERDITE DI CARICO G.I. G.II. G.III. G.IV. G.V. G.VI. Efflusso da serbatoio Codotto di vetilazioe Pompaggio di ua portata d acqua
Cotrollo Termico dei Sistemi di Calcolo Es.G/0 ESERCIZI UNITA G SOMMARIO G. PERDITE DI CARICO G.I. G.II. G.III. G.IV. G.V. G.VI. Efflusso da serbatoio Codotto di vetilazioe Pompaggio di ua portata d acqua
Introduzione all Analisi di Fourier. Prof. Luigi Landini Ing. Nicola Vanello. (presentazione a cura di N. Vanello)
 Itroduzioe all Aalisi di Prof. Luigi Ladii Ig. Nicola Vaello (presetazioe a cura di N. Vaello) ANALII DI FOURIER egali tempo cotiui: egali periodici egali aperiodici viluppo i serie di Itroduzioe alla
Itroduzioe all Aalisi di Prof. Luigi Ladii Ig. Nicola Vaello (presetazioe a cura di N. Vaello) ANALII DI FOURIER egali tempo cotiui: egali periodici egali aperiodici viluppo i serie di Itroduzioe alla
Sistemi e Tecnologie della Comunicazione
 Sistemi e ecologie della Comuicazioe Lezioe 4: strato fisico: caratterizzazioe del segale i frequeza Lo strato fisico Le pricipali fuzioi dello strato fisico soo defiizioe delle iterfacce meccaiche (specifiche
Sistemi e ecologie della Comuicazioe Lezioe 4: strato fisico: caratterizzazioe del segale i frequeza Lo strato fisico Le pricipali fuzioi dello strato fisico soo defiizioe delle iterfacce meccaiche (specifiche
Università degli Studi di Cassino, Anno accademico Corso di Statistica 2, Prof. M. Furno
 Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Algoritmi e Strutture Dati (Elementi)
 Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!)
 COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
RAPPRESENTAZIONE ANALITICA DEI PUNTALI OGIVALI PER PROIETTILI
 M. G. BUSATO RAPPRESENTAZIONE ANALITIA DEI PUNTALI OGIVALI PER PROIETTILI mgbstudio.et SOMMARIO I umerose applicazioi balistiche, ed i particolare per calcolare la resisteza aerodiamica di u proiettile,
M. G. BUSATO RAPPRESENTAZIONE ANALITIA DEI PUNTALI OGIVALI PER PROIETTILI mgbstudio.et SOMMARIO I umerose applicazioi balistiche, ed i particolare per calcolare la resisteza aerodiamica di u proiettile,
Insiemi numerici. Sono noti l insieme dei numeri naturali: N = {1, 2, 3, }, l insieme dei numeri interi relativi:
 Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
Isiemi umerici Soo oti l isieme dei umeri aturali: N {1,, 3,, l isieme dei umeri iteri relativi: Z {0, ±1, ±, ±3, N {0 ( N e, l isieme dei umeri razioali: Q {p/q : p Z, q N. Si ottiee questo ultimo isieme,
2.5 Convergenza assoluta e non
 .5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
.5 Covergeza assoluta e o Per le serie a termii complessi, o a termii reali di sego o costate, i criteri di covergeza si qui visti o soo applicabili. L uico criterio geerale, rozzo ma efficace, è quello
UNIVERSITA DEGLI STUDI DI PERUGIA STATISTICA MEDICA. Prof.ssa Donatella Siepi tel:
 UNIVERSITA DEGLI STUDI DI PERUGIA STATISTICA MEDICA Prof.ssa Doatella Siepi doatella.siepi@uipg.it tel: 075 5853525 05 dicembre 2014 6 LEZIONE Statistica descrittiva STATISTICA DESCRITTIVA Rilevazioe dei
UNIVERSITA DEGLI STUDI DI PERUGIA STATISTICA MEDICA Prof.ssa Doatella Siepi doatella.siepi@uipg.it tel: 075 5853525 05 dicembre 2014 6 LEZIONE Statistica descrittiva STATISTICA DESCRITTIVA Rilevazioe dei
( ) = J s m
 CAPITOO 9 a meccaica quatistica QUESITI Quesito A ogi particella materiala co ua quatità di moto! p corrispode ua lughezza d oda, detta di De Broglie, data da: λ = h p. () Nel modello corpuscolare di Bohr
CAPITOO 9 a meccaica quatistica QUESITI Quesito A ogi particella materiala co ua quatità di moto! p corrispode ua lughezza d oda, detta di De Broglie, data da: λ = h p. () Nel modello corpuscolare di Bohr
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE 1
 ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
( 4) ( ) ( ) ( ) ( ) LE DERIVATE ( ) ( ) (3) D ( x ) = 1 derivata di un monomio con a 0 1. GENERALITÀ
 LE DERIVATE. GENERALITÀ Defiizioe A) Ituitiva. La derivata, a livello ituitivo, è u operatore tale che: a) ad ua fuzioe f associa u altra fuzioe; b) obbedisce alle segueti regole di derivazioe: () D a
LE DERIVATE. GENERALITÀ Defiizioe A) Ituitiva. La derivata, a livello ituitivo, è u operatore tale che: a) ad ua fuzioe f associa u altra fuzioe; b) obbedisce alle segueti regole di derivazioe: () D a
Alcuni concetti di statistica: medie, varianze, covarianze e regressioni
 A Alcui cocetti di statistica: medie, variaze, covariaze e regressioi Esistoo svariati modi per presetare gradi quatità di dati. Ua possibilità è presetare la cosiddetta distribuzioe, raggruppare cioè
A Alcui cocetti di statistica: medie, variaze, covariaze e regressioi Esistoo svariati modi per presetare gradi quatità di dati. Ua possibilità è presetare la cosiddetta distribuzioe, raggruppare cioè
CAPITOLO 1 RISONATORI AD ANELLO
 CAPITOLO 1 RISONATORI AD ANELLO Pag.3/105 1.1 Premessa U risoatore ottico ad aello ( micro-rig resoator ) è u positivo ottico itegrato che cosiste di ua guida d oda chiusa i retroazioe positiva accoppiata
CAPITOLO 1 RISONATORI AD ANELLO Pag.3/105 1.1 Premessa U risoatore ottico ad aello ( micro-rig resoator ) è u positivo ottico itegrato che cosiste di ua guida d oda chiusa i retroazioe positiva accoppiata
Statistica. Esercitazione 12. Alfonso Iodice D Enza Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
TEORIA DELLE MATRICI. dove aij K. = di ordine n, gli elementi aij con i = j (cioè gli elementi a 11
 1 TEORIA DELLE MATRICI Dato u campo K, defiiamo matrice ad elemeti i K di tipo (m, ) u isieme di umeri ordiati secodo m righe ed coloe i ua tabella rettagolare del tipo a11 a12... a1 a21 a22... a2 A =.........
1 TEORIA DELLE MATRICI Dato u campo K, defiiamo matrice ad elemeti i K di tipo (m, ) u isieme di umeri ordiati secodo m righe ed coloe i ua tabella rettagolare del tipo a11 a12... a1 a21 a22... a2 A =.........
Diagramma polare e logaritmico
 Diagramma polare e aritmico ariatori discotiui del moto di taglio Dalla relazioe π D c si ota che la velocità di taglio dipede, oltre che dal umero di giri del madrio, ache dal diametro dell elemeto rotate
Diagramma polare e aritmico ariatori discotiui del moto di taglio Dalla relazioe π D c si ota che la velocità di taglio dipede, oltre che dal umero di giri del madrio, ache dal diametro dell elemeto rotate
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
Appendice A1 Termodinamica Statistica.
 Appedice A Termodiamica Statistica. A. - La distribuzioe biomiale di probabilità. Si cosideri u sistema isolato, macroscopicamete i equilibrio e omogeeo. Ache se la termodiamica covezioale stabilisce che
Appedice A Termodiamica Statistica. A. - La distribuzioe biomiale di probabilità. Si cosideri u sistema isolato, macroscopicamete i equilibrio e omogeeo. Ache se la termodiamica covezioale stabilisce che
Metodi di valutazione delle prestazioni di rete
 Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
c n OTTICA GEOMETRICA RIFLESSIONE E RIFRAZIONE INDICE DI RIFRAZIONE
 OTTICA GEOMETRICA U oda e.m. si propaga rettilieamete i u mezzo omogeeo ed isotropo co velocità c v = > si chiama idice di rifrazioe e dipede sia dal mezzo sia dalla lughezza d oda della radiazioe RIFLESSIONE
OTTICA GEOMETRICA U oda e.m. si propaga rettilieamete i u mezzo omogeeo ed isotropo co velocità c v = > si chiama idice di rifrazioe e dipede sia dal mezzo sia dalla lughezza d oda della radiazioe RIFLESSIONE
ESAME DI STATO DI LICEO SCIENTIFICO 2005 CORSO DI ORDINAMENTO Sessione ordinaria Tema di MATEMATICA - 23 giugno 2005
 ESAME DI STATO DI LICEO SCIENTIFICO 005 CORSO DI ORDINAMENTO Sessioe ordiaria Tema di MATEMATICA - 3 giugo 005 Svolgimeto a cura del prof. Luigi Tomasi (luigi.tomasi@libero.it) RISPOSTE AI QUESITI DEL
ESAME DI STATO DI LICEO SCIENTIFICO 005 CORSO DI ORDINAMENTO Sessioe ordiaria Tema di MATEMATICA - 3 giugo 005 Svolgimeto a cura del prof. Luigi Tomasi (luigi.tomasi@libero.it) RISPOSTE AI QUESITI DEL
Università degli Studi di Padova. Corso di Laurea in Medicina e Chirurgia - A.A
 Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
STUDIO DEL LANCIO DI 3 DADI
 Leoardo Latella STUDIO DEL LANCIO DI 3 DADI Il calcolo delle probabilità studia gli eveti casuali probabili, cioè quegli eveti che possoo o o possoo verificarsi e che dipedoo uicamete dal caso. Tale studio
Leoardo Latella STUDIO DEL LANCIO DI 3 DADI Il calcolo delle probabilità studia gli eveti casuali probabili, cioè quegli eveti che possoo o o possoo verificarsi e che dipedoo uicamete dal caso. Tale studio
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Serie di potenze / Esercizi svolti
 MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
Def. R si dice raggio di convergenza; nel caso i) R = 0, nel caso ii)
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Pompa di calore a celle di Peltier. ( 3 ) Analisi dei dati
 Pompa di calore a celle di Peltier ( 3 ) Aalisi dei dati Scuola estiva di Geova 2 6 settembre 2008 1 Primo esperimeto : riscaldameto per effetto Joule Come descritto ella guida, misuriamo tesioe di alimetazioe
Pompa di calore a celle di Peltier ( 3 ) Aalisi dei dati Scuola estiva di Geova 2 6 settembre 2008 1 Primo esperimeto : riscaldameto per effetto Joule Come descritto ella guida, misuriamo tesioe di alimetazioe
Distribuzione normale
 Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Calcolo I - Corso di Laurea in Fisica - 31 Gennaio 2018 Soluzioni Scritto
 Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
Circuiti Opto Elettronici Integrati
 Circuiti Opto lettroici Itegrati Quello che vogliamo realizzare soo chip di semicoduttore i cui soo itegrate tutte le fuzioi Sorge quidi la ecessità oltre le altre cosedi realizzare i caali che trasportao
Circuiti Opto lettroici Itegrati Quello che vogliamo realizzare soo chip di semicoduttore i cui soo itegrate tutte le fuzioi Sorge quidi la ecessità oltre le altre cosedi realizzare i caali che trasportao
LE MISURE DI TENDENZA CENTRALE
 STATISTICA DESCRITTIVA LE MISURE DI TENDENZA CENTRALE http://www.biostatistica.uich.itit OBIETTIVO Esempio: Nella tabella seguete soo riportati i valori del tasso glicemico rilevati su 0 pazieti: Idividuare
STATISTICA DESCRITTIVA LE MISURE DI TENDENZA CENTRALE http://www.biostatistica.uich.itit OBIETTIVO Esempio: Nella tabella seguete soo riportati i valori del tasso glicemico rilevati su 0 pazieti: Idividuare
Statistica I - A.A
 Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioi di Aalisi Matematica per i corsi di Laurea i Igegeria Chimica e Igegeria per l Ambiete e il Territorio dell Uiversità di Bologa. Ao Accademico
Ottavio Serra La costante C di Eulero-Mascheroni e la funzione Gamma. 1. =
 Ottavio Serra La costate C di Eulero-Mascheroi e la fuzioe Gamma la costate C di Eulero Mascheroi è defiita come il limite della seguete successioe: [] a = +/+/3+ +/ log(+) Il termie a è la differeza tra
Ottavio Serra La costate C di Eulero-Mascheroi e la fuzioe Gamma la costate C di Eulero Mascheroi è defiita come il limite della seguete successioe: [] a = +/+/3+ +/ log(+) Il termie a è la differeza tra
Inferenza Statistica. L inferenza statistica cerca di risalire al modello del fenomeno sulla base delle osservazioni.
 Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Compito di Matematica II - 12 Settembre 2017
 Compito di Matematica II - Settembre 7 Corso di Laurea i Ottica e Optometria - A.A. 6/7 Soluzioi degli esercizi. Esercizio. a) Il domiio C è il cerchio di raggio uitario. La fuzioe fx y) = x + y è defiita
Compito di Matematica II - Settembre 7 Corso di Laurea i Ottica e Optometria - A.A. 6/7 Soluzioi degli esercizi. Esercizio. a) Il domiio C è il cerchio di raggio uitario. La fuzioe fx y) = x + y è defiita
PROPRIETÀ DELLE POTENZE IN BASE 10
 PROPRIETÀ DELLE POTENZE IN BASE Poteze i base co espoete itero positivo Prediamo u umero qualsiasi che deotiamo co la lettera a e u umero itero positivo che deotiamo co la lettera Per defiizioe (cioè per
PROPRIETÀ DELLE POTENZE IN BASE Poteze i base co espoete itero positivo Prediamo u umero qualsiasi che deotiamo co la lettera a e u umero itero positivo che deotiamo co la lettera Per defiizioe (cioè per
La legge di Hooke. Alessio Bianchi 5 aprile 2017
 La legge di Hooke Alessio Biachi 5 aprile 2017 Sommario Determiazioe delle costati elastiche k di alcue molle e di ua massa m icogita sfruttado la legge di Hooke. Verifica del legame tra costate elastica
La legge di Hooke Alessio Biachi 5 aprile 2017 Sommario Determiazioe delle costati elastiche k di alcue molle e di ua massa m icogita sfruttado la legge di Hooke. Verifica del legame tra costate elastica
n 1 = n b) {( 1) n } = c) {n!} In questo caso la successione è definita per ricorrenza: a 0 = 1, a n = n a n 1 per ogni n 1.
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi 0: Riferimeti: R.Adams, Calcolo Differeziale - Si cosiglia vivamete di fare gli esercizi del testo. Successioi umeriche:
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi 0: Riferimeti: R.Adams, Calcolo Differeziale - Si cosiglia vivamete di fare gli esercizi del testo. Successioi umeriche:
Universitá di Roma Tor Vergata Analisi 1, Ingegneria (CIO-FR), Prof. A. Porretta Esame del 19 febbraio 2018
 Uiversitá di Roma Tor Vergata Aalisi, Igegeria CIO-FR), Prof. A. Porretta Esame del 9 febbraio 08 Esame orale : Esercizio [7 puti] Studiare la fuzioe f) = + 4 ) disegadoe u grafico qualitativo e idicado:
Uiversitá di Roma Tor Vergata Aalisi, Igegeria CIO-FR), Prof. A. Porretta Esame del 9 febbraio 08 Esame orale : Esercizio [7 puti] Studiare la fuzioe f) = + 4 ) disegadoe u grafico qualitativo e idicado:
Fisica Generale B. Esercizio 1. Esercizio 1 (II) Esercizio 1 (III) 3. Esercizi di ottica. June 17, 2009
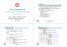 Esercizio Fisica Geerale B La fiamma di u forello, cotiuamete e regolarmete riforita di sale da cucia, costituisce ua sorgete estesa di luce gialla. Si trova che tale luce gialla è composta di due ode
Esercizio Fisica Geerale B La fiamma di u forello, cotiuamete e regolarmete riforita di sale da cucia, costituisce ua sorgete estesa di luce gialla. Si trova che tale luce gialla è composta di due ode
CAPITOLO 3. Quicksort
 CAPITOLO 3 Quicksort I questa lezioe presetiamo l algoritmo di ordiameto Quicksort(vedi []). L algoritmo Quicksort riceve i iput u array A e idici p r ed ordia l array A[p,, r] el modo seguete. L array
CAPITOLO 3 Quicksort I questa lezioe presetiamo l algoritmo di ordiameto Quicksort(vedi []). L algoritmo Quicksort riceve i iput u array A e idici p r ed ordia l array A[p,, r] el modo seguete. L array
Precorso di Matematica. Parte IV : Funzioni e luoghi geometrici
 Facoltà di Igegeria Precorso di Matematica 1. Equazioi e disequazioi Parte IV : Fuzioi e luoghi geometrici Richiamiamo brevemete la ozioe di fuzioe, che sarà utilizzato i quest ultima parte del precorso.
Facoltà di Igegeria Precorso di Matematica 1. Equazioi e disequazioi Parte IV : Fuzioi e luoghi geometrici Richiamiamo brevemete la ozioe di fuzioe, che sarà utilizzato i quest ultima parte del precorso.
Soluzioni degli esercizi del corso di Analisi Matematica I
 Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
A8 - Campi vettoriali conservativi e solenoidali
 A8 - Campi vettoriali coservativi e soleoidali A8.1 Campi coservativi e campi irrotazioali Sia V(x,y,z) u campo vettoriale defiito i ua regioe di spazio Ω, e sia u cammio, di estremi A e B, defiito i Ω.
A8 - Campi vettoriali coservativi e soleoidali A8.1 Campi coservativi e campi irrotazioali Sia V(x,y,z) u campo vettoriale defiito i ua regioe di spazio Ω, e sia u cammio, di estremi A e B, defiito i Ω.
Probabilità e Statistica (cenni)
 robabilità e Statistica (cei) remettiamo la distizioe tra i due cocetti: Defiizioe: dato il verificarsi di u eveto si defiisce la probabilità per l eveto cosiderato il rapporto tra il umero dei casi favorevoli
robabilità e Statistica (cei) remettiamo la distizioe tra i due cocetti: Defiizioe: dato il verificarsi di u eveto si defiisce la probabilità per l eveto cosiderato il rapporto tra il umero dei casi favorevoli
Caratteristiche I-V Qualitativamente, la caratteristica di uscita di un MOSFET è la seguente:
 l sistema MOFE l MOFE è u FE che utilizza come caale la regioe di iversioe che si crea i ua struttura MO opportuamete polarizzata. l cotatto di gate del trasistor coicide co il Metallo della struttura
l sistema MOFE l MOFE è u FE che utilizza come caale la regioe di iversioe che si crea i ua struttura MO opportuamete polarizzata. l cotatto di gate del trasistor coicide co il Metallo della struttura
Solidi e volumi Percorso: Il problema della misura
 Solidi e volumi Percorso: Il problema della misura Abilità Coosceze Nuclei Collegameti esteri Calcolare perimetri e aree Equivaleza el piao ed Spazio e figure Fisica di poligoi. equiscompoibilità tra Disego
Solidi e volumi Percorso: Il problema della misura Abilità Coosceze Nuclei Collegameti esteri Calcolare perimetri e aree Equivaleza el piao ed Spazio e figure Fisica di poligoi. equiscompoibilità tra Disego
Laboratorio di Fisica per Scienze Naturali Esperienza n 1. Verifica della legge di Hooke Misura dei coefficiente di elasticità di molle di acciaio.
 Scopo dell'esperieza Laboratorio di isica per Scieze aturali Esperieza Verifica della legge di Hooe Misura dei coefficiete di elasticità di molle di acciaio. ) verifica del fatto che l allugameto di ua
Scopo dell'esperieza Laboratorio di isica per Scieze aturali Esperieza Verifica della legge di Hooe Misura dei coefficiete di elasticità di molle di acciaio. ) verifica del fatto che l allugameto di ua
Intervalli di Fiducia
 di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
