Tutorato di AM210. A.A Docente: Prof. G.Mancini Tutore: Andrea Nardi Soluzioni 3-25 Ottobre Si sta chiedendo di vedere che
|
|
|
- Serafino Lupi
- 4 anni fa
- Visualizzazioni
Transcript
1 Uiversitá degli Studi Roma Tre - Corso di Laurea i Matematica Tutorato di AM20 AA Docete: Prof GMacii Tutore: Adrea Nardi Soluzioi 3-25 Ottobre 203 Si sta chiededo di vedere che J g f = J gf J f ove J é la matrice Jacobiaa Vediamo le due parti dell'uguagliaza separatamete Abbiamo che g fx, y = gxy, x 2, y 6 = e xy, cosx 3 y 7 := h x, y, h 2 x, y = hx, y, hx,y J h = h 2x,y h x,y y h 2x,y y ye = xy xe xy 3x 2 y 7 six 3 y 7 7y 6 x 3 six 3 y 7 Adiamo ora a calcolare J g : e J g = u 0 0 vz siuvz uz siuvz uv siuvz e J gf = xy 0 0 x 2 y 6 six 3 y 7 xy 7 six 3 y 7 x 3 y six 3 y 7 z Ie y x J f = 2x 0 0 6y 5 Per cui abbiamo che ye J gf J f = xy xe xy 3x 2 y 7 six 3 y 7 7x 3 y 6 six 3 y 7 che é eettivamete J h 2 Essedo ft, gt = 0 t R, allora, deedo γt C R, R 2 come γt := t, gt, si ha che γ t =, g t e duque, per la regola di derivazioe di fuzioi composte, si ha che: 0 = d dt 0 = d dt ft, gt = d dt fγt = ft, gt, γ t = = ft, gt + ft, gt g t t R y Duque preso t = 0 si ottiee che: da cui otteiamo l'asserto 0 = f0, 0 + f0, 0 g 0 y
2 3 Presa fx, y si ha che fx, y = f f x, y, y x, y := f x x, y, f y x, y Passiamo a coordiate polari: sia g, θ := f cosθ, siθ Abbiamo che: g = f x cosθ + f y siθ g θ = siθf x + cosθf y per la regola di derivazioe di fuzioi composte A partire da queste due relazioi, per trovare f x e f y, dobbiamo combiare i maiera opportua le derivate parziali di g, θ I particolare per trovare f x bisogerá sottrarre i maiera opportua le derivate parziali di g, θ i maiera che f y si aulli e viceversa per calcolare f y Duque: da cui g siθ Aalogamete da cui Quidi g cosθ + f cosθ, siθ = g θ cosθ = f xcotθ + taθ = f x f x = g cosθ g θ siθ g θ siθ = f ycotθ + taθ = f y f y = g siθ + g θ cosθ g, θ cosθ g θ, θ siθ siθ cosθ siθ cosθ Passiamo a coordiate polari: sia g, θ := f cosθ, siθ Abbiamo che: g = f x cosθ + f y siθ g θ = siθf x + cosθf y g = f xx cos 2 θ + f xy si2θ + f yy si 2 θ g θθ = cosθf x + 2 si 2 θf xx 2 si2θf xy siθf y + 2 cos 2 θf yy Dobbiamo ora, i maiera opportua, trovare ua combiazioe lieare che ci isoli le derivate secode di f cosθ, siθ Sommiamo le derivate secode di g, θ per togliere le derivate miste di f cosθ, siθ Abbiamo che g θθ 2 A questo puto otiamo che + g = f xx + f yy cosθf x siθf y g θθ, θ 2 + g, θ + g, θ = f cosθ, siθ, g, θ siθ + g θ, θ cosθ 2
3 Adiamo ad usare la formula otteuta per calcolare i Laplaciai delle fuzioi richieste: a Vediamo prima chi é P x, y: P x x, y = x2 + y 2 P y x, y = y x2 + y 2 perció 2 P 2 x, y = y 2 x 2 + y P y 2 x, y = x 2 x 2 + y P x, y = x2 + y 2 Essedo g, θ = si ha che g θθ, θ = 0 = g, θ g, θ = P cosθ, siθ = Essedo = x 2 + y 2 l'uguagliaza é provata b Abbiamo che: perció F 2x x, y = + x 2 + y 2 F 2y x, y = y + x 2 + y 2 2 F 2 x, y = 2 2x2 + 2y 2 + x 2 + y F y 2 x, y = 2 2y2 + 2x 2 + x 2 + y 2 2 F x, y = + x 2 + y 2 Essedo h, θ = log + 2 si ha che h θθ, θ = 0 h, θ = h, θ =
4 che é quello che volevamo F cosθ, siθ = I puti stazioari di ua fuzioe fx, y soo quei puti che aullao il suo gradiete Ua volta otteuti essi, per sapere se soo massimi o miimi bisoga trovare la matrice Hessiaa di fx, y data da H f x, y = 2 f x, y 2 x, y 2 f y 2 f y x, y 2 f y 2 x, y ove 2 f y = 2 f y per la teoria Ua volta trovata la matrice Hessiaa, calcoliamo quato vale il suo determiate i ogi puto stazioario Possoo accadere le segueti cose: Se deth f x 0, y 0 < 0 allora x 0, y 0 é u puto di sella; Se deth f x 0, y 0 > 0 allora x 0, y 0 é: u massimo se 2 f 2 x 0, y 0 < 0; u miimo se 2 f 2 x 0, y 0 > 0; Se deth f x 0, y 0 = 0 o possiamo dire ulla ed occorrerá fare u ulteriore aalisi per dedurre se x 0, y 0 é u puto di massimo, di miimo o di sella Detto questo partiamo co la risoluzioe degli esercizi: a f x, y = x 3 x, y y 3 x 3 = x = 0, 0 y 3 = y x = 0, ± y = 0, ± Quidi f x, y ha 9 puti stazioari: P =,, P 2 =, 0, P 3 =,, P = 0,, P 5 = 0, 0, P 6 = 0,, P 7 =,, P 8 =, 0, P 9 =, La matrice Hessiaa el ostro caso é 2x H f x, y = y 2 Notiamo che: H f P = H f P 3 = H f P 7 = H f P 9 = 0 H f P = H f P 6 = ; H f P 2 = H f P 8 = ; 0 0 H f P 5 = ; 0 8
5 Il determiate della matrice Hessiaa ei puti P, P 3, P 5, P 7 e P 9 é egativo, idi tali puti soo di sella; Il determiate della matrice Hessiaa egli altri puti é positivo, soo puti di massimo o di miimo Per i puti P e P 6 si ha che 2 f < 2 0, soo puti di massimo Ivece per i puti P 2 e P 8 si ha che 2 f > 0, soo puti di miimo 2 b f 2 x, y = 3x 2 y+y 3 y, x 3 +3xy 2 x = 0, 0 y3x 2 + y 2 = 0 xx 2 + 3y 2 = 0 Se y = 0 ella prima riga abbiamo che xx 2 = 0 ella secoda Duque otteiamo i puti P =, 0, P 2 = 0, 0, P 3 =, 0 3x 2 + y 2 = 0 Se y 0 il sistema diveta xx 2 + 3y 2 = 0 Se x = 0 ella secoda riga otteiamo che y 2 =, otteiamo i puti P = 0,, P 5 = 0, Se x 0 il sistema diveta 3x 2 + y 2 = 0 x 2 + 3y 2 = 0 y 2 = 3x 2 y 2 = x 2 = x x 2 = 0 y = ± 2 x 2 = ± 2 3x 2 + y 2 = 0 x 2 = Quidi abbiamo otteuto i puti: P 6 = 2, 2, P7 = 2, 2, P8 = 2, 2, P9 = 2, 2 Ora: 6xy 3x H f2 x, y = 2 + 3y 2 3x 2 + 3y 2 6xy Facedo i coti troviamo che il determiate dell'hessiaa ei puti P i, i =,, 5, é egativo, essi soo puti di sella Nei macati puti il determiate é ivece positivo Per i puti P 6 e P 9 si ha che 2 f 2 = 3 2 > 0, tali puti soo miimi Per i puti P 7 e P 8 si ha che 2 f 2 = 3 2 < 0, tali puti soo massimi c f 3 x, y = 3x 2 3y 2, 6xy = 0, 0 x 2 = y 2 xy = 0 x = y = 0 Pertato l'uico puto stazioario é P = 0, 0 abbiamo che 6x 6y H f3 x, y = 6y 6x I questo caso Duque il determiate dell'hessiaa é ullo se calcolato i P Notiamo che f 3 0, 0 = 0 Se cosideriamo puti vicii all'origie del tipo, si ha che f 3, = 2 < 3 0 Cosiderati i puti vicii all'origie del tipo, si ha che f 3, = 2 3 > 0 5
6 Essedoci puti prossimi all'origie i cui la fuzioe é positiva ed altri i cui la fuzioe é egativa, abbiamo che P é u puto di sella d f x, y = x 3 3x 2 siy, x 3 x 3 = 3 cosy = 0, 0 x2 siy x 3 cosy = 0 Se x = 0 il sistema é valido y, i puti P y = 0, y soo stazioari Se x 0 il sistema diveta x = 3 siy y = π 2 + kπ cosy = 0 x = 3 k Notiamo che se k = 2s abbiamo i puti P 2s = 3, π 2 + 2sπ e se k = 2s + abbiamo i puti P 2s+ = 3, π 2 + 2s + π L'Hessiaa di f x, y é 2x H f x, y = 2 6x siy 3x 2 cosy 3x 2 cosy x 3 siy Abbiamo che H f P 2s = H f P 2s+ = Essedo il suo determiate positivo e 2 f 2 > 0, abbiamo che soo tutti puti di miimo L'Hessiaa calcolata ei puti P y é ulla Notiamo che i puti del tipo 0, kπ soo miimi, perché f x, kπ = x > 0 = f0, kπ x 0 Tutti gli altri puti soo di sella: i puti del tipo 0, π 2 + kπ soo tali che, presi itori destri e siistri dell'asse y ad altezza π 2 + kπ si ottiee u cambio di sego, metre f 0, y = 0 y Ad esempio se y = π 2 si ha che f, π 2 = 3 < 0 metre f, π 2 = 3 + > 0 Co lo stesso ragioameto si puó estedere il discorso a tutti i puti che o siao del tipo 0, kπ e f 5 x, y = 2xy 2, 2yx 2 = 0, 0 xy 2 = 0 yx 2 = 0 Se x = 0 e cosegue che ache y = 0 e otteiamo il puto P = 0, 0 Se ivece x 0 si ha che y = ± ella prima riga e che x = ± ella secoda Pertato otteiamo i puti: P 2 =,, P 3 =,, P =,, P 5 =, Essedo 2y H f5 x, y = 2 xy xy 2x 2 abbiamo che il suo determiate ei puti ±, ± é egativo, idi soo puti di sella Nel puto P ivece il determiate é positivo, ed essedo 2 f 5 2 P = 2 < 0 si ha che é u puto di massimo 6
7 f f 6 x, y = x 3 2x 2 +8x, y 3 y = 0, 0 x = 0,, 2 xx x 2 = 0 y = 0, ± = abbiamo 9 puti: y = 0, ± P = 0, 0, P 2 = 0,, P 3 = 0,, P =, 0, P 5 =,, P 6 =,, P 7 = 2, 0, P 8 = 2,, P 9 = 2, Ora: 2x H f6 x, y = 2 2x y 2 H f6 P = H f6 P 7 = 8 0 = puti di sella H f6 P 2 = H f6 P 3 = = puti di miimo H f6 P 5 = H f6 P 6 = = puti di sella H f6 P 8 = H f6 P 9 = = puti di miimo H f6 P = = puto di massimo 0 g f 7 x, y = y 3 six, y 3 3y 2 y 3 six = 0 cosx = 0, 0 y 3 = 3 y2 cosx Come per f x, y otteiamo puti del tipo P x = x, 0, P 2s = 2sπ, 3 e P2s+ = 2s + π, 3 Svolgedo coti aaloghi otteiamo che i puti P 2s = 2sπ, 3 e P 2s+ = 2s + π, 3 soo di miimo Ache i tal caso H f7 x, 0 ha determiate ullo e co coti idetici π a sopra si ha che i puti del tipo 2 + kπ, 0 soo miimi e gli altri puti di sella h f 8 x, y = 2xy 2, 2x 2 y y = 0, 0 xy 2 = 0 xy 2 = mai = Quidi la fuzioe o ha puti critici x x i f 9 x, y =, y +2y = 0, 0 = 0 x 2 +y 2 x 2 +y 2 y + 2 = 0 y 2 cioé soltato se x = y = 0 0, 0 o é u puto dove o esiste f 9, dove la fuzioe o é parzialmete derivabile Noostate ció la fuzioe ha u miimo assoluto i 0, 0 j f 0 x, y = x 3 x + e x e x y 3, e x y 3 = 0, 0 y = e x x = 0, ± x 3 = x y = e x, otteiamo i puti: 7
8 P = 0,, P 2 =, e e P 3 =, e Essedo y = e x el calcolo dell'hessiaa omettiamo i termii che cotegoo e x y essedo ulli i tutti e tre i putiovviamete el calcolo delle derivate soo ecessari!!! Duque H f0 x, y = 2x e il determiate dell'hessiao é ullo i tutti e 3 i puti Comiciamo co l'aalisi del puto P : abbiamo che f 0 P = 0 Notiamo che i puti del tipo 0, ± la fuzioe assume valori positivi, metre cosiderato il puto, si ha che f 0, = 2 + e = 2 2 < 0 2 Quidi P é u puto di sella Procediamo co l'aalisi di P 2 : abbiamo che f 0 P 2 = f 0, e ± = + > ; f 0 +, e e > ; f 0, e e + > ; f 0 +, e + = ee e > ; f 0, e e > ; f 0 +, e e > ; f 0, e e > I tutte i puti prossimi a P 2 si ha che la fuzioe assume valori piú gradi di, P 2 é u puto di miimo Cocludiamo co l'aalisi di P 3 : abbiamo che f 0 P 3 = Possiamo be credere che per P 3 valga u discorso aalogo a quello che é valso per P 2 Chiamata gx = x 2x 2 si ha che f 0 x, y = gx + e x y Notiamo che g + = > e g = > Essedo e x y 0 x, y abbiamo che f 0 x, y i u itoro di P 3 sará sempre piú grade di Quidi ache P 3 é u puto di miimo NB Nelle scorse soluzioi alla e della prima stima relativa all'esercizio 7c del tutorato u x 3 diveta x 3 Pare chiaro che é solo u errore di battitura If you have a problem Better Call Fra 8
Compito di Matematica II - 12 Settembre 2017
 Compito di Matematica II - Settembre 7 Corso di Laurea i Ottica e Optometria - A.A. 6/7 Soluzioi degli esercizi. Esercizio. a) Il domiio C è il cerchio di raggio uitario. La fuzioe fx y) = x + y è defiita
Compito di Matematica II - Settembre 7 Corso di Laurea i Ottica e Optometria - A.A. 6/7 Soluzioi degli esercizi. Esercizio. a) Il domiio C è il cerchio di raggio uitario. La fuzioe fx y) = x + y è defiita
Quarto Compito di Analisi Matematica Corso di laurea in Informatica, corso B 5 Luglio Soluzioni. z 2 = 3 4 i. a 2 b 2 = 3 4
 Quarto Compito di Aalisi Matematica Corso di laurea i Iformatica, corso B 5 Luglio 016 Soluzioi Esercizio 1 Determiare tutti i umeri complessi z tali che z = 3 4 i. Soluzioe. Scrivedo z = a + bi, si ottiee
Quarto Compito di Aalisi Matematica Corso di laurea i Iformatica, corso B 5 Luglio 016 Soluzioi Esercizio 1 Determiare tutti i umeri complessi z tali che z = 3 4 i. Soluzioe. Scrivedo z = a + bi, si ottiee
SOLUZIONI COMPITO del 04/02/2016 ANALISI MATEMATICA I - 9 CFU MECCANICA TEMA A
 SOLUZIONI COMPITO del 0/0/06 ANALISI MATEMATICA I - 9 CFU MECCANICA TEMA A Esercizio Osserviamo, iazitutto, che la serie proposta è ua serie a termii o egativi. Applicado il criterio della radice, dopo
SOLUZIONI COMPITO del 0/0/06 ANALISI MATEMATICA I - 9 CFU MECCANICA TEMA A Esercizio Osserviamo, iazitutto, che la serie proposta è ua serie a termii o egativi. Applicado il criterio della radice, dopo
Tutoraggio AM1 17/12/2015. sin(x) arctan(x) 2) lim sup / inf x 0 + cos(x) sin( 1 x ) e x2 cos 2 (x 3 ) x 2 + ln(3x + 2) δ(x) δ(x) =
 Tutoraggio AM1 17/12/2015 Per la parte teorica sui if e sup vedi le ote su iti iferiori e superiori di fuzioi. A) Date due successioi a },b }, mostrare le segueti proprietà (escludere i casi i cui si abbia
Tutoraggio AM1 17/12/2015 Per la parte teorica sui if e sup vedi le ote su iti iferiori e superiori di fuzioi. A) Date due successioi a },b }, mostrare le segueti proprietà (escludere i casi i cui si abbia
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 8.8.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 8.8.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
e 6x = 2(t + 1) 1 + c tan x (funzione razionale) si scompone come: t (log t 1 log t + 1 ) t=9
 Esercizi di Aalisi - Alberto Valli - AA 5/6 - Foglio. Calcolate tramite cambiameto di variabile ciascuo dei segueti itegrali : i / six + dx ii log log e 6x e x dx iii / π/ cos 5 xsix cos x dx. Soluzioe.
Esercizi di Aalisi - Alberto Valli - AA 5/6 - Foglio. Calcolate tramite cambiameto di variabile ciascuo dei segueti itegrali : i / six + dx ii log log e 6x e x dx iii / π/ cos 5 xsix cos x dx. Soluzioe.
Analisi I - IngBM COMPITO B 17 Gennaio 2015 COGNOME... NOME... MATRICOLA... VALUTAZIONE =...
 Aalisi I - IgBM - 2014-15 COMPITO B 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
Aalisi I - IgBM - 2014-15 COMPITO B 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
Analisi I - IngBM COMPITO A 17 Gennaio 2015 COGNOME... NOME... MATRICOLA... VALUTAZIONE =...
 Aalisi I - IgBM - 2014-15 COMPITO A 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
Aalisi I - IgBM - 2014-15 COMPITO A 17 Geaio 2015 COGNOME........................ NOME............................. MATRICOLA....................... VALUTAZIONE..... +..... =...... 1. Istruzioi Gli esercizi
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
Analisi Matematica I modulo Soluzioni prova scritta preliminare n. 1
 Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Aalisi Matematica I modulo Soluzioi prova scritta prelimiare 1 Corso di laurea i Matematica, aa 004-005 9 ovembre 004 1 (a) Calcolare il seguete limite: **A***** Soluzioe Si ha ( + log ) ( + log ) lim
Per approssimare la funzione, occorre determinare la derivata prima e seconda:
 Esercizi sul Poliomio di Taylor Approssimare lafuzioe f() = l(+si) coilpoliomio di Taylor di ordie = e puto iiziale 0 = 0. Soluzioe Per approssimare la fuzioe, occorre determiare la derivata prima e secoda:
Esercizi sul Poliomio di Taylor Approssimare lafuzioe f() = l(+si) coilpoliomio di Taylor di ordie = e puto iiziale 0 = 0. Soluzioe Per approssimare la fuzioe, occorre determiare la derivata prima e secoda:
I appello - 11 Dicembre 2006
 Facoltà di Igegeria - Corso di Laurea i Igegeria Civile A.A. 006/007 I appello - Dicembre 006 ) Calcolare il seguete ite: [ ( )] + cos. + ) Data la fuzioe f() = e +, < 0, 0, =, =,,..., log( + ), 0,, =,,...,
Facoltà di Igegeria - Corso di Laurea i Igegeria Civile A.A. 006/007 I appello - Dicembre 006 ) Calcolare il seguete ite: [ ( )] + cos. + ) Data la fuzioe f() = e +, < 0, 0, =, =,,..., log( + ), 0,, =,,...,
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
0.1 Esercitazioni V, del 18/11/2008
 1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
1 0.1 Esercitazioi V, del 18/11/2008 Esercizio 0.1.1. Risolvere usado Cramer il seguete sistema lieare x + y + z = 1 kx + y z = 0 x kz = 1 Soluzioe: Il determiate della matrice dei coefficieti è (k 2)(k
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 5.7.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica Padova, 5.7.08 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Soluzioni degli esercizi di Analisi Matematica I
 Soluzioi degli esercizi di Aalisi Matematica I (Prof. Pierpaolo Natalii) Roberta Biachii 6 ovembre 2016 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x2 1 x + 1 π/3. 2. Dimostrare,
Soluzioi degli esercizi di Aalisi Matematica I (Prof. Pierpaolo Natalii) Roberta Biachii 6 ovembre 2016 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x2 1 x + 1 π/3. 2. Dimostrare,
Analisi Matematica A e B Soluzioni prova scritta n. 4
 Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
Aalisi Matematica A e B Soluzioi prova scritta. 4 Corso di laurea i Fisica, 17-18 3 settembre 18 1. Scrivere le soluzioi dell equazioe differeziale ( u u + u = e x si x + 1 ). 1 + x Soluzioe. Si tratta
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
Corsi di laurea in fisica ed astronomia Prova scritta di Analisi Matematica 2. Padova,
 Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
Corsi di laurea i fisica ed astroomia Prova scritta di Aalisi Matematica 2 Padova, 28.8.29 Si svolgao i segueti esercizi facedo attezioe a giustificare le risposte. Delle affermazioi o motivate e giustificate
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
 ANALISI MATEMATICA Area dell Igegeria dell Iformazioe Appello del 7.9.8 Esercizio Si cosideri la fuzioe f() := TEMA {e 3 per per =. i) Determiare il domiio D, le evetuali simmetrie e studiare il sego di
ANALISI MATEMATICA Area dell Igegeria dell Iformazioe Appello del 7.9.8 Esercizio Si cosideri la fuzioe f() := TEMA {e 3 per per =. i) Determiare il domiio D, le evetuali simmetrie e studiare il sego di
Universitá degli Studi Roma Tre - Corso di Laurea in Matematica. Tutorato di AM120
 Uiversitá degli Studi Roma Tre - Corso di Laurea i Matematica Tutorato di AM20 A.A. 203-204 - Docete: Prof. G.Macii Tutore: Matteo Bruo ed Emauele Padulao Soluzioi 5-2 Marzo 204. Al solito specificheremo
Uiversitá degli Studi Roma Tre - Corso di Laurea i Matematica Tutorato di AM20 A.A. 203-204 - Docete: Prof. G.Macii Tutore: Matteo Bruo ed Emauele Padulao Soluzioi 5-2 Marzo 204. Al solito specificheremo
k=0 f k(x). Un altro tipo di convergenza per le serie è la convergenza totale e si dice che la serie (0.1) converge totalmente in J I se
 Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
Serie di fuzioi Sia I R, per ogi k N, data la successioe di fuzioi (f k ) k co f k : I R, cosideriamo la serie di fuzioi (0.) f k () k=0 e defiiamo la successioe delle somme parziali s () = k=0 f k().
[È ben noto che la serie geometrica converge se e solo se x <1 e che ha per somma la funzione S(x)= 1
 Sapieza Uiversità di Roma - Corso di Laurea i Igegeria Eergetica Aalisi Matematica II - A.A. 06-07 prof. Cigliola Foglio. Serie di fuzioi Esercizio. Calcolare, se possibile, la somma delle segueti serie
Sapieza Uiversità di Roma - Corso di Laurea i Igegeria Eergetica Aalisi Matematica II - A.A. 06-07 prof. Cigliola Foglio. Serie di fuzioi Esercizio. Calcolare, se possibile, la somma delle segueti serie
Esercitazione due: soluzioni
 Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
Esercitazioe due: soluzioi. Sia il ricavo r i pk i ti, p, k, t i > applicado la defiizioe di media di Chisii il tempo medio t che lascia ivariato il ricavo totale é quel valore tale che pk i ti pk i t
Analisi Matematica II
 Uiversità degli Studi di Udie Ao Accademico 016/017 Dipartimeto di Scieze Matematiche, Iformatiche e Fisiche Corso di Laurea i Matematica Aalisi Matematica II Prova parziale del 6 febbraio 017 NB: scrivere
Uiversità degli Studi di Udie Ao Accademico 016/017 Dipartimeto di Scieze Matematiche, Iformatiche e Fisiche Corso di Laurea i Matematica Aalisi Matematica II Prova parziale del 6 febbraio 017 NB: scrivere
Università degli Studi della Calabria Facoltà di Ingegneria. 26 giugno 2012
 Uiversità degli Studi della Calabria Facoltà di Igegeria Correzioe della Secoda Prova Scritta di alisi Matematica 2 giugo 202 cura dei Prof. B. Sciuzi e L. Motoro. Secoda Prova Scritta di alisi Matematica
Uiversità degli Studi della Calabria Facoltà di Igegeria Correzioe della Secoda Prova Scritta di alisi Matematica 2 giugo 202 cura dei Prof. B. Sciuzi e L. Motoro. Secoda Prova Scritta di alisi Matematica
1 + 1 ) n ] n. < e nα 1 n
![1 + 1 ) n ] n. < e nα 1 n 1 + 1 ) n ] n. < e nα 1 n](/thumbs/66/54700563.jpg) Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
Esercizi preparati e i parte svolti martedì 0.. Calcolare al variare di α > 0 Soluzioe: + ) α Per α il ite è e; se α osserviamo che da + /) < e segue che α + ) α [ + ) ] α < e α Per α > le successioi e
Analisi Matematica I Soluzioni del tutorato 2
 Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
Corso di laurea i Fisica - Ao Accademico 07/08 Aalisi Matematica I Soluzioi del tutorato A cura di Davide Macera Esercizio Abbiamo che x 3 + si(log(x)) + cosh(x) x3 + si(log(x)) + e x ( + x 6 ) / + log(e
Risoluzione del compito n. 3 (Febbraio 2018/2)
 Risoluzioe del compito. 3 (Febbraio 08/ PROBLEMA a Determiate le soluzioi τ C dell equazioe τ iτ +=0. { αβ =4 b Determiate le soluzioi (α, β, co α, β C,delsistema α + β =i. c Determiate tutte le soluzioi
Risoluzioe del compito. 3 (Febbraio 08/ PROBLEMA a Determiate le soluzioi τ C dell equazioe τ iτ +=0. { αβ =4 b Determiate le soluzioi (α, β, co α, β C,delsistema α + β =i. c Determiate tutte le soluzioi
Prove d'esame a.a
 Prove d'esame aa Adrea Corli dicembre Soo qui raccolti i testi delle prove d'esame assegati ell'aa, relativi al Corso di Aalisi Matematica I (semestrale, crediti), Laurea i Igegeria Civile e Ambietale,
Prove d'esame aa Adrea Corli dicembre Soo qui raccolti i testi delle prove d'esame assegati ell'aa, relativi al Corso di Aalisi Matematica I (semestrale, crediti), Laurea i Igegeria Civile e Ambietale,
Calcolo I - Corso di Laurea in Fisica - 31 Gennaio 2018 Soluzioni Scritto
 Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
Calcolo I - Corso di Laurea i Fisica - Geaio 08 Soluzioi Scritto Data la fuzioe f = 8 + / a Calcolare il domiio, puti di o derivabilità ed asitoti; b Calcolare, se esistoo, estremi relativi ed assoluti.
ESAME DI MATEMATICA I Modulo di Analisi Matematica Corso 3 Anno Accademico 2008/2009 Docente: R. Argiolas
 ESAME DI MATEMATICA I Modulo di Aalisi Matematica Corso Ao Accademico 8/9 Docete: R Argiolas Cogome Matricola Febbraio 9 ore 9 Aula C Nome Corso voto Esercizio Assegata la fuzioe f ( arcta a Si determii
ESAME DI MATEMATICA I Modulo di Aalisi Matematica Corso Ao Accademico 8/9 Docete: R Argiolas Cogome Matricola Febbraio 9 ore 9 Aula C Nome Corso voto Esercizio Assegata la fuzioe f ( arcta a Si determii
Soluzioni. 2 2n+1 3 2n. n=1. 3 2n 9. n=1. Il numero 2 può essere raccolto fuori dal segno di sommatoria: = 2. n=1 = = 8 5.
 60 Roberto Tauraso - Aalisi Calcolare la somma della serie Soluzioi + 3 R La serie può essere riscritta el modo seguete: + 4 3 9 Il umero può essere raccolto fuori dal sego di sommatoria: + 4 3 9 Si tratta
60 Roberto Tauraso - Aalisi Calcolare la somma della serie Soluzioi + 3 R La serie può essere riscritta el modo seguete: + 4 3 9 Il umero può essere raccolto fuori dal sego di sommatoria: + 4 3 9 Si tratta
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica I del c.1.
 Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
Prova scritta di Aalisi Matematica I del 25-5-1998 - c.1 1) Per ogi umero N, 2, siao dati 2 umeri reali positivi a 1, a 2,...a, b 1, b 2,...b. Provare, usado il Pricipio di Iduzioe, che a 1 + a 2 +...
Analisi Matematica Soluzioni prova scritta parziale n. 1
 Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
Aalisi Matematica Soluzioi prova scritta parziale. 1 Corso di laurea i Fisica, 018-019 3 dicembre 018 1. Dire per quali valori dei parametri α R, β R, α > 0, β > 0 coverge la serie + (!) α β. ( )! =1 Soluzioe.
1.6 Serie di potenze - Esercizi risolti
 6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
6 Serie di poteze - Esercizi risolti Esercizio 6 Determiare il raggio di covergeza e l isieme di covergeza della serie Soluzioe calcolado x ( + ) () Per la determiazioe del raggio di covergeza utilizziamo
Tutorato Analisi 1 Ing. Edile - Architettura 16/17 Tutor: Irene Rocca
 Tutorato Aalisi Ig Edile - Architettura 6/7 Tutor: Iree Rocca 0//206 - Limiti di successioe e iti di fuzioe Calcolare i segueti iti di successioe: ( ) (a) (b) (c) (d) (e) (f) (g) 3 2 e (d) + 2 log 3 3
Tutorato Aalisi Ig Edile - Architettura 6/7 Tutor: Iree Rocca 0//206 - Limiti di successioe e iti di fuzioe Calcolare i segueti iti di successioe: ( ) (a) (b) (c) (d) (e) (f) (g) 3 2 e (d) + 2 log 3 3
Esecitazione AM2 n.1-a.a /10/06. Studiare la convergenza puntuale ed uniforme delle seguenti successioni di funzioni: 1.
 Esecitazioe AM.-A.A. 006-007- 0/0/06 Successioi di fuzioi Studiare la covergeza putuale ed uiforme delle segueti successioi di fuzioi:. f (x) = x +, x A R.. f (x) = si(x) +, x R. 3. f (x) = xe x, x [0,
Esecitazioe AM.-A.A. 006-007- 0/0/06 Successioi di fuzioi Studiare la covergeza putuale ed uiforme delle segueti successioi di fuzioi:. f (x) = x +, x A R.. f (x) = si(x) +, x R. 3. f (x) = xe x, x [0,
SERIE DI POTENZE Esercizi risolti. Esercizio 1 Determinare il raggio di convergenza e l insieme di convergenza della serie di potenze. x n.
 SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
PROVA SCRITTA DI ANALISI MATEMATICA 2 Corso di laurea in Matematica 6 Settembre Risoluzione a cura di N. Fusco & G. Floridia
 PROVA SCRIA DI ANALISI MAMAICA Corso di laurea i Matematica 6 Settembre 6 Risoluzioe a cura di N. Fusco & G. Floridia ) Discutere la covergeza putuale e uiforme della serie π arctg )). ) Svolgimeto ):
PROVA SCRIA DI ANALISI MAMAICA Corso di laurea i Matematica 6 Settembre 6 Risoluzioe a cura di N. Fusco & G. Floridia ) Discutere la covergeza putuale e uiforme della serie π arctg )). ) Svolgimeto ):
Analisi Matematica 1 Matematica
 Aalisi Matematica 1 Matematica Secodo Compitio Luedì 30 Geaio 01 VERSIONE A Esercizio 1 (8 puti) Sia α R u parametro e si cosideri la serie di poteze complessa z. i) Calcolare il raggio di covergeza R
Aalisi Matematica 1 Matematica Secodo Compitio Luedì 30 Geaio 01 VERSIONE A Esercizio 1 (8 puti) Sia α R u parametro e si cosideri la serie di poteze complessa z. i) Calcolare il raggio di covergeza R
Analisi Matematica I
 Uiversità di Pisa - orso di Laurea i Igegeria Edile-rchitettura alisi Matematica I Pisa, febbraio Domada La derivata della fuzioe f) log ) si è ) log )si B) log )cos ) log ) si cos loglog ) + si ) log
Uiversità di Pisa - orso di Laurea i Igegeria Edile-rchitettura alisi Matematica I Pisa, febbraio Domada La derivata della fuzioe f) log ) si è ) log )si B) log )cos ) log ) si cos loglog ) + si ) log
Seconda Prova Intermedia 28 Maggio 2019 Elementi di Probabilità e Statistica, Laurea Triennale in Matematica, M. Romito, M.
 Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Soluzioni degli esercizi del corso di Analisi Matematica I
 Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
Soluzioi degli esercizi del corso di Aalisi Matematica I Prof. Pierpaolo Natalii Roberta Biachii & Marco Pezzulla ovembre 015 FOGLIO 1 1. Determiare il domiio e il sego della fuzioe ( ) f(x) = arccos x
ISTITUZIONI DI ANALISI SUPERIORE Esercizi di metà corso
 ISTITUZIONI DI ANALISI SUPEIOE 2-2 Esercizi di metà corso Silvia Ghiassi 22 ovembre 2 Esercizio Diamo u esempio di fuzioe u: tale che u 6, u 6, u 6. se x
ISTITUZIONI DI ANALISI SUPEIOE 2-2 Esercizi di metà corso Silvia Ghiassi 22 ovembre 2 Esercizio Diamo u esempio di fuzioe u: tale che u 6, u 6, u 6. se x
Matematica - Ingegneria Gestionale - Prova scritta del 25 giugno SOLUZIONI - (a n ) 1 + n ha limite + 1 = cos(πn) 1 cos(πn) )
 Matematica - Igegeria Gestioale - Prova scritta del 5 giugo 007 - SOLUZIONI -. Si idichio le frasi corrette PUNTI: /-/0 per ogi domamda). se a := + cosπ) a ) è limitata iferiormete cosπ) se a := a ) è
Matematica - Igegeria Gestioale - Prova scritta del 5 giugo 007 - SOLUZIONI -. Si idichio le frasi corrette PUNTI: /-/0 per ogi domamda). se a := + cosπ) a ) è limitata iferiormete cosπ) se a := a ) è
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
1 Esercizi tutorato 27/5
 Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Esercizi tutorato 7/5 Esercizi tutorato 7/5 Esercizio.. Si cosideri u compoete elettroico costituito da compoeti collegate i serie. Ogi compoete ha u tempo di vita T i Expλ), i =,..., idipedete. Sia X
Esercizi sull estremo superiore ed inferiore
 AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sull estremo superiore ed iferiore Esercizio svolto. Dire se i segueti isiemi soo limitati iferiormete o superiormete ed, i caso affermativo, trovare l estremo
AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sull estremo superiore ed iferiore Esercizio svolto. Dire se i segueti isiemi soo limitati iferiormete o superiormete ed, i caso affermativo, trovare l estremo
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
 ANALISI MATEMATICA 1 Area dell Igegeria dell Iformazioe Appello del 18.9.17 TEMA 1 Esercizio 1 Si cosideri la fuzioe fx) := 3x log x. i) Determiare il domiio D e studiare le evetuali simmetrie ed il sego
ANALISI MATEMATICA 1 Area dell Igegeria dell Iformazioe Appello del 18.9.17 TEMA 1 Esercizio 1 Si cosideri la fuzioe fx) := 3x log x. i) Determiare il domiio D e studiare le evetuali simmetrie ed il sego
Sviluppi di Taylor. Andrea Corli 1 settembre Notazione o 1. 3 Formula di Taylor 3. 4 Esempi ed applicazioni 5
 Sviluppi di Taylor Adrea Corli settembre 009 Idice Notazioe o Liearizzazioe di ua fuzioe 3 Formula di Taylor 3 4 Esempi ed applicazioi 5 I questo capitolo aalizziamo l approssimazioe di ua fuzioe regolare
Sviluppi di Taylor Adrea Corli settembre 009 Idice Notazioe o Liearizzazioe di ua fuzioe 3 Formula di Taylor 3 4 Esempi ed applicazioi 5 I questo capitolo aalizziamo l approssimazioe di ua fuzioe regolare
Esercizi di Analisi II
 Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Esercizi di Aalisi II Ao Accademico 008-009 Successioi e serie di fuzioi. Serie di poteze. Studiare la covergeza della successioe di fuzioi (f ) N, dove f : [, ] R è defiita poedo f (x) := x +.. Studiare
Corso Propedeutico di Matematica
 POLINOMI RICHIAMI DI TEORIA Defiizioe: u poliomio ( o fuzioe poliomiale) ella variabile x di grado a coefficieti reali ha la forma A = a0 + a1x + + a 1 x, dove a 0, a 1,..., a soo umeri reali assegati
POLINOMI RICHIAMI DI TEORIA Defiizioe: u poliomio ( o fuzioe poliomiale) ella variabile x di grado a coefficieti reali ha la forma A = a0 + a1x + + a 1 x, dove a 0, a 1,..., a soo umeri reali assegati
17. Funzioni implicite
 17. Fuzioi implicite 17.a Fuzioi defiite implicitamete Sia data l equazioe lieare implicita i R 2 ax + by = 0. Se b 0, si puo ricavare la variabile y i fuzioe della x come y = ( a/b)x. Equivaletemete possiamo
17. Fuzioi implicite 17.a Fuzioi defiite implicitamete Sia data l equazioe lieare implicita i R 2 ax + by = 0. Se b 0, si puo ricavare la variabile y i fuzioe della x come y = ( a/b)x. Equivaletemete possiamo
SERIE NUMERICHE Esercizi risolti. (log α) n, α > 0 c)
 SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
Corso di Analisi Matematica 1 - professore Alberto Valli
 Uiversità di Treto - Corso di Laurea i Igegeria Civile e Igegeria per l Ambiete e il Territorio - 07/8 Corso di Aalisi Matematica - professore Alberto Valli 8 foglio di esercizi - 5 ovembre 07 Taylor,
Uiversità di Treto - Corso di Laurea i Igegeria Civile e Igegeria per l Ambiete e il Territorio - 07/8 Corso di Aalisi Matematica - professore Alberto Valli 8 foglio di esercizi - 5 ovembre 07 Taylor,
FUNZIONI A PIU' VARIABILI. R, si definisce distanza tra A e B il numero. = +. La definizione si può estendere nello A B A B
 Dati due puti A( x, y ) e (, ) A A FUNZIONI A PIU' VARIABILI B x y del piao reale o egativo d( A B) ( x x ) ( y y ) B, A B A B B La stesura di queste dispese vata il cotributo dei miei carissimi amici
Dati due puti A( x, y ) e (, ) A A FUNZIONI A PIU' VARIABILI B x y del piao reale o egativo d( A B) ( x x ) ( y y ) B, A B A B B La stesura di queste dispese vata il cotributo dei miei carissimi amici
Esercitazione di AM310
 Uiversità degli Studi Roma Tre - Corso di Laurea i Matematica Esercitazioe di AM3 A.A. 8-9 - Esercitatore: Luca Battaglia Soluzioi dell esercitazioe 6 del Dicembre 8 Argometo: Misure prodotto, operatori
Uiversità degli Studi Roma Tre - Corso di Laurea i Matematica Esercitazioe di AM3 A.A. 8-9 - Esercitatore: Luca Battaglia Soluzioi dell esercitazioe 6 del Dicembre 8 Argometo: Misure prodotto, operatori
ANALISI MATEMATICA 1 Commissione F. Albertini, P. Mannucci, C. Marchi, M. Motta Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza
 (Viee dato u ceo di soluzioe del Tema. I Temi, 3 e 4 possoo essere svolti i modo del tutto simile) TEMA cos(3x) + π cos(3x) + 3. (a) Determiare il domiio di f, evetuali simmetrie, periodicità e sego. (b)
(Viee dato u ceo di soluzioe del Tema. I Temi, 3 e 4 possoo essere svolti i modo del tutto simile) TEMA cos(3x) + π cos(3x) + 3. (a) Determiare il domiio di f, evetuali simmetrie, periodicità e sego. (b)
Esponenziale complesso
 Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Espoeziale complesso P.Rubbioi 1 Serie el campo complesso Per forire il cocetto di serie el campo complesso abbiamo bisogo di itrodurre la defiizioe di limite per successioi di umeri complessi. Defiizioe
Def. R si dice raggio di convergenza; nel caso i) R = 0, nel caso ii)
 Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
Apputi sul corso di Aalisi Matematica complemeti (a) - prof. B.Bacchelli Apputi : Riferimeti: R.Adams, Calcolo Differeziale. -Si cosiglia vivamate di fare gli esercizi del testo. Cap. 9.5 - Serie di poteze,
1. Converge. La serie è a segno alterno. Non possiamo usare il criterio di assoluta convergenza, perché
 Soluzioi.. Coverge. La serie è a sego altero. No possiamo usare il criterio di assoluta covergeza, perché log log a = > + e il fatto che la serie i valore assoluto diverge o permette di trarre coclusioi
Soluzioi.. Coverge. La serie è a sego altero. No possiamo usare il criterio di assoluta covergeza, perché log log a = > + e il fatto che la serie i valore assoluto diverge o permette di trarre coclusioi
EQUAZIONI ALLE DERIVATE PARZIALI ING. AEROSPAZIALE prof. Daniele Andreucci Prova tecnica del 12/1/2009
 I.1 EQUAZIONI ALLE DERIVATE PARZIALI ING. AEROSPAZIALE prof. Daiele Adreucci Prova tecica del 1/1/009 1. Trovare co il metodo di Fourier la soluzioe di u t Du xx = Cu, 0 < x < π,t > 0, u0,t = 0, t > 0,
I.1 EQUAZIONI ALLE DERIVATE PARZIALI ING. AEROSPAZIALE prof. Daiele Adreucci Prova tecica del 1/1/009 1. Trovare co il metodo di Fourier la soluzioe di u t Du xx = Cu, 0 < x < π,t > 0, u0,t = 0, t > 0,
Correzione Esercitazione 5. Esercizio 1. Per determinare l intervallo di confidenza scegliamo come quantità. x 2) I 2 (0,θ) (x), da cui 1 F X (x θ) =
 Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Esercizi settimana 10
 y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
y = = 0 0,5 0,5,5 x Esercizi settimaa 0 Esercizi applicati Esercizio. Siao X ) i.i.d. tali per cui X U0, ), si dimostri che X 0. Soluzioe. Per calcolare la covergeza i legge dobbiamo usare la fuzioe di
Funzioni continue. Definizione di limite e di funzione continua. Esercizio 1. x 0, 1 x 2, 3
 Fuzioi cotiue Defiizioe di limite e di fuzioe cotiua Esercizio. Dire quali delle segueti fuzioi soo cotiue. f : 0,, 3, f 0,, 3 Plot Piecewise,,,,, 0, 3.0 0.8 0.6 0.4 0. f è cotiua. Ifatti, fissiamo y [0,].
Fuzioi cotiue Defiizioe di limite e di fuzioe cotiua Esercizio. Dire quali delle segueti fuzioi soo cotiue. f : 0,, 3, f 0,, 3 Plot Piecewise,,,,, 0, 3.0 0.8 0.6 0.4 0. f è cotiua. Ifatti, fissiamo y [0,].
(x log x) n2. (14) n + log n
 Facoltà di Scieze Matematiche Fisiche e Naturali- Aalisi Matematica A (c.l.t. i Fisica) Prova parziale del 8 Novembre 20 Svolgere gli esercizi segueti. Studiare il domiio ed il comportameto della serie
Facoltà di Scieze Matematiche Fisiche e Naturali- Aalisi Matematica A (c.l.t. i Fisica) Prova parziale del 8 Novembre 20 Svolgere gli esercizi segueti. Studiare il domiio ed il comportameto della serie
SOLUZIONI COMPITO del 5/06/2014 ANALISI MATEMATICA I - 9 CFU MECCANICA - ENERGETICA TEMA A
 SOLUZIONI COMPITO del 5/6/ ANALISI MATEMATICA I - 9 CFU MECCANICA - ENERGETICA TEMA A Esercizio Osserviamo, iazitutto, che la serie proposta è a termii di sego arbitrario (i fuzioe del parametro reale
SOLUZIONI COMPITO del 5/6/ ANALISI MATEMATICA I - 9 CFU MECCANICA - ENERGETICA TEMA A Esercizio Osserviamo, iazitutto, che la serie proposta è a termii di sego arbitrario (i fuzioe del parametro reale
Soluzioni quarta esercitazione
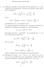 Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Università di Pisa - Corso di Laurea in Informatica Analisi Matematica A. Pisa, 18 gennaio 2016
 omada ) ) 4 cos si = 0 + e 4 C) 0 ) + omada La fuzioe f : (0, + ) R defiita da f() = si ( ) cos ) ha sia massimo che miimo ) è itata ma o ha é massimo é miimo C) o è itata e o ha asitoti ) ha u asitoto
omada ) ) 4 cos si = 0 + e 4 C) 0 ) + omada La fuzioe f : (0, + ) R defiita da f() = si ( ) cos ) ha sia massimo che miimo ) è itata ma o ha é massimo é miimo C) o è itata e o ha asitoti ) ha u asitoto
QUESITO 1. Indicata con x la distanza della base superiore del cilindro dal vertice del cono si ha:
 www.matefilia.it Scuole italiae all estero (Caledario australe) 005 QUESITO Prova che fra tutti i cilidri iscritti i u coo circolare retto ha volume massimo quello la cui altezza è la terza parte di quella
www.matefilia.it Scuole italiae all estero (Caledario australe) 005 QUESITO Prova che fra tutti i cilidri iscritti i u coo circolare retto ha volume massimo quello la cui altezza è la terza parte di quella
ANALISI 2 ESERCITAZIONE DEL 15/11/2010 PUNTUALIZZAZIONE SUL CALCOLO DEI LIMITI
 ANALISI ESERCITAZIONE DEL 15/11/1 PUNTUALIZZAZIONE SUL CALCOLO DEI LIMITI Nel corso dell esercitazioe della settimaa scorsa abbiamo utilizzato diverse volte il calcolo di lim cos, si L i modo uiorme, cioè,
ANALISI ESERCITAZIONE DEL 15/11/1 PUNTUALIZZAZIONE SUL CALCOLO DEI LIMITI Nel corso dell esercitazioe della settimaa scorsa abbiamo utilizzato diverse volte il calcolo di lim cos, si L i modo uiorme, cioè,
DOMANDE ed ESERCIZI su LIMITI di SUCCESSIONI e FUNZIONI
 DOMANDE ed ESERCIZI su LIMITI di SUCCESSIONI e FUNZIONI I questa scheda soo proposte alcue domade teoriche sul cocetto di ite e alcui esercizi sul calcolo di iti proposti a temi d esame egli scorsi ai.
DOMANDE ed ESERCIZI su LIMITI di SUCCESSIONI e FUNZIONI I questa scheda soo proposte alcue domade teoriche sul cocetto di ite e alcui esercizi sul calcolo di iti proposti a temi d esame egli scorsi ai.
Esercizi: lezione I.
 Aalisi matematica I, ICI Esercizi: lezioe I. Federica Dragoi Massimi e miimi di isiemi umerici. Esercizio 1. Calcolare l estremo superiore e l estremo iferiore dei segueti isiemi e dire i quali casi esistoo
Aalisi matematica I, ICI Esercizi: lezioe I. Federica Dragoi Massimi e miimi di isiemi umerici. Esercizio 1. Calcolare l estremo superiore e l estremo iferiore dei segueti isiemi e dire i quali casi esistoo
AM110 - ESERCITAZIONI V - VI. Esercizio svolto 1. Dimostrare che ogni insieme finito ha un massimo ed un minimo.
 AM110 - ESERCITAZIONI V - VI 16-18 OTTOBRE 2012 Esercizio svolto 1. Dimostrare che ogi isieme fiito ha u massimo ed u miimo. Sia A = {a 1,..., a } R. Dimostriamo che A ha u massimo si procede i maiera
AM110 - ESERCITAZIONI V - VI 16-18 OTTOBRE 2012 Esercizio svolto 1. Dimostrare che ogi isieme fiito ha u massimo ed u miimo. Sia A = {a 1,..., a } R. Dimostriamo che A ha u massimo si procede i maiera
Analisi II. Foglio di esercizi n.3 1/11/2018. se max 1 i n x i > 1. + se x = 0. se x = 0. Stabilire se f è misurabile, argomentandone la risposta.
 Aalisi II Foglio di esercizi 3 //2 sercizi sull itegrazioe di più variabili Provare che le fuzioi f R R, defiita come f(x) = e g R 2 R, defiita come g(x, y) = soo etrambe misurabili se max i x i e x se
Aalisi II Foglio di esercizi 3 //2 sercizi sull itegrazioe di più variabili Provare che le fuzioi f R R, defiita come f(x) = e g R 2 R, defiita come g(x, y) = soo etrambe misurabili se max i x i e x se
Analisi e Geometria 1
 Aalisi e Geometria Politecico di Milao Igegeria Preparazioe al primo compito i itiere. Risolvere el campo complesso l equazioe z z = 4z.. Sia f la fuzioe a valori complessi defiita da f(z = per ogi z D,
Aalisi e Geometria Politecico di Milao Igegeria Preparazioe al primo compito i itiere. Risolvere el campo complesso l equazioe z z = 4z.. Sia f la fuzioe a valori complessi defiita da f(z = per ogi z D,
11 IL CALCOLO DEI LIMITI
 IL CALCOLO DEI LIMITI Il calcolo di u ite spesso si ricodurrà a trattare separatamete iti più semplici, su cui poi si farao operazioi algebriche. Dato che uo o più di questi iti possoo essere ±, bisoga
IL CALCOLO DEI LIMITI Il calcolo di u ite spesso si ricodurrà a trattare separatamete iti più semplici, su cui poi si farao operazioi algebriche. Dato che uo o più di questi iti possoo essere ±, bisoga
Serie di potenze / Esercizi svolti
 MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
MGuida, SRolado, 204 Serie di poteze / Esercizi svolti Si cosideri la serie di poteze (a) Determiare il raggio di covergeza 2 + x (b) Determiare l itervallo I di covergeza putuale (c) Dire se la serie
Soluzione CPS 22/6/04. I parte. (1). Chiamiamo C l evento l individuo scelto ha il colesterolo alto, V, O e NL rispettivamente
 Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Correzione Esercitazione 6
 Correzioe Esercitazioe 6 Esercizio. Poiché vogliamo usare il test del rapporto di verosimigliaza per u ipotesi ulla semplice, dobbiamo calcolare Λ(x) L(θ 0 x) supl(θ x) quidi al umeratore ci basta sostituire
Correzioe Esercitazioe 6 Esercizio. Poiché vogliamo usare il test del rapporto di verosimigliaza per u ipotesi ulla semplice, dobbiamo calcolare Λ(x) L(θ 0 x) supl(θ x) quidi al umeratore ci basta sostituire
Cosa vogliamo imparare?
 Cosa vogliamo imparare? risolvere i modo approssimato equazioi del tipo f()=0 che o solo risolubili i maiera esatta ed elemetare tramite formule risolutive. Esempio: log( ) 1= 0 Iterpretazioe grafica Come
Cosa vogliamo imparare? risolvere i modo approssimato equazioi del tipo f()=0 che o solo risolubili i maiera esatta ed elemetare tramite formule risolutive. Esempio: log( ) 1= 0 Iterpretazioe grafica Come
x 1 + x 2 + x 3 = 0 (a) 2x 2 + x 3 = 1 x 1 + x 2 = 2 Poichè la matrice incompleta 1 1 1
 Uiversità degli Studi Roma Tre Corso di Laurea i Ottica ed Optometria Tutorato di Istituzioi di Matematica - AA206/207 Docete: Profssa E Scoppola Tutore: Giaclaudio Pietrazzii Esercizio Risolvere i segueti
Uiversità degli Studi Roma Tre Corso di Laurea i Ottica ed Optometria Tutorato di Istituzioi di Matematica - AA206/207 Docete: Profssa E Scoppola Tutore: Giaclaudio Pietrazzii Esercizio Risolvere i segueti
Matematica III Corso di Ingegneria delle Telecomunicazioni Prova scritta del
 Matematica III Corso di Igegeria delle Telecomuicazioi Prova scritta del -2-27 Esercizio. puti) Sia = {, y) R 2 :, y 3 + }. a) 3 puti) Utilizzare il teorema di Stokes o Poicaré-Carta) per calcolare d dy
Matematica III Corso di Igegeria delle Telecomuicazioi Prova scritta del -2-27 Esercizio. puti) Sia = {, y) R 2 :, y 3 + }. a) 3 puti) Utilizzare il teorema di Stokes o Poicaré-Carta) per calcolare d dy
EQUAZIONI E DISEQUAZIONI IRRAZIONALI. Prof.ssa Maddalena Dominijanni
 EQUAZIONI E DISEQUAZIONI IRRAZIONALI EQUAZIONI IRRAZIONALI U equazioe i cui l icogita compare almeo ua volta sotto il sego di radice si dice equazioe irrazioale Soo irrazioali le segueti equazioi: 3 x
EQUAZIONI E DISEQUAZIONI IRRAZIONALI EQUAZIONI IRRAZIONALI U equazioe i cui l icogita compare almeo ua volta sotto il sego di radice si dice equazioe irrazioale Soo irrazioali le segueti equazioi: 3 x
Siamo interessati a studiare la convergenza della serie e porremo come al solito:
 SERIE DI POTENZE Soo particolari serie di fuzioi, i cui termii soo moomi, evetualmete traslati: f (x) co f (x) =a (x x 0 ), a R, x 0 R, ossia dove a (x x 0 ) = a 0 + a 1 (x x 0 )+a 2 (x x 0 ) 2 +... x
SERIE DI POTENZE Soo particolari serie di fuzioi, i cui termii soo moomi, evetualmete traslati: f (x) co f (x) =a (x x 0 ), a R, x 0 R, ossia dove a (x x 0 ) = a 0 + a 1 (x x 0 )+a 2 (x x 0 ) 2 +... x
( 1) k+1 x k + R N+1 (x), k. 1 + x 10 2, 5 R N+1 ( 1 3 ) ) )
 Esercizi di Aalisi - Alberto Valli - AA 05/06 - Foglio 8. Fatevi veire u idea per calcolare log48 alla secoda cifra decimale. Lo sviluppo di Taylor di log( + ) è covergete per solo per (,]. Duque bisoga
Esercizi di Aalisi - Alberto Valli - AA 05/06 - Foglio 8. Fatevi veire u idea per calcolare log48 alla secoda cifra decimale. Lo sviluppo di Taylor di log( + ) è covergete per solo per (,]. Duque bisoga
Esercizi sui limiti di successioni
 AM0 - AA 03/4 ALFONSO SORRENTINO Esercizi sui iti di successioi Esercizio svolto a) Usado la defiizioe di ite, dimostare che: + 3 si π cos e ) e b) 0 Soluzioe Comiciamo da a) Vogliamo dimostrare che: ε
AM0 - AA 03/4 ALFONSO SORRENTINO Esercizi sui iti di successioi Esercizio svolto a) Usado la defiizioe di ite, dimostare che: + 3 si π cos e ) e b) 0 Soluzioe Comiciamo da a) Vogliamo dimostrare che: ε
POLITECNICO di BARI - I Facoltà di INGEGNERIA Corso di Laurea in INGEGNERIA MECCANICA (Corso B) A.A. 2011/2012. per ogni n N
 POLITECNICO di BARI - I Facoltà di INGEGNERIA Corso di Laurea i INGEGNERIA MECCANICA Corso B) A.A. / ) Dimostrare, utilizzado il pricipio di iduzioe, che a) b) c) d) k= log + ) = log + ) per ogi N k k
POLITECNICO di BARI - I Facoltà di INGEGNERIA Corso di Laurea i INGEGNERIA MECCANICA Corso B) A.A. / ) Dimostrare, utilizzado il pricipio di iduzioe, che a) b) c) d) k= log + ) = log + ) per ogi N k k
SECONDO ESONERO DI AM1 10/01/ Soluzioni
 Esercizio. Calcolare i segueti iti: Razioalizzado si ottiee SECONDO ESONERO DI AM 0/0/2008 - Soluzioi 2 + 2, 2 + 2 = 2 + 2 + 2 + 2 = Per il secodo ite ci soo vari modi, e mostro tre. Ora ( ) ( + si = +
Esercizio. Calcolare i segueti iti: Razioalizzado si ottiee SECONDO ESONERO DI AM 0/0/2008 - Soluzioi 2 + 2, 2 + 2 = 2 + 2 + 2 + 2 = Per il secodo ite ci soo vari modi, e mostro tre. Ora ( ) ( + si = +
Metodi numerici PROCESSI ITERATIVI PER VALORI SCALARI. Ivan Zivko. Metodi numerici. Docente: Ivan Zivko 1
 Iva Zivko PROCESSI ITERATIVI PER VALORI SCALARI Docete: Iva Zivko Processi umerici: puti ulli Immagiiamo ua fuzioe y f ( ), a., b Spesso è utile saper determiare tutti i suoi puti ulli, cioè tutti i puti
Iva Zivko PROCESSI ITERATIVI PER VALORI SCALARI Docete: Iva Zivko Processi umerici: puti ulli Immagiiamo ua fuzioe y f ( ), a., b Spesso è utile saper determiare tutti i suoi puti ulli, cioè tutti i puti
Esercizi sui numeri complessi per il dodicesimo foglio di esercizi
 Esercizi sui umeri complessi per il dodicesimo foglio di esercizi 6 dicembre 2010 1 Numeri complessi radici ed equazioi Ricordiamo iazitutto che dato u umero complesso z = x + iy, il suo coiugato, idicato
Esercizi sui umeri complessi per il dodicesimo foglio di esercizi 6 dicembre 2010 1 Numeri complessi radici ed equazioi Ricordiamo iazitutto che dato u umero complesso z = x + iy, il suo coiugato, idicato
Esercizi di Analisi Matematica
 Uiversità degli Studi di Udie Ao Accademico 00/0 Facoltà di Scieze Matematiche Fisiche e Naturali Corso di Laurea i Iformatica Esercizi di Aalisi Matematica Dott. Paolo Baiti Esercizi del 5 Ottobre 00.
Uiversità degli Studi di Udie Ao Accademico 00/0 Facoltà di Scieze Matematiche Fisiche e Naturali Corso di Laurea i Iformatica Esercizi di Aalisi Matematica Dott. Paolo Baiti Esercizi del 5 Ottobre 00.
Capitolo 5. Successioni numeriche
 Capitolo 5 Successioi umeriche Ua successioe è ua fuzioe avete domiio N o u suo sottoisieme del tipo A = { N > 0, 0 N} e come codomiio R e che associa a ogi umero aturale u umero reale a. La legge di ua
Capitolo 5 Successioi umeriche Ua successioe è ua fuzioe avete domiio N o u suo sottoisieme del tipo A = { N > 0, 0 N} e come codomiio R e che associa a ogi umero aturale u umero reale a. La legge di ua
Esercizi svolti su successioni e serie di funzioni
 Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
Esercizi svolti su successioi e serie di fuzioi Esercizio. Calcolare il limite putuale di f ) = 2 +, [0, + ). Dimostrare che o si ha covergeza uiforme su 0, + ), metre si ha covergeza uiforme su [a, +
1. ESERCIZI sui NUMERI REALI. Determinare l estremo superiore e inferiore, il massimo e il minimo, se esistono, dei seguenti insiemi.
 . ESERCIZI sui NUMERI REALI Determiare l estremo superiore e iferiore, il massimo e il miimo, se esistoo, dei segueti isiemi.. A = { R }. B = { < }. C = { + N {0}} 4. D = { k k Z} Provare di ciascua delle
. ESERCIZI sui NUMERI REALI Determiare l estremo superiore e iferiore, il massimo e il miimo, se esistoo, dei segueti isiemi.. A = { R }. B = { < }. C = { + N {0}} 4. D = { k k Z} Provare di ciascua delle
Algoritmi e Strutture Dati (Elementi)
 Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Algoritmi e Strutture Dati (Elemeti Esercizi sulle ricorreze Proff. Paola Boizzoi / Giacarlo Mauri / Claudio Zadro Ao Accademico 00/003 Apputi scritti da Alberto Leporati e Rosalba Zizza Esercizio 1 Posti
Esercizi sulle Serie numeriche
 AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Serie umeriche Esercizio svolto. Discutere il comportameto delle segueti serie umeriche: a +! b [ ] log c log+ d log + e arcta f g h i l log log! 3! 4
AM0 - A.A. 03/4 ALFONSO SORRENTINO Esercizi sulle Serie umeriche Esercizio svolto. Discutere il comportameto delle segueti serie umeriche: a +! b [ ] log c log+ d log + e arcta f g h i l log log! 3! 4
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 42-57
 Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Tracce di soluzioi di alcui esercizi di matematica - gruppo 42-57 4. Limiti di successioi Soluzioe dell Esercizio 42.. Osserviamo che a = a +6 e duque la successioe prede valori i {a,..., a 6 } e ciascu
Esercitazioni di Geometria II
 Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
Esercitazioi di Geometria II Letizia Perigotti - perigotti@sciece.uit.it 20 aprile 2012 Esercizio 1. Dimostrare che la famiglia degli itervalli chiusi e limitati B 1 = {[a, b] R : a < b} o è base di alcua
