A5 - Integrali di campi scalari e vettoriali su linee, superfici e volumi

Transcript

1 A5 - Itegli di cmpi scli e ettoili s liee, spefici e olmi A5.1 - INTEGRALE DI LINEA i c oiett di R 3, di estemi 1 e. ppoimo che si descitt i fom pmetic dll fioe ettoile, dipedete dl pmeto scle : 1 : [, ] R [ ] R 3 () 1 () i h petto: ( ) + + () è il ettoe, fioe del pmeto, che idii il geeico pto dell c. i o f fioe defiit sll isieme [] dei pti di. E oto dll Alisi che l qtità: 1 f d chimt itegle cilieo, è idipedete dll pmetiioe scelt ed iolte islt sempe: d. i peiee così fcilmete ll foml isolti dell itegle cilieo: i ossei che se f ( ( )) 1, l itegle f ( ( )) d f ( ) 1 d foisce l lghe dell c. L fioe f pò essee si fioe scle che fioe ettoile. Ad esempio, si cosidei cmpo scle φ cotio e defiito lgo l c. L gde: I 1 ( φ ) φ( ( )) d φ( ( )) è dett itegle di lie del cmpo scle φ lgo l lie. i o cmpo ettoile defiito e cotio lgo. L gde:

2 I ( ) d d + d + 1 d è dett itegle del cmpo ettoile lgo l lie. Osseimo che l qtità d d + d + d è ettoe tgete e di lghe ifiitesim d. d + d etto l itegle sddetto è l somm lgo delle compoeti tgeili di ispetto ll c stess. L gde itegd d d + d d è fom diffeeile di gdo 1. i pò sciee che: I + ( ) i d c doe î è il esoe tgete el geeico pto, ete eso cocode co l oietioe dell c. e è c chis semplice (cioè o itesec se stess i lc pto) llo l itegle lgo tle c: è detto cicitioe di lgo. I ( ) d i d Osseimo che l itegle di lie di cmpo ettoile è cso pticole di itegle cilieo, el qle l fioe f è così defiit: f ( )) ( Il cotito dell pmetiioe è coteto el esoe tgete. i pò iftti dimoste che islt: i h qidi: 1 d ( ) i d 1 che ppeset l foml isolti pe l itegle di lie del cmpo ettoile. d 1

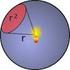
3 Esempio icitioe di ettoe (,,) lgo cechio di ggio R cetto ell oigie e gicete sl pio (edi fig). Le eqioi di i coodite cilidiche soo: ρ R 0 I fom ctesi: + R L eqioe dell c i fom pmetic è: R cos Φ R siφ 0 I fom ettoile: i h qidi: (,,) d π π [ - R siφ dφ + R cosφ dφ] 0 0 ( Φ) R cosφ + R siφ + 0 ( Φ) dφ π 0 φ ρ [ R siφ + R cosφ + 0 ] R d dφ iccome,, soo fioi di φ, st espimee i fioe di φ e si pò solgee fcilmete l itegle. Allo stesso isltto si pote peeie che sciedo l itegle ell fom d i, e icoddo che l cicofee sl pio è l secod lie coodit del sistem di coodite cilidiche. etto, pe isolee l itegle è sfficiete ossee che i qesto cso islt - siφ + cosφ + 0, e iolte che l elemeto di lie d coicide co il secodo co φ elemete ds h dφ, peciò d R dφ. A5. - INTEGRALE UERFIIALE E FLUO DI UN AMO ETTORIALE i speficie oiett di R 3 descitt i fom pmetic dll fioe ettoile, dipedete di pmeti scli,: 3 {[,] [ c,d] } R [ ] : (, ) D R

4 Usdo l otioe ettoile: (, ) (, ) + (, ) + (, ) è il ettoe, fioe dei pmeti e, che idii il geeico pto dell speficie. i o f fioe scle o ettoile defiit sll isieme [] dei pti di. E oto dll Alisi che l qtità: f d chimt itegle speficile, è idipedete dll pmetiioe scelt ed iolte islt sempe: d d, doe : i peiee così fcilmete ll foml isolti dell itegle di speficie: i ossei che se f d f ( (, )) d f ( (, )) D f ( (, )) 1, l itegle d c d d d foisce l e dell speficie. L fioe f pò essee si fioe scle che fioe ettoile. Ad esempio, si cosidei cmpo scle φ cotio e defiito lgo l speficie. L gde: I d c ( φ ) φ d φ( (, )) d è dett itegle speficile del cmpo scle φ lgo l speficie. i o (,,) cmpo ettoile defiito e cotio lgo. i iolte î il esoe omle ll speficie el geeico pto. e qto igd il eso di î, pe coeioe iee cosideto dietto eso l esteo el cso di speficie chis. e è speficie pet, î è dietto dll fcci positi qell egti, edo stilito pioi qle si l fcci positi dell speficie. e h pe cotoo lie chis oiett γ, si ssme pe ite che ot el eso positio fissto s γ. L qtità: F ( ) i d î il eso i ci

5 è dett flsso del cmpo ettoile tteso l speficie. Alogmete idiieemo co il flsso di tteso speficie chis. F ( ) i d i ossei che il flsso di cmpo ettoile è cso pticole di itegle speficile, el qle l fioe f è così defiit: f ( (, )) Il cotito dell pmetiioe è coteto el esoe omle î. i pò iftti dimoste che: i h qidi: i i d d [ ] d d c che ppeset l foml isolti pe l itegle di flsso del cmpo ettoile. d c i d [ ] d d c Esempio Flsso del ettoe (,,) tteso speficie sfeic cett ell oigie di ggio R (fig). i L eqioe i coodite sfeiche è R. I fom ctesi: + + R

6 L eqioe dell speficie i fom pmetic è: R siθ cosφ R siθ siφ R cosθ e cioè: ( θ, Φ) R siθ cosφ + R siθ siφ + R cos θ L itegle si pò isolee fcilmete ossedo che l speficie sfeic coicide co l pim speficie coodit del sistem di coodite sfeiche. eciò i qesto cso islt: (θ, Φ) i (θ, Φ) R i Ricoddo iolte che: i siθ cos Φ i + siθ si Φ i + cosθ î e teedo coto che l elemeto ifiitesimo di speficie sfeic è (fig): d d h h d θ d Φ R siθ dθ dφ 1 3 (L elemeto ifiitesimo di speficie d si pò otteee che sdo l foml θ Φ d θ dφ, tlmete) si h ifie: i π π d ( si θcosφ + si θsiφ cosθ) R siθ dθ dφ Osseimo che il flsso di tteso si pote ice che medite l foml isolti geele del flsso di cmpo ettoile, iché sfttdo l coosce delle gdee ote î e d (eificlo pe eseciio). U metodo ltetio che si pò tilie qdo è ichiesto di effette itegle s di speficie sfeic cosiste ell tilio dell defiiioe di golo solido. A tl poposito, si icodi che l golo solido ΔΩ sotteso d elemeto di speficie Δ le: Δ ΔΩ [sted]

7 L elemeto di speficie sfeic pò sciesi petto el segete modo: d dω doe l golo sotteso ll elemeto ifiitesimo di speficie sfeic le: dω si θ dθ dφ etto, il flsso tteso pò isciesi come: i d dω I dω 4π 4π cioè come itegle ell iile Ω. L pplicioe di qesto metodo è pticolmete tggios qdo l qtità islt iesmete popoiole (qesto è il cso, d esempio, dell pote idit d te gde dist): iftti, i qesto cso, il polem si icoce ll itegioe di fioe scle I che o dipede d. A5.3 - INTEGRALE DI OLUME i cosidei speficie chis che cchide egioe dello spio R 3. i possoo llo ee i segeti itegli di olme: d d Itegle di o scle Itegle di ettoe Ntlmete, se è espesso, d esempio, i fom ctesi: + + islt : d d i + d i + d e ci si icoce qidi ll itegle di 3 fioi scli.

8 Gli itegli di olme, come qelli ciliei o di speficie, possoo essee effettti, scelt, i o dei sistemi di ifeimeto dispoiili. Nel cso di coodite ctesie, d diet, lmete, d d d. I sistem di ifeimeto sfeico iece, occoeà espimee il olme elemete el modo segete (edi fig): θ d dφ d h h h d d θ d Φ siθ d dθ dφ 1 3 φ seθ seθ dφ