pdv + p ponendo v T v p

Транскрипт

1 Nel aso artiolare in i δl sia esresso in fnzione delle oordinate e, è er trasformazione internamente reersibile ari a : δl d laoro di ariazione di olme, essendo d d d esso si ò osì esrimere δl d d onendo β e si ha he δl βd d Coeffiiente di dilatazione isobara Coeffiiente di omrimibilità isoterma

2 COEFFICIENI ELASICI ρ ρ Coeffiiente di dilatazione isobara: aratterizza la ariazione erentale di olme seifio (o della densità) onsegente alla la ariazione isobaria della temeratra. ρ ρ Coeffiiente di omrimibilità isoterma: aratterizza la ariazione erentale di olme seifio (o della otenza qarta della densità) onsegente alla ariazione isoterma della ressione. S s ρ ρ s Coeffiiente di omrimibilità isoentroia: aratterizza la ariazione erentale di olme seifio (o della otenza qarta della densità nsità) onsegente alla ariazione isoentroia della ressione.

3 CAPACIA EMICA E CALOE SPECIFICO Per n sistema he sbisa na trasformazione termodinamia si definise Caaità termia er qella trasformazione il raorto tra la qantità di alore sambiata dal sistema e la onsegente ariazione di temeratra del sistema stesso. C dq d in termini infinitesimi [J/K] C Q he è in realtà na aaità media. La aaità termia di n oro raresenta l oosizione di n oro alla ariazione di temeratra in segito ad no sambio di energia termia: tra de ori he rieono na stessa qantità di alore, qello a aaità termia minore arà n maggiore amento di temeratra. La relatia grandezza estensia è detta alore seifio: dq md in termini infinitesimi [J/gK] Q m alore seifio medio.

4 Calori seifii e oeffiienti elastii Calore seifio a olme ostante Per na trasformazione internamente reersibile: δ l d er i la forma differenziale della rima legge er n sistema hiso he eole in modo internamente reersibile è: Se la trasformazione è isoora (ost): d δ q d d δ q er i ( q) d Qantità elementare di energia termia seifia trasferita a olme seifio ostante. è na orrelazione tra la definizione matematia e fenomenologia del alore seifio:orrela il alore seifio (rorietà seifia) a olme ostante on il raorto tra la qantità di energia termia seifia trasferita al sistema e la orrisondente ariazione della temeratra, in na trasformazione internamente reersibile a olme ostante.

5 h Calore seifio a ressione ostante Per na trasformazione internamente reersibile: er i ( q) d dh δq d Qantità elementare di energia termia seifia trasferita a ressione ostante. Correla la definizione formale della rorietà seifia a qella fenomenologia. β e s

6 Un altro modo er definire i alori seifii a ressione e olme seifio ostanti si ottiene sfrttando le eqazioni di Gibbs ds d d d d d ; ds d dh d d d er i se è ost s se è ost s h

7 GAS Una sostanza è in fase gassosa (gas) se ale la relazione: z è la ostante del gas J gk z è il fattore di omrimibilità r z ( 0) si riaa l'eqazione dei gas ideali o erfetti in genere è z < er alori eleati di e :noto z è ossibile dall'eqazione riaare, ore.

8 PAAMEI IDOI iferiamo e allo stato ritio e introdiamo i arametri ridotti: π π è la ressione ridotta e θ è la ressione ritia θ è la temeratra ridotta e è la temeratra ritia Lo stato orrisondente è lo stato termodinamio aratterizzato dai arametri ridotti definiti. De sostanze dierse he hanno le stesse ondizioni di ressione e temeratra ridotta, si troano nello stesso stato orrisondente.

9 PAAMEI IDOI Van der Walls enniò il riniio degli stati orrisondenti: sostanze dierse resentano gli stessi z se si troano nello stesso stato di eqilibrio orrisondente (in ogni stato di eqilibrio l eqazione di stato f(,,) è del tio /ost). Per ttti i gas è alido lo stesso legame fnzionale z f(π, θ): nota la sostanza e noti ressione e temeratra, si ò altare z. Si ò arlare di gas ideale, ommettendo n errore < 8% se: π 0,5 er 0 θ er > ottenendo he il alore di z sia

10 GAS IDEALE ore V m ln ln ln ln d d d ostante f (,, ) 0 in na arte della serfiie aratteristia EQUAZIONE DI SAO

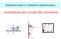
11 PE VIA SPEIMENALE: ESPEIENZA DI JOULE f() le notò he nell arire la alola di arazione tra il serbatoio ontenente ia e qello ontenente il oto, drante sansione dell aria, la temeratra ll aqa restaa ostante e non erano ambi di energia nel modo alore, bbene olme seifio e ressione riaano: AIA EMOMEO ACQUA LIQUIDA VUOO d δq δl δq 0 0, 0 Anhe se e sono ambiati, e non lo sono;ertanto essi selti insieme non aratterizzano lo stato, oero non

12 PE VIA ANALIICA PE VIA ANALIICA f() f() h() h h() h roede er analogamente si n differenziale esatto essendo ) ( ) ( 0 / 0 / 0 / / f ds d d d d ds

13 E era anhe l imliazione ontraria: h f ( ) g( ) eqazione di stato è ostante

14 Se il gas è ideale: d dh h d d ) ( ) ( ) ( ) ( β

15 Inoltre: MAYE ELAZIONE DI β

16 CALCOLO PE, h, s NEL CASO DI GAS IDEALE d ( ) d dh ( ) d ds d d ( ) d d ds dh d ( ) d d essendo d d d si ha ds ( ) d ( ) d

17 ( ) ( ) ln ln ln ln ln ln d d s d h d CALCOLO PE, h, s NEL CASO DI GAS IDEALE a alori seifii ostanti on

18 ASFOMAZIONI: ADIABAICA INENAMENE EVESIBILE ds 0 d d 0 er n gas ideale ale er i d d 0 se i alori seifii sono ostanti on, si ha ln ln ost oihè ln ln ost da i

19 ASFOMAZIONI: ADIABAICA INENAMENE EVESIBILE ( ) ost ost ost ost ost ost ost ln ln -

20 Adiabatia: ost Isoterma: ost, ost Sl iano la trasformazione isoentroia er gas ideale on alori seifii ostanti è raresentata da n ierbole non eqilatera

21 [ ] [ ] l d d l Per sistemi hisi e er Per sistemi hisi e er trasf trasf. Int. Int. e e : l area sottesa in senso ertiale a : l area sottesa in senso ertiale a tale ra raresenta il laoro sambiato on l ambiente da n tale ra raresenta il laoro sambiato on l ambiente da n sistema sistema hiso hiso

22 d d l Per sistemi aerti e er Per sistemi aerti e er trasf trasf. Int. Int. e.: e.: l area sottesa in senso orizzontale a l area sottesa in senso orizzontale a tale ra raresenta, ritenendo trasrabili le ariazioni di tale ra raresenta, ritenendo trasrabili le ariazioni di energia energia inetia e otenziale, il laoro sambiato da n V.C. on l ambi inetia e otenziale, il laoro sambiato da n V.C. on l ambiente. ente.

23 Basta onosere na delle de: f ( ) f ( ) f ( ) ore f ( ) In genere () è esresso ome na serie di otenze di : ( ) 3 a b d... a, b,, d, diendono dalla sostanza e deono altarsi serimentalmente a meno di teorie he ne onsentano la altazione er la sostanza in esame (ab.a.9). I orrisondenza di erti interalli non molto ami di temeratra (he diendono dalla sostanza) si ha he (e qindi ) non aria, è ratiamente ostante: in tal aso si arlerà di gas ideali a alori seifii ostanti. In genere nell interallo di temeratra [0,00] onsidereremo semre i alori seifii indiendenti da.