Lezione 15 - La teoria lineare
|
|
|
- Floriana Viola
- 4 anni fa
- Visualizzazioni
Transcript
1 Leone 5 - La teora lneare [Ultmarevsone revsone6 6gennao gennao009] In questa leone s esamnano le conseguene d una ragonevole potes sulla grandea d alcune quantta' d nteresse fsco. L'potes d pccole deformaon E' spesso evdente, nella pratca tecnca, che le varaon percentual d lunghea E x, E x ed E x, asseme con le varaon angolar g, g e g possano consderars quantta' pccole rspetto all'unta'. Quando co' sa accettable, s dra' che s e' nell'ambto delle pccole deformaon: E x ` ; E x `; E x `; γ ` ; γ ` ; γ ` ; In tale potes s hanno alcune nteressant semplfcaon d svarate formule. Le (7-9) della Leone precedente, che qu s rportano per comodta': () E x = è!!!!!!!!!!!!!!!!!!!! d E x = è!!!!!!!!!!!!!!!!!!!! d E x = è!!!!!!!!!!!!!!!!!!!! d s semplfcano utlando lo svluppo n sere della radce quadrata, ed arrestandos al prmo termne: da cu s ha: è!!!!!!!!!!!!!!!!!!!! d = d d d O@d D 4 E x = d E x = d () () (4) (5) (6) (7) E x = d Ne segue che n queste potes gl element dagonal del tensore d Green-Lagrange fornscono drettamente gl allungament percentual d segment passant per un punto M e parallel agl ass. Inoltre, per qualsas segmento MN øøøö la deformaone MN, data dalla () della Leone precedente: (8) s semplfca n: ε MN = E MN J E MN N ε MN = E MN (9) (0)
2 94 Leone 5 - Pccole deformaon.nb da cu, come ga' suggerto, s vede che la defnone matematca e quella ngegnerstca vengono a concdere. Infne, occorre semplfcare le (-5) della Leone precedente: sn γ = sn γ = d H E x L H E x L d H E x L H E x L () () sn γ = d H E x L H E x L I sen degl angol, come noto, possono confonders con gl angol stess, se gl angol sono pccol: sn γ = γ γ 6 O@γ D 4 ed l denomnatore a secondo membro puo' confonders con l'unta'. S ha qund: () (4) d = g ÅÅÅÅÅÅÅÅ d = g ÅÅÅÅÅÅÅÅ (5) (6) d = g ÅÅÅÅÅÅÅÅ Qund, nelle potes semplfcatve d questa leone, le tre component d, d, d concdono con la meta' della varaone angolare dell'angolo retto tra element passant per M ed orgnaramente dstes lungo gl ass. (7) L'potes d pccol gradent d spostamento Una ulterore potes semplfcatva rguarda l'ampea delle dervate degl spostament. Se s assume che tutte le dervate del tpo u ê x,... u ê x sano tanto pccole da poter trascurare loro quadrat rspetto ad esse, allora la defnone del tensore d Green-Lagrange vene a semplfcars drastcamente, n quanto l'ultmo termne della (8) della Leone precedente: D = HH HT H T HL vene a trascurars, e qund s ha: (8) D = E = HH HT L (9) In altr termn, l tensore d Green-Lagrange vene a concdere con la parte smmetrca del gradente d spostamento.
3 Leone 5 - Pccole deformaon.nb 95 La decomposone dello spostamento Nell'potes d pccol gradent d spostamento, gl element della matrce H de gradent d spostamento sono tutt dello stesso ordne d grandea, cos' come gl element della parte smmetrca E d H, e della parte antsmmetrca W. Co' permette una utle decomposone del processo deformatvo n esame. à La rotaone rgda S consder la (0) della Leone, che s rporta per comodta': ossa: du du = du u x x x u u u x x x u u u x x x u u dx dx dx (0) con: du = Hdx = HE ΩL dx () E = u x H u x u x L H u x u x L H u x u u x L x H u x u x L H u x u x L H u x u u x L x () Ω = 0 H u x u H u x u x L H u x u x L x L 0 H x u x u L H u x u S defnsca ora l vettore w d component: ω = J u u N x x ω = J u u N x x ω = J u u N x x n modo da scrvere: H u x u x L x L 0 () (4) (5) (6) Ω = 0 ω ω ω 0 ω ω ω 0 (7) Ora, e' noto che l generco atto d moto d un corpo rgdo, s puo' scomporre n tre traslaon u 0, u 0, u 0, rspetto a tre ass cartesan d rfermento, e n tre rotaon d ampea W, W, W ntorno agl ass passant per un punto P 0 (detto polo) e parallel agl ass d rfermento.
4 96 Leone 5 - Pccole deformaon.nb A seguto d questo atto d moto, lo spostamento d un generco punto P del corpo, puo' scrvers: u u u P = u 0 u 0 u 0 0 Ω Ω Ω 0 Ω Ω Ω 0 Ne segue che l'alquota d spostamento della (): du r = Ωdx = ω dx x x 0 x x 0 x x 0 e' nterpretable come una rotaone rgda con vettore rotaone d component: ω = J u u N x x ω = J u u N x x ω = J u u N x x (8) (9) (0) () () à La deformaone pura La restante alquota della (): du e = Edx () e' qund responsable dell'effettva deformaone del segmento MN, e la matrce E s dce anche matrce della deformaone pura. I corrspondent spostament s dcono spostament da deformaone pura. Nota - Il concetto d decomposone della deformaone, come llustrato n questa seone, rsale a G.Stoes, 845. Fgura - G. Stoes
5 Leone 5 - Pccole deformaon.nb 97 L'nterpretaone fsca delle dreon prncpal d deformaone La (), combnata con la (9), permette una semplce nterpretaone fsca della rcerca delle deformaon prncpal con le corrspondent dreon prncpal d deformaone, operata nella Leone precedente sul tensore d Green-Lagrange. S consder nfatt un punto M, e sa p una dreone prncpale passante per M. Sa po N un punto appartenente alla retta p, ed a dstana dx da M. Il punto N, per effetto della deformaone pura, s porta n N', con spostament fornt dalla (): du = e dx e dx e dx du = e dx e dx e dx du = e dx e dx e dx (4) D'altro canto, poche' N appartene ad una dreone prncpale, anche N' dovra' appartenere alla stessa dreone, e qund MN' deve essere proporonale ad MN (cfr. Fgura ): X u M dx x du N x x N' u ξ ξ X ξ X Fgura - Gl spostament da deformaone pura e le dreon prncpal d deformaone du = εdx du = εdx du = εdx Paragonando le (5) e (4) s gunge al sstema: He εldx e dx e dx = 0 e dx He εl dx e dx = 0 e dx e dx He εl dx = 0 dentco alla (8) della Leone precedente. (5) (6)
6 98 Leone 5 - Pccole deformaon.nb Le condon d compatblta' In quest'ultma seone s affronta l seguente problema: - date le tre funon spostamento u Hx, x, x L, u Hx, x, x L e u Hx, x, x L, e' da esse possble rcavare, tramte dervaone, le se component del tensore d deformaone. - assegnate le se funon e Hx, x, x L,, =,,, e' sempre possble rcavare le tre funon spostamento da cu esse sarebbero generate? In altr termn, assegnate se funon del tpo descrtto, sono sempre esse nterpretabl come component d deformaone, relatve ad un campo d spostament? La rsposta alla domanda precedente e': non sempre, ma solo quando le se funon sano legate tra loro da tre condon, dette condon d compatblta'. S puo' dmostrare l seguente: Teorema - Condone necessara e suffcente affnche' le se funon contnue ed unform e Hx, x, x L,, =,, sano component d deformaone lneare e' che sano verfcate le relaon: e x x = J e e e N x x x x (7) e = x x e = x x J e e e N x x x x J e e e N x x x x (8) (9) e = e x x x e x e = e e x x x x (40) (4) e = e x x x e x (4) Nota - Prma d nare la dmostraone, s osserv che l gruppo delle prme tre condon s puo' ottenere a partre da una qualsas equaone, tramte permutaone crcolare degl ndc x Ø x Ø x Ø x, cos' come possono otteners le altre tre condon. Dm. La condone e' necessara. Ed nfatt l secondo gruppo d condon puo' essere faclmente dmostrato n base alla seguente relaone: e = u u x x u x x v x x = ed alla permutaone crcolare degl ndc. e = x x x J u x N x J u N = e x x e x (4)
7 Leone 5 - Pccole deformaon.nb 99 Per dmostrare l prmo gruppo d condon, s consder che s ha: e = J u u N e = x x x x J u x x x u x N x (44) e = J u u N e = x x x x J u x x x e = J u u N e = x x x x J u x x x e sommando s ha: e x x e x x J u x x x J u x x x u = x x x e = x x J u x x x u N x x x u N = x x x u = e x x x x x La condone e' suffcente. S consult Mushelshvl.[Mushelshvl] ð u N x x x u N x x x u N x x x (45) (46) (47) Nota - La necessareta' delle condon d compatblta' e' stata dmostrata da B. De Sant Venant n una brevssma nota d due pagne, pubblcata nel 86, mentre la dmostraone della loro suffcena e' dovuta ad Eugeno Beltram ("Sull'nterpretaone meccanca delle formule d Maxwell", Rendcont del Crcolo Matematco d Palermo,, 886). Tale nota puo' anche essere letta sul sto nella seone Rcerca. Fgura - Adhemar Jean Claude Barre' de Sant-Venant
8 00 Leone 5 - Pccole deformaon.nb Nota - Le equaon d congruena possono sntetars nell'unca formula: curlcurle = 0 (48) dove l rotore d un tensore e' defnto, ad esempo, nel Complemento 6, sul sto Le dentta' d Banch E' faclmente potable che non tutte le condon d congruena appena scrtte sano ndpendent tra d loro. Ed nfatt, s rscrvano le se condon sotto forma d dentta' a ero: G = e e e = 0 x x x x (49) G = e e e = 0 x x x x G = e e e = 0 x x x x (50) (5) G = G = e x x e x x e e = 0 x x x (5) G = G = e x x e x x e e x x x = 0 (5) G = G = e x x e x x e e x x x = 0 S puo' verfcare, per sosttuone dretta, che sussstono le cosddette dentta' d Banch: (54) G G G = 0 x x x G G G = 0 x x x (55) (56) G G G = 0 x x x (57) che legano tra loro le se condon d congruena, e facendo s' che solo tre d esse sano ndpendent. S not che utlando la convenone degl ndc rpetut, le dentta' d Banch s scrvono: G x = 0, =,, (58)
9 Leone 5 - Pccole deformaon.nb 0 Fgura 4 - Lug Banch Note [] N. Mushelshvl, "Some basc Problems of the Mathematcal Theor of Elastct", Noordhoff 96, pp [Torna al testo] Grafc
Esercitazioni 2 - Analisi della deformazione
 Eserctaon - Anals della deformaone In questa eserctaone s studano alcun stat deformatv Infne, s danno alcune semplc funon Mathematca, che permettono l'automaone dello studo per qualsas stato deformatvo
Eserctaon - Anals della deformaone In questa eserctaone s studano alcun stat deformatv Infne, s danno alcune semplc funon Mathematca, che permettono l'automaone dello studo per qualsas stato deformatvo
Lezione 13 - Il gradiente di deformazione
 eone - Il gradente d deformaone [Ultmarevsone revsone dcembre dcembre008] In questa leone s comnca ad affrontare l'anals della deformaone, cu compto prncpale e' rspondere al seguente problema: - assegnate
eone - Il gradente d deformaone [Ultmarevsone revsone dcembre dcembre008] In questa leone s comnca ad affrontare l'anals della deformaone, cu compto prncpale e' rspondere al seguente problema: - assegnate
θ 2 i r 2 r La multifunzione f (z) = z z i
 1-19 1.4 1.4.1. La multfunone f () = + 1 3 è l prodotto d 2 multfunon Z Z e W 3 W. È qund ragonevole supporre che Z =, coè = 1 e W =, coè = sano punt d dramaone d f. Con rfermento alla fgura a lato, e
1-19 1.4 1.4.1. La multfunone f () = + 1 3 è l prodotto d 2 multfunon Z Z e W 3 W. È qund ragonevole supporre che Z =, coè = 1 e W =, coè = sano punt d dramaone d f. Con rfermento alla fgura a lato, e
Complementi 1 - Le trasformazioni lineari
 Complement 1 - Le trasformaon lnear [Ultmarevsone revsone20 20dcembre dcembre2008] In questa Leone s studano le propreta delle trasformaon lnear rappresentate da: ξ 1 = a 11 +a 12 +a 13 ξ 2 = a 21 +a 22
Complement 1 - Le trasformaon lnear [Ultmarevsone revsone20 20dcembre dcembre2008] In questa Leone s studano le propreta delle trasformaon lnear rappresentate da: ξ 1 = a 11 +a 12 +a 13 ξ 2 = a 21 +a 22
Complementi 4 - Materiali non isotropi
 Complement 4 - Materal non sotrop [Ultmarevsone revsone9gennao gennao2009] In questo noteboo s parte dalla legge d Hooe per sold ansotrop, e s deducono le opportune restron sulle 21 costant elastche, potando
Complement 4 - Materal non sotrop [Ultmarevsone revsone9gennao gennao2009] In questo noteboo s parte dalla legge d Hooe per sold ansotrop, e s deducono le opportune restron sulle 21 costant elastche, potando
Lezione 5 - Analisi cinematica
 eone 5 - nals cnematca [Ultmarevsone: revsone:25 25novembre 28] S consder ora una struttura bdmensonale, ossa un nseme d trav collegate tra loro ed al suolo da opportun vncol. In questa leone s voglono
eone 5 - nals cnematca [Ultmarevsone: revsone:25 25novembre 28] S consder ora una struttura bdmensonale, ossa un nseme d trav collegate tra loro ed al suolo da opportun vncol. In questa leone s voglono
asse fisso nel tempo in rotazione attorno ad un asse fisso dell asse di rotazione rimarranno fermi al passar del temporispetto al sistema inerziale
 Rotaon rgde attorno ad un asse fsso nel tempo un corpo rgdo n rotaone attorno ad un asse fsso ha un solo grado d lberta n quest cas per descrvere l moto converra rferrs ad un polo fsso se l asse d rotaone
Rotaon rgde attorno ad un asse fsso nel tempo un corpo rgdo n rotaone attorno ad un asse fsso ha un solo grado d lberta n quest cas per descrvere l moto converra rferrs ad un polo fsso se l asse d rotaone
Complementi 2 - Le trasformazioni simmetriche ed antisimmetriche
 Complement - Le trasformaon smmetrche ed antsmmetrche [Ultmarevsone revsone5 5dcembre dcembre008] gn matrce A puo essere espressa come somma d una matrce smmetrca ed una matrce antsmmetrca: A = 1 HA +AT
Complement - Le trasformaon smmetrche ed antsmmetrche [Ultmarevsone revsone5 5dcembre dcembre008] gn matrce A puo essere espressa come somma d una matrce smmetrca ed una matrce antsmmetrca: A = 1 HA +AT
Dinamica del corpo rigido
 Anna Nobl 1 Defnzone e grad d lbertà S consder un corpo d massa totale M formato da N partcelle cascuna d massa m, = 1,..., N. Il corpo s dce rgdo se le dstanze mutue tra tutte le partcelle che lo compongono
Anna Nobl 1 Defnzone e grad d lbertà S consder un corpo d massa totale M formato da N partcelle cascuna d massa m, = 1,..., N. Il corpo s dce rgdo se le dstanze mutue tra tutte le partcelle che lo compongono
Propagazione degli errori
 Propagaone degl error Voglamo rcavare le ncertee nelle msure ndrette. Abbamo gà vsto leone un prma stma degl error sulle grandee dervate valda n generale. Consderamo ora l caso specco d grandee aette da
Propagaone degl error Voglamo rcavare le ncertee nelle msure ndrette. Abbamo gà vsto leone un prma stma degl error sulle grandee dervate valda n generale. Consderamo ora l caso specco d grandee aette da
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO
 PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
Corpi rigidi (prima parte)
 Corp rgd (prma parte) Corp rgd Un corpo rgdo è un corpo n cu le dstane tra le vare par che lo compongono rmangono costan3. r CM d CM È un po parcolare d sstema d N parcelle. Valgono ancora le legg dp dt
Corp rgd (prma parte) Corp rgd Un corpo rgdo è un corpo n cu le dstane tra le vare par che lo compongono rmangono costan3. r CM d CM È un po parcolare d sstema d N parcelle. Valgono ancora le legg dp dt
Dinamica dei sistemi particellari
 Dnamca de sstem partcellar Marco Favrett Aprl 11, 2010 1 Cnematca Sa dato un sstema d rfermento nerzale (O, e ), = 1, 2, 3 e consderamo un sstema d punt materal (sstema partcellare) S = {(OP, m )}, = 1,,
Dnamca de sstem partcellar Marco Favrett Aprl 11, 2010 1 Cnematca Sa dato un sstema d rfermento nerzale (O, e ), = 1, 2, 3 e consderamo un sstema d punt materal (sstema partcellare) S = {(OP, m )}, = 1,,
Principio di massima verosimiglianza
 Prncpo d massma verosmglana Sa data una grandea d cu s conosce la unone denstà d probabltà ; che dpende da un nseme de parametr ndcat con d valore sconoscuto. S vuole determnare la mglor stma de parametr.
Prncpo d massma verosmglana Sa data una grandea d cu s conosce la unone denstà d probabltà ; che dpende da un nseme de parametr ndcat con d valore sconoscuto. S vuole determnare la mglor stma de parametr.
Principio di massima verosimiglianza
 Prncpo d massma verosmglana Sa data una grandea d cu s conosce la unone denstà d probabltà ; che dpende da un nseme de parametr ndcat con d valore sconoscuto. S vuole determnare la mglor stma de parametr.
Prncpo d massma verosmglana Sa data una grandea d cu s conosce la unone denstà d probabltà ; che dpende da un nseme de parametr ndcat con d valore sconoscuto. S vuole determnare la mglor stma de parametr.
Fisica dei semiconduttori: prova del
 6114.nb 1 Fsca de semconduttor: prova del 6 11 4 ü 1. 1. Un elettrone è descrtto da una funone d onda (n 1 dmensone) u(x) = a u 1 (x) + b u (x) dove u 1 (x) ed u (x) sono autofunon dell Hamltonana del
6114.nb 1 Fsca de semconduttor: prova del 6 11 4 ü 1. 1. Un elettrone è descrtto da una funone d onda (n 1 dmensone) u(x) = a u 1 (x) + b u (x) dove u 1 (x) ed u (x) sono autofunon dell Hamltonana del
Meccanica Dinamica del corpo rigido
 Meccanca 8-9 6 Fora peso sul corpo rgdo Corpo sottoposto alla fora peso: Su ogn elemento nfntesmo d massa dm agsce la fora Rsultante delle fore: F peso V g dm Momento rsultante (polo ): M V Energa potenale:
Meccanca 8-9 6 Fora peso sul corpo rgdo Corpo sottoposto alla fora peso: Su ogn elemento nfntesmo d massa dm agsce la fora Rsultante delle fore: F peso V g dm Momento rsultante (polo ): M V Energa potenale:
4.2 IL PRINCIPIO DEI LAVORI VIRTUALI 4.1 INTRODUZIONE
 Cap 4 PRINCIPIO DEI LAORI IRTUALI 4. IL PRINCIPIO DEI LAORI IRTUALI 4. INTRODUZIONE Fno ad ora s è condotto lo stdo del problema della deformazone e d qello della tensone per n corpo contno gngendo alla
Cap 4 PRINCIPIO DEI LAORI IRTUALI 4. IL PRINCIPIO DEI LAORI IRTUALI 4. INTRODUZIONE Fno ad ora s è condotto lo stdo del problema della deformazone e d qello della tensone per n corpo contno gngendo alla
Geometria 1 a.a. 2011/12 Esonero del 23/01/12 Soluzioni (Compito A) sì determinarla, altrimenti dimostrare che ciò è impossibile.
 Geometra 1 a.a. 2011/12 Esonero del 23/01/12 Soluzon (Compto A) (1) S consder su C 2 l prodotto Hermtano, H assocato alla matrce ( ) 2 H =. 2 (a) Dmostrare che, H è defnto postvo e determnare una base
Geometra 1 a.a. 2011/12 Esonero del 23/01/12 Soluzon (Compto A) (1) S consder su C 2 l prodotto Hermtano, H assocato alla matrce ( ) 2 H =. 2 (a) Dmostrare che, H è defnto postvo e determnare una base
links utili:
 dspensa d Govann Bachelet Meccanca de Sstem, maggo 2003 lnks utl: http://scenceworld.wolfram.com/physcs/angularmomentum.html http://hyperphyscs.phy-astr.gsu.edu/hbase/necon.html Momento della quanttà d
dspensa d Govann Bachelet Meccanca de Sstem, maggo 2003 lnks utl: http://scenceworld.wolfram.com/physcs/angularmomentum.html http://hyperphyscs.phy-astr.gsu.edu/hbase/necon.html Momento della quanttà d
Meccanica Dinamica del corpo rigido
 Meccanca 08-09 Dnamca del corpo rgdo 7 ω L Equaon del moto: Momento angolare: Energa cnetca: Sstem corpo rgdo E F K dp dt L L + L ω M otaone d un corpo rgdo L ω Momento d nera: r dm V dl dt r m L L ω L
Meccanca 08-09 Dnamca del corpo rgdo 7 ω L Equaon del moto: Momento angolare: Energa cnetca: Sstem corpo rgdo E F K dp dt L L + L ω M otaone d un corpo rgdo L ω Momento d nera: r dm V dl dt r m L L ω L
Funzione di matrice. c i λ i. i=0. i=0. m 1. γ i A i. i=0. Moltiplicando entrambi i membri di questa equazione per A si ottiene. α i 1 A i α m 1 A m
 Captolo INTRODUZIONE Funzone d matrce Sa f(λ) una generca funzone del parametro λ svluppable n sere d potenze f(λ) Sa A una matrce quadrata d ordne n La funzone d matrce f(a) èdefnta nel modo seguente
Captolo INTRODUZIONE Funzone d matrce Sa f(λ) una generca funzone del parametro λ svluppable n sere d potenze f(λ) Sa A una matrce quadrata d ordne n La funzone d matrce f(a) èdefnta nel modo seguente
F E risultante t delle forze esterne agenti su P i. F forza esercitata t sul generico punto P ij del sistema da P : forza interna al sistema
 DINAMICA DEI SISTEMI Sstema costtuto da N punt materal P 1, P 2,, P N F E rsultante t delle forze esterne agent su P F E F forza eserctata t sul generco punto P j del sstema da P : forza nterna al sstema
DINAMICA DEI SISTEMI Sstema costtuto da N punt materal P 1, P 2,, P N F E rsultante t delle forze esterne agent su P F E F forza eserctata t sul generco punto P j del sstema da P : forza nterna al sstema
Esercizi sulle reti elettriche in corrente continua (parte 2)
 Esercz sulle ret elettrche n corrente contnua (parte ) Eserczo 3: etermnare gl equvalent d Thevenn e d Norton del bpolo complementare al resstore R 5 nel crcuto n fgura e calcolare la corrente che crcola
Esercz sulle ret elettrche n corrente contnua (parte ) Eserczo 3: etermnare gl equvalent d Thevenn e d Norton del bpolo complementare al resstore R 5 nel crcuto n fgura e calcolare la corrente che crcola
di una delle versioni del compito di Geometria analitica e algebra lineare del 12 luglio 2013 distanza tra r ed r'. (punti 2 + 3)
 Esempo d soluzone d una delle verson del compto d Geometra analtca e algebra lneare del luglo 3 Stablre se la retta r, d equazon parametrche x =, y = + t, z = t (nel parametro reale t), è + y + z = sghemba
Esempo d soluzone d una delle verson del compto d Geometra analtca e algebra lneare del luglo 3 Stablre se la retta r, d equazon parametrche x =, y = + t, z = t (nel parametro reale t), è + y + z = sghemba
2.1 Parabola nella forma canonica
 5 Clc per tutt gl appunt (AUTOMAZIONE TRATTAMENTI TERMICI ACCIAIO SCIENZA delle COSTRUZIONI ) e-mal per suggerment. Paraola nella forma canonca Studamo con metod general la conca nella espressone canonca
5 Clc per tutt gl appunt (AUTOMAZIONE TRATTAMENTI TERMICI ACCIAIO SCIENZA delle COSTRUZIONI ) e-mal per suggerment. Paraola nella forma canonca Studamo con metod general la conca nella espressone canonca
INTRODUZIONE ALL ESPERIENZA 4: STUDIO DELLA POLARIZZAZIONE MEDIANTE LAMINE DI RITARDO
 INTODUZION ALL SPINZA 4: STUDIO DLLA POLAIZZAZION DIANT LAIN DI ITADO Un utle rappresentazone su come agscono le lamne su fasc coerent è ottenuta utlzzando vettor e le matrc d Jones. Vettore d Jones e
INTODUZION ALL SPINZA 4: STUDIO DLLA POLAIZZAZION DIANT LAIN DI ITADO Un utle rappresentazone su come agscono le lamne su fasc coerent è ottenuta utlzzando vettor e le matrc d Jones. Vettore d Jones e
10 Modelli di dispersione
 10 Modell d dspersone Smulare l comportamento d un nqunante, rlascato n atmosfera, sgnfca determnare l campo d concentraone da esso prodotto n qualunque punto dello spao e n qualunque stante successvo
10 Modell d dspersone Smulare l comportamento d un nqunante, rlascato n atmosfera, sgnfca determnare l campo d concentraone da esso prodotto n qualunque punto dello spao e n qualunque stante successvo
Risposta in frequenza
 Rsposta n frequenza www.de.ng.unbo.t/pers/mastr/ddattca.htm (versone del 6--6 Dagramm d Bode Le funzon d trasfermento (f.d.t de crcut lnear tempo nvarant sono funzon razonal (coè rapport tra due polnom
Rsposta n frequenza www.de.ng.unbo.t/pers/mastr/ddattca.htm (versone del 6--6 Dagramm d Bode Le funzon d trasfermento (f.d.t de crcut lnear tempo nvarant sono funzon razonal (coè rapport tra due polnom
Dipartimento di Matematica per le scienze economiche e sociali Università di Bologna. Matematica aa lezione marzo 2009
 Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2008-2009 lezone 25 17 marzo 2009 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/26? Convesstà Sa I un ntervallo
Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2008-2009 lezone 25 17 marzo 2009 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/26? Convesstà Sa I un ntervallo
Rotazione rispetto ad asse fisso Asse z : asse di rotazione
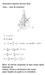 Rotaone rspetto ad asse fsso Asse : asse d rotaone 1 1 1 Ek= ω = ω= ω om. d nera: propreta d ogn corpo rgdo Dpende da: massa, forma e dmenson del corpo asse rspetto al quale lo s consdera Asta omogenea:
Rotaone rspetto ad asse fsso Asse : asse d rotaone 1 1 1 Ek= ω = ω= ω om. d nera: propreta d ogn corpo rgdo Dpende da: massa, forma e dmenson del corpo asse rspetto al quale lo s consdera Asta omogenea:
Sistemi Intelligenti Stimatori e sistemi lineari - III
 Sstem Intellgent Stmator e sstem lnear - III Alberto Borghese Unverstà degl Stud d Mlano Laboratory of Appled Intellgent Systems (AIS-Lab) Dpartmento d Informatca borghese@d.unm.t /6 http:\\borghese.d.unm.t\
Sstem Intellgent Stmator e sstem lnear - III Alberto Borghese Unverstà degl Stud d Mlano Laboratory of Appled Intellgent Systems (AIS-Lab) Dpartmento d Informatca borghese@d.unm.t /6 http:\\borghese.d.unm.t\
Equilibrio e stabilità di sistemi dinamici. Stabilità dell equilibrio di sistemi dinamici non lineari per linearizzazione
 Equlbro e stabltà d sstem dnamc Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem NL TC Crter d stabltà
Equlbro e stabltà d sstem dnamc Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem NL TC Crter d stabltà
Elasticità nei mezzi continui
 Elastctà ne mezz contnu l tensore degl sforz o tensore d stress, σ j Consderamo un cubo d dmenson untare n un mezzo elastco deformato. l cubo è deformato dalle forze eserctate sulle sue facce dal resto
Elastctà ne mezz contnu l tensore degl sforz o tensore d stress, σ j Consderamo un cubo d dmenson untare n un mezzo elastco deformato. l cubo è deformato dalle forze eserctate sulle sue facce dal resto
Numeri complessi, polinomi - Risposte pagina 1 di 11 23
 Numer compless, polnom - Rsposte pagna d 0. a. I numer compless con Re () sono quell a destra della retta vertcale (retta compresa). Quell con modulo mnore d 4 sono all nterno della crconferena d centro
Numer compless, polnom - Rsposte pagna d 0. a. I numer compless con Re () sono quell a destra della retta vertcale (retta compresa). Quell con modulo mnore d 4 sono all nterno della crconferena d centro
Soluzioni 3.1. n(n 1) (n k + 1) z n k! k + 1 n k. lim k
 (1) La sere bnomale è B n (z) = k=0 Con l metodo del rapporto s ottene R = lm k Soluzon 3.1 n(n 1) (n k + 1) z n k! c k c k+1 = lm k k + 1 n k lm k c k z k. k=0 1 + 1 k 1 n k = 1 (2) La multfunzone f(z)
(1) La sere bnomale è B n (z) = k=0 Con l metodo del rapporto s ottene R = lm k Soluzon 3.1 n(n 1) (n k + 1) z n k! c k c k+1 = lm k k + 1 n k lm k c k z k. k=0 1 + 1 k 1 n k = 1 (2) La multfunzone f(z)
Esercizio 1. Esercitazione 14 Dicembre 2012 Sistemi trifase e potenze R 3 R 1 R 2. simmetrico L 1 L 3
 serctazone 4 Dcembre 0 Sstem trfase e potenze serczo L L L 00 f 50 Hz smmetrco Fg : Sstema trfase a stella S consder l crcuto d Fg e s calcolno le tre corrent d fase e le potenze attve, reattve ed apparent
serctazone 4 Dcembre 0 Sstem trfase e potenze serczo L L L 00 f 50 Hz smmetrco Fg : Sstema trfase a stella S consder l crcuto d Fg e s calcolno le tre corrent d fase e le potenze attve, reattve ed apparent
NATURA ATOMICA DELLA MATERIA
 NATURA ATOMICA DLLA MATRIA Un qualunque fludo è costtuto da un gran numero d partcelle (sa sngol atom che molecole) n un contnuo moto dsordnato defnto agtaone termca. Questo fenomeno sta alla base de cosddett
NATURA ATOMICA DLLA MATRIA Un qualunque fludo è costtuto da un gran numero d partcelle (sa sngol atom che molecole) n un contnuo moto dsordnato defnto agtaone termca. Questo fenomeno sta alla base de cosddett
Stabilità dei Sistemi Dinamici. Stabilità Semplice. Stabilità Asintotica. Stabilità: concetto intuitivo che può essere formalizzato in molti modi
 Gustavo Belforte Stabltà de Sstem Dnamc Gustavo Belforte Stabltà de Sstem Dnamc Stabltà de Sstem Dnamc Il Pendolo Stabltà: concetto ntutvo che può essere formalzzato n molt mod Intutvamente: Un oggetto
Gustavo Belforte Stabltà de Sstem Dnamc Gustavo Belforte Stabltà de Sstem Dnamc Stabltà de Sstem Dnamc Il Pendolo Stabltà: concetto ntutvo che può essere formalzzato n molt mod Intutvamente: Un oggetto
I.5. FORMULAZIONE DIFFERENZIALE DELL ELETTROSTATICA
 I.5. FORMULAZIONE DIFFERENZIALE DELL ELETTROTATICA I.5.. Propretà ntegral del campo elettrostatco Le propretà gà consderate del campo elettrostatco, descrtte dal teorema d Gauss e dal fatto che l campo
I.5. FORMULAZIONE DIFFERENZIALE DELL ELETTROTATICA I.5.. Propretà ntegral del campo elettrostatco Le propretà gà consderate del campo elettrostatco, descrtte dal teorema d Gauss e dal fatto che l campo
Spostamento, velocità, accelerazione
 Spostamento, veloctà, acceleraone Posone e spostamento Due stan assegna t 1 e t, con t t 1 >0 Posone al tempo t 1 : r r t ) ( ( t ), ( t ), ( 1 ( 1 1 1 t1 Posone al tempo t : r r t ) ( ( t ), ( t ), (
Spostamento, veloctà, acceleraone Posone e spostamento Due stan assegna t 1 e t, con t t 1 >0 Posone al tempo t 1 : r r t ) ( ( t ), ( t ), ( 1 ( 1 1 1 t1 Posone al tempo t : r r t ) ( ( t ), ( t ), (
Algebra 2. 6 4. Sia A un anello commutativo. Si ricorda che in un anello commutativo vale il teorema binomiale, cioè. (a + b) n = a i b n i i.
 Testo Fac-smle 2 Durata prova: 2 ore 8 1. Un gruppo G s dce semplce se suo unc sottogrupp normal sono 1 e G stesso. Sa G un gruppo d ordne pq con p e q numer prm tal che p < q. (a) Il gruppo G può essere
Testo Fac-smle 2 Durata prova: 2 ore 8 1. Un gruppo G s dce semplce se suo unc sottogrupp normal sono 1 e G stesso. Sa G un gruppo d ordne pq con p e q numer prm tal che p < q. (a) Il gruppo G può essere
Riccardo Sabatino 463/1 Progetto di un telaio in c.a. A.A. 2003/04
 Rccardo Sabatno 463/1 Progetto d un telao n c.a. A.A. 003/04 3.3 Il metodo degl spostament per la rsoluzone del telao Il metodo degl spostament è basato sulla valutazone de moment flettent ce agscono sugl
Rccardo Sabatno 463/1 Progetto d un telao n c.a. A.A. 003/04 3.3 Il metodo degl spostament per la rsoluzone del telao Il metodo degl spostament è basato sulla valutazone de moment flettent ce agscono sugl
6 Prodotti scalari e prodotti Hermitiani
 6 Prodott scalar e prodott Hermtan 6.1 Prodott scalar S fss K = R. Defnzone 6.1 Sa V un R-spazo vettorale. Un prodotto scalare su V è un applcazone che gode delle seguent propretà: ) (lneartà rspetto al
6 Prodott scalar e prodott Hermtan 6.1 Prodott scalar S fss K = R. Defnzone 6.1 Sa V un R-spazo vettorale. Un prodotto scalare su V è un applcazone che gode delle seguent propretà: ) (lneartà rspetto al
I.5. FORMULAZIONE DIFFERENZIALE DELL ELETTROSTATICA
 I.5. FORMULZIOE DIFFEREZILE DELL ELETTROTTIC I.5.. Propretà ntegral del campo elettrostatco Le propretà gà consderate del campo elettrostatco, descrtte dal teorema d Gauss e dal fatto che l campo elettrostatco
I.5. FORMULZIOE DIFFEREZILE DELL ELETTROTTIC I.5.. Propretà ntegral del campo elettrostatco Le propretà gà consderate del campo elettrostatco, descrtte dal teorema d Gauss e dal fatto che l campo elettrostatco
B - ESERCIZI: IP e TCP:
 Unverstà d Bergamo Dpartmento d Ingegnera dell Informazone e Metod Matematc B - ESERCIZI: IP e TCP: F. Martgnon Archtetture e Protocoll per Internet Eserczo b. S consder l collegamento n fgura A C =8 kbt/s
Unverstà d Bergamo Dpartmento d Ingegnera dell Informazone e Metod Matematc B - ESERCIZI: IP e TCP: F. Martgnon Archtetture e Protocoll per Internet Eserczo b. S consder l collegamento n fgura A C =8 kbt/s
Corsi di Laurea in Farmacia e CTF Prova di Matematica
 Cors d Laurea n Farmaca e CTF Prova d Matematca S O L U Z I O N I Effettua uno studo qualtatvo della funzone 4 f + con partcolare rfermento a seguent aspett: a trova l domno della funzone b trova gl ntervall
Cors d Laurea n Farmaca e CTF Prova d Matematca S O L U Z I O N I Effettua uno studo qualtatvo della funzone 4 f + con partcolare rfermento a seguent aspett: a trova l domno della funzone b trova gl ntervall
METODO DEGLI ELEMENTI FINITI
 METODO DEGLI ELEMENTI FINITI Introduzone al metodo degl element fnt Il concetto base nella nterpretazone fsca del metodo degl element fnt è la decomposzone d un sstema meccanco complesso n pù semplc component
METODO DEGLI ELEMENTI FINITI Introduzone al metodo degl element fnt Il concetto base nella nterpretazone fsca del metodo degl element fnt è la decomposzone d un sstema meccanco complesso n pù semplc component
LE FREQUENZE CUMULATE
 LE FREQUENZE CUMULATE Dott.ssa P. Vcard Introducamo questo argomento con l seguente Esempo: consderamo la seguente dstrbuzone d un campone d 70 sttut d credto numero flal present nel terrtoro del comune
LE FREQUENZE CUMULATE Dott.ssa P. Vcard Introducamo questo argomento con l seguente Esempo: consderamo la seguente dstrbuzone d un campone d 70 sttut d credto numero flal present nel terrtoro del comune
Analisi Modale. Le evoluzioni libere dei due sistemi a partire dalla condizione iniziale x(0) = x 0 sono
 Captolo 1 INTRODUZIONE 21 Anals Modale S facca rfermento al sstema tempo-dscreto e al sstema tempo-contnuo x(k +1)=Ax(k) ẋ(t) =Ax(t) Le evoluzon lbere de due sstem a partre dalla condzone nzale x() = x
Captolo 1 INTRODUZIONE 21 Anals Modale S facca rfermento al sstema tempo-dscreto e al sstema tempo-contnuo x(k +1)=Ax(k) ẋ(t) =Ax(t) Le evoluzon lbere de due sstem a partre dalla condzone nzale x() = x
Introduzione... 2 Equazioni dei telegrafisti... 3 Parametri per unità di lunghezza... 7 Soluzione nel dominio della frequenza... 7 Risoluzione delle
 Appunt d amp Elettromagnetc aptolo 8 parte I nee d trasmssone Introduone... Equaon de telegrafst... 3 Parametr per untà d lunghea... 7 Soluone nel domno della frequena... 7 soluone delle equaon de telegrafst...
Appunt d amp Elettromagnetc aptolo 8 parte I nee d trasmssone Introduone... Equaon de telegrafst... 3 Parametr per untà d lunghea... 7 Soluone nel domno della frequena... 7 soluone delle equaon de telegrafst...
Intorduzione alla teoria delle Catene di Markov
 Intorduzone alla teora delle Catene d Markov Mchele Ganfelce a.a. 2014/2015 Defnzone 1 Sa ( Ω, F, {F n } n 0, P uno spazo d probabltà fltrato. Una successone d v.a. {ξ n } n 0 defnta su ( Ω, F, {F n }
Intorduzone alla teora delle Catene d Markov Mchele Ganfelce a.a. 2014/2015 Defnzone 1 Sa ( Ω, F, {F n } n 0, P uno spazo d probabltà fltrato. Una successone d v.a. {ξ n } n 0 defnta su ( Ω, F, {F n }
Ad esempio, potremmo voler verificare la legge di caduta dei gravi che dice che un corpo cade con velocità uniformemente accellerata: v = v 0 + g t
 Relazon lnear Uno de pù mportant compt degl esperment è quello d nvestgare la relazone tra due varabl. Il caso pù mportante (e a cu spesso c s rconduce, come vedremo è quello n cu la relazone che s ntende
Relazon lnear Uno de pù mportant compt degl esperment è quello d nvestgare la relazone tra due varabl. Il caso pù mportante (e a cu spesso c s rconduce, come vedremo è quello n cu la relazone che s ntende
LABORATORIO II. 1 La retta di regressione. NB create un nuovo foglio di lavoro
 LABORATORIO II B create un nuovo foglo d lavoro La retta d regressone Eserco. U PRIMO ESEMPIO DI RETTA DI REGRESSIOE LIEARE. Leggere attentamente paragraf.,. e. tutto Costrure la retta d regressone lneare
LABORATORIO II B create un nuovo foglo d lavoro La retta d regressone Eserco. U PRIMO ESEMPIO DI RETTA DI REGRESSIOE LIEARE. Leggere attentamente paragraf.,. e. tutto Costrure la retta d regressone lneare
Appunti: Scomposizione in fratti semplici ed antitrasformazione
 Appunt: Scomposzone n fratt semplc ed anttrasformazone Gulo Cazzol v0. (AA. 017-018) 1 Fratt semplc 1.1 Funzone ntera.............................................. 1. Funzone razonale fratta strettamente
Appunt: Scomposzone n fratt semplc ed anttrasformazone Gulo Cazzol v0. (AA. 017-018) 1 Fratt semplc 1.1 Funzone ntera.............................................. 1. Funzone razonale fratta strettamente
Lezione 6 - Analisi statica
 eone 6 - nals statca [Ultmarevsone: revsone:5 5novembre 8] S consder la stessa struttura bdmensonale della leone precedente, ossa un nseme d trav collegate tra loro ed al suolo da opportun vncol. S vuole
eone 6 - nals statca [Ultmarevsone: revsone:5 5novembre 8] S consder la stessa struttura bdmensonale della leone precedente, ossa un nseme d trav collegate tra loro ed al suolo da opportun vncol. S vuole
Propagazione delle incertezze
 Propagazone delle ncertezze In questa Sezone vene trattato l problema della propagazone delle ncertezze quando s msurano pù grandezze dfferent,,,z soggette a error d tpo casuale e po s utlzzano tal grandezze
Propagazone delle ncertezze In questa Sezone vene trattato l problema della propagazone delle ncertezze quando s msurano pù grandezze dfferent,,,z soggette a error d tpo casuale e po s utlzzano tal grandezze
Metodi e Modelli per l Ottimizzazione Combinatoria Progetto: Metodo di soluzione basato su generazione di colonne
 Metod e Modell per l Ottmzzazone Combnatora Progetto: Metodo d soluzone basato su generazone d colonne Lug De Govann Vene presentato un modello alternatvo per l problema della turnazone delle farmace che
Metod e Modell per l Ottmzzazone Combnatora Progetto: Metodo d soluzone basato su generazone d colonne Lug De Govann Vene presentato un modello alternatvo per l problema della turnazone delle farmace che
Propagazione degli errori
 Propagazone degl error Msure drette: la grandezza sca vene msurata drettamente (ad es. Spessore d una lastrna). Per questo tpo d msure, la teora dell errore svluppata nelle lezone precedent é sucente per
Propagazone degl error Msure drette: la grandezza sca vene msurata drettamente (ad es. Spessore d una lastrna). Per questo tpo d msure, la teora dell errore svluppata nelle lezone precedent é sucente per
Calcolo Scientifico e Matematica Applicata Secondo Parziale, Ingegneria Ambientale
 Calcolo Scentfco e Matematca Applcata Secondo Parzale, 7.2.28 Ingegnera Ambentale Rsolvere gl esercz, 2, 4 oppure, n alternatva, gl esercz, 3, 4. Valutazone degl esercz: 4, 2 8, 3 8, 4 8.. Illustrare,
Calcolo Scentfco e Matematca Applcata Secondo Parzale, 7.2.28 Ingegnera Ambentale Rsolvere gl esercz, 2, 4 oppure, n alternatva, gl esercz, 3, 4. Valutazone degl esercz: 4, 2 8, 3 8, 4 8.. Illustrare,
{ 1, 2,..., n} Elementi di teoria dei giochi. Giovanni Di Bartolomeo Università degli Studi di Teramo
 Element d teora de goch Govann D Bartolomeo Unverstà degl Stud d Teramo 1. Descrzone d un goco Un generco goco, Γ, che s svolge n un unco perodo, può essere descrtto da una Γ= NSP,,. Ess sono: trpla d
Element d teora de goch Govann D Bartolomeo Unverstà degl Stud d Teramo 1. Descrzone d un goco Un generco goco, Γ, che s svolge n un unco perodo, può essere descrtto da una Γ= NSP,,. Ess sono: trpla d
5.1 Controllo di un sistema non lineare
 5.1 Controllo d un sstema non lneare Sa dato l sstema non lneare rappresentato n fgura 5.1, con h g θ Θ,m,r Fgura 5.1: Sstema non lneare F m (,d) = k m la forza che esercta l elettromagnete percorso da
5.1 Controllo d un sstema non lneare Sa dato l sstema non lneare rappresentato n fgura 5.1, con h g θ Θ,m,r Fgura 5.1: Sstema non lneare F m (,d) = k m la forza che esercta l elettromagnete percorso da
Il modello markoviano per la rappresentazione del Sistema Bonus Malus. Prof. Cerchiara Rocco Roberto. Materiale e Riferimenti
 Il modello marovano per la rappresentazone del Sstema Bonus Malus rof. Cercara Rocco Roberto Materale e Rferment. Lucd dstrbut n aula. Lemare 995 (pag.6- e pag. 74-78 3. Galatoto G. 4 (tt del VI Congresso
Il modello marovano per la rappresentazone del Sstema Bonus Malus rof. Cercara Rocco Roberto Materale e Rferment. Lucd dstrbut n aula. Lemare 995 (pag.6- e pag. 74-78 3. Galatoto G. 4 (tt del VI Congresso
Tecniche di approssimazione Differenze finite
 Tecnche d approssmaone Derene nte Derene nte t Il metodo delle derene nte permette d trasormare un problema derenale n uno algebrco approssmato. Lmtando nalmente l problema al caso d una unone ncognta
Tecnche d approssmaone Derene nte Derene nte t Il metodo delle derene nte permette d trasormare un problema derenale n uno algebrco approssmato. Lmtando nalmente l problema al caso d una unone ncognta
5. Baricentro di sezioni composte
 5. Barcentro d sezon composte Barcentro del trapezo Il barcentro del trapezo ( FIURA ) s trova sull asse d smmetra oblqua (medana) della fgura; è suffcente, qund, determnare la sola ordnata. A tal fne,
5. Barcentro d sezon composte Barcentro del trapezo Il barcentro del trapezo ( FIURA ) s trova sull asse d smmetra oblqua (medana) della fgura; è suffcente, qund, determnare la sola ordnata. A tal fne,
Lezione 20 Maggio 29
 PSC: Progettazone d sstem d controllo III Trm 2007 Lezone 20 Maggo 29 Docente: Luca Schenato Stesor: Maran F, Marcon R, Marcassa A, Zanella F Fnora s sono sempre consderat sstem tempo-nvarant, ovvero descrtt
PSC: Progettazone d sstem d controllo III Trm 2007 Lezone 20 Maggo 29 Docente: Luca Schenato Stesor: Maran F, Marcon R, Marcassa A, Zanella F Fnora s sono sempre consderat sstem tempo-nvarant, ovvero descrtt
3 = 3 Ω. quindi se v g = 24 V, i = 1,89 A Dobbiamo studiare tre circuiti; in tutti e tre i casi si ottiene un partitore di corrente.
 5. Per la propretà d lneartà la tensone può essere espressa come = k g, doe g è la corrente del generatore. Utlzzando dat n Fgura a abbamo - = k 6, qund k = - ½. In Fgura b la corrente del generatore è
5. Per la propretà d lneartà la tensone può essere espressa come = k g, doe g è la corrente del generatore. Utlzzando dat n Fgura a abbamo - = k 6, qund k = - ½. In Fgura b la corrente del generatore è
Lezione 14 - Il tensore di Green- Lagrange
 Lezione 14 - Il tensore di Green- Lagrange [Ultimarevisione: revisione:4 4novembre novembre009] In questa lezione si generalizza quanto detto nella lezione precedente, considerando la trasformazione subita
Lezione 14 - Il tensore di Green- Lagrange [Ultimarevisione: revisione:4 4novembre novembre009] In questa lezione si generalizza quanto detto nella lezione precedente, considerando la trasformazione subita
ANALISI STATISTICA DELLE INCERTEZZE CASUALI
 AALISI STATISTICA DELLE ICERTEZZE CASUALI Consderamo l caso della msura d una grandezza fsca che sa affetta da error casual. Per ottenere maggor nformazone sul valore vero della grandezza rpetamo pù volte
AALISI STATISTICA DELLE ICERTEZZE CASUALI Consderamo l caso della msura d una grandezza fsca che sa affetta da error casual. Per ottenere maggor nformazone sul valore vero della grandezza rpetamo pù volte
I coefficienti di elasticità della domanda: un esposizione algebrico-grafica 1
 ppendce 4 I coeffcent d elastctà della domanda: un esposzone algebrco-grafca 1 Il calcolo de coeffcent d elastctà della domanda La teora e l ndagne economca hanno dentfcato numerosevarablchenflusconosullaquanttàdomandatadunbeneoservzo.traquestevsonol
ppendce 4 I coeffcent d elastctà della domanda: un esposzone algebrco-grafca 1 Il calcolo de coeffcent d elastctà della domanda La teora e l ndagne economca hanno dentfcato numerosevarablchenflusconosullaquanttàdomandatadunbeneoservzo.traquestevsonol
Le soluzioni della prova scritta di Matematica per il corso di laurea in Farmacia (raggruppamento M-Z)
 Le soluzon della prova scrtta d Matematca per l corso d laurea n Farmaca (raggruppamento M-Z). Data la funzone a. trova l domno d f f ( ) ln + b. scrv, esplctamente e per esteso, qual sono gl ntervall
Le soluzon della prova scrtta d Matematca per l corso d laurea n Farmaca (raggruppamento M-Z). Data la funzone a. trova l domno d f f ( ) ln + b. scrv, esplctamente e per esteso, qual sono gl ntervall
ESERCIZIARIO SUI NUMERI COMPLESSI
 ESERCIZIARIO SUI NUMERI COMPLESSI I numer regnano sull unverso. PITAGORA Perché numer sono bell? È come chedere perché la Nona Snfona d Beethoven è bella. Se non ved perché, nessuno può spegartelo. Io
ESERCIZIARIO SUI NUMERI COMPLESSI I numer regnano sull unverso. PITAGORA Perché numer sono bell? È come chedere perché la Nona Snfona d Beethoven è bella. Se non ved perché, nessuno può spegartelo. Io
CAPITOLO 3 CIRCUITI DI RESISTORI
 CAPITOLO 3 CIRCUITI DI RESISTORI Pagna 3. Introduzone 70 3. Connessone n sere e connessone n parallelo 70 3.. Bpol resstv n sere 7 3.. Bpol resstv n parallel 77 3.3 Crcut resstv lnear e sovrapposzone degl
CAPITOLO 3 CIRCUITI DI RESISTORI Pagna 3. Introduzone 70 3. Connessone n sere e connessone n parallelo 70 3.. Bpol resstv n sere 7 3.. Bpol resstv n parallel 77 3.3 Crcut resstv lnear e sovrapposzone degl
PROVA SCRITTA DI MECCANICA RAZIONALE (13 gennaio 2017) (Prof. A. Muracchini)
 PRV SCRITT DI ECCNIC RZINLE (13 gennao 017) (Prof.. uracchn) Il sstema rappresentato n fgura è costtuto da: a) una lamna pesante, omogenea a forma d trangolo soscele (massa m, base l, altezza h) vncolata
PRV SCRITT DI ECCNIC RZINLE (13 gennao 017) (Prof.. uracchn) Il sstema rappresentato n fgura è costtuto da: a) una lamna pesante, omogenea a forma d trangolo soscele (massa m, base l, altezza h) vncolata
1 Le equazioni per le variabili macroscopiche: i momenti dell equazione di Boltzmann
 FISICA DEI FLUIDI Lezone 5-5 Maggo 202 Le equazon per le varabl macroscopche: moment dell equazone d Boltzmann Teorema H a parte, non è facle estrarre altre consderazon general sulla funzone denstà d probabltà
FISICA DEI FLUIDI Lezone 5-5 Maggo 202 Le equazon per le varabl macroscopche: moment dell equazone d Boltzmann Teorema H a parte, non è facle estrarre altre consderazon general sulla funzone denstà d probabltà
ANELLI E SOTTOANELLI. contrassegna gli esercizi (relativamente) più complessi.
 ESERCIZI SU ANELLI E SOTTOANELLI N.B.: l smbolo contrassegna gl esercz relatvamente pù compless. 1 Sa X un nseme, e sa PX l suo nseme delle part. Indcando con l operazone d dfferenza smmetrca tra element
ESERCIZI SU ANELLI E SOTTOANELLI N.B.: l smbolo contrassegna gl esercz relatvamente pù compless. 1 Sa X un nseme, e sa PX l suo nseme delle part. Indcando con l operazone d dfferenza smmetrca tra element
La soluzione delle equazioni differenziali con il metodo di Galerkin
 Il metodo de resdu pesat per gl element fnt a soluzone delle equazon dfferenzal con l metodo d Galerkn Tra le procedure generalmente adottate per formulare e rsolvere le equazon dfferenzal con un metodo
Il metodo de resdu pesat per gl element fnt a soluzone delle equazon dfferenzal con l metodo d Galerkn Tra le procedure generalmente adottate per formulare e rsolvere le equazon dfferenzal con un metodo
Matematica Computazionale(6cfu) Ottimizzazione(8cfu)
 Docente: Marco Gavano (e-mal:gavano@unca.t) Corso d Laurea n Infomatca Corso d Laurea n Matematca Matematca Computazonale(6cfu) Ottmzzazone(8cfu) (a.a. 205-6, lez.8) Matematca Computazonale, Ottmzzazone,
Docente: Marco Gavano (e-mal:gavano@unca.t) Corso d Laurea n Infomatca Corso d Laurea n Matematca Matematca Computazonale(6cfu) Ottmzzazone(8cfu) (a.a. 205-6, lez.8) Matematca Computazonale, Ottmzzazone,
urto v 2f v 2i e forza impulsiva F r F dt = i t
 7. Urt Sstem a due partcelle Defnzone d urto elastco, urto anelastco e mpulso L urto è un nterazone fra corp che avvene n un ntervallo d tempo normalmente molto breve, al termne del quale le quanttà d
7. Urt Sstem a due partcelle Defnzone d urto elastco, urto anelastco e mpulso L urto è un nterazone fra corp che avvene n un ntervallo d tempo normalmente molto breve, al termne del quale le quanttà d
Intelligenza Artificiale II. Ragionamento probabilistico Rappresentazione. Marco Piastra. Intelligenza Artificiale II - AA 2007/2008
 Intellgenza rtfcale II Ragonamento probablstco Rappresentazone Marco astra Ragonamento probablstco: rappresentazone - arte Mond possbl sottonsem event artzon e varabl aleatore robabltà Margnalzzazone Condzonal
Intellgenza rtfcale II Ragonamento probablstco Rappresentazone Marco astra Ragonamento probablstco: rappresentazone - arte Mond possbl sottonsem event artzon e varabl aleatore robabltà Margnalzzazone Condzonal
i 2 + i 1 v 2 Comportamento elettrico descritto in vari modi equivalenti Piu' comuni, quadripolo lineare: = z i + z i Parametri di ammettenza
 Quadrpolo: Rete generca (passa o atta, lneare o non lneare) coppe d termnal: ngresso - uscta Caratterata dall'esterno da 4 grandee elettrche:,,, Input Rete Output Comportamento elettrco descrtto n ar mod
Quadrpolo: Rete generca (passa o atta, lneare o non lneare) coppe d termnal: ngresso - uscta Caratterata dall'esterno da 4 grandee elettrche:,,, Input Rete Output Comportamento elettrco descrtto n ar mod
Soluzione del compito di Fisica febbraio 2012 (Udine)
 del compto d Fsca febbrao (Udne) Elettrodnamca È data una spra quadrata d lato L e resstenza R, ed un flo percorso da corrente lungo z (ved fgura). Dcamo a e b le dstanze del lato parallelo pù vcno e pù
del compto d Fsca febbrao (Udne) Elettrodnamca È data una spra quadrata d lato L e resstenza R, ed un flo percorso da corrente lungo z (ved fgura). Dcamo a e b le dstanze del lato parallelo pù vcno e pù
3 CAMPIONAMENTO DI BERNOULLI E DI POISSON
 3 CAMPIOAMETO DI ROULLI E DI POISSO 3. ITRODUZIOE In questo captolo esamneremo due schem d camponamento che dversamente dal camponamento casuale semplce non producono campon d dmensone fssa ma varable.
3 CAMPIOAMETO DI ROULLI E DI POISSO 3. ITRODUZIOE In questo captolo esamneremo due schem d camponamento che dversamente dal camponamento casuale semplce non producono campon d dmensone fssa ma varable.
Corso di laurea in Ingegneria Meccatronica. DINAMICI CA - 04 ModiStabilita
 Automaton Robotcs and System CONTROL Unverstà degl Stud d Modena e Reggo Emla Corso d laurea n Ingegnera Meccatronca MODI E STABILITA DEI SISTEMI DINAMICI CA - 04 ModStablta Cesare Fantuzz (cesare.fantuzz@unmore.t)
Automaton Robotcs and System CONTROL Unverstà degl Stud d Modena e Reggo Emla Corso d laurea n Ingegnera Meccatronca MODI E STABILITA DEI SISTEMI DINAMICI CA - 04 ModStablta Cesare Fantuzz (cesare.fantuzz@unmore.t)
Ettore Limoli. Lezioni di Matematica Prof. Ettore Limoli. Sommario. Calcoli di regressione
 Sto Personale d Ettore Lmol Lezon d Matematca Prof. Ettore Lmol Sommaro Calcol d regressone... 1 Retta d regressone con Ecel... Uso della funzone d calcolo della tendenza... 4 Uso della funzone d regressone
Sto Personale d Ettore Lmol Lezon d Matematca Prof. Ettore Lmol Sommaro Calcol d regressone... 1 Retta d regressone con Ecel... Uso della funzone d calcolo della tendenza... 4 Uso della funzone d regressone
REGRESSIONE LINEARE. È caratterizzata da semplicità: i modelli utilizzati sono basati essenzialmente su funzioni lineari
 REGRESSIONE LINEARE Ha un obettvo mportante: nvestgare sulle relazon emprche tra varabl allo scopo d analzzare le cause che possono spegare un determnato fenomeno È caratterzzata da semplctà: modell utlzzat
REGRESSIONE LINEARE Ha un obettvo mportante: nvestgare sulle relazon emprche tra varabl allo scopo d analzzare le cause che possono spegare un determnato fenomeno È caratterzzata da semplctà: modell utlzzat
L arcobaleno. Giovanni Mancarella. n = n = n = α( o )
 Govann Mancarella L arcobaleno I(α) (a.u.) n =.3338 n =.336 39 40 4 4 43 α( o ) In questa nota utlzzeremo l termne dstrbuzone per ndcare la denstà d probabltà d una varable casuale. Il fenomeno dell arcobaleno
Govann Mancarella L arcobaleno I(α) (a.u.) n =.3338 n =.336 39 40 4 4 43 α( o ) In questa nota utlzzeremo l termne dstrbuzone per ndcare la denstà d probabltà d una varable casuale. Il fenomeno dell arcobaleno
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa lezione 17: 16 maggio 2013
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 17: 16 maggo 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/22? Eserczo Un Btp trennale, d valore nomnale C
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 17: 16 maggo 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/22? Eserczo Un Btp trennale, d valore nomnale C
Determinarelatranscaratteristicav out (v in ) del seguente circuito R. V out. V in V ٧ = 0.7V D Z D V R = 5V. R o V R V Z = -8V
 ESECZO SU DOD (Metodo degl Scatt) Determnarelatranscaratterstcav out (v n ) del seguente crcuto Dat del problema 5 o kω Ω 0 Ω Z -8 n ٧ 0.7 r D 0 Ω r Z 0 Ω r Ω D Z D o out Metodo degl scatt S determnano
ESECZO SU DOD (Metodo degl Scatt) Determnarelatranscaratterstcav out (v n ) del seguente crcuto Dat del problema 5 o kω Ω 0 Ω Z -8 n ٧ 0.7 r D 0 Ω r Z 0 Ω r Ω D Z D o out Metodo degl scatt S determnano
L ANALISI MONOVARIATA: Variabilità e mutabilità. Prof. Maria Carella
 L AALISI MOOVARIATA: Varabltà e mutabltà Prof. Mara Carella Varabltà Le msure d tendenza centrale non sono suffcent alla comprensone de fenomen. Una sntes approprata deve tener conto del modo n cu s dstrbuscono
L AALISI MOOVARIATA: Varabltà e mutabltà Prof. Mara Carella Varabltà Le msure d tendenza centrale non sono suffcent alla comprensone de fenomen. Una sntes approprata deve tener conto del modo n cu s dstrbuscono
Risposta in frequenza e filtri
 Rsposta n frequenza e fltr www.de.ng.unbo.t/pers/mastr/ddattca.htm (versone del 3-3-9) Funzon d rete S consdera un crcuto con un solo ngresso (coè un solo generatore) operante n condzon d regme snusodale
Rsposta n frequenza e fltr www.de.ng.unbo.t/pers/mastr/ddattca.htm (versone del 3-3-9) Funzon d rete S consdera un crcuto con un solo ngresso (coè un solo generatore) operante n condzon d regme snusodale
NUMERI GRANDI DI FIBONACCI come trovare velocemente i loro esatti valori numerici Cristiano Teodoro
 NUMERI GRANDI DI FIBONACCI come trovare velocemente loro esatt valor numerc Crstano Teodoro crstanoteodoro@vrglo.t Sommaro: n questo artcolo vene proposto, n alternatva al metodo classco per l calcolo
NUMERI GRANDI DI FIBONACCI come trovare velocemente loro esatt valor numerc Crstano Teodoro crstanoteodoro@vrglo.t Sommaro: n questo artcolo vene proposto, n alternatva al metodo classco per l calcolo
Analisi agli elementi finiti di campi vettoriali
 Anals agl element fnt d camp vettoral Carlo Forestere December, 04 Formulazone n forma debole d equazon d campo vettorale Sa R un domno bdmensonale Fg. rempto da un materale lneare, sotropo, tempo nvarante,
Anals agl element fnt d camp vettoral Carlo Forestere December, 04 Formulazone n forma debole d equazon d campo vettorale Sa R un domno bdmensonale Fg. rempto da un materale lneare, sotropo, tempo nvarante,
Si dice corpo rigido un oggetto ideale che mantiene la stessa forma e le stesse dimensioni qualunque sia la sollecitazione cui lo si sottopone.
 Captolo 7 I corp estes 1. I movment d un corpo rgdo Che cosa s ntende per corpo esteso? Con l termne d corpo esteso c s rfersce ad oggett per qual non è lecto adoperare l approssmazone d partcella, coè
Captolo 7 I corp estes 1. I movment d un corpo rgdo Che cosa s ntende per corpo esteso? Con l termne d corpo esteso c s rfersce ad oggett per qual non è lecto adoperare l approssmazone d partcella, coè
POLINOMIO MINIMO E FORMA CANONICA DI JORDAN NOTA AGGIUNTIVA PER IL CORSO DI GEOMETRIA ANALITICA E ALGEBRA LINEARE A.A DOCENTE: PAOLO LISCA
 POLINOMIO MINIMO E FORMA CANONICA DI JORDAN NOTA AGGIUNTIVA PER IL CORSO DI GEOMETRIA ANALITICA E ALGEBRA LINEARE AA 2009-2010 DOCENTE: PAOLO LISCA 1 Polnomo mnmo Avvertenza: con V ndcheremo uno spazo
POLINOMIO MINIMO E FORMA CANONICA DI JORDAN NOTA AGGIUNTIVA PER IL CORSO DI GEOMETRIA ANALITICA E ALGEBRA LINEARE AA 2009-2010 DOCENTE: PAOLO LISCA 1 Polnomo mnmo Avvertenza: con V ndcheremo uno spazo
materiale didattico I incontro
 Pano Nazonale Lauree Scentfche (PLS 2016-2017) Statstca Laboratoro d Statstca Le relazon tra varabl prof.ssa Angela Mara D'Uggento angelamara.duggento@unba.t materale ddattco I ncontro Dall anals statstca
Pano Nazonale Lauree Scentfche (PLS 2016-2017) Statstca Laboratoro d Statstca Le relazon tra varabl prof.ssa Angela Mara D'Uggento angelamara.duggento@unba.t materale ddattco I ncontro Dall anals statstca
Risposta in frequenza e filtri
 Rsposta n frequenza e fltr www.de.ng.unbo.t/pers/mastr/ddattca.htm (versone del 5-4-7) Funzon d rete S consdera un crcuto con un solo ngresso (coè un solo generatore) operante n condzon d regme snusodale
Rsposta n frequenza e fltr www.de.ng.unbo.t/pers/mastr/ddattca.htm (versone del 5-4-7) Funzon d rete S consdera un crcuto con un solo ngresso (coè un solo generatore) operante n condzon d regme snusodale
3) Entropie condizionate, entropie congiunte ed informazione mutua
 Argoment della Lezone ) Coppe d varabl aleatore 2) Canale dscreto senza memora 3) Entrope condzonate, entrope congunte ed nformazone mutua 4) Esemp d canal Coppe d varabl aleatore Fno ad ora è stata consderata
Argoment della Lezone ) Coppe d varabl aleatore 2) Canale dscreto senza memora 3) Entrope condzonate, entrope congunte ed nformazone mutua 4) Esemp d canal Coppe d varabl aleatore Fno ad ora è stata consderata
x 0 x 50 x 20 x 100 CASO 1 CASO 2 CASO 3 CASO 4 X n X n X n X n
 Corso d Statstca docente: Domenco Vstocco La msura della varabltà per varabl qualtatve ordnal Lo studo della varabltà per varabl qualtatve ordnal può essere condotto servendos degl ndc d omogenetà/eterogenetà
Corso d Statstca docente: Domenco Vstocco La msura della varabltà per varabl qualtatve ordnal Lo studo della varabltà per varabl qualtatve ordnal può essere condotto servendos degl ndc d omogenetà/eterogenetà
