Calcolo Scientifico e Matematica Applicata Secondo Parziale, Ingegneria Ambientale
|
|
|
- Filippo Forti
- 4 anni fa
- Visualizzazioni
Transcript
1 Calcolo Scentfco e Matematca Applcata Secondo Parzale, Ingegnera Ambentale Rsolvere gl esercz, 2, 4 oppure, n alternatva, gl esercz, 3, 4. Valutazone degl esercz: 4, 2 8, 3 8, Illustrare, medante l metodo delle dfferenze fnte, la rsoluzone numerca del seguente problema perbolco u tt = u xx + 4x 2 u x ( + 2x 2 u + cos 2 (x, x 3, t 8, u(, t = f, u(3, t = f 2, u(x, = x 2, u t (x, = x + 2. Dscutere le condzon su pass affnché le matrc de sstem sano nvertbl. 2. Illustrare la rsoluzone numerca del seguente problema debolmente non lneare: u xx + (3 + sn xu x + (sn(u u 5 = sn 2 (x, x 4, u( = f, u(4 = f Illustrare la rsoluzone numerca del seguente problema parabolco: u t = [( + x 4 u x ] x (3 + 2 sn(xu + f(x, x, u(, t = u(, t =, u(x, = g(x. Dscutere le propretà prncpal delle matrc del sstema. 4. a. Illustrare l procedmento d rsoluzone, medante gl element fnt, del seguente problema ellttco: ( [ + x 4 y 2 ] u ( [ + x 4 y 2 ] u x x y y sotto la condzone al contorno u Ω =. + (2 + cos[x + y]u = x 2 y 2, (x, y Ω,
2 b. Indcat con ϕ la box splne che assume l valore nel punto nodale (3, 4 e zero negl altr punt nodal e con ψ la box splne che assume l valore nel punto nodale (3 h, 4 + h e zero negl 2 altr, llustrare l procedmento per l calcolo del seguente ntegrale I = ϕ ψ dxdy, essendo T l trangolo d vertc { (3 2 h, 4 + h, (3, 4, (3 + 2 h, h}. Utlzzare l trangolo d rfermento. T
3 Calcolo Scentfco e Matematca Applcata Secondo Parzale, Ingegnera Meccanca. Illustrare, medante l metodo delle dfferenze fnte, la rsoluzone numerca del seguente problema perbolco u tt = u xx + 4x 2 u x ( + 2x 2 u + cos 2 (x, x 3, t 8, u(, t = f, u(3, t = f 2, u(x, = x 2, u t (x, = x + 2. Dscutere le condzon su pass affnché le matrc de sstem sano nvertbl. 2. Illustrare la rsoluzone numerca del seguente problema debolmente non lneare: u xx + (3 + sn xu x + (sn(u u 5 = sn 2 (x, x 4, u( = f, u(4 = f Illustrare, medante l metodo delle dfferenze fnte, la rsoluzone numerca del seguente problema parabolco u t = u xx + 4x 2 u x ( + 2x 2 sn 2 (2tu + 3 sn 2 (x, x 4, t 2, u(, t = f, u(4, t = f 2, u(x, = x 4 +. Dscutere le condzon su pass affnché le matrc de sstem sano nvertbl. Rsolvere tutt gl esercz. Valutazone degl esercz: 4, 2 8, 3 8.
4 Soluzon per l ngegnera ambentale:. Sano = x < x <... < x n < x n+ = 3 nod spazal equdstant [h = 3, x n+ = h] e = t < t <... < t m < t m+ = 8 nod temporal equdstant [k = 8, t m+ j = jk]. Allora u,j+ 2u j + u,j k 2 = [ u+,j+ 2u,j+ + u,j+ + u ] +,j 2u,j + u,j 2 h [ 2 + 4x2 u+,j+ u,j+ + u ] +,j u,j 2 ( + 2x 2 u j + cos 2 (x, dove =,..., n e j =,..., m. S conoscono dat u,j = f, u n+,j = f 2, u = x 2, dove =,,..., n, n + e j =,,..., m, m +. Qund bsogna rsolvere l sstema per u,j+ [ =,..., n] ( h + ( ( u 2 k 2,j+ + 2x2 u 2 +,j+ 2x2 u 2,j+ = 2u j u,j + u +,j 2u,j + u,j k x 2 u +,j u,j ( + 2x 2 u j + cos 2 (x, dove =,..., n e termn con pedc per = e + per = n sono da spostare alla parte a destra. La matrce del sstema è trdagonale. Essa è strettamente dagonalmente domnante e qund nvertble se + 2x x2 2 < h + 2 k. 2 Cò è vero se 2x2 per =,..., n, coè se < h [/2 max x 2 2 ] =, coè se n 53. 8
5 (,j+ (+,j+ (,j+ (,j (,j (,j (+,j C rmane l calcolo d u. S ha: u = u(x, k u(x, + ku t (x, + 2 k2 u tt (x, u + ku t (x, + 2 k2 [ u+, 2u + u, + 4x 2 u +, u, dove u = x 2, u t (x, = x + 2 e =,..., n. ] ( + 2x 2 u + cos 2 (x, 2. Sano = x < x <... < x n < x n+ = 4 nod equdstant [h = 4 n+, x = h]. Sa u = u(x, f = f(x. Allora bsogna trovare le soluzon del sstema d equazon non lnear dove F (u, u, u + F (u, u, u + =, =, 2,..., n, := u + 2u + u + (3 + sn x u + u + (sn(u u 5 sn 2 (x.
6 Sceglendo l punto d nnesco u [] = f + n + (f 2 f = (n + f + f 2, n + s applch l metodo d Newton-Raphson rsultando nell terazone u [k+] = u [k], u[k] F u (u [k], u[k] F (u [k], u [k] +, u [k] +. D conseguenza, per < ph 2 [con p = max(3 + sn x = 4, coè se < h oppure se n 7] s ha: 2 u [k+] = u [k] + u[k] + 2u[k] + u [k] + h 3+sn x (u [k] 2 + u[k] + (sn(u[k] u [k] 5 sn 2 (x, (sn(u [k] u [k] 4 ( cos(u [k] dove =,..., n e k =,, 2,.... S osserv che l denomnatore della frazone è postvo. 3. Sano = x < x <... < x n < x n+ = nod non necessaramente equdstant e sano, x x, x x x φ (x = x, x x x, x + x x + x, x x x +,, x + x, le funzon splne tal che φ (x = e φ (x j = per j. Allora la formulazone varazonale del problema è l seguente: Trovare, per t >, una funzone u(, t H(, tale che per ogn v H(, s ha: d dt = + u(x, tv(x dx ( ( + x 4 u x (x, tv (x + (3 + 2 sn(xu(x, tv(x dx f(x, tv(x dx.
7 Sosttuendo u = n j= c jφ j e v = φ s arrva al sstema lneare n c j(t j= n c j ( j= φ φ j dx = + φ φ j dx = ( ( + x 4 φ φ j + (3 + 2 sn(xφ φ j dx f(x, tφ (x dx, G(xφ (x dx, dove =,..., n. Introducendo le matrc real, smmetrche e trdagonal M e K (quest ultma chamata la stffness matrx come M j = φ φ j dx, K j = s ottene l problema d Cauchy { Mc (t = Kc(t + f(t, Mc( = g, ( ( + x 4 φ φ j +(3 + 2 sn(xφ φ j dx, dove c(t è l vettore colonna de coeffcent e f(t e g sono vettor colonna degl ntegral che rguardano f e g. Charamente, M è la matrce d Gram [rspetto al prodotto nterno n L 2 (, ] delle funzon splne. Sccome le splnes sono lnearmente ndpendent, gl autovalor d M sono tutt postv e qund M è nvertble. La stessa cosa vale per la stffness matrx K, pochè essa è la matrce d Gram [rspetto al prodotto nterno [u, v] = ( ( + x 4 u v + (3 + 2 sn(xuv dx n H (, che genera la topologa d H (, ]. Qund { c (t = M Kc(t + M f(t, c( = M g. 4a. Il problema ellttco con condzon d Drchlet ([ + x 4 y 2 ] u + (2 + cos[x + y]u = x 2 y 2,
8 ammette la seguente formulazone varazonale: Trovare u H(Ω tale che per ogn v H(Ω s ha: ( [ + x 4 y 2 ] u v+(2 + cos[x + y]uv dxdy = x 2 y 2 v(x, y dxdy. Ω Sano φ (x, y [ =,..., N] le funzon splne con supporto l unone d al massmo se trangol. Ponendo u = N j= c jφ j e v = φ s ha: N c j j= = Ω Ω ( [ + x 4 y 2 ] φ φ j + (2 + cos[x + y]φ φ j dxdy x 2 y 2 φ (x, y dxdy, dove =,..., N. Scrvendo quest ultmo sstema d equazon lnear nella forma Kc = f, dove la stffness matrx K è reale, smmetrca e sparsa, bsogna dmostrare l nvertbltà d K. Sccome +x 4 y 2 e 2+cos[x+y] sono funzon postve, la stffness matrx è la matrce d Gram [rspetto a un prodotto nterno d H (Ω che genera la topologa d H (Ω] delle funzon splne e quest ultme sono lnearmente ndpendent. D conseguenza, K ha soltanto autovalor postv e qund è nvertble. 4b. La trasformazone lneare che porta punt (s, t {(,, (,, (, } ne rspettatv punt { (3, 4, (3 2 h, 4 + h, (3 + 2 h, h} ha la forma { x = 3 2 hs + 2 ht, y = 4 + hs + 4 ht. Essa ha la matrce Jacobana ( ( xs x J = t = h h 2 2 y s y t h h, 4 essendo u 2 H (, [u, u] u 2 H (, Ω
9 per cu det J = 5 8 h2. Abbamo ora γ(s, t = s t e δ(s, t = s per le funzon lnear n (s, t T R [l trangolo d rfermento con vertc (,, (, e (, ] che s annullano n due delle tre vertc e prendono l valore nella terza. S calcol ( h h ( ( 4 6/5h Qund I = J T γ = 8 5 J T δ = 8 5 T h h = 2 2 ( h h ( 4 h h = 2 2 8/5h ( 2/5h 4/5h. ϕ ψ dxdy = (J T γ (J T δ det J dsdt T R = h2 = 4, essendo 2 = T R dsdt l area del trangolo d rfermento., T R T
10 Soluzon per l ngegnera meccanca:. Sano = x < x <... < x n < x n+ = 3 nod spazal equdstant [h = 3, x n+ = h] e = t < t <... < t m < t m+ = 8 nod temporal equdstant [k = 8, t m+ j = jk]. Allora u,j+ 2u j + u,j k 2 = [ u+,j+ 2u,j+ + u,j+ + u ] +,j 2u,j + u,j 2 h [ 2 + 4x2 u+,j+ u,j+ + u ] +,j u,j 2 ( + 2x 2 u j + cos 2 (x, dove =,..., n e j =,..., m. S conoscono dat u,j = f, u n+,j = f 2, u = x 2, dove =,,..., n, n + e j =,,..., m, m +. Qund bsogna rsolvere l sstema per u,j+ [ =,..., n] ( h + ( ( u 2 k 2,j+ + 2x2 u 2 +,j+ 2x2 u 2,j+ = 2u j u,j + u +,j 2u,j + u,j k x 2 u +,j u,j ( + 2x 2 u j + cos 2 (x, dove =,..., n e termn con pedc per = e + per = n sono da spostare alla parte a destra. La matrce del sstema è trdagonale. Essa è strettamente dagonalmente domnante e qund nvertble se + 2x x2 2 < h + 2 k. 2 Cò è vero se 2x2 per =,..., n, coè se < h [/2 max x 2 2 ] =, coè se n 53. 8
11 (,j+ (+,j+ (,j+ (,j (,j (,j (+,j C rmane l calcolo d u. S ha: u = u(x, k u(x, + ku t (x, + 2 k2 u tt (x, u + ku t (x, + 2 k2 [ u+, 2u + u, + 4x 2 u +, u, dove u = x 2, u t (x, = x + 2 e =,..., n. ] ( + 2x 2 u + cos 2 (x, 2. Sano = x < x <... < x n < x n+ = 4 nod equdstant [h = 4 n+, x = h]. Sa u = u(x, f = f(x. Allora bsogna trovare le soluzon del sstema d equazon non lnear dove F (u, u, u + F (u, u, u + =, =, 2,..., n, := u + 2u + u + (3 + sn x u + u + (sn(u u 5 sn 2 (x.
12 Sceglendo l punto d nnesco u [] = f + n + (f 2 f = (n + f + f 2, n + s applch l metodo d Newton-Raphson rsultando nell terazone u [k+] = u [k], u[k] F u (u [k], u[k] F (u [k], u [k] +, u [k] +. D conseguenza, per < ph 2 [con p = max(3 + sn x = 4, coè se < h oppure se n 7] s ha: 2 u [k+] = u [k] + u[k] + 2u[k] + u [k] + h 3+sn x (u [k] 2 + u[k] + (sn(u[k] u [k] 5 sn 2 (x, (sn(u [k] u [k] 4 ( cos(u [k] dove =,..., n e k =,, 2,.... S osserv che l denomnatore della frazone è postvo. 3. Sano = x < x <... < x n < x n+ = 4 nod spazal equdstant [h = 3, x n+ = + h] e = t < t <... < t m < t m+ = 2 nod temporal equdstant [k = 2, t m+ j = jk]. Allora t j t,j k = u +,j 2u j + u,j + 4x 2 u +,j u,j ( + 2x 2 sn 2 (2t j u j + 3 sn 2 (x, u j = f, u n+,j = f 2, u = x 4 +, dove =,..., n e j =,..., m +. Qund ( 2 h x2 sn 2 (2t j + k ( + 4x2 u 2 +,j = t,j k + 3 sn 2 (x, u j ( 4x2 2 u,j dove =,..., n, j =,..., m + e termn con prmo pedce per = e + per = n sono da spostare nella parte a destra. Per
13 ogn pedce j =,..., m + la matrce del sstema è trdagonale. Essa è strettamente dagonalmente domnante e qund nvertble se + 4x x2 2 < 2 h x2 sn 2 (2t j + k. Cò è vero se 4x2 per =,..., n, coè se < h [/ max 4x 2 ] =, coè se n
Equilibrio e stabilità di sistemi dinamici. Stabilità dell equilibrio di sistemi dinamici non lineari per linearizzazione
 Equlbro e stabltà d sstem dnamc Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem NL TC Crter d stabltà
Equlbro e stabltà d sstem dnamc Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem NL TC Crter d stabltà
Metodi variazionali. ed agiscono sulla FORMA DEBOLE DEL PROBLEMA
 Metod varazonal OBIETTIVO: determnare funzon ncognte, chamate varabl dpendent, che soddsfano un certo nseme d equazon dfferenzal n un determnato domno e condzon al contorno STRUMETO: Metod varazonal: servono
Metod varazonal OBIETTIVO: determnare funzon ncognte, chamate varabl dpendent, che soddsfano un certo nseme d equazon dfferenzal n un determnato domno e condzon al contorno STRUMETO: Metod varazonal: servono
Metodi variazionali. ed agiscono sulla FORMA DEBOLE DEL PROBLEMA
 Metod varazonal OBIETTIVO: determnare funzon ncognte, chamate varabl dpendent, che soddsfano un certo nseme d equazon dfferenzal n un determnato domno e condzon al contorno STRUMETO: Metod varazonal: servono
Metod varazonal OBIETTIVO: determnare funzon ncognte, chamate varabl dpendent, che soddsfano un certo nseme d equazon dfferenzal n un determnato domno e condzon al contorno STRUMETO: Metod varazonal: servono
Analisi agli elementi finiti di campi vettoriali
 Anals agl element fnt d camp vettoral Carlo Forestere December, 04 Formulazone n forma debole d equazon d campo vettorale Sa R un domno bdmensonale Fg. rempto da un materale lneare, sotropo, tempo nvarante,
Anals agl element fnt d camp vettoral Carlo Forestere December, 04 Formulazone n forma debole d equazon d campo vettorale Sa R un domno bdmensonale Fg. rempto da un materale lneare, sotropo, tempo nvarante,
Integrazione numerica dell equazione del moto per un sistema lineare viscoso a un grado di libertà. Prof. Adolfo Santini - Dinamica delle Strutture 1
 Integrazone numerca dell equazone del moto per un sstema lneare vscoso a un grado d lbertà Prof. Adolfo Santn - Dnamca delle Strutture 1 Introduzone 1/2 L equazone del moto d un sstema vscoso a un grado
Integrazone numerca dell equazone del moto per un sstema lneare vscoso a un grado d lbertà Prof. Adolfo Santn - Dnamca delle Strutture 1 Introduzone 1/2 L equazone del moto d un sstema vscoso a un grado
Metodi di analisi R 1 =15Ω R 2 =40Ω R 3 =16Ω
 Metod d anals Eserczo Anals alle magle n presenza d sol generator ndpendent d tensone R s J R Determnare le tenson sulle resstenze sapendo che: s s 0 R R 5.Ω s J R J R R 5Ω R 0Ω R 6Ω R 5 Dsegnamo l grafo,
Metod d anals Eserczo Anals alle magle n presenza d sol generator ndpendent d tensone R s J R Determnare le tenson sulle resstenze sapendo che: s s 0 R R 5.Ω s J R J R R 5Ω R 0Ω R 6Ω R 5 Dsegnamo l grafo,
Corsi di Laurea in Farmacia e CTF Prova di Matematica
 Cors d Laurea n Farmaca e CTF Prova d Matematca S O L U Z I O N I Effettua uno studo qualtatvo della funzone 4 f + con partcolare rfermento a seguent aspett: a trova l domno della funzone b trova gl ntervall
Cors d Laurea n Farmaca e CTF Prova d Matematca S O L U Z I O N I Effettua uno studo qualtatvo della funzone 4 f + con partcolare rfermento a seguent aspett: a trova l domno della funzone b trova gl ntervall
Funzione di matrice. c i λ i. i=0. i=0. m 1. γ i A i. i=0. Moltiplicando entrambi i membri di questa equazione per A si ottiene. α i 1 A i α m 1 A m
 Captolo INTRODUZIONE Funzone d matrce Sa f(λ) una generca funzone del parametro λ svluppable n sere d potenze f(λ) Sa A una matrce quadrata d ordne n La funzone d matrce f(a) èdefnta nel modo seguente
Captolo INTRODUZIONE Funzone d matrce Sa f(λ) una generca funzone del parametro λ svluppable n sere d potenze f(λ) Sa A una matrce quadrata d ordne n La funzone d matrce f(a) èdefnta nel modo seguente
Geometria 1 a.a. 2011/12 Esonero del 23/01/12 Soluzioni (Compito A) sì determinarla, altrimenti dimostrare che ciò è impossibile.
 Geometra 1 a.a. 2011/12 Esonero del 23/01/12 Soluzon (Compto A) (1) S consder su C 2 l prodotto Hermtano, H assocato alla matrce ( ) 2 H =. 2 (a) Dmostrare che, H è defnto postvo e determnare una base
Geometra 1 a.a. 2011/12 Esonero del 23/01/12 Soluzon (Compto A) (1) S consder su C 2 l prodotto Hermtano, H assocato alla matrce ( ) 2 H =. 2 (a) Dmostrare che, H è defnto postvo e determnare una base
Elettronica dello Stato Solido Esercitazione di Laboratorio 1: Soluzione numerica dell equazione di Schrödinger 1D
 Elettronca dello Stato Soldo Eserctazone d Laboratoro 1: Soluzone nuerca dell equazone d Schrödnger 1D Danele Ieln DEI Poltecnco d Mlano eln@elet.pol.t Contenut del Laboratoro Costruzone d un etodo nuerco
Elettronca dello Stato Soldo Eserctazone d Laboratoro 1: Soluzone nuerca dell equazone d Schrödnger 1D Danele Ieln DEI Poltecnco d Mlano eln@elet.pol.t Contenut del Laboratoro Costruzone d un etodo nuerco
Dipartimento di Statistica Università di Bologna. Matematica Finanziaria aa lezione 17: 8 maggio 2012
 Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 17: 8 maggo 2012 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/20? Costture n regme semplce al tasso = 0, 025 l
Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 17: 8 maggo 2012 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/20? Costture n regme semplce al tasso = 0, 025 l
La soluzione delle equazioni differenziali con il metodo di Galerkin
 Il metodo de resdu pesat per gl element fnt a soluzone delle equazon dfferenzal con l metodo d Galerkn Tra le procedure generalmente adottate per formulare e rsolvere le equazon dfferenzal con un metodo
Il metodo de resdu pesat per gl element fnt a soluzone delle equazon dfferenzal con l metodo d Galerkn Tra le procedure generalmente adottate per formulare e rsolvere le equazon dfferenzal con un metodo
Le soluzioni della prova scritta di Matematica per il corso di laurea in Farmacia (raggruppamento M-Z)
 Le soluzon della prova scrtta d Matematca per l corso d laurea n Farmaca (raggruppamento M-Z). Data la funzone a. trova l domno d f f ( ) ln + b. scrv, esplctamente e per esteso, qual sono gl ntervall
Le soluzon della prova scrtta d Matematca per l corso d laurea n Farmaca (raggruppamento M-Z). Data la funzone a. trova l domno d f f ( ) ln + b. scrv, esplctamente e per esteso, qual sono gl ntervall
4.6 Dualità in Programmazione Lineare
 4.6 Dualtà n Programmazone Lneare Ad ogn PL n forma d mn (max) s assoca un PL n forma d max (mn) Spaz e funzon obettvo dvers ma n genere stesso valore ottmo! Esempo: l valore massmo d un flusso ammssble
4.6 Dualtà n Programmazone Lneare Ad ogn PL n forma d mn (max) s assoca un PL n forma d max (mn) Spaz e funzon obettvo dvers ma n genere stesso valore ottmo! Esempo: l valore massmo d un flusso ammssble
Equilibrio e stabilità di sistemi dinamici. Stabilità interna di sistemi dinamici LTI
 Equlbro e stabltà d sstem dnamc Stabltà nterna d sstem dnamc LTI Stabltà nterna d sstem dnamc LTI Stabltà nterna d sstem dnamc LTI TC Crter d stabltà per sstem dnamc LTI TC Stabltà nterna d sstem dnamc
Equlbro e stabltà d sstem dnamc Stabltà nterna d sstem dnamc LTI Stabltà nterna d sstem dnamc LTI Stabltà nterna d sstem dnamc LTI TC Crter d stabltà per sstem dnamc LTI TC Stabltà nterna d sstem dnamc
Riccardo Sabatino 463/1 Progetto di un telaio in c.a. A.A. 2003/04
 Rccardo Sabatno 463/1 Progetto d un telao n c.a. A.A. 003/04 3.3 Il metodo degl spostament per la rsoluzone del telao Il metodo degl spostament è basato sulla valutazone de moment flettent ce agscono sugl
Rccardo Sabatno 463/1 Progetto d un telao n c.a. A.A. 003/04 3.3 Il metodo degl spostament per la rsoluzone del telao Il metodo degl spostament è basato sulla valutazone de moment flettent ce agscono sugl
5.1 Controllo di un sistema non lineare
 5.1 Controllo d un sstema non lneare Sa dato l sstema non lneare rappresentato n fgura 5.1, con h g θ Θ,m,r Fgura 5.1: Sstema non lneare F m (,d) = k m la forza che esercta l elettromagnete percorso da
5.1 Controllo d un sstema non lneare Sa dato l sstema non lneare rappresentato n fgura 5.1, con h g θ Θ,m,r Fgura 5.1: Sstema non lneare F m (,d) = k m la forza che esercta l elettromagnete percorso da
Stabilità dei Sistemi Dinamici. Stabilità Semplice. Stabilità Asintotica. Stabilità: concetto intuitivo che può essere formalizzato in molti modi
 Gustavo Belforte Stabltà de Sstem Dnamc Gustavo Belforte Stabltà de Sstem Dnamc Stabltà de Sstem Dnamc Il Pendolo Stabltà: concetto ntutvo che può essere formalzzato n molt mod Intutvamente: Un oggetto
Gustavo Belforte Stabltà de Sstem Dnamc Gustavo Belforte Stabltà de Sstem Dnamc Stabltà de Sstem Dnamc Il Pendolo Stabltà: concetto ntutvo che può essere formalzzato n molt mod Intutvamente: Un oggetto
Calcolo Scientifico e Matematica Applicata Scritto Generale, , Ingegneria Meccanica
 Calcolo Scientifico e Matematica Applicata Scritto Generale, 17.12.2018, Ingegneria Meccanica Valutazione degli esercizi: 1 4, 2 10, 3 8, 4 8 1. Risolvere, con il metodo degli integrali generali, il seguente
Calcolo Scientifico e Matematica Applicata Scritto Generale, 17.12.2018, Ingegneria Meccanica Valutazione degli esercizi: 1 4, 2 10, 3 8, 4 8 1. Risolvere, con il metodo degli integrali generali, il seguente
Verifica reti con più serbatoi (II)
 Verfca ret con pù serbato (I) Condzon al contorno per gl N nod della rete e corrspondent ncognte: Condzone mposta Incognta A) carco pezometrco portata concentrata B) portata concentrata carco pezometrco
Verfca ret con pù serbato (I) Condzon al contorno per gl N nod della rete e corrspondent ncognte: Condzone mposta Incognta A) carco pezometrco portata concentrata B) portata concentrata carco pezometrco
Teoremi dei circuiti
 Teorem de crcut www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del --04) Teorema d Tellegen potes: Crcuto con n nod e l lat ers d rfermento scelt per tutt lat secondo la conenzone dell utlzzatore {,...,
Teorem de crcut www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del --04) Teorema d Tellegen potes: Crcuto con n nod e l lat ers d rfermento scelt per tutt lat secondo la conenzone dell utlzzatore {,...,
Ingegneria Elettrica Politecnico di Torino. Luca Carlone. ControlliAutomaticiI LEZIONE III
 Ingegnera Elettrca Poltecnco d Torno Luca Carlone ControllAutomatcI LEZIONE III Sommaro LEZIONE III Trasformata d Laplace Propretà e trasformate notevol Funzon d trasfermento Scomposzone n fratt semplc
Ingegnera Elettrca Poltecnco d Torno Luca Carlone ControllAutomatcI LEZIONE III Sommaro LEZIONE III Trasformata d Laplace Propretà e trasformate notevol Funzon d trasfermento Scomposzone n fratt semplc
Metodi iterativi per sistemi di equazioni lineari algebriche
 Captolo 17 Metod teratv per sstem d equazon lnear algebrche 171 Generaltà su metod teratv S fornsce la defnzone d convergnza per vettor e matrc Convergenza d vettor Una successone d vettor d n component
Captolo 17 Metod teratv per sstem d equazon lnear algebrche 171 Generaltà su metod teratv S fornsce la defnzone d convergnza per vettor e matrc Convergenza d vettor Una successone d vettor d n component
Appunti: Scomposizione in fratti semplici ed antitrasformazione
 Appunt: Scomposzone n fratt semplc ed anttrasformazone Gulo Cazzol v0. (AA. 017-018) 1 Fratt semplc 1.1 Funzone ntera.............................................. 1. Funzone razonale fratta strettamente
Appunt: Scomposzone n fratt semplc ed anttrasformazone Gulo Cazzol v0. (AA. 017-018) 1 Fratt semplc 1.1 Funzone ntera.............................................. 1. Funzone razonale fratta strettamente
2.1 Parabola nella forma canonica
 5 Clc per tutt gl appunt (AUTOMAZIONE TRATTAMENTI TERMICI ACCIAIO SCIENZA delle COSTRUZIONI ) e-mal per suggerment. Paraola nella forma canonca Studamo con metod general la conca nella espressone canonca
5 Clc per tutt gl appunt (AUTOMAZIONE TRATTAMENTI TERMICI ACCIAIO SCIENZA delle COSTRUZIONI ) e-mal per suggerment. Paraola nella forma canonca Studamo con metod general la conca nella espressone canonca
Analisi Modale. Le evoluzioni libere dei due sistemi a partire dalla condizione iniziale x(0) = x 0 sono
 Captolo 1 INTRODUZIONE 21 Anals Modale S facca rfermento al sstema tempo-dscreto e al sstema tempo-contnuo x(k +1)=Ax(k) ẋ(t) =Ax(t) Le evoluzon lbere de due sstem a partre dalla condzone nzale x() = x
Captolo 1 INTRODUZIONE 21 Anals Modale S facca rfermento al sstema tempo-dscreto e al sstema tempo-contnuo x(k +1)=Ax(k) ẋ(t) =Ax(t) Le evoluzon lbere de due sstem a partre dalla condzone nzale x() = x
1 Le equazioni per le variabili macroscopiche: i momenti dell equazione di Boltzmann
 FISICA DEI FLUIDI Lezone 5-5 Maggo 202 Le equazon per le varabl macroscopche: moment dell equazone d Boltzmann Teorema H a parte, non è facle estrarre altre consderazon general sulla funzone denstà d probabltà
FISICA DEI FLUIDI Lezone 5-5 Maggo 202 Le equazon per le varabl macroscopche: moment dell equazone d Boltzmann Teorema H a parte, non è facle estrarre altre consderazon general sulla funzone denstà d probabltà
Elettronica dello Stato Solido Esercitazione di Laboratorio 1: Soluzione numerica dell equazione
 Elettronca dello Stato Soldo Eserctazone d Laboratoro 1: Soluzone nuerca dell equazone d Scrödnger 1D Danele Ieln DEI Poltecnco d Mlano eln@elet.pol.t Contenut del Laboratoro Costruzone d un etodo nuercoper
Elettronca dello Stato Soldo Eserctazone d Laboratoro 1: Soluzone nuerca dell equazone d Scrödnger 1D Danele Ieln DEI Poltecnco d Mlano eln@elet.pol.t Contenut del Laboratoro Costruzone d un etodo nuercoper
Corso di. Gasdinamica II Tommaso Astarita
 Corso d Gasdnamca II Tommaso Astarta astarta@unna.t www.docent.unna.t Gasdnamca II Tommaso Astarta 5.0.008 Metodo d Eulero S supponga d avere una equazone dfferenzale del prmo ordne: f ( x, ) x xo o Defnendo
Corso d Gasdnamca II Tommaso Astarta astarta@unna.t www.docent.unna.t Gasdnamca II Tommaso Astarta 5.0.008 Metodo d Eulero S supponga d avere una equazone dfferenzale del prmo ordne: f ( x, ) x xo o Defnendo
6 Prodotti scalari e prodotti Hermitiani
 6 Prodott scalar e prodott Hermtan 6.1 Prodott scalar S fss K = R. Defnzone 6.1 Sa V un R-spazo vettorale. Un prodotto scalare su V è un applcazone che gode delle seguent propretà: ) (lneartà rspetto al
6 Prodott scalar e prodott Hermtan 6.1 Prodott scalar S fss K = R. Defnzone 6.1 Sa V un R-spazo vettorale. Un prodotto scalare su V è un applcazone che gode delle seguent propretà: ) (lneartà rspetto al
Teoremi dei circuiti
 Teorem de crcut www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del 0-0-03) Teorema d Tellegen Ipotes: Crcuto con n nod e l lat ers d rfermento scelt per tutt lat secondo la conenzone dell utlzzatore {,...,
Teorem de crcut www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del 0-0-03) Teorema d Tellegen Ipotes: Crcuto con n nod e l lat ers d rfermento scelt per tutt lat secondo la conenzone dell utlzzatore {,...,
Generalità. Problema: soluzione di una equazione differenziale alle derivate ordinarie di ordine n: ( )
 Generaltà Problema: soluzone d una equazone derenzale alle dervate ordnare d ordne n: n n K soggetta alle n condzon nzal: K n Ovvero rcercare la soluzone d un sstema d n equazon derenzal ordnare del prmo
Generaltà Problema: soluzone d una equazone derenzale alle dervate ordnare d ordne n: n n K soggetta alle n condzon nzal: K n Ovvero rcercare la soluzone d un sstema d n equazon derenzal ordnare del prmo
Esercizi sulle reti elettriche in corrente continua (parte 2)
 Esercz sulle ret elettrche n corrente contnua (parte ) Eserczo 3: etermnare gl equvalent d Thevenn e d Norton del bpolo complementare al resstore R 5 nel crcuto n fgura e calcolare la corrente che crcola
Esercz sulle ret elettrche n corrente contnua (parte ) Eserczo 3: etermnare gl equvalent d Thevenn e d Norton del bpolo complementare al resstore R 5 nel crcuto n fgura e calcolare la corrente che crcola
di una delle versioni del compito di Geometria analitica e algebra lineare del 12 luglio 2013 distanza tra r ed r'. (punti 2 + 3)
 Esempo d soluzone d una delle verson del compto d Geometra analtca e algebra lneare del luglo 3 Stablre se la retta r, d equazon parametrche x =, y = + t, z = t (nel parametro reale t), è + y + z = sghemba
Esempo d soluzone d una delle verson del compto d Geometra analtca e algebra lneare del luglo 3 Stablre se la retta r, d equazon parametrche x =, y = + t, z = t (nel parametro reale t), è + y + z = sghemba
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO
 PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa lezione 2: 21 febbraio 2013
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 2: 21 febbrao 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/25? Defnzone. f : R R s dce addtva se per ogn
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 2: 21 febbrao 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/25? Defnzone. f : R R s dce addtva se per ogn
3 = 3 Ω. quindi se v g = 24 V, i = 1,89 A Dobbiamo studiare tre circuiti; in tutti e tre i casi si ottiene un partitore di corrente.
 5. Per la propretà d lneartà la tensone può essere espressa come = k g, doe g è la corrente del generatore. Utlzzando dat n Fgura a abbamo - = k 6, qund k = - ½. In Fgura b la corrente del generatore è
5. Per la propretà d lneartà la tensone può essere espressa come = k g, doe g è la corrente del generatore. Utlzzando dat n Fgura a abbamo - = k 6, qund k = - ½. In Fgura b la corrente del generatore è
Risoluzione numerica di problemi differenziali alle derivate parziali
 Rsolzone nmerca d problem dfferenzal alle dervate parzal Rsolzone nmerca d PDE Dscretzzazone Sosttre al problema contno n problema dscreto Qal è l problema contno? Rsolzone nmerca d PDE Il problema contno:
Rsolzone nmerca d problem dfferenzal alle dervate parzal Rsolzone nmerca d PDE Dscretzzazone Sosttre al problema contno n problema dscreto Qal è l problema contno? Rsolzone nmerca d PDE Il problema contno:
Principi di ingegneria elettrica. Lezione 6 a. Analisi delle reti resistive
 Prncp d ngegnera elettrca Lezone 6 a Anals delle ret resste Anals delle ret resste L anals d una rete elettrca (rsoluzone della rete) consste nel determnare tutte le corrent ncognte ne ram e tutt potenzal
Prncp d ngegnera elettrca Lezone 6 a Anals delle ret resste Anals delle ret resste L anals d una rete elettrca (rsoluzone della rete) consste nel determnare tutte le corrent ncognte ne ram e tutt potenzal
Corso di Elettrotecnica
 Unerstà degl Stud d Paa Facoltà d Ingegnera orso d orso d Elettrotecnca Teora de rcut rcut elettrc n funzonamento perturbato rcut elettrc n funzonamento perturbato I IRUITI OMPRENONO: Sorgent nterne d
Unerstà degl Stud d Paa Facoltà d Ingegnera orso d orso d Elettrotecnca Teora de rcut rcut elettrc n funzonamento perturbato rcut elettrc n funzonamento perturbato I IRUITI OMPRENONO: Sorgent nterne d
Support Vector Machines. Macchine a vettori di supporto
 Support Vector Machnes Macchne a vettor d supporto Separator Lnear Percettrone La classfcazone bnara può essere vsta come un problema d separazone d class nello spazo delle feature m b b b > 0 b 0 b
Support Vector Machnes Macchne a vettor d supporto Separator Lnear Percettrone La classfcazone bnara può essere vsta come un problema d separazone d class nello spazo delle feature m b b b > 0 b 0 b
POLINOMIO MINIMO E FORMA CANONICA DI JORDAN NOTA AGGIUNTIVA PER IL CORSO DI GEOMETRIA ANALITICA E ALGEBRA LINEARE A.A DOCENTE: PAOLO LISCA
 POLINOMIO MINIMO E FORMA CANONICA DI JORDAN NOTA AGGIUNTIVA PER IL CORSO DI GEOMETRIA ANALITICA E ALGEBRA LINEARE AA 2009-2010 DOCENTE: PAOLO LISCA 1 Polnomo mnmo Avvertenza: con V ndcheremo uno spazo
POLINOMIO MINIMO E FORMA CANONICA DI JORDAN NOTA AGGIUNTIVA PER IL CORSO DI GEOMETRIA ANALITICA E ALGEBRA LINEARE AA 2009-2010 DOCENTE: PAOLO LISCA 1 Polnomo mnmo Avvertenza: con V ndcheremo uno spazo
Il logaritmo discreto in Z p Il gruppo moltiplicativo Z p delle classi resto modulo un primo p è un gruppo ciclico.
 Il logartmo dscreto n Z p Il gruppo moltplcatvo Z p delle class resto modulo un prmo p è un gruppo cclco. Defnzone (Logartmo dscreto). Sa p un numero prmo e sa ā una radce prmtva n Z p. Sa ȳ Z p. Il logartmo
Il logartmo dscreto n Z p Il gruppo moltplcatvo Z p delle class resto modulo un prmo p è un gruppo cclco. Defnzone (Logartmo dscreto). Sa p un numero prmo e sa ā una radce prmtva n Z p. Sa ȳ Z p. Il logartmo
Fondamenti di Fisica Matematica: Secondo parziale Cognome e nome:...matricola:... es.1 es.2 es.3 es.4 es.5 somma
 Fondamenti di Fisica Matematica: Secondo parziale 6..03 Cognome e nome:....................................matricola:......... es. es. es.3 es.4 es.5 somma 7 7 0 6 6 30 Voto: es.+es.+es.3+max(es.4,es.5).
Fondamenti di Fisica Matematica: Secondo parziale 6..03 Cognome e nome:....................................matricola:......... es. es. es.3 es.4 es.5 somma 7 7 0 6 6 30 Voto: es.+es.+es.3+max(es.4,es.5).
Predimensionamento reti chiuse
 Predmensonamento ret chuse Rspetto ad una rete aperta, ogn magla aggunge un grado d lbertà (una nfntà d soluzon) nella determnazone delle portate Q,Q 1, e Q 2, utlzzando le sole equazon d contnutà. La
Predmensonamento ret chuse Rspetto ad una rete aperta, ogn magla aggunge un grado d lbertà (una nfntà d soluzon) nella determnazone delle portate Q,Q 1, e Q 2, utlzzando le sole equazon d contnutà. La
Macchine. 5 Esercitazione 5
 ESERCITAZIONE 5 Lavoro nterno d una turbomacchna. Il lavoro nterno massco d una turbomacchna può essere determnato not trangol d veloctà che s realzzano all'ngresso e all'uscta della macchna stessa. Infatt
ESERCITAZIONE 5 Lavoro nterno d una turbomacchna. Il lavoro nterno massco d una turbomacchna può essere determnato not trangol d veloctà che s realzzano all'ngresso e all'uscta della macchna stessa. Infatt
Predimensionamento reti chiuse
 Predmensonamento ret chuse Rspetto ad una rete aperta, ogn magla aggunge un grado d lbertà (una nfntà d soluzon) nella determnazone delle portate Q,Q 1, e Q 2, utlzzando le sole equazon d contnutà. a dfferenza
Predmensonamento ret chuse Rspetto ad una rete aperta, ogn magla aggunge un grado d lbertà (una nfntà d soluzon) nella determnazone delle portate Q,Q 1, e Q 2, utlzzando le sole equazon d contnutà. a dfferenza
Analisi Matematica Lezione 16 3 novembre 2014 Limiti di funzioni
 Dpartmento d Scenze Statstche Anals Matematca Lezone 6 3 novembre 204 Lmt d funzon prof. Danele Rtell danele.rtell@unbo.t /7? Eserczo 9 Determnare l ordne d nfntesmo e la parte prncpale dell nfntesmo rspetto
Dpartmento d Scenze Statstche Anals Matematca Lezone 6 3 novembre 204 Lmt d funzon prof. Danele Rtell danele.rtell@unbo.t /7? Eserczo 9 Determnare l ordne d nfntesmo e la parte prncpale dell nfntesmo rspetto
Esercitazione sulle Basi di di Definizione
 Eserctazone sulle as d d Defnzone ESERIZIO Un bpolo ressto (dodo) ha la seguente equazone: = k [ 0 + 00] con k 0 nella quale ed sono descrtt dalla conenzone degl utlzzator come n fgura. Stablre se l bpolo
Eserctazone sulle as d d Defnzone ESERIZIO Un bpolo ressto (dodo) ha la seguente equazone: = k [ 0 + 00] con k 0 nella quale ed sono descrtt dalla conenzone degl utlzzator come n fgura. Stablre se l bpolo
METODO DEGLI ELEMENTI FINITI
 METODO DEGLI ELEMENTI FINITI Introduzone al metodo degl element fnt Il concetto base nella nterpretazone fsca del metodo degl element fnt è la decomposzone d un sstema meccanco complesso n pù semplc component
METODO DEGLI ELEMENTI FINITI Introduzone al metodo degl element fnt Il concetto base nella nterpretazone fsca del metodo degl element fnt è la decomposzone d un sstema meccanco complesso n pù semplc component
I Appello di Calcolo delle Probabilità Cognome: Laurea Triennale in Matematica 2014/15 Nome: 29 gennaio
 I Appello d Calcolo delle Probabltà Cognome: Laurea Trennale n Matematca 24/5 Nome: 29 gennao 25 Emal: Se non è espressamente ndcato l contraro, per la soluzone degl esercz è possble usare tutt rsultat
I Appello d Calcolo delle Probabltà Cognome: Laurea Trennale n Matematca 24/5 Nome: 29 gennao 25 Emal: Se non è espressamente ndcato l contraro, per la soluzone degl esercz è possble usare tutt rsultat
Gestione della produzione e della supply chain Logistica distributiva. Paolo Detti Dipartimento di Ingegneria dell Informazione Università di Siena
 Gestone della produzone e della supply chan Logstca dstrbutva Paolo Dett Dpartmento d Ingegnera dell Informazone Unverstà d Sena Un algortmo per l flusso su ret a costo mnmo: l smplesso su ret Convergenza
Gestone della produzone e della supply chan Logstca dstrbutva Paolo Dett Dpartmento d Ingegnera dell Informazone Unverstà d Sena Un algortmo per l flusso su ret a costo mnmo: l smplesso su ret Convergenza
VII esercitazione. Corso di Laurea in Informatica Calcolo Scientifico II a.a. 07/08
 VII eserctazone Una fattorzzazone che rvela propretà della matrce: La Sngular value decomposton (SVD) fattorzza una matrce rettangolare reale o complessa è utlzzata nelle applcazon: nella trasmssone d
VII eserctazone Una fattorzzazone che rvela propretà della matrce: La Sngular value decomposton (SVD) fattorzza una matrce rettangolare reale o complessa è utlzzata nelle applcazon: nella trasmssone d
Lezione n. 10. Legge di Raoult Legge di Henry Soluzioni ideali Deviazioni dall idealit. idealità Convenzioni per le soluzioni reali
 Chmca Fsca - Chmca e Tecnologa Farmaceutche Lezone n. 10 Legge d Raoult Legge d Henry Soluzon deal Devazon dall dealt dealtà Convenzon per le soluzon real Relazon tra coeffcent d attvtà 02/03/2008 Antonno
Chmca Fsca - Chmca e Tecnologa Farmaceutche Lezone n. 10 Legge d Raoult Legge d Henry Soluzon deal Devazon dall dealt dealtà Convenzon per le soluzon real Relazon tra coeffcent d attvtà 02/03/2008 Antonno
Elettrotecnica - Modulo 1 - Ing. Biomedica, Ing. Elettronica per l Energia e l Informazione A.A. 2017/18 - Prova n luglio 2018.
 ognome Nome Matrcola Frma 1 Part svolte: E1 E E3 D Eserczo 1 A G7 6 B V G6 T V 1 D V 5 g11 0 G g1 g Supponendo not parametr de component e della matrce d conduttanza del trpolo T, llustrare l procedmento
ognome Nome Matrcola Frma 1 Part svolte: E1 E E3 D Eserczo 1 A G7 6 B V G6 T V 1 D V 5 g11 0 G g1 g Supponendo not parametr de component e della matrce d conduttanza del trpolo T, llustrare l procedmento
Elasticità nei mezzi continui
 Elastctà ne mezz contnu l tensore degl sforz o tensore d stress, σ j Consderamo un cubo d dmenson untare n un mezzo elastco deformato. l cubo è deformato dalle forze eserctate sulle sue facce dal resto
Elastctà ne mezz contnu l tensore degl sforz o tensore d stress, σ j Consderamo un cubo d dmenson untare n un mezzo elastco deformato. l cubo è deformato dalle forze eserctate sulle sue facce dal resto
Dipartimento di Statistica Università di Bologna. Matematica Finanziaria aa lezione 3:
 Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 3: 21022012 professor Danele Rtell www.unbo.t/docdent/danele.rtell 1/31? Captalzzazone msta S usa l regme composto per l
Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 3: 21022012 professor Danele Rtell www.unbo.t/docdent/danele.rtell 1/31? Captalzzazone msta S usa l regme composto per l
Dipartimento di Statistica Università di Bologna. Matematica Finanziaria aa lezione 21: 29 maggio 2013
 Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 21: 29 maggo 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/35? Eserczo Dmostrare che l portafoglo d mnmo rscho
Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 21: 29 maggo 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/35? Eserczo Dmostrare che l portafoglo d mnmo rscho
Analisi Numerica I, a.a Docente: M.Gaviano
 Eserctazone n.1 Anals Numerca I, a.a. 2004-2005 Medante MatLab 1) Costrusc le seguent matrc 0.9501 0.8913 0.2311 0.7621 0.6068 0.4565 0.4860 0.0185 0.8214 0.4447 0.6154 0.7919 0.9218 0.7382 0.1763 0.4057
Eserctazone n.1 Anals Numerca I, a.a. 2004-2005 Medante MatLab 1) Costrusc le seguent matrc 0.9501 0.8913 0.2311 0.7621 0.6068 0.4565 0.4860 0.0185 0.8214 0.4447 0.6154 0.7919 0.9218 0.7382 0.1763 0.4057
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa lezione 2: 18 febbraio 2014
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2013-2014 lezone 2: 18 febbrao 2014 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/19? Defnzone. f : R R s dce moltplcatva se per
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2013-2014 lezone 2: 18 febbrao 2014 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/19? Defnzone. f : R R s dce moltplcatva se per
Risposta in frequenza
 Rsposta n frequenza www.de.ng.unbo.t/pers/mastr/ddattca.htm (versone del 6--6 Dagramm d Bode Le funzon d trasfermento (f.d.t de crcut lnear tempo nvarant sono funzon razonal (coè rapport tra due polnom
Rsposta n frequenza www.de.ng.unbo.t/pers/mastr/ddattca.htm (versone del 6--6 Dagramm d Bode Le funzon d trasfermento (f.d.t de crcut lnear tempo nvarant sono funzon razonal (coè rapport tra due polnom
Dipartimento di Matematica per le scienze economiche e sociali Università di Bologna. Modelli 1 lezione novembre 2011 Media e varianza
 Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Modell 1 lezone 17 30 novembre 2011 Meda e varanza professor Danele Rtell www.unbo.t/docent/danele.rtell 1/23? Teorema er ogn funzone
Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Modell 1 lezone 17 30 novembre 2011 Meda e varanza professor Danele Rtell www.unbo.t/docent/danele.rtell 1/23? Teorema er ogn funzone
B - ESERCIZI: IP e TCP:
 Unverstà d Bergamo Dpartmento d Ingegnera dell Informazone e Metod Matematc B - ESERCIZI: IP e TCP: F. Martgnon Archtetture e Protocoll per Internet Eserczo b. S consder l collegamento n fgura A C =8 kbt/s
Unverstà d Bergamo Dpartmento d Ingegnera dell Informazone e Metod Matematc B - ESERCIZI: IP e TCP: F. Martgnon Archtetture e Protocoll per Internet Eserczo b. S consder l collegamento n fgura A C =8 kbt/s
Soluzioni 3.1. n(n 1) (n k + 1) z n k! k + 1 n k. lim k
 (1) La sere bnomale è B n (z) = k=0 Con l metodo del rapporto s ottene R = lm k Soluzon 3.1 n(n 1) (n k + 1) z n k! c k c k+1 = lm k k + 1 n k lm k c k z k. k=0 1 + 1 k 1 n k = 1 (2) La multfunzone f(z)
(1) La sere bnomale è B n (z) = k=0 Con l metodo del rapporto s ottene R = lm k Soluzon 3.1 n(n 1) (n k + 1) z n k! c k c k+1 = lm k k + 1 n k lm k c k z k. k=0 1 + 1 k 1 n k = 1 (2) La multfunzone f(z)
V n. =, e se esiste, il lim An
 Parttore resstvo con nfnte squadre n cascata. ITIS Archmede CT La Fg. rappresenta un parttore resstvo, formato da squadre d restor tutt ugual ad, conness n cascata, e l cu numero n s fa tendere ad nfnto.
Parttore resstvo con nfnte squadre n cascata. ITIS Archmede CT La Fg. rappresenta un parttore resstvo, formato da squadre d restor tutt ugual ad, conness n cascata, e l cu numero n s fa tendere ad nfnto.
Intorduzione alla teoria delle Catene di Markov
 Intorduzone alla teora delle Catene d Markov Mchele Ganfelce a.a. 2014/2015 Defnzone 1 Sa ( Ω, F, {F n } n 0, P uno spazo d probabltà fltrato. Una successone d v.a. {ξ n } n 0 defnta su ( Ω, F, {F n }
Intorduzone alla teora delle Catene d Markov Mchele Ganfelce a.a. 2014/2015 Defnzone 1 Sa ( Ω, F, {F n } n 0, P uno spazo d probabltà fltrato. Una successone d v.a. {ξ n } n 0 defnta su ( Ω, F, {F n }
ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, A.A. 2003/04, GEMMA PARMEGGIANI
 ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, A.A. 3/4, GEMMA PARMEGGIANI Unverstà degl Stud d Padova Dpartmento d Matematca Pura e Applcata va Belzon, 7 353 Padova. Programma. Esercz tpo svolt 3. Eserctazon
ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, A.A. 3/4, GEMMA PARMEGGIANI Unverstà degl Stud d Padova Dpartmento d Matematca Pura e Applcata va Belzon, 7 353 Padova. Programma. Esercz tpo svolt 3. Eserctazon
INDICE. Scaricabile su: Derivate TEORIA. Derivata in un punto. Significato geometrico della derivata
 P r o f Gu d of r a n c n Anteprma Anteprma Anteprma www l e z o n j md o c o m Scarcable su: ttp://lezonjmdocom/ INDICE TEORIA Dervata n un punto Sgnfcato geometrco della dervata Funzone dervata e dervate
P r o f Gu d of r a n c n Anteprma Anteprma Anteprma www l e z o n j md o c o m Scarcable su: ttp://lezonjmdocom/ INDICE TEORIA Dervata n un punto Sgnfcato geometrco della dervata Funzone dervata e dervate
Esercizio 1. Esercitazione 14 Dicembre 2012 Sistemi trifase e potenze R 3 R 1 R 2. simmetrico L 1 L 3
 serctazone 4 Dcembre 0 Sstem trfase e potenze serczo L L L 00 f 50 Hz smmetrco Fg : Sstema trfase a stella S consder l crcuto d Fg e s calcolno le tre corrent d fase e le potenze attve, reattve ed apparent
serctazone 4 Dcembre 0 Sstem trfase e potenze serczo L L L 00 f 50 Hz smmetrco Fg : Sstema trfase a stella S consder l crcuto d Fg e s calcolno le tre corrent d fase e le potenze attve, reattve ed apparent
La sincronizzazione. (Libro) Trasmissione dell Informazione
 La sncronzzazone (Lbro) Problem d sncronzzazone La trasmssone e la dverstà tra gl OL del trasmetttore e del rcevtore ntroducono (anche n assenza d fadng) un errore d d frequenza, d fase e d camponamento
La sncronzzazone (Lbro) Problem d sncronzzazone La trasmssone e la dverstà tra gl OL del trasmetttore e del rcevtore ntroducono (anche n assenza d fadng) un errore d d frequenza, d fase e d camponamento
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa Lezione 4: Martedì 24/2/2015
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2014-2015 Lezone 4: Martedì 24/2/2015 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/31? Attualzzazone I fattor d attualzzazone conugat
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2014-2015 Lezone 4: Martedì 24/2/2015 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/31? Attualzzazone I fattor d attualzzazone conugat
Approssimazione minimax
 Approssmazone mnmax 1 Il problema dell approssmazone lneare Data una f(x) appartenente allo spazo vettorale F delle funzon real d varable reale, s scegle n F un modello, coè un nseme d funzon φ (x), =
Approssmazone mnmax 1 Il problema dell approssmazone lneare Data una f(x) appartenente allo spazo vettorale F delle funzon real d varable reale, s scegle n F un modello, coè un nseme d funzon φ (x), =
Introduzione e modellistica dei sistemi
 Introduzone e modellstca de sstem Element fondamental Rappresentazone n arabl d stato Esemp d rappresentazone n arabl d stato 007 Poltecnco d Torno Resstore deale Resstore deale d resstenza R R R equazone
Introduzone e modellstca de sstem Element fondamental Rappresentazone n arabl d stato Esemp d rappresentazone n arabl d stato 007 Poltecnco d Torno Resstore deale Resstore deale d resstenza R R R equazone
6. METODO DELLE FORZE IMPOSTAZIONE GENERALE
 aptolo6 ETODO DEE FORZE - IOSTZIOE GEERE 6. ETODO DEE FORZE IOSTZIOE GEERE ssocamo al sstema perstatco un altro sstema, denomnato sstema prncpale. Il sstema prncpale è un sstema statcamente determnato,
aptolo6 ETODO DEE FORZE - IOSTZIOE GEERE 6. ETODO DEE FORZE IOSTZIOE GEERE ssocamo al sstema perstatco un altro sstema, denomnato sstema prncpale. Il sstema prncpale è un sstema statcamente determnato,
Metodi ad un passo espliciti con passo adattivo Metodi Runge - Kutta
 Metod ad un passo esplct con passo adattvo Metod Runge - Kutta Scrvere un programma che approssm l problema d Cauchy: u (t) = f(t, u), t 0 t T, u R d, u(t 0 ) = v per un sstema d equazon dfferenzal ordnare
Metod ad un passo esplct con passo adattvo Metod Runge - Kutta Scrvere un programma che approssm l problema d Cauchy: u (t) = f(t, u), t 0 t T, u R d, u(t 0 ) = v per un sstema d equazon dfferenzal ordnare
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa lezione 9: 3 marzo 2014
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2013-2014 lezone 9: 3 marzo 2014 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/25? Eserczo Consderamo una rendta perodca d 2n termn
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2013-2014 lezone 9: 3 marzo 2014 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/25? Eserczo Consderamo una rendta perodca d 2n termn
urto v 2f v 2i e forza impulsiva F r F dt = i t
 7. Urt Sstem a due partcelle Defnzone d urto elastco, urto anelastco e mpulso L urto è un nterazone fra corp che avvene n un ntervallo d tempo normalmente molto breve, al termne del quale le quanttà d
7. Urt Sstem a due partcelle Defnzone d urto elastco, urto anelastco e mpulso L urto è un nterazone fra corp che avvene n un ntervallo d tempo normalmente molto breve, al termne del quale le quanttà d
Matematica Computazionale(6cfu) Ottimizzazione(8cfu)
 Docente: Marco Gavano (e-mal:gavano@unca.t) Corso d Laurea n Infomatca Corso d Laurea n Matematca Matematca Computazonale(6cfu) Ottmzzazone(8cfu) (a.a. 205-6, lez.8) Matematca Computazonale, Ottmzzazone,
Docente: Marco Gavano (e-mal:gavano@unca.t) Corso d Laurea n Infomatca Corso d Laurea n Matematca Matematca Computazonale(6cfu) Ottmzzazone(8cfu) (a.a. 205-6, lez.8) Matematca Computazonale, Ottmzzazone,
La teoria del consumo
 La teora del consumo L equazone d Slutsky. Problema dell ntegrabltà. Maro Sortell Dartmento d Matematca Unverstà degl Stud d Bar Va E. Orabona, 4 I-70125 Bar (Italy) (Tel.: +39 (0)99 7720 626; fax: +39
La teora del consumo L equazone d Slutsky. Problema dell ntegrabltà. Maro Sortell Dartmento d Matematca Unverstà degl Stud d Bar Va E. Orabona, 4 I-70125 Bar (Italy) (Tel.: +39 (0)99 7720 626; fax: +39
Dipartimento di Matematica per le scienze economiche e sociali Università di Bologna. Matematica aa lezione 18
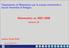 Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2007-2008 lezone 18 professor Danele Rtell danele.rtell@unbo.t 1/11? Questo esempo nteressa la gestone delle scorte.
Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2007-2008 lezone 18 professor Danele Rtell danele.rtell@unbo.t 1/11? Questo esempo nteressa la gestone delle scorte.
Tangenti a una conica: il metodo del Doppio sdoppiamento 1
 Tangent a una conca: l metodo del Doppo sdoppamento 1 Franco Goacchno Sunto Ecco un metodo alternatvo per determnare le tangent a una conca da un qualsas punto del pano. Esso consste nell applcare volte
Tangent a una conca: l metodo del Doppo sdoppamento 1 Franco Goacchno Sunto Ecco un metodo alternatvo per determnare le tangent a una conca da un qualsas punto del pano. Esso consste nell applcare volte
Dipartimento di Statistica Università di Bologna. Matematica Finanziaria aa lezione 7: 6 marzo 2012
 Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 7: 6 marzo 2012 professor Danele Rtell www.unbo.t/docdent/danele.rtell 1/29? Defnzone Se è un prestto se m {1, 2,..., n}
Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 7: 6 marzo 2012 professor Danele Rtell www.unbo.t/docdent/danele.rtell 1/29? Defnzone Se è un prestto se m {1, 2,..., n}
6. Catene di Markov a tempo continuo (CMTC)
 6. Catene d Markov a tempo contnuo (CMTC) Defnzone Una CMTC è un processo stocastco defnto come segue: lo spazo d stato è dscreto: X{x,x 2, }. L nseme X può essere sa fnto sa nfnto numerable. L nseme de
6. Catene d Markov a tempo contnuo (CMTC) Defnzone Una CMTC è un processo stocastco defnto come segue: lo spazo d stato è dscreto: X{x,x 2, }. L nseme X può essere sa fnto sa nfnto numerable. L nseme de
3 Partizioni dell unità 6
 Partzon dell untà Alessandro Ghg 29 ottobre 2014 Indce 1 Funzon lsce a supporto compatto 1 2 Rcoprment localmente fnt 5 3 Partzon dell untà 6 1 Funzon lsce a supporto compatto Lemma 1. Sano f C 1 (a, b)
Partzon dell untà Alessandro Ghg 29 ottobre 2014 Indce 1 Funzon lsce a supporto compatto 1 2 Rcoprment localmente fnt 5 3 Partzon dell untà 6 1 Funzon lsce a supporto compatto Lemma 1. Sano f C 1 (a, b)
Dipartimento di Matematica per le scienze economiche e sociali Università di Bologna. Matematica aa lezione marzo 2009
 Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2008-2009 lezone 25 17 marzo 2009 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/26? Convesstà Sa I un ntervallo
Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2008-2009 lezone 25 17 marzo 2009 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/26? Convesstà Sa I un ntervallo
Teorema di Thévenin-Norton
 87 Teorema d Téenn-Norton E detto ance teorema d rappresentazone del bpolo, consente nfatt d rappresentare una rete lneare a due morsett (A, B) con: un generatore d tensone ed un resstore sere (Téenn)
87 Teorema d Téenn-Norton E detto ance teorema d rappresentazone del bpolo, consente nfatt d rappresentare una rete lneare a due morsett (A, B) con: un generatore d tensone ed un resstore sere (Téenn)
6.1- Sistemi punti, forze interne ed esterne
 1 CAP 6 - SISTEMI DI PUNTI MATERIALI Parte I 1 Cap 6 - Sstem d punt materal Cap 6 - Sstem d punt materal Il punto materale è un astrazone alla quale poch cas s possono assmlare. La maggor parte degl oggett
1 CAP 6 - SISTEMI DI PUNTI MATERIALI Parte I 1 Cap 6 - Sstem d punt materal Cap 6 - Sstem d punt materal Il punto materale è un astrazone alla quale poch cas s possono assmlare. La maggor parte degl oggett
y x x 20 e gli assi delle ascisse e delle ordinate. Tracce assegnate durante l anno scolastico
 Tracce assegnate durante l anno scolastco. Dsegna nel pano cartesano la retta d equazone, dopo averla scrtta n orma esplcta. Stablsc, sa gracamente ce analtcamente, se l B ; 3 appartene alla retta. punto.
Tracce assegnate durante l anno scolastco. Dsegna nel pano cartesano la retta d equazone, dopo averla scrtta n orma esplcta. Stablsc, sa gracamente ce analtcamente, se l B ; 3 appartene alla retta. punto.
Rappresentazione dei numeri PH. 3.1, 3.2, 3.3
 Rappresentazone de numer PH. 3.1, 3.2, 3.3 1 Tp d numer Numer nter, senza segno calcolo degl ndrzz numer che possono essere solo non negatv Numer con segno postv negatv Numer n vrgola moble calcol numerc
Rappresentazone de numer PH. 3.1, 3.2, 3.3 1 Tp d numer Numer nter, senza segno calcolo degl ndrzz numer che possono essere solo non negatv Numer con segno postv negatv Numer n vrgola moble calcol numerc
* PROBABILITÀ - SCHEDA N. 2 LE VARIABILI ALEATORIE *
 * PROBABILITÀ - SCHEDA N. LE VARIABILI ALEATORIE *. Le varabl aleatore Nella scheda precedente abbamo defnto lo spazo camponaro come la totaltà degl est possbl d un espermento casuale; abbamo vsto che
* PROBABILITÀ - SCHEDA N. LE VARIABILI ALEATORIE *. Le varabl aleatore Nella scheda precedente abbamo defnto lo spazo camponaro come la totaltà degl est possbl d un espermento casuale; abbamo vsto che
Fisica Generale LA N.1 Prova Scritta del 12 Febbraio 2018 Prof. Nicola Semprini Cesari
 Fsca Generale A N. Prova Scrtta del Febbrao 8 Prof. Ncola Semprn Cesar Meccanca: quest ) Al tempo t= una carrozza ferrovara comnca a muovers d moto rettlneo unformemente accelerato (a). Al tempo t=t, da
Fsca Generale A N. Prova Scrtta del Febbrao 8 Prof. Ncola Semprn Cesar Meccanca: quest ) Al tempo t= una carrozza ferrovara comnca a muovers d moto rettlneo unformemente accelerato (a). Al tempo t=t, da
Rappresentazione dei numeri
 Rappresentazone de numer PH. 3.1, 3.2, 3.3 1 Tp d numer Numer nter, senza segno calcolo degl ndrzz numer che possono essere solo non negatv Numer con segno postv negatv Numer n vrgola moble calcol numerc
Rappresentazone de numer PH. 3.1, 3.2, 3.3 1 Tp d numer Numer nter, senza segno calcolo degl ndrzz numer che possono essere solo non negatv Numer con segno postv negatv Numer n vrgola moble calcol numerc
Dipartimento di Matematica per le scienze economiche e sociali Università di Bologna
 Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Modell 1 lezone 18 1 dcembre 2011 Covaranza, Varabl aleatore congunte professor Danele Rtell www.unbo.t/docent/danele.rtell 1/19?
Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Modell 1 lezone 18 1 dcembre 2011 Covaranza, Varabl aleatore congunte professor Danele Rtell www.unbo.t/docent/danele.rtell 1/19?
Esercizi sui circuiti magnetici
 Esercz su crcut magnetc Eserczo a. Nel crcuto magnetco llustrato calcolare, trascurando la rluttanza del ferro, coeffcent d auto nduzone degl avvolgment e e l coeffcente d mutua nduzone tra due avvolgment
Esercz su crcut magnetc Eserczo a. Nel crcuto magnetco llustrato calcolare, trascurando la rluttanza del ferro, coeffcent d auto nduzone degl avvolgment e e l coeffcente d mutua nduzone tra due avvolgment
Esercizi di Probabilità e Statistica
 Esercz d Probabltà e Statstca Samuel Rota Bulò 25 maggo 2007 Funzon d v.a., meda, varanza, moda, medana, quantl e quartl. Vettor aleator, denst condzonata, covaranza, correlazone. Eserczo 1 Sa Y ax + b
Esercz d Probabltà e Statstca Samuel Rota Bulò 25 maggo 2007 Funzon d v.a., meda, varanza, moda, medana, quantl e quartl. Vettor aleator, denst condzonata, covaranza, correlazone. Eserczo 1 Sa Y ax + b
FUNZIONAMENTO IN REGIME ALTERNATO SINUSOIDALE
 FUNZIONAMENTO IN REGIME ALTERNATO SINUSOIDALE In presenza d una almentazone alternata snusodale tutte le grandezze elettrche saranno alternate snusodal. Le equazon d funzonamento n regme comunque varale
FUNZIONAMENTO IN REGIME ALTERNATO SINUSOIDALE In presenza d una almentazone alternata snusodale tutte le grandezze elettrche saranno alternate snusodal. Le equazon d funzonamento n regme comunque varale
Lezione n. 7. Legge di Raoult Legge di Henry Soluzioni ideali Deviazioni dall idealit. idealità. Antonino Polimeno 1
 Chmca Fsca Botecnologe santare Lezone n. 7 Legge d Raoult Legge d Henry Soluzon deal Devazon dall dealt dealtà Antonno Polmeno 1 Soluzon / comportamento deale - Il dagramma d stato d una soluzone bnara,
Chmca Fsca Botecnologe santare Lezone n. 7 Legge d Raoult Legge d Henry Soluzon deal Devazon dall dealt dealtà Antonno Polmeno 1 Soluzon / comportamento deale - Il dagramma d stato d una soluzone bnara,
Dipartimento di Matematica per le scienze economiche e sociali Università di Bologna
 Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Modell 1 lezone 12 10 novembre 2011 Teorema d Lebesgue Vtal-Generazone d msure professor Danele Rtell www.unbo.t/docent/danele.rtell
Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Modell 1 lezone 12 10 novembre 2011 Teorema d Lebesgue Vtal-Generazone d msure professor Danele Rtell www.unbo.t/docent/danele.rtell
