PONTE DI WHEATSTONE. Fig. 1. Schema elettrico del Ponte di Wheatstone
|
|
|
- Mattia Salvatore
- 7 anni fa
- Visualizzazioni
Transcript
1 PONTE DI WHEATSTONE Fi.. Shem elettio del Ponte di Whettone. Genelità Un metodo lio pe l mi di eitenze di odine medio è il ponte di Whettone. Un hemtizzzione di tle ponte è ipott in Fi.. Come i pò vedee dllo hem elettio, il ponte di Whettone ilt fomto d qtto eitenze onnee in modo d elizze n mli on qtto lti e qtto vetii. T de vetii oppoti viene ollet n oente di limentzione in oente ontin, mente t li lti de viene ineito n lvnometo. In e ll onfizione, è poiile definie le pti otitenti il ponte ome: lti del ponte, oipondenti i qtto mi otititi di eitoi; dionli del ponte, oipondenti i mi he ontenono l oente di limentzione o il lvnometo; in ptiole, è dett dionle di limentzione qell he è ifeit ll oente di limentzione, e dionle di ilevzione qell in i è ineito il lvnometo. Uno qlii dei qtto lti è otitito dl eitoe di eitenz inonit, mente li lti te lti ono otititi d eitoi le i eitenze mono vloi noti. Almeno n
2 delle eitenze note deve eee nhe viile, ed in ptiole nell eempio di op ipotto vò n eitoe viile dedi. Il ilevtoe di zeo, poto t i nodi A e B, è eniile l pio di oente nel lto teo, o ll diffeenz di potenzile t i nodi A e B. Il ponte è in eqiliio qndo è nll l oente he ttve l dionle di ivelzione, ondizione he pò eee individt dll indie del lvnometo nell poizione di zeo. In ondizione di fnzionmento, il enetoe di tenione ontin E f oee n oente he i iptie t i de mi in i ono ineite ed ompendenti ipettivmente il nodo A e il nodo B. Applindo i pinipi di Kihhoff l ponte, qndo è veifit l ondizione di eqiliio, i h: eqzione l nodo A I I () eqzione l nodo B eqzione ll mli ABC eqzione ll mli ABD I I () I I (3) I I () Sotitendo () e () in (), i ottiene: I I (5) I I (6) Dividendo memo memo, i iv: d i: (7) E tt oi tovt l elzione he le le qtto eitenze del ponte, in ondizioni di eqiliio: il podotto delle eitenze dei de lti oppoti eli il podotto delle lte de. E qindi poiile lole il vloe dell eitenz inonit: (8) Pe inee l ondizione di eqiliio è poiile opee l ppoto o ll eitenz. Nel eito i fà ifeimento qet eond olzione. (ponti filo)
3 . Poed di mi Poihé inizilmente il vloe di potee nhe eee molto dive d qello he oddif l (8), l oente nel mo AB potee eee elevt e qindi dnneie il lvnometo. Di oneenz i pefeie limente il iito on vloi di tenione vi vi eenti fino l vloe nominle, inementndo ontemponemente l eniilità del lvnometo. Nomlmente ll mente dell tenione di limentzione e dell eniilità del lvnometo, ooe opee lle dedi più piole dll eitenz mpione. Anhe on n eniilità del ponte elevt ed in ondizioni di tenione di limentzione nominle, del nmeo finito di dedi dell eitenz dipoizione, pò dee di non iie d ottenee n pefetto zzemento del lvnometo: in tl o, è neeio poedee ll intepolzione linee, poedimento vlido in qnto i il iito i lo tmento (lvnometo) hnno ompotmento linee nell intono dello zeo. Pe eempio, ponendo Ω, ipotizzndo 875, Ω ed vendo dipoizione n on dede più piol pi d Ω, non i iià pote zeo l indie del lvnometo né on 875 Ω né on 876 Ω. E neeio qindi effette l intepolzione del vloe di ol eente poedimento. Spponendo he on 875 Ω l indie devi d n lto (pe eempio init dello zeo), di δ diviioni e on 876 Ω devi, invee, dll lto lto di δ diviioni, e detto il vloe di eitenz d omme l vloe più piolo di pe ottenee l zzemento del lvnometo, è poiile otie l eente fi: Fi.. ppeentzione fi dell intepolzione dove il emento AC ppeent l diffeenz f i de vloi di (ovveo Ω) ed i ementi AB e CD ppeentno ipettivmente le de devizioni δ e δ, ipotte in eno oppoto ipetto l emento AC. Coninendo li etemi B e D, i ottenono de tinoli ettnoli ABO e OCD he iltno eee imili (eendo AB pllelo CD ed 3
4 entmi pependioli d AC, e li noli BOA e COD eli pehé oppoti l vetie). Si AO δ h, qindi:, e dto he AO ed OC (-), à no : OC δ d i: δ δ δ δ δ Se d eempio è δ diviioni e δ diviioni, à, Ω 35 e qindi he è il vloe di d onidee nell (8). 875, Ω
5 3. Vltzione dell inetezz L inetezz ll mi di pò eee vltt pplindo l lee di popzione dell inetezz eit dlle Nom UNICEI 9 ll elzione (8). Bion peò tenee peente he l eniilità del lvnometo non è infinit, e he qindi pò de n indizione di zeo nhe qndo in eltà iol n oente non nll. Dett I min l oente limite l di otto dell qle il lvnometo è ineniile (ovveo fonie omnqe n indizione di zeo), l elzione (8) v iitt pe tene onto he il ponte non è eniile vizioni dell eitenz he deteminno il pio di n oente infeioe I min : dove è il vloe di eitenz oipondente ll oente limite I min. Conidendo l nt dell eitenz (he pò eei o meno, e pò mee qlii vloe fino d n vloe mimo pi popio d ), e pò eee onidet ome n ndezz letoi vloe medio nllo m on n inetezz dive d zeo, d vlte. Di oneenz: L inetezz i ottiene pplindo l lee di popzione delle inetezze nel o di n podotto o di n ppoto: & & & & ( & & & ) &. L inetezz lle inole eitenze,, pò eee ilevt on metodi di vltzione di teoi A, ioè eeendo mie ipette, o di tipo B, tilizzndo i dti foniti dl otttoe. Pe vlte ion ione ome ee. Pe ome è tt definit, l eitenz ppeent il vloe limite di vizione dell eitenz inonit he dà loo d no potmento dell o del lvnometo dell minim qntità ppezzile. Pe l vltzione di i pò poedee in de modi ditinti: ppoio poteioi (peimentle) o ppoio pioi (teoio). Un volt detemint l, è poiile dotte n metodo di vltzione dell inetezz di tipo B, ipotizzndo n ditizione ettnole medi nll e di mpiezz ± ; i h qindi:. 3 Nel eito venono peentti entmi li ppoi pe l vltzione di. 5
6 3.. Appoio poteioi Ipotizzndo n ompotmento linee del lvnometo intono llo zeo, è poiile ivee: Ovveo: : dλ d : dλ Δ : Δλ Δ : Δλ (9) dove i è indito on: il vloe dell minim vizione d dell i il ponte è eniile; dλ minim devizione ppezzile dello tmento; Δ vizione finit di ; Δλ il nmeo di devizioni oipondenti ll vizione finit Δ. Dll elzione (9) i h: Δ Δλ dλ pe i è poiile vlte imponendo n vizione inifitiv li pplizioni, tle vizione non i pò fiimente impoe in qnto eitenz inonit e nomlmente non è viile. Dll elzione(8), i h: Δ Δ in qnto l ni eitenz viile è l i h: Δ Δ Δ. Dividendo pe di oneenz, eendo, l () diviene: Δ dλ Δλ Δ Δ (). Tttvi, nelle è l e iodndo empe l (8), Δ dλ Δλ Qindi l i pò vlte imponendo n vizione inifitiv ll eitenz mpione e vltndo l oipondente devizione Δλ del lvnometo. Con ifeimento ll eempio nmeio peedentemente ipotto ( 875, Ω; ; 875 Ω e 876 Ω, e qindi pe n vizione Δ Ω) on le ipettive devizioni ( δ diviioni init e δ det, pe n totle di Δλ 35 diviioni), e onidendo di pote ppezze l lvnometo l mezz diviione (dλ,5), i h: dλ,5 Δ. Ω Δλ 35 6
7 3.. Appoio pioi L ppoio pioi i l teoem di Thevenin, ovveo ll nlii del iito eqivlente del ponte vito i pi del lvnometo: Fi. 3. Ciito eqivlente di Thevenin Pe definie i vloi di eq e di E i poede ome ee. Con ifeimento llo hem elettio del ponte di Fi., i onidei il iito eqivlente vito di vetii di ilevzione A e B ottento otoiitndo il enetoe (Fi. 5): Fi.. Shem elettio del ponte Fi. 5. Ciito eqivlente vito i pi del lvnometo d i: eq Con ifeimento empe llo hem di Fi., è poiile ive: 7
8 V A E ; V B E E o VB VA E () In ondizione di eqiliio I e qindi V AB E. Pe ilie l vloe di i iodi he e è definit ome l vizione di eitenz ll qle oiponde n pio di oente I nel lvnometo pi ll minim oente ll qle il lvnometo è eniile. Anlizzndo il iito di Fi. 3 i h: dove I ΔE () eq Δ Eo è l vizione di tenione dovt ll ed è l eitenz inten del lvnometo. Pe ive Δ E i pò vilppe l elzione () in eie di Tylo nell intono di i oiponde E, etndoi l pimo odine (tle ppoimzione è vlid poihé l vizione di ono piole); i h: ΔE d (3) Dlle () e (3) i h: ioè ( ) eq I ( eq ) I ΔE () L oente I i pò epimee ome: I K Δλ (5) dove K è l otnte tmentle del lvnometo, epe in A/div. Qet otnte è let in mnie inve ll eniilità dello tmento, in qnto tnto più piol è K tnto milioe è l eniilità dello tmento. Dll () i h: E pe i l () divent: ( ) ( ) E E E (6) 8
9 ( ) eq K E Δλ Poihé nell elzione () il temine ompe l denomintoe, è inteente nde vlte, onde dimenione l melio il iito, qndo eo me il vloe mimo pe pote oì ottenee il minimo vloe di e qindi l ondizione di mim eniilità. Ponendo m nell (6), i h: E m ( m) Pe individe il mimo in fnzione di m i deve poe, ioè: m ( m) ( m) m m m m m m ( m) ( m) ( m) he è veifit pe m ±, ovveo l ondizione di mim eniilità del ponte è ottent pe ; in tl o, ovvimente, nhe. E poiile inolte dimote he l milioe ondizione in olto è qell pe l qle. Conidendo olo l olzione poitiv ( ) e otitendo tle vloe nell (6), i h: pe i l () divent: E ( ) E ( ) eq K E Δλ Si pò, qindi, ffeme he: no tmento on n K più piolo ide l eoe di eniilità; qnto più è elevt l tenione E tnto più o è l eoe di eniilità; tttvi, il vloe mimo di E dipende dll oente mim mmiiile pe i omponenti; qnto più piolo è il temine ( eq ) tnto più è ; qindi l eoe di eniilità non dipende olo dllo tmento tilizzto, m nhe dlle tteitihe del iito; il metodo peent n limite l eee di, in qnto ment l dipendenz diett i pehé ment l eniilità. eq i pe, e di oneenz diminie l 9
10 . Miliomento dell peiione del metodo del ponte di Whettone Il ponte di Whettone viene tilizzto pe mie di eitenz di vloe medio, indo peiioni dell odine di n pte dieimil. Semeee qindi he, tttndoi di peiioni non ptiolmente elevte, eo po eee otitit d n on mltimeto nmeio. In eltà ttveo le de tenihe: doppi pet otitzione i h n miliomento delle petzioni tle d itifie l tilizzo del ponte nhe pe mie di peiione... Teni dell doppi pet Come detto ilt empe onveniente tilizze de eitoi ed tei vloi nominli. Effettndo de mie e mindo di poto tteizzte dli ed (7) (8) i h: A dell inetezz e, p vendo nominlmente i và. Moltiplindo i de memi delle elzioni (7) e (8) i h: d i: (9) () on in qnto l diffeenz f i de vloi è dovt olmente ll inetezz e. Utilizzndo pe n eitenz dedi, è poiile onidee: in i è l pte omne dell L () diviene qindi: nelle de mie ed ovvimente () >> ed >>. ( ) ( ) ( ) ()
11 in qnto il temine ilt tile. iodndo inolte he ( ) n on << pò eee ppoimto ome ( ) n n, ed eendo empe ed << pe i <<, l () diviene e ioè il vloe di i ottiene ome medi delle de mie. Vltzione dell inetezz Pe vlte l inetezz ion tene onto nhe dell inetezz let ll eniilità del ponte. A tl fine le eqzioni (7) e (8), onfomemente qnto vito in peedenz, vnno oì iitte: qindi, moltiplindo memo memo: dto he ( ) e ponendo ome pim e, i h: ( ) ( ) ( ) eendo << e << e potendo te il temine, i h: eendo il temine <<, è poiile pplie l ppoimzione ( ) n n, pe i:
12 eendo e qindi: : X S S.. Teni dell otitzione Tle metodo onente di ottenee n inetezz idott nell mi del ppoto t de eitenze he diffeiono f loo di n qntità piol. Qet itzione è nhe qell he i h nelle pplizioni on eitenze inonite viili in i i è inteeti mie l vizione eltiv dell eitenz inonit ipetto d n ondizione di ifeimento. Si poede nel eente modo. Si pone n delle de eitenze inonite nel ponte e i ine l eqiliio: Qindi i otitie l on l lt eitenz inonit ondizione di eqiliio: Qindi dividendo memo memo: e i iv n nov Pe vlte l inetezz l ppoto ion tene onto dell inetezz lle de ondizioni di eqiliio; i h: (3) Dto he e ono de vloi divei dello teo eitoe dedi, è poiile poe: dove e ono piole ipetto e e ono molto poime t loo. L epeione (3) divent qindi:
13 3 e >>, pplindo l ppoimzione ( ) n n, l epeione divent: ( ) ( ) ( ) ( ) poihé e oì ome e ono molto minoi di, è poiile te l ltimo temine, pe i i h: ( ) ( ) qindi l inetezz olt divent: ( ) ( ) ( ) S S A volte il metodo di otitzione viene tilizzto pe mie n eitenz inonit on n inetezz più di qell iniile ol metodo tdizionle, m ihiede l impieo di de eitoi mpioni viili. Si poizion l eitenz inonit nel ponte e i ine n pim ondizione di eqiliio: Si otitie l eitenz inonit on n'lt eitenz mpione viile e i ie olo qet ltim mntenendo fio fino inee n nov ondizione d eqiliio: Confontndo i de eqilii, i dede he: Dl pnto di vit dell vltzione dell inetezz, l elzione peedente pò eee itt ome: in qnto e è tit d de ondizioni di eqiliio. Ne ee he l inetezz olt è dt d: S C X pe i l inetezz e non ient in qet elzione e qindi l mi è tteizzt d n inetezz minoe ipetto l ponte tdizionle.
PONTE DI WHEATSTONE. Fig.4.1- Schema elettrico del Ponte di Wheatstone. <lati> del ponte sono detti i quattro rami costituiti da resistori
 PONTE DI WHEATSTONE Fig.4.- Shem elettio del Ponte di Whettone 4. Genelit Un metodo lio pe l miu di eitenze di odine medio, è il ponte di Whettone. Un hemtizzzione di tle ponte è ipott in figu 4.. Come
PONTE DI WHEATSTONE Fig.4.- Shem elettio del Ponte di Whettone 4. Genelit Un metodo lio pe l miu di eitenze di odine medio, è il ponte di Whettone. Un hemtizzzione di tle ponte è ipott in figu 4.. Come
d r da informazione r r y x Cinematica seconda parte
 Cinemic econd pe Moo nello pzio e nel pino L elocià nel pino L ccelezione nel pino Moo cicole Moo cicole nifome Moo cicole nifomemene cceleo ozione eoile del moo cicole Moo pbolico Moo pbolico Moo pbolico
Cinemic econd pe Moo nello pzio e nel pino L elocià nel pino L ccelezione nel pino Moo cicole Moo cicole nifome Moo cicole nifomemene cceleo ozione eoile del moo cicole Moo pbolico Moo pbolico Moo pbolico
θ 2 º Esercizio 1
 ecizio ) Si θ l ngolo ipetto ll veticle dell fune di lunghezz pim che m veng lcit lie di muovei velocità v di m l momento dell uto con m i ottiene imponendo l conevzione dell enegi: m v m g ( coθ ) v g
ecizio ) Si θ l ngolo ipetto ll veticle dell fune di lunghezz pim che m veng lcit lie di muovei velocità v di m l momento dell uto con m i ottiene imponendo l conevzione dell enegi: m v m g ( coθ ) v g
Facoltà di Ingegneria Fisica I 1 marzo 2005 Compito C
 Eecizio n. Fcoltà di Inenei Fiic I zo 00 Copito C Nell cchin di twood dell iu, nell qule l cucol può eee conidet idele, Clcole le ccelezioni delle due e e ipondee lle euenti donde:. il odulo dell ccelezione
Eecizio n. Fcoltà di Inenei Fiic I zo 00 Copito C Nell cchin di twood dell iu, nell qule l cucol può eee conidet idele, Clcole le ccelezioni delle due e e ipondee lle euenti donde:. il odulo dell ccelezione
Analisi del ponte di Wheatstone
 Anlisi del ponte di Whetstone Ponte limentto on genetoe idele di tensione Umeto Pisni: Stumentzione e sistemi di misu 1 Ponte di Whetstone 1 Shem del ponte limentto d un genetoe idele di tensione B A V
Anlisi del ponte di Whetstone Ponte limentto on genetoe idele di tensione Umeto Pisni: Stumentzione e sistemi di misu 1 Ponte di Whetstone 1 Shem del ponte limentto d un genetoe idele di tensione B A V
In generale i piani possono essere tra loro
 Leione 7 - Alge e Geometi - Anno emio 9/ In genele i pini possono essee t loo Pini istinti inienti in un ett ppesentt l sistem sop sitto se. Pini plleli se istinti se, oinienti se. Eseiio tem esme) Si
Leione 7 - Alge e Geometi - Anno emio 9/ In genele i pini possono essee t loo Pini istinti inienti in un ett ppesentt l sistem sop sitto se. Pini plleli se istinti se, oinienti se. Eseiio tem esme) Si
1) Una carica puntiforme q si trova al centro di una sfera cava conduttrice di raggio
 1) Un cic puntifome si tov l cento di un sfe cv conduttice di ggio inteno e spessoe. Clcole nel cso di conduttoe isolto: il cmpo elettico, il potenzile e l enegi elettosttic in tutto lo spzio. Cso ()
1) Un cic puntifome si tov l cento di un sfe cv conduttice di ggio inteno e spessoe. Clcole nel cso di conduttoe isolto: il cmpo elettico, il potenzile e l enegi elettosttic in tutto lo spzio. Cso ()
Momento di una forza rispettto ad un punto
 Momento di un fo ispettto d un punto Rihimimo lune delle definiioni e popietà sui vettoi già disusse ll iniio del oso Podotto vettoile: ϑ ϑ sin sin θ Il vettoe è dietto lungo l pependiole l pino individuto
Momento di un fo ispettto d un punto Rihimimo lune delle definiioni e popietà sui vettoi già disusse ll iniio del oso Podotto vettoile: ϑ ϑ sin sin θ Il vettoe è dietto lungo l pependiole l pino individuto
Tecniche volt-amperometriche in DC Tecniche volt-amperometriche in AC. Tecniche di zero: ponte in DC
 Misu di impedenze Misue di impedenze Tecniche volt-mpeometiche in DC Tecniche volt-mpeometiche in AC Tecniche di zeo: ponte in AC Tecniche di isonnz: Il Q-meto 006 Politecnico di Toino 1 Oiettivi dell
Misu di impedenze Misue di impedenze Tecniche volt-mpeometiche in DC Tecniche volt-mpeometiche in AC Tecniche di zeo: ponte in AC Tecniche di isonnz: Il Q-meto 006 Politecnico di Toino 1 Oiettivi dell
Motore CC. Motore a corrente continua. Motore in corrente continua Schema elettrico Modello Motore+Carico. (medio) (piccolo)
 CC in coente continu Schem elettico Modello Cico (medio) (piccolo) G.U FdA coente continu G.U FdA 2 Cicuito con un pi G.U FdA 3 Coppi indott dl pggio di coente Vloe dell Coppi G.U FdA 4 con più pie Rotoe
CC in coente continu Schem elettico Modello Cico (medio) (piccolo) G.U FdA coente continu G.U FdA 2 Cicuito con un pi G.U FdA 3 Coppi indott dl pggio di coente Vloe dell Coppi G.U FdA 4 con più pie Rotoe
1 VETTORI. 1.1 Operazioni tra vettori
 1 VETTORI Ttte le gndee pe l ci definiione non concoono lti elementi l di foi dell loo mis engono dette gndee scli; sono esempi di gndee scli l intello di tempo l mss l tempet ecc Esistono ttti delle gndee
1 VETTORI Ttte le gndee pe l ci definiione non concoono lti elementi l di foi dell loo mis engono dette gndee scli; sono esempi di gndee scli l intello di tempo l mss l tempet ecc Esistono ttti delle gndee
3. Calcolare l angolo di carico nelle condizioni di cui al punto precedente [ ] m Reattanza di dispersione
![3. Calcolare l angolo di carico nelle condizioni di cui al punto precedente [ ] m Reattanza di dispersione 3. Calcolare l angolo di carico nelle condizioni di cui al punto precedente [ ] m Reattanza di dispersione](/thumbs/71/65755893.jpg) .. SAPENZA - UNESÀ D OMA OS D LAUEA MAGSAL in NGEGNEA ELEA ed ENEGEA MAHNE E AZONAMEN ELE MAHNE ELEHE POA SA DEL GENNAO 5. Un genetoe incono tife è collegto d un tubin g. L ettnz incon è i 4 Ω e uò eee
.. SAPENZA - UNESÀ D OMA OS D LAUEA MAGSAL in NGEGNEA ELEA ed ENEGEA MAHNE E AZONAMEN ELE MAHNE ELEHE POA SA DEL GENNAO 5. Un genetoe incono tife è collegto d un tubin g. L ettnz incon è i 4 Ω e uò eee
Fondamenti di Geometria nello spazio 3D. Corso di Robotica Prof. Davide Brugali Università degli Studi di Bergamo
 Fondamenti di Geometia nello pazio 3D Coo di obotia Pof. Davide Bugali Univeità degli Studi di Begamo Geometia delle talazioni Q T Q Semplie talazione Q T Q y z y z Q T qz qy q b a qz qy q T T obotia -
Fondamenti di Geometia nello pazio 3D Coo di obotia Pof. Davide Bugali Univeità degli Studi di Begamo Geometia delle talazioni Q T Q Semplie talazione Q T Q y z y z Q T qz qy q b a qz qy q T T obotia -
CONTROLLO TERMICO DEI SISTEMI DI CALCOLO A.A. 2011/2012. H A s = L H. U.08 Trasmissione del calore 1/28. U.08 Trasmissione del calore 2/28
 CONOLLO EMICO DEI SISEMI DI CALCOLO A.A. 20/202 CONOLLO EMICO DEI SISEMI DI CALCOLO A.A. 20/202 U08 U.08 miione del loe H A L H L U.08 miione del loe /28 CONOLLO EMICO DEI SISEMI DI CALCOLO A.A. 20/202
CONOLLO EMICO DEI SISEMI DI CALCOLO A.A. 20/202 CONOLLO EMICO DEI SISEMI DI CALCOLO A.A. 20/202 U08 U.08 miione del loe H A L H L U.08 miione del loe /28 CONOLLO EMICO DEI SISEMI DI CALCOLO A.A. 20/202
Pozzetti a sezione quadrata per rete fognaria
 SCHEDA TECNICA POZZETTI A SEZIONE QUADRATA PER RETE FOGNARIA 1 Pozzetti ezione qudt pe ete fogni 2 SCHEDA TECNICA POZZETTI A SEZIONE QUADRATA PER RETE FOGNARIA DESCRIZIONE DEL PRODOTTO Il pozzetto ezion
SCHEDA TECNICA POZZETTI A SEZIONE QUADRATA PER RETE FOGNARIA 1 Pozzetti ezione qudt pe ete fogni 2 SCHEDA TECNICA POZZETTI A SEZIONE QUADRATA PER RETE FOGNARIA DESCRIZIONE DEL PRODOTTO Il pozzetto ezion
Appello di Fisica IA (ii) 25 febbraio 2009 Ore 9 Testo I
 Appeo di Fii IA (ii) 5 febbio 9 Oe 9 eto I Indie u popio eboto NOME e COGNOME e NUMEO DI MAICOLA 1) po è id e ffontt indiiduente; oni tipo di ounizione, eifit dunte o dopo po, opot inidzione de te. L itento
Appeo di Fii IA (ii) 5 febbio 9 Oe 9 eto I Indie u popio eboto NOME e COGNOME e NUMEO DI MAICOLA 1) po è id e ffontt indiiduente; oni tipo di ounizione, eifit dunte o dopo po, opot inidzione de te. L itento
Classe 4 G dicembre 2010.
 Clsse 4 G dicembe 2010. Legge di Newton pe il ffeddmento (iscldmento). Due copi tempetu diffeente se posti in conttto temico si scmbino cloe. L'ossevzione speimentle indic che essi si potno d un tempetu
Clsse 4 G dicembe 2010. Legge di Newton pe il ffeddmento (iscldmento). Due copi tempetu diffeente se posti in conttto temico si scmbino cloe. L'ossevzione speimentle indic che essi si potno d un tempetu
Fluidodinamica applicata Esercizi (Navier Stokes)
 ESERCIZIO (N.S.: COETTE p) Cnle iimensionle infinito. Pete speioe in moto con velocità. iente i pessione. Clcole: Pe qle vloe i è nllo lo sfozo viscoso sll pete speioe? Pe qle vloe i è nllo lo sfozo viscoso
ESERCIZIO (N.S.: COETTE p) Cnle iimensionle infinito. Pete speioe in moto con velocità. iente i pessione. Clcole: Pe qle vloe i è nllo lo sfozo viscoso sll pete speioe? Pe qle vloe i è nllo lo sfozo viscoso
4) Ebollizione-Condensazione come convezione ma con cambiamento di fase
 Fiic ecnic G. Gzzini UNIVERSIA DI FIRENZE Fcoltà di Ingegnei RASMISSIONE DEL CALORE INERAZIONE ENERGIA MAERIA II Pincipio emodinmic Q p d con > L tmiione dell'enegi temic è influenzt non olo dll diffeenz
Fiic ecnic G. Gzzini UNIVERSIA DI FIRENZE Fcoltà di Ingegnei RASMISSIONE DEL CALORE INERAZIONE ENERGIA MAERIA II Pincipio emodinmic Q p d con > L tmiione dell'enegi temic è influenzt non olo dll diffeenz
Elementi di Cinematica COORDINATE CARTESIANE. r r. & r COOORDINATE LOCALI COORDINATE POLARI. r = r. λ r
 Elementi di Cinemtic COORDINTE CRTESINE O P j y i x j y i x j y i x COOORDINTE LOCLI ( ) µ ϑ ϑ λ ϑ ) ( - µ λ ϑ λ COORDINTE POLRI τ ϑ ρ τ ρ n Elementi di Cinemtic MOTO RETTILINEO j O i COORDINTE CRTESINE
Elementi di Cinemtic COORDINTE CRTESINE O P j y i x j y i x j y i x COOORDINTE LOCLI ( ) µ ϑ ϑ λ ϑ ) ( - µ λ ϑ λ COORDINTE POLRI τ ϑ ρ τ ρ n Elementi di Cinemtic MOTO RETTILINEO j O i COORDINTE CRTESINE
Il modello binomiale di Ross-RubinsteinRubinstein (1979)
 Il moello binomiale i Cox-Ro Ro-RbinteinRbintein (979) Il teoema fonamentale i valtazione in n meato emplifiato Si tatta el moello i meato finanziaio più emplie. È n moello a tempo ieto, e intoe gli impotanti
Il moello binomiale i Cox-Ro Ro-RbinteinRbintein (979) Il teoema fonamentale i valtazione in n meato emplifiato Si tatta el moello i meato finanziaio più emplie. È n moello a tempo ieto, e intoe gli impotanti
GONIOMETRIA GONIOMETRIA E TRIGONOMETRIA LEZIONI. Introduzione alla goniometria e alla trigonometria
 GNIMETRIA E TRIGNMETRIA LEZINI GNIMETRIA Intoduzione ll goniometi e ll tigonometi Goniometi e tigonometi ono due temini che deivno dl geco e ignificno ipettivmente miu degli ngoli e miu dei tingoli. Le
GNIMETRIA E TRIGNMETRIA LEZINI GNIMETRIA Intoduzione ll goniometi e ll tigonometi Goniometi e tigonometi ono due temini che deivno dl geco e ignificno ipettivmente miu degli ngoli e miu dei tingoli. Le
11. Geometria piana ( ) ( ) 1. Formule fondamentali. Rettangolo. A = b = h = = b h. b = base h = altezza. Quadrato
 11. Geometi pin 1. Fomule fonmentli Rettngolo = h = h = h p= + h p= + h h= p = p h + ( ) = h = h h = = se = igonle p = peimeto h = ltezz = e p = semipeimeto Quto = l l = = l l = l = lto = igonle = e p
11. Geometi pin 1. Fomule fonmentli Rettngolo = h = h = h p= + h p= + h h= p = p h + ( ) = h = h h = = se = igonle p = peimeto h = ltezz = e p = semipeimeto Quto = l l = = l l = l = lto = igonle = e p
Geometria elementare. Sezione Prima Geometria nel piano
 pitolo 3 Geometi elemente Sezione Pim Geometi nel pino 1 Enti geometii fondmentli 113 on il temine Geometi, pol ompost di oigine ge he signifi lettelmente misuzione dell te, s intende l sienz zionle he
pitolo 3 Geometi elemente Sezione Pim Geometi nel pino 1 Enti geometii fondmentli 113 on il temine Geometi, pol ompost di oigine ge he signifi lettelmente misuzione dell te, s intende l sienz zionle he
Soluzioni A - Test d ingresso alla Prova Scritta di Controlli Automatici A del 8 Maggio 2004
 Soluzioni A - Tet d ingreo ll Prov Sritt di Controlli Automtii A del 8 Mggio 004 ) Srivere l funzione di trferimento di un item dinmio vente i modi{ t in(4 t e t ϕ), te in(4 t ϕ) } T() ( ) 6 ( ) ) Dto
Soluzioni A - Tet d ingreo ll Prov Sritt di Controlli Automtii A del 8 Mggio 004 ) Srivere l funzione di trferimento di un item dinmio vente i modi{ t in(4 t e t ϕ), te in(4 t ϕ) } T() ( ) 6 ( ) ) Dto
Capitolo 16. La teoria dell equilibrio generale. Soluzioni delle Domande di ripasso
 eanko & aeutigam icoeconomia anuale delle oluzioni Capitolo 16 La teoia dell equilibio geneale Soluzioni delle Domande di ipao 1. L analii di equilibio paziale tudia la deteminazione del pezzo e della
eanko & aeutigam icoeconomia anuale delle oluzioni Capitolo 16 La teoia dell equilibio geneale Soluzioni delle Domande di ipao 1. L analii di equilibio paziale tudia la deteminazione del pezzo e della
I PROBLEMI DI MASSIMO E DI MINIMO
 I PROBLEMI DI MASSIMO E DI MINIMO Souzioni di pobemi ttti d ibo: Coso Bse Bu di Mtemti, vo. 5 [1] (Pobem n. pg. 1 ) Individu i punto de ett xy5 pe i que è minim distnz d oigine degi ssi oodinti. Consideimo
I PROBLEMI DI MASSIMO E DI MINIMO Souzioni di pobemi ttti d ibo: Coso Bse Bu di Mtemti, vo. 5 [1] (Pobem n. pg. 1 ) Individu i punto de ett xy5 pe i que è minim distnz d oigine degi ssi oodinti. Consideimo
Esempi di campi magnetici e calcolo di induttanze.
 5d_EAEE_APPLCAZON CAMP MAGNETC STATC (ultim modific 7/10/017) Esempi di cmpi mgnetici e clcolo di induttnze. M. Usi 5d_EAEE_APPLCAZON CAMP MAGNETC STATC 1 Conduttoe ettilineo indefinito Si considei un
5d_EAEE_APPLCAZON CAMP MAGNETC STATC (ultim modific 7/10/017) Esempi di cmpi mgnetici e clcolo di induttnze. M. Usi 5d_EAEE_APPLCAZON CAMP MAGNETC STATC 1 Conduttoe ettilineo indefinito Si considei un
Esame di allineamento di Fisica - 24 novembre Facoltà di Ingegneria - Università di Bologna, sede di Cesena -a-
 --. lcole l e del pllelo indiiduo di eueni eoi: i j k ( ) ( ) ( ) i j 9 k 6 i j k i j k ( ) ( ) ( ) 9 lcole il odulo del podoo eoile:. Un copo pendo d feo ccele pe un fino d un elocià di / ucceiene i uoe
--. lcole l e del pllelo indiiduo di eueni eoi: i j k ( ) ( ) ( ) i j 9 k 6 i j k i j k ( ) ( ) ( ) 9 lcole il odulo del podoo eoile:. Un copo pendo d feo ccele pe un fino d un elocià di / ucceiene i uoe
Qualche appunto sulle trasformazioni affini.
 Qulhe ppunto sulle tsfomzioni ffini. Due efinizioni i ffinità. Def. si ie ff i n ità un oisponenz iunivo t punti el pino A : he h ome invinti l llinemento ei punti e il pllelismo. Ossevzioni * A un ffinità
Qulhe ppunto sulle tsfomzioni ffini. Due efinizioni i ffinità. Def. si ie ff i n ità un oisponenz iunivo t punti el pino A : he h ome invinti l llinemento ei punti e il pllelismo. Ossevzioni * A un ffinità
Strutture AB x semplici
 Chimi fisi speioe Modlo Sttte AB x semplii Segio Btti Sttte intestizili L imphettmento omptto esgonle o io D pò ite l ostzione nhe di sttte più omplesse ispetto gli elementi in i tomi di dives nt fomino
Chimi fisi speioe Modlo Sttte AB x semplii Segio Btti Sttte intestizili L imphettmento omptto esgonle o io D pò ite l ostzione nhe di sttte più omplesse ispetto gli elementi in i tomi di dives nt fomino
Angoli e funzioni. goniometriche
 UNITÀ 1 ngoli e funzioni goniometihe TEORI 1 Definizioni di ngolo Misu degli ngoli 3 Funzioni goniometihe seno e oseno 4 Funzioni goniometihe tngente e otngente 5 Vloi delle funzioni goniometihe 6 Gfii
UNITÀ 1 ngoli e funzioni goniometihe TEORI 1 Definizioni di ngolo Misu degli ngoli 3 Funzioni goniometihe seno e oseno 4 Funzioni goniometihe tngente e otngente 5 Vloi delle funzioni goniometihe 6 Gfii
Programmazione dinamica: dal Problema della diligenza all'ottimizzazione della Logistica
 Pogammazione dinamica: dal Poblema della diligenza all'ottimizzazione della Logistica Lca Betazzi ) Il poblema della diligenza Dato il segente gafo 9 8 5 7 5 7 8 deteminae n cammino a costo minimo dal
Pogammazione dinamica: dal Poblema della diligenza all'ottimizzazione della Logistica Lca Betazzi ) Il poblema della diligenza Dato il segente gafo 9 8 5 7 5 7 8 deteminae n cammino a costo minimo dal
Università degli Studi di Teramo Facoltà di Scienze Politiche
 Uivesità degli Studi di Temo Foltà di Sieze Politihe Coso di Lue i Sttisti Lezioi del Coso di Mtemti u di D. Todii.. 00/004 CAPITOLO I GLI INTEGRALI. GENERALITÀ Defiizioe di itegle defiito pe u fuzioe
Uivesità degli Studi di Temo Foltà di Sieze Politihe Coso di Lue i Sttisti Lezioi del Coso di Mtemti u di D. Todii.. 00/004 CAPITOLO I GLI INTEGRALI. GENERALITÀ Defiizioe di itegle defiito pe u fuzioe
Dischi e cilindri assialsimmetrici. Accoppiamenti forzati Dischi e cilindri
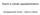 Dischi e cilini ssilsimmetici Accoppimenti fozti Dischi e cilini sempi Copi ssilsimmetici elstici elzioni i se O y h x Se Rh Stto pino i tensione z 0 0 z z R Ipotesi i se
Dischi e cilini ssilsimmetici Accoppimenti fozti Dischi e cilini sempi Copi ssilsimmetici elstici elzioni i se O y h x Se Rh Stto pino i tensione z 0 0 z z R Ipotesi i se
METODO VOLTAMPEROMETRICO
 METODO OLTAMPEOMETCO Tle etodo consente di isrre indirettente n resistenz elettric ed ipieg l definizione stess di resistenz : doe rppresent l tensione i cpi dell resistenz e l corrente che l ttrers coe
METODO OLTAMPEOMETCO Tle etodo consente di isrre indirettente n resistenz elettric ed ipieg l definizione stess di resistenz : doe rppresent l tensione i cpi dell resistenz e l corrente che l ttrers coe
I equazione cardinale della dinamica
 I equzione cdinle dell dinic I Sistei di pticelle Un siste di pticelle è un insiee di punti teili, definito dll ss e dll posizione di ciscun pticell. Il più seplice siste di pticelle è foto d due soli
I equzione cdinle dell dinic I Sistei di pticelle Un siste di pticelle è un insiee di punti teili, definito dll ss e dll posizione di ciscun pticell. Il più seplice siste di pticelle è foto d due soli
Matematica FORMULARIO RICHIAMI DI ALGEBRA. Un equazione di secondo grado è riconducibile alla forma normale: ax 2 bx c 0, a 0. c 0: impossibile.
 FRMULRI Mtemti RIHIMI DI LGER LE EQUZINI DI SEND GRD Un equzione di seondo gdo è ionduiile ll fom nomle: 0, 0 0, 0 (equzione pu) 0 se 0: impossiile se 0, 0, 0 (equzione spui) 0 ( ) 0 0, 0 (equzione monomi)
FRMULRI Mtemti RIHIMI DI LGER LE EQUZINI DI SEND GRD Un equzione di seondo gdo è ionduiile ll fom nomle: 0, 0 0, 0 (equzione pu) 0 se 0: impossiile se 0, 0, 0 (equzione spui) 0 ( ) 0 0, 0 (equzione monomi)
Corso di Complementi di gasdinamica
 oso di oleenti di gsdinic Toso stit stit@nin.it www.docenti.nin.it oleenti di Gsdinic T stit odlo 8 del 30/0/05 ocede di clcolo Si è già isto che in coodinte oli si h: d e cos t d e cos t Si ò ense di
oso di oleenti di gsdinic Toso stit stit@nin.it www.docenti.nin.it oleenti di Gsdinic T stit odlo 8 del 30/0/05 ocede di clcolo Si è già isto che in coodinte oli si h: d e cos t d e cos t Si ò ense di
maurizio pizzonia sicurezza dei sistemi informatici e delle reti. esercizi su controllo di accesso e sicurezza di sistema
 eseizi su ontollo di esso e siuezz di sistem 1 ess mtix e onfidenzilità S={,,} O={,,} R={ed,ite} il modello è DAC o MAC? può sivee i file? può leee i file? può venie onosenz del ontenuto dei file? ome?
eseizi su ontollo di esso e siuezz di sistem 1 ess mtix e onfidenzilità S={,,} O={,,} R={ed,ite} il modello è DAC o MAC? può sivee i file? può leee i file? può venie onosenz del ontenuto dei file? ome?
La molla con attrito
 La molla con attito L equazione di patenza è mx + x + kx 0 () con condizioni iniziali x(0) l ed x (0) 0, ipettivamente lunghezza iniziale e velocità iniziale. Tafomando otteniamo l equazione: m[ X() x(0)
La molla con attito L equazione di patenza è mx + x + kx 0 () con condizioni iniziali x(0) l ed x (0) 0, ipettivamente lunghezza iniziale e velocità iniziale. Tafomando otteniamo l equazione: m[ X() x(0)
j Verso la scuola superiore +l calcolo letterale Monomi Polinomi e prodotti notevoli Equazioni
 j Verso l suol superiore +l lolo letterle Monomi Polinomi e prodotti notevoli Equzioni Monomi Il monomio x 4 y è simile : x 4 y 5 +x 4 y x y Due monomi sono simili se hnno l prte letterle ugule e, siome
j Verso l suol superiore +l lolo letterle Monomi Polinomi e prodotti notevoli Equzioni Monomi Il monomio x 4 y è simile : x 4 y 5 +x 4 y x y Due monomi sono simili se hnno l prte letterle ugule e, siome
Fisica II. 6 Esercitazioni
 Esecizi svolti Esecizio 61 Un spi cicole di ggio è pecos d un coente di intensità i Detemine il cmpo B podotto dll spi in un punto P sul suo sse, distnz x dl cento dell spi un elemento infinitesimo di
Esecizi svolti Esecizio 61 Un spi cicole di ggio è pecos d un coente di intensità i Detemine il cmpo B podotto dll spi in un punto P sul suo sse, distnz x dl cento dell spi un elemento infinitesimo di
Ehningen, 12 luglio 2014, Giovanni Bianchi 1
 Intouzione L toi i queto pempifitoe h lunghe ii. L mi vventu i tootuttoe omini intono l 980. Ci iei nni opo, eii i tente on le vlvole. im ompei qulhe lio e lt oumentzione te, poi pli on nzini olleghi i
Intouzione L toi i queto pempifitoe h lunghe ii. L mi vventu i tootuttoe omini intono l 980. Ci iei nni opo, eii i tente on le vlvole. im ompei qulhe lio e lt oumentzione te, poi pli on nzini olleghi i
Anno 2. Triangoli rettangoli e teorema delle corde
 Anno Tringoli rettngoli e teorem delle orde 1 Introduzione In quest lezione impreri d pplire i teoremi di Eulide e di Pitgor e sopriri quli prtiolrità nsondono i tringoli rettngoli on ngoli prtiolri. Infine,
Anno Tringoli rettngoli e teorem delle orde 1 Introduzione In quest lezione impreri d pplire i teoremi di Eulide e di Pitgor e sopriri quli prtiolrità nsondono i tringoli rettngoli on ngoli prtiolri. Infine,
Definiamo ora alcuni vettori particolarmente importanti detti versori.
 Prof. A. Di Mro I versori Definimo or lcni vettori prticolrmente importnti detti versori. Un versore è semplicemente n vettore di modlo nitrio. Normlmente gli ssi, e z vengono ssociti i versori i ˆ, ˆj,
Prof. A. Di Mro I versori Definimo or lcni vettori prticolrmente importnti detti versori. Un versore è semplicemente n vettore di modlo nitrio. Normlmente gli ssi, e z vengono ssociti i versori i ˆ, ˆj,
Compito di Fisica I. Ingegneria elettronica. A. A luglio 2010
 omito di Fisic I. Ingegnei elettonic... 9- - 7 luglio Esecizio Un unto mteile uo` muovesi in un dimensione soggetto d un foz F kx. ove: ) l enegi otenzile U(x) eltiv tle foz, onendo come zeo dell enegi
omito di Fisic I. Ingegnei elettonic... 9- - 7 luglio Esecizio Un unto mteile uo` muovesi in un dimensione soggetto d un foz F kx. ove: ) l enegi otenzile U(x) eltiv tle foz, onendo come zeo dell enegi
Campo elettrico in un conduttore
 Cmpo elettico in un conduttoe In entmbi i csi se il conduttoe è isolto e possiede un cic totle, dett cic si dispone sull supeficie esten del conduttoe; se così non fosse inftti ci sebbe un foz sulle ciche
Cmpo elettico in un conduttoe In entmbi i csi se il conduttoe è isolto e possiede un cic totle, dett cic si dispone sull supeficie esten del conduttoe; se così non fosse inftti ci sebbe un foz sulle ciche
come per coppia di punt
 Anello di m M: cmpo ull e g x G Mx ( x + ), come pe coppi di punt Inftti: L nello i puo pene compoto in tnte coppie di me puntifomi m,m in poizioni dimetlmente oppote u un ciconfeenz di ggio. Ogni coppi
Anello di m M: cmpo ull e g x G Mx ( x + ), come pe coppi di punt Inftti: L nello i puo pene compoto in tnte coppie di me puntifomi m,m in poizioni dimetlmente oppote u un ciconfeenz di ggio. Ogni coppi
Per ogni domanda ci può essere più di una risposta esatta. Puoi confrontarti con i tuoi compagni. Domanda Risposta A Risposta B Risposta C Risposta D
 CON UN MICO CON UN MICO Pe ogni domnd ci può eee più di un ipo e. Puoi confoni con i uoi compgni. SRCIZI Domnd Ripo Ripo Ripo C Ripo D 1 Le due ee ono pependicoli pllele incideni pni enmbe pe Z z 2 Le
CON UN MICO CON UN MICO Pe ogni domnd ci può eee più di un ipo e. Puoi confoni con i uoi compgni. SRCIZI Domnd Ripo Ripo Ripo C Ripo D 1 Le due ee ono pependicoli pllele incideni pni enmbe pe Z z 2 Le
Controllo di Azionamenti Elettrici. Lezione n 9. Controllo degli azionamenti elettrici con motore in corrente alternata
 Controllo di Azionmenti Elettrici Lezione n 9 Coro di Lure in Ingegneri dell Automzione Fcoltà di Ingegneri Univerità degli Studi di Plermo Controllo degli zionmenti elettrici con motore in corrente lternt
Controllo di Azionmenti Elettrici Lezione n 9 Coro di Lure in Ingegneri dell Automzione Fcoltà di Ingegneri Univerità degli Studi di Plermo Controllo degli zionmenti elettrici con motore in corrente lternt
Appello del 18/07/2005 di Microonde I
 Appello del 8/7/5 di Mioonde I Eseizio In un avo oassiale di impedenza aatteistia 5 Ω, ostante dielettia elativa 3 (tanδ) e onduibilità 5.8. 7 S, si vuole assiuae un attoe di meito alla equenza di 3 GHz.
Appello del 8/7/5 di Mioonde I Eseizio In un avo oassiale di impedenza aatteistia 5 Ω, ostante dielettia elativa 3 (tanδ) e onduibilità 5.8. 7 S, si vuole assiuae un attoe di meito alla equenza di 3 GHz.
Bibliografia: Elettrotecnica Luciano De Menna
 Indice: Intoduzione 1 Pima Legge di Kichhoff 1 Seconda Legge di Kichhoff 1 Il gafo di una ete e le equazioni indipendenti 2 Metodo dei Potenziali 3 Metodo delle coenti di maglia 3 Teoema di Tellegen (o
Indice: Intoduzione 1 Pima Legge di Kichhoff 1 Seconda Legge di Kichhoff 1 Il gafo di una ete e le equazioni indipendenti 2 Metodo dei Potenziali 3 Metodo delle coenti di maglia 3 Teoema di Tellegen (o
MINI-MWS FORATURA (METALLO DURO) MWS L METALLO DURO NEW
 ( ) MINI-MWS ++ MWS y SB (Pe foi pilot) tempto inoidbile ( inteno) NEW Leg legge Leg eitente l cloe ++ ++ + + Micopunte con cnli di ffeddmento inteni pe un fotu pofond tbile. Pe un fotu efficiente ed etemmente
( ) MINI-MWS ++ MWS y SB (Pe foi pilot) tempto inoidbile ( inteno) NEW Leg legge Leg eitente l cloe ++ ++ + + Micopunte con cnli di ffeddmento inteni pe un fotu pofond tbile. Pe un fotu efficiente ed etemmente
Unità Didattica N 11 Le equazioni di secondo grado ad una incognita Unità Didattica N 11 Le equazioni di secondo grado ad una incognita
 86 Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di
86 Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di
La misura della resistenza
 Parte II (Metodi e strmenti di misra in ) Metodi di zero I metodi di zero onsentono il onfronto diretto tra na grandezza inognita X e na fnzione nota di n ampione f(c). Il risltato del onfronto viene tilizzato
Parte II (Metodi e strmenti di misra in ) Metodi di zero I metodi di zero onsentono il onfronto diretto tra na grandezza inognita X e na fnzione nota di n ampione f(c). Il risltato del onfronto viene tilizzato
Unità Didattica N 11 Le equazioni di secondo grado ad una incognita
 Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di seondo
Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di seondo
1 Integrali doppi di funzioni a scala su rettangoli
 INEGRALI DOPPI L prim motivzione per lo studio degli integrli di funzioni di due vribili è il lolo di volumi, in nlogi on l pplizione degli integrli di funzioni di un vribile l lolo di ree. L proedur di
INEGRALI DOPPI L prim motivzione per lo studio degli integrli di funzioni di due vribili è il lolo di volumi, in nlogi on l pplizione degli integrli di funzioni di un vribile l lolo di ree. L proedur di
- determinare il modulo della densita di corrente di spostamento J s e il valore
 Un ondenatoe a fae piane e paallele viene aiato ollegandolo ad un geneatoe di oente di modo he duante la aia del ondenatoe la oente di onduzione ia otante. Le amatue del ondenatoe hanno upefiie A π R ono
Un ondenatoe a fae piane e paallele viene aiato ollegandolo ad un geneatoe di oente di modo he duante la aia del ondenatoe la oente di onduzione ia otante. Le amatue del ondenatoe hanno upefiie A π R ono
Sforzo normale 187. sapendo che esso deve portare uno sforzo normale di compressione NEd pari a 1750 kn. Utilizzando l espressione proposta si ottiene
 Sorzo normale 187 apendo he eo deve portare uno orzo normale di ompreione Ed pari a 175 k. Utilizzando l epreione propoa i ottiene 175 1 3 Ed, ne 1 135 m d 14.17.. 175 1 3 Ed, ne 1 8.94 m 391.3 Se i vuole
Sorzo normale 187 apendo he eo deve portare uno orzo normale di ompreione Ed pari a 175 k. Utilizzando l epreione propoa i ottiene 175 1 3 Ed, ne 1 135 m d 14.17.. 175 1 3 Ed, ne 1 8.94 m 391.3 Se i vuole
Esercitazione Matlab. Giovanni Palmieri Università degli Studi del Sannio Dipartimento di Ingegneria
 Esecitzione Mtlb Giovnni Plmiei 4-0-007 Univesità deli Stdi del Snnio Diptimento di Inenei ppesentzione dei sistemi nello spzio di stto Vibili ltezz sebtoio Flsso di inesso Flsso di scit Velocità di scit
Esecitzione Mtlb Giovnni Plmiei 4-0-007 Univesità deli Stdi del Snnio Diptimento di Inenei ppesentzione dei sistemi nello spzio di stto Vibili ltezz sebtoio Flsso di inesso Flsso di scit Velocità di scit
Vettori e scalari. Scalari: sono completamente definite quando se ne conosce la sola misura (es. tempo, massa, temperatura, GRANDEZZE FISICHE
 Vettoi e scli GRNDEZZE FISICHE Scli: sono completmente definite qundo se ne conosce l sol misu (es. tempo, mss, tempetu, volume ) Vettoili: ichiedono un mggio contenuto infomtivo (es. velocità, cceleione,
Vettoi e scli GRNDEZZE FISICHE Scli: sono completmente definite qundo se ne conosce l sol misu (es. tempo, mss, tempetu, volume ) Vettoili: ichiedono un mggio contenuto infomtivo (es. velocità, cceleione,
F I S S I A M O I C O N C E T T I
 F I S S I M O I C O N C E T T I 3UHSDUDWL? DOOD?YHULILFD MULTI OOK L gndzz fih li ono ttizzt d un modulo (o intnità) d un unità di miu Empi di gndzz fih li ono : il tmpo, l lunghzz, l m, l tmptu, l pion
F I S S I M O I C O N C E T T I 3UHSDUDWL? DOOD?YHULILFD MULTI OOK L gndzz fih li ono ttizzt d un modulo (o intnità) d un unità di miu Empi di gndzz fih li ono : il tmpo, l lunghzz, l m, l tmptu, l pion
SUPERFICI. Definizione.
 SUPERICI Definiione. Si l chis di n peto connesso limitto A R l ci fontie A è n c semplice, chis, egole ttti. Un pplicione ettoile: che h le segenti popietà: - è contin s - è inietti in A : R, (, (, i
SUPERICI Definiione. Si l chis di n peto connesso limitto A R l ci fontie A è n c semplice, chis, egole ttti. Un pplicione ettoile: che h le segenti popietà: - è contin s - è inietti in A : R, (, (, i
Circuiti a tempo discreto Raffaele Parisi
 Univeità di Roma La Sapienza Lauea peialitia in Ingegneia Elettonia Ciuiti a tempo dieto Raffaele Paii : Campionamento e iotuzione Relazione ta iuiti C e iuiti D, elaboazione numeia di un egnale C (invaianza
Univeità di Roma La Sapienza Lauea peialitia in Ingegneia Elettonia Ciuiti a tempo dieto Raffaele Paii : Campionamento e iotuzione Relazione ta iuiti C e iuiti D, elaboazione numeia di un egnale C (invaianza
Verifica di matematica
 Nome Cognome. Clsse D 7 Mrzo Verifi di mtemti ) Dt l equzione: (punti ) k ) Srivi per quli vlori di k rppresent un ellisse, preisndo per quli vlori è un ironferenz b) Srivi per quli vlori di k rppresent
Nome Cognome. Clsse D 7 Mrzo Verifi di mtemti ) Dt l equzione: (punti ) k ) Srivi per quli vlori di k rppresent un ellisse, preisndo per quli vlori è un ironferenz b) Srivi per quli vlori di k rppresent
UTILIA SULL INTEGRALE MULTIPLO SECONDO RIEMANN
 UTILIA SULL INTGRAL MULTIPLO SCONDO RIMANN Avvertenz: tutto iò detto nel seguito vle in R n e non solo in R 2. 1. INTGRAL DI RIMANN SU RTTANGOLI Un insieme R 2 si die essere un rettngolo (hiuso) se = [,b]
UTILIA SULL INTGRAL MULTIPLO SCONDO RIMANN Avvertenz: tutto iò detto nel seguito vle in R n e non solo in R 2. 1. INTGRAL DI RIMANN SU RTTANGOLI Un insieme R 2 si die essere un rettngolo (hiuso) se = [,b]
8. Calcolo integrale.
 Politenio di Milno - Foltà di Arhitettur Corso di Lure in Edilizi Istituzioni di Mtemtihe - Appunti per le lezioni - Anno Ademio 200/20 26 8 Clolo integrle 8 Signifito geometrio dell integrle definito
Politenio di Milno - Foltà di Arhitettur Corso di Lure in Edilizi Istituzioni di Mtemtihe - Appunti per le lezioni - Anno Ademio 200/20 26 8 Clolo integrle 8 Signifito geometrio dell integrle definito
= det b, a, b, c R 3. In quest ottica, il determinante del terzo ordine e caratterizzato dalle seguenti proprieta : a a. c c
 Determinnti n = 3. Propriet Possimo rigurdre il determinnte di un mtrie del terzo ordine ome un funzione delle sue olonne: det b = det [, b,,, b, R 3. In quest otti, il determinnte del terzo ordine e rtterizzto
Determinnti n = 3. Propriet Possimo rigurdre il determinnte di un mtrie del terzo ordine ome un funzione delle sue olonne: det b = det [, b,,, b, R 3. In quest otti, il determinnte del terzo ordine e rtterizzto
Posizionamento degli autovalori nei sistemi completamente controllabili
 Gstvo Belfote Retozioe deli Stti ed Ossevtoe sitotico Posiziometo deli tovloi ei sistemi completmete cotollbili Si dto sistem: Sppoimo di costie l iesso come = K dove K è mtice di dimesioi oppote che scelimo
Gstvo Belfote Retozioe deli Stti ed Ossevtoe sitotico Posiziometo deli tovloi ei sistemi completmete cotollbili Si dto sistem: Sppoimo di costie l iesso come = K dove K è mtice di dimesioi oppote che scelimo
Il lavoro è quindi una grandezza scalare le cui unita di misura sono: = Joule = J
 Ve. el 9/0/09 Lvoo e Eneg Denzone lvoo pe un oz cotnte Se un oz cotnte gce u un copo che eettu uno potmento ce che l oz compe un lvoo ento come: co ( co ) ove è l componente ell oz pllel llo potmento.
Ve. el 9/0/09 Lvoo e Eneg Denzone lvoo pe un oz cotnte Se un oz cotnte gce u un copo che eettu uno potmento ce che l oz compe un lvoo ento come: co ( co ) ove è l componente ell oz pllel llo potmento.
Sistemi a Radiofrequenza II
 Sistemi Rdiofequenz II meti d ntenn - Geneic secizio 6. Clcole l densità di potenz dit Km di distnz lungo l diezione del mssimo di dizione di un ntenn, spendo che: l W, A eq.5 m e f GHz Soluzione 6. G
Sistemi Rdiofequenz II meti d ntenn - Geneic secizio 6. Clcole l densità di potenz dit Km di distnz lungo l diezione del mssimo di dizione di un ntenn, spendo che: l W, A eq.5 m e f GHz Soluzione 6. G
PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA
 PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA 1 2 RIEPILOGO GENERALE RESIDUI ATTIVI CONSERVATI 3 4 Pgm. CPA0099R ***-----------------------------------------------------------***
PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA 1 2 RIEPILOGO GENERALE RESIDUI ATTIVI CONSERVATI 3 4 Pgm. CPA0099R ***-----------------------------------------------------------***
Contenuto e scopo presentazione. Programmazione Lineare. Problema di programmazione lineare. Problema di programmazione lineare
 Contento e opo preentione Progrmmione Linere Teorem fondmentle e impleo primle 9//. Contento vengono preentti i teoremi e dell PL he gitifino l o dell lgoritmo del impleo viene introdotto l lgoritmo del
Contento e opo preentione Progrmmione Linere Teorem fondmentle e impleo primle 9//. Contento vengono preentti i teoremi e dell PL he gitifino l o dell lgoritmo del impleo viene introdotto l lgoritmo del
Il moto circolare uniforme
 Il moto cicolae unifome Il moto cicolae unifome: peiodo e fequenza Un copo che i muoe lungo una taiettoia cicolae con elocità calae cotante ipaa pe la poizione iniziale a intealli fii di tempo. Definiamo
Il moto cicolae unifome Il moto cicolae unifome: peiodo e fequenza Un copo che i muoe lungo una taiettoia cicolae con elocità calae cotante ipaa pe la poizione iniziale a intealli fii di tempo. Definiamo
[ ] Posizionamento degli autovalori nei sistemi completamente controllabili. Risulta: Sia dato un sistema:
![[ ] Posizionamento degli autovalori nei sistemi completamente controllabili. Risulta: Sia dato un sistema: [ ] Posizionamento degli autovalori nei sistemi completamente controllabili. Risulta: Sia dato un sistema:](/thumbs/95/124367392.jpg) Posiziometo deli utovloi ei sistemi completmete cotollbili Si dto u sistem: Suppoimo di costuie l iesso u come u K dove K è u mtice di dimesioi oppotue che scelimo oi. Bu Risult: Si ottiee u sistem co
Posiziometo deli utovloi ei sistemi completmete cotollbili Si dto u sistem: Suppoimo di costuie l iesso u come u K dove K è u mtice di dimesioi oppotue che scelimo oi. Bu Risult: Si ottiee u sistem co
Prova scritta di Algebra lineare e Geometria- 22 Gennaio 2018 = L (( 3, 2, 6)) = L ( 3, 2, 6, 5).
 Corso di Lure in Ingegneri Informti (A-Co, J-Pr) - Ingegneri Elettroni (A-Co, J-Pr) - Ingegneri Industrile (F-O) - Ingegneri Gestionle - Ingegneri Elettri - Ingegneri Meni - Ingegneri REA Prov sritt di
Corso di Lure in Ingegneri Informti (A-Co, J-Pr) - Ingegneri Elettroni (A-Co, J-Pr) - Ingegneri Industrile (F-O) - Ingegneri Gestionle - Ingegneri Elettri - Ingegneri Meni - Ingegneri REA Prov sritt di
I vettori. Grandezze scalari e grandezze vettoriali
 I vetto Gndee sl e gndee vettol Vettoe: ente mtemto tteto d te qunttà modulo deone veso I vetto sono pplt n un punto (esste un numeo nfnto d vetto equpollent, oé on modulo, deone e veso ugul, m pplt n
I vetto Gndee sl e gndee vettol Vettoe: ente mtemto tteto d te qunttà modulo deone veso I vetto sono pplt n un punto (esste un numeo nfnto d vetto equpollent, oé on modulo, deone e veso ugul, m pplt n
Chimica fisica dei materiali. Recupero di matematica. Sergio Brutti
 Chimi fisi dei mterili Repero di mtemti Sergio Brtti Nmeri omplessi Un nmero omplesso è n espressione mtemti ostitit d 3 elementi ( nmeri reli, e l nità immginri i: i i definiione Re Im Dti de nmeri omplessi:
Chimi fisi dei mterili Repero di mtemti Sergio Brtti Nmeri omplessi Un nmero omplesso è n espressione mtemti ostitit d 3 elementi ( nmeri reli, e l nità immginri i: i i definiione Re Im Dti de nmeri omplessi:
Un modello di ricerca operativa per le scommesse sportive
 Un modello di iceca opeativa pe le commee potive Di Citiano Amellini citianoamellini@aliceit Supponiamo di dove giocae una ceta omma di denao (eempio euo ulla patita MILAN- JUVE Le quote SNAI ono quelle
Un modello di iceca opeativa pe le commee potive Di Citiano Amellini citianoamellini@aliceit Supponiamo di dove giocae una ceta omma di denao (eempio euo ulla patita MILAN- JUVE Le quote SNAI ono quelle
Es1 Es2 Es3 Es4 Es5 tot
 Ottore lsse E Verifi sommtiv Cognome Nome rgomenti: onihe, funzione esponenzile e grfii derivti Tempo disposizione: ore Voto Es Es Es Es Es tot.... Considert l ellisse vente ome sse fole l sse, eentriità
Ottore lsse E Verifi sommtiv Cognome Nome rgomenti: onihe, funzione esponenzile e grfii derivti Tempo disposizione: ore Voto Es Es Es Es Es tot.... Considert l ellisse vente ome sse fole l sse, eentriità
Fluidodinamica applicata Esercizi 1-2 (Ugello De Laval)
 Politcnico di oino C Flidodinic lict.4 Escizi - (Ugllo D Lvl) ESECIZIO (UELLO DE LVL) Un gllo convgnt divgnt collg n sbtoio infinito con l tosf. L szion isttt dll gllo h d in ss si isno. L tosf h ssion
Politcnico di oino C Flidodinic lict.4 Escizi - (Ugllo D Lvl) ESECIZIO (UELLO DE LVL) Un gllo convgnt divgnt collg n sbtoio infinito con l tosf. L szion isttt dll gllo h d in ss si isno. L tosf h ssion
Costruzione della matrice di rotazione noti 3 suoi elementi
 Univesità Politecnic delle Mche PRIN5 Sistemi mini-obotici pe ppliczioni tecnologiche vnzte UNIT OPERTIV DI NCON Dispositivi di oientmento pe stzioni di ssemblggio minituizzte Rppoto scientifico n Costuzione
Univesità Politecnic delle Mche PRIN5 Sistemi mini-obotici pe ppliczioni tecnologiche vnzte UNIT OPERTIV DI NCON Dispositivi di oientmento pe stzioni di ssemblggio minituizzte Rppoto scientifico n Costuzione
14. Richiami di analisi vettoriale
 14. Richimi di nlisi vettoile Richimi di nlisi vettoile 341 14.1. Scli, vettoi, tensoi Le gndee che entno in gioco nei enomeni isici possono essee ppesentte tmite unioni del tempo, t e delle coodinte di
14. Richimi di nlisi vettoile Richimi di nlisi vettoile 341 14.1. Scli, vettoi, tensoi Le gndee che entno in gioco nei enomeni isici possono essee ppesentte tmite unioni del tempo, t e delle coodinte di
COMBINAZIONI DI CARICO SOLAI
 COMBINAZIONI DI CARICO SOLAI (ppunti di Mrio Zfonte in fse di elorzione) Ai fini delle verifihe degli stti limite, seondo unto indito dll normtiv, in generle le ondizioni di rio d onsiderre, sono uelle
COMBINAZIONI DI CARICO SOLAI (ppunti di Mrio Zfonte in fse di elorzione) Ai fini delle verifihe degli stti limite, seondo unto indito dll normtiv, in generle le ondizioni di rio d onsiderre, sono uelle
Modulazione QAM: idea base
 Modulzione QAM: ide se x I i di sono ppeseni Alenivmene d e d x q x i Si iese smeee l sess inomzione on un empo di i eeivo doppio Modulzione QAM: shem di pinipio Il lusso di di poveniene dll sogene viene
Modulzione QAM: ide se x I i di sono ppeseni Alenivmene d e d x q x i Si iese smeee l sess inomzione on un empo di i eeivo doppio Modulzione QAM: shem di pinipio Il lusso di di poveniene dll sogene viene
Vettori e scalari. Scalari: sono completamente definite quando se ne conosce la sola misura (es. tempo, massa, temperatura, GRANDEZZE FISICHE
 Vettoi e scli GRNDEZZE FISICHE Scli: sono completmente definite qundo se ne conosce l sol misu (es. tempo, mss, tempetu, volume ) Vettoili: ichiedono un mggio contenuto infomtivo (es. velocità, cceleione,
Vettoi e scli GRNDEZZE FISICHE Scli: sono completmente definite qundo se ne conosce l sol misu (es. tempo, mss, tempetu, volume ) Vettoili: ichiedono un mggio contenuto infomtivo (es. velocità, cceleione,
Lezioni L4. 1. Potenziale Elettrico; 3. Generatore di Van de Graff. FISICA GENERALE II, Cassino A.A Carmine E.
 Lezioni L4 1. Potenzile Elettico; 2. Potenzile Elettico vs Enegi Potenzile; 3. Genetoe di Vn de Gff. 2005 Cmine E. Pglione Potentile Elettico Un cic q in un Cmpo Elettico si compot in mnie nlog d un mss
Lezioni L4 1. Potenzile Elettico; 2. Potenzile Elettico vs Enegi Potenzile; 3. Genetoe di Vn de Gff. 2005 Cmine E. Pglione Potentile Elettico Un cic q in un Cmpo Elettico si compot in mnie nlog d un mss
L(s) y(t) = = A sua volta la determinazione della fase critica ϕ C è definita dalla relazione di seguito riportata:
 ESERCIZIO : Si onidei il itema etoazionato il ui hema a blohi è motato in figua. Si detemini il valoe della otante di tempo T atta a gaantie a) una pulazione itia data da ω C ad/e;b) una fae magine tale
ESERCIZIO : Si onidei il itema etoazionato il ui hema a blohi è motato in figua. Si detemini il valoe della otante di tempo T atta a gaantie a) una pulazione itia data da ω C ad/e;b) una fae magine tale
Fisica II. 1 Esercitazioni
 isic II Esecizi svolti Esecizio. Clcole l foz che gisce sull cic Q µc, dovut lle ciche Q - µc e Q 7 µc disposte come ipotto in figu Q Q α 5 cm 6 cm Q Soluzione: L foz che gisce sull cic Q è dt dll composizione
isic II Esecizi svolti Esecizio. Clcole l foz che gisce sull cic Q µc, dovut lle ciche Q - µc e Q 7 µc disposte come ipotto in figu Q Q α 5 cm 6 cm Q Soluzione: L foz che gisce sull cic Q è dt dll composizione
Facoltà di Ingegneria Prova scritta di Fisica II
 Fcoltà di ngegnei Pov scitt di Fisic..7 7 Tm Not: ε = 8.85, 4 = π Nm A Esecizio n. Dto il cmpo elettico E = î x y z ( V / m) si detemini l densità di cic ρ nel punto P=(,,) e l cic totle in un cuo vente
Fcoltà di ngegnei Pov scitt di Fisic..7 7 Tm Not: ε = 8.85, 4 = π Nm A Esecizio n. Dto il cmpo elettico E = î x y z ( V / m) si detemini l densità di cic ρ nel punto P=(,,) e l cic totle in un cuo vente
UNIVERSITA DEL SANNIO CORSO DI FISICA 1 ESERCIZI + SVOLGIMENTO CINEMATICA II
 UNIVERSITA DEL SANNIO CORSO DI FISICA 1 ESERCIZI + SVOLGIMENTO CINEMATICA II 1. Un oeo i muoe u una aieoia cicolae. Deeminae di quano aia la elocià quando l oeo paa da un puno della ciconfeenza al puno,
UNIVERSITA DEL SANNIO CORSO DI FISICA 1 ESERCIZI + SVOLGIMENTO CINEMATICA II 1. Un oeo i muoe u una aieoia cicolae. Deeminae di quano aia la elocià quando l oeo paa da un puno della ciconfeenza al puno,
Introduction to the study of matching models of unemployment
 MPRA Munih Peonal RePE Ahive Intodution to the tud of mathing model of unemploment Gaetano Lii Univeit of Caino 6. Ma 200 Online at http://mpa.u.uni-muenhen.de/22735/ MPRA Pape No. 22735, poted 7. Ma 200
MPRA Munih Peonal RePE Ahive Intodution to the tud of mathing model of unemploment Gaetano Lii Univeit of Caino 6. Ma 200 Online at http://mpa.u.uni-muenhen.de/22735/ MPRA Pape No. 22735, poted 7. Ma 200
r v E r = Quadrilatero articolato 3 β α ω 1 v r δ v r E v r E/B 1 = manovella 2 = bilanciere 3 = biella
 Qudilteo ticolto Si uole detemine l elocità ngole del bilnciee M V / / / / mnoell bilnciee biell N copi igidi Vincoli ceniee estene intene dl -() Si suppong di conoscee l elocità ngole dell mnoell e l
Qudilteo ticolto Si uole detemine l elocità ngole del bilnciee M V / / / / mnoell bilnciee biell N copi igidi Vincoli ceniee estene intene dl -() Si suppong di conoscee l elocità ngole dell mnoell e l
Visita di un Grafo Università degli Studi di Milano
 Viita di n Gafo Unieità degli Stdi di Milano La iita di n gafo conite nell'eploae na ola olta ttti il contento (cioè le infomaioni) dei nodi di n gafo E.: iitae n ottogafo del Web Difficoltà: Cammini molteplici
Viita di n Gafo Unieità degli Stdi di Milano La iita di n gafo conite nell'eploae na ola olta ttti il contento (cioè le infomaioni) dei nodi di n gafo E.: iitae n ottogafo del Web Difficoltà: Cammini molteplici
ageometria rafforzata per una lavorazione stabile. aper un elevata qualità di foratura. Lega resistente al calore Tolleranza D1 Tolleranza D4
 ( ) l cbonio legto tempto ++ inoidbile Ghi Leg legge Leg eitente l cloe + Tollenz Tollenz D =. UWC VP
( ) l cbonio legto tempto ++ inoidbile Ghi Leg legge Leg eitente l cloe + Tollenz Tollenz D =. UWC VP
esercizi su controllo di accesso e sicurezza di sistema 2006-2008 maurizio pizzonia sicurezza dei sistemi informatici e delle reti
 eseizi su ontollo di esso e siuezz di sistem 2006-2008 muizio pizzoni siuezz dei sistemi infomtii e delle eti 1 ess mtix e onfidenzilità S={,,} O={f,f,} R={ed,ite} il modello è DAC o MAC? può sivee i file?
eseizi su ontollo di esso e siuezz di sistem 2006-2008 muizio pizzoni siuezz dei sistemi infomtii e delle eti 1 ess mtix e onfidenzilità S={,,} O={f,f,} R={ed,ite} il modello è DAC o MAC? può sivee i file?
Problema Q & SOLUZIONE
 Problem 2..2.2 Un portt di,00 0 4 m / di ri umid, inizilmente ll tempertur di 2,0 C con umidità reltiv del 60% viene rffreddt e deumidifict. L tempertur in ucit è di 0,0 C ed il grdo igrometrico del 00%
Problem 2..2.2 Un portt di,00 0 4 m / di ri umid, inizilmente ll tempertur di 2,0 C con umidità reltiv del 60% viene rffreddt e deumidifict. L tempertur in ucit è di 0,0 C ed il grdo igrometrico del 00%
22. Geometria analitica dello spazio (piani e rette).
 . Geometia analitia dello spazio (piani e ette)... Definizione. Siano O un punto dello spazio e (i, j, k) una ase otonomale dello spazio dei vettoi liei. Diemo he la quatena odinata (O, i, j, k) è un ifeimento
. Geometia analitia dello spazio (piani e ette)... Definizione. Siano O un punto dello spazio e (i, j, k) una ase otonomale dello spazio dei vettoi liei. Diemo he la quatena odinata (O, i, j, k) è un ifeimento
INSTABILITA PANNELLO PIANO SOGGETTO A COMPRESSIONE
 Politecico di Milo Diptieto di Igegei Aeospzile INSTABILITA PANNLLO PIANO SOGGTTO A COMPRSSION DISPNS DL CORSO DI STRUTTUR MATRIALI AROSPAZIALI II VITTORIO GIAVOTTO CHIARA BISAGNI ANNO ACCADMICO 1/ Mteile
Politecico di Milo Diptieto di Igegei Aeospzile INSTABILITA PANNLLO PIANO SOGGTTO A COMPRSSION DISPNS DL CORSO DI STRUTTUR MATRIALI AROSPAZIALI II VITTORIO GIAVOTTO CHIARA BISAGNI ANNO ACCADMICO 1/ Mteile
