Cognome e nome (in stampatello) n di matricola n d'ordine (v. elenco) Equazioni differenziali. a) Scrivere l'integrale generale dell'equazione
|
|
|
- Amanda De Marco
- 7 anni fa
- Visualizzazioni
Transcript
1 Es Tot. Punti Prima prova in itinere di Analisi Matematica Ing. Elettronica. Ing. Telecomunicazioni Politecnico di Milano A.A. 00/0. Prof. M. Bramanti Tema n ú Ing. Elettronica (arrare il proprio corso) ú Ing. Telecomunicazioni ognome e nome (in stampatello) n di matricola n d'ordine (v. elenco) on riferimento al D.Lgs. 96/00 ("Legge sulla privacy"), il docente del corso chiede allo studente il consenso a pulicare nel sito e del corso i seguenti dati dello studente: Nome, ognome, numero di matricola, esito di questa prova scritta. (Barrare e firmare) ú Dò il mio consenso ú Nego il mio consenso. Firma dello studente Equazioni differenziali. a) Scrivere l'integrale generale dell'equazione ab$ ab%ab œ!þ ) Determinare una soluzione particolare dell'equazione %B ab$ ab%ab œ &/ Þ
2 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Tema. Si consideri l'equazione differenziale: œ Þ B" a. Determinare tutte le soluzioni dell'equazione.. Risolvere il prolema di auchy per l'equazione precedente con la condizione iniziale a! œ "Þ c. Precisare qual è il più ampio intervallo su cui la soluzione del prolema di auchy è definita. urve e integrali di linea. alcolare il momento d'inerzia di una linea materiale omogenea rappresentata da una circonferenza di raggio V e massa Q, rispetto a un asse passante per un punto della circonferenza e perpendicolare al piano che la contiene. (Prestare particolare cura nell'impostazione dell'esercizio, scrivendo esplicitamente le equazioni parametriche della curva in un opportuno riferimento e indicando qual è l'asse di rotazione in questo riferimento).
3 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Tema alcolo differenziale per funzioni reali di più variaili 4. alcolare il seguente limite, ossia: dimostrare che il limite esiste e vale j, oppure dimostrare che non esiste, applicando criteri o teoremi studiati. B $B lim Œ abßä a!ß! % % B & 5. Sia 0 À 8 Ä definita da `0 0aB œ log kbkß per B 8 Ï a!ß! Þ a. alcolare `B ab per œ "ßßÞÞÞß8Þ. Detta < a> À M Ä 8 un arco di curva regolare, calcolare..> c0 a< a> d, dove 0 è la funzione del punto a, e semplificare l'espressione ottenuta. c. Applicare la formula trovata al punto alla curva < À a!ß" Ä $ data da e semplificare l'espressione trovata. <a> œ a> cos>ß> sin>ß>
4 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Tema 6. Dopo aver determinato tutti i punti stazionari della seguente funzione, studiarne la natura (cioè decidere se sono punti di minimo, massimo o sella). B 0aBß œ / ˆ B 4
5 Es Tot. Punti Prima prova in itinere di Analisi Matematica Ing. Elettronica. Ing. Telecomunicazioni Politecnico di Milano A.A. 00/0. Prof. M. Bramanti Tema n ú Ing. Elettronica (arrare il proprio corso) ú Ing. Telecomunicazioni ognome e nome (in stampatello) n di matricola n d'ordine (v. elenco) on riferimento al D.Lgs. 96/00 ("Legge sulla privacy"), il docente del corso chiede allo studente il consenso a pulicare nel sito e del corso i seguenti dati dello studente: Nome, ognome, numero di matricola, esito di questa prova scritta. (Barrare e firmare) ú Dò il mio consenso ú Nego il mio consenso. Firma dello studente Equazioni differenziali. a) Scrivere l'integrale generale dell'equazione ) Risolvere il prolema di auchy: ab$ ab œ BÞ Ú ab$ ab œ B Û a! œ! Ü " a! œ Þ $
6 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Tema. a) Scrivere l'integrale generale dell'equazione ) Risolvere il prolema di auchy: B " œ Þ "B B B "B œ a " œ œ " B precisando il più ampio intervallo su cui è definita la soluzione del prolema. urve e integrali di linea. alcolare la lunghezza dell'arco di curva piana la cui equazione in forma polare è: * œ Œsin ß * c!ß dþ
7 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Tema alcolo differenziale per funzioni reali di più variaili 4. Sia l'insieme di definizione della funzione I 0aBß œ loga"b %. sinb Dopo aver determinato analiticamente l'insieme I ed averlo disegnato, dire se: I è aperto SI' ú NO ú I è chiuso SI' ú NO ú I è limitato SI' ú NO ú I è connesso SI' ú NO ú 5. Data la funzione $ $ B B B Bß 0aBß œ B B per a Á a!ß! ā! per abß œ a!ß! Þ ) Stailire se 0 è continua o meno nell'origine. ) Stailire se 0 è derivaile o meno nell'origine. ) Stailire se 0 è differenziaile o meno nell'origine. (Si chiede di dimostrare ogni affermazione fatta in ase a criteri o teoremi studiati, non di limitarsi ad affermare come vanno le cose).
8 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Tema 6. Dopo aver determinato tutti i punti stazionari della seguente funzione, studiarne la natura (cioè decidere se sono punti di minimo, massimo o sella). 0aBß œ B ab" 4
9 Es Tot. Punti Prima prova in itinere di Analisi Matematica Ing. Elettronica. Ing. Telecomunicazioni Politecnico di Milano A.A. 00/0. Prof. M. Bramanti Tema n ú Ing. Elettronica (arrare il proprio corso) ú Ing. Telecomunicazioni ognome e nome (in stampatello) n di matricola n d'ordine (v. elenco) on riferimento al D.Lgs. 96/00 ("Legge sulla privacy"), il docente del corso chiede allo studente il consenso a pulicare nel sito e del corso i seguenti dati dello studente: Nome, ognome, numero di matricola, esito di questa prova scritta. (Barrare e firmare) ú Dò il mio consenso ú Nego il mio consenso. Firma dello studente Equazioni differenziali. a) Scrivere l'integrale generale dell'equazione abab œ!þ ) Determinare una soluzione particolare dell'equazione B abab œ $/ sinbþ
10 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Tema. Risolvere il prolema di auchy: sinb ' œ cos ā ˆ œ e precisare qual è il più ampio intervallo su cui la soluzione del prolema di auchy è definita. urve e integrali di linea. alcolare l'integrale di linea ( È D.= ÚB œ > cos> dove è l'arco di curva: Û œ > sin> > c!ß d. Ü D œ >
11 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Tema alcolo differenziale per funzioni reali di più variaili 4. alcolare il seguente limite, ossia: dimostrare che il limite esiste e vale j, oppure dimostrare che non esiste, applicando criteri o teoremi studiati. B loga"b lim abßä a!ß! B sin B Þ 5. Data la funzione B Bß 0aBß œ B % per a Á a!ß! ā! per abß œ a!ß! Þ ) alcolare la derivata direzionale di 0 nell'origine rispetto al generico versore acos* ß sin* Þ ) Stailire se nell'origine vale la formula del gradiente. ) Stailire se 0 è differenziaile o meno nell'origine. (Si chiede di dimostrare ogni affermazione fatta in ase a criteri o teoremi studiati, non di limitarsi ad affermare come vanno le cose).
12 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Tema 6. Dopo aver determinato tutti i punti stazionari della seguente funzione, studiarne la natura (cioè decidere se sono punti di minimo, massimo o sella). 0aBß œ / ˆ B %B 4
13 Es Tot. Punti Prima prova in itinere di Analisi Matematica Ing. Elettronica. Ing. Telecomunicazioni Politecnico di Milano A.A. 00/0. Prof. M. Bramanti Tema n 4 ú Ing. Elettronica (arrare il proprio corso) ú Ing. Telecomunicazioni ognome e nome (in stampatello) n di matricola n d'ordine (v. elenco) on riferimento al D.Lgs. 96/00 ("Legge sulla privacy"), il docente del corso chiede allo studente il consenso a pulicare nel sito e del corso i seguenti dati dello studente: Nome, ognome, numero di matricola, esito di questa prova scritta. (Barrare e firmare) ú Dò il mio consenso ú Nego il mio consenso. Firma dello studente Equazioni differenziali. a) Scrivere l'integrale generale dell'equazione ) Risolvere il prolema di auchy: ab' ab*ab œ!þ Ú ab' ab*ab œ! Û a! œ Ü a! œ "Þ
14 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Tema 4. a) Scrivere l'integrale generale dell'equazione ) Risolvere il prolema di auchy: "B œ "B Þ "B œ "B œ a! œ " precisando il più ampio intervallo su cui è definita la soluzione del prolema. urve e integrali di linea. alcolare l'integrale di linea (.= dove è l'arco di sinusoide œ sinb per B c!ßdþ
15 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Tema 4 alcolo differenziale per funzioni reali di più variaili 4. Sia l'insieme di definizione della funzione I 0aBß œ " loga" log ab. Dopo aver determinato analiticamente l'insieme I ed averlo disegnato, dire se: I è aperto SI' ú NO ú I è chiuso SI' ú NO ú I è limitato SI' ú NO ú I è connesso SI' ú NO ú 5. Data la funzione ' B ' Bß 0aBß œ B % per a Á a!ß! ā! per abß œ a!ß! Þ ) Stailire in quali punti del piano è derivaile, calcolando esplicitamente le derivate in tal caso (semplificare le espressioni trovate!); ) Stailire in quali punti del piano è differenziaile; (Si chiede di dimostrare ogni affermazione fatta in ase a criteri o teoremi studiati, non di limitarsi ad affermare come vanno le cose).
16 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Tema 4 6. Dopo aver determinato tutti i punti stazionari della seguente funzione, studiarne la natura (cioè decidere se sono punti di minimo, massimo o sella). 0aBß œ B ab" 4
17 Es Tot. Punti Prima prova in itinere di Analisi Matematica Ing. Elettronica. Ing. Telecomunicazioni Politecnico di Milano A.A. 00/0. Prof. M. Bramanti Svolgimento Tema n ú Ing. Elettronica (arrare il proprio corso) ú Ing. Telecomunicazioni Equazioni differenziali. a) Scrivere l'integrale generale dell'equazione ab$ ab%ab œ!þ ) Determinare una soluzione particolare dell'equazione a) Integrale generale dell'omogenea: %B ab$ ab%ab œ &/ Þ! $! % œ! a! " a! % œ!à! œ "ß! œ % Þ B %B DaB œ -"/ - / Þ ) Poiché il termine noto è soluzione dell'omogenea, cerchiamo una soluzione particolare dell'equazione nella forma %B ab œ EB/ œ E/ %B a%b" œ E/ %B a"' B) %B %B E/ ca"' B) $ a%b" %Bd œ &/. Si consideri l'equazione differenziale: & E œ &àe œ " ab œ B/ %B œ Þ B" a. Determinare tutte le soluzioni dell'equazione.. Risolvere il prolema di auchy per l'equazione precedente con la condizione iniziale a! œ "Þ
18 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Svolgimento Tema c. Precisare qual è il più ampio intervallo su cui la soluzione del prolema di auchy è definita. a. Soluzioni costanti: œ!þ Per Á!ß..B " " œ à œ logkb" k- B" " œ " logk B" k - ". " œ a! œ à- œ "Þ - " ab œ " " logkb" k " " / poiché dev'essere B Á e logkb" k Á ß cioè B Á, la soluzione è definita nell'intervallo: " / " Œ ß Þ urve e integrali di linea. alcolare il momento d'inerzia di una linea materiale omogenea rappresentata da una circonferenza di raggio V e massa Q, rispetto a un asse passante per un punto della circonferenza e perpendicolare al piano che la contiene. (Prestare particolare cura nell'impostazione dell'esercizio, scrivendo esplicitamente le equazioni parametriche della curva in un opportuno riferimento e indicando qual è l'asse di rotazione in questo riferimento). irconferenza passante per l'origine: <a* œ av Vcos* ßVsin* ß* c!ß d Asse di rotazione: l'asse dall'origine nel piano abß: D, quindi la distanza del punto dall'asse è la sua distanza Q Q M œ ( ˆ B.= œ ( V a" cos* sin * V. * œ P V! QV QV QV œ ( a" cos *. * œ (.* œ % œ QV Þ!! alcolo differenziale per funzioni reali di più variaili 4. alcolare il seguente limite, ossia: dimostrare che il limite esiste e vale j, oppure dimostrare che non esiste, applicando criteri o teoremi studiati. B $B lim Œ abßä a!ß! % % B &
19 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Svolgimento Tema perciò 0aBß Ä!Þ B $B B $B B & œ B & B & 0 a Bß % % % % % % a Bß Þ B kbk k0abß k œ º º Ÿ œ kbk Ä!, B% &% abßb œ $B B 'B $ % µ $B Ä!à $B $ ˆ BßB % œ Ä Þ B% &B ) Perciò non esiste il limite di, e pertanto neanche il limite di partenza. 5. Sia 0 À 8 Ä definita da 0aB œ log kbkß per B 8 Ï a!ß! Þ `0 a. alcolare ab per œ "ßßÞÞÞß8Þ `B. Detta <a> À M Ä 8 un arco di curva regolare, calcolare..> 0 a<a> dove 0 è la funzione del punto a, e semplificare l'espressione ottenuta. c. Applicare la formula trovata al punto alla curva < À a!ß" Ä $ data da <a> œ a> cos>ß> sin>ß> e semplificare l'espressione trovata. Attenzione: i primi due punti di questo esercizio sono amientati in 8 con 8 qualsiasi. Vanno quindi svolti per 8 qualsiasi (e non per 8 œ o $ ), usando le opportune notazioni. a.. ` logkbk B BlogkBk ˆ log kbk œ œ Þ `B kbk kbk kbk 8 8. < > > >.> 0 > œ f0 > > œ a logk< a k a a a a a " > < a > œ logk< a k " > < a > < < < < a > k< a k k< a k Þ œ" œ" c.. >.> 0 > œ logk< a k a a " > < a > < < a > k< a k $ œ" <a> œ a> cos>ß> sin>ß> à
20 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Svolgimento Tema k< a> k œ È> œ > Èà < a> œ acos>> sin>ß sin>> cos>ß" $ " < a> < a> œ > cos> acos>> sin> > sin> asin>> cos> > œ >Þ œ". logš > È logš > È log> log 0 a< a> œ > œ œ Þ.> > > > 6. Dopo aver determinato tutti i punti stazionari della seguente funzione, studiarne la natura (cioè decidere se sono punti di minimo, massimo o sella). B 0aBß œ / ˆ B B B 0B œ / abab œ / ab B" œ! ā B B 0 œ / ab œ / ab œ!þ I punti stazionari sono: a!ß! à a"ß" àa"ß" Þ Matrice hessiana: L0 a Bß $ B 'B%B B %B %B œ / Œ a a Þ a%b %B! L0 a!ß! œ Œ indef.; a!ß! punto di sella L0 a"ß" œ / ' Œ def. neg. a"ß" punto di max. rel. " " ' L0 a"ß " œ / Œ def. neg. a"ß " punto di max. rel 4
21 Es Tot. Punti Prima prova in itinere di Analisi Matematica Ing. Elettronica. Ing. Telecomunicazioni Politecnico di Milano A.A. 00/0. Prof. M. Bramanti Svolgimento Tema n ú Ing. Elettronica (arrare il proprio corso) ú Ing. Telecomunicazioni Equazioni differenziali. a) Scrivere l'integrale generale dell'equazione ) Risolvere il prolema di auchy: a) Soluzione omogenea: Integrale generale dell'omogenea: ab$ ab œ BÞ Ú ab$ ab œ B Û a! œ! Ü " a! œ Þ $! $! œ!! œ!à! œ $ DaB œ -" - / $B Þ Soluzione particolare della non omogenea: cerco ab œ EB FBà ab œ EBFà ab œ EÞ E$ aebf œ BÞ E$F œ! ā'e œ E œ āf œ " $ * Integrale generale: a B " œ - " - / $B B B $ * Þ ) Soluzione del prolema di auchy: $B ab œ - / B $ *
22 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Svolgimento Tema œ a! œ -" - œ! a! œ $ - * œ " $ & & - œ à-" œ Þ ( ( & B " ab œ a"/ B BÞ ( $ *. a) Scrivere l'integrale generale dell'equazione ) Risolvere il prolema di auchy: B " œ Þ "B B B "B œ a " œ œ " B precisando il più ampio intervallo su cui è definita la soluzione del prolema. B + ab œ "B à EaB œ ' + ab.b œ log a"b " " " B œ - "B.B œ - B Þ "B œ ( ˆ B "B œ logk k ) " " ( œ a" œ œ- à- œ à " ( B œ B B "B œ log per a!ß_ Þ urve e integrali di linea. alcolare la lunghezza dell'arco di curva piana la cui equazione in forma polare è: * œ Œsin ß * c!ß dþ œ * * sin cos à % * * * *.= œ É.* œ ËŒsin Œsin cos.* œ º sin º.* * P œ ( º sin º. * œ ( sin>.> œ c cos> d! œ %Þ!!
23 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Svolgimento Tema alcolo differenziale per funzioni reali di più variaili 4. Sia l'insieme di definizione della funzione I 0aBß œ loga"b %. sinb Dopo aver determinato analiticamente l'insieme I ed averlo disegnato, dire se: I è aperto SI' ú NO ú I è chiuso SI' ú NO ú I è limitato SI' ú NO ú I è connesso SI' ú NO ú I œ abß À B % "àb Á!ß Á! Þ I è aperto SI' úx NO ú I è chiuso SI' ú NO úx I è limitato SI' úx NO ú I è connesso SI' ú NO úx 5. Data la funzione $ $ B B B Bß 0aBß œ B B per a Á a!ß! ā! per abß œ a!ß! Þ ) Stailire se 0 è continua o meno nell'origine. ) Stailire se 0 è derivaile o meno nell'origine. ) Stailire se 0 è differenziaile o meno nell'origine. (Si chiede di dimostrare ogni affermazione fatta in ase a criteri o teoremi studiati, non di limitarsi ad affermare come vanno le cose). ) Proviamo che lim abßä a!ß! 0 a Bß œ!þ $ $ $ $ kb k kbk kbk kb k kbk kbk k0abßk Ÿ Ÿ œ B B B $ $ kb k kb k kbk œ Þ B B B " $ Ora: 0 " è positivamente omogenea di grado, 0 è positivamente omogenea di grado ", 0$ è positivamente omogenea di grado ", sono tutte continue fuori dall'origine, quindi ciascuna delle tre tende a! per abß Ä a!ß!. Per il teorema del confronto anche 0aBß Ä!, quindi è continua. ) $ B `0 0aBß! œ œ Bà a!ß! œ Þ B `B
24 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Svolgimento Tema 0 a!ß œ!à In particolare, 0 è derivaile nell'origine. ) 0 differenziaile nell'origine se e solo se: `0!ß! œ!þ ` a 0aBßB Ä! per abß Ä a!ß! Þ ÈB B$ B$ B 0aBßB B B» È» È» È» B œ B $ $ B B â B œ â ab B B œ $ $ $ $ kb k kbk kb k kbk Ÿ Ÿ œ ab B ÈB ab $Î $ kb k kbk œ Þ ab $Î ab $Î " Ora: " è positivamente omogenea di grado ", è positivamente omogenea di grado, quindi entrame tendono a zero. Per il teorema del confronto, il limite desiderato è zero, e 0 è differenziaile nell'origine. 6. Dopo aver determinato tutti i punti stazionari della seguente funzione, studiarne la natura (cioè decidere se sono punti di minimo, massimo o sella). 0aBß œ B ab" 0B œ $B B B œ B a$b œ! œ $ 0 œ B B B œ B ab" œ!þ $ I punti stazionari sono: " " a" ß! à Œ ß à e la retta a!ß! Þ % Matrice hessiana: L0 a Bß "$B B $B% œ Œ a a Þ B a$b% B! " L0 a" ß! œ Œ indef.; a" ß! punto di sella " $ " " " ) % " " L0Œ ß œ " " def. neg. Œ ß punto di max. rel. % % % 4
25 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Svolgimento Tema! a"!! L0 a!ß! œ Œ semidef. a!ß! casi dui.!! Studiamo i punti della retta B œ! mediante il segno, poiché 0 a!ß! œ!. Lo studio del segno ci dice che: i punti a!ß! per! ā " e per!! sono punti di massimo relativo (perché in quei punti 0 è nulla e in un intorno è negativa); per!! " sono punti di minimo relativo (perché in quei punti 0 è nulla e in un intorno è positiva); i punti a!ß! e a!ß" sono di sella (perché in quei punti 0 è nulla e in ogni intorno camia di segno). 5
26 Es Tot. Punti Prima prova in itinere di Analisi Matematica Ing. Elettronica. Ing. Telecomunicazioni Politecnico di Milano A.A. 00/0. Prof. M. Bramanti Svolgimento Tema n ú Ing. Elettronica (arrare il proprio corso) ú Ing. Telecomunicazioni Equazioni differenziali. a) Scrivere l'integrale generale dell'equazione abab œ!þ ) Determinare una soluzione particolare dell'equazione a) Integrale generale dell'omogenea: ) B abab œ $/ sinbþ! œ!! œ È DaB œ - cosš ÈB - sinš ÈB Þ " B Ba" $/ sinb œ Imˆ $/ erchiamo una soluzione particolare dell'equazione complessa della forma A A œ $/ AaB œ E/ Ba" Ba" A œ Ea" / Ba" Ba" Ba" E/ a" œ $/ $ a"% $ E œ œ $ œ a"% "% ""' "(
27 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Svolgimento Tema $ Ba" $ B AaB œ a"%/ œ / a"%acosb sinb "( "(. Risolvere il prolema di auchy: $ ab œ ImAaB œ / B asinb% cosb "( sinb ' œ cos ā ˆ œ e precisare qual è il più ampio intervallo su cui la soluzione del prolema di auchy è definita. Risolviamo l'equazione a variaili separaili: ( cos. œ ( sinb.b sin œ cosb- Imponiamo la condizione iniziale: sin œ cos - ' " œ - " sin œ cosbþ Devo risolvere l'equazione in, quando B varia in un intorno di B œ. La condizione " " $ " Ÿ Ÿ B Ÿ Ÿ B Ÿ cos B Ÿ " dà cos, quindi $. $ In questo intervallo risulta ab œ arcsin Œ " B cos B per $ $ (negli estremi dell'intervallo la funzione arcsin non è derivaile). urve e integrali di linea. alcolare l'integrale di linea ( È D.=
28 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Svolgimento Tema dove è l'arco di curva: ÚB œ > cos> Û œ > sin> Ü D œ > > c!ß d. < a> œ acos>> sin>ß sin>> cos>ß> k< a> k œ Éacos>> sin> asin>> cos> a>.> œ œ È "&>.>Þ ( È ( È " D.= œ > "&>.> œ ˆ "&> œ "&! $Î! " œ "! " Þ "& ˆ $Î alcolo differenziale per funzioni reali di più variaili 4. alcolare il seguente limite, ossia: dimostrare che il limite esiste e vale j, oppure dimostrare che non esiste, applicando criteri o teoremi studiati. B loga"b lim abßä a!ß! B sin B Þ alcoliamo il limite di qualche restrizione. 0 BßB œ B "B $ loga a B sin BB µ B B µ B œ B B% B B Ä!Þ $ $ B "B B B " 0ˆ loga BßB œ µ œ Þ B sin BB% B% B % $ Poiché restrizioni di 0 lungo curve diverse hanno limiti diversi, il limite di partenza non esiste. 5. Data la funzione B Bß 0aBß œ B % per a Á a!ß! ā! per abß œ a!ß! Þ ) alcolare la derivata direzionale di 0 nell'origine rispetto al generico versore acos* ß sin* Þ ) Stailire se nell'origine vale la formula del gradiente. ) Stailire se 0 è differenziaile o meno nell'origine. (Si chiede di dimostrare ogni affermazione fatta in ase a criteri o teoremi studiati, non di limitarsi ad affermare come vanno le cose).
29 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Svolgimento Tema. $ > cos* sin * > cos* sin * > sin * a> œ 0 a> cos* ß> sin* œ œ µ per > Ä!ß > cos * > % sin% * cos * > sin% * cos* purché sia cos* Á 0. Per cos* Á 0 si ha H acos* ßsin* sin * 0 a!ß! œ a! œ à cos* per cos* œ! è a>! e Ha0ß 0 a!ß! œ!þ. La formula del gradiente non vale nell'origine perché la generica derivata direzionale non è cominazione lineare di cos* ß sin*.. Pertanto 0 non è differenziaile nell'origine. 6. Dopo aver determinato tutti i punti stazionari della seguente funzione, studiarne la natura (cioè decidere se sono punti di minimo, massimo o sella). I punti stazionari sono: Matrice hessiana: 0aBß œ / ˆ B %B 0B œ / ab% œ / ab œ! œ 0 œ / a B %B% œ!þ Š ß" È$ Þ a%b L0aBß œ / Œ Þ a%b %BB a% L0 Š ß" È Š " È$! $ œ / Œ Š ß" È$! % È indef.; punto di sella $ L0 Š ß" È " È$! $ œ / Œ Š ß" È$! % È def. pos.; punto di min. rel. $ 4
30 Es Tot. Punti Prima prova in itinere di Analisi Matematica Ing. Elettronica. Ing. Telecomunicazioni Politecnico di Milano A.A. 00/0. Prof. M. Bramanti Svolgimento Tema n 4 ú Ing. Elettronica (arrare il proprio corso) ú Ing. Telecomunicazioni Equazioni differenziali. a) Scrivere l'integrale generale dell'equazione ) Risolvere il prolema di auchy: a) ab' ab*ab œ!þ Ú ab' ab*ab œ! Û a! œ Ü a! œ "Þ! '! * œ! Integrale generale:! œ $ $B ab œ / a- B- Þ " ) $B ab œ / a$ - B$- - " " œ a! œ - œ a! œ $- - œ " " - œ à- œ ( " $B ab œ / a(b Þ. a) Scrivere l'integrale generale dell'equazione ) Risolvere il prolema di auchy: "B œ "B Þ "B œ "B œ a! œ " precisando il più ampio intervallo su cui è definita la soluzione del prolema.
31 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Svolgimento Tema 4 a). + ab œ "B à EaB œ ' + ab.b œ log ˆ "B "B "B "B "B œ Œ œ- ( Œ ˆ "B.B œ Œ œ- ( "B.B œ "B "B a "B "B a"b $ œ Œ - Þ "B ā $ Ÿ " ) " œ a! œ œ- à- œ à $ $ "B a"b $ œ Œ B "B ā$ $ Ÿ per a"ß" perché a"ß" è il più ampio intervallo contenente B! œ!, in cui la soluzione e i coefficienti dell'equazione sono definiti. E' accettaile anche la risposta "per B a"ß_ " in quanto la soluzione è definita in questo intervallo; in B œ " la soluzione si annulla, il denominatore del coefficiente + ab si annulla ma, nel senso dei limiti, l'equazione è ancora soddisfatta. urve e integrali di linea. alcolare l'integrale di linea (.= dove è l'arco di sinusoide œ sinb per B c!ßdþ.= œ É"0 ab.b œ È" cos B.B (.= œ (! sinb È " cos B.B œ ccosb œ > d " " " œ ( È">.> œ ( È">.> œ ( È">.> œ c> œ Sh? d " "! SettSh" œ ( h?.? œ csh? h?? d œ È SettSh ".! SettSh"!
32 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Svolgimento Tema 4 alcolo differenziale per funzioni reali di più variaili 4. Sia l'insieme di definizione della funzione I 0aBß œ " loga" log ab. Dopo aver determinato analiticamente l'insieme I ed averlo disegnato, dire se: I è aperto SI' ú NO ú I è chiuso SI' ú NO ú I è limitato SI' ú NO ú I è connesso SI' ú NO ú I œ abß À! B " o " B / Þ I è aperto SI' úx NO ú I è chiuso SI' ú NO úx I è limitato SI' ú NO úx I è connesso SI' ú NO úx 5. Data la funzione ' B ' Bß 0aBß œ B % per a Á a!ß! ā! per abß œ a!ß! Þ ) Stailire in quali punti del piano è derivaile, calcolando esplicitamente le derivate in tal caso (semplificare le espressioni trovate!); ) Stailire in quali punti del piano è differenziaile; (Si chiede di dimostrare ogni affermazione fatta in ase a criteri o teoremi studiati, non di limitarsi ad affermare come vanno le cose). ) Fuori dall'origine 0 è certamente derivaile. alcoliamo: `0 `B œ `0 ` œ & 'B ˆ % B ' ' BaB B œ %B 'B B % B % a a ( & % ' & ' ˆ % B $ ' ' % ab B œ 'B %B % B % a a & * ' $ Nell'origine: % `0 $ `0 0aBß! œ B à abß! œ %B à a!ß! œ!à `B `B `0 `0 0 a!ß œ à a!ß œ à a!ß! œ!þ ` ` ) Le derivate parziali calcolate al punto precedente sono evidentemente continue fuori " dall'origine, quindi 0 G a Ï a!ß! e pertanto è differenziaile fuori dall'origine. Studiamo la differenziailità nell'origine.
33 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Svolgimento Tema 4 0 differenziaile in a!ß! se e solo se 0aBß B Ä! per abß Ä a!ß! Þ È 0aBß» È» œ B ' ' B ab % ÈB œ ' ' ' ' B B œ Ÿ ab % ÈB ab % ÈB B ÈB % È œ $ B kk Ä! 0aBß B per abß Ä a!ß!. Per il teorema del confronto, anche Ä!, e 0 è differenziaile nell'origine. È 6. Dopo aver determinato tutti i punti stazionari della seguente funzione, studiarne la natura (cioè decidere se sono punti di minimo, massimo o sella). 0aBß œ B ab" 0B œ a"b œ! œ 0 œ BaB$ œ!þ I punti stazionari sono: " " a!ß" à Œ ß à e la retta ab! ß! Þ % Matrice hessiana: a%b$ L0aBß œ Œ Þ a%b$ Ba"B$ " L0 a!ß" œ Œ "! indef.; a!ß" punto di sella " " L0Œ " " % ß œ Œ " " " $ def. pos. ß punto di min. rel. % % % )!! L0aB! ß! œ Œ ab ß! B a semidef.! "B! casi dui.!! Studiamo i punti della retta œ! mediante il segno, poiché 0aB! ß! œ!. Lo studio del segno ci dice che: i punti ab! ß! per B! ā " e per B!! sono punti di minimo relativo (perché in quei punti 0 è nulla e in un intorno è positiva); per! B! " sono punti di massimo relativo (perché in quei punti 0 è nulla e in un intorno è negativa); 4
34 Prima prova in itinere di Analisi Matematica. Prof. Bramanti. A.A. 00/. Svolgimento Tema 4 i punti a!ß! e a!ß" sono di sella (perché in quei punti 0 è nulla e in ogni intorno camia di segno). 5
Secondo Appello di Analisi Matematica 2 Ing. Elettronica Politecnico di Milano A.A. 2014/2015. Prof. M. Bramanti Tema n 1
 Es. 2 3 4 5 6 7 8 Tot. Punti Secondo Appello di Analisi Matematica 2 Ing. Elettronica Politecnico di Milano A.A. 204/205. Prof. M. ramanti Tema n Cognome e nome (in stampatello) codice persona n d'ordine
Es. 2 3 4 5 6 7 8 Tot. Punti Secondo Appello di Analisi Matematica 2 Ing. Elettronica Politecnico di Milano A.A. 204/205. Prof. M. ramanti Tema n Cognome e nome (in stampatello) codice persona n d'ordine
Prima prova in itinere di Analisi Matematica 1 Ingegneria Elettronica Politecnico di Milano A.A. 2008/2009. Prof. M.
 Es. 5 6 Tot. Punti Prima prova in itinere di Analisi Matematica Ingegneria Elettronica Politecnico di Milano A.A. 008/009. Prof. M. Bramanti Tema n Cognome e nome (in stampatello) n di matricola n d'ordine
Es. 5 6 Tot. Punti Prima prova in itinere di Analisi Matematica Ingegneria Elettronica Politecnico di Milano A.A. 008/009. Prof. M. Bramanti Tema n Cognome e nome (in stampatello) n di matricola n d'ordine
Primo Appello di Analisi Matematica 2 Ing. Elettronica. Ing. Telecomunicazioni Politecnico di Milano A.A. 2010/2011. Prof. M.
 Es. 2 3 4 5 6 7 8 Tot. Punti Primo Appello di Analisi Matematica 2 Ing. Elettronica. Ing. Telecomunicazioni Politecnico di Milano A.A. 200/20. Prof. M. Bramanti Tema n ú Ing. Elettronica (arrare il proprio
Es. 2 3 4 5 6 7 8 Tot. Punti Primo Appello di Analisi Matematica 2 Ing. Elettronica. Ing. Telecomunicazioni Politecnico di Milano A.A. 200/20. Prof. M. Bramanti Tema n ú Ing. Elettronica (arrare il proprio
Prima prova in itinere di Analisi Matematica 1 Ingegneria Elettronica Politecnico di Milano A.A. 2011/2012. Prof. M.
 Es. 5 6 Tot. Punti Prima prova in itinere di Analisi Matematica Ingegneria Elettronica Politecnico di Milano A.A. 0/0. Prof. M. ramanti Tema n Cognome e nome (in stampatello) n di matricola n d'ordine
Es. 5 6 Tot. Punti Prima prova in itinere di Analisi Matematica Ingegneria Elettronica Politecnico di Milano A.A. 0/0. Prof. M. ramanti Tema n Cognome e nome (in stampatello) n di matricola n d'ordine
Secondo appello di Analisi Matematica 1 Ingegneria Elettronica Politecnico di Milano A.A. 2011/2012. Prof. M. Bramanti Tema n 1
 Es. 4 6 7 Tot. Punti Secondo appello di Analisi Matematica Ingegneria Elettronica Politecnico di Milano A.A. 0/0. Prof. M. ramanti Tema n Cognome e nome in stampatello) n di matricola n dordine v. elenco)
Es. 4 6 7 Tot. Punti Secondo appello di Analisi Matematica Ingegneria Elettronica Politecnico di Milano A.A. 0/0. Prof. M. ramanti Tema n Cognome e nome in stampatello) n di matricola n dordine v. elenco)
Seconda prova in itinere di Analisi Matematica 1 Ingegneria Elettronica Politecnico di Milano A.A. 2011/2012. Prof. M.
 Es. 2 3 4 5 6 Tot. Punti Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica Politecnico di Milano A.A. 20/202. Prof. M. ramanti Tema n Cognome e nome (in stampatello) n di matricola
Es. 2 3 4 5 6 Tot. Punti Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica Politecnico di Milano A.A. 20/202. Prof. M. ramanti Tema n Cognome e nome (in stampatello) n di matricola
Secondo appello di Analisi Matematica 1 Ingegneria Elettronica Politecnico di Milano A.A. 2013/2014. Prof. M. Bramanti Tema n 1
 Es. 2 3 4 5 6 7 8 Tot. Punti Secondo appello di Analisi Matematica Ingegneria Elettronica Politecnico di Milano A.A. 203/204. Prof. M. ramanti Tema n Cognome e nome (in stampatello) n di matricola n d'ordine
Es. 2 3 4 5 6 7 8 Tot. Punti Secondo appello di Analisi Matematica Ingegneria Elettronica Politecnico di Milano A.A. 203/204. Prof. M. ramanti Tema n Cognome e nome (in stampatello) n di matricola n d'ordine
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Recupero sul 1 compitino di Analisi Matematica 2 Ing. Elettronica Politecnico di Milano A.A. 2014/2015. Prof. M. Bramanti Tema n 1
 Es. 4 5 6 Tot. Punti Recupero sul compitino di Analisi Matematica Ing. Elettronica Politecnico di Milano A.A. 04/05. Prof. M. ramanti Tema n Cognome e nome (in stampatello) codice persona n d'ordine (v.
Es. 4 5 6 Tot. Punti Recupero sul compitino di Analisi Matematica Ing. Elettronica Politecnico di Milano A.A. 04/05. Prof. M. ramanti Tema n Cognome e nome (in stampatello) codice persona n d'ordine (v.
Primo Appello di Analisi Matematica 1 Ingegneria Elettronica. Politecnico di Milano A.A. 2008/2009. Prof. M. Bramanti Svolgimento Tema n 1
 Es. 3 4 5 6 7 8 Tot. Punti Primo Appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 008/009. Prof. M. ramanti Svolgimento Tema n 0 crediti (ord. L.70). Numeri complessi. Risolvere
Es. 3 4 5 6 7 8 Tot. Punti Primo Appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano A.A. 008/009. Prof. M. ramanti Svolgimento Tema n 0 crediti (ord. L.70). Numeri complessi. Risolvere
Recupero sul 1 compitino di Analisi Matematica 1 Ingegneria Elettronica Politecnico di Milano A.A. 2013/2014. Prof. M.
 Es. 2 4 5 6 Tot. Punti Recupero sul compitino di Analisi Matematica Ingegneria Elettronica Politecnico di Milano A.A. 20/204. Prof. M. Bramanti Tema n Cognome e nome (in stampatello) codice persona (o
Es. 2 4 5 6 Tot. Punti Recupero sul compitino di Analisi Matematica Ingegneria Elettronica Politecnico di Milano A.A. 20/204. Prof. M. Bramanti Tema n Cognome e nome (in stampatello) codice persona (o
Cognome e nome (in stampatello) n di matricola n d'ordine (v. elenco)
 Es. 2 4 5 6 Tot. Punti Seconda prova in itinere di Analisi Matematica 2 Ing. Elettronica. Ing. Telecomunicazioni Politecnico di Milano A.A. 200/20. Prof. M. Bramanti Tema n ú Ing. Elettronica (barrare
Es. 2 4 5 6 Tot. Punti Seconda prova in itinere di Analisi Matematica 2 Ing. Elettronica. Ing. Telecomunicazioni Politecnico di Milano A.A. 200/20. Prof. M. Bramanti Tema n ú Ing. Elettronica (barrare
Prima prova in itinere di Analisi Matematica 1 Ingegneria Elettronica. Politecnico di Milano. A.A. 2015/2016. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 0/06. Prof. M. Bramanti Tema n 4 6 Tot. Cognome e nome (in stampatello) codice persona (o n di
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 0/06. Prof. M. Bramanti Tema n 4 6 Tot. Cognome e nome (in stampatello) codice persona (o n di
Seconda prova in itinere di Analisi Matematica 2 Ingegneria Elettronica Politecnico di Milano A.A. 2014/2015. Prof. M.
 Es. 3 4 5 6 Tot. Punti Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica Politecnico di Milano A.A. 04/05. Prof. M. Bramanti Tema n Cognome e nome (in stampatello) codice persona n
Es. 3 4 5 6 Tot. Punti Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica Politecnico di Milano A.A. 04/05. Prof. M. Bramanti Tema n Cognome e nome (in stampatello) codice persona n
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
Estremi. 5. Determinare le dimensioni di una scatola rettangolare di volume v assegnato, che abbia la superficie minima.
 Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
Primo appello di Analisi Matematica 1 Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 2015/2016. Prof. M. Bramanti.
 Primo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 5/6. Prof. M. Bramanti Tema n 5 6 7 Tot. Cognome e nome in stampatello codice persona o n di matricola n
Primo appello di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 5/6. Prof. M. Bramanti Tema n 5 6 7 Tot. Cognome e nome in stampatello codice persona o n di matricola n
Domande da 6 punti. Prima parte del programma
 Domande da 6 punti Prima parte del programma Domanda. Dare la definizione di arco di curva continua, di sostegno di una curva, di curva chiusa, di curva semplice e di curva piana fornendo qualche esempio.
Domande da 6 punti Prima parte del programma Domanda. Dare la definizione di arco di curva continua, di sostegno di una curva, di curva chiusa, di curva semplice e di curva piana fornendo qualche esempio.
ESAME DI MATEMATICA I parte Vicenza, 05/06/2017. x log 2 x?
 A. Peretti Svolgimento dei temi d esame di Matematica A.A. 6/7 ESAME DI MATEMATICA I parte Vicenza, 5/6/7 log? Domanda. Per quali valori di è definita l espressione L espressione è definita se l argomento
A. Peretti Svolgimento dei temi d esame di Matematica A.A. 6/7 ESAME DI MATEMATICA I parte Vicenza, 5/6/7 log? Domanda. Per quali valori di è definita l espressione L espressione è definita se l argomento
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
1. Disegnare nel piano di Gauss i seguenti insiemi di numeri complessi:
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Test di autovalutazione 1. Disegnare nel piano di Gauss i seguenti insiemi di numeri complessi: (a) A = {z C : z, 0 arg z /} (b) B = {w
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Test di autovalutazione 1. Disegnare nel piano di Gauss i seguenti insiemi di numeri complessi: (a) A = {z C : z, 0 arg z /} (b) B = {w
a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;
![a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [; a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;](/thumbs/69/60588320.jpg) ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
Corso di Laurea in Ingegneria Gestionale - Sede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame
 Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Analisi Matematica 2, Scritto Generale, Per quali valori di > e uniformemente convergente per ogni x 2 [; +) la serie di funzioni n x + n 4 x
 Analisi Matematica 2, Scritto Generale, 6-5-994. Consideriamo la serie di Fourier f (x) = a k= [a k cos(kx) + b k sen (kx)] ; dove f (x) = jxj per x 2 ( ; ) e una funzione pari. a. Calcolare i coecienti
Analisi Matematica 2, Scritto Generale, 6-5-994. Consideriamo la serie di Fourier f (x) = a k= [a k cos(kx) + b k sen (kx)] ; dove f (x) = jxj per x 2 ( ; ) e una funzione pari. a. Calcolare i coecienti
Maturità Scientifica, Corso di ordinamento, Sessione Ordinaria
 Matematica per la nuova maturità scientifica A. Bernardo M. Pedone 7 Problema 1 Maturità Scientifica, Corso di ordinamento, Sessione Ordinaria 001-00 In un piano, riferito a un sistema di assi cartesiani
Matematica per la nuova maturità scientifica A. Bernardo M. Pedone 7 Problema 1 Maturità Scientifica, Corso di ordinamento, Sessione Ordinaria 001-00 In un piano, riferito a un sistema di assi cartesiani
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti sulle funzioni di variabile complessa (1)
 Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti sulle funzioni di variabile complessa 1) Marco Bramanti Politecnico di Milano November 7, 2016 1 Funzioni olomorfe e campi di
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti sulle funzioni di variabile complessa 1) Marco Bramanti Politecnico di Milano November 7, 2016 1 Funzioni olomorfe e campi di
Corso di Laurea in Chimica e Tecnologia Farmaceutiche Matematica con Elementi di Informatica COMPITO 19 Febbraio 2016
 Corso di Laurea in Chimica e Tecnologia Farmaceutiche Matematica con Elementi di Informatica COMPITO 19 Febbraio 2016 Nome Cognome Matricola Punteggi 10 cfu Teoria Ex.1 Ex.2 Ex.3 Ex. 4 Ex.5 /6 /5 /5 /5
Corso di Laurea in Chimica e Tecnologia Farmaceutiche Matematica con Elementi di Informatica COMPITO 19 Febbraio 2016 Nome Cognome Matricola Punteggi 10 cfu Teoria Ex.1 Ex.2 Ex.3 Ex. 4 Ex.5 /6 /5 /5 /5
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Secondo compito in itinere 3 Febbraio 2014
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Febbraio 04 Cognome: Nome: Matricola: Compito A Es: 8 punti Es: 8 punti Es: 8 punti Es4: 8 punti Totale a) Determinare
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Febbraio 04 Cognome: Nome: Matricola: Compito A Es: 8 punti Es: 8 punti Es: 8 punti Es4: 8 punti Totale a) Determinare
ESERCIZIO SVOLTO N 1 ESERCIZIO SVOLTO N 2. Determinare e rappresentare graficamente il dominio della funzione
 ESERCIZIO SVOLTO N 1 Determinare e rappresentare graficamente il dominio della funzione f(x, y) = y 2 x 2 Trovare gli eventuali punti stazionari e gli estremi di f Il dominio della funzione è dato da dom
ESERCIZIO SVOLTO N 1 Determinare e rappresentare graficamente il dominio della funzione f(x, y) = y 2 x 2 Trovare gli eventuali punti stazionari e gli estremi di f Il dominio della funzione è dato da dom
A Analisi Matematica 2 (Corso di Laurea in Informatica) Simulazione compito d esame
 COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/0/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/0/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/0/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/0/03) Università di Verona - Laurea in Biotecnologie
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Esercizi su massimi e minimi locali
 Esercizi su massimi e minimi locali Determinare i punti di massimo locale, di minimo locale o di sella delle seguenti funzioni: 1. f(x, y = (x 1 2 + y 2 2. f(x, y = (x 1 2 y 2 3. f(x, y = x 2 + xy + y
Esercizi su massimi e minimi locali Determinare i punti di massimo locale, di minimo locale o di sella delle seguenti funzioni: 1. f(x, y = (x 1 2 + y 2 2. f(x, y = (x 1 2 y 2 3. f(x, y = x 2 + xy + y
Svolgimento. f y (x, y) = 8 y 2 x. 1 x 2 y = 0. y 2 x = 0. (si poteva anche ricavare la x dalla seconda equazione e sostituire nella prima)
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 2013-2014 (dott.ssa Vita Leonessa) Esercizi svolti: Ricerca di massimi e minimi di funzioni a
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 2013-2014 (dott.ssa Vita Leonessa) Esercizi svolti: Ricerca di massimi e minimi di funzioni a
Soluzioni delle Esercitazioni VIII 21-25/11/2016. = lnx ln1 = lnx. f(t)dt.
 Esercitazioni di Matematica Esercitazioni VIII -5//6 Soluzioni delle Esercitazioni VIII -5//6 A. Funzione integrale. La funzione integrale di f nell intervallo [, ] è per definizione F() = dt con [,].
Esercitazioni di Matematica Esercitazioni VIII -5//6 Soluzioni delle Esercitazioni VIII -5//6 A. Funzione integrale. La funzione integrale di f nell intervallo [, ] è per definizione F() = dt con [,].
(a) Le derivate parziali f x. f y = x2 + 2xy + 3 si annullano contemporaneamente in (1, 2) e ( 1, 2). Le derivate seconde di f valgono.
 Esercizio 1 Si consideri la funzione f(x, y) = x 2 y + xy 2 + y (a) Determinare i punti di massimo e minimo relativo e di sella del grafico di f. (b) Determinare i punti di massimo e minimo assoluto di
Esercizio 1 Si consideri la funzione f(x, y) = x 2 y + xy 2 + y (a) Determinare i punti di massimo e minimo relativo e di sella del grafico di f. (b) Determinare i punti di massimo e minimo assoluto di
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
ORDINAMENTO 2011 QUESITO 1
 www.matefilia.it ORDINAMENTO 0 QUESITO Consideriamo la sezione della sfera e del cilindro con un piano passante per l asse del cilindro: Indicando con x il diametro di base del cilindro, con y la sua altezza
www.matefilia.it ORDINAMENTO 0 QUESITO Consideriamo la sezione della sfera e del cilindro con un piano passante per l asse del cilindro: Indicando con x il diametro di base del cilindro, con y la sua altezza
Corso di Laurea in Informatica/Informatica Multimediale Esercizi Analisi Matematica 2
 a.a 2005/06 Corso di Laurea in Informatica/Informatica Multimediale Esercizi Analisi Matematica 2 Funzioni di due variabili a cura di Roberto Pagliarini Vediamo prima di tutto degli esercizi sugli insiemi
a.a 2005/06 Corso di Laurea in Informatica/Informatica Multimediale Esercizi Analisi Matematica 2 Funzioni di due variabili a cura di Roberto Pagliarini Vediamo prima di tutto degli esercizi sugli insiemi
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f è crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f è crescente nell intervallo (a, b) se
Richiami sullo studio di funzione
 Richiami sullo studio di funzione Per studiare una funzione y = f() e disegnarne un grafico approssimativo, possiamo procedere in ordine secondo i seguenti passi:. determinare il campo di esistenza (o
Richiami sullo studio di funzione Per studiare una funzione y = f() e disegnarne un grafico approssimativo, possiamo procedere in ordine secondo i seguenti passi:. determinare il campo di esistenza (o
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2007 Sessione suppletiva
 ESAME DI STAT DI LIE SIENTIFI RS DI RDINAMENT 7 Sessione suppletiva Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PRBLEMA Rispetto a un sistema di assi cartesiani
ESAME DI STAT DI LIE SIENTIFI RS DI RDINAMENT 7 Sessione suppletiva Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PRBLEMA Rispetto a un sistema di assi cartesiani
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Bacchelli - a.a. 2010/2011.
 Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
Derivate delle funzioni di una variabile.
 Derivate delle funzioni di una variabile. Il concetto di derivata di una funzione di una variabile è uno dei più fecondi della matematica ed è quello su cui si basa il calcolo differenziale. I problemi
Derivate delle funzioni di una variabile. Il concetto di derivata di una funzione di una variabile è uno dei più fecondi della matematica ed è quello su cui si basa il calcolo differenziale. I problemi
Soluzione. Il dominio E consiste nella parte di spazio contenuta nella sfera ma esterna al cono rappresentata in Figura 1. Infatti
 Esercizio 1 (G. Ziglio). (6 punti) Calcolare il volume della porzione di spazio E interna alla sfera di equazione x 2 + y 2 + z 2 = 1 ed esterna al cono di equazione z 2 = x 2 + y 2 E = (x, y, z) R x 2
Esercizio 1 (G. Ziglio). (6 punti) Calcolare il volume della porzione di spazio E interna alla sfera di equazione x 2 + y 2 + z 2 = 1 ed esterna al cono di equazione z 2 = x 2 + y 2 E = (x, y, z) R x 2
Studiamo adesso il comportamento di f(x) alla frontiera del dominio. Si. x 0 lim f(x) = lim. x 2 +
 Esercizi del 2//09. Data la funzione f(x) = ln(x 2 2x) (a) trovare il dominio, gli eventuali asintoti e gli intervalli in cui la funzione cresce o decresce. Disegnare il grafico della funzione. (b) Scrivere
Esercizi del 2//09. Data la funzione f(x) = ln(x 2 2x) (a) trovare il dominio, gli eventuali asintoti e gli intervalli in cui la funzione cresce o decresce. Disegnare il grafico della funzione. (b) Scrivere
Matematica 2. Derivate Esercizi. y=sen( x 4 3x) y' =cos(x 4 3x)(4x 3 3) y=logsen( x x) y' = sen(x 4 +3x) cos(x4 +3x)(4x 3 +3)
 Matematica 2 Derivate Esercizi y=sen( 4 3) y' =cos( 4 3)(4 3 3) y=logsen( 4 1 3) y' = sen( 4 +3) cos(4 +3)(4 3 +3) y=sen 2 ( 4 3) y' =2sen( 4 3 )cos( 4 3)(4 3 3) Funzioni ad una sola variabile y=f() è
Matematica 2 Derivate Esercizi y=sen( 4 3) y' =cos( 4 3)(4 3 3) y=logsen( 4 1 3) y' = sen( 4 +3) cos(4 +3)(4 3 +3) y=sen 2 ( 4 3) y' =2sen( 4 3 )cos( 4 3)(4 3 3) Funzioni ad una sola variabile y=f() è
INTEGRALI INDEFINITI e DEFINITI Esercizi risolti
 INTEGRALI INDEFINITI e DEFINITI Esercizi risolti E data la funzione f( = (a Provare che la funzione F ( = + arcsin è una primitiva di f( sull intervallo (, (b Provare che la funzione G( = + arcsin π è
INTEGRALI INDEFINITI e DEFINITI Esercizi risolti E data la funzione f( = (a Provare che la funzione F ( = + arcsin è una primitiva di f( sull intervallo (, (b Provare che la funzione G( = + arcsin π è
Istituzioni di Matematiche Modulo B (SG)
 Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
Soluzioni dei quesiti della maturità scientifica A.S. 2007/2008
 Soluzioni dei quesiti della maturità scientifica A.S. 007/008 Nicola Gigli Sun-Ra Mosconi 19 giugno 008 1. La proposizione è falsa. Per trovare un controesempio ad essa, si consideri un qualunque piano
Soluzioni dei quesiti della maturità scientifica A.S. 007/008 Nicola Gigli Sun-Ra Mosconi 19 giugno 008 1. La proposizione è falsa. Per trovare un controesempio ad essa, si consideri un qualunque piano
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Universita degli Studi di Ancona - Facolta di Ingegneria Laurea in Ing. Elettronica (VO) Ing. Informatica e Automatica - Ing. delle Telecomunicazioni
 Universita degli Studi di Ancona - Facolta di Ingegneria Laurea in Ing. Elettronica (VO) Ing. Informatica e Automatica - Ing. delle Telecomunicazioni ANALISI NUMERICA - Primo Parziale - TEMA A (Prof. A.M.Perdon)
Universita degli Studi di Ancona - Facolta di Ingegneria Laurea in Ing. Elettronica (VO) Ing. Informatica e Automatica - Ing. delle Telecomunicazioni ANALISI NUMERICA - Primo Parziale - TEMA A (Prof. A.M.Perdon)
Problema ( ) = 0,!
 Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Applicazioni delle serie e degli integrali generalizzati al calcolo delle probabilità
 Applicazioni delle serie e degli integrali generalizzati al calcolo delle proailità Marco Bramanti Gennaio 202 Questi appunti, scritti per il corso di Analisi Matematica, esulano in realtà dal programma
Applicazioni delle serie e degli integrali generalizzati al calcolo delle proailità Marco Bramanti Gennaio 202 Questi appunti, scritti per il corso di Analisi Matematica, esulano in realtà dal programma
LE COORDINATE CARTESIANE
 CORSO ZERO DI MATEMATICA per Ing. Chimica e Ing. delle Telecomunicazioni GEOMETRIA ANALITICA Prof. Erasmo Modica erasmo@galois.it LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate
CORSO ZERO DI MATEMATICA per Ing. Chimica e Ing. delle Telecomunicazioni GEOMETRIA ANALITICA Prof. Erasmo Modica erasmo@galois.it LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate
SESSIONE SUPPLETIVA QUESTIONARIO QUESITO 1
 www.matefilia.it SESSIONE SUPPLETIVA 216 - QUESTIONARIO QUESITO 1 Si consideri questa equazione differenziale: y + 2y + 2y = x. Quale delle seguenti funzioni ne è una soluzione? Si giustifichi la risposta.
www.matefilia.it SESSIONE SUPPLETIVA 216 - QUESTIONARIO QUESITO 1 Si consideri questa equazione differenziale: y + 2y + 2y = x. Quale delle seguenti funzioni ne è una soluzione? Si giustifichi la risposta.
Tutorato di Analisi 2 - AA 2014/15
 Tutorato di Analisi - AA / Emanuele Fabbiani marzo Funzioni in più variabili. Dominio Determinare e rappresentare gracamente il più grande insieme di R n che può essere dominio delle seguenti funzioni.
Tutorato di Analisi - AA / Emanuele Fabbiani marzo Funzioni in più variabili. Dominio Determinare e rappresentare gracamente il più grande insieme di R n che può essere dominio delle seguenti funzioni.
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Seconda prova in itinere 31 gennaio 2011
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Seconda prova in itinere 3 gennaio Cognome: Nome: Matricola: Compito A Es. : 8 punti Es. : 8 punti Es. 3: 8 punti Es. 4: 8 punti Es. 5:
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Seconda prova in itinere 3 gennaio Cognome: Nome: Matricola: Compito A Es. : 8 punti Es. : 8 punti Es. 3: 8 punti Es. 4: 8 punti Es. 5:
Soluzioni degli esercizi proposti nella sessione estiva Terni Perugia. F NdS. div F = 2 div F dxdydz = 2volume (V ) = 36π.
 Soluzioni degli esercizi proposti nella sessione estiva 2-2 Terni Perugia ) Sia F = (2x, y, z) e V il volume delimitato dalle superfici: la semisfera S := z = 9 x 2 y 2 ed il disco S 2 di equazione z =,
Soluzioni degli esercizi proposti nella sessione estiva 2-2 Terni Perugia ) Sia F = (2x, y, z) e V il volume delimitato dalle superfici: la semisfera S := z = 9 x 2 y 2 ed il disco S 2 di equazione z =,
Analisi Matematica II - INGEGNERIA Gestionale - B 20 luglio 2017 Cognome: Nome: Matricola:
 Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = e (x3 +x) y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Alcuni esercizi: funzioni di due variabili e superfici
 ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.008-009 - Prof. G.Cupini Alcuni esercizi: funzioni di due variabili e superfici
ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.008-009 - Prof. G.Cupini Alcuni esercizi: funzioni di due variabili e superfici
10 - Applicazioni del calcolo differenziale
 Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del secondo appello, 1 febbraio 2017 Testi 1
 Analisi Matematica I per Ingegneria Gestionale, a.a. 206-7 Scritto del secondo appello, febbraio 207 Testi Prima parte, gruppo.. Trovare le [0, π] che risolvono la disequazione sin(2) 2. 2. Dire se esistono
Analisi Matematica I per Ingegneria Gestionale, a.a. 206-7 Scritto del secondo appello, febbraio 207 Testi Prima parte, gruppo.. Trovare le [0, π] che risolvono la disequazione sin(2) 2. 2. Dire se esistono
FUNZIONI TRIGONOMETRICHE
 FUNZIONI TRIGONOMETRICHE RICHIAMI DI TEORIA Definizione: si dice angolo positivo individuato dalla coppia di semirette r e r' uscenti dal punto O, l'insieme dei punti del piano descritti dai punti di r
FUNZIONI TRIGONOMETRICHE RICHIAMI DI TEORIA Definizione: si dice angolo positivo individuato dalla coppia di semirette r e r' uscenti dal punto O, l'insieme dei punti del piano descritti dai punti di r
Analisi Matematica I Primo Appello ( ) - Fila 1
 Analisi Matematica I Primo Appello (4-11-003) - Fila 1 1. Determinare la retta tangente alla funzione f() = (1 + ) 1+ in = 0. R. f(0) = 1, mentre la derivata è f () = ( e (1+) log(1+)) ( ) = e (1+) log(1+)
Analisi Matematica I Primo Appello (4-11-003) - Fila 1 1. Determinare la retta tangente alla funzione f() = (1 + ) 1+ in = 0. R. f(0) = 1, mentre la derivata è f () = ( e (1+) log(1+)) ( ) = e (1+) log(1+)
Esame di Analisi Funzionale e Trasformate Prima prova in itinere. Maggio 2017 A.A. 2016/2017. Prof. M. Bramanti Tema A
 Esame di Analisi Funzionale e Trasformate Prima prova in itinere. Maggio 7 A.A. 6/7. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom Dom Dom 3 Es Es Es 3 Tot. Punti Domande di teoria
Esame di Analisi Funzionale e Trasformate Prima prova in itinere. Maggio 7 A.A. 6/7. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom Dom Dom 3 Es Es Es 3 Tot. Punti Domande di teoria
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
b 2 4c. Stabiliamo se le seguenti equazioni rappresentano delle circonferenze e, in caso affermativo, determiniamone centro e raggio.
 LA CIRCONFERENZA Rivedi la teoria L'equazione della circonferenza e le sue caratteristiche La circonferenza eá il luogo dei punti del piano che hanno la stessa distanza da un punto fisso chiamato centro;
LA CIRCONFERENZA Rivedi la teoria L'equazione della circonferenza e le sue caratteristiche La circonferenza eá il luogo dei punti del piano che hanno la stessa distanza da un punto fisso chiamato centro;
Matematica e Statistica (A-E, F-O, P-Z)
 Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (24/06/20) Università di Verona - Laurea in Biotecnologie - A.A. 200/ Tema A Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O,
Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (24/06/20) Università di Verona - Laurea in Biotecnologie - A.A. 200/ Tema A Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O,
Nel caso particolare in cui il vertice si trovi nell'origine, la parabola assume la forma: y ˆ ax 2.
 LA PARABOLA Rivedi la teoria La parabola e la sua equazione La parabola eá il luogo dei punti del piano che hanno la stessa distanza da un punto fisso chiamato fuoco e da una retta fissa chiamata direttrice.
LA PARABOLA Rivedi la teoria La parabola e la sua equazione La parabola eá il luogo dei punti del piano che hanno la stessa distanza da un punto fisso chiamato fuoco e da una retta fissa chiamata direttrice.
Curve e lunghezza di una curva
 Curve e lunghezza di una curva Definizione 1 Si chiama curva il luogo geometrico dello spazio di equazioni parametriche descritto da punto p, chiuso e limitato. Definizione 2 Si dice che il luogo C è una
Curve e lunghezza di una curva Definizione 1 Si chiama curva il luogo geometrico dello spazio di equazioni parametriche descritto da punto p, chiuso e limitato. Definizione 2 Si dice che il luogo C è una
Quaderno per il recupero del debito MATEMATICA ANNO SCOLASTICO 2016/2017 Prof.ssa Migliaccio Gabriella CLASSE III
 Quaderno per il recupero del debito MATEMATICA ANNO SCOLASTICO 016/017 Prof.ssa Migliaccio Gabriella CLASSE III Gli esercizi vanno svolti e consegnati, anche su un quaderno, il giorno dell esame per il
Quaderno per il recupero del debito MATEMATICA ANNO SCOLASTICO 016/017 Prof.ssa Migliaccio Gabriella CLASSE III Gli esercizi vanno svolti e consegnati, anche su un quaderno, il giorno dell esame per il
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 2010/2011
 LUISS Laurea specialistica in Economia e Finanza Anno Accademico 1/11 Corso di Metodi Matematici per la Finanza Prof. Fausto Gozzi, Dr. Davide Vergni Soluzioni esercizi 4,5,6 esame scritto del 13/9/11
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 1/11 Corso di Metodi Matematici per la Finanza Prof. Fausto Gozzi, Dr. Davide Vergni Soluzioni esercizi 4,5,6 esame scritto del 13/9/11
Esempio di grafico di una funzione reale di due variabili reali
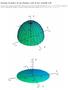 Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
Esercizi su serie numeriche, integrali ed equazioni differenziali utili per la preparazione all esame scritto 1
 Esercizi di Analisi Matematica Paola Gervasio Esercizi su serie numeriche, integrali ed equazioni differenziali utili per la preparazione all esame scritto Es Determinare il carattere delle seguenti serie
Esercizi di Analisi Matematica Paola Gervasio Esercizi su serie numeriche, integrali ed equazioni differenziali utili per la preparazione all esame scritto Es Determinare il carattere delle seguenti serie
ESAME DI STATO DI LICEO SCIENTIFICO Corso Sperimentale P.N.I. Tema di MATEMATICA - 17 giugno 2004
 ESAME DI STATO DI LICEO SCIENTIFICO 00-004 Corso Sperimentale PNI Tema di MATEMATICA - 7 giugno 004 Svolgimento a cura della profssa Sandra Bernecoli e del prof Luigi Tomasi (luigitomasi@liberoit) RISOLUZIONE
ESAME DI STATO DI LICEO SCIENTIFICO 00-004 Corso Sperimentale PNI Tema di MATEMATICA - 7 giugno 004 Svolgimento a cura della profssa Sandra Bernecoli e del prof Luigi Tomasi (luigitomasi@liberoit) RISOLUZIONE
Limite. Se D non è limitato si può fare il limite di f(x) per x che tende
 Appunti sul corso di Complementi di Matematica,mod.Analisi, prof. B.Bacchelli - a.a. 200/20. 05 - Limiti continuità: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3., 3.2. - Esercizi 3., 3.2.
Appunti sul corso di Complementi di Matematica,mod.Analisi, prof. B.Bacchelli - a.a. 200/20. 05 - Limiti continuità: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3., 3.2. - Esercizi 3., 3.2.
COMPITO IN CLASSE DI MATEMATICA Funzioni di due variabili Classe 5ª D. Fila A
 Esercizio 1 Determinare il dominio della seguente funzione: COMPITO IN CLASSE DI MATEMATICA Funzioni di due variabili Classe 5ª D Fila A (a) f (, ln( + 4 Esercizio Calcolare le derivate parziali delle
Esercizio 1 Determinare il dominio della seguente funzione: COMPITO IN CLASSE DI MATEMATICA Funzioni di due variabili Classe 5ª D Fila A (a) f (, ln( + 4 Esercizio Calcolare le derivate parziali delle
LOGARITMI ED ESPONENZIALI
 1 LOGARITMI ED ESPONENZIALI 1. (Da Veterinaria 2013) Riscrivendo 9 3x+2 nel formato 3 y, quale sarà il valore di y? a) 3x b) 3x + 4 c) 6x + 2 d) 6x + 4 e) 9x + 6 2. (Da Odontoiatria 2009) Qual è la soluzione
1 LOGARITMI ED ESPONENZIALI 1. (Da Veterinaria 2013) Riscrivendo 9 3x+2 nel formato 3 y, quale sarà il valore di y? a) 3x b) 3x + 4 c) 6x + 2 d) 6x + 4 e) 9x + 6 2. (Da Odontoiatria 2009) Qual è la soluzione
{ x + 2y = 3 αx + 2y = 1 αx + y = 0. f(x) = e x 2 +3x+4 x 5. f(x) = x 3 e 7x.
 0 Gennaio 006 Teoria: Definizione di derivata puntuale e suo significato geometrico Esercizio Determinare l equazione del piano contenente i vettori u = (,, 3 e v = (,, e passante per P o = (,, Scrivere
0 Gennaio 006 Teoria: Definizione di derivata puntuale e suo significato geometrico Esercizio Determinare l equazione del piano contenente i vettori u = (,, 3 e v = (,, e passante per P o = (,, Scrivere
Teoria in sintesi 10. Teoria in sintesi 14
 Indice L attività di recupero Funzioni goniometriche Teoria in sintesi 0 Obiettivo Calcolare il valore di espressioni goniometriche in seno e coseno Obiettivo Determinare massimo e minimo di funzioni goniometriche
Indice L attività di recupero Funzioni goniometriche Teoria in sintesi 0 Obiettivo Calcolare il valore di espressioni goniometriche in seno e coseno Obiettivo Determinare massimo e minimo di funzioni goniometriche
Derivata di una funzione
 Derivata di una funzione Prof. E. Modica http://www.galois.it erasmo@galois.it Il problema delle tangenti Quando si effettua lo studio delle coniche viene risolta una serie di esercizi che richiedono la
Derivata di una funzione Prof. E. Modica http://www.galois.it erasmo@galois.it Il problema delle tangenti Quando si effettua lo studio delle coniche viene risolta una serie di esercizi che richiedono la
Analisi Matematica 2 (prof.g.cupini) A.A CdL Astronomia - Univ. Bologna REGISTRO DELLE LEZIONI
 Analisi Matematica 2 (prof.g.cupini) A.A.2016-2017 - CdL Astronomia - Univ. Bologna REGISTRO DELLE LEZIONI GLI ARGOMENTI IN GIALLO SARANNO OGGETTO DI VERIFICA SOLO NELL'ESAME DI TEORIA. Lu, 26 settembre
Analisi Matematica 2 (prof.g.cupini) A.A.2016-2017 - CdL Astronomia - Univ. Bologna REGISTRO DELLE LEZIONI GLI ARGOMENTI IN GIALLO SARANNO OGGETTO DI VERIFICA SOLO NELL'ESAME DI TEORIA. Lu, 26 settembre
1 - Estremo superiore ed estremo inferiore di insiemi
 - Estremo superiore ed estremo inferiore di insiemi Prima di affrontare gli esercizi su estremo superiore ed inferiore, ricordiamo alcune definizioni ed alcuni teoremi che ci verranno utili. Definizione.
- Estremo superiore ed estremo inferiore di insiemi Prima di affrontare gli esercizi su estremo superiore ed inferiore, ricordiamo alcune definizioni ed alcuni teoremi che ci verranno utili. Definizione.
I Esame di maturità 2012
 I. ESAME DI MATURITÀ I Esame di maturità Quesito Cosa rappresenta? Portando fuori il 5 abbiamo 5( lim + h)4 5 4 h h ( 5 lim + h)4 4 h h che assomiglia ad un rapporto incrementale del tipo: f(x + h) f(x)
I. ESAME DI MATURITÀ I Esame di maturità Quesito Cosa rappresenta? Portando fuori il 5 abbiamo 5( lim + h)4 5 4 h h ( 5 lim + h)4 4 h h che assomiglia ad un rapporto incrementale del tipo: f(x + h) f(x)
CALENDARIO BOREALE 2 AMERICHE 2015 QUESITO 1
 www.matefilia.it Indirizzi: LI0, EA0 SCIENTIFICO; LI0 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE AMERICHE 0 QUESITO Determinare il volume del solido generato dalla rotazione attorno alla
www.matefilia.it Indirizzi: LI0, EA0 SCIENTIFICO; LI0 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE AMERICHE 0 QUESITO Determinare il volume del solido generato dalla rotazione attorno alla
3 ) (5) Determinare la proiezione ortogonale del punto (2, 1, 2) sul piano x + 2y + 3z + 4 = 0.
 1 Calcolo vettoriale 1 Scrivere il vettore w =, 6 sotto forma di combinazione lineare dei vettori u = 1, e v = 3, 1 R w = v 4u Determinare la lunghezza o il modulo del vettore, 6, 3 R 7 3 Determinare la
1 Calcolo vettoriale 1 Scrivere il vettore w =, 6 sotto forma di combinazione lineare dei vettori u = 1, e v = 3, 1 R w = v 4u Determinare la lunghezza o il modulo del vettore, 6, 3 R 7 3 Determinare la
Sul concetto di derivata di una funzione con riferimento ad alcune sue applicazioni nel campo matematico e fisico.
 Sul concetto di derivata di una funzione con riferimento ad alcune sue applicazioni nel campo matematico e fisico. Introduzione In matematica la derivata di una funzione è uno dei cardini dellanalisi matematica
Sul concetto di derivata di una funzione con riferimento ad alcune sue applicazioni nel campo matematico e fisico. Introduzione In matematica la derivata di una funzione è uno dei cardini dellanalisi matematica
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Le Funzioni. Modulo Esponenziali Logaritmiche. Prof.ssa Maddalena Dominijanni
 Le Funzioni Modulo Esponenziali Logaritmiche Definizione di modulo o valore assoluto Se x è un generico numero reale, il suo modulo o valore assoluto è: x = x se x 0 -x se x
Le Funzioni Modulo Esponenziali Logaritmiche Definizione di modulo o valore assoluto Se x è un generico numero reale, il suo modulo o valore assoluto è: x = x se x 0 -x se x
Esercizi sulle funzioni di due variabili: parte II
 ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) A.A.009-00 - Università di Bologna - Prof. G.Cupini Esercizi sulle funzioni di due variabili: parte II (Grazie agli studenti del corso
ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) A.A.009-00 - Università di Bologna - Prof. G.Cupini Esercizi sulle funzioni di due variabili: parte II (Grazie agli studenti del corso
Prima parte: DOMINIO E INSIEMI DI LIVELLO
 FUNZIONI DI DUE VARIABILI 1 Prima parte: DOMINIO E INSIEMI DI LIVELLO Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia insiemi aperti, chiusi, limitati, convessi, connessi
FUNZIONI DI DUE VARIABILI 1 Prima parte: DOMINIO E INSIEMI DI LIVELLO Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia insiemi aperti, chiusi, limitati, convessi, connessi
Soluzioni dei quesiti della maturità scientifica A.S. 2009/2010
 Soluzioni dei quesiti della maturità scientifica AS 009/010 Nicola Gigli Sun-Ra Mosconi giugno 010 Quesito 1 Un generico polinomio di grado n si può scrivere nella forma p(x) a 0 + a 1 x + + a n x n dove
Soluzioni dei quesiti della maturità scientifica AS 009/010 Nicola Gigli Sun-Ra Mosconi giugno 010 Quesito 1 Un generico polinomio di grado n si può scrivere nella forma p(x) a 0 + a 1 x + + a n x n dove
Le Derivate. Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri
 Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
Temid esamesvolti-1. Analisi delle funzioni
 Temi d esame svolti - 1 1 Temid esamesvolti-1 Analisi delle funzioni (91003) 1 Si consideri la funzione definita a tratti su tutto R: ½ + sin 1 f() =, 6= 0 k, =0 (a) Per quale valore di k la funzione è
Temi d esame svolti - 1 1 Temid esamesvolti-1 Analisi delle funzioni (91003) 1 Si consideri la funzione definita a tratti su tutto R: ½ + sin 1 f() =, 6= 0 k, =0 (a) Per quale valore di k la funzione è
1. (Da Medicina e Odontoiatria 2012) Determinare l'area del triangolo che ha come vertici i punti (0,0), (0,1), (13,12) del piano cartesiano:
 QUESITI 1 PIANO CARTESIANO 1. (Da Medicina e Odontoiatria 2012) Determinare l'area del triangolo che ha come vertici i punti (0,0), (0,1), (13,12) del piano cartesiano: a) 6 b) 13/2 c) 12 d) 13 e) 78 2.
QUESITI 1 PIANO CARTESIANO 1. (Da Medicina e Odontoiatria 2012) Determinare l'area del triangolo che ha come vertici i punti (0,0), (0,1), (13,12) del piano cartesiano: a) 6 b) 13/2 c) 12 d) 13 e) 78 2.
