ELOGIO DELLA PIGRIZIA: IL PRINCIPIO DI MINIMA AZIONE
|
|
|
- Norma Mauri
- 4 anni fa
- Visualizzazioni
Transcript
1 ELOGIO DELLA PIGRIZIA: IL PRINCIPIO DI MINIMA AZIONE CARLANGELO LIVERANI 1. Lagrangana Dato un sstema N partcelle soggette a forze conservatve, possamo scrvere le equazon Newton come (1.1) Mẍ = U ove x : R R, M è una matrce efnta postva e U C 2 (R, R) una funzone etta potenzale. Accae che tal equazon possono essere alternatvamente escrtte attraverso una funzone L C 2 (R 2, R) efnta a (1.2) L(x, y) = 1 y, My U(x). 2 Tale funzone L è etta Lagrangana e etermna elle equazon fferenzal, per la funzone ncognta x C 2 (R, R ), efnte a (1.3) t yl(x(t), ẋ(t)) x L(x(t), ẋ(t)) = 0. Tal equazon sono ette equazon Lagrange. Eserczo 1.1. S mostr che le equazon Lagrange assocate alla Lagrangana (1.2) sono esattamente le equazon Newton (1.1). Lo scrvere le equazon el moto n forma lagrangana ha svarat vantagg, l prmo è una maggore facltà nel cambo coornate. Infatt, sa Ξ C 2 (R, R ) un ffeomorfsmo allora s ha l seguente fonamentale fatto. Teorema 1.2. S conser l cambo coornate x = Ξ(q) allora the equazon Newton (1.1) nelle coornate q concono con le equazon Lagrange per la Lagrangana L(ξ, η) = L(Ξ(ξ), DΞ(ξ)η). 1 Proof. Prma tutto occorre calcolare come sono fatte le equazon (1.1) nelle nuove coornate. S not che ẋ = DΞ(q) q (1.4) ẍ = qj qk Ξ (q) q j q k + qj Ξ (q) q j j,k j q (U Ξ)(q) = ( xj U) Ξ(q) q Ξ j (q). j Date: Versone May 15, Normalmente s abusano le notazon e la nuova funzone L vene chamata nuovamente L, sebbene sa ovvamente una funzone fferente. Inoltre s tene a scrvere ql(q, q) e q L(q, q) (nvece ξ L(ξ, η) e η L(ξ, η)) sebbene tal espresson, per quanto ntutve, non abbano molto senso. Nel seguto m conformerò a questa scutble, ma convenente, trazone. 1
2 2 CARLANGELO LIVERANI Pochè Ξ è un ffeomorfsmo DΞ eve essere nvertble, qun le equazon (1.1) sono equvalent a DΞ T Mẍ = DΞ T U(x) = [ (U Ξ)] Ξ 1 (x). Ovvero, poneno Ũ = U Ξ e usano le (1.4) s ha (1.5) q Ξ l M l,r qj Ξ r q j = q Ũ. D altro canto l,j,k,r q Ξ l M l,r qj qk Ξ r q j q k + l,j,r L(q, q) = 1 2 q, DΞT (q)mdξ(q) q Ũ(q) q L = j,k,l qr Ξ j M j,k q ql Ξ k q l q r q Ũ q L = l,r,j q Ξ l M l,r qj Ξ r q j t q L = l,r,j,k qk q Ξ l M l,r qk qj Ξ r q j q k + l,r,j q Ξ l M l,r qj Ξ r q j e nsereno queste espressone nelle equazon Lagrange (1.3) s ottengono esattamente le (1.5), come annuncato. Il vantaggo cambare faclmente coornate è partcolarmente evente quanto s conserano sstem vncolat. S conser l caso Mẍ(t) = U(x) + R(t) (1.6) Φ(x) = 0 R(t), v = 0 per tutt v R tal che DΦ(x(t))v = 0. Dove R sono le reazon vncolar ncognte. Φ C 2 (R, R m ), m <, esprme l vncolo e s assume che DΦ abba rango massmo a ogn punto. Infne, l ultma rga esprme l prncpo e lavor vrtual ovvero (parlano un poco mpropramente) che le forze vncolar al tempo t non compono lavoro su qualunque moto compatble col vncolo nel punto x(t). Pochè l rango DΦ è massmo, l teorema ella funzone mplcta c ce che localmente (ovvero nell ntorno qualunque punto assegnato) esste una funzone Ξ C 2 (V, R ), ove V è un aperto R m, tale che per ogn q V s ha Φ(Ξ(q)) = 0. Dunque se conseramo solo mot el tpo x(t) = Ξ(q(t)), quest sosfano automatcamente l vncolo. Inoltre, fferenzano, s ha DΦDΞ = 0. Infne, pochè l kernel Φ eve essere m mensonale, tutt vettor tal Dφ v = 0 s possono esprme come v = DΞw per qualche w R m. Questo sgnfca che, per ogn w R m eve essere R(t), DΞ(q(t))w = 0 ovvero l prncpo e lavor vrtual è equvalente a (1.7) DΞ(q(t)) T R(t) = 0. Possamo qun moltplcare la prma elle (1.6) per DΞ T e ottenere (1.8) DΞ T Mẍ = DΞ T U(x) Queste sono m equazon fferenzal per le m funzon ncognte q(t). C samo unque rott a un problema n cu a un lato sono state elmnate le reazon
3 ELOGIO DELLA PIGRIZIA 3 vncolar e che ha l gusto numero equazon per etermnare le rmanent ncognte. Eserczo 1.3. S usno le (1.4) per scrvere esplctamente le (1.8) n termn elle funzon q e s verfch che concono con le equazon Lagrange per la Lagrangana L(q, q) = 1 2 q, DΞT (q)mdξ(q) q U(Ξ(q)). Remark 1.4. Abbamo unque vsto, che ato un sstema vncolato con vncol eal (ovvero che sosfano l prncpo e lavor vrtual), le equazon el moto possono essere faclmente ervate prma cambano varable nella Lagrangana e po usano le equazon Lagrange per la Lagrangana così ottenuta. 2. Azone Un altro mportante uso ella Lagrangana è quello efne un altra sorprenente funzone: l azone. Questa è una funzone efnta su un nseme un poco strano: un nseme funzon! Veamo essere pù precs: per ogn, t 1 R e A, B R s conser l nseme (etto nseme e mot) M t0,t 1 (A, B) = {q C 1 ([, t 1 ], R ) : q( ) = A, q(t 1 ) = B}. 2 Possamo unque efnre la funzone S : M t0,t 1 (A, B) R come (2.1) S(q) = L(q(s), q(s))s. Sccome una funzone funzon può sembrare alquanto nusuale, vene spontaneo cheers qual propretà abba, per esempo: è contnua? è fferenzable? è convessa? etc. Un attmo rflessone mostra che per rsponere a tal omane occorre prma tutto charre che sgnfcano. Per esempo, una funzone f : R n R è contnua se solo se per ogn successone convergente x n s ha lm n f(x n ) = f(lm n x). C s può cheere se la stessa cosa sa vera per S, ma per rsponere occorre prma spegare che sgnfca convergere per una successone element M t0,t 1 (A, B). A questa omana s possono are molte rsposte e approfonre questo tema c porterebbe allo stuo elle possbl topologe per uno spazo nfnto mensonale. Questo è al fuor e nostr scop attual, c accontentamo qun ella seguente efnzone che, sperablmente, l lettore troverà naturale: remo che una successone {q n } M t0,t 1 (A, B) converge a q M t0,t 1 (A, B) se lm sup n s [,t 1] q n (s) q(s) + sup s [,t 1] q n (s) q(s) = 0. Eserczo 2.1. S mostr che con la nozone convergenza appena ntrootta M t0,t 1 (A, B) è uno spazo completo, ovvero: ogn successone Cauchy è convergente. In analoga col caso fnto mensonale remo unque che S è contnua n q se, per ogn {q n } che converge a q s ha lm n S(q n ) = S( q). Eserczo 2.2. S mostr che se L C 0 allora S è contnua. B. 2 Ovvero tutt mot che, pateno al tempo t0, nel tempo t 1 vanno al punto A al punto
4 4 CARLANGELO LIVERANI Che re ella fferenzabltà? Una funzone a f : R n R è fferenzable n x se esste una funzone lneare L : R n R n tale che f(x + h) f(x) L(h) lm = 0. h 0 h Tale funzone L s chama ervata e s scrve D x f h = x f, h = L(h). 3 Dunque per parlare fferenzabltà occorre ntrourre una funzone lneare. Sfortunatamente M t0,t 1 (A, B) non è uno spazo lneare e qun non ha senso parlare funzon lnear su M t0,t 1 (A, B). Eserczo 2.3. S mostr che se q, q M t0,t 1 (A, B) allora q q M t0,t 1 (0, 0). Inoltre s most che M t0,t 1 (0, 0) è uno spazo vettorale sul campo e real. In analoga con l caso fnto mensonale possamo unque stuare S(q + h) S(q) ove q M t0,t 1 (A, B) e h M t0,t 1 (0, 0). Inoltre su M t0,t 1 (0, 0) possamo ntrourre la norma h C 1 = sup h(s) + s [,t 1] sup s [,t 1] ḣ(s). Eserczo 2.4. S mostr che C 1 è una norma su M t0,t 1 (0, 0). 4 Eserczo 2.5. S mostr che M t0,t 1 (0, 0) è uno spazo completo rspetto alla norma C 1, ovvero che ogn successone Cauchy è convergente. 5 Dremo unque che S è fferenzable n q M t0,t 1 (A, B) se esste una funzone lneare L q : M t0,t 1 (0, 0) R tale che, per ogn successone {h n } M t0,t 1 (0, 0) tale che lm n h n C 1 = 0 s ha Oppure, pù brevemente, S(q + h n ) S(q) L q (h n ) lm = 0. n h n C 1 S(q + h) S(q) L q (h) lm = 0. h 0 h C 1 Naturalmente remo che L q è l fferenzale S n q (per essere precs s chama fferenzale Fréchet). Lemma 2.6. Se L C 1 allora la funzone S è fferenzable n ogn q M t0,t 1 (A, B) e s ha che { } L q (h) = q L(q(s), q(s))ḣ + q L(q(s), q(s))h (s) s. Proof. Usano la formula Taylor al prmo orne s ha L(q(s) + h(s), q(s) + ḣ(s)) =L(q(s), q(s)) + q L(q(s), q(s))h (s) + q L(q(s), q(s))ḣ(s) + o( h C 1). 3 Infatt una funzone lneare a R n a R è entfcata unvocamente a un vettore, tale vettore è appunto xf cu element sono le ervate parzal ella f, ovvero x f. 4 S rcor che, ato uno spazo vettorale V sul campo e real, una funzone : V R+ è una norma se: 1) x > 0 per ogn x V, x 0; 2) λx = λ x per ogn x V e λ R; 3) x + y x + y per ogn x, y V. 5 Gl spaz vettoral normat e complet s chamano spaz Banach.
5 ELOGIO DELLA PIGRIZIA 5 Dunque S(q + h) S(q) = + q L(q(s), q(s))h (s)s q L(q(s), q(s))ḣ(s)s + o( h C 1). Il Lemma segue mmeatamente all ultma equazone. Vsto che abbamo l fferenzale, è naturale stuare punt stazonar, ovvero mot q per cu L q = 0. Rsulta che tal mot sono molto specal, comncamone lo stuo. Come al solto, se assumamo un poco pù ottenamo un rsultato pù precso. Lemma 2.7. Se L C 2 e q C 2 allora s ha che L q (h) = 0 per ogn h M t0,t 1 (0, 0) se e solo se q sosfa le equazon Lagrange con conzon q( ) = A, q(t 1 ) = B. Proof. Per la necesstà basta notare che L q (h) = q L(q(s), q(s))h (s)s t q L(q(s), q(s)) h (s)s ove abbamo ntegrato per part e rcorato che h( ) = h(t 1 ) = 0 e che, per potes, q L(q( ), q( )) C 1. Se nfatt le equazon Langrange non fossero sosfatte, allora essterebbe un e un ntervallo temp n cu q L(q(s), q(s)) t q L(q(s), q(s)) non s annulla ma. Moltplcano per una h supportata n tale ntervallo e con h 0 s avrebbe qun un ntegrale non nullo contraramente alle potes. La suffcenza segue al fatto che se q sosfa le equazon Lagrange allora L q (h) = 0. È nteressante notare che l potes q C 2 n realtà è molto meno forte quanto possa sembare a prma vsta. Lemma 2.8. Se L C 2 e q M t0,t 1 (A, B) è stazonara e la matrce q qj L(q, q) è nvertble, allora q C 2 ((, t 1 ), R ). Proof. Il fatto che q sa stazonaro sgnfca che per ogn h M t0,t 1 (0, 0) s ha L q (h) = 0. Qun L q (h) = + = q L(q(s), q(s)) ḣ (s 1 )s 1 s q L(q(s), q(s)) ḣ(s)s { s } q L(q(s 1 ), q(s 1 ))s 1 + q L(q(s), q(s)) ḣ (s)s.
6 6 CARLANGELO LIVERANI Ora s not che se g C 0 ([, t 1 ], R ), allora h(t) = t g(s)s t t0 t1 t 1 g(s)s M t0,t 1 (0, 0). Pochè ḣ = g 1 g(s)s =: g α g, segue che se G C 1 e t 1 G, ḣ = 0 per ogn h M,t 1 (0, 0), allora [ 0 = G(s), g(s) α g s = G(s) 1 t 1 ] G(s 1 )s 1, g(s) s, per ogn g C 0 ([, t 1 ], R ). Questo mplca che, per ogn s [, t 1 ], s q L(q(s 1 ), q(s 1 ))s 1 + q L(q(s), q(s)) c = 0 per opportune costant c. A questo punto s not che la conzone nvertbltà ella matrce q qj L(q, q) è esattamente quello che occorre per applcare l teorema ella funzone mplcta e esprmere q come una funzone C 1. Infatt H(s) = t 1 s ql(q(s 1 ), q(s 1 ))s 1 e G(s, x) = q L(q(s), x) sono C 1 per potes. Dunque, poneno F (s, x) = H(s) + G(s, x) c, l teorema ella funzone mplcta afferma che F (s, x) = 0 ha una unca soluzone q(s) e q C 1. Abbamo unque l fatto notevole che S ha ervata nulla sulle soluzon elle equazon Lagrange. Certo rmane la cosa un poco strana che nvece avere un problema Cauchy (ovvero specfcare q( ), q( )) s specfcano valor elle sole poszon agl estrem ell ntervallo temporale conserato. Vene naturale omanars che relazone c sa tra questo problema a bor e l problema Cauchy. Prma affrontare questo problema mostramo un altra propretà sorprenente ell azone. In questo caso assumamo che L C 3 (R 2, R). Teorema 2.9. Se = 1 e esste m > 0 tale che nf x,y 2 yl(x, y) m, allora mot che sosfano le equazon Lagrange con conzon a bor q( ) = A, q(t 1 ) = B sono mnm local ell azone. Proof. Argomentamo come nel Lemma 2.6, ma questa volta svluppamo la Lagrangana fno al secono orne 6 L(q(s) + h(s), q(s) + ḣ(s)) = L(q(s), q(s)) + ql(q(s), q(s))h(s) + q L(q(s), q(s))ḣ(s) q q L(q(s), q(s))h(s) 2 + q q L(q(s), q(s))h(s)ḣ(s) q q L(q(s), q(s))(ḣ(s))2 + o(h(s) 2 + (ḣ(s))2 ). A questo punto s not che, pochè le ervate mste sono ugual vsto che L C 2, (2.2) q q L(q(s), q(s))h(s)ḣ(s) = 1 q q L(q(s), q(s)) 2 s (h(s)2 ) = 1 2 s q q L(q(s), q(s)) h(s) 2. 6 Vsto che sappamo allo stuo elle funzon a R n a R che massm e mnm penono alle proprtà ella ervata secona.
7 ELOGIO DELLA PIGRIZIA 7 D altro canto, pochè L C 3 e qun anche l orne elle ervate terze non ha mportanza, s q q L(q(s), q(s)) = q q q L(q(s), q(s)) q + q q q L(q(s), q(s)) q = q [ q q L(q(s), q(s)) q + q q L(q(s), q(s)) q] [ ] = q s ql(q(s), q(s)). Possamo unque usare le relazon preceent per scrvere, rcorano che le q sosfano le equazon Lagrange, (2.3) S(q + h) S(q) = 1 2 = 1 2 [ q q L(q(s), q(s))h(s) 2 + q q L(q(s), q(s))ḣ(s)2] s q 1 2 [ ] ( t1 s ql(q(s), q(s)) h(s) 2 s + o q q L(q(s), q(s))(ḣ(s))2 s + o ( m ( ) 2 (ḣ(s))2 s + o h(s) 2 + (ḣ(s))2. Per concluere s not che, usano la suguaglanza Schwarz, ) 2 h(s) 2 = ( ḣ(τ)τ (ḣ(τ))2 τ (t 1 ) h(s) 2 + (ḣ(s))2 h(s) 2 + (ḣ(s))2 ) (ḣ(s))2 s. Questo sgnfca che se h C 1 è suffcentemente pccolo, l errore n (2.3) è pù pccolo el prmo termne (che è postvo). In altre parole, per qualunque moto suffcentemente vcno a q l azone ha un valore pù grane S(q), ovvero q è un mnmo locale ell azone. A questo punto vene naturale cheers che cosa accae se > 1. Ovvamente s può proceere nello stesso moo anche se ora lo svluppo Taylor ella Lagrangana è pù complesso. Tuttava l argomento usato nell equazone (2.2) è sostanzalmente unmensonale. Non è qun strano che n pù menson l rsultato sa leggermente pù ebole. v, Teorema Se esste m > 0 tale che nf x,y nf 2 y L(x,y)v v v m e se t 2 1 è suffcentemente pccolo, allora mot che sosfano le equazon Lagrange con conzon a bor q( ) = A, q(t 1 ) = B sono mnm local ell azone. Proof. Nuovamente svluppamo la Lagrangana fno al secono orne L(q(s) + h(s), q(s) + ḣ(s)) = L(q(s), q(s)) + q L(q(s), q(s))h (s) + q L(q(s), q(s))ḣ(s) + 1 q qj L(q(s), q(s))h (s)h j (s) 2 j + q qj L(q(s), q(s))h (s)ḣj(s) + 1 q qj L(q(s), q(s))ḣ(s)ḣj(s) 2 j j + o( h(s) 2 + ḣ(s) 2 ). )
8 8 CARLANGELO LIVERANI In analoga con quanto fatto prma possamo scrvere S(q + h) S(q) = 1 2 m q qj L(q(s), q(s))h (s)h j (s),j + + o + o q qj L(q(s), q(s))ḣ(s)ḣj(s)s,j q qj L(q(s), q(s)) h (s)ḣj(s)s,j ( ( h(s) 2 + ḣ(s) 2 ḣ(s) 2 s C ) ) h(s) 2 + ḣ(s) 2, [ h(s) 2 + ḣ(s) h(s) ] s ove C è una costante etermnata al massmo el valore assoluto elle ervate secone lungo la curva q e abbamo usato la suguaglanza Schwartz nella forma [ ] 12 a a 2. =1 =1 D altro canto, n manera smle a quanto fatto nel caso unmensonale, 2 h(s) 2 = ḣ(τ)τ ḣ(τ) 2 τ (t 1 ) ḣ(s) 2 s. Per trattare l termne msto s not che 7 2 Da cu segue che h(s) ḣ(s) = S(q + h) S(q) 1 2 (t 1 ) 1 2 h(s) 2 + (t 1 ) 1 2 ḣ(s) 2 s. [ ] t 1 1 C(t 1 ) 1 2 ( ḣ(s) 2 s + o ḣ(s) 2). Qun nuovamente q è un mnmo locale a patto che C(t 1 ) 1 2 < 1. Tuttava s not che non abbamo mostrato che l azone ha sempre e mnm o, pù n generale, e punt stazonar. La cosa non è ovva come mostra l seguente esempo. Eserczo S conser la Lagrangana L(q, q) = 1 2 q2 1 2 q2, q R, e = 0 e t 1 = 2π. S mostr che l azone non ha punt stazonar n M t0,t 1 (0, 1). (Suggermento: se avesse punt stazonar allora ovrebbero sosfare le equazon Lagrange e q(0) = 0, q(2π) = 1. S rsolvano le equazon Lagrange e s vea che tal soluzon non esstono.) 7 Qu stamo usano la suguaglanza 2 ab δ 2 a 2 +δ 2 b 2 che s ottene banalmente al fatto che (δa δ 1 b) 2 0 e (δa + δ 1 b) 2 0.
9 ELOGIO DELLA PIGRIZIA 9 3. Esstenza e mnm e equazon fferenzal con conzon al boro Per concluere scutamo un attmo la relazone tra l problema Cauchy e l problema al boro che s ottene mnmzzano l azone. Come abbamo gà fatto nello stuo ell azone assumamo che essta m > 0 tale che, per ogn v R, (3.1) nf x,y v, 2 yl(x, y)v m v 2. Eserczo 3.1. S mostr che (3.1) mplca che la matrce con element q qj L è nvertble S not che le equazon Lagrange hanno la forma 2 q L q = G(q, q) per una qualche funzone G. Dunque possamo scrvere (3.2) q = [ 2 q L ] 1 G(q, q) = F (q, q). C samo così rott a elle equazon fferenzal el secono orne nella forma solta. S not che se L C 4 allora F C 2. Il rsultato base per charfcare l problema che c samo post è l seguente. Teorema 3.2. Data F C 2 (R 2, R ),, t 1 R e A, B R l problema q = F (q, q) q( ) = A, q(t 1 ) = B ammette una unca soluzone a patto che t 1 sa suffcentemente pccolo. Proof. L ea base è quella confrontare l problema con quello Cauchy per cu abbamo gà molt rsultat. A questo scopo è meglo trasformare l equazone partenza n una equazone el prmo orne: sa z = (q, p) R 2, q, p R, e F (z, λ) = (p, λf (q, p)), λ [0, 1], allora l equazone che c nteressa può essere scrtta come 8 ż = F (z, 1). La ragone per cu abbamo ntrootto l parametro λ è che l equazone ż = F (z, 0), z( ) = A, z(t 1 ) = B s può faclmente rsolvere esplctamente e la sua unca soluzone è z(t) = (A + (B A) t t0 t 1, (B A)(t 1 ) 1 ). Possamo qun conserare l problema Cauchy ż = F (z, λ) z(0) = (A, v). Sappamo che tale problema ha una unca soluzone z(t, v, λ) = (q(t, v, λ), p(t, v, λ)). Sembra qun naturale esprmere tale soluzone come funzone v, λ e cercare rsolvere l equazone (3.3) q(t 1, v, λ) B = 0. Se è possble (per λ = 1) questo fornsce una soluzone el nostro problema. L approcco ovvo è quello cercare usare l teorema ella funzone mplcta. Questo c ce che, n un ntorno λ = 0 e v = (B A)(t 1 ) 1 la equazone (3.3) 8 Questo non è un sstema molto furbo trasformare le equazon Lagrange n un sstema el prmo orne. Esste un formalsmo (l formalsmo Hamltonano) che permette farlo n manera molto pù effcente e profona. Tuttava per nostr scop è suffcente.
10 10 CARLANGELO LIVERANI ha una unca soluzone a patto che la matrce ata a ξ(t, v, λ) = v q(t, v, λ) sa nvertble per t = t 1. Il teorema sulla penenza fferenzable alle conzon nzal e a parametr mplca che z(t 1, v, λ) è una funzone fferenzable v e λ e noltre, poneno η(t, v, λ) = v p(t, v, λ) abbamo ξ = η η = q F (z)ξ + p F (z)η ξ(0) = 0 η(0) = 1. Pochè le equazon sono lnear sappamo che esste una costante C F C 1, tale che ξ(t) + η(t) e C(t t0). Dunque t t ξ(t) = η(s)s = 1(t ) + s q F (z(s 1 ))ξ(s 1 ) + p F (z(s 1 ))η(s 1 )s 1. Remark 3.3. S not che nelle rghe sopra abbamo ntrootto la norma una matrce. Questa non è efnta n moo canonco, esste tuttava una scelta partcolarmente felce: sa D una matrce allora efnamo Dv (3.4) D = sup v R \{0} v. Qun ξ(t 1 ) 1(t 1 ) s 2Ce C(s1 t0) s 1 Ce C(t1 t0) (t 1 ) 2. Possamo qun scrvere ξ(t 1, v, λ) = (t 1 ) [1 D] ove D Ce C(t1 t0) (t 1 ). Eserczo 3.4. S mostr che la (3.4) efnsce una norma nello spazo ella matrc. Inoltre s mostr che, ate comunque ue matrc D, E, s ha che DE D E. Eserczo 3.5. S mostr che se D < 1 allora 1 D è nvertble. (suggermento: s mostr che la sere n=0 Dn converge n norma e che qun efnsce una matrce E. S verfch che E(1 D) = (1 D)E = 1.) Dunque se Ce C(t1 t0) (t 1 ) < 1, allora ξ(t 1 ) è nvertble e l teorema ella funzone mplcta s applca per ogn λ suffcentemente pccolo. Questo sgnfca che per tal λ l nostro problema ha un unca soluzone e questa pene con contnutà a λ. Questo mplca che l nseme e λ per cu esste la soluzone è chuso. Sa λ 1 l suo supremo. Ma ora possamo fare lo stesso argomento parteno a λ 1 nvece che a zero. Per gl stess esatt argoment l teorema ella funzone mplcta s applcherà e otterremo una unca soluzone per tutt λ n un ntorno λ 1, contraramente all potes che λ 1 fosse l pù grane λ per cu essteva una soluzone. Qun l nostro problema ha una soluzone per tutt λ, e n partcolare per λ = 1, l che mplca l teorema. Abbamo così vsto che l problema al contorno etermnato al mnmzzare l azone ha una unca soluzone (a patto che lo s conser per temp suffcentemente pccol) e qun a un lato è equvalente a un qualche (pù convenzonale) problema Cauchy e all altro sgnfca che l azone eve avere un mnmo. S not nfne che sebbene la soluzone possa esstere per temp pù lungh, essa può non essere unca, come s evnce rsolveno seguent esercz.
11 ELOGIO DELLA PIGRIZIA 11 Eserczo 3.6. S conser la Lagrangana L 1 (x, ẋ) = 1 2 ẋ 2, q R 3 e sa ato l vncolo x = 1 (ovvero l moto s svolge sulla superfce ella sfera untara). S scrva la Lagrangana nelle coornate x = (cos θ sn ϕ, sn θ sn ϕ, cos ϕ) ove θ [0, 2π] e ϕ [0, π]. S facca lo stesso per la Lagrangana L 2 = ẋ e s mostr che ha gl stess punt stazonar L 1. Eserczo 3.7. S mostr che, per ogn T > 0, e M 0,T (A, B) con A = (0, 0, 1) e B = (0, 0, 1), l azone assocata alla Lagrangana L 1 ha nfnt punt stazonar. Eserczo 3.8. S not che l azone assocata alla lagrangana L 2 non è altro che la lunghezza ella curva su cu avvene l moto. S us questo fatto per are una nterpretazone geometrca egl esercz preceent. Carlangelo Lveran, Dpartmento Matematca, II Unverstà Roma (Tor Vergata), Va ella Rcerca Scentfca, Roma, Italy. E-mal aress: lveran@mat.unroma2.t
Qualità dell adattamento di una funzione y=f(x) ad un insieme di misure (y in funzione di x)
 Qualtà ell aattamento una funzone y=f() a un nseme msure (y n funzone ) Date N msure coppe valor elle granezze e y, legate alla relazone y=f(;a,b), nell potes che le ncertezze sulle sano trascurabl e y
Qualtà ell aattamento una funzone y=f() a un nseme msure (y n funzone ) Date N msure coppe valor elle granezze e y, legate alla relazone y=f(;a,b), nell potes che le ncertezze sulle sano trascurabl e y
Funzione di matrice. c i λ i. i=0. i=0. m 1. γ i A i. i=0. Moltiplicando entrambi i membri di questa equazione per A si ottiene. α i 1 A i α m 1 A m
 Captolo INTRODUZIONE Funzone d matrce Sa f(λ) una generca funzone del parametro λ svluppable n sere d potenze f(λ) Sa A una matrce quadrata d ordne n La funzone d matrce f(a) èdefnta nel modo seguente
Captolo INTRODUZIONE Funzone d matrce Sa f(λ) una generca funzone del parametro λ svluppable n sere d potenze f(λ) Sa A una matrce quadrata d ordne n La funzone d matrce f(a) èdefnta nel modo seguente
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO
 PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
Intorduzione alla teoria delle Catene di Markov
 Intorduzone alla teora delle Catene d Markov Mchele Ganfelce a.a. 2014/2015 Defnzone 1 Sa ( Ω, F, {F n } n 0, P uno spazo d probabltà fltrato. Una successone d v.a. {ξ n } n 0 defnta su ( Ω, F, {F n }
Intorduzone alla teora delle Catene d Markov Mchele Ganfelce a.a. 2014/2015 Defnzone 1 Sa ( Ω, F, {F n } n 0, P uno spazo d probabltà fltrato. Una successone d v.a. {ξ n } n 0 defnta su ( Ω, F, {F n }
6 Prodotti scalari e prodotti Hermitiani
 6 Prodott scalar e prodott Hermtan 6.1 Prodott scalar S fss K = R. Defnzone 6.1 Sa V un R-spazo vettorale. Un prodotto scalare su V è un applcazone che gode delle seguent propretà: ) (lneartà rspetto al
6 Prodott scalar e prodott Hermtan 6.1 Prodott scalar S fss K = R. Defnzone 6.1 Sa V un R-spazo vettorale. Un prodotto scalare su V è un applcazone che gode delle seguent propretà: ) (lneartà rspetto al
Algebra 2. 6 4. Sia A un anello commutativo. Si ricorda che in un anello commutativo vale il teorema binomiale, cioè. (a + b) n = a i b n i i.
 Testo Fac-smle 2 Durata prova: 2 ore 8 1. Un gruppo G s dce semplce se suo unc sottogrupp normal sono 1 e G stesso. Sa G un gruppo d ordne pq con p e q numer prm tal che p < q. (a) Il gruppo G può essere
Testo Fac-smle 2 Durata prova: 2 ore 8 1. Un gruppo G s dce semplce se suo unc sottogrupp normal sono 1 e G stesso. Sa G un gruppo d ordne pq con p e q numer prm tal che p < q. (a) Il gruppo G può essere
Esercizi 3 Scattering elettromagnetico e fattori di forma elastici. 1. Sez. d urto di Rutherford (statica)
 Esercz Scatterng elettromagnetco e fattor forma elastc 1. Sez. urto Rutherfor (statca) Scatterng a un potenzale coulombano statco: Sez. urto Rutherfor (v. cors preceent ): m 4 4 4 p sn. Sez. urto Rutherfor
Esercz Scatterng elettromagnetco e fattor forma elastc 1. Sez. urto Rutherfor (statca) Scatterng a un potenzale coulombano statco: Sez. urto Rutherfor (v. cors preceent ): m 4 4 4 p sn. Sez. urto Rutherfor
Dipartimento di Matematica per le scienze economiche e sociali Università di Bologna. Matematica aa lezione marzo 2009
 Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2008-2009 lezone 25 17 marzo 2009 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/26? Convesstà Sa I un ntervallo
Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2008-2009 lezone 25 17 marzo 2009 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/26? Convesstà Sa I un ntervallo
Integrazione numerica dell equazione del moto per un sistema lineare viscoso a un grado di libertà. Prof. Adolfo Santini - Dinamica delle Strutture 1
 Integrazone numerca dell equazone del moto per un sstema lneare vscoso a un grado d lbertà Prof. Adolfo Santn - Dnamca delle Strutture 1 Introduzone 1/2 L equazone del moto d un sstema vscoso a un grado
Integrazone numerca dell equazone del moto per un sstema lneare vscoso a un grado d lbertà Prof. Adolfo Santn - Dnamca delle Strutture 1 Introduzone 1/2 L equazone del moto d un sstema vscoso a un grado
Calcolo Scientifico e Matematica Applicata Secondo Parziale, Ingegneria Ambientale
 Calcolo Scentfco e Matematca Applcata Secondo Parzale, 7.2.28 Ingegnera Ambentale Rsolvere gl esercz, 2, 4 oppure, n alternatva, gl esercz, 3, 4. Valutazone degl esercz: 4, 2 8, 3 8, 4 8.. Illustrare,
Calcolo Scentfco e Matematca Applcata Secondo Parzale, 7.2.28 Ingegnera Ambentale Rsolvere gl esercz, 2, 4 oppure, n alternatva, gl esercz, 3, 4. Valutazone degl esercz: 4, 2 8, 3 8, 4 8.. Illustrare,
ANELLI E SOTTOANELLI. contrassegna gli esercizi (relativamente) più complessi.
 ESERCIZI SU ANELLI E SOTTOANELLI N.B.: l smbolo contrassegna gl esercz relatvamente pù compless. 1 Sa X un nseme, e sa PX l suo nseme delle part. Indcando con l operazone d dfferenza smmetrca tra element
ESERCIZI SU ANELLI E SOTTOANELLI N.B.: l smbolo contrassegna gl esercz relatvamente pù compless. 1 Sa X un nseme, e sa PX l suo nseme delle part. Indcando con l operazone d dfferenza smmetrca tra element
Soluzioni 3.1. n(n 1) (n k + 1) z n k! k + 1 n k. lim k
 (1) La sere bnomale è B n (z) = k=0 Con l metodo del rapporto s ottene R = lm k Soluzon 3.1 n(n 1) (n k + 1) z n k! c k c k+1 = lm k k + 1 n k lm k c k z k. k=0 1 + 1 k 1 n k = 1 (2) La multfunzone f(z)
(1) La sere bnomale è B n (z) = k=0 Con l metodo del rapporto s ottene R = lm k Soluzon 3.1 n(n 1) (n k + 1) z n k! c k c k+1 = lm k k + 1 n k lm k c k z k. k=0 1 + 1 k 1 n k = 1 (2) La multfunzone f(z)
2. La base monetaria e i mercati dei depositi e del credito
 2. La base monetara e mercat e epost e el creto Esercz svolt Eserczo 2.1 (a) Conserate l moello che rappresenta l equlbro el mercato ella base monetara e el mercato e epost (fate l potes che coe cent c;
2. La base monetara e mercat e epost e el creto Esercz svolt Eserczo 2.1 (a) Conserate l moello che rappresenta l equlbro el mercato ella base monetara e el mercato e epost (fate l potes che coe cent c;
La soluzione delle equazioni differenziali con il metodo di Galerkin
 Il metodo de resdu pesat per gl element fnt a soluzone delle equazon dfferenzal con l metodo d Galerkn Tra le procedure generalmente adottate per formulare e rsolvere le equazon dfferenzal con un metodo
Il metodo de resdu pesat per gl element fnt a soluzone delle equazon dfferenzal con l metodo d Galerkn Tra le procedure generalmente adottate per formulare e rsolvere le equazon dfferenzal con un metodo
# STUDIO DELLA FEDELTA DI RISPOSTA
 # STUDIO DELLA FEDELTA DI RISOSTA # er poter formulare n manera approprata problem sntes (progetto) sstem controllo, e necessaro a questo punto nteressarc elle loro propreta n termn feelta rsposta agl
# STUDIO DELLA FEDELTA DI RISOSTA # er poter formulare n manera approprata problem sntes (progetto) sstem controllo, e necessaro a questo punto nteressarc elle loro propreta n termn feelta rsposta agl
Geometria 1 a.a. 2011/12 Esonero del 23/01/12 Soluzioni (Compito A) sì determinarla, altrimenti dimostrare che ciò è impossibile.
 Geometra 1 a.a. 2011/12 Esonero del 23/01/12 Soluzon (Compto A) (1) S consder su C 2 l prodotto Hermtano, H assocato alla matrce ( ) 2 H =. 2 (a) Dmostrare che, H è defnto postvo e determnare una base
Geometra 1 a.a. 2011/12 Esonero del 23/01/12 Soluzon (Compto A) (1) S consder su C 2 l prodotto Hermtano, H assocato alla matrce ( ) 2 H =. 2 (a) Dmostrare che, H è defnto postvo e determnare una base
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa lezione 3: 27 febbraio 2013
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 3: 27 febbrao 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/26? S può dmostrare che 1. se 0 < t < 1 allora
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 3: 27 febbrao 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/26? S può dmostrare che 1. se 0 < t < 1 allora
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa lezione 9: 3 marzo 2014
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2013-2014 lezone 9: 3 marzo 2014 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/25? Eserczo Consderamo una rendta perodca d 2n termn
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2013-2014 lezone 9: 3 marzo 2014 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/25? Eserczo Consderamo una rendta perodca d 2n termn
Ingegneria Elettrica Politecnico di Torino. Luca Carlone. ControlliAutomaticiI LEZIONE III
 Ingegnera Elettrca Poltecnco d Torno Luca Carlone ControllAutomatcI LEZIONE III Sommaro LEZIONE III Trasformata d Laplace Propretà e trasformate notevol Funzon d trasfermento Scomposzone n fratt semplc
Ingegnera Elettrca Poltecnco d Torno Luca Carlone ControllAutomatcI LEZIONE III Sommaro LEZIONE III Trasformata d Laplace Propretà e trasformate notevol Funzon d trasfermento Scomposzone n fratt semplc
POLINOMIO MINIMO E FORMA CANONICA DI JORDAN NOTA AGGIUNTIVA PER IL CORSO DI GEOMETRIA ANALITICA E ALGEBRA LINEARE A.A DOCENTE: PAOLO LISCA
 POLINOMIO MINIMO E FORMA CANONICA DI JORDAN NOTA AGGIUNTIVA PER IL CORSO DI GEOMETRIA ANALITICA E ALGEBRA LINEARE AA 2009-2010 DOCENTE: PAOLO LISCA 1 Polnomo mnmo Avvertenza: con V ndcheremo uno spazo
POLINOMIO MINIMO E FORMA CANONICA DI JORDAN NOTA AGGIUNTIVA PER IL CORSO DI GEOMETRIA ANALITICA E ALGEBRA LINEARE AA 2009-2010 DOCENTE: PAOLO LISCA 1 Polnomo mnmo Avvertenza: con V ndcheremo uno spazo
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energa e Lavoro Fnora abbamo descrtto l moto de corp (puntform) usando le legg d Newton, tramte le forze; abbamo scrtto l equazone del moto, determnato spostamento e veloctà n funzone del tempo. E possble
Energa e Lavoro Fnora abbamo descrtto l moto de corp (puntform) usando le legg d Newton, tramte le forze; abbamo scrtto l equazone del moto, determnato spostamento e veloctà n funzone del tempo. E possble
Metodi variazionali. ed agiscono sulla FORMA DEBOLE DEL PROBLEMA
 Metod varazonal OBIETTIVO: determnare funzon ncognte, chamate varabl dpendent, che soddsfano un certo nseme d equazon dfferenzal n un determnato domno e condzon al contorno STRUMETO: Metod varazonal: servono
Metod varazonal OBIETTIVO: determnare funzon ncognte, chamate varabl dpendent, che soddsfano un certo nseme d equazon dfferenzal n un determnato domno e condzon al contorno STRUMETO: Metod varazonal: servono
Metodi variazionali. ed agiscono sulla FORMA DEBOLE DEL PROBLEMA
 Metod varazonal OBIETTIVO: determnare funzon ncognte, chamate varabl dpendent, che soddsfano un certo nseme d equazon dfferenzal n un determnato domno e condzon al contorno STRUMETO: Metod varazonal: servono
Metod varazonal OBIETTIVO: determnare funzon ncognte, chamate varabl dpendent, che soddsfano un certo nseme d equazon dfferenzal n un determnato domno e condzon al contorno STRUMETO: Metod varazonal: servono
Enrico Borghi LA LEGGE FONDAMENTALE DELLA MECCANICA NEWTONIANA PER UN SISTEMA DI PARTICELLE
 Enrco Borgh LA LEGGE FONDAMENTALE DELLA MECCANICA NEWTONIANA PE UN SISTEMA DI PATICELLE La meccanca newtonana e sstem costtut a pú partcelle puntform può essere svluppata parteno alla legge fonamentale
Enrco Borgh LA LEGGE FONDAMENTALE DELLA MECCANICA NEWTONIANA PE UN SISTEMA DI PATICELLE La meccanca newtonana e sstem costtut a pú partcelle puntform può essere svluppata parteno alla legge fonamentale
3 Partizioni dell unità 6
 Partzon dell untà Alessandro Ghg 29 ottobre 2014 Indce 1 Funzon lsce a supporto compatto 1 2 Rcoprment localmente fnt 5 3 Partzon dell untà 6 1 Funzon lsce a supporto compatto Lemma 1. Sano f C 1 (a, b)
Partzon dell untà Alessandro Ghg 29 ottobre 2014 Indce 1 Funzon lsce a supporto compatto 1 2 Rcoprment localmente fnt 5 3 Partzon dell untà 6 1 Funzon lsce a supporto compatto Lemma 1. Sano f C 1 (a, b)
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa lezione 17: 16 maggio 2013
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 17: 16 maggo 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/22? Eserczo Un Btp trennale, d valore nomnale C
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 17: 16 maggo 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/22? Eserczo Un Btp trennale, d valore nomnale C
Propagazione degli errori
 Propagaone degl error Voglamo rcavare le ncertee nelle msure ndrette. Abbamo gà vsto leone un prma stma degl error sulle grandee dervate valda n generale. Consderamo ora l caso specco d grandee aette da
Propagaone degl error Voglamo rcavare le ncertee nelle msure ndrette. Abbamo gà vsto leone un prma stma degl error sulle grandee dervate valda n generale. Consderamo ora l caso specco d grandee aette da
Il logaritmo discreto in Z p Il gruppo moltiplicativo Z p delle classi resto modulo un primo p è un gruppo ciclico.
 Il logartmo dscreto n Z p Il gruppo moltplcatvo Z p delle class resto modulo un prmo p è un gruppo cclco. Defnzone (Logartmo dscreto). Sa p un numero prmo e sa ā una radce prmtva n Z p. Sa ȳ Z p. Il logartmo
Il logartmo dscreto n Z p Il gruppo moltplcatvo Z p delle class resto modulo un prmo p è un gruppo cclco. Defnzone (Logartmo dscreto). Sa p un numero prmo e sa ā una radce prmtva n Z p. Sa ȳ Z p. Il logartmo
6. Catene di Markov a tempo continuo (CMTC)
 6. Catene d Markov a tempo contnuo (CMTC) Defnzone Una CMTC è un processo stocastco defnto come segue: lo spazo d stato è dscreto: X{x,x 2, }. L nseme X può essere sa fnto sa nfnto numerable. L nseme de
6. Catene d Markov a tempo contnuo (CMTC) Defnzone Una CMTC è un processo stocastco defnto come segue: lo spazo d stato è dscreto: X{x,x 2, }. L nseme X può essere sa fnto sa nfnto numerable. L nseme de
Matematica Computazionale(6cfu) Ottimizzazione(8cfu)
 Docente: Marco Gavano (e-mal:gavano@unca.t) Corso d Laurea n Infomatca Corso d Laurea n Matematca Matematca Computazonale(6cfu) Ottmzzazone(8cfu) (a.a. 205-6, lez.8) Matematca Computazonale, Ottmzzazone,
Docente: Marco Gavano (e-mal:gavano@unca.t) Corso d Laurea n Infomatca Corso d Laurea n Matematca Matematca Computazonale(6cfu) Ottmzzazone(8cfu) (a.a. 205-6, lez.8) Matematca Computazonale, Ottmzzazone,
urto v 2f v 2i e forza impulsiva F r F dt = i t
 7. Urt Sstem a due partcelle Defnzone d urto elastco, urto anelastco e mpulso L urto è un nterazone fra corp che avvene n un ntervallo d tempo normalmente molto breve, al termne del quale le quanttà d
7. Urt Sstem a due partcelle Defnzone d urto elastco, urto anelastco e mpulso L urto è un nterazone fra corp che avvene n un ntervallo d tempo normalmente molto breve, al termne del quale le quanttà d
Laboratorio 2B A.A. 2012/2013. Elaborazione Dati. Lab 2B CdL Fisica
 Laboratoro B A.A. 01/013 Elaborazone Dat Lab B CdL Fsca Lab B CdL Fsca Elaborazone dat spermental Prncpo della massma verosmglanza Quando eseguamo una sere d msure relatve ad una data grandezza fsca, quanto
Laboratoro B A.A. 01/013 Elaborazone Dat Lab B CdL Fsca Lab B CdL Fsca Elaborazone dat spermental Prncpo della massma verosmglanza Quando eseguamo una sere d msure relatve ad una data grandezza fsca, quanto
6. Catene di Markov a tempo continuo (CMTC)
 6. Catene d Markov a tempo contnuo (CMTC) Carla Seatzu, 8 Marzo 28 Defnzone Una CMTC è un processo stocastco defnto come segue: lo spazo d stato è dscreto: X{x,x 2, }. L nseme X può essere sa fnto sa nfnto
6. Catene d Markov a tempo contnuo (CMTC) Carla Seatzu, 8 Marzo 28 Defnzone Una CMTC è un processo stocastco defnto come segue: lo spazo d stato è dscreto: X{x,x 2, }. L nseme X può essere sa fnto sa nfnto
Dipartimento di Statistica Università di Bologna. Matematica Finanziaria aa lezione 16: 2 maggio 2012
 Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 16: 2 maggo 2012 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/19? CCT/CCTEu S tratta d un ttolo a cedola varable:
Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 16: 2 maggo 2012 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/19? CCT/CCTEu S tratta d un ttolo a cedola varable:
Equilibrio e stabilità di sistemi dinamici. Stabilità dell equilibrio di sistemi dinamici non lineari per linearizzazione
 Equlbro e stabltà d sstem dnamc Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem NL TC Crter d stabltà
Equlbro e stabltà d sstem dnamc Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem NL TC Crter d stabltà
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa lezione 2: 21 febbraio 2013
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 2: 21 febbrao 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/25? Defnzone. f : R R s dce addtva se per ogn
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 2: 21 febbrao 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/25? Defnzone. f : R R s dce addtva se per ogn
ω 0 =, abbiamo L = 1 H. LC 8.1 Per t il condensatore si comporta come un circuito aperto pertanto la corrente tende a zero: la R
 8. Per t l condensatore s comporta come un crcuto aperto pertanto la corrente tende a zero: la funzone non può essere la (c). caando α e ω 0 s ottengono seguent alor: α 5 0 e ω 0 0. Essendo α > ω 0 l crcuto
8. Per t l condensatore s comporta come un crcuto aperto pertanto la corrente tende a zero: la funzone non può essere la (c). caando α e ω 0 s ottengono seguent alor: α 5 0 e ω 0 0. Essendo α > ω 0 l crcuto
Stabilità dei Sistemi Dinamici. Stabilità Semplice. Stabilità Asintotica. Stabilità: concetto intuitivo che può essere formalizzato in molti modi
 Gustavo Belforte Stabltà de Sstem Dnamc Gustavo Belforte Stabltà de Sstem Dnamc Stabltà de Sstem Dnamc Il Pendolo Stabltà: concetto ntutvo che può essere formalzzato n molt mod Intutvamente: Un oggetto
Gustavo Belforte Stabltà de Sstem Dnamc Gustavo Belforte Stabltà de Sstem Dnamc Stabltà de Sstem Dnamc Il Pendolo Stabltà: concetto ntutvo che può essere formalzzato n molt mod Intutvamente: Un oggetto
Ad esempio, potremmo voler verificare la legge di caduta dei gravi che dice che un corpo cade con velocità uniformemente accellerata: v = v 0 + g t
 Relazon lnear Uno de pù mportant compt degl esperment è quello d nvestgare la relazone tra due varabl. Il caso pù mportante (e a cu spesso c s rconduce, come vedremo è quello n cu la relazone che s ntende
Relazon lnear Uno de pù mportant compt degl esperment è quello d nvestgare la relazone tra due varabl. Il caso pù mportante (e a cu spesso c s rconduce, come vedremo è quello n cu la relazone che s ntende
5.1 Controllo di un sistema non lineare
 5.1 Controllo d un sstema non lneare Sa dato l sstema non lneare rappresentato n fgura 5.1, con h g θ Θ,m,r Fgura 5.1: Sstema non lneare F m (,d) = k m la forza che esercta l elettromagnete percorso da
5.1 Controllo d un sstema non lneare Sa dato l sstema non lneare rappresentato n fgura 5.1, con h g θ Θ,m,r Fgura 5.1: Sstema non lneare F m (,d) = k m la forza che esercta l elettromagnete percorso da
Dipartimento di Scienze Statistiche Università di Bologna. Matematica finanziaria aa lezione 16: 13 marzo 2014
 Dpartmento d Scenze Statstche Unverstà d Bologna Matematca fnanzara aa 2013-2014 lezone 16: 13 marzo 2014 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/20? Eserczo Nell ammortamento d un prestto
Dpartmento d Scenze Statstche Unverstà d Bologna Matematca fnanzara aa 2013-2014 lezone 16: 13 marzo 2014 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/20? Eserczo Nell ammortamento d un prestto
MODELLI MULTISTATO. Introduzione ai modelli multistato. Esempio di modello multistato per descrivere la progressione di una malattia
 MODELLI MULTISTATO Introuzone a moell multstato Esempo moello multstato per escrvere la progressone una malatta I moell multstato Un moello multstato per l asscurazone malatta Introuzone a moell multstato
MODELLI MULTISTATO Introuzone a moell multstato Esempo moello multstato per escrvere la progressone una malatta I moell multstato Un moello multstato per l asscurazone malatta Introuzone a moell multstato
INTERPOLAZIONE MEDIANTE CURVE SPLINE. '' ( b ) = 0
 INTERPOLAZIONE EDIANTE CURVE SPLINE Defnzone del problema Sovente, nelle applcazon grafche (CAD Computer Aed Desgn), s ha la necesstà d traccare, dat alcun punt, una lnea che l raccord e che sa suffcentemente
INTERPOLAZIONE EDIANTE CURVE SPLINE Defnzone del problema Sovente, nelle applcazon grafche (CAD Computer Aed Desgn), s ha la necesstà d traccare, dat alcun punt, una lnea che l raccord e che sa suffcentemente
Dipartimento di Matematica per le scienze economiche e sociali Università di Bologna. Matematica aa lezione febbraio 2009
 Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2008-2009 lezone 17 13 febbrao 2009 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/19? 2/19? Fgura 1: ( 5y
Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2008-2009 lezone 17 13 febbrao 2009 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/19? 2/19? Fgura 1: ( 5y
B - ESERCIZI: IP e TCP:
 Unverstà d Bergamo Dpartmento d Ingegnera dell Informazone e Metod Matematc B - ESERCIZI: IP e TCP: F. Martgnon Archtetture e Protocoll per Internet Eserczo b. S consder l collegamento n fgura A C =8 kbt/s
Unverstà d Bergamo Dpartmento d Ingegnera dell Informazone e Metod Matematc B - ESERCIZI: IP e TCP: F. Martgnon Archtetture e Protocoll per Internet Eserczo b. S consder l collegamento n fgura A C =8 kbt/s
Ricerca di radici di equazioni non lineari
 Rcerca rac equazon non lnear Il problema consste nella rcerca elle soluzon ell'equazone sotto forma mplcta f( ) Torna all'nce generale f e possono essere n generale ue vettor a n component, anche se la
Rcerca rac equazon non lnear Il problema consste nella rcerca elle soluzon ell'equazone sotto forma mplcta f( ) Torna all'nce generale f e possono essere n generale ue vettor a n component, anche se la
Propagazione degli errori
 Propagazone degl error Msure drette: la grandezza sca vene msurata drettamente (ad es. Spessore d una lastrna). Per questo tpo d msure, la teora dell errore svluppata nelle lezone precedent é sucente per
Propagazone degl error Msure drette: la grandezza sca vene msurata drettamente (ad es. Spessore d una lastrna). Per questo tpo d msure, la teora dell errore svluppata nelle lezone precedent é sucente per
Corso di. Gasdinamica II Tommaso Astarita
 Corso d Gasdnamca II Tommaso Astarta astarta@unna.t www.docent.unna.t Gasdnamca II Tommaso Astarta 5.0.008 Metodo d Eulero S supponga d avere una equazone dfferenzale del prmo ordne: f ( x, ) x xo o Defnendo
Corso d Gasdnamca II Tommaso Astarta astarta@unna.t www.docent.unna.t Gasdnamca II Tommaso Astarta 5.0.008 Metodo d Eulero S supponga d avere una equazone dfferenzale del prmo ordne: f ( x, ) x xo o Defnendo
Dipartimento di Matematica per le scienze economiche e sociali Università di Bologna
 Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Modell 1 lezone 12 10 novembre 2011 Teorema d Lebesgue Vtal-Generazone d msure professor Danele Rtell www.unbo.t/docent/danele.rtell
Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Modell 1 lezone 12 10 novembre 2011 Teorema d Lebesgue Vtal-Generazone d msure professor Danele Rtell www.unbo.t/docent/danele.rtell
Appunti: Scomposizione in fratti semplici ed antitrasformazione
 Appunt: Scomposzone n fratt semplc ed anttrasformazone Gulo Cazzol v0. (AA. 017-018) 1 Fratt semplc 1.1 Funzone ntera.............................................. 1. Funzone razonale fratta strettamente
Appunt: Scomposzone n fratt semplc ed anttrasformazone Gulo Cazzol v0. (AA. 017-018) 1 Fratt semplc 1.1 Funzone ntera.............................................. 1. Funzone razonale fratta strettamente
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa lezione 2: 18 febbraio 2014
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2013-2014 lezone 2: 18 febbrao 2014 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/19? Defnzone. f : R R s dce moltplcatva se per
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2013-2014 lezone 2: 18 febbrao 2014 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/19? Defnzone. f : R R s dce moltplcatva se per
Sorgenti Numeriche - Soluzioni
 Sorgent umerche - Soluzon *) L anals delle frequenze con cu compaono le vare lettere n un documento n talano, comprendente 5975 caratter, ha fornto seguent dat: Lettera umero Frequenza relatva A 666. B
Sorgent umerche - Soluzon *) L anals delle frequenze con cu compaono le vare lettere n un documento n talano, comprendente 5975 caratter, ha fornto seguent dat: Lettera umero Frequenza relatva A 666. B
Elasticità nei mezzi continui
 Elastctà ne mezz contnu l tensore degl sforz o tensore d stress, σ j Consderamo un cubo d dmenson untare n un mezzo elastco deformato. l cubo è deformato dalle forze eserctate sulle sue facce dal resto
Elastctà ne mezz contnu l tensore degl sforz o tensore d stress, σ j Consderamo un cubo d dmenson untare n un mezzo elastco deformato. l cubo è deformato dalle forze eserctate sulle sue facce dal resto
Esercizi sulle reti elettriche in corrente continua (parte 2)
 Esercz sulle ret elettrche n corrente contnua (parte ) Eserczo 3: etermnare gl equvalent d Thevenn e d Norton del bpolo complementare al resstore R 5 nel crcuto n fgura e calcolare la corrente che crcola
Esercz sulle ret elettrche n corrente contnua (parte ) Eserczo 3: etermnare gl equvalent d Thevenn e d Norton del bpolo complementare al resstore R 5 nel crcuto n fgura e calcolare la corrente che crcola
Generalità. Problema: soluzione di una equazione differenziale alle derivate ordinarie di ordine n: ( )
 Generaltà Problema: soluzone d una equazone derenzale alle dervate ordnare d ordne n: n n K soggetta alle n condzon nzal: K n Ovvero rcercare la soluzone d un sstema d n equazon derenzal ordnare del prmo
Generaltà Problema: soluzone d una equazone derenzale alle dervate ordnare d ordne n: n n K soggetta alle n condzon nzal: K n Ovvero rcercare la soluzone d un sstema d n equazon derenzal ordnare del prmo
Analisi Matematica Lezione 16 3 novembre 2014 Limiti di funzioni
 Dpartmento d Scenze Statstche Anals Matematca Lezone 6 3 novembre 204 Lmt d funzon prof. Danele Rtell danele.rtell@unbo.t /7? Eserczo 9 Determnare l ordne d nfntesmo e la parte prncpale dell nfntesmo rspetto
Dpartmento d Scenze Statstche Anals Matematca Lezone 6 3 novembre 204 Lmt d funzon prof. Danele Rtell danele.rtell@unbo.t /7? Eserczo 9 Determnare l ordne d nfntesmo e la parte prncpale dell nfntesmo rspetto
Support Vector Machines. Macchine a vettori di supporto
 Support Vector Machnes Macchne a vettor d supporto Separator Lnear Percettrone La classfcazone bnara può essere vsta come un problema d separazone d class nello spazo delle feature m b b b > 0 b 0 b
Support Vector Machnes Macchne a vettor d supporto Separator Lnear Percettrone La classfcazone bnara può essere vsta come un problema d separazone d class nello spazo delle feature m b b b > 0 b 0 b
Le soluzioni della prova scritta di Matematica per il corso di laurea in Farmacia (raggruppamento M-Z)
 Le soluzon della prova scrtta d Matematca per l corso d laurea n Farmaca (raggruppamento M-Z). Data la funzone a. trova l domno d f f ( ) ln + b. scrv, esplctamente e per esteso, qual sono gl ntervall
Le soluzon della prova scrtta d Matematca per l corso d laurea n Farmaca (raggruppamento M-Z). Data la funzone a. trova l domno d f f ( ) ln + b. scrv, esplctamente e per esteso, qual sono gl ntervall
Dipartimento di Statistica Università di Bologna. Matematica Finanziaria aa lezione 3:
 Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 3: 21022012 professor Danele Rtell www.unbo.t/docdent/danele.rtell 1/31? Captalzzazone msta S usa l regme composto per l
Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 3: 21022012 professor Danele Rtell www.unbo.t/docdent/danele.rtell 1/31? Captalzzazone msta S usa l regme composto per l
di una delle versioni del compito di Geometria analitica e algebra lineare del 12 luglio 2013 distanza tra r ed r'. (punti 2 + 3)
 Esempo d soluzone d una delle verson del compto d Geometra analtca e algebra lneare del luglo 3 Stablre se la retta r, d equazon parametrche x =, y = + t, z = t (nel parametro reale t), è + y + z = sghemba
Esempo d soluzone d una delle verson del compto d Geometra analtca e algebra lneare del luglo 3 Stablre se la retta r, d equazon parametrche x =, y = + t, z = t (nel parametro reale t), è + y + z = sghemba
I Appello di Calcolo delle Probabilità Cognome: Laurea Triennale in Matematica 2014/15 Nome: 29 gennaio
 I Appello d Calcolo delle Probabltà Cognome: Laurea Trennale n Matematca 24/5 Nome: 29 gennao 25 Emal: Se non è espressamente ndcato l contraro, per la soluzone degl esercz è possble usare tutt rsultat
I Appello d Calcolo delle Probabltà Cognome: Laurea Trennale n Matematca 24/5 Nome: 29 gennao 25 Emal: Se non è espressamente ndcato l contraro, per la soluzone degl esercz è possble usare tutt rsultat
Analisi Modale. Le evoluzioni libere dei due sistemi a partire dalla condizione iniziale x(0) = x 0 sono
 Captolo 1 INTRODUZIONE 21 Anals Modale S facca rfermento al sstema tempo-dscreto e al sstema tempo-contnuo x(k +1)=Ax(k) ẋ(t) =Ax(t) Le evoluzon lbere de due sstem a partre dalla condzone nzale x() = x
Captolo 1 INTRODUZIONE 21 Anals Modale S facca rfermento al sstema tempo-dscreto e al sstema tempo-contnuo x(k +1)=Ax(k) ẋ(t) =Ax(t) Le evoluzon lbere de due sstem a partre dalla condzone nzale x() = x
LE FREQUENZE CUMULATE
 LE FREQUENZE CUMULATE Dott.ssa P. Vcard Introducamo questo argomento con l seguente Esempo: consderamo la seguente dstrbuzone d un campone d 70 sttut d credto numero flal present nel terrtoro del comune
LE FREQUENZE CUMULATE Dott.ssa P. Vcard Introducamo questo argomento con l seguente Esempo: consderamo la seguente dstrbuzone d un campone d 70 sttut d credto numero flal present nel terrtoro del comune
Introduzione al calcolo numerico. Derivazione Integrazione Soluzione di equazioni
 Introduzone al calcolo numerco Dervazone Integrazone Soluzone d equazon Dervazone numerca Il calcolo della dervata d una unzone n un punto mplca un processo al lmte ce può solo essere approssmato da un
Introduzone al calcolo numerco Dervazone Integrazone Soluzone d equazon Dervazone numerca Il calcolo della dervata d una unzone n un punto mplca un processo al lmte ce può solo essere approssmato da un
Metodi di analisi R 1 =15Ω R 2 =40Ω R 3 =16Ω
 Metod d anals Eserczo Anals alle magle n presenza d sol generator ndpendent d tensone R s J R Determnare le tenson sulle resstenze sapendo che: s s 0 R R 5.Ω s J R J R R 5Ω R 0Ω R 6Ω R 5 Dsegnamo l grafo,
Metod d anals Eserczo Anals alle magle n presenza d sol generator ndpendent d tensone R s J R Determnare le tenson sulle resstenze sapendo che: s s 0 R R 5.Ω s J R J R R 5Ω R 0Ω R 6Ω R 5 Dsegnamo l grafo,
1 La domanda di moneta
 La domanda d moneta Eserczo.4 (a) Keynes elenca tre motv per detenere moneta: Scopo transattvo Scopo precauzonale Scopo speculatvo Il modello d domanda d moneta a scopo speculatvo d Keynes consdera la
La domanda d moneta Eserczo.4 (a) Keynes elenca tre motv per detenere moneta: Scopo transattvo Scopo precauzonale Scopo speculatvo Il modello d domanda d moneta a scopo speculatvo d Keynes consdera la
La sincronizzazione. (Libro) Trasmissione dell Informazione
 La sncronzzazone (Lbro) Problem d sncronzzazone La trasmssone e la dverstà tra gl OL del trasmetttore e del rcevtore ntroducono (anche n assenza d fadng) un errore d d frequenza, d fase e d camponamento
La sncronzzazone (Lbro) Problem d sncronzzazone La trasmssone e la dverstà tra gl OL del trasmetttore e del rcevtore ntroducono (anche n assenza d fadng) un errore d d frequenza, d fase e d camponamento
Lezione 7. Numeri primi. Teorema Fondamentale dell'aritmetica.
 Lezone 7 Prereqst: L'nseme de nmer nter Lezone 6 Nmer prm Teorema Fondamentale dell'artmetca Defnzone 7 Un nmero ntero p dverso da 0 e s dce prmo se per ogn a b Z Altrment p s dce composto p ab p a oppre
Lezone 7 Prereqst: L'nseme de nmer nter Lezone 6 Nmer prm Teorema Fondamentale dell'artmetca Defnzone 7 Un nmero ntero p dverso da 0 e s dce prmo se per ogn a b Z Altrment p s dce composto p ab p a oppre
Analisi Matenatica Lezione 5 1 ottobre 2013
 Dpartmento d Scenze Statstche Anals Matenatca Lezone 5 1 ottobre 2013 prof. Danele Rtell danele.rtell@unbo.t 1/13? Fattorale d un numero naturale Sa n N {0}. Il fattorale d n, n! s defnsce nduttvamente
Dpartmento d Scenze Statstche Anals Matenatca Lezone 5 1 ottobre 2013 prof. Danele Rtell danele.rtell@unbo.t 1/13? Fattorale d un numero naturale Sa n N {0}. Il fattorale d n, n! s defnsce nduttvamente
Dipartimento di Statistica Università di Bologna. Matematica Finanziaria aa lezione 21: 29 maggio 2013
 Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 21: 29 maggo 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/35? Eserczo Dmostrare che l portafoglo d mnmo rscho
Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 21: 29 maggo 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/35? Eserczo Dmostrare che l portafoglo d mnmo rscho
x 0 x 50 x 20 x 100 CASO 1 CASO 2 CASO 3 CASO 4 X n X n X n X n
 Corso d Statstca docente: Domenco Vstocco La msura della varabltà per varabl qualtatve ordnal Lo studo della varabltà per varabl qualtatve ordnal può essere condotto servendos degl ndc d omogenetà/eterogenetà
Corso d Statstca docente: Domenco Vstocco La msura della varabltà per varabl qualtatve ordnal Lo studo della varabltà per varabl qualtatve ordnal può essere condotto servendos degl ndc d omogenetà/eterogenetà
Analisi Class info sul corso Lezione 1 22 settembre 2014
 CLASS Bologna Anals Matematca @ Class nfo sul corso Lezone 1 22 settembre 2014 professor Danele Rtell danele.rtell@unbo.t 1/27? Codce docente 030508 Codce corso 00013 Anals Matematca roflo scentfco del
CLASS Bologna Anals Matematca @ Class nfo sul corso Lezone 1 22 settembre 2014 professor Danele Rtell danele.rtell@unbo.t 1/27? Codce docente 030508 Codce corso 00013 Anals Matematca roflo scentfco del
S O L U Z I O N I. 1. Effettua uno studio qualitativo della funzione. con particolare riferimento ai seguenti aspetti:
 S O L U Z I O N I 1 Effettua uno studo qualtatvo della funzone con partcolare rfermento a seguent aspett: f ( ) ln( ) a) trova l domno della funzone b) ndca qual sono gl ntervall n cu f() rsulta postva
S O L U Z I O N I 1 Effettua uno studo qualtatvo della funzone con partcolare rfermento a seguent aspett: f ( ) ln( ) a) trova l domno della funzone b) ndca qual sono gl ntervall n cu f() rsulta postva
SOLUZIONI. p T. p T. nella quale la temperatura va espressa in Kelvin e non in gradi Celsius, per cui occorre convertire:
 SOLUZIONI POBLEA N. I at el problema sono seguent: 0 C (temperatura nzale ell ara) 50 C (temperatura nale ell ara) p. bar p.? Il processo è approssmable con una trasormazone a volume costante, e l ara
SOLUZIONI POBLEA N. I at el problema sono seguent: 0 C (temperatura nzale ell ara) 50 C (temperatura nale ell ara) p. bar p.? Il processo è approssmable con una trasormazone a volume costante, e l ara
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa Lezione 1: Martedì 17/2/2015
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2014-2015 Lezone 1: Martedì 17/2/2015 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/40? Codce docente 030508 Codce corso 00675 Matematca
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2014-2015 Lezone 1: Martedì 17/2/2015 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/40? Codce docente 030508 Codce corso 00675 Matematca
RICHIAMI SULLA RAPPRESENTAZIONE IN COMPLEMENTO A 2
 RICHIAMI SULLA RAPPRESENTAZIONE IN COMPLEMENTO A La rappresentazone n Complemento a Due d un numero ntero relatvo (.-3,-,-1,0,+1,+,.) una volta stablta la precsone che s vuole ottenere (coè l numero d
RICHIAMI SULLA RAPPRESENTAZIONE IN COMPLEMENTO A La rappresentazone n Complemento a Due d un numero ntero relatvo (.-3,-,-1,0,+1,+,.) una volta stablta la precsone che s vuole ottenere (coè l numero d
Corsi di Laurea in Farmacia e CTF Prova di Matematica
 Cors d Laurea n Farmaca e CTF Prova d Matematca S O L U Z I O N I Effettua uno studo qualtatvo della funzone 4 f + con partcolare rfermento a seguent aspett: a trova l domno della funzone b trova gl ntervall
Cors d Laurea n Farmaca e CTF Prova d Matematca S O L U Z I O N I Effettua uno studo qualtatvo della funzone 4 f + con partcolare rfermento a seguent aspett: a trova l domno della funzone b trova gl ntervall
1. Il Teorema Ergodico per le catene di Markov * Definizione Una catena di Markov discreta con spazio degli stati E; si dice regolare se, detta P = (P
 . Il Teorema Ergodco er le catene d Markov * Defnzone Una catena d Markov dscreta con sazo degl stat E; s dce regolare se, detta P = (P ) la matrce delle robablt a d transzone assocata, esstono un ntero
. Il Teorema Ergodco er le catene d Markov * Defnzone Una catena d Markov dscreta con sazo degl stat E; s dce regolare se, detta P = (P ) la matrce delle robablt a d transzone assocata, esstono un ntero
ESERCITAZIONE N 8 VALUTAZIONE DEL LIVELLO DI SERVIZIO DI UNA INTERSEZIONE A T SEMAFORIZZATA
 ESERITAZIONE N 8 VALUTAZIONE DEL LIVELLO DI SERVIZIO DI UNA INTERSEZIONE A T SEMAFORIZZATA 1. Introuzone Nel presente elaborato c s pone l obettvo etermnare l lvello servzo una ntersezone a tre bracc semaforzzata.
ESERITAZIONE N 8 VALUTAZIONE DEL LIVELLO DI SERVIZIO DI UNA INTERSEZIONE A T SEMAFORIZZATA 1. Introuzone Nel presente elaborato c s pone l obettvo etermnare l lvello servzo una ntersezone a tre bracc semaforzzata.
Corso di Elettrotecnica
 Unerstà degl Stud d Paa Facoltà d Ingegnera orso d orso d Elettrotecnca Teora de rcut rcut elettrc n funzonamento perturbato rcut elettrc n funzonamento perturbato I IRUITI OMPRENONO: Sorgent nterne d
Unerstà degl Stud d Paa Facoltà d Ingegnera orso d orso d Elettrotecnca Teora de rcut rcut elettrc n funzonamento perturbato rcut elettrc n funzonamento perturbato I IRUITI OMPRENONO: Sorgent nterne d
Dipartimento di Statistica Università di Bologna. Matematica Finanziaria aa lezione 7: 6 marzo 2012
 Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 7: 6 marzo 2012 professor Danele Rtell www.unbo.t/docdent/danele.rtell 1/29? Defnzone Se è un prestto se m {1, 2,..., n}
Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 7: 6 marzo 2012 professor Danele Rtell www.unbo.t/docdent/danele.rtell 1/29? Defnzone Se è un prestto se m {1, 2,..., n}
Soluzione del compito di Fisica febbraio 2012 (Udine)
 del compto d Fsca febbrao (Udne) Elettrodnamca È data una spra quadrata d lato L e resstenza R, ed un flo percorso da corrente lungo z (ved fgura). Dcamo a e b le dstanze del lato parallelo pù vcno e pù
del compto d Fsca febbrao (Udne) Elettrodnamca È data una spra quadrata d lato L e resstenza R, ed un flo percorso da corrente lungo z (ved fgura). Dcamo a e b le dstanze del lato parallelo pù vcno e pù
Verifica reti con più serbatoi (II)
 Verfca ret con pù serbato (I) Condzon al contorno per gl N nod della rete e corrspondent ncognte: Condzone mposta Incognta A) carco pezometrco portata concentrata B) portata concentrata carco pezometrco
Verfca ret con pù serbato (I) Condzon al contorno per gl N nod della rete e corrspondent ncognte: Condzone mposta Incognta A) carco pezometrco portata concentrata B) portata concentrata carco pezometrco
STATISTICA DESCRITTIVA - SCHEDA N. 5 REGRESSIONE LINEARE
 Matematca e statstca: da dat a modell alle scelte www.dma.unge/pls_statstca Responsabl scentfc M.P. Rogantn e E. Sasso (Dpartmento d Matematca Unverstà d Genova) STATISTICA DESCRITTIVA - SCHEDA N. REGRESSIONE
Matematca e statstca: da dat a modell alle scelte www.dma.unge/pls_statstca Responsabl scentfc M.P. Rogantn e E. Sasso (Dpartmento d Matematca Unverstà d Genova) STATISTICA DESCRITTIVA - SCHEDA N. REGRESSIONE
SOLUZIONE ESERCIZI: STRUTTURA DI MERCATO. ECONOMIA INDUSTRIALE Università degli Studi di Milano-Bicocca. Christian Garavaglia
 SOLUZIONE ESERCIZI: STRUTTURA DI MERCATO ECONOMIA INDUSTRIALE Unverstà degl Stud d Mlano-Bcocca Chrstan Garavagla Soluzone 7 a) L ndce d concentrazone C (o CR k ) è la somma delle uote d mercato (o share)
SOLUZIONE ESERCIZI: STRUTTURA DI MERCATO ECONOMIA INDUSTRIALE Unverstà degl Stud d Mlano-Bcocca Chrstan Garavagla Soluzone 7 a) L ndce d concentrazone C (o CR k ) è la somma delle uote d mercato (o share)
Il lavoro L svolto da una forza costante è il prodotto scalare della forza per lo spostamento del punto di applicazione della forza medesima
 avoro ed Energa F s Fs cos θ F// s F 0 0 se: s 0 θ 90 Il lavoro svolto da una orza costante è l prodotto scalare della orza per lo spostamento del punto d applcazone della orza medesma [] [M T - ] N m
avoro ed Energa F s Fs cos θ F// s F 0 0 se: s 0 θ 90 Il lavoro svolto da una orza costante è l prodotto scalare della orza per lo spostamento del punto d applcazone della orza medesma [] [M T - ] N m
Dipartimento di Matematica per le scienze economiche e sociali Università di Bologna
 Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Modell 1 lezone 15 23 novembre 211 Funzon Eulerane - robabltà professor Danele Rtell www.unbo.t/docent/danele.rtell 1/2? Cambo
Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Modell 1 lezone 15 23 novembre 211 Funzon Eulerane - robabltà professor Danele Rtell www.unbo.t/docent/danele.rtell 1/2? Cambo
ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2016/2017. Esercizi 3
 ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2016/2017 Esercz 3 Pan d ammortamento Eserczo 1. Un prestto d 12000e vene rmborsato n 10 ann con rate mensl e pano all
ESERCIZI DI MATEMATICA FINANZIARIA DIPARTIMENTO DI ECONOMIA E MANAGEMENT UNIFE A.A. 2016/2017 Esercz 3 Pan d ammortamento Eserczo 1. Un prestto d 12000e vene rmborsato n 10 ann con rate mensl e pano all
LA CORRENTE ELETTRICA CONTINUA
 CAPITOLO 33 LA CORRENTE ELETTRICA CONTINUA 1 L INTENSITÀ DELLA CORRENTE ELETTRICA 1! v! a t! F m e! E m t v! e t m! E Fssato l ntervallo d tempo t, s può scrvere! v! E 2 Q t 4,0 10 2 A 5,0 s 0,20 C 3 t
CAPITOLO 33 LA CORRENTE ELETTRICA CONTINUA 1 L INTENSITÀ DELLA CORRENTE ELETTRICA 1! v! a t! F m e! E m t v! e t m! E Fssato l ntervallo d tempo t, s può scrvere! v! E 2 Q t 4,0 10 2 A 5,0 s 0,20 C 3 t
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa Lezione 4: Martedì 24/2/2015
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2014-2015 Lezone 4: Martedì 24/2/2015 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/31? Attualzzazone I fattor d attualzzazone conugat
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2014-2015 Lezone 4: Martedì 24/2/2015 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/31? Attualzzazone I fattor d attualzzazone conugat
Dipartimento di Matematica per le scienze economiche e sociali Università di Bologna. Modelli 1 lezione novembre 2011 Media e varianza
 Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Modell 1 lezone 17 30 novembre 2011 Meda e varanza professor Danele Rtell www.unbo.t/docent/danele.rtell 1/23? Teorema er ogn funzone
Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Modell 1 lezone 17 30 novembre 2011 Meda e varanza professor Danele Rtell www.unbo.t/docent/danele.rtell 1/23? Teorema er ogn funzone
Statistica di Bose-Einstein
 Statstca d Bose-Ensten Esstono sstem compost d partcelle dentche e ndstngubl che non sono soggette al prncpo d esclusone. In quest sstem non esste un lmte al numero d partcelle che possono essere osptate
Statstca d Bose-Ensten Esstono sstem compost d partcelle dentche e ndstngubl che non sono soggette al prncpo d esclusone. In quest sstem non esste un lmte al numero d partcelle che possono essere osptate
COMPORTAMENTO DINAMICO DI ASSI E ALBERI
 COMPORTAMENTO DNAMCO D ASS E ALBER VBRAZON TORSONAL Costruzone d Macchne Generaltà l problema del progetto d un asse o d un albero non è solo statco Gl ass e gl alber, come sstem elastc, sotto l azone
COMPORTAMENTO DNAMCO D ASS E ALBER VBRAZON TORSONAL Costruzone d Macchne Generaltà l problema del progetto d un asse o d un albero non è solo statco Gl ass e gl alber, come sstem elastc, sotto l azone
Dipartimento di Matematica per le scienze economiche e sociali Università di Bologna. Matematica aa lezione febbraio 2009
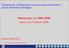 Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2008-2009 lezone 18 20 febbrao 2009 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/23? Ottmzzazone 2/23?
Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2008-2009 lezone 18 20 febbrao 2009 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/23? Ottmzzazone 2/23?
Unità Didattica N 5. Impulso e quantità di moto
 Imnpulso e quanttà d moto - - Impulso e quanttà d moto ) Sstema solato : orze nterne ed esterne...pag. 2 2) Impulso e quanttà d moto...pag. 3 3) Teorema d conservazone della quanttà d moto...pag. 6 4)
Imnpulso e quanttà d moto - - Impulso e quanttà d moto ) Sstema solato : orze nterne ed esterne...pag. 2 2) Impulso e quanttà d moto...pag. 3 3) Teorema d conservazone della quanttà d moto...pag. 6 4)
θ 2 i r 2 r La multifunzione f (z) = z z i
 1-19 1.4 1.4.1. La multfunone f () = + 1 3 è l prodotto d 2 multfunon Z Z e W 3 W. È qund ragonevole supporre che Z =, coè = 1 e W =, coè = sano punt d dramaone d f. Con rfermento alla fgura a lato, e
1-19 1.4 1.4.1. La multfunone f () = + 1 3 è l prodotto d 2 multfunon Z Z e W 3 W. È qund ragonevole supporre che Z =, coè = 1 e W =, coè = sano punt d dramaone d f. Con rfermento alla fgura a lato, e
Statica del corpo rigido Sistemi equivalenti di forze
 Statca el copo go Sstem equvalent foze S efnsce Copo Rgo un copo che è nefomable: Tutt punt el copo go mantengono nalteata la ecpoca stanza qualunque foza estena agsca su ess E ovvamente un astazone Con
Statca el copo go Sstem equvalent foze S efnsce Copo Rgo un copo che è nefomable: Tutt punt el copo go mantengono nalteata la ecpoca stanza qualunque foza estena agsca su ess E ovvamente un astazone Con

 Sulla teora d Z n L = {+,
Sulla teora d Z n L = {+,