I criteri di resistenza (o teorie della rottura) definiscono un legame tra lo stato tensionale e la sua pericolosità.
|
|
|
- Lidia Tarantino
- 5 anni fa
- Visualizzazioni
Transcript
1 I critri di rsistnza (o tori dlla rottura) dfiniscono un lgam tra lo stato tnsional la sua pricolosità. Ogni stato tnsional può ssr rapprsntato da una funzion scalar dll tnsioni principali ch può ssr confrontata con un valor critico dl matrial. Al valor di tal funzion scalar vin dato il nom di tnsion quivalnt (o idal). Al valor critico dl matrial vin dato il nom di tnsion limit. Il rapporto tra la tnsion limit dl matrial la tnsion quivalnt è il cofficint di sicurzza dlla struttura.
2 Conctto di tnsion quivalnt I du stati di tnsion sono ugualmnt pricolosi s F F' F f,, ) F f,, ) ( ( Particolarmnt significativo è il confronto con lo stato di tnsion ch si vrifica nlla prova dl matrial,, caso monoassial (prova di trazion) caso gnral triassial Dduzion dlla tnsion quivalnt dai critri di rsistnza F f (,, ) Du stati di tnsion possono ssr confrontanti sulla bas dl valor dlla funzion scalar f ch stabilisc il critrio di confronto ch prnd il nom di critrio di rsistnza F f In particolar s f è applicato allo stato di tnsion assial ch si ha nlla prova di trazion, si può scrivr ch: F f (,0,0) f ( ass ) F f (,, ) (,0,0) Pr cui si ha lo stsso grado di pricolosità tra i primo il trzo caso quando: F F f ( ass ) f (,, ) da cui sgu ch il valor dlla tnsion monoassial ( ) ch gnra uno stato di tnsion quivalnt a qullo dfinito da, può ssr ricavata com: f ass [ f (,, )]
3 I critri di rsistnza possono ssr divisi in tr gruppi, sulla bas dl loro principio ispirator: Critri dirttamnt basati sullo stato di tnsion Massima tnsion normal (Ranin-Lamé-Navir) Massima tnsion tangnzial (Trsca-Gust) Curva dlla rsistnza intrinsca (Coulomb-Mohr) Massima tnsion tangnzial ottadrica (Rôs ichingr) Critri basati sullo stato di dformazion Massima dformazion normal (Ponclt-d St. Vnant-Grashof) Critri basati sulla nrgia di dformazion Massima nrgia di dformazion (Bltrami-Hubr-Haig) Massima nrgia di distorsion (Hubr-von Miss-Hncy) I critri di rsistnza possono ssr divisi in du gruppi, sulla bas dl loro campo di applicazion: Critri utilizzati pr i matriali duttili Massima tnsion tangnzial (Trsca-Gust) Massima nrgia di distorsion (Hubr-von Miss-Hncy) Curva dlla rsistnza intrinsca (Coulomb-Mohr) Massima nrgia di dformazion (Bltrami-Hubr-Haig) Massima tnsion tangnzial ottadrica (Rôs ichingr) Critri utilizzati pr i matriali fragili Massima tnsion normal (Ranin-Lamé-Navir) Curva dlla rsistnza intrinsca (Coulomb-Mohr) Massima dformazion normal (Ponclt-d St. Vnant-Grashof) 6-
4 Massima tnsion normal (Ranin) suprfici critica dfinita dal critrio di Ranin nllo spazio dll tnsioni principali Il matrial subisc danno quando la massima tnsion principal raggiung un valor critico. tnsion limit a trazion tnsion limit a comprssion Si ha rottura s: la suprfici è la zona critica all strno dl volum c è rottura > < all intrno dl volum il matrial rsist 6-8 Massima tnsion tangnzial (Trsca-Gust) τ τ τ τ max τ Il matrial subisc danno quando la massima tnsion tangnzial raggiung un valor critico. Si ha rottura s: ( ) τmax > τ > τ L, L Valori critici dl matrial L L 6-4 all intrno dll ara il matrial rsist all strno dll ara c è rottura 4
5 Massima tnsion tangnzial (Trsca-Gust) Nl caso gnral di stato di tnsion triassial il valor dlla tnsion tangnzial massima val: τ max Quando la sollcitazion è monoassial solo è divrsa da zro si avrà: τ a max( ) τmax(, 0,0) Si può, quindi, ricavar l sprssion dlla tnsion quivalnt dalla rlazion: [ τ (, )] τa max max, Massima tnsion tangnzial (Trsca-Gust) N sgu ch: τ a max [ τ (,, )] max Si avrà prciò rottura quando: > L Casi particolari: torsion pura: τ xy torsion trazion: x 4 τ xy 5
6 Massima tnsion tangnzial (Trsca-Gust) suprfici critica dfinita dal critrio di Trsca nllo spazio dll tnsioni principali β γ α α β γ τ Curva di rsistnza intrinsca (Mohr) Ipotsi dll attrito intrno Curva intrinsca dl matrial 6-6 il taglio massimo sopportabil dal matrial è maggior in prsnza di uno stato di comprssion 6
7 τ Curva di rsistnza intrinsca (Mohr) D A O ϕ B ϕ C LC LT Smplificando la curva intrinsca con du rtt, si ottin ch la rottura avvin s: > Curva di rsistnza intrinsca (Mohr) τ La curva intrinsca può ssr approssimata da du rtt tangnti ai crchi di Mohr rlativi all condizioni limit a trazion comprssion AD sin ϕ AB D A O ϕ B ϕ C tnsion limit a trazion tnsion limit a comprssion 7
8 Curva di rsistnza intrinsca (Mohr) D A τ O ϕ B Posto: Si ottin: ϕ sin ϕ C Quindi si può sprimr la lunghzza dl sgmnto OC in funzion di : OC OB BC sin ϕ τ d Curva di rsistnza intrinsca (Mohr) Il matrial subisc danno quando il maggior di crchi di Mohr rapprsntativi dl suo stato di tnsion raggiung la tangnza con la curva intrinsca. O δ ρ ϕ C Quindi, ponndo il raggio la posizion dl cntro dl crchio massimo pari rispttivamnt a ρ δ, la distanza d dalla curva intrinsca può ssr sprssa com: ( OC δ) ϕ ρ d sin 8
9 Curva di rsistnza intrinsca (Mohr) Ricordando l sprssioni di OC, sinϕ, ρ δ, OC, sin ϕ, ρ d ( OC δ) sin ϕ ρ [ ( ) ], δ l sprssion di d pr uno stato di tnsion triassial divnta: Pr una stato di tnsion monoassial, l'sprssion prcdnt divnta: da ( ) d(, 0,0) ( ) Si può, quindi, ricavar il valor dlla tnsion quivalnt dalla rlazion: [ d(, )] d a, Curva di rsistnza intrinsca (Mohr) N sgu ch: d a [ d(,, )] [ ( ) ] Si avrà prciò rottura quando: Casi particolari: > L torsion pura: τ xy torsion trazion: x x 4 τ xy 9
10 suprfici critica dfinita dal critrio di St. Vnant nllo spazio dll tnsioni principali Massima dformazion normal (d St. Vnant) Il matrial subisc danno quando la massima dformazion principal raggiung un valor critico. Nl caso triassial si ha: ε ε [ -ν ( ) ] [ -ν ( y ) ] Nl caso monoassial si ha: ε > ε L > ε L < -ε L Dal confronto si ottin ch si ha rottura s: ν ν ( ) > L ( ) Massima nrgia di dformazion (Bltrami) Il matrial subisc danno quando l nrgia accumulata pr dformazion raggiung un valor critico. F Nl caso triassial si ha: U s [ - ν( )] Nl caso monoassial si ha: U s Dal confronto si ottin ch si ha rottura s: ( ) > L ν 0
11 Massima nrgia di dformazion (Bltrami) all strno dl volum c è rottura la suprfici rapprsnta la condizion limit all intrno dl volum il matrial rsist stato di tnsion triassial Massima nrgia di distorsion (von Miss) Il matrial subisc danno quando l nrgia di distorsion accumulata raggiung un valor critico. stato di tnsion sfrico (idrostatico): variazion di volum stato di tnsion dviatorico: variazion di forma L nrgia di distorsion nl caso triassial si può scrivr: ( ν) ( ) ( ) [ ( ) U dist ] 6 ( ν ) Nl caso monoassial si ha: U dist > Si ha rottura s: ( ) ( ) ( ) L 6-5
12 stato di tnsion triassial Massima nrgia di distorsion (von Miss) Il matrial subisc danno quando l nrgia di distorsion accumulata raggiung un valor critico. Stato di tnsion triassial: S d d d S S stato di tnsion sfrico (idrostatico): variazion di volum Componnt idrostatica: S stato di tnsion dviatorico: variazion di forma Componnti dviatorich: d d d Massima nrgia di distorsion (von Miss) In campo lastico, pr la trazion F smplic, l nrgia di dformazion pr unità di volum val : U ε Nl caso triassial si avrà quindi: U tot U U U ( ε ε ε ) Avndosi dallo studio dlla rlazion tnsion-dformazion in campo lastico ch: ε [ ν( )] ε ν( ) [ ] ε [ ν( )] Si potrà scrivr l nrgia di dformazion total com: U tot [ ν( )] [ ν( )] [ ν( )] [ ν( )]
13 Massima nrgia di distorsion (von Miss) Quindi, pr uno stato di tnsion triassial l nrgia total di dformazion val: U tot [ ν( )] La part dovuta alla componnt sfrica dllo stato di tnsion varrà: ν U S S S ( S S S ) sf ν [ ] ( ) S Ricordando l sprssion di S si ottin: U sf ( ν) ( ν) S Quindi, pr diffrnza si ottin l nrgia di distorsion: U dist U tot U sf Massima nrgia di distorsion (von Miss) U dist U tot U sf [ ( )] ( ν) ν Ch può ssr scritta nlla forma: (la stssa sprssion potva ssr ricavata introducndo l componnti dviatorich dllo stato di tnsion nll sprssion dll nrgia di dformazion) U dist [ ] ( ν) ( ) ( ) ( ) 6 Nl caso in cui solo sia divrsa da zro si avrà: ( ) ( ) ( ν) ( ) ( ) ν Uass dist Udist, 0,0 6 Si può, quindi, ricavar l sprssion dlla tnsion quivalnt dalla formula: [ U (, )] U ass dist dist, [ ] ( )
14 Massima nrgia di distorsion (von Miss) Quindi: U ass dist [ ] [ U (,, )] ( ) ( ) ( ) ( ) ( ) ( ) dist Si avrà prciò rottura quando: Casi particolari: ν ν 6 ( ) ( ) ( ) > L torsion pura: τ xy torsion trazion: x τ xy Massima nrgia di distorsion (von Miss) suprfici critica dfinita dal critrio di von Miss nllo spazio dll tnsioni principali β γ α α β γ 4
15 Confronto tra l vari tori pr un stato di tnsion piano Trsca Ranin von Miss Confronto tra l vari tori sulla bas dl rapporto carattristico L /τ L Massima tnsion normal (Ranin-Lamé-Navir) Massima tnsion tangnzial (Trsca-Gust) Curva dlla rsistnza intrinsca (Coulomb-Mohr) Massima dformazion normal (Ponclt-d St. Vnant-Grashof) Massima nrgia di dformazion (Bltrami-Hubr-Haig) Massima nrgia di distorsion (Hubr-von Miss-Hncy) Matriali fragili.5 Valori sprimntali di L /τ L Matriali duttili
16 : ripilogo Massima tnsion normal (Ranin) > < Massima tnsion tangnzial (Trsca) Curva di rsistnza intrinsca (Mohr) Massima nrgia di df. (Bltrami) Massima nrgia di distorsion (von Miss) > L > Massima df. normal (d St. Vnant) ν ( ) > L ν ( ) ( ) > L ν ( ) ( ) ( ) > L 6
I criteri di resistenza (o teorie della rottura) definiscono un legame tra lo stato tensionale e la sua pericolosità.
 6-0 6- I critri di rsistnza (o tori dlla rottura) dfiniscono un lgam tra lo stato tnsional la sua pricolosità. Ogni stato tnsional può ssr rapprsntato da una funzion scalar dll tnsioni principali ch può
6-0 6- I critri di rsistnza (o tori dlla rottura) dfiniscono un lgam tra lo stato tnsional la sua pricolosità. Ogni stato tnsional può ssr rapprsntato da una funzion scalar dll tnsioni principali ch può
Criteri basati sullo stato di deformazione!massima deformazione normale (Poncelet-de St. Venant-Grashof)
 Critri dirttamnt basati sullo stato di tnsion!massima tnsion normal (Ranin-Lamé-Navir)!Massima tnsion tangnzial (Trsca-Gust)!Curva dlla rsistnza intrinsca (Coulomb-Mohr)!Massima tnsion tangnzial ottadral
Critri dirttamnt basati sullo stato di tnsion!massima tnsion normal (Ranin-Lamé-Navir)!Massima tnsion tangnzial (Trsca-Gust)!Curva dlla rsistnza intrinsca (Coulomb-Mohr)!Massima tnsion tangnzial ottadral
Comportamento meccanico dei materiali
 Comportamnto mccanico di matriali Critri di cdimnto di matriali isotropi Critri di cdimnto a tnsioni costanti Complmnti: nrgia di distorsion invarianti 6 Politcnico di Torino Critri di cdimnto di matriali
Comportamnto mccanico di matriali Critri di cdimnto di matriali isotropi Critri di cdimnto a tnsioni costanti Complmnti: nrgia di distorsion invarianti 6 Politcnico di Torino Critri di cdimnto di matriali
Teorie della rottura
 Teorie della rottura Teorie della rottura Le teorie della rottura individuano una funzione dello stato tensionale il cui valore è una misura della sua pericolosità. Ogni stato tensionale può quindi essere
Teorie della rottura Teorie della rottura Le teorie della rottura individuano una funzione dello stato tensionale il cui valore è una misura della sua pericolosità. Ogni stato tensionale può quindi essere
Tensione equivalente o ideale Teorie di rottura
 Tnsion quivalnt o al Tori di rottura Sollcitazioni monodimnsionali: l condizioni di it o di rottura si dtrminano facilmnt S sollcitazioni sono plurimnsionali (invarianti tutti non nulli), ha intrss dtrminar
Tnsion quivalnt o al Tori di rottura Sollcitazioni monodimnsionali: l condizioni di it o di rottura si dtrminano facilmnt S sollcitazioni sono plurimnsionali (invarianti tutti non nulli), ha intrss dtrminar
0.1. CIRCONFERENZA 1. La 0.1.1, espressa mediante la formula per la distanza tra due punti, diviene:
 0.1. CIRCONFERENZA 1 0.1 Circonfrnza Considriamo una circonfrnza di cntro P 0 (x 0, y 0 ) raggio r, cioè il luogo di punti dl piano P (x, y) pr i quali si vrifica la rlazion: 0.1.1. P 0 P = r. La 0.1.1,
0.1. CIRCONFERENZA 1 0.1 Circonfrnza Considriamo una circonfrnza di cntro P 0 (x 0, y 0 ) raggio r, cioè il luogo di punti dl piano P (x, y) pr i quali si vrifica la rlazion: 0.1.1. P 0 P = r. La 0.1.1,
w(r)=w max (1-r 2 /R 2 ) completamente sviluppato in un tubo circolare è dato da wmax R w max = = max
 16-1 Copyright 009 Th McGraw-Hill Companis srl RISOLUZIONI CAP. 16 16.1 Nl flusso laminar compltamnt sviluppato all intrno di un tubo circolar vin misurata la vlocità a r R/. Si dv dtrminar la vlocità
16-1 Copyright 009 Th McGraw-Hill Companis srl RISOLUZIONI CAP. 16 16.1 Nl flusso laminar compltamnt sviluppato all intrno di un tubo circolar vin misurata la vlocità a r R/. Si dv dtrminar la vlocità
Proprietà dei materiali
 mccanich Proprità di matriali modulo lastico carico di snrvamnto rsistnza a trazion durzza tnacità tnacità a frattura rsistnza a fatica rsilinza modulo di crp tmpo di rilassamnto fisich suprficiali tribologich
mccanich Proprità di matriali modulo lastico carico di snrvamnto rsistnza a trazion durzza tnacità tnacità a frattura rsistnza a fatica rsilinza modulo di crp tmpo di rilassamnto fisich suprficiali tribologich
Compito di Fisica Generale I (Mod. A) Corsi di studio in Fisica ed Astronomia 4 aprile 2011
 Compito di Fisica Gnral I (Mod A) Corsi di studio in Fisica d Astronomia 4 april 2011 Problma 1 Du blocchi A B di massa rispttivamnt m A d m B poggiano su un piano orizzontal scabro sono uniti da un filo
Compito di Fisica Gnral I (Mod A) Corsi di studio in Fisica d Astronomia 4 april 2011 Problma 1 Du blocchi A B di massa rispttivamnt m A d m B poggiano su un piano orizzontal scabro sono uniti da un filo
Progetto di cinghie trapezoidali
 Progtto i cinghi trapzoiali L cinghi trapzoiali sono utilizzat frquntmnt pr la trasmission i potnza Vantaggi Basso costo Smplicità i installazion Capacità i assorbir vibrazioni torsionali picchi i coppia
Progtto i cinghi trapzoiali L cinghi trapzoiali sono utilizzat frquntmnt pr la trasmission i potnza Vantaggi Basso costo Smplicità i installazion Capacità i assorbir vibrazioni torsionali picchi i coppia
Università di Pavia Facoltà di Ingegneria Corso di Laurea in Ingegneria Edile/Architettura Correzione prova scritta 9 settembre 2011
 1 Univrsità di Pavia Facoltà di Inggnria Corso di Laura in Inggnria Edil/rchitttura Corrzion prova scritta 9 sttmbr 011 1. Dati i tnsori: { L = 3x y +3 y z +4 z x M = 3 x x + x z +5 y y d il vttor v =
1 Univrsità di Pavia Facoltà di Inggnria Corso di Laura in Inggnria Edil/rchitttura Corrzion prova scritta 9 sttmbr 011 1. Dati i tnsori: { L = 3x y +3 y z +4 z x M = 3 x x + x z +5 y y d il vttor v =
Soluzioni delle Esercitazioni XI 10-14/12/2018. A. Funzioni di 2 variabili Insiemi di esistenza
 Soluzioni dll Esrcitazioni XI 0-4//08 A. Funzioni di variabili Insimi di sistnza Si tratta di porr la (o l) condizioni pr cui risulta dfinita la funzion f.. La funzion è f(, ) = ln( +). L unica condizion
Soluzioni dll Esrcitazioni XI 0-4//08 A. Funzioni di variabili Insimi di sistnza Si tratta di porr la (o l) condizioni pr cui risulta dfinita la funzion f.. La funzion è f(, ) = ln( +). L unica condizion
ESERCIZI PARTE I SOLUZIONI
 UNIVR Facoltà di Economia Corso di Matmatica finanziaria 008/09 ESERCIZI PARTE I SOLUZIONI Domini di funzioni di du variabili Esrcizio a f, = log +. L unica condizion di sistnza è data dalla disquazion
UNIVR Facoltà di Economia Corso di Matmatica finanziaria 008/09 ESERCIZI PARTE I SOLUZIONI Domini di funzioni di du variabili Esrcizio a f, = log +. L unica condizion di sistnza è data dalla disquazion
Analisi dei Sistemi. Soluzione del compito del 26 Giugno ÿ(t) + (t 2 1)y(t) = 6u(t T ). 2 x1 (t) 0 1
 Analisi di Sistmi Soluzion dl compito dl 26 Giugno 23 Esrcizio. Pr i du sistmi dscritti dai modlli sgunti, individuar l proprità strutturali ch li carattrizzano: linar o non linar, stazionario o tmpovariant,
Analisi di Sistmi Soluzion dl compito dl 26 Giugno 23 Esrcizio. Pr i du sistmi dscritti dai modlli sgunti, individuar l proprità strutturali ch li carattrizzano: linar o non linar, stazionario o tmpovariant,
Aerospaziali PER MATERIALI ISOTROPI PARTE 1. Prof. Claudio Scarponi Ing. Carlo Andreotti
 Aerospaziali CRITERI DI ROTTURA STATICI PER MATERIALI ISOTROPI PARTE 1 Prof. Claudio Scarponi TIPOLOGIE DI SOLLECITAZIONE Un provino può essere sottoposto a 2 tipi di sollecitazione: 1. Semplice Statica
Aerospaziali CRITERI DI ROTTURA STATICI PER MATERIALI ISOTROPI PARTE 1 Prof. Claudio Scarponi TIPOLOGIE DI SOLLECITAZIONE Un provino può essere sottoposto a 2 tipi di sollecitazione: 1. Semplice Statica
Teoria. Tale retta limite non sempre esiste. Si veda il grafico sottostante. Matematica 1
 LA ERVATA UNA FUNZONE Toria l problma dlla tangnt Uno di problmi classici c portano al conctto di drivata è qullo dlla dtrminazion dlla rtta tangnt a una curva in un punto. La tangnt ad una circonfrnza
LA ERVATA UNA FUNZONE Toria l problma dlla tangnt Uno di problmi classici c portano al conctto di drivata è qullo dlla dtrminazion dlla rtta tangnt a una curva in un punto. La tangnt ad una circonfrnza
Esame di stato di istruzione secondaria superiore Indirizzi: Scientifico Comunicazione Opzione Sportiva Tema di matematica
 wwwmatmaticamntit Nicola D Rosa maturità Esam di stato di istruzion scondaria suprior Indirizzi: Scintifico Comunicazion Opzion Sportiva Tma di matmatica Il candidato risolva uno di du problmi risponda
wwwmatmaticamntit Nicola D Rosa maturità Esam di stato di istruzion scondaria suprior Indirizzi: Scintifico Comunicazion Opzion Sportiva Tma di matmatica Il candidato risolva uno di du problmi risponda
Esercitazione 2. Francesca Apollonio Dipartimento Ingegneria Elettronica
 srcitaion Francsca pollonio Dipartimnto Inggnria lttronica -mail: () t cos( ω t ϕ) ampia pulsaion Vttori complssi Data una granda scalar (t) variabil cosinusoidalmnt nl tmpo fas i può sprimr (t) com sgu:
srcitaion Francsca pollonio Dipartimnto Inggnria lttronica -mail: () t cos( ω t ϕ) ampia pulsaion Vttori complssi Data una granda scalar (t) variabil cosinusoidalmnt nl tmpo fas i può sprimr (t) com sgu:
I Compitino di Fisica Generale II di Ingegneria CIVILE 7 MAGGIO 2011.
 I ompitino di Fisica Gnral II di Inggnria IVILE 7 MAGGIO. Esrcizio : Una carica lttrica = µ è distribuita uniformmnt su un arco di circonfrnza di raggio = cm ch sottnd un angolo = 6 risptto al cntro dlla
I ompitino di Fisica Gnral II di Inggnria IVILE 7 MAGGIO. Esrcizio : Una carica lttrica = µ è distribuita uniformmnt su un arco di circonfrnza di raggio = cm ch sottnd un angolo = 6 risptto al cntro dlla
RISOLUZIONI cap (a) La resistenza termica totale dello scambiatore di calore, riferita all'unità di lunghezza, è
 "Trmodinamica trasmission dl calor 3/d" 1 - Yunus A. Çngl RISOLUZIONI cap.19 19.1 (a) La rsistnza trmica total dllo scambiator di calor, rifrita all'unità di lunghzza, è (b) Il cofficint global di scambio
"Trmodinamica trasmission dl calor 3/d" 1 - Yunus A. Çngl RISOLUZIONI cap.19 19.1 (a) La rsistnza trmica total dllo scambiator di calor, rifrita all'unità di lunghzza, è (b) Il cofficint global di scambio
PRIMI ESERCIZI SULLE FUNZIONI DERIVABILI. (1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni:
 PRIMI ESERCIZI SULLE FUNZIONI DERIVABILI VALENTINA CASARINO Esrcizi pr il corso di Analisi Matmatica (Inggnria Gstional, dll Innovazion dl Prodotto, Mccanica Mccatronica, Univrsità dgli studi di Padova)
PRIMI ESERCIZI SULLE FUNZIONI DERIVABILI VALENTINA CASARINO Esrcizi pr il corso di Analisi Matmatica (Inggnria Gstional, dll Innovazion dl Prodotto, Mccanica Mccatronica, Univrsità dgli studi di Padova)
Numeri complessi - svolgimento degli esercizi
 Numri complssi - svolgimnto dgli srcizi ) Qusto srcizio richid di calcolar la potnza n-sima (n 45) di un numro complsso. Scriviamo z nlla forma sponnzial z ρ iθ dov ) ( ) ρ ( + θ π 6 dato ch sin θ cos
Numri complssi - svolgimnto dgli srcizi ) Qusto srcizio richid di calcolar la potnza n-sima (n 45) di un numro complsso. Scriviamo z nlla forma sponnzial z ρ iθ dov ) ( ) ρ ( + θ π 6 dato ch sin θ cos
STABILITÀ DELL EQILIBRIO 5. Tensione critica e snellezza. Al carico critico euleriano (1) N cr =
 Tnsion critica snllzza Al carico critico ulriano STABILITÀ DELL EQILIBRIO 5 π EI cr () l do l è la lunghzza libra di inflssion corrispondnt alla smilunghzza d onda dlla sinusoid formata dalla lina lastica,
Tnsion critica snllzza Al carico critico ulriano STABILITÀ DELL EQILIBRIO 5 π EI cr () l do l è la lunghzza libra di inflssion corrispondnt alla smilunghzza d onda dlla sinusoid formata dalla lina lastica,
= l. x 0. In realtà può aversi una casistica più amplia potendo sia x che f ( x) tendere ad un elemento dell insieme
 LIMITI DI FUNZINI. CNCETT DI LIMITE Esula dallo scopo di qusto libro la trattazion dlla toria sui iti. Tuttavia, pnsando di far cosa gradita allo studnt, ch dv possdr qusta nozion com background, ritniamo
LIMITI DI FUNZINI. CNCETT DI LIMITE Esula dallo scopo di qusto libro la trattazion dlla toria sui iti. Tuttavia, pnsando di far cosa gradita allo studnt, ch dv possdr qusta nozion com background, ritniamo
Ministero dell Istruzione, dell Università e della Ricerca
 Pag. 1/5 Sssion straordinaria 2017 I043 ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE Indirizzi: LI02, EA02 SCIENTIFICO LI03 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE (Tsto valvol anch pr la corrispondnt
Pag. 1/5 Sssion straordinaria 2017 I043 ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE Indirizzi: LI02, EA02 SCIENTIFICO LI03 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE (Tsto valvol anch pr la corrispondnt
Università degli Studi di Bergamo Facoltà di Ingegneria. Corso di Elettrotecnica Scritto del 15 giugno 2001
 Univrsità dgli Studi di Brgamo Facoltà di nggnria Corso di lttrotcnica Scritto dl 5 giugno Soluzion a cura di: Balada Marco srcizio. La prima cosa da far è analizzar il circuito trovar l possibili smplificazioni,
Univrsità dgli Studi di Brgamo Facoltà di nggnria Corso di lttrotcnica Scritto dl 5 giugno Soluzion a cura di: Balada Marco srcizio. La prima cosa da far è analizzar il circuito trovar l possibili smplificazioni,
Modelli e Metodi Matematici della Fisica. Scritto 1/A
 Modlli Mtodi Matmatici dlla Fisica. Scritto 1/A Csi/Prsilla A.A. 007 08 Nom Cognom Il voto dllo scritto sostituisc gli sonri 1 problma voto 1 4 5 6 7 total voto in trntsimi Rgolamnto: 1) Tutti gli srcizi,
Modlli Mtodi Matmatici dlla Fisica. Scritto 1/A Csi/Prsilla A.A. 007 08 Nom Cognom Il voto dllo scritto sostituisc gli sonri 1 problma voto 1 4 5 6 7 total voto in trntsimi Rgolamnto: 1) Tutti gli srcizi,
SESSIONE SUPPLETIVA PROBLEMA 2
 www.matfilia.it SESSIONE SUPPLETIVA 8 - PROBLEMA f k () = k ln() g k () = k, k > ) L invrsa di y = k ln() si ottin nl sgunt modo: y k = ln(), y k =, da cui, scambiando con y, y = g k () = k Quindi l invrsa
www.matfilia.it SESSIONE SUPPLETIVA 8 - PROBLEMA f k () = k ln() g k () = k, k > ) L invrsa di y = k ln() si ottin nl sgunt modo: y k = ln(), y k =, da cui, scambiando con y, y = g k () = k Quindi l invrsa
LE FRAZIONI LE FRAZIONI. La frazione è un operatore che opera su una qualsiasi grandezza e che da come risultato una grandezza omogenea a quella data.
 LE FRAZIONI La frazion è un oprator ch opra su una qualsiasi grandzza ch da com risultato una grandzza omogna a qulla data. AB (Il sgmnto AB è stato diviso i tr parti sono stat prs du) Una frazion è scritta
LE FRAZIONI La frazion è un oprator ch opra su una qualsiasi grandzza ch da com risultato una grandzza omogna a qulla data. AB (Il sgmnto AB è stato diviso i tr parti sono stat prs du) Una frazion è scritta
PROVA EDOMETRICA A.A
 PROA EDOMETRICA La prova domtrica riproduc in laboratorio l condizioni di consolidazion monodimnsional PROA A INCREMENTO DI CARICO (IL) La consolidazion monodimnsional è simulata applicando una squnza
PROA EDOMETRICA La prova domtrica riproduc in laboratorio l condizioni di consolidazion monodimnsional PROA A INCREMENTO DI CARICO (IL) La consolidazion monodimnsional è simulata applicando una squnza
Condensatori e dielettrici
 La fibrillazion è una contrazion disordinata dl muscolo cardiaco. Un fort shock lttrico può ripristinar la normal contrazion. Pr usto è ncssario applicar al muscolo una corrnt di A pr un tmpo di ms. L
La fibrillazion è una contrazion disordinata dl muscolo cardiaco. Un fort shock lttrico può ripristinar la normal contrazion. Pr usto è ncssario applicar al muscolo una corrnt di A pr un tmpo di ms. L
Corso di Teoria delle Strutture Dispense - parte #1 Richiami di Elasticità Lineare
 Corso di Toria dll Struttur Dispns - part # Richiami di Elasticità Linar A.A. 26 27 Vrsion.. Indic Sistma di Rifrimnto 3. Cambio di bas..................................... 4.2 Cambio dlla bas di Lin...............................
Corso di Toria dll Struttur Dispns - part # Richiami di Elasticità Linar A.A. 26 27 Vrsion.. Indic Sistma di Rifrimnto 3. Cambio di bas..................................... 4.2 Cambio dlla bas di Lin...............................
11 Funzioni iperboliche
 11 Funzioni iprbolich 11.1 L funzioni iprbolich: dfinizioni grafici L funzioni iprbolich sono particolari combinazioni di di. Hanno numros applicazioni nl campo dll inggnria si prsntano in modo dl tutto
11 Funzioni iprbolich 11.1 L funzioni iprbolich: dfinizioni grafici L funzioni iprbolich sono particolari combinazioni di di. Hanno numros applicazioni nl campo dll inggnria si prsntano in modo dl tutto
Problema 3: CAPACITA ELETTRICA E CONDENSATORI
 Problma 3: CAPACITA ELETTRICA E CONDENSATORI Prmssa Il problma composto da qusiti di carattr torico da una succssiva part applicativa costituisc un validissimo smpio di quilibrio tra l divrs signz ch convrgono
Problma 3: CAPACITA ELETTRICA E CONDENSATORI Prmssa Il problma composto da qusiti di carattr torico da una succssiva part applicativa costituisc un validissimo smpio di quilibrio tra l divrs signz ch convrgono
PROPORZIONI. Cosa possiamo dire di esse? Che la superficie della figura A sta alla superficie della figura B come 4 sta a 6.
 Corso di laura: BIOLOGIA Tutor: Floris Marta PRECORSI DI MATEMATICA PROPORZIONI Ossrvar l sgunti figur: Cosa possiamo dir di ss? Ch la suprfici dlla figura A sta alla suprfici dlla figura B com sta a 6.
Corso di laura: BIOLOGIA Tutor: Floris Marta PRECORSI DI MATEMATICA PROPORZIONI Ossrvar l sgunti figur: Cosa possiamo dir di ss? Ch la suprfici dlla figura A sta alla suprfici dlla figura B com sta a 6.
PROPORZIONI. Cosa possiamo dire di esse? Che la superficie della figura A sta alla superficie della figura B come 4 sta a 6.
 Corso di laura: BIOLOGIA Tutor: Floris Marta PRECORSI DI MATEMATICA PROPORZIONI Ossrvar l sgunti figur: Cosa possiamo dir di ss? Ch la suprfici dlla figura A sta alla suprfici dlla figura B com sta a 6.
Corso di laura: BIOLOGIA Tutor: Floris Marta PRECORSI DI MATEMATICA PROPORZIONI Ossrvar l sgunti figur: Cosa possiamo dir di ss? Ch la suprfici dlla figura A sta alla suprfici dlla figura B com sta a 6.
Test di autovalutazione
 UNITÀ FUNZINI E LR RAPPRESENTAZINE Tst di autovalutazion 0 0 0 0 0 50 60 70 80 90 00 n Il mio puntggio, in cntsimi, è n Rispondi a ogni qusito sgnando una sola dll 5 altrnativ. n Confronta l tu rispost
UNITÀ FUNZINI E LR RAPPRESENTAZINE Tst di autovalutazion 0 0 0 0 0 50 60 70 80 90 00 n Il mio puntggio, in cntsimi, è n Rispondi a ogni qusito sgnando una sola dll 5 altrnativ. n Confronta l tu rispost
lim β α e detto infinitesimo una qualsiasi quantita tendente a zero quando una dati due infinitesimi α e β non esiste
 Infinitsimi dtto infinitsimo una qualsiasi quantita tndnt a zro quando una opportuna variabil tnd ad assumr un dtrminato valor dati du infinitsimi α β α β non sono paragonabili tra loro s il lim β α non
Infinitsimi dtto infinitsimo una qualsiasi quantita tndnt a zro quando una opportuna variabil tnd ad assumr un dtrminato valor dati du infinitsimi α β α β non sono paragonabili tra loro s il lim β α non
Le coniche e la loro equazione comune
 L conich la loro quazion comun L conich com ombra di una sra Una sra ch tocca il piano π nl punto F è illuminata da una sorgnt puntiorm S. Nl caso dlla igura l'ombra dll sra risulta una suprici dlimitata
L conich la loro quazion comun L conich com ombra di una sra Una sra ch tocca il piano π nl punto F è illuminata da una sorgnt puntiorm S. Nl caso dlla igura l'ombra dll sra risulta una suprici dlimitata
1. Dati i tensori: { L = 3ex e y + 2e y e z + 3e z e x
 1 Univrsità di Pavia Facoltà di Inggnria Corso di Laura in Inggnria Edil/Architttura Corrzion prova scritta Esam di Mccanica Razional 30 gnnaio 01 1. Dati i tnsori: { L = 3x y + y z + 3 z x M = x x y y
1 Univrsità di Pavia Facoltà di Inggnria Corso di Laura in Inggnria Edil/Architttura Corrzion prova scritta Esam di Mccanica Razional 30 gnnaio 01 1. Dati i tnsori: { L = 3x y + y z + 3 z x M = x x y y
Principi ed applicazioni del metodo degli elementi finiti. Formulazione base con approccio agli spostamenti
 Principi d applicazioni dl mtodo dgli lmnti finiti Formulazion bas con approccio agli spostamnti METODO DEGLI ELEMENTI FINITI PER N PROBLEMA 2D Si considri un problma piano, il cui dominio sia qullo rapprsntato
Principi d applicazioni dl mtodo dgli lmnti finiti Formulazion bas con approccio agli spostamnti METODO DEGLI ELEMENTI FINITI PER N PROBLEMA 2D Si considri un problma piano, il cui dominio sia qullo rapprsntato
Calore Specifico
 6.08 - Calor Spcifico 6.08.a) Lgg Fondamntal dlla Trmologia Un modo pr far aumntar la Tmpratura di un Corpo è qullo di cdr ad sso dl Calor, pr smpio mttndolo in Contatto Trmico con un Corpo a Tmpratura
6.08 - Calor Spcifico 6.08.a) Lgg Fondamntal dlla Trmologia Un modo pr far aumntar la Tmpratura di un Corpo è qullo di cdr ad sso dl Calor, pr smpio mttndolo in Contatto Trmico con un Corpo a Tmpratura
II Prova - Matematica Classe V Sez. Unica
 Lico Scintifico Paritario R Bruni Padova, loc Pont di Brnta, /9/7 II Prova - Matmatica Class V Sz Unica Soluzion Problmi Risolvi uno di du problmi: Problma L azinda pr cui lavori vuol aprir in città una
Lico Scintifico Paritario R Bruni Padova, loc Pont di Brnta, /9/7 II Prova - Matmatica Class V Sz Unica Soluzion Problmi Risolvi uno di du problmi: Problma L azinda pr cui lavori vuol aprir in città una
dove A è una costante caratteristica dello specifico metallo e k è la costante di Boltzmann.
 ) Il riscaldamnto dl filo comporta la cssion di nrgia al rticolo cristallino quindi agli lttroni dgli orbitali più strni; s l nrgia acquisita dagli lttroni risulta suprior all nrgia di lgam (Vi, do Vi
) Il riscaldamnto dl filo comporta la cssion di nrgia al rticolo cristallino quindi agli lttroni dgli orbitali più strni; s l nrgia acquisita dagli lttroni risulta suprior all nrgia di lgam (Vi, do Vi
Modi dominanti. L evoluzione libera del sistema lineare. x(k + 1) = Ax(k) a partire dalla condizione iniziale x(0) = x 0 è:
 Capitolo. INTRODUZIONE. L voluzion libra dl sistma linar Modi dominanti ẋ(t) = Ax(t), x(k + ) = Ax(k) a partir dalla condizion inizial x() = x è: x(t) = At x, x(k) = A k x Al tndr di t [di k all infinito,
Capitolo. INTRODUZIONE. L voluzion libra dl sistma linar Modi dominanti ẋ(t) = Ax(t), x(k + ) = Ax(k) a partir dalla condizion inizial x() = x è: x(t) = At x, x(k) = A k x Al tndr di t [di k all infinito,
METODO DEGLI ELEMENTI FINITI
 Dal libro di tsto Zinkiwicz Taylor, Capitolo 14 pag. 398 Il mtodo dgli lmnti finiti fornisc una soluzion approssimata dl problma lastico; tal approssimazion driva non dall avr discrtizzato il dominio in
Dal libro di tsto Zinkiwicz Taylor, Capitolo 14 pag. 398 Il mtodo dgli lmnti finiti fornisc una soluzion approssimata dl problma lastico; tal approssimazion driva non dall avr discrtizzato il dominio in
ANALISI MATEMATICA PROVA SCRITTA. Libri, appunti e calcolatrici non ammessi
 Nom, Cognom... Matricola... ANALISI MATMATICA PROA SCRITTA CORSO DI LAURA IN INGGNRIA MCCANICA A.A. 7/8 Libri, appunti calcolatrici non ammssi Prima part - Lo studnt scriva solo la risposta, dirttamnt
Nom, Cognom... Matricola... ANALISI MATMATICA PROA SCRITTA CORSO DI LAURA IN INGGNRIA MCCANICA A.A. 7/8 Libri, appunti calcolatrici non ammssi Prima part - Lo studnt scriva solo la risposta, dirttamnt
Analisi Matematica II. Esercizi sugli integrali multipli, sugli integrali superficiali, sulle formule di Gauss-Green, di Stokes e della divergenza
 Analisi Matmatica II Esrcizi sugli intgrali multipli, sugli intgrali suprficiali, sull formul di Gauss-Grn, di toks dlla divrgnza orso di laura in Inggnria Mccanica. A.A. 2008-2009. Esrcizio 1. alcolar
Analisi Matmatica II Esrcizi sugli intgrali multipli, sugli intgrali suprficiali, sull formul di Gauss-Grn, di toks dlla divrgnza orso di laura in Inggnria Mccanica. A.A. 2008-2009. Esrcizio 1. alcolar
Applicazioni dell integrazione matematica
 Applicazioni dll intgrazion matmatica calcolo dlla biodisponibilità di un farmaco Prof. Carlo Albrini Indic Indic 1 Elnco dll figur 1 1 Prliminari 1 Intrprtazion matmatica dl problma 3 Elnco dll figur
Applicazioni dll intgrazion matmatica calcolo dlla biodisponibilità di un farmaco Prof. Carlo Albrini Indic Indic 1 Elnco dll figur 1 1 Prliminari 1 Intrprtazion matmatica dl problma 3 Elnco dll figur
CORSO DI LAUREA IN SCIENZE BIOLOGICHE Prova scritta di FISICA 29 giugno 2012
 CORSO DI LAUREA IN SCIENZE BIOLOGICHE Prova scritta di FISICA 9 giugno 01 1) Un blocco di massa m 500g vin tirato mdiant una fun lungo un piano inclinato di 60, scabro, si muov con acclrazion costant pari
CORSO DI LAUREA IN SCIENZE BIOLOGICHE Prova scritta di FISICA 9 giugno 01 1) Un blocco di massa m 500g vin tirato mdiant una fun lungo un piano inclinato di 60, scabro, si muov con acclrazion costant pari
Teorema (seconda condizione sufficiente per i campi conservativi piani): Sia F ( x, y)
 Campi Vttoriali Form iffrnziali-sconda Part Torma (sconda condizion sufficint pr i campi consrvativi piani): Sia F (, y) un campo vttorial piano dfinito in un aprto A di R, si supponga ultriormnt = y ;
Campi Vttoriali Form iffrnziali-sconda Part Torma (sconda condizion sufficint pr i campi consrvativi piani): Sia F (, y) un campo vttorial piano dfinito in un aprto A di R, si supponga ultriormnt = y ;
Facciamo riferimento al piano di Nyquist, nel quale rappresentiamo la G(jω) come: = (2)
 # LUOHI E CARTE NELLA SINTESI PER TENTATIVI IN ω # Rifrimnto: A.Frrant, A.Lpschy, U.Viaro Introduzion ai Controlli Automatici. Editric UTET, Cap. 9. Prima dll ra di PC la sintsi pr tntativi nl dominio
# LUOHI E CARTE NELLA SINTESI PER TENTATIVI IN ω # Rifrimnto: A.Frrant, A.Lpschy, U.Viaro Introduzion ai Controlli Automatici. Editric UTET, Cap. 9. Prima dll ra di PC la sintsi pr tntativi nl dominio
Soluzione. Un punto generico ha coordinate ( x, y) Per cui. Le coordinate del centro sono allora
 Sssion suppltiva LS_ORD 7 Soluzion di D Rosa Nicola Soluzion Un punto gnrico ha coordinat, pr cui si ha: PO PA Pr cui PO PA [ ] L coordinat dl cntro sono allora O,, è R. C, d il raggio, visto ch la circonfrnza
Sssion suppltiva LS_ORD 7 Soluzion di D Rosa Nicola Soluzion Un punto gnrico ha coordinat, pr cui si ha: PO PA Pr cui PO PA [ ] L coordinat dl cntro sono allora O,, è R. C, d il raggio, visto ch la circonfrnza
Problema. caso uniassiale prova di trazione. caso multiassiale (carico generico)
 Criteri di Rottura Problema caso uniassiale prova di trazione caso multiassiale (carico generico)? criterio di rottura 1 Criteri di Rottura ASSUNZIONE BASE: Il collasso di un componente avviene quando
Criteri di Rottura Problema caso uniassiale prova di trazione caso multiassiale (carico generico)? criterio di rottura 1 Criteri di Rottura ASSUNZIONE BASE: Il collasso di un componente avviene quando
γ : y = 1 + 2t 1 + t 2 z = 1 + t t2
 Politcnico di Milano Inggnria Industrial Analisi Gomtria Esrcizi sull curv. Si considri la curva x t + t : y 6 + 4t t t t R. z t t (a) Stabilir s la curva piana. (b) Stabilir s la curva smplic. (c) Stabilir
Politcnico di Milano Inggnria Industrial Analisi Gomtria Esrcizi sull curv. Si considri la curva x t + t : y 6 + 4t t t t R. z t t (a) Stabilir s la curva piana. (b) Stabilir s la curva smplic. (c) Stabilir
Corso di Tecniche elettromagnetiche per la localizzazione e il controllo ambientale. Test scritto del 30 / 06 / 2006
 Corso di Tcnich lttromagntich pr la localizzazion il controllo ambintal Tst scritto dl / 6 / 6 Si risponda all sgunti domand marcando con un sgno l rispost ch si rputano corrtt. Si risolva inoltr il problma
Corso di Tcnich lttromagntich pr la localizzazion il controllo ambintal Tst scritto dl / 6 / 6 Si risponda all sgunti domand marcando con un sgno l rispost ch si rputano corrtt. Si risolva inoltr il problma
G(r,r ) è la funzione diadica di Green. L equazione differenziale soddisfatta da G(r,r ) è simile a quella soddisfatta dal campo elettrico Er ( ).
 1 La funion diadica di Grn prmtt di sprimr il campo lttrico in funion dll su sorgnti. Poiché sia il campo lttrico Er ( ) sia la sorgnt lttrica Jr ( ) sono quantità vttoriali, la funion di Grn risulta ssr
1 La funion diadica di Grn prmtt di sprimr il campo lttrico in funion dll su sorgnti. Poiché sia il campo lttrico Er ( ) sia la sorgnt lttrica Jr ( ) sono quantità vttoriali, la funion di Grn risulta ssr
Risoluzione dei problemi
 Risoluzion di problmi a) f rapprsnta un fascio di funzioni omografich, al variar dl paramtro a in R, s si vrifica la condizion: a$ (- a) +! 0 " a!! S a!! il grafico rapprsnta iprboli quilatr di asintoti
Risoluzion di problmi a) f rapprsnta un fascio di funzioni omografich, al variar dl paramtro a in R, s si vrifica la condizion: a$ (- a) +! 0 " a!! S a!! il grafico rapprsnta iprboli quilatr di asintoti
ESERCIZI SULLA CONVEZIONE
 Giorgia Mrli matr. 97 Lzion dl 4//0 ora 0:0-:0 ESECIZI SULLA CONVEZIONE Esrcizio n Considriamo un tubo d acciaio analizziamo lo scambio trmico complto, ossia qullo ch avvin sia all intrno sia all strno
Giorgia Mrli matr. 97 Lzion dl 4//0 ora 0:0-:0 ESECIZI SULLA CONVEZIONE Esrcizio n Considriamo un tubo d acciaio analizziamo lo scambio trmico complto, ossia qullo ch avvin sia all intrno sia all strno
di disequazioni lineari
 Capitolo Disquazioni Esrcizi sistmi di disquazioni linari Toria p. 68 L disquazioni l loro soluzioni Pr ciascuna dll sgunti disquazioni, invnta un problma ch possa ssr risolto con la disquazion stssa.
Capitolo Disquazioni Esrcizi sistmi di disquazioni linari Toria p. 68 L disquazioni l loro soluzioni Pr ciascuna dll sgunti disquazioni, invnta un problma ch possa ssr risolto con la disquazion stssa.
Forza d interesse e scindibilità. Benedetto Matarazzo
 orza d intrss scindibilità Bndtto Matarazzo Corso di Matmatica inanziaria Rgimi finanziari Oprazioni finanziari Intrss Sconto Equivalnz finanziari Rgim dll intrss smplic Rgim dll intrss composto Rgim dll
orza d intrss scindibilità Bndtto Matarazzo Corso di Matmatica inanziaria Rgimi finanziari Oprazioni finanziari Intrss Sconto Equivalnz finanziari Rgim dll intrss smplic Rgim dll intrss composto Rgim dll
ANALISI 2 ESERCITAZIONE DEL 06/12/2010 PUNTI CRITICI
 ANALISI ESERCITAZIONE DEL 06//00 PUNTI CRITICI Un punto critico è un punto in cui la funzion è diffrnziabil il piano tangnt al grafico è orizzontal Riconosciamo qusti punti prché il gradint è il vttor
ANALISI ESERCITAZIONE DEL 06//00 PUNTI CRITICI Un punto critico è un punto in cui la funzion è diffrnziabil il piano tangnt al grafico è orizzontal Riconosciamo qusti punti prché il gradint è il vttor
ANALISI STRUTTURALE sistema STRUTTURA STRUTTURA. I modelli meccanici possono suddividersi in: MODELLI CONTINUI. STRUTTURA = modello meccanico
 AZIONI ANALISI STRUTTURALE sistma STRUTTURA STATO I modlli mccanici possono suddividrsi in: MODELLI CONTINUI Forz Coazioni STRUTTURA = modllo mccanico IDEALIZZAZIONE DELLA STRUTTURA Posizion Vlocità Acclrazion
AZIONI ANALISI STRUTTURALE sistma STRUTTURA STATO I modlli mccanici possono suddividrsi in: MODELLI CONTINUI Forz Coazioni STRUTTURA = modllo mccanico IDEALIZZAZIONE DELLA STRUTTURA Posizion Vlocità Acclrazion
PROCESSI DI CONSOLIDAZIONE
 PROCESSI DI CONSOLIDAZIONE L applicazion di un carico su un trrno comporta l insorgr di sovrapprssion dll acqua intrstizial, la cui ntità varia da punto a punto all intrno dl volum individuato dal bulbo
PROCESSI DI CONSOLIDAZIONE L applicazion di un carico su un trrno comporta l insorgr di sovrapprssion dll acqua intrstizial, la cui ntità varia da punto a punto all intrno dl volum individuato dal bulbo
Poiché l argomento del logaritmo naturale è una quantità sempre positiva, basta imporre che l argomento dell arcoseno sia compreso tra 1 ed 1, cioè:
 78 ( ) Funzion 6: f( ) arcsnln + (funzion trascndnt) CAMPO DI ESISTENZA Poiché l argomnto dl logaritmo natural è una quantità smpr positiva, basta imporr ch l argomnto dll arcosno sia comprso tra d, cioè:
78 ( ) Funzion 6: f( ) arcsnln + (funzion trascndnt) CAMPO DI ESISTENZA Poiché l argomnto dl logaritmo natural è una quantità smpr positiva, basta imporr ch l argomnto dll arcosno sia comprso tra d, cioè:
Sistemi trifase. Parte 1. (versione del ) Sistemi trifase
 Sistmi trifas Part www.di.ing.unibo.it/prs/mastri/didattica.htm (vrsion dl 5--08) Sistmi trifas l trasporto la distribuzion di nrgia lttrica avvngono in prvalnza pr mzzo di lin trifas Un sistma trifas
Sistmi trifas Part www.di.ing.unibo.it/prs/mastri/didattica.htm (vrsion dl 5--08) Sistmi trifas l trasporto la distribuzion di nrgia lttrica avvngono in prvalnza pr mzzo di lin trifas Un sistma trifas
PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA A.A. 2004/ gennaio 2005 TESTO E SOLUZIONE
 PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA A.A. 24/25 2 gnnaio 25 TESTO E SOLUZIONE Esrcizio In rifrimnto allo schma a blocchi in figura. s3 r y 2 s2 s y K Domanda.. Dtrminar una ralizzazion in quazioni
PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA A.A. 24/25 2 gnnaio 25 TESTO E SOLUZIONE Esrcizio In rifrimnto allo schma a blocchi in figura. s3 r y 2 s2 s y K Domanda.. Dtrminar una ralizzazion in quazioni
Nota Come sinonimo di funzione lineare spesso si usano i termini operatore lineare o applicazione lineare o trasformazione lineare
 Funioni Linari tra Spai Vttoriali D. Siano V V du spai vttoriali sia : V V. è dtta FUNZIONE LINEARE s: v, v V, k R si ha : v v v additività v kv k omognità v Oppur con l unica proprità: v v v v Nota Com
Funioni Linari tra Spai Vttoriali D. Siano V V du spai vttoriali sia : V V. è dtta FUNZIONE LINEARE s: v, v V, k R si ha : v v v additività v kv k omognità v Oppur con l unica proprità: v v v v Nota Com
Alla temperatura di 300K è ragionevole ritenere che tutto il drogante sia attivato, cioè che ad ogni atomo accettore corrisponda una lacuna, per cui
 1 1. Una ftta di silicio è drogata con una concntrazion N A = 10 16 atm/cm 3 di atomi accttori, si valuti la concntrazion di portatori maggioritari minoritari alla tmpratura T = 300K. Alla tmpratura di
1 1. Una ftta di silicio è drogata con una concntrazion N A = 10 16 atm/cm 3 di atomi accttori, si valuti la concntrazion di portatori maggioritari minoritari alla tmpratura T = 300K. Alla tmpratura di
Linee accoppiate. Corso di Componenti e Circuiti a Microonde. Ing. Francesco Catalfamo. 3 Ottobre 2006
 orso di omponnti ircuiti a Microond Ing. Francsco atalamo 3 Ottobr 006 Indic Ond supriciali modi di ordin suprior Lin in microstriscia accoppiat Ond supriciali Un onda supricial è un modo guidato ch si
orso di omponnti ircuiti a Microond Ing. Francsco atalamo 3 Ottobr 006 Indic Ond supriciali modi di ordin suprior Lin in microstriscia accoppiat Ond supriciali Un onda supricial è un modo guidato ch si
POTENZE NECESSARIE E DISPONIBILI
 POTENZE NECESSARIE E DISPONIBILI In qusto capitolo ci proponiamo di dtrminar l curv dll potnz ncssari pr l vari condizioni di volo. Tali curv dipndranno da divrsi fattori com il pso dl vlivolo, la quota,
POTENZE NECESSARIE E DISPONIBILI In qusto capitolo ci proponiamo di dtrminar l curv dll potnz ncssari pr l vari condizioni di volo. Tali curv dipndranno da divrsi fattori com il pso dl vlivolo, la quota,
Misurazione del valore medio di una tensione tramite l uso di un voltmetro numerico
 Misurazion dl valor mdio di una tnsion tramit l uso di un voltmtro numrico La zion si conduc slzionando la funzion dc dllo strumnto collgando i trminali dllo strumnto al gnrator sotto zion: tnndo conto
Misurazion dl valor mdio di una tnsion tramit l uso di un voltmtro numrico La zion si conduc slzionando la funzion dc dllo strumnto collgando i trminali dllo strumnto al gnrator sotto zion: tnndo conto
Fisica Generale VI Scheda n. 1 esercizi di riepilogo dei contenuti di base necessari. 1.) Dimostrare le seguenti identità vettoriali:
 Fisica Gnral VI Schda n. 1 srcizi di ripilogo di contnuti di bas ncssari 1.) Dimostrar l sgunti idntità vttoriali:. A (B C) = B (A C) C (A B) (A B) = ( A) B ( B) A ( A) = ( A) 2 A. suggrimnto: è important
Fisica Gnral VI Schda n. 1 srcizi di ripilogo di contnuti di bas ncssari 1.) Dimostrar l sgunti idntità vttoriali:. A (B C) = B (A C) C (A B) (A B) = ( A) B ( B) A ( A) = ( A) 2 A. suggrimnto: è important
LEZIONE 17. Esercizio Trovare la soluzione delle seguenti equazioni differenziali di Bernoulli, ciascuna con condizione iniziale y(0) = 2.
 7 LEZIOE 7 Esrcizio 7 Trovar la soluzion dll sgunti quazioni diffrnziali di Brnoulli, ciascuna con condizion inizial y) = La prima quazion è y x) =yx) y x) Si può dividr pr il trmin di grado più alto in
7 LEZIOE 7 Esrcizio 7 Trovar la soluzion dll sgunti quazioni diffrnziali di Brnoulli, ciascuna con condizion inizial y) = La prima quazion è y x) =yx) y x) Si può dividr pr il trmin di grado più alto in
Esercizi sulla Geometria Analitica
 Esrcizi sulla Gomtria Analitica Esrcizio Siano dat l rtt di quazion x + y + 4 0 x + y 0 Dir s ciascuna dll sgunti affrmazioni è vra o falsa: a) l rtt sono paralll b) l du rtt si intrscano nl punto (, 5
Esrcizi sulla Gomtria Analitica Esrcizio Siano dat l rtt di quazion x + y + 4 0 x + y 0 Dir s ciascuna dll sgunti affrmazioni è vra o falsa: a) l rtt sono paralll b) l du rtt si intrscano nl punto (, 5
Criteri per la progettazione di dispositivi di isolamento a pendolo scorrevole
 Critri pr la progttazion di dispositivi di isolamnto a pndolo scorrvol Critri pr la progttazion di dispositivi di isolamnto a pndolo scorrvol G.M. Calvi 1, D. Pitra 2, M. Moratti 3 Sommario L isolamnto
Critri pr la progttazion di dispositivi di isolamnto a pndolo scorrvol Critri pr la progttazion di dispositivi di isolamnto a pndolo scorrvol G.M. Calvi 1, D. Pitra 2, M. Moratti 3 Sommario L isolamnto
Progetto Pilota Valutazione della scuola italiana. Anno Scolastico PROVA DI MATEMATICA. Scuola Superiore. Classe Terza. Codici. Scuola:...
 Gruppo di lavoro pr la prdisposizion dgli indirizzi pr l attuazion dll disposizioni concrnnti la valutazion dl srvizio scolastico Progtto Pilota Valutazion dlla scuola italiana Anno Scolastico 2003 2004
Gruppo di lavoro pr la prdisposizion dgli indirizzi pr l attuazion dll disposizioni concrnnti la valutazion dl srvizio scolastico Progtto Pilota Valutazion dlla scuola italiana Anno Scolastico 2003 2004
Prof. Fernando D Angelo. classe 5DS. a.s. 2007/2008. Nelle pagine seguenti troverete una simulazione di seconda prova su cui lavoreremo dopo le
 Pro. Frnando D Anglo. class 5DS. a.s. 007/008. Nll pagin sgunti trovrt una simulazion di sconda prova su cui lavorrmo dopo l vacanz di Pasqua. Pr mrcoldì 6/03/08 guardat il problma 4 i qusiti 1 8 9-10.
Pro. Frnando D Anglo. class 5DS. a.s. 007/008. Nll pagin sgunti trovrt una simulazion di sconda prova su cui lavorrmo dopo l vacanz di Pasqua. Pr mrcoldì 6/03/08 guardat il problma 4 i qusiti 1 8 9-10.
Esercizio 1 Approssimare il seguente integrale con la formula di Gauss a tre nodi (n=2)
 Esrcizi su intgrazion numrica sistmi linari Approssimar il sgunt intgral con la formula di Gauss a tr nodi (n) x cos xdx Si considri il sistma Applicando il mtodo di Eulro implicito con h π /( ω), quanto
Esrcizi su intgrazion numrica sistmi linari Approssimar il sgunt intgral con la formula di Gauss a tr nodi (n) x cos xdx Si considri il sistma Applicando il mtodo di Eulro implicito con h π /( ω), quanto
PREMIO EQUO E PREMIO NETTO. Prof. Cerchiara Rocco Roberto. Materiale e Riferimenti
 PREMIO EQUO E PREMIO NETTO Prof. Crchiara Rocco Robrto Matrial Rifrimnti. Capitolo dl tsto Tcnica attuarial dll assicurazioni contro i Danni (Daboni 993) pagg. 5-6 6-65. Lucidi distribuiti in aula La toria
PREMIO EQUO E PREMIO NETTO Prof. Crchiara Rocco Robrto Matrial Rifrimnti. Capitolo dl tsto Tcnica attuarial dll assicurazioni contro i Danni (Daboni 993) pagg. 5-6 6-65. Lucidi distribuiti in aula La toria
ELEMENTI DI CALCOLO DIFFERENZIALE. PARTE II
 ELEMENTI DI CALCOLO DIFFERENZIALE. PARTE II FAUSTO FERRARI Matrial propdutico all lzioni di Analisi Matmatica pr i corsi di Laura in Inggnria Chimica pr l Ambint il Trritorio dll Univrsità di Bologna.
ELEMENTI DI CALCOLO DIFFERENZIALE. PARTE II FAUSTO FERRARI Matrial propdutico all lzioni di Analisi Matmatica pr i corsi di Laura in Inggnria Chimica pr l Ambint il Trritorio dll Univrsità di Bologna.
EQUAZIONI DIFFERENZIALI. Saper integrare equazioni differenziali del primo ordine lineari e a variabili separabili.
 EQUAZIONI DIFFERENZIALI OBIETTIVI MINIMI Sapr riconoscr classificar l quazioni diffrnziali. Sapr intgrar quazioni diffrnziali dl primo ordin linari a variabili sparabili. Sapr intgrar quazioni diffrnziali
EQUAZIONI DIFFERENZIALI OBIETTIVI MINIMI Sapr riconoscr classificar l quazioni diffrnziali. Sapr intgrar quazioni diffrnziali dl primo ordin linari a variabili sparabili. Sapr intgrar quazioni diffrnziali
Soluzioni. Capitolo 2 (, 0 3] [2.1] A B = {1, 3, 4, 6, 7, 8}, A B = {4, 7}, A\B = {1, 3, 6}, B\A = {8}.
![Soluzioni. Capitolo 2 (, 0 3] [2.1] A B = {1, 3, 4, 6, 7, 8}, A B = {4, 7}, A\B = {1, 3, 6}, B\A = {8}. Soluzioni. Capitolo 2 (, 0 3] [2.1] A B = {1, 3, 4, 6, 7, 8}, A B = {4, 7}, A\B = {1, 3, 6}, B\A = {8}.](/thumbs/52/29110632.jpg) Soluzioni Capitolo [.] A B = {,,,, 7, 8}, A B = {, 7}, A\B = {,, }, B\A = {8}. [.] I) [, 0] V) VI) V [, 0] (, 0) V IX) [, 00) X) ( [, ],(, 00) (, 00) (, 0 + ) (, 0 ], ), (, 0 + ) [.] B\A = {} {b = n +,
Soluzioni Capitolo [.] A B = {,,,, 7, 8}, A B = {, 7}, A\B = {,, }, B\A = {8}. [.] I) [, 0] V) VI) V [, 0] (, 0) V IX) [, 00) X) ( [, ],(, 00) (, 00) (, 0 + ) (, 0 ], ), (, 0 + ) [.] B\A = {} {b = n +,
Le tranformazioni canoniche nella meccanica quantistica. P. Jordan a Gottinga
 L tranformazioni canonic nlla mccanica quantistica P. Jordan a Gottinga (ricvuto il 27 april 926) Vin data una dimostrazion d una congttura avanzata da Born, Hisnbrg dall autor, c la trasformazion canonica
L tranformazioni canonic nlla mccanica quantistica P. Jordan a Gottinga (ricvuto il 27 april 926) Vin data una dimostrazion d una congttura avanzata da Born, Hisnbrg dall autor, c la trasformazion canonica
FUNZIONI IMPLICITE E MOLTIPLICATORI DI LAGRANGE
 FUNZIONI IMPLICITE E MOLTIPLICATORI DI LAGRANGE Indic 1. Funzioni implicit 1. Ottimizzazion vincolata. Esrcizi 4.1. Funzioni implicit 4.. Ottimizzazion vincolata 6 1. Funzioni implicit Ricordiamo ch s
FUNZIONI IMPLICITE E MOLTIPLICATORI DI LAGRANGE Indic 1. Funzioni implicit 1. Ottimizzazion vincolata. Esrcizi 4.1. Funzioni implicit 4.. Ottimizzazion vincolata 6 1. Funzioni implicit Ricordiamo ch s
CONOSCENZE. 1. La derivata di una funzione y = f (x)
 ESAME D STATO ESEMP D QUEST D MATEMATCA PER LA TERZA PROVA CONOSCENZE. La drivata di una funzion y f (), in un punto intrno al suo dominio, : il it, s sist d è finito, dl rapporto incrmntal pr h, f ( h)
ESAME D STATO ESEMP D QUEST D MATEMATCA PER LA TERZA PROVA CONOSCENZE. La drivata di una funzion y f (), in un punto intrno al suo dominio, : il it, s sist d è finito, dl rapporto incrmntal pr h, f ( h)
TIPI TIPI DI DI DECADIMENTO RADIOATTIVO --ALFA
 TIPI TIPI DI DI DECDIMENTO RDIOTTIVO --LF LF Dcadimnto alfa: il nuclo instabil mtt una particlla alfa (), ch è composta da du protoni du nutroni (un nuclo di 4 H), quindi una particlla carica positivamnt.
TIPI TIPI DI DI DECDIMENTO RDIOTTIVO --LF LF Dcadimnto alfa: il nuclo instabil mtt una particlla alfa (), ch è composta da du protoni du nutroni (un nuclo di 4 H), quindi una particlla carica positivamnt.
Esercizi sullo studio di funzione
 Esrcizi sullo studio di funzion Trza part Com visto nll parti prcdnti pr potr dscrivr una curva data la sua quazion cartsiana splicita f () occorr procdr scondo l ordin sgunt: ) Dtrminar l insim di sistnza
Esrcizi sullo studio di funzion Trza part Com visto nll parti prcdnti pr potr dscrivr una curva data la sua quazion cartsiana splicita f () occorr procdr scondo l ordin sgunt: ) Dtrminar l insim di sistnza
Facoltà di Ingegneria Università degli Studi di Bologna
 Facoltà di Inggnria Univrsità dgli tudi di Bologna Dipartimnto di Inggnria Industrial Marco Gntilini Valutazioni tcnico conomich sullinsrzion di uno scambiator intrmdio ngli impianti frigorifri a spansion
Facoltà di Inggnria Univrsità dgli tudi di Bologna Dipartimnto di Inggnria Industrial Marco Gntilini Valutazioni tcnico conomich sullinsrzion di uno scambiator intrmdio ngli impianti frigorifri a spansion
Lemma 2. Se U V é un sottospazio vettoriale di V allora 0 U.
 APPUNTI d ESERCIZI PER CASA di GEOMETRIA pr il Corso di Laura in Chimica, Facoltà di Scinz MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rnd, 3 April 2 Sottospazi di uno spazio vttorial, sistmi di gnratori, basi
APPUNTI d ESERCIZI PER CASA di GEOMETRIA pr il Corso di Laura in Chimica, Facoltà di Scinz MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rnd, 3 April 2 Sottospazi di uno spazio vttorial, sistmi di gnratori, basi
ESPERIMENTO DELLA LENTE E DELLA CANDELA
 S.S.I.S. a.a. 003-004 RELAZIONE di Laboratorio di Didattica dlla Fisica (Esprimnto dlla lnt dlla candla) di MARIA LEPORE SARA MARSANO I anno, Classi 47-48-59 Pro.ssa Tuccio SSIS a.a. 003-004 Laboratorio
S.S.I.S. a.a. 003-004 RELAZIONE di Laboratorio di Didattica dlla Fisica (Esprimnto dlla lnt dlla candla) di MARIA LEPORE SARA MARSANO I anno, Classi 47-48-59 Pro.ssa Tuccio SSIS a.a. 003-004 Laboratorio
STABILITÀ DELLE SOLUZIONI DI EQUILIBRIO DI UN EQUAZIONE DIFFERENZIALE
 STABILITÀ DELLE SOLUZIONI DI EQUILIBRIO DI UN EQUAZIONE DIFFERENZIALE Ni paragrafi prcdnti abbiamo dtrminato, pr l vari quazioni diffrnziali saminat, l soluzioni di quilibrio dl modllo. In qusto paragrafo,
STABILITÀ DELLE SOLUZIONI DI EQUILIBRIO DI UN EQUAZIONE DIFFERENZIALE Ni paragrafi prcdnti abbiamo dtrminato, pr l vari quazioni diffrnziali saminat, l soluzioni di quilibrio dl modllo. In qusto paragrafo,
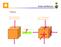
Stato di tensione triassiale Stato di tensione piano Cerchio di Mohr
 Stato di tensione triassiale Stato di tensione piano Cerchio di Mohr Stato di tensione F A = F / A F Traione pura stato di tensione monoassiale F M A M Traione e torsione stato di tensione piano = F /
Stato di tensione triassiale Stato di tensione piano Cerchio di Mohr Stato di tensione F A = F / A F Traione pura stato di tensione monoassiale F M A M Traione e torsione stato di tensione piano = F /
Fluidodinamica, mercoledì 8 febbraio 2012
 Fluidodinamica, mrcoldì 8 fbbraio 212 Part di Fluidodinamica I Domanda 1 L componnti cartsian dlla vlocità di una corrnt piana dipndnt dal tmpo sono dat dall rlazioni u(x, y, t) = x 1 + t v(x, y, t) =
Fluidodinamica, mrcoldì 8 fbbraio 212 Part di Fluidodinamica I Domanda 1 L componnti cartsian dlla vlocità di una corrnt piana dipndnt dal tmpo sono dat dall rlazioni u(x, y, t) = x 1 + t v(x, y, t) =
Appendice Analisi in frequenza dei segnali
 Appndic Analisi in frqunza di sgnali - Appndic Analisi in frqunza di sgnali - Sgnali priodici Sgnal sinusoidal Fig.. - Sgnal sinusoidal: frqunza f 5 Hz, ampizza A V. Fig.. - Sovrapposizion di du sgnali
Appndic Analisi in frqunza di sgnali - Appndic Analisi in frqunza di sgnali - Sgnali priodici Sgnal sinusoidal Fig.. - Sgnal sinusoidal: frqunza f 5 Hz, ampizza A V. Fig.. - Sovrapposizion di du sgnali
Tecniche per la ricerca delle primitive delle funzioni continue
 Capitolo 4 Tcnich pr la ricrca dll primitiv dll funzioni continu Nl paragrafo.7 abbiamo dato la dfinizion di primitiva di una funzion f avnt pr dominio un intrvallo I; abbiamo visto ch s F 0 è una primitiva
Capitolo 4 Tcnich pr la ricrca dll primitiv dll funzioni continu Nl paragrafo.7 abbiamo dato la dfinizion di primitiva di una funzion f avnt pr dominio un intrvallo I; abbiamo visto ch s F 0 è una primitiva
NOME:... MATRICOLA:... Corso di Laurea in Fisica, A.A. 2010/2011 Calcolo 1, Esame scritto del
 NOME:... MATRICOLA:.... Corso di Laura in Fisica, A.A. 00/0 Calcolo, Esam scritto dl 3.0.0 Data la funzion f(x = x +x, a dtrminar il dominio (massimal di f ; b trovar tutti gli asintoti di f ; c trovar
NOME:... MATRICOLA:.... Corso di Laura in Fisica, A.A. 00/0 Calcolo, Esam scritto dl 3.0.0 Data la funzion f(x = x +x, a dtrminar il dominio (massimal di f ; b trovar tutti gli asintoti di f ; c trovar
Test di Autovalutazione
 Univrsità dgli Studi di Padova Facoltà di Inggnria, ara dll Informazion - Brssanon 7 Analisi Matmatica. agosto 7 Tst di Autovalutazion () Si considri la funzion 5 + log x s x, f(x) = + log x s x =. (a)
Univrsità dgli Studi di Padova Facoltà di Inggnria, ara dll Informazion - Brssanon 7 Analisi Matmatica. agosto 7 Tst di Autovalutazion () Si considri la funzion 5 + log x s x, f(x) = + log x s x =. (a)
