Lezione 26 I TRANSITORI NEGLI IMPIANTI IDRAULICI. IL MOTO VARIO NELLE CORRENTI
|
|
|
- Raffaela Marino
- 7 anni fa
- Visualizzazioni
Transcript
1 Appuni ei cori i Irulic e Iroinmic Lezione 6 I TRANSITORI NEGLI IMPIANTI IRALICI. IL MOTO VARIO NELLE CORRENTI L compleià ello uio el moo vrio nelle correni ipene lle ipoei ce i inroucono, le quli loro vol ipenono ll nur ell impino in cui i relizz il rniorio. Si poono iniviure ue ivere iuzioni. Nell prim le vrizioni i preione ono moee e quini il fluio può eere coniero enià cone. Nell econ, invece, i nno vrizioni i preione noevoli e è necerio conierre l enià vribile. Conierimo ue ci eemplificivi. CASO : ENSITA COSTANTE Nei erboi ell impino in fiur l iribuzione i preione può eere rienu pri quell iroic, eeno il fluio conenuo in ei pricmene fermo
2 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) Queo fo impone ei limii l vlore ce l preione può umere ll imbocco e llo bocco ell cono e quini lle vrizioni i preione ce poono eere oerve in uo l impino. L enià el fluio può quini eere conier cone coì come cone può eere un l ezione ell cono. Al uo inerno l equzione i coninuià impone unque Menre l equzione el moo fornice ( ) H λ j ove j n emplice nlii elle rnezze ce compiono nell epreione i j mor ce j non ipene coì come il ermine. L equzione el moo può quini eere iner ll ezione inizile quell finle forneno H H j L ove H e H rppreenno il crico ole nelle ezioni finli e inizili ripeivmene, menre è ivenuo in quno non ipene. I vlori H e H poono eere lei l livello nei erboi meeno in cono le iipzioni concenre i eneri H z ζ H z ζ
3 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) ove i è inico con z il livello nel erboio ripeo quello in conizioni ice. Aveno uno l uperficie ell ezione ei ue erboi uule, eriv ce il livello nel erboio riul pri z. ζ vle menre ζ è pri.5, quno è poiivo. Quno è neivo, ζ vle.5 e ζ è pri. Si unque z ζ z ζ λ L L λl z ζ ζ (NOTA ) n emplice bilncio i m ll inerno el erboio mor ce zs Eeno l uperficie ell ezione ell cono e S l uperficie liber ei ue erboi. Seue quini ce S z e L S z S z z λl z. 5 Tle equzione può fcilmene eere iner uilizzno un meoo numerico. n ie ul compormeno ell oluzione può eere oenu rcurno le iipzioni i eneri, umeno cioè il fluio iele. In l co z z LS L oluzione è unque z c en c co LS LS NOTA : Si noi ce i le perie i crico iribuie, i quelle concenre ono e une proporzionli invece ce in quno il moo può inverire l u irezione ripeo ll irezione
4 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) Le coni c e c poono eere eermine imponeno le conizioni inizili. A eempio e per il fluio è fermo e z è pri z i z c c L oluzione mor quini ce i il livello nei erboi i l velocià nell cono ocillno nel empo con perioo T π LS Inolre fr velocià e pelo libero eie uno fmeno i 9 S z LS L preenz elle iipzioni inuce un enuzione elle ocillzioni e il fenomeno non è più perioico. L enuzione è no miore quno più rne riul il ermine S λl.5 L Per vlori elevi elle iipzioni i può vere un len ice i z prire z enz ce il livello nel erboio um vlori neivi
5 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) CASO : LIO COMPRIMIBILE Conierimo or l impino in fiur, coiuio un erboio, un cono e un vlvol po nell ezione erminle ell cono (ezione A). Quno l vlvol po in A è complemene per e il moo è reime, il fluio efluice con un velocià mei. Eeno il imero ell cono, l por Q è pri π 4. Aumimo ce il crico cineico, pri i rcurbile ripeo. Ciò cce quno l cono ermin con un rerinimeno (vei fiur) e l velocià el eo ucene ll cono è molo miore ell velocià ll inerno ell cono
6 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) Ponimoci il problem i uire co uccee quno l vlvol po in A i ciue in un empo τ, eo empo i ciuur. In le inervllo emporle l ezione i effluo p l vlore ω (vei fiur) zero con un lee ce è e lee i ciuur ω η ( ) ( ) ω
7 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) Nonone i rcurbile ripeo, l velocià è peo elev e quini elev è l inerzi el fluio. Se il empo i ciuur τ è piccolo, ono necerie forze e quini preioni eleve per fermre il fluio. In le iuzione l comprimibilià el fluio non può eere rcur coì come non poono eere rcure le vrizioni ell ezione ell cono ce i moific eeno il merile ell cono oo i elicià. Per uire ciò ce cce è quini necerio fre riferimeno lle equzioni elle correni in form comple H ( ) ( ) Ee venono comunque emplifice inrouceno lcune ipoei. In primo luoo il fluio può eere ipoizzo iele. Infi eeno rcuro nell equzione el moo ce iviene j molo minore i il ermine j può eere H Il fluio è uppoo inolre broropico, i ume cioè ce l enià ipen olo ll preione ( p) Le ulime ipoei riurno l nur ell oluzione ce i uppone i ipo proporio, cioè le ce con c cone imenionle [ c ] Eeno riul e c. Quini Si ume infine ce ( LT ) (, ) ( c, ) c c c
8 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) Ciò implic ce c Seue unque ce Le ipoei ce l oluzione i propori e ce c non poono eere verifice in queo momeno, ee rnno conrolle un vol ce l oluzione rà eermin. L equzione el moo conuce Tuvi, riul per le ipoei fe, molo minore i eeno c e quini E coiuice l prim elle equzioni emplifice el fenomeno in eme enomino COLPO ARIETE. L econ equzione eriv ll equzione i coninuià ce conuce Per le rioni preceenemene epoe i econi ermini ll inerno elle prenei qure ono rcurbili ripeo i primi e coneuenemene poono eere rcuri
9 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) Or le vrizioni nel empo ell enià e ell ezione evono eere lee lle vrizioni ell preione ce loro vol ono lee lle vrizioni i. Si infi z p γ Tuvi l quo z ell cono non vri nel empo e peno ce γ γ ( p), i p γ L equzione i o (LEZIONE 5) per un fluio broropico impone Seue quini p p p γ p Imponeno l equilibrio ll rlzione vericle i mezz cono oe lle forze ce l eerno eerci u i e, riul (rcurno il peo el fluio) p σ eeno lo peore ell cono e σ l enione ll inerno el merile con cui e è relizz
10 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) E eviene unque ce vrizioni i preioni comporno vrizioni ell enione σ ce loro vol ono lee ll eformzione ell ezione rvero il moulo i elicià E el merile ell cono. Riul p E p E σ σ Teneno inolre cono ce 4,, 4 / / / / π π π π eue E p p E / / Infine p p E γ L equzione i coninuià iviene unque E E E E γ γ veno inrooo l cone. E
11 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) le equzioni ce overnno il moo vrio nell cono poono eere crie nell form e coiuicono le coiee equzioni emplifice el colpo riee percé veremo nel euio ce urne il rniorio i poono mnifere noevoli ovrppreioni ce poono nneire l cono e. L oluzione elle equzioni può eere eermin olo opo ver pecifico le conizioni l conorno. Nel problem in eme, nell ezione immeimene vlle el erboio i : Sezione B Infi veno rcuro il crico cineico ripeo e le perie i crico, i può ffermre ce H. L conizione l conorno nell ezione erminle ell cono può eere oenu pplicno il eorem i Bernoulli fr l ezione A e l ezione el eo immeimene vlle ell ezione conr (ezione C). A A C C
12 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) Nell ezione C l preione reliv è null. Inolre l quo z può eere rcur ripeo l crico A coì come il crico cineico A. Seue unque C A Il principio i conervzione ell m impone inolre A A ω C ω C C A C ( ) eeno C C il coefficiene i conrzione ce le l ezione conr ll ezione i effluo el fluio l ermine el ro converene. L relzione preceene eve vlere qulunque empo e in pricolre nce ll ine inizile. A A A C C ω Seue quini ( ) ω A A A A ω veno uno A A e C C C C. Quini nell Sezione A η ( )
13 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) Riumeno e inrouceno un e x ireo ll ezione A vero l ezione B con oriine nell ezione A, i x x in x L (NOTA ) η ( ) in x e x L oluzione el problem formulo preceenemene ipene ll form ell funzione η ( ) cioè ll lee i ciuur. Tuvi è poibile bilire lcune ue proprieà enerli. In primo luoo noimo ce e oifno l e equzione ce form x Ciò può eere fcilmene verifico per, erivno l prim equzione per x, moliplicnol per e oreno l econ equzione eriv ripeo l empo. In moo nloo è poibile verificre ce l meeim equzione è oif. Le ue funzioni inconie unque ono crerizze ll meeim ipenenz pzio emporle. Per eerminre le ipenenz inroucimo le ue nuove vribili inipeneni x ; x NOTA L cone inroo nell equzione el moo le imenioni i un velocià. E poibile imorre ce e corripone ll velocià el uono nell cono. Nelle conoe in cciio il vlore i i ir orno m menre in un fluio inefinio 4 m
14 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) Noimo inolre ce ; ; x x Soiueno li epreioni nell equzione inizile i Tle equzione, e equzione i Almber o equzione ell cor vibrne, come oluzione enerle ( ) ( ) f f eeno f e f funzioni opporune. Ricorno le epreioni i e i x f x f E quini fcile verificre ce i f ce f verificno l efinizione i funzioni proporie con c e c ripeivmene. Infi f x f f c x f f f f x f f c x f f f Inolre eeno c e peno ce l orine i è pri m 3 è poibile verificre ce c, coniero ce l velocià el fluio nell cono è in enerle ell orine i m. Noimo ce l funzione ( ) f f i prop, non cmbino l u form, nell irezione poiiv (neiv) ell e x con velocià ( ). A queo puno ue le ipoei formule inizilmene riulno verifice. Conclueno i
15 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) x x f f x x L inrouzione elle coni e è poibile eeno le funzioni f, f,, rbirrie. Le funzioni f, f,, ono lee fr i loro, come è poibile morre conierno le equzioni inizili x f f oveno le equzione eere verific qulunque vlore uno e emere unque ; f f x x f f Inizilmene eeno e, le funzioni fr f e f ono enrmbe nulle. Non ppen inizi l mnovr i ciuur, nell ezione A l conizione l conorno f ì ce e i moificino. Ciò può vvenire olo e f e f umono vlori iveri zero. I vlori i f eneri in A non ono qui i ineree percé f i prop nell irezione neiv ell e x e quini i vlori eneri in A non vnno inerere l cono, efini vlori i x li ce x L. L funzione f un vol ener in A, i prop ll inerno ell cono vero B ove iune opo un empo pri L. In B, i vlori i f iveri zero, ce rrivno provenieni A, enerebbero fr umere vlori iveri. Tuvi l conizione l conorno impone e unque in B, per miori i L, i enerno vlori i f iveri zero e in pricolri uuli f. Tli vlori non nulli i f, eneri in B, i propno vero A con velocià e iunono in A olo opo un
16 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) empo θ L ll inizio ell mnovr i ciuur. Il empo ce un on ce vii con velocià impie percorrere l inz L è eo ur i fe. Nell ezione A per ui i empi minori i θ, il vlore i f è nullo e i Quini eliminno f i oiene x f x f Se il empo i ciuur τ è inferiore θ, in A per ( ) τ θ i e quini Il vlore è il ovrccrico ce i mnife in A, in occione i un ciuur ce vviene in un empo τ minore i θ (ciuur bruc), e ce un ur pri θ τ. E poibile poi imorre ce le ovrccrico è il mimo ovrccrico poibile. E poibile ricvre l mim ovrppreione ll conocenz el leme fr p e. p mx p Teneno preene ce m, K m 3 / e può riunere vlori i m, è fcile veere ce le ovrppreioni ce i poono enerre poono cure l rour ell cono e. Per vlori i miori i θ, f ume vlori iveri zero nce in A e non è più poibile ricvre e in moo emplice. Speo è necerio ricorrere meoi numerici ce, uvi, uilizzno un form iver elle equzioni ce verrà ricv nel euio
17 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) LE EQAZIONI LNGO LE CRVE CARATTERISTICHE Primo lle equzioni emplifice el colpo riee x x e moliplicimo l prim equzione per un cone e ommimo l econ equzione x x Se x il ermine i inir iviene. Se x nce il ermine fr prenei qure iviene l eriv i ripeo l empo. Si unque Ciò è poibile e e olo e e cioè e quini e L equzione ± x ± o ± può eere fcilmene iner forneno ± ( ) Tli relzioni fr e nno però vliià olo quno ono oife le equzioni ce conucono x ± x ± cone
18 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) In lre prole olo un oervore ce i muove con velocià ( ) cioè con lee x co ( x co) nel pino orrio verà il crico e l velocià lee ll ( ) relzione ( ) ( ) ( ) ( ). Le curve (ree) el pino orrio efinie x ± co ono ee curve creriice e le vlono olo luno li curve. equzioni ± ( ) n emplice meoo (rfico) per eerminre il vlore i e nelle ezioni A e B è quello i nlizzre il fenomeno nel pino (, ). Per eempio conierimo un ciuur bruc, con lee i ciuur rppreen in fiur Anlizzimo il fenomeno nel pino (, ) - 5 -
19 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) Per quno icuo in preceenz, il puno nel pino (, ) ce rppreen l iuzione in B per qulunque empo inferiore o uule θ è il puno ( ) nell ezione B e nell ezione A ripeivmene l enerico empo in ( ),. Inicno con Bn e A n l iuzione nθ, il puno B. 5 i roverà,. n oervore ce i rov in B ll ine.5 θ e i muove con velocià vero A, vi iunerà l empo θ. urne il movimeno l oervore verà un crico e un velocià lei ll relzione ( ) rppreen in fiur ll re. E unque eviene ce il puno A ce rppreen l iuzione in A ll ine ezione A impone ce θ eve rovri u le re. ove? L conizione l conorno nell η ( ) ino il vlore i, le conizione l conorno rppreen nel pino (, ) un curv ull qule eve rovri il puno A l empo coniero. Nel co in eme τ θ e per θ η vle zero. L curv ce rppreen l conizione l conorno in A eener quini nell e. Il puno A ovenoi rovre conempornemene luno l re e luno l curv, vrà - 5 -
20 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) coorine O, (vei fiur). L proceur può eere coninu per eempio per rovre l poizione i B. 5. Infi un oervore ce i rov in A ll ine θ e i muove vero B con velocià, vi iunerà l empo.5θ. urne il uo movimeno verà un velocià e un crico lei ll relzione ( ) A A (re ). Quini il puno B. 5 ovrà rovri luno le re. Inolre in B, l conizione l conorno impone ce e è quini fcile eerminre B. 5 come inerezione ell re e ell re. Proeueno nel empo è poi poibile eerminre l poizione i, B.5, A3 oervi ce, opo ce nell ezione A l empo empo A e coì vi. Si θ i è prooo il mimo ovrccrico, l θ il crico cene l i oo i i un qunià pri ( ). Se il vlore i ( ) è elevo e non è rne, è poibile ce l preione riun il vlore ell enione el vpore e ce quini il fluio cvii. In l co i formno ll inerno ell cono elle bolle ce poi imploono quno l preione umen nuovmene. Aveno rcuro le iipzioni, lo o el iem ocill con perioo θ, infi B. 5 coincie con B. 5, A 3 coincie con A e coì vi. I riuli oenui morno ce eie un fe in cui il fluio, inizilmene nimo velocià, rllen comprimenoi e rformno l u eneri cineic in eneri elic i compreione. Que fe ermin quno il fluio è fermo e l preione mim. A queo puno il fluio i il invereno l u velocià ce ume vlori neivi vi vi creceni, menre l preione iminuice. Quno l preione riune il vlore inizile, l velocià neiv è mim e pri. A queo puno il fluio rllen nce e coninu epneri e quini vere un velocià neiv. L fe i epnione ermin quno l preione riune il vlore minimo. In le iuzione. Inizi quini un fe i compreione le l fo ce l velocià riorn poiiv. opo mezz fe l velocià vle e l preione riorn vere il uo vlore oriinrio e il fenomeno i ripee ienicmene per l mncnz i iipzioni. Quee ulime cuno nell relà un len enuzione el fenomeno (vei fiur) e l ermine el proceo i riune un iuzione zionri ecri e
21 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) Veimo or co uccee in preenz i un mnovr len le ce τ θ. In pricolre eminimo il co in cui l funzione η i quell rppreen nell fiur oone Anlizzimo il fenomeno nel pino (, ) Come nel co preceene ( ) B e un oervore ce preno B ll ine.5θ i.5, muove vero l ezione A, l riune l empo ecrii ll re θ oervno, urne il rio, vlori i e
22 LEZIONE 6 I rniori neli impini irulici Il moo vrio nelle correni (Novembre 7) ove eve cere il puno A. Al empo. ( ) θ l vlvol po in A non è ncor ciu e quini ( ) η θ Nel co in eme η ( θ ) è pri.5 e l conizione l conorno in A è ecri, nel pino (, ) ll prbol. E eviene unque ce A crà nell inerezione fr l re e l curv. n oervore ce, rovnoi in A ll ine iunerà l empo θ, i muove con velocià vero l ezione B vi.5θ, oervno vlori i e lei ll relzione (re 3) ( ) A A Teneno cono ce in B eve eere uule, è fcile poizionre B. 5. Coninuno nell proceur è poi poibile oenere A,..., B. 5 Si noi ce il ovrccrico ce i relizz in A è in queo co inferiore ( )
MOTO del PROIETTILE. Velocità: cambia continuamente in direzione e modulo secondo le equazioni:
 Eerizioni mrzo, inemi el puno merile MOO el PROIEILE rieorie i proieili, ui pri on eloià pri (in moulo) m/ m on irezioni ripeo l uolo iere o Veloià: mbi oninumene in irezione e moulo eono le equzioni:
Eerizioni mrzo, inemi el puno merile MOO el PROIEILE rieorie i proieili, ui pri on eloià pri (in moulo) m/ m on irezioni ripeo l uolo iere o Veloià: mbi oninumene in irezione e moulo eono le equzioni:
Scelto l asse del moto y orientato verso l alto, nella prima fase del lancio si ha: v = a t ; y = ½ a t 2 e dopo t = 1 min = 60 s
 Eercizione n 3 FISICA SPERIMENTALE (C.L. Ing. Edi.) (Prof. Gbriele F)A.A. 1/11 Cinemic (b) 1. Un rzzo eore, lncio in ericle, le per 1 min con ccelerzione cone = m/, dopodiché, conumo uo il combuibile,
Eercizione n 3 FISICA SPERIMENTALE (C.L. Ing. Edi.) (Prof. Gbriele F)A.A. 1/11 Cinemic (b) 1. Un rzzo eore, lncio in ericle, le per 1 min con ccelerzione cone = m/, dopodiché, conumo uo il combuibile,
Funzioni a valori vettoriali
 Funzioni vlori veorili Definizione. Un ppliczione defini u un inieme di numeri reli il cui codominio è un n inieme dir è per definizione un funzione vlori veorili. F è un veore che h n componeni e i crive
Funzioni vlori veorili Definizione. Un ppliczione defini u un inieme di numeri reli il cui codominio è un n inieme dir è per definizione un funzione vlori veorili. F è un veore che h n componeni e i crive
5. La trasformata di Laplace Esercizi
 5. L rform di Lplce Eercizi Aggiornmeno: febbrio 3 p://www.cirm.unibo.i/~brozzi/mi/pdf/mi-cp.5-ee.pdf 5.. Inroduzione ll rform di Lplce 5.. Proprieà dell rform di Lplce 5.-. Coniderimo l funzione limi
5. L rform di Lplce Eercizi Aggiornmeno: febbrio 3 p://www.cirm.unibo.i/~brozzi/mi/pdf/mi-cp.5-ee.pdf 5.. Inroduzione ll rform di Lplce 5.. Proprieà dell rform di Lplce 5.-. Coniderimo l funzione limi
Facoltà di Ingegneria 1 a prova intracorso di Fisica I Compito B
 Eercizio n. Un punto terile i Fcoltà i Ingegneri pro intrcoro i Fiic I 5--00-Copito = 5kg i uoe lungo l e x con legge orri x( t) α t 8 =, oe x è epreo in etri, t in econi e α =. Deterinre: l poizione el
Eercizio n. Un punto terile i Fcoltà i Ingegneri pro intrcoro i Fiic I 5--00-Copito = 5kg i uoe lungo l e x con legge orri x( t) α t 8 =, oe x è epreo in etri, t in econi e α =. Deterinre: l poizione el
MOTI. Per descrivere un moto è necessario specificare la posizione del corpo in ogni istante. E quindi necessario definire un sistema di coordinate:
 MOTI Meccnic: Cinemic: Dinmic: brnc dell fiic che udi il moo dei corpi e le fore che lo fnno rire decrie il moo dei corpi en fre riferimeno eplicio lle fore che gicono u di ei è lo udio dell relione eplici
MOTI Meccnic: Cinemic: Dinmic: brnc dell fiic che udi il moo dei corpi e le fore che lo fnno rire decrie il moo dei corpi en fre riferimeno eplicio lle fore che gicono u di ei è lo udio dell relione eplici
Cinematica 1-1. Università degli Studi di Bari Aldo Moro Dip. DiSAAT - Ing. Francesco Santoro Corso di Fisica
 Cinetic - Si eterini l itnz el punto i cut ripetto l punto i lncio i un punto terile che ll itnte inizile i trovi un quot h e è otto i un velocità inizile orizzontle v non null. Cinetic - Fito il ite i
Cinetic - Si eterini l itnz el punto i cut ripetto l punto i lncio i un punto terile che ll itnte inizile i trovi un quot h e è otto i un velocità inizile orizzontle v non null. Cinetic - Fito il ite i
τ = 0.6 efficacia dell equilibratore
 TABILITA LONGITUDINALE DIMENIONAMENTO PIANO DI CODA ORIZZONTALE Il dienioneno del pino di cod orizzonle conie nel ricercre l coppi di vlori b perur geoerici che oddif le due condizioni criiche : uperficie
TABILITA LONGITUDINALE DIMENIONAMENTO PIANO DI CODA ORIZZONTALE Il dienioneno del pino di cod orizzonle conie nel ricercre l coppi di vlori b perur geoerici che oddif le due condizioni criiche : uperficie
11 DIMENSIONAMENTO DEL PIANO DI CODA ORIZZONTALE
 11 DIMENSIONAMENTO DEL PIANO DI CODA ORIZZONTALE Avendo già fo un dimensionmeno preliminre del pino di cod orizzonle, riporimo i di oenui d le sim: S.7m b 3.7m profilo: NACA 0006 AR 5.15 Per effeure il
11 DIMENSIONAMENTO DEL PIANO DI CODA ORIZZONTALE Avendo già fo un dimensionmeno preliminre del pino di cod orizzonle, riporimo i di oenui d le sim: S.7m b 3.7m profilo: NACA 0006 AR 5.15 Per effeure il
INTEGRALI IMPROPRI. TEORIA in sintesi. , sappiamo che sotto tali condizioni esiste. Sia f ( x) l integrale definito fra a e b della funzione f ( x)
 INTEGRALI IMPROPRI Prerequiii: Oieivi : Clcolo degli inegrli indefinii Inegrle definio di un funzione coninu Teorem e formul fondmenle del clcolo inegrle Appliczioni del clcolo inegrle Sper riconocere
INTEGRALI IMPROPRI Prerequiii: Oieivi : Clcolo degli inegrli indefinii Inegrle definio di un funzione coninu Teorem e formul fondmenle del clcolo inegrle Appliczioni del clcolo inegrle Sper riconocere
Cinematica. Le equazioni del moto di A sono: v A = v 0 a A t ; s A = d + v 0 t ½ a A t 2
 Esercitzione n FISIC SPERIMENTLE I (C.L. In. Ei.) (Prof. Gbriele F).. / Cinemtic. Due uto e B iino con l stess elocità = 7 km/h su un str pin e rettiline, istnz l un ll ltr. un certo istnte t = il uitore
Esercitzione n FISIC SPERIMENTLE I (C.L. In. Ei.) (Prof. Gbriele F).. / Cinemtic. Due uto e B iino con l stess elocità = 7 km/h su un str pin e rettiline, istnz l un ll ltr. un certo istnte t = il uitore
b 9 Il metodo costruisce iterativamente tale insieme W, fino ad inserire t in W.
 Eerizio u mmino minimo Clolre meine il meoo i Djikr un mmino i oo minimo nel eguene grfo orieno, in ui per ogni ro (i, j) è inio il oo oio q ij. 7 4 1 7 9 1 4 e 9 Riferimeno: M. Fihei, Lezioni i Rier Operiv
Eerizio u mmino minimo Clolre meine il meoo i Djikr un mmino i oo minimo nel eguene grfo orieno, in ui per ogni ro (i, j) è inio il oo oio q ij. 7 4 1 7 9 1 4 e 9 Riferimeno: M. Fihei, Lezioni i Rier Operiv
Differenza tra microeconomia (analisi dei comportamenti individuali) e macroeconomia (analisi dei comportamenti aggregati).
 Capitolo 2 Domana e offerta pagina 1 CAPITOLO 2 DOMANDA E OFFERTA Differenza tra microeconomia (analii ei comportamenti iniviuali) e macroeconomia (analii ei comportamenti aggregati). La prima i fona ui
Capitolo 2 Domana e offerta pagina 1 CAPITOLO 2 DOMANDA E OFFERTA Differenza tra microeconomia (analii ei comportamenti iniviuali) e macroeconomia (analii ei comportamenti aggregati). La prima i fona ui
Cinematica. Il confronto e la classificazione dei moti, chiamata cinematica, si presenta come un compito arduo.
 Cineic Il ondo, con uo quello che coniene, i uoe ripeo l reo dell Uniero. Anche ciò che in pprenz è iobile, coe un rd, i uoe con l rozione dell Terr, con l orbi dell Terr inorno l Sole, con l orbi del
Cineic Il ondo, con uo quello che coniene, i uoe ripeo l reo dell Uniero. Anche ciò che in pprenz è iobile, coe un rd, i uoe con l rozione dell Terr, con l orbi dell Terr inorno l Sole, con l orbi del
ECONOMIA POLITICA II - ESERCITAZIONE 8 Curva di Phillips Legge di Okun - AD
 ECOOMIA POLITICA II - ESERCITAZIOE 8 Curv di Phillips Legge di Okun - AD Esercizio 1 Sino β = 0.5, α = 1, u = u n = 6%, λ = 0.5, g y = 0.03. Supponee che nell nno 0 l disoccupzione si 6% e che l bnc cenrle
ECOOMIA POLITICA II - ESERCITAZIOE 8 Curv di Phillips Legge di Okun - AD Esercizio 1 Sino β = 0.5, α = 1, u = u n = 6%, λ = 0.5, g y = 0.03. Supponee che nell nno 0 l disoccupzione si 6% e che l bnc cenrle
Esame di allineamento di Fisica - 24 novembre Facoltà di Ingegneria - Università di Bologna, sede di Cesena -a-
 --. lcole l e del pllelo indiiduo di eueni eoi: i j k ( ) ( ) ( ) i j 9 k 6 i j k i j k ( ) ( ) ( ) 9 lcole il odulo del podoo eoile:. Un copo pendo d feo ccele pe un fino d un elocià di / ucceiene i uoe
--. lcole l e del pllelo indiiduo di eueni eoi: i j k ( ) ( ) ( ) i j 9 k 6 i j k i j k ( ) ( ) ( ) 9 lcole il odulo del podoo eoile:. Un copo pendo d feo ccele pe un fino d un elocià di / ucceiene i uoe
Monomi e polinomi. Verifica per la classe prima COGNOME... NOME... Classe... Data...
 Cpitolo Monomi e polinomi Monomi Verifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Cpitolo Monomi e polinomi Monomi Verifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Fisica Generale A. 2. Esercizi di Cinematica. Esercizio 1. Esercizio 1 (III) Esercizio 1 (II)
 Fisic Generle A. Esercizi di Cinemic hp://cmpus.cib.unibo.i/57/ Esercizio 1 Un puno merile è incolo muoersi luno un uid reiline. Al empo il puno merile si ro in quiee. Il puno merile cceler con ccelerzione:
Fisic Generle A. Esercizi di Cinemic hp://cmpus.cib.unibo.i/57/ Esercizio 1 Un puno merile è incolo muoersi luno un uid reiline. Al empo il puno merile si ro in quiee. Il puno merile cceler con ccelerzione:
Sistemi Intelligenti Reinforcement Learning: Iterative policy evaluation
 Siemi Inelligeni Reinforcemen Lerning: Ierive policy evluion Albero Borghee Univerià degli Sudi di Milno Lbororio di Siemi Inelligeni Applici (AIS-Lb Diprimeno di Informic borghee@di.unimi.i /28 Sommrio
Siemi Inelligeni Reinforcemen Lerning: Ierive policy evluion Albero Borghee Univerià degli Sudi di Milno Lbororio di Siemi Inelligeni Applici (AIS-Lb Diprimeno di Informic borghee@di.unimi.i /28 Sommrio
GRANDEZZE PERIODICHE
 GRNDEZZE PERIODICHE Un grndezz empodipendene (), che supponimo rele, si definisce periodic qundo d u- guli inervlli ssume vlori uguli, cioè qundo vle l relzione (con n inero qulsisi): ( ) ( n) + () - Il
GRNDEZZE PERIODICHE Un grndezz empodipendene (), che supponimo rele, si definisce periodic qundo d u- guli inervlli ssume vlori uguli, cioè qundo vle l relzione (con n inero qulsisi): ( ) ( n) + () - Il
Principi di Ingegneria Chimica Anno Accademico Cognome Nome Matricola Firma
 Principi i Ingegneria Chimica Anno Accaemico 2010 2011 Cognome Nome Maricola Firma Problema 1. Uno cambiaore i calore è coiuio a ue ubi coaiali i iameri D 1 e D 2, con parei i peore racurabile e lunghezza
Principi i Ingegneria Chimica Anno Accaemico 2010 2011 Cognome Nome Maricola Firma Problema 1. Uno cambiaore i calore è coiuio a ue ubi coaiali i iameri D 1 e D 2, con parei i peore racurabile e lunghezza
INTEGRALE IN SENSO IMPROPRIO E INTEGRALE DI LEBESGUE
 INTEGRALE IN SENSO IMPROPRIO E INTEGRALE DI LEBESGUE OSSERVAZIONI ED ESEMPI Si f : [,+ ) : R inegrbile in senso improprio. Se,, f() llor f è inegrbile secondo Lebesgue, e i due inegrli coincidono. Infi
INTEGRALE IN SENSO IMPROPRIO E INTEGRALE DI LEBESGUE OSSERVAZIONI ED ESEMPI Si f : [,+ ) : R inegrbile in senso improprio. Se,, f() llor f è inegrbile secondo Lebesgue, e i due inegrli coincidono. Infi
Cinematica del punto
 Cinemic del puno L meccnic è l pre dell fisic ce sudi il moimeno dei corpi e le cuse ce lo enerno. Ess si diide in re pri: Cinemic: ess sudi il moo dei corpi senz ineressrsi lle cuse ce lo enerno Sic:
Cinemic del puno L meccnic è l pre dell fisic ce sudi il moimeno dei corpi e le cuse ce lo enerno. Ess si diide in re pri: Cinemic: ess sudi il moo dei corpi senz ineressrsi lle cuse ce lo enerno Sic:
Regime dell interesse composto.
 Regime dell ineresse composo Formule d usre : M = monne ; I = ineresse ; C = cpile ; r = fore di cpilizzzione K = somm d sconre ; s = sso di scono unirio ; i = sso di ineresse unirio V = vlore ule ; ν
Regime dell ineresse composo Formule d usre : M = monne ; I = ineresse ; C = cpile ; r = fore di cpilizzzione K = somm d sconre ; s = sso di scono unirio ; i = sso di ineresse unirio V = vlore ule ; ν
Principi di Ingegneria Chimica Anno Accademico Cognome Nome Matricola Firma
 Principi i Ingegneria Chimica Anno Accaemico 5 Cognome Nome Maricola Firma E mail: Problema. Un erbaoio ferico, i raggio inerno e coruio in maeriale plaico conucibilià, peore, è compleamene pieno i acqua
Principi i Ingegneria Chimica Anno Accaemico 5 Cognome Nome Maricola Firma E mail: Problema. Un erbaoio ferico, i raggio inerno e coruio in maeriale plaico conucibilià, peore, è compleamene pieno i acqua
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria di Primo Grado Classe Prima. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
Meccanica quantistica (3)
 Meccanica quanisica 3 03/11/13 1-MQ-3.oc 0 03/11/13 1-MQ-3.oc 1 Equazione i Scröinger La funzione 'ona Ψ, per le paricelle quanisice è soluzione all'equazione i Scröinger: i V m,,, Ψ Ψ + Ψ Se si pone:,
Meccanica quanisica 3 03/11/13 1-MQ-3.oc 0 03/11/13 1-MQ-3.oc 1 Equazione i Scröinger La funzione 'ona Ψ, per le paricelle quanisice è soluzione all'equazione i Scröinger: i V m,,, Ψ Ψ + Ψ Se si pone:,
Zona Frattura critica. Tenacità del materiale
 1 Perché l frur frgile si verifichi è necessrio il conemporneo verificrsi delle re segueni condizioni: livello di sollecizione elevo (nche se inferiore ll ensione di rour); presenz di un difeo (cricc)
1 Perché l frur frgile si verifichi è necessrio il conemporneo verificrsi delle re segueni condizioni: livello di sollecizione elevo (nche se inferiore ll ensione di rour); presenz di un difeo (cricc)
Calcolo della funzione di trasferimento P(s) Progetto del controllore in base alle specifiche
 Calolo ella funzione i raferimeno P( Traformano eono Laplae il moello impliio ingreo-uia lineare e azionario ell impiano P y( y( y( u( + + + u( oengo: Y ( + Y ( + Y ( U ( + U ( Da ale relazione i riava:
Calolo ella funzione i raferimeno P( Traformano eono Laplae il moello impliio ingreo-uia lineare e azionario ell impiano P y( y( y( u( + + + u( oengo: Y ( + Y ( + Y ( U ( + U ( Da ale relazione i riava:
SOLUZIONE PROBLEMI Insegnamento di Fisica dell Atmosfera Seconda prova in itinere
 Doente: rof Dino Zri serittore: in lessio Bertò OLUZION PROBLMI Insenento i Fisi ell tosfer eon rov in itinere /3 Vlori elle ostnti Rio terrestre eio: 637 Rio solre eio: 7 5 Distnz ei terr-sole : 9 6 Vlore
Doente: rof Dino Zri serittore: in lessio Bertò OLUZION PROBLMI Insenento i Fisi ell tosfer eon rov in itinere /3 Vlori elle ostnti Rio terrestre eio: 637 Rio solre eio: 7 5 Distnz ei terr-sole : 9 6 Vlore
a a = 1, a a = 0; a a = 1, a a = 0; e quindi, = (a a ) (a a ) = (a a) a = 0 a = a
 Definizione 1. Si R un insieme otto i ue leggi i composizione interne e. Si ice che l struttur lgebric (R,, ) è un reticolo (lgebrico) se e verificno le proprietà: (1) x, y, z R, (x y) z = x (y z); (x
Definizione 1. Si R un insieme otto i ue leggi i composizione interne e. Si ice che l struttur lgebric (R,, ) è un reticolo (lgebrico) se e verificno le proprietà: (1) x, y, z R, (x y) z = x (y z); (x
Principi di Ingegneria Chimica Anno Accademico Cognome Nome Matricola Firma
 Principi i Ingegneria Chimica Anno Accaemico -3 Cognome Nome Matricola Firma Problema. Una latra quarata i un olio con caratteritiche fiiche cotanti (enità, conucibilità, calore pecifico ), i lato e peore,
Principi i Ingegneria Chimica Anno Accaemico -3 Cognome Nome Matricola Firma Problema. Una latra quarata i un olio con caratteritiche fiiche cotanti (enità, conucibilità, calore pecifico ), i lato e peore,
2. In un mercato concorrenziale senza intervento pubblico non si ha perdita di benessere sociale netto.
 Beanko & Breautigam Microeconomia Manuale elle oluzioni Capitolo 10 Mercati concorrenziali: applicazioni Soluzioni elle Domane i ripao 1. In corriponenza ell equilibrio i lungo perioo, un mercato concorrenziale
Beanko & Breautigam Microeconomia Manuale elle oluzioni Capitolo 10 Mercati concorrenziali: applicazioni Soluzioni elle Domane i ripao 1. In corriponenza ell equilibrio i lungo perioo, un mercato concorrenziale
Introduzione e modellistica dei sistemi
 Fondmeni di Auomic Modellisic dei sisemi eleromeccnici Inroduzione e modellisic dei sisemi Modellisic dei sisemi eleromeccnici Principi fisici di funzionmeno Moore elerico in correne coninu (DC-moor) DC-moor
Fondmeni di Auomic Modellisic dei sisemi eleromeccnici Inroduzione e modellisic dei sisemi Modellisic dei sisemi eleromeccnici Principi fisici di funzionmeno Moore elerico in correne coninu (DC-moor) DC-moor
1 REGOLE DI INTEGRAZIONE
 UNIVERSITÀ DEGLI STUDI DI ROMA LA SAPIENZA - Fcolà di Frmci e Medicin - Corso di Lure in CTF REGOLE DI INTEGRAZIONE. REGOLA DI INTEGRAZIONE PER PARTI f(x)g (x)dx = f(x)g(x) g(x)f (x)dx f(x)dg(x) = f(x)g(x)
UNIVERSITÀ DEGLI STUDI DI ROMA LA SAPIENZA - Fcolà di Frmci e Medicin - Corso di Lure in CTF REGOLE DI INTEGRAZIONE. REGOLA DI INTEGRAZIONE PER PARTI f(x)g (x)dx = f(x)g(x) g(x)f (x)dx f(x)dg(x) = f(x)g(x)
Problema 1: Una collisione tra meteoriti
 Problema : Una colliione ra meeorii Problemi di imulazione della econda prova di maemaica Eami di ao liceo cienifico 5 febbraio 05 Lo udene deve volgere un olo problema a ua cela Tempo maimo aegnao alla
Problema : Una colliione ra meeorii Problemi di imulazione della econda prova di maemaica Eami di ao liceo cienifico 5 febbraio 05 Lo udene deve volgere un olo problema a ua cela Tempo maimo aegnao alla
F (r(t)), d dt r(t) dt
 Cmpi vettorili Un cmpo vettorile è un funzione vlori vettorili F : A R, con A R n, ove in questo cso l imensione el ominio e el coominio è l stess. F ( 1, 2,..., n ) (f 1 ( 1, 2,..., n ), f 2 ( 1, 2,...,
Cmpi vettorili Un cmpo vettorile è un funzione vlori vettorili F : A R, con A R n, ove in questo cso l imensione el ominio e el coominio è l stess. F ( 1, 2,..., n ) (f 1 ( 1, 2,..., n ), f 2 ( 1, 2,...,
COLPO D ARIETE: MANOVRE DI CHIUSURA
 Università degli studi di Rom Tor Vergt Corso di Idrulic. Prof. P. Smmrco COLPO D ARIETE: MANOVRE DI CHIUSURA Appunti integrtivi l testo E. Mrchi, A. Rubtt - Meccnic dei Fluidi dlle lezioni del prof. P.
Università degli studi di Rom Tor Vergt Corso di Idrulic. Prof. P. Smmrco COLPO D ARIETE: MANOVRE DI CHIUSURA Appunti integrtivi l testo E. Mrchi, A. Rubtt - Meccnic dei Fluidi dlle lezioni del prof. P.
Principi di Ingegneria Chimica Anno Accademico Cognome Nome Matricola Firma
 Principi i Ingegneria Chimica Anno Accaemico 17 18 Cognome Nome Matricola Firma E mail: Problema 1. Un ottile parallelepipeo a bae quarata i lato e peore S è ee i una generazione termica volumetrica G,
Principi i Ingegneria Chimica Anno Accaemico 17 18 Cognome Nome Matricola Firma E mail: Problema 1. Un ottile parallelepipeo a bae quarata i lato e peore S è ee i una generazione termica volumetrica G,
Disequazioni di primo grado
 Cpitolo Disequzioni i primo gro Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Cpitolo Disequzioni i primo gro Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Esempio: accelerazione media
 Segno ell ccelerzione L ccelerzione è posii quno è ire nel erso posiio ell sse, negi nel cso opposo. Aenzione l significo el segno!!! Il segno ell ccelerzione non uol sempre ire che l oggeo s umenno o
Segno ell ccelerzione L ccelerzione è posii quno è ire nel erso posiio ell sse, negi nel cso opposo. Aenzione l significo el segno!!! Il segno ell ccelerzione non uol sempre ire che l oggeo s umenno o
Test di autovalutazione
 UNITÀ 2 GLI ELEMENTI FONMENTLI ELL GEOMETRI T T i uovluzion 0 10 20 30 40 0 0 70 80 90 100 n Il mio punggio, in nimi, è 1 2 3 Ov l figu gn l uni popoizion o. ppin L. ppin l. ppin l. ppin l ppin l. l ppin.
UNITÀ 2 GLI ELEMENTI FONMENTLI ELL GEOMETRI T T i uovluzion 0 10 20 30 40 0 0 70 80 90 100 n Il mio punggio, in nimi, è 1 2 3 Ov l figu gn l uni popoizion o. ppin L. ppin l. ppin l. ppin l ppin l. l ppin.
Dispositivi e Sistemi Meccanici. 11 Esercizi. Politecnico di Torino CeTeM. Esercizio 11
 Poliecnico i Torino ete Dipoiivi e Siemi eccanici Eercizi Eercizio Un moore o è collegao a un argano A i ollevameno econo lo chema in figura. Sull albero moore è ineria una frizione conica Fr, che ramee
Poliecnico i Torino ete Dipoiivi e Siemi eccanici Eercizi Eercizio Un moore o è collegao a un argano A i ollevameno econo lo chema in figura. Sull albero moore è ineria una frizione conica Fr, che ramee
Pressioni nelle condotte
 10 Pressioni nelle condotte 10.1 Sovrppressioni ccidentli L e sovrppressioni ccidentli si possono verificre cus delle vrizioni del moto dell cqu nell tubzione. In questo cso si dirà che il moto non viene
10 Pressioni nelle condotte 10.1 Sovrppressioni ccidentli L e sovrppressioni ccidentli si possono verificre cus delle vrizioni del moto dell cqu nell tubzione. In questo cso si dirà che il moto non viene
Omotopia, forme chiuse e esatte
 Omotopi, forme chiuse e estte Per curv intenimo un curv orientt regolre trtti. Dt un curv enoteremo con l curv ottenut cmbino orientzione, si h ω = ω per ogni form ω (1) Due curve, tli che il punto finle
Omotopi, forme chiuse e estte Per curv intenimo un curv orientt regolre trtti. Dt un curv enoteremo con l curv ottenut cmbino orientzione, si h ω = ω per ogni form ω (1) Due curve, tli che il punto finle
Sistemi Intelligenti Reinforcement Learning: Iterative policy evaluation. Sommario
 Siemi Inelligeni Reinforcemen Lerning: Ierive policy evluion Albero Borghee Univerià degli Sudi di Milno Lbororio di Siemi Inelligeni Applici (AIS-Lb) Diprimeno di Scienze dell Informzione borghee@di.unimi.i
Siemi Inelligeni Reinforcemen Lerning: Ierive policy evluion Albero Borghee Univerià degli Sudi di Milno Lbororio di Siemi Inelligeni Applici (AIS-Lb) Diprimeno di Scienze dell Informzione borghee@di.unimi.i
A.A.2009/10 Fisica 1 1
 Mhine termihe e frigoriferi Un mhin termi è un mhin he, grzie un sequenz i trsformzioni termoinmihe i un t sostnz, proue lvoro he può essere utilizzto. Un mhin solitmente lvor su i un ilo i trsformzioni
Mhine termihe e frigoriferi Un mhin termi è un mhin he, grzie un sequenz i trsformzioni termoinmihe i un t sostnz, proue lvoro he può essere utilizzto. Un mhin solitmente lvor su i un ilo i trsformzioni
UNIVERSITÁ DEGLISTUDIDISALERNO C.d.L. in INGEGNERIA GESTIONALE Ricerca Operativa 12 Gennaio 2009 Prof. Saverio Salerno. Compito A
 1. Risolvere i seguenti problemi: 12 Gennio 2009 Compito A () stbilire se il vettore (3, 2, 0) è combinzione convess i u 1 =(3, 0, 6) e u 2 =(3, 3, 3); (b) per il poliero S = (x 1,x 2 ) R 2 :0 x 1 1, 0
1. Risolvere i seguenti problemi: 12 Gennio 2009 Compito A () stbilire se il vettore (3, 2, 0) è combinzione convess i u 1 =(3, 0, 6) e u 2 =(3, 3, 3); (b) per il poliero S = (x 1,x 2 ) R 2 :0 x 1 1, 0
Risolvi i seguenti esercizi rispondi a 4 quesiti a scelta tra quelli proposti nel questionario
 Risolvi i segueni esercizi rispondi quesii scel r quelli proposi nel quesionrio Clcol le segueni primiive. Quindi c ln e. Pongo d cui segue, llor: ( e ) d ( e ) c ( e ) c e e d. sin ( ) Pongo d cui segue,
Risolvi i segueni esercizi rispondi quesii scel r quelli proposi nel quesionrio Clcol le segueni primiive. Quindi c ln e. Pongo d cui segue, llor: ( e ) d ( e ) c ( e ) c e e d. sin ( ) Pongo d cui segue,
Componenti per l aritmetica binaria
 Componenti per l ritmetic inri Introduzione 2 Introduzione Motivzioni 3 Appliczioni di n-it dder 4 Sommtore CLA I itemi di clcolo neceitno di componenti che relizzino operzioni di tipo ritmetico (omme,
Componenti per l ritmetic inri Introduzione 2 Introduzione Motivzioni 3 Appliczioni di n-it dder 4 Sommtore CLA I itemi di clcolo neceitno di componenti che relizzino operzioni di tipo ritmetico (omme,
Problema 1. Una distribuzione continua di carica vale, in coordinate cilindriche,
 Corso i Lure in Mtemtic Prim prov in itinere i Fisic 2 (Prof. E. Sntovetti) 18 novemre 2016 Nome: L rispost numeric eve essere scritt nell pposito riquro e giustifict cclueno i clcoli reltivi. Prolem 1.
Corso i Lure in Mtemtic Prim prov in itinere i Fisic 2 (Prof. E. Sntovetti) 18 novemre 2016 Nome: L rispost numeric eve essere scritt nell pposito riquro e giustifict cclueno i clcoli reltivi. Prolem 1.
Lavoro di una forza. Si definisce lavoro elementare della forza F agente sul punto materiale P che si sposta di dr la quantità scalare:
 Loro i un forz Consierio un punto terile P in oto lungo un cur L per effetto i un forz F, si r il ettore posizione el punto in un siste i riferiento inerzile: in un interllo i tepo t il punto copie uno
Loro i un forz Consierio un punto terile P in oto lungo un cur L per effetto i un forz F, si r il ettore posizione el punto in un siste i riferiento inerzile: in un interllo i tepo t il punto copie uno
Disequazioni di secondo grado
 Disequzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Disequzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
STABILITA DEI SISTEMI IN RETROAZIONE CRITERIO DI ROUTH ESERCIZI
 STABILITA DEI SISTEMI IN RETROAZIONE CRITERIO DI ROUTH ESERCIZI U( ) + Stilità dei itemi in retrozione G( ) Y ( ) G( ) N ( ) G DG ( ) W ( ) G( ) NG ( ) 1 + G( ) D ( ) + N ( ) G G Nel co di un itemi G()
STABILITA DEI SISTEMI IN RETROAZIONE CRITERIO DI ROUTH ESERCIZI U( ) + Stilità dei itemi in retrozione G( ) Y ( ) G( ) N ( ) G DG ( ) W ( ) G( ) NG ( ) 1 + G( ) D ( ) + N ( ) G G Nel co di un itemi G()
CORSO di POLITICA ECONOMICA, 10 cfu. Prof. Francesco Aiello. Corso di Laurea Triennale in Economica (DM 270) ESERCIZIO
 CORSO i POLITIC ECONOMIC, 0 cfu Prof. Franceco iello Coro i Laurea Triennale in Economica (DM 70) ESERCIZIO Siano Q=450-p e Q=-50+p le curve, ripettivamente, i omana interna e i offerta interna i un paee
CORSO i POLITIC ECONOMIC, 0 cfu Prof. Franceco iello Coro i Laurea Triennale in Economica (DM 70) ESERCIZIO Siano Q=450-p e Q=-50+p le curve, ripettivamente, i omana interna e i offerta interna i un paee
UNIVERSITÀ DEGLI STUDI DI TERAMO
 UNIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA IN TUTELA E BENESSERE ANIMALE Corso di : FISICA MEDICA A.A. 015 /016 Docente: Dott. Chiucchi Riccrdo il:rchiucchi@unite.it Medicin Veterinri: CFU 5 (corso
UNIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA IN TUTELA E BENESSERE ANIMALE Corso di : FISICA MEDICA A.A. 015 /016 Docente: Dott. Chiucchi Riccrdo il:rchiucchi@unite.it Medicin Veterinri: CFU 5 (corso
Soluzione N.3. Soluzione T.1]. Sia F la primitiva della nostra funzione f, in altre parole. F 0 (s) =f (s),
![Soluzione N.3. Soluzione T.1]. Sia F la primitiva della nostra funzione f, in altre parole. F 0 (s) =f (s), Soluzione N.3. Soluzione T.1]. Sia F la primitiva della nostra funzione f, in altre parole. F 0 (s) =f (s),](/thumbs/95/123720090.jpg) Soluzione N3 Soluzione T] Si F l primiiv dell nosr funzione f, in lre prole F (s) =f (s), per definizione di inegrle definio oenimo β() α() f (s) ds = F (β ()) F (α ()) derivndo oenimo β() d f (s) ds =
Soluzione N3 Soluzione T] Si F l primiiv dell nosr funzione f, in lre prole F (s) =f (s), per definizione di inegrle definio oenimo β() α() f (s) ds = F (β ()) F (α ()) derivndo oenimo β() d f (s) ds =
Compito di Campi Elettromagnetici del 31 Gennaio 2003
 Compito i Campi Elettromagnetici el 31 Gennaio 2003 1. Un'ona piana monocromatica a frequenza ~ 4/', proveniente allo pazio vuoto e avente enita' i potenza : ~ >, incie ortogonalmente u un emipazio ielettrico
Compito i Campi Elettromagnetici el 31 Gennaio 2003 1. Un'ona piana monocromatica a frequenza ~ 4/', proveniente allo pazio vuoto e avente enita' i potenza : ~ >, incie ortogonalmente u un emipazio ielettrico
Definizione. Si chiama similitudine una corrispondenza biunivoca dal piano in sé tale che,
 CAPITOLO 6 LE SIMILITUDINI 6 Rihimi i teori Definizione Si him similituine un orrisponenz iunivo l pino in sé tle he presi ue punti qulunque A B el pino e etti A B i loro orrisponenti si h he esiste un
CAPITOLO 6 LE SIMILITUDINI 6 Rihimi i teori Definizione Si him similituine un orrisponenz iunivo l pino in sé tle he presi ue punti qulunque A B el pino e etti A B i loro orrisponenti si h he esiste un
Si considera un corpo solido a forma di parallelepipedo, di spessore d [m] e facce maggiori con superficie S [m 2 ], tale che sia T 1
![Si considera un corpo solido a forma di parallelepipedo, di spessore d [m] e facce maggiori con superficie S [m 2 ], tale che sia T 1 Si considera un corpo solido a forma di parallelepipedo, di spessore d [m] e facce maggiori con superficie S [m 2 ], tale che sia T 1](/thumbs/98/134926211.jpg) I itemi termici La reitenza termica Se ue corpi aventi temperature ivere vengono mei a contatto, i ha un paaggio i quantità i calore al corpo a temperatura maggiore vero quello a temperatura minore, fino
I itemi termici La reitenza termica Se ue corpi aventi temperature ivere vengono mei a contatto, i ha un paaggio i quantità i calore al corpo a temperatura maggiore vero quello a temperatura minore, fino
Equazioni di secondo grado Capitolo
 Equzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Equzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Per ogni domanda ci può essere più di una risposta esatta. Puoi confrontarti con i tuoi compagni. Domanda Risposta A Risposta B Risposta C Risposta D
 CON UN MICO CON UN MICO Pe ogni domnd ci può eee più di un ipo e. Puoi confoni con i uoi compgni. SRCIZI Domnd Ripo Ripo Ripo C Ripo D 1 Le due ee ono pependicoli pllele incideni pni enmbe pe Z z 2 Le
CON UN MICO CON UN MICO Pe ogni domnd ci può eee più di un ipo e. Puoi confoni con i uoi compgni. SRCIZI Domnd Ripo Ripo Ripo C Ripo D 1 Le due ee ono pependicoli pllele incideni pni enmbe pe Z z 2 Le
A.A Ingegneria Gestionale Soluzioni della 3 prova
 FISICA A.A. 03-04 Ingegneri Geionle 3 ro - Mrzo 04 Lo uene ecri il roceimeno e l oluzione egli eercizi rooi. Gli elbori errnno riiri Luneì 4 Mrzo e rnno lui i fini el uermeno ell eme finle.. Su i un ino
FISICA A.A. 03-04 Ingegneri Geionle 3 ro - Mrzo 04 Lo uene ecri il roceimeno e l oluzione egli eercizi rooi. Gli elbori errnno riiri Luneì 4 Mrzo e rnno lui i fini el uermeno ell eme finle.. Su i un ino
Maturità scientifica, corso di ordinamento, sessione ordinaria 2000-2001
 Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone Mturità scientific, corso di ordinmento, sessione ordinri 000-001 PROBLEMA 1 Si consideri l seguente relzione tr le vribili reli x, y: 1 1 1 +
Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone Mturità scientific, corso di ordinmento, sessione ordinri 000-001 PROBLEMA 1 Si consideri l seguente relzione tr le vribili reli x, y: 1 1 1 +
Lezione 4. Risposte canoniche dei sistemi del primo e del secondo ordine
 Lezione 4 Ripoe canoniche dei iemi del primo e del econdo ordine Parameri caraeriici della ripoa allo calino Per ripoe canoniche i inendono le ripoe dei iemi dinamici ai egnali coiddei canonici (impulo,
Lezione 4 Ripoe canoniche dei iemi del primo e del econdo ordine Parameri caraeriici della ripoa allo calino Per ripoe canoniche i inendono le ripoe dei iemi dinamici ai egnali coiddei canonici (impulo,
Esercizi & Domande per il Compito di Elettrotecnica del 24 giugno 2002
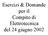 Eercizi & Domande per il ompio di Eleroecnica del 4 iuno 00 ESEZO - Traniorio nel dominio di aplace Svolimeno Eercizio - Traniorio nel dominio di aplace coninua i a v v () i a Ω Ω F v (0 - ) v (0 - ) alcolare
Eercizi & Domande per il ompio di Eleroecnica del 4 iuno 00 ESEZO - Traniorio nel dominio di aplace Svolimeno Eercizio - Traniorio nel dominio di aplace coninua i a v v () i a Ω Ω F v (0 - ) v (0 - ) alcolare
VERIFICA A PRESSOFLESSIONE ALLO SLU DI SEZIONI IN C.A.
 PROGETTO DI STRUTTURE - Ing. F. Paolacci - A/A 9-1 ESERCITAZIONE N 1 VERIFICA A PRESSOFLESSIONE ALLO SLU DI SEZIONI IN C.A. Si eve realizzare un eiicio con truttura portante cotituita a una erie i telai
PROGETTO DI STRUTTURE - Ing. F. Paolacci - A/A 9-1 ESERCITAZIONE N 1 VERIFICA A PRESSOFLESSIONE ALLO SLU DI SEZIONI IN C.A. Si eve realizzare un eiicio con truttura portante cotituita a una erie i telai
b) La velocità del centro di massa è identica prima e dopo l urto a causa della conservazione della quantità di moto del sistema: v CM = v.
 Esercizio a) Il sistema elle ue masse è sottoposto a una risultante elle forze nulla in irezione orizzontale nell istante ell urto. Si conserva la quantità i moto in tale irezione. Assumeno come positiva
Esercizio a) Il sistema elle ue masse è sottoposto a una risultante elle forze nulla in irezione orizzontale nell istante ell urto. Si conserva la quantità i moto in tale irezione. Assumeno come positiva
BOZZA. Lezione n. 20. Stati limite nel cemento armato Stato limite ultimo per tensioni normali
 Lezione n. Stati limite nel cemento armato Stato limite ultimo per tenioni normali Determinazione elle configurazioni i rottura per la ezione Una volta introotti i legami cotitutivi, è poibile eterminare
Lezione n. Stati limite nel cemento armato Stato limite ultimo per tenioni normali Determinazione elle configurazioni i rottura per la ezione Una volta introotti i legami cotitutivi, è poibile eterminare
Comportamento Meccanico dei Materiali. 5 Soluzione degli esercizi proposti. Esercizio 5-1
 Esercizio 5- lcolre lo sposmeno dell esremo e le sollecizioni preseni nell sruur in figur, compos d due se in serie con sezione circolre di dimero D 0 e D 8, lunghe enrme 00 e soggee d un crico di 0 k.
Esercizio 5- lcolre lo sposmeno dell esremo e le sollecizioni preseni nell sruur in figur, compos d due se in serie con sezione circolre di dimero D 0 e D 8, lunghe enrme 00 e soggee d un crico di 0 k.
Controllo di Azionamenti Elettrici. Lezione n 9. Controllo degli azionamenti elettrici con motore in corrente alternata
 Controllo di Azionmenti Elettrici Lezione n 9 Coro di Lure in Ingegneri dell Automzione Fcoltà di Ingegneri Univerità degli Studi di Plermo Controllo degli zionmenti elettrici con motore in corrente lternt
Controllo di Azionmenti Elettrici Lezione n 9 Coro di Lure in Ingegneri dell Automzione Fcoltà di Ingegneri Univerità degli Studi di Plermo Controllo degli zionmenti elettrici con motore in corrente lternt
Analisi Matematica 1 Ingegneria Informatica Gruppo 4, canale 6. Argomenti 19 ottobre 2017
 Analisi Maemaica Ingegneria Informaica Gruppo 4, canale 6 Argomeni 9 oobre 207. Esercizio. Da p://www.ma.unip.i/~moni/a_ing_205/appuni2.pf (Maeriali iaici Successioni numerice.) suiare il capiolo 3 fino
Analisi Maemaica Ingegneria Informaica Gruppo 4, canale 6 Argomeni 9 oobre 207. Esercizio. Da p://www.ma.unip.i/~moni/a_ing_205/appuni2.pf (Maeriali iaici Successioni numerice.) suiare il capiolo 3 fino
Problema Q & SOLUZIONE
 Problem 2..2.2 Un portt di,00 0 4 m / di ri umid, inizilmente ll tempertur di 2,0 C con umidità reltiv del 60% viene rffreddt e deumidifict. L tempertur in ucit è di 0,0 C ed il grdo igrometrico del 00%
Problem 2..2.2 Un portt di,00 0 4 m / di ri umid, inizilmente ll tempertur di 2,0 C con umidità reltiv del 60% viene rffreddt e deumidifict. L tempertur in ucit è di 0,0 C ed il grdo igrometrico del 00%
Sistemi Intelligenti Reinforcement Learning: Equazioni di Bellman
 Siemi Inelligeni Reinforcemen Lerning: quzioni di Bellmn Albero Borghee Univerià degli Sudi di Milno Lbororio di Siemi Inelligeni Applici (AIS-Lb) Diprimeno di Scienze dell Informzione borghee@di.unimi.i
Siemi Inelligeni Reinforcemen Lerning: quzioni di Bellmn Albero Borghee Univerià degli Sudi di Milno Lbororio di Siemi Inelligeni Applici (AIS-Lb) Diprimeno di Scienze dell Informzione borghee@di.unimi.i
273 CAPITOLO 18: PALI DI FONDAZIONE IN CONDIZIONI DI ESERCIZIO
 27 nrouzione Per i pali si può fare un iscorso analogo a quello viso per le fonazioni superficiali. Si è viso che nel caso elle fonazioni superficiali l analisi ella eformabilià ella sruura non poeva essere
27 nrouzione Per i pali si può fare un iscorso analogo a quello viso per le fonazioni superficiali. Si è viso che nel caso elle fonazioni superficiali l analisi ella eformabilià ella sruura non poeva essere
Università di Cagliari DIT Idraulica Corso di Costruzioni Marittime. Corso di Costruzioni Marittime. (modulo B) A. A
 (modulo B) A. A. 010-011 Esercizione N. Su un fondle sbbioso di rofondià ssegn si deve relizzre un sisem di briccole er l ccoso di nvi eroliere. Sono revise briccole flessibili cosiuie d n li d cciio sezione
(modulo B) A. A. 010-011 Esercizione N. Su un fondle sbbioso di rofondià ssegn si deve relizzre un sisem di briccole er l ccoso di nvi eroliere. Sono revise briccole flessibili cosiuie d n li d cciio sezione
Equazioni e disequazioni logaritmiche ed esponenziali. Sintesi delle teoria e guida alla risoluzione di esercizi
 Equzioni e disequzioni rimiche ed esponenzili Sinesi delle eori e guid ll risoluzione di esercizi Esponenzile Definizione: si definisce funzione esponenzile, con come vlori l qunià elev ll poenz. è l rgomeno
Equzioni e disequzioni rimiche ed esponenzili Sinesi delle eori e guid ll risoluzione di esercizi Esponenzile Definizione: si definisce funzione esponenzile, con come vlori l qunià elev ll poenz. è l rgomeno
Circuiti in regime sinusoidale
 ircuii in regime sinusoiale are www.ie.ing.unibo.i/pers/masri/iaica.hm versione el -0-03 Funzioni sinusoiali a cos ampiezza fase iniziale raiani, ra pulsazione ra/s f frequenza herz, Hz T perioo seconi,
ircuii in regime sinusoiale are www.ie.ing.unibo.i/pers/masri/iaica.hm versione el -0-03 Funzioni sinusoiali a cos ampiezza fase iniziale raiani, ra pulsazione ra/s f frequenza herz, Hz T perioo seconi,
Studio di una funzione razionale fratta (autore Carlo Elce)
 Stuio i funzioni Carlo Elce 1 Stuio i una funzione razionale fratta (autore Carlo Elce) Per rappresentare graficamente una funzione reale i una variabile reale bisogna seguire i seguenti passi: Passo 1)
Stuio i funzioni Carlo Elce 1 Stuio i una funzione razionale fratta (autore Carlo Elce) Per rappresentare graficamente una funzione reale i una variabile reale bisogna seguire i seguenti passi: Passo 1)
GIUNTO SALDATO: ESEMPIO [EC3 Appendice J]
![GIUNTO SALDATO: ESEMPIO [EC3 Appendice J] GIUNTO SALDATO: ESEMPIO [EC3 Appendice J]](/thumbs/39/19573251.jpg) GIUNTO SALDATO: ESEPIO [EC3 Appenice J] (revisione..3) HE A h (mm) b (mm) tw (mm) 7 tf (mm) r (mm) 8 A (cm) 64,34 Iy (cm4) 54 Wy (cm3) 55, Wpl,y (cm3) 568,5 IPE 3 h (mm) 3 b (mm) 5 tw (mm) 7, tf (mm),7
GIUNTO SALDATO: ESEPIO [EC3 Appenice J] (revisione..3) HE A h (mm) b (mm) tw (mm) 7 tf (mm) r (mm) 8 A (cm) 64,34 Iy (cm4) 54 Wy (cm3) 55, Wpl,y (cm3) 568,5 IPE 3 h (mm) 3 b (mm) 5 tw (mm) 7, tf (mm),7
PROVA SCRITTA DI TECNICA DELLE COSTRUZIONI DEL 12/10/2006. Esercizio n 1
 PROVA SCRITTA DI TECNICA DELLE COSTRUZIONI DEL 1/10/006 Eerizio n 1 Sia ata la trave a menola i.a. i lue l =,50 m e avente all inatro la ezione rappreentata in figura. Il ario i ervizio appliato, uniformemente
PROVA SCRITTA DI TECNICA DELLE COSTRUZIONI DEL 1/10/006 Eerizio n 1 Sia ata la trave a menola i.a. i lue l =,50 m e avente all inatro la ezione rappreentata in figura. Il ario i ervizio appliato, uniformemente
Nicola De Rosa, Liceo scientifico Americhe sessione ordinaria 2010, matematicamente.it. si determini quella che passa per il punto di coordinate 1
 Nicol De Ros, Liceo scienifico Americhe sessione ordinri, memicmene.i PROBLEMA Nel pino riferio coordine cresino Oy:. si sudi l funzione f e se ne rcci il grfico.. Si deermini l mpiezz degli ngoli individui
Nicol De Ros, Liceo scienifico Americhe sessione ordinri, memicmene.i PROBLEMA Nel pino riferio coordine cresino Oy:. si sudi l funzione f e se ne rcci il grfico.. Si deermini l mpiezz degli ngoli individui
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria di Primo Grado Classe Prima. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
STATO TENSIONALE IN SITO
 STATO TENSIONAE IN SITO 1.1 Preione totle verticle W z W = γ z A A σ = W/A = γ z preione totle verticle è pri l peo dell unità di volume del terreno γ moltiplict per l profondità z dl pino cmpgn σ=γ z
STATO TENSIONAE IN SITO 1.1 Preione totle verticle W z W = γ z A A σ = W/A = γ z preione totle verticle è pri l peo dell unità di volume del terreno γ moltiplict per l profondità z dl pino cmpgn σ=γ z
SISTEMA DI FISSAGGIO EDILFIX
 SISTEM I ISSGGIO EILIX Il itema i fiaggio EILIX offre una oluzione rapia e veratile a ogni problema i ancoraggio tra elementi i calcetruzzo, quali: pannelli/travi, parapetti/olette, ecc. e in carpenteria
SISTEM I ISSGGIO EILIX Il itema i fiaggio EILIX offre una oluzione rapia e veratile a ogni problema i ancoraggio tra elementi i calcetruzzo, quali: pannelli/travi, parapetti/olette, ecc. e in carpenteria
Componenti combinatori speciali. Componenti speciali. Sommario. Sommario
 Sommario Componenti combinatori peciali 2 Componenti peciali Sommario Si é ecritto un approccio top-own al progetto i reti combinatorie Alcune funzioni ono i utilizzo talmente comune a eere tate inerite
Sommario Componenti combinatori peciali 2 Componenti peciali Sommario Si é ecritto un approccio top-own al progetto i reti combinatorie Alcune funzioni ono i utilizzo talmente comune a eere tate inerite
Momento Massimo in campata M d [kn m] =
![Momento Massimo in campata M d [kn m] = Momento Massimo in campata M d [kn m] =](/thumbs/97/133455343.jpg) PRO INTERORSO N el 15.5. ESERIZIO N 1 Traccia on riferimento alla truttura i c.a. in figura, ollecitata a un carico uniformemente ripartito il cui valore i calcolo (incluo il peo proprio ella trave) è
PRO INTERORSO N el 15.5. ESERIZIO N 1 Traccia on riferimento alla truttura i c.a. in figura, ollecitata a un carico uniformemente ripartito il cui valore i calcolo (incluo il peo proprio ella trave) è
PROVA SCRITTA DI TECNICA DELLE COSTRUZIONI DEL 16/02/2007
 PROVA SCRITTA DI TECNICA DELLE COSTRUZIONI DEL 16/02/2007 Eercizio n 1 Sia ata una trave continua i cemento armato a ue campate i luci L 1 = 5,00 m e L 2 = 6.00 m. La trave, alta 60 cm e larga 30, ha ezione
PROVA SCRITTA DI TECNICA DELLE COSTRUZIONI DEL 16/02/2007 Eercizio n 1 Sia ata una trave continua i cemento armato a ue campate i luci L 1 = 5,00 m e L 2 = 6.00 m. La trave, alta 60 cm e larga 30, ha ezione
Le equazioni di grado superiore al secondo
 Le equzioni di grdo superiore l secondo ITIS Feltrinelli nno scolstico 007-008 R. Folgieri 007-008 1 Teorem fondmentle dell lger Ogni equzione lgeric di grdo n h sempre n soluzioni, che possono essere
Le equzioni di grdo superiore l secondo ITIS Feltrinelli nno scolstico 007-008 R. Folgieri 007-008 1 Teorem fondmentle dell lger Ogni equzione lgeric di grdo n h sempre n soluzioni, che possono essere
Chimica Fisica dei Materiali
 Chimic Fiic dei Mterili Dr. Serio Brutti Accumulo di idroeno Idroeno come vettore eneretico L idroeno oo può eere uto come vettore eneretico. Il rilcio di eneri viene relizzto fruttndo due differenti poibili
Chimic Fiic dei Mterili Dr. Serio Brutti Accumulo di idroeno Idroeno come vettore eneretico L idroeno oo può eere uto come vettore eneretico. Il rilcio di eneri viene relizzto fruttndo due differenti poibili
Esercizi per il corso di Calcolatori Elettronici
 Eserizi per il orso i loltori Elettronii svolti Muro IOVIELLO & io LUDNI Prte prim : mppe i Krnugh, metoo QM ESERIZIO : Mppe i Krnugh Minimizzre l rete rppresentt ll funzione: = {,,, 3, 4, 5,, } D = Ø
Eserizi per il orso i loltori Elettronii svolti Muro IOVIELLO & io LUDNI Prte prim : mppe i Krnugh, metoo QM ESERIZIO : Mppe i Krnugh Minimizzre l rete rppresentt ll funzione: = {,,, 3, 4, 5,, } D = Ø
Componenti combinatori speciali. Componenti speciali. Sommario. Sommario. M. Favalli
 Sommario Componenti combinatori peciali M. Favalli ngineering Department in Ferrara 2 (NDIF) Reti logiche / 29 (NDIF) Reti logiche 2 / 29 Componenti peciali Sommario Si é ecritto un approccio top-own al
Sommario Componenti combinatori peciali M. Favalli ngineering Department in Ferrara 2 (NDIF) Reti logiche / 29 (NDIF) Reti logiche 2 / 29 Componenti peciali Sommario Si é ecritto un approccio top-own al
Equazioni e disequazioni logaritmiche ed esponenziali. Guida alla risoluzione di esercizi
 Equzioni e disequzioni rimiche ed esponenzili Guid ll risoluzione di esercizi Esponenzile Definizione: si definisce funzione esponenzile, con come vlori l qunià elev ll poenz. è l rgomeno dell esponenzile,
Equzioni e disequzioni rimiche ed esponenzili Guid ll risoluzione di esercizi Esponenzile Definizione: si definisce funzione esponenzile, con come vlori l qunià elev ll poenz. è l rgomeno dell esponenzile,
Definizione opposto: Somma. Definizione vettore 0:
 Somm Operzioni in R n : somm :... n n Definizione ettore : Definizione opposto: :... :... n Rispetto tle operzione R n risult un gruppo elino. Cioè l somm h le seguenti proprietà: S5) Commutti S) Intern
Somm Operzioni in R n : somm :... n n Definizione ettore : Definizione opposto: :... :... n Rispetto tle operzione R n risult un gruppo elino. Cioè l somm h le seguenti proprietà: S5) Commutti S) Intern
Componenti combinatori speciali. Componenti speciali. Sommario. Sommario. M. Favalli
 Sommario Componenti combinatori peciali M. Favalli ngineering Department in Ferrara 2 Analii e intei ei circuiti igitali / Componenti peciali Sommario Analii e intei ei circuiti igitali 2 / Si é ecritto
Sommario Componenti combinatori peciali M. Favalli ngineering Department in Ferrara 2 Analii e intei ei circuiti igitali / Componenti peciali Sommario Analii e intei ei circuiti igitali 2 / Si é ecritto
Lezione 10. Idrodinamica di un liquido ideale
 Lezione 0 Iroinamica i un liquio ieale Fluioinamica La fluioinamica stuia il moto i un fluio, per esempio all interno i un conotto. Il parametro principale el moto el fluio a eterminare è la elocità el
Lezione 0 Iroinamica i un liquio ieale Fluioinamica La fluioinamica stuia il moto i un fluio, per esempio all interno i un conotto. Il parametro principale el moto el fluio a eterminare è la elocità el
Istituzioni di Probabilità Laurea magistrale in Matematica prova scritta del 20/6/2013
 Iiuzioni di Probabilià Laurea magirale in Maemaica prova cria del 0/6/03 Exercie. (puni 8 circa) Sia W un moo browniano reale. Sia ϕ : 0, + 0, + una funzione crecene, ia c : 0, + 0, + una funzione miurabile;
Iiuzioni di Probabilià Laurea magirale in Maemaica prova cria del 0/6/03 Exercie. (puni 8 circa) Sia W un moo browniano reale. Sia ϕ : 0, + 0, + una funzione crecene, ia c : 0, + 0, + una funzione miurabile;
CORSO DI LAUREA IN SCIENZE BIOLOGICHE Prova scritta di FISICA 18 Luglio 2007
 COSO DI UE IN SCIENZE IOOGICHE Proa cria i FISIC 8 ulio 7 Un coro i aa r i uoe u un iano orizzonale cabro, con coefficiene i ario inaico µ.4, areno con elocià. Doo aere ercoro un rao, al erine el quale
COSO DI UE IN SCIENZE IOOGICHE Proa cria i FISIC 8 ulio 7 Un coro i aa r i uoe u un iano orizzonale cabro, con coefficiene i ario inaico µ.4, areno con elocià. Doo aere ercoro un rao, al erine el quale
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del quinto appello, 3 luglio 2017 Testi 1
 nlisi Mtemti I per Ingegneri Gestionle,.. 6-7 Sritto el quinto ppello, 3 luglio 7 Testi Prim prte, gruppo.. Dire per quli R l funzione f() := sin( 3 ) + 3 è resente su tutto R.. Disporre le seguenti funzioni
nlisi Mtemti I per Ingegneri Gestionle,.. 6-7 Sritto el quinto ppello, 3 luglio 7 Testi Prim prte, gruppo.. Dire per quli R l funzione f() := sin( 3 ) + 3 è resente su tutto R.. Disporre le seguenti funzioni
