CAPITOLO 4. Struttura e potere di mercato
|
|
|
- Olimpia Giusti
- 8 anni fa
- Visualizzazioni
Transcript
1 CAPITOLO 4 Struttura e potere d merato 4.. Moopolo e potere d merato Quado ua mpresa può fluezare l prezzo he reve per l propro prodotto s de he ha u potere d moopolo, o potere d merato. U mpresa he ha u potere d merato fssa l prezzo al d sopra del lvello oorrezale, vale a dre al d sopra del osto margale. Ua mpresa he e- serta u potere d merato può osegure proftt postv, ma può ahe osegure proftt ull, ome el aso u v sao ost fss abbastaza elevat. Quado l merato o opera maera ottmale v è u osto per la soetà detto deadweght loss, (perdta sea o perdta etta). La perdta sea è data dalla dffereza tra la somma del surplus del osumatore e del produttore stuazoe d equlbro oorrezale, e la somma de due surplus ua stuazoe o oorrezale aratterzzata da ua quattà sambata ferore a quella d equlbro. Nel grafo l tragolo ABC rappreseta l surplus totale equlbro oorrezale, dato dalla somma del surplus del osumatore ABp e e l surplus del produttore CBp e. Se la quattà sambata s rdue a Q *, s avrà u prezzo p *, al quale orrspodoo uov lvell del surplus del produttore e del osumatore, par rspettvamete a CEDp * e ADp *. La perdta d surplus totale è par a EDB. S ot he oltre alla perdta omplessva d surplus l allotaameto dall equlbro oorrezale determa ua redstrbuzoe del surplus dal osumatore al produttore, ella msura del quadrato DFp e p *. Nel aso del moopolo è fale msurare l potere d merato a partre dalle odzo d equlbro. All equlbro l moopolsta uguagla l ravo margale al osto margale: MRMC ()
2 8 Captolo 4 Tale uguaglaza derva dalla odzoe del prmo orde per la massmzzazoe del proftto π RT CT p( Q) Q CT ( Q) : dπ dq drt dq dct dq S ot he l ravo margale, defto ome l ambameto el ravo totale he derva dalla vedta d ua utà aggutva d Q è dato da: 0 d( pq) dp MR p Q p () dq dq ε dove è l elasttà della domada. dq ε dp p Q Fgura - Perdta etta d moopolo I fgura è rappresetata la perdta d beessere ua stuazoe d moopolo e potzzado ost margal ostat. L area ACB msura la perdta detta deadweght loss e l area EADC msura proftt del moopolsta 3. La parte sottostate della fgura evdeza ahe la relazoe he v è tra proftt e ravo
3 Struttura e potere d merato 9 margale. I proftt resoo fo a quado l ravo margale è maggore del osto margale e soo massm quado l ravo margale è par al osto margale; s aullao orrspodeza dell equlbro oorrezale, quado l ravo totale è uguale al osto totale. Il ravo margale a sua volta è postvo f tato he la urva d domada è elasta ( ε < ) ed è egatvo quado la urva d domada è elasta 4 ( < ε < 0). Sosttuedo la () ella () s ha: p MC p ε (3) La relazoe trovata evdeza ome l markup (vale a dre la dffereza tra l prezzo e l osto margale rapporto al prezzo, detto de d Lerer) he u moopolsta può applare dpede solo dall elasttà della domada o la quale l moopolsta s ofrota. Pù la domada è elasta more è l markup, e l potere d merato, he l moopolsta può esertare. S ot he al dmure dell elasttà della domada rese ahe la perdta sea assoata al moopolo. La relazoe tra perdta etta ed elasttà della domada può essere rappresetata grafamete faedo ruotare la urva d domada modo he rmaga varata la quattà d equlbro d moopolo e oorreza ma he per tal quattà d equlbro l elasttà sa more per la uova urva. I fgura 3 s vede ome la perdta etta assoata alla urva d domada ruotata D par a ABE sa maggore d quella assoata alla urva orgara D, par a ABC. V soo var mod u s rea e s matee u moopolo. Geeralmete u moopolo esste o perhé le eoome d sala soo osì elevate he l raggugmeto della sala mma effete mpla la preseza d ua ua mpresa (moopol atural); o perhé l moopolsta ha partolar ooseze he gl permettoo d lavorare meglo rspetto a potezal etrat; o perhé l moopolsta ha l otrollo eslusvo d alu fattor produttv (possesso d ua rsorsa aturale ua o sfruttameto de brevett); o perhé l moopolsta è tale base a vol sttuzoal (moopolo d stato). La legslazoe su brevett etvado la rera d soluzo tehe he sao sfruttabl uamete dalle mprese he regstrao l brevetto etva e promuove moopol. La dfesa de drtt d propretà tellettuale è spesso gudata vataggosa per l bee omue, quato etva la rera e lo svluppo teologo. Tuttava va otato he gl etv alla rera s perdoo e prm a d sfruttameto del brevetto, quato o v è la maa d altre mprese ed aora o è eessaro trovare l uovo prodotto he sostturà l veho alla sadeza del brevetto. Ioltre rmae la questoe d fodo he gl obettv d rera delle mprese prvate rspodoo all obettvo prmaro d massmzzazoe de proftt e o del beessere soale. Iovazo he potrebbero avvataggare ua gra parte della popolazoe vegoo sosttute da ovazo
4 0 Captolo 4 he rspodoo a bsog d u lmtato umero d persoe apa però d pagare prezz elevat. L dustra farmaeuta è u aso tpo d tale dstorsoe. Metre all ogg esstoo farma ostosssm per la ura d malatte rare preset e paes rh, o esstoo farma per malatte ome la malara e la febbre d Degue he afflggoo grad fette della popolazoe de paes pù pover del modo. U moopolsta spesso matee l propro potere dsetvado l etrata d uove mprese sul propro merato, vale a dre attuado stratege d deterreza all etrata. Spesso l osto sosteuto per tale prata stratega vee osderato ome u altra fote d effeza de moopol, da sommare alla fote prmara osttuta dall eserzo del potere d merato. Ife va rordata u u altra fote d effeza del moopolo hamata -effey (Lebeste, 966). Quado ua mpresa su d u merato oorrezale opera modo effete, l ofroto o le mprese pù effet (e apa pertato d operare a ost mor) la spgerà fuor dal merato. U mpresa moopolsta al otraro può rmaere sul merato ahe se produe a ost elevat, e otuado a otteere proftt postv. I proftt postv o soo eessaramete assoat alla preseza d moopol. V possoo essere mprese he oseguoo proftt postv pur o esertado u potere d moopolo. Cò può aadere quado el omputo de proftt radoo le redte assoate al possesso d alu fattor produttv (ad e- sempo u propretaro terrero he s omporta ome pre taker può osegure de proftt postv he dervao dal possesso d u elevato aptale fodaro). Nel breve perodo u moopolsta può osegure proftt egatv; ad e- sempo se ua brusa aduta della domada lo ostrge ad abbassare l prezzo, l moopolsta rmarrà sul merato ahe se l lvello de guadag è tale he gl vestmet d tpo suk (vale a dre rreuperabl) offroo ua redta ferore a quella oorrezale. Rassumedo, l omportameto moopolsta è aratterzzato da ua mpresa he reve u prezzo superore al osto margale. Nel lugo perodo ua mpresa oorrezale osegue proftt ull metre ua mpresa moopolsta osegue proftt he al lmte soo ull. Nel breve perodo etrambe le mprese possoo osegure proftt postv, ull o egatv. 4.. Moopsoo Quado l potere d moopolo vee esertato su merat d aqusto, azhé su quell d vedta, s parla d moopsoo. Ua mpresa moopsosta è l uo aqurete sul merato d u prodotto he essa aqusta e su tale merato eserta u potere d moopsoo, vale a dre he è pre-maker luogo d pre-taker.
5 Fgura - Moopolo o ost margal ostat Struttura e potere d merato
6 Captolo 4 Fgura 3 - Relazoe tra perdta sea d moopolo ed elasttà della domada Così ome l moopolsta deve fare ot o ua urva d domada lata egatvamete, l moopsosta deve fare ot o ua urva d offerta (del bee aqustato) lata postvamete. Essedo l uo aqurete, l mpresa sa he al resere della propra domada l prezzo sul merato d aqusto tede a resere, e veversa. Il problema del moopsosta è quello d seglere la quattà d prodotto da aqustare he oseta d osegure l massmo proftto: ma pf ( ) w( ) dove: f()y è la fuzoe d produzoe del bee y veduto dal moopsosta sul merato d vedta; p è l prezzo d y, he s assume ome dato el aso u l merato d y sa oorrezale; è l fattore produttvo sul merato del quale l mpresa è l uo aqurete; w è l prezzo d ; w() è la fuzoe d offerta versa del fattore. La odzoe eessara perhé l proftto sa massmo è he la dervata prma s aull:
7 Struttura e potere d merato 3 dy dw p w 0 () d d S ot he l prmo terme dell espressoe 5 defse l valore del prodotto margale 6. La () s può pertato rsrvere ome: dw pmp w( ) () d S ot he l membro a sstra rappreseta l ravo margale dervate dall mpego d ua utà aggutva del fattore. Il membro d destra dell uguaglaza rappreseta vee l osto margale assoato all mpego d ua utà aggutva del fattore 7. La odzoe del prmo orde pertato asserse he l lvello d mpego del fattore he osete d massmzzare proftt è tale he l ravo margale assoato al suo uso sa uguale al osto margale assoato al suo uso. Moltplado l terme a destra della () per w w s ottee: dw pf '( ) w( )( ) w( ) (3) d w η dove η è l elasttà dell offerta del fattore produttvo. Il osto margale assoato all mpego d dpede pertato dal prezzo e dall elasttà dell offerta del fattore. S ot he pohé l elasttà è sempre postva l osto margale sarà sempre pù elevato del prezzo del fattore. Il grafo 4 llustra l equlbro del moopsosta sul merato del fattore osderado ua urva d offerta versa del fattore defta ome w ( ) a b. Il osto totale assoato all mpego del fattore da parte del moopsosta è par a C ( ) w( ) a b e l osto margale d ua utà addzoale d put è dato da MC ( ) a b. Il moopsosta aqusta la quattà * he rspetta la odzoe del prmo orde e fssa u prezzo w* he orrspode al prezzo he, per l lvello d produzoe *, rspetta l equlbro de produttor del fattore (dato per l apputo dall tersezoe tra la quattà domadata * e la urva d offerta del fattore). Il ofroto o la stuazoe oorrezale ( w, ) evdeza ome l eserzo del potere d moopsoo determ ua rduzoe sa del prezzo he della quattà sambata del fattore. I term d beessere s hao seguet effett: u aumeto del surplus dell aqurete par alla dffereza tra l area del rettagolo w dw* e del tragolo deb ; ua rduzoe del
8 4 Captolo 4 surplus del produttore par all area del trapezo w bw * ; ua perdta soale etta par all area del tragolo eb. È teressate aalzzare l equlbro el aso u l mpresa he aqusta l put, oltre ad avere u potere d moopsoo sul merato del fattore produttvo, abba ahe u potere d moopolo sul propro merato d vedta. A tal fe aalzzamo dapprma l omportameto d aqusto del fattore produttvo d ua mpresa o potere d moopolo, potzzado u merato del fattore oorrezale. Suessvamete aggugamo l potes d moopsoo sul merato del fattore. Fgura 4 - Moopsoo
9 Struttura e potere d merato Combazo d moopol MONOPOLIO A VALLE E CONCORRENZA A MONTE. (LA DOMANDA DI UN FATTORE DA PARTE DI UNA IMPRESA MONOPOLISTA) Il problema per l mpresa è sempre quello d seglere l lvello d mpego del fattore, dato y f (), he osete d massmzzare l proftto: ma p( f ( )) f ( ) w () La dffereza o l aso preedete è he l prezzo del prodotto o è pù ostate ma dpede dal lvello d produzoe (he a sua volta dpede dal lvello d mpego dell put, y f () ), metre l prezzo del fattore è ora assuto ome ostate. La odzoe del prmo orde per la massmzzazoe del proftto è la seguete 8 : p '( y) f '( ) f ( ) p( y) f '( ) w () La () può essere rsrtta ome: Moltplado l terme a sstra della (3) per dp dy dy y p( y) w (3) dy d d dy d p( y) s ha: p( y) dp y p( y) w dy p (4) dy dp y S ot he è l prodotto margale d (MP) e he d p ( y) è l ravo margale. dy p Il prodotto tra l prodotto margale d (he defse la varazoe del prodotto totale dovuta all mpego d ua utà aggutva d ) e l ravo margale (he defse la varazoe del ravo totale dovuta alla vedta d ua utà aggutva d y) è detto prodotto del ravo margale (MRP) ed da la varazoe del ravo totale dovuto all mpego d ua utà aggutva d. Il ravo margale del prodotto oorreza perfetta è par a pmp, vale a dre al valore del prodotto margale All equlbro pertato l moopolsta utlzzerà u lvello del fattore produttvo tale da uguaglare l osto margale del fattore ( questo aso rappresetato dal prezzo w) al ravo margale del prodotto.
10 6 Captolo 4 Fgura 5 - Domada d u fattore per u moopolsta S ot he l ravo margale del prodotto è ferore al valore del prodotto margale e tede ad uguaglarlo quado l elasttà tede ad fto. Pertato, trae he el aso d ua urva d domada perfettamete elasta, orrspodeza d u qualsas lvello d mpego, l valore margale d ua utà aggutva d put per l moopolsta sarà more he per l mpresa oorrezale. I fgura 5 s vede he pohé la urva del ravo margale del prodotto (MRP) gae al d sotto del valore del prodotto margale (pmp) per u dato prezzo w l moopolsta mpegherà ua quattà del fattore ( m ) ferore a quella mpegata dall mpresa oorrezale ( ). MONOPOLIO A VALLE E MONOPSONIO A MONTE Il produttore moopolsta-moopsosta questo aso deve utlzzare l fattore modo da massmzzare la seguete fuzoe del proftto: ma p( f ( )) f ( ) w( ) () la odzoe del prmo orde sarà data da:
11 Struttura e potere d merato 7 f '( ) p( y) f ( ) p' ( y) f '( ) w' ( ) w( ) 0 () vale a dre, utlzzado le deomazo sopra date: MRPMC. Fgura 6 - Moopolo a valle e moopsoo a mote Sul grafo 6 he omba due graf preedet, s vede he quado l mpresa he aqusta u fattore produttvo, somma al potere d moopsoo quello d moopolo, s ha ua ulterore dmuzoe sa del prezzo he della quattà sambata del fattore produttvo. Gl equlbr delle tre stuazo d merato soo dat o le tre oppe d valor: (, w ) per l aso d oorreza;, w ) per l aso d moopsoo a mote e oorreza a valle; ( m m * * (, w ) per l aso d moopsoo a mote e moopolo a valle. Quado l moopsosta è ahe moopolsta sul propro merato d vedta s ha ua perdta d beessere aggutva, rspetto al aso del moopsoo semple, par all area abd el grafo 6.
12 8 Captolo 4 IL DOPPIO MONOPOLIO Ife osderamo l aso u sa l mpresa he produe l fattore he quella he lo aqusta abbao u potere d moopolo. Ipotzzamo oè v sa ua ua mpresa he produe l fattore produttvo e he l mpresa he lo aqusta sa l uo produttore del bee otteuto utlzzado l fattore. S ot he l mpresa aqurete o è l ua possble mpresa aqurete pohé l fattore produttvo può essere utlzzato per la produzoe d be dvers (stamo pertato esludedo stuazo d moopsoo). È questo l aso del doppo moopolo (detto ahe della atea d moopol), he mpla u moopolo sa a mote he a valle del proesso produttvo. L esemplfazoe pù omue rguarda u produttore moopolsta a mote he vede ad ua mpresa d dstrbuzoe (dettaglate) he detee ah essa u potere d moopolo. Quado è presete u doppo moopolo, l aquszoe delle attvtà d ua delle due mprese da parte dell altra mpresa determa u mglorameto dell effeza omplessva dello sambo, o u aumeto sa del surplus del osumatore he del lvello de proftt del settore. Il osto soale assoato al doppo moopolo è llustrato fgura 7. S potzz u rapporto d sambo tale he l mpresa a valle (u dettaglate) aqust u bee prodotto dall mpresa a mote (ua mpresa mafatturera) al prezzo p w per po rvederlo al prezzo p r. S potzz ahe he l osto margale per la produzoe del bee (a aro dell mpresa a mote) sa ostate e par a MC, metre ost d dstrbuzoe (sosteut dall mpresa a valle) sao ull. Nella fgura 7 la urva D rappreseta la domada d merato per l output del moopolsta a valle e MR la urva del ravo margale da essa dervata. Pohé l moopolsta a valle vorrà vedere quella quattà del bee tale he l valore del ravo margale uguagl l prezzo d aqusto del bee (s ot he l prezzo d aqusto pagato al produttore a mote rappreseta l osto margale per l mpresa a valle, dato he ost d dstrbuzoe soo ull), l ravo margale rappreseta la urva d domada rvolta all mpresa a mote. Dalla urva MR è possble pertato dervare la urva del ravo margale per l mpresa a mote MRp. Il produttore a mote seglerà d vedere al dettaglate quella quattà Q* tale he l ravo margale MRp uguagl l osto margale MC, fssado u prezzo p w. Tale prezzo p w rappreseta l osto margale per l dettaglate he vederà la quattà Q* tale he p w MR al prezzo p r ompatble o la urva d domada D. S ot he se l produttore gestsse ahe l attvtà d dstrbuzoe, attraverso ua tegrazoe a valle (l aals rmae varata se s potzza he l dettaglate s appropr dell attvtà d produzoe) sarebbe equlbro per la quattà Q (tale he MCMR) fssado u prezzo p.
13 Struttura e potere d merato 9 S ot he l equlbro aso d tegrazoe vertale (Q, p ) mpla u maggore surplus del osumatore (he passa dall area p rab, all area p CB) e maggor proftt (he passao dall area p raed all area p CFD) rspetto al aso dell equlbro del doppo moopolo (Q*, p r). I rsultat appea otteut possoo essere ravat ahe a partre da u semple esempo umero. Sa q D( p) p la fuzoe d domada del bee esame. Sa p w l prezzo pagato dal dettaglate al produttore per l aqusto del bee e l osto margale ostate per la produzoe del bee. S assuma oltre he l dettaglate o abba altr ost al d fuor d quello per l aqusto del bee da rvedere. La fuzoe d proftto del dettaglate è defta da: La fuzoe d proftto del produttore è defta da: π ( p p ) D( p) () r w π p (p w )D(p) () La odzoe del prmo orde per la massmzzazoe della fuzoe d proftto del dettaglate è data da: dπ r p pw 0 (3) dp Da u s ravao l prezzo e la quattà d equlbro del dettaglate fuzoe del prezzo fssato dal produttore: pw p (4) p w p q p w (5) Sosttuedo tal valor d equlbro d p e q (vale a dre la (4) e la (5)) ella fuzoe d proftto del dettaglate, la () vee rsrtta ome fuzoe del prezzo p fssato dal produttore: w pw pw pw π r ( p pw ) q pw (6) Sosttuedo l valore della quattà d equlbro del dettaglate (la (5)) ella fuzoe d proftto del produttore (la ()) s ha:
14 30 Captolo 4 pw pw pw pw π p ( pw ) (7) La odzoe del prmo orde per la massmzzazoe della fuzoe d proftto del produttore è data da: dπ p pw 0 (8) dp w da u s rava l prezzo d equlbro del produttore: p w (9) Sosttuedo tale prezzo d equlbro (la (9)) ella fuzoe d proftto del produttore data dalla (7) s ottee l lvello d proftto d equlbro del produttore: ( ) ( ) π p (0) 8 Ife, sosttuedo l valore d equlbro del prezzo del produttore ella fuzoe d proftto del dettaglate data dalla (6) s ottee l lvello d proftto d equlbro del dettaglate: ( ) ( ) π r () 6 Ioltre sosttuedo l valore trovato d p w ell espressoe del prezzo d e- qulbro del dettaglate data dalla (4) s ottee l valore d equlbro del prezzo sul merato fale, fuzoe uamete del osto margale del bee: 3 p () 4 La somma de proftt del dettaglate e del produttore determa l valore del proftto totale aso d o tegrazoe: 3 π π r π p ( ) (3) 6 Nel aso ua delle due mprese deda d aqusre l otrollo dell altra mpresa, vale a dre opt per ua polta d tegrazoe vertale, la fuzoe del proftto sarà data da: π ( p ) D( p) ( p )( p) p p p (4)
15 Struttura e potere d merato 3 La odzoe d massmzzazoe del prmo orde sarà allora: dπ p 0 (5) dp da u s ottee l prezzo d equlbro: p (6) Sosttuedo l prezzo d equlbro ella fuzoe d proftt aso d tegrazoe data dalla (4) s ottee l lvello d proftto per l settore tegrato: ( ) π (7) 4 Tale proftto della struttura tegrata rsulta maggore de proftt ogut del settore o tegrato: 3 ( ) π π r π p ( ) < π 6 4 Fgura 7 - La doppa margalzzazoe Il aso del doppo moopolo, detto ahe della doppa margalzzazoe, è l uo aso u s dmostra equvoablmete he l tegrazoe vertale o omporta ua perdta d effeza. Nel aptolo 7 s vedrà ome le polthe d tegrazoe vertale sao spesso esamate o attezoe dalla legslazoe attrust he e deua possbl effett atoorrezal.
16 3 Captolo Moopolo blaterale e goh d otrattazoe U merato dove opera u moopolsta dal lato dell offerta e u moopsosta dal lato della domada s de he è aratterzzato da u moopolo blaterale. Cas d moopolo blaterale s verfao geeralmete su que merat de fattor dove u partolare put, per la u produzoe esste ua ua mpresa spealzzata, è utlzzato per la produzoe d u bee partolare, ella produzoe del quale s è spealzzata ua partolare mpresa he detee l eslusva della produzoe. S ot he l moopolo blaterale o assume ua stuazoe d moopolo sul merato a valle dell mpresa aqurete. Ua grade mpresa multazoale può rhedere la fabbrazoe d u partolare ompoete (per l quale esstoo elevate eoome d loalzzazoe assoate alla produzoe del bee fale) u determato paese, per la produzoe del quale s spealzza ua u- a mpresa. Il bee fale può essere prodotto ahe da altre mprese e altr paes oshé l mpresa moopsosta deve ofrotars o altr oorret sul propro merato d vedta. Può aadere oltre he l mpresa moopsosta sa ahe u moopolsta; ò avvee quado l bee fale è dotato d elevata speftà ed esstoo ad esempo barrere all etrata oesse alle ooseze spefhe del produttore e\o alla essteza d brevett. La fgura 8 rappreseta l merato del fattore produttvo aratterzzato da moopolo blaterale. La urva D rappreseta la urva d domada del merato, data dal ravo margale dervate all mpresa aqurete dall mpego d ua utà aggutva del fattore (s rveda l paragrafo relatvo al moopsoo). La urva MC rappreseta la urva d offerta del fattore e orrspode alla urva del osto margale dell mpresa produttre del fattore. Il produttore moopolsta massmzza la sua fuzoe del proftto quado la sua urva del ravo margale MR dervata dalla urva d domada D uguagla la propra urva de ost margal MC. Egl pertato vorrà vedere ua quattà q v al prezzo p v. L mpresa aqurete massmzza la propra fuzoe del proftto quado la propra urva de ost margal MC, dervata dalla urva d offerta MC del merato, uguagla la propra urva de rav margal D. L aqurete pertato vorrà aqustare la quattà q a al prezzo p a. S ot he og parte s trova equlbro (vale a dre l ompratore sulla propra urva d domada e l vedtore sulla propra urva d offerta) solo se l altra parte tratta p ome u parametro, ma ò omporta u dsaordo su valor d p e d q desderat. Perhé lo sambo abba luogo pertato le part devoo aordars sa sul prezzo he sulla quattà da sambare. I u merato aratterzzato da moopolo blaterale possoo avers le seguet tre soluzo: - ua delle part assume l otrollo della otroparte (tegrazoe vertale); -.lo sambo o ha luogo (l merato fallse); 3- le part
17 Struttura e potere d merato 33 s aordao per u partolare valore del prezzo e della quattà (equlbro d otrattazoe) Fgura 8 - Merato d u fattore aratterzzato da moopolo blaterale I aso d tegrazoe vertale s avrà ua ua mpresa he otrolla etrambe le fas produttve a mote e a valle del proesso produttvo el quale l fattore è mpegato. La quattà d equlbro del fattore utlzzata da tale mpresa sarà par a q e ella fgura 8, determata dall otro delle urve d offerta MC e d domada D del merato del fattore. S ot he tale quattà d equlbro è maggore d etrambe le quattà he l aqurete moopsosta e l vedtore moopolsta sarebbero dspost a sambare. Pertato l tegrazoe vertale determa u aumeto dell effeza. L evetualtà he lo sambo o abba luogo è relatvamete remota. Ftatohé lo sambo è effete (vale a dre he l osto d opportutà del vedtore è more del beefo dello sambo per l ompratore) s può attedere he le part sao etvate a trovare u aordo modo da approprars d almeo ua parte de beef dello sambo. Cò he geeralmete avvee è he s avv ua otrattazoe. L aals della rera d u aordo aso d moopolo blaterale è u tema partolarmete omplesso della letteratura eooma. Gl svlupp maggo-
18 34 Captolo 4 r s soo avut ell ambto della teora de goh, a partre dall aals semale d Nash (950). Il problema vee geeralmete affrotato due mod alteratv. U approo è quello d mporre ua sere d odzo he s può attedere sao soddsfatte da u aordo e trovare quelle soluzo d equlbro (aord) he soddsfo tal odzo. L altro approo s oetra sul proesso d otrattazoe, defedo orzzot temporal e regole del goo he permettoo d trovare delle soluzo d equlbro. Seza etrare el merto d tale letteratura lmtamo, ella sezoe he segue, a dare ua esemplfazoe d ome l assuzoe dell potes d massmzzazoe de proftt ogut gra parte de modell propost aut a rdurre la omplesstà del problema d otrattazoe. IL PROBLEMA DI CONTRATTAZIONE E L IPOTESI DI MASSIMIZZAZIONE DEL PROFITTO CONGIUNTO 9 ** Sa dato l merato del fattore produttvo aratterzzato da moopolo blaterale e sa w l prezzo del fattore mpegato dal ompratore per otteere b l output y o fuzoe d produzoe yf(). S dh o π R( f ( )) w s e π w C() rspettvamete le fuzo d proftto del ompratore e del vedtore. Se etrambe le part vogloo massmzzare l propro proftto allora valor w e d equlbro d otrattazoe sarao tal da massmzzare proftt b s ogut π π. Ifatt se tale somma o fosse massmzzata allora sarebbe possble trovare u altro aordo tale da far aumetare l proftto d almeo ua delle part. L assuto he aget razoal he massmzzao proftt o stpulo u aordo he o sa grado d massmzzare l proftto oguto, restrge d molto l seme de possbl aord (soluzo d equlbro). La odzoe del prmo orde per la massmzzazoe del proftto oguto è data da: b s d( π π ) R' f ' C' 0. d Le part pertato vogloo sambare la quattà * orrspodeza dell uguaglaza tra l ravo margale del prodotto del ompratore e l valore del osto margale del vedtore, date rspettvamete ome MRP e MC() fgura. La varable su u le part devoo aordars è l prezzo w. S ot he w o flueza l lvello del proftto oguto, ma e flueza la rpartzoe dπ tra le due part. S ot he b dπ e s, vale a dre he a mao a mao he w aumeta l proftto del ompratore s rdue al tasso, metre dw dw quello
19 Struttura e potere d merato 35 del vedtore aumeta allo stesso tasso. Qud l ompratore vorrà fssare u prezzo l pù basso possble e l vedtore u prezzo l pù alto possble. Dato he etrambe le part vogloo osegure proftt postv, l aordo d equlbro dovrà soddsfare le seguet dsuguaglaze: b π R w py wp 0 s π w C( z) 0 S ot he la prma d tal dsuguaglaze mpla w py e la seoda mpla w C, oshé w deve soddsfare la odzoe: AC( ) w pap. Co rfermeto alla fgura 9 pertato l aordo apae d massmzzare proftt ogut sarà tale da prevedere ua quattà sambata * ed u prezzo u l ompreso tra w e w. Mao a mao he l prezzo oordato s avva a u w l proftto del vedtore aumeta rapporto a quello del ompratore. Il veversa aade quado l prezzo s avva al lmte ferore w. l S ot he la quattà sambata * u equlbro d otrattazoe (he rspett ome el aso esame l volo d massmzzazoe del proftto oguto) è maggore della quattà sambata e as u vega esertato l solo potere d moopolo da parte del vedtore ( ) o l solo potere d moop- s b soo da parte dell aqurete ( ) La tes he l moopolo blaterale possa essere alu as preferble alle stuazo d solo moopolo o d solo moopsoo è stata avazata per la prma volta modo esplto da Galbrath (95) he trodusse a tal proposto l oetto d outervalg power. I u rapporto d sambo l potere d moopolo (moopsoo) esertato da ua delle part può servre a otroblaare (outerval) l potere d moopsoo (moopolo) esertato dalla otroparte. L eserzo del outervalg power determa geeralmete u aumeto del beessere soale, trae el aso u l moopsosta detega ahe u potere d moopolo sul propro merato d vedta 0. Al fe d rsolvere l problema d otrattazoe, vale a dre determare le quattà ed l prezzo d equlbro, soo stat propost dvers modell. Uo de prm modell è quello proposto da Zeuthe el 930. Zeuthe potzza ua stuazoe d sambo del tutto aaloga a quella daz llustrata per esemplfare gl effett dell potes d massmzzazoe de proftt ogut. Il ompratore e l vedtore soo oord sul lvello della quattà da sambare (quello ott-
20 36 Captolo 4 male, ossa he osete d massmzzare proftt ogut) e devoo trovare u aordo sul lvello del prezzo. Il measmo d otrattazoe proposto da Zeuthe, o offerte e otroofferte he otuao fo a he l prezzo he l ompratore vuole pagare sa par a quello rhesto dal vedtore, odue ad ua soluzoe d equlbro per la quale l proftto oguto è rpartto equamete tra le due part. Il modello d Zeuthe fa rfermeto ad ua stuazoe molto semplfata, o potes molto restrttve sul omportameto delle otropart (d mera massmzzazoe), sul measmo d otrattazoe (offerte reterate, seza spefazoe del protoollo, de ost e del tempo) e sul otesto formatvo (d ertezza; le part oosoo perfettamete sa l valore dello sambo sa la propesoe al rsho d u maato aordo della propra otroparte). Fgura 9 - Massmzzazoe de proftt ogut Stuazo d moopolo blaterale soo frequet el modo reale. Quado l bee sambato preseta ua elevata speftà sa per l ompratore he per l vedtore (vale a dre he etramb sosterrebbero de ost elevat se volessero
21 Struttura e potere d merato 37 ambare otroparte (swthg osts)), lo sambo avvee u otesto he s avva alla stuazoe deale del moopolo blaterale. Esemp tp soo rapport d fortura basat sull adattameto el tempo del bee prodotto dal vedtore alle esgeze tehe e orgazzatve del ompratore. Altr esemp s rvegoo el merato del lavoro, ad esempo quado le partolar ooseze ed abltà aquste da u lavoratore all tero d ua mpresa restrgoo le alteratve d selta d u uovo mpego (assuzoe) per l lavoratore (datore d lavoro). CONTRATTAZIONE BILATERALE E TEORIA DEI GIOCHI** A partre dagl a quarata la teora de goh ha offerto uov strumet e quadr oettual per l aals de problem d otrattazoe. La teora de goh permette d ofgurare l problema maera flessble, potzzado otest e regole del goo apa d raffgurare ua varetà d protooll d otrattazoe sotto dverse potes relatve all formazoe e al omportameto degl aget. La letteratura sulla otrattazoe blaterale he utlzza la teora de goh è attualmete tato ampa quato omplessa. Ua buoa troduzoe sull argometo, aessble ahe al lettore o possesso d ooseze a- vazate d teora de goh, s trova Kreps (990). Nelle sezo he seguoo vee offerta ua llustrazoe molto semplfata d alu modell d otrattazoe he hao aperto la strada alla suessva letteratura. Ua evdeza mportate d tale letteratura è he preseza d otest ad elevata ompletezza formatva ed ad elevata ertezza goh d otrattazoe he vogloo smulare stuazo ve a quelle del modo reale o ammettoo soluzo d equlbro o e ammettoo ua moltepltà. Ioltre rsultat teor spesso otraddoo l evdeza empra, sa quella del modo reale he quella rprodotta otest spermetal. U rsultato partolarmete teressate emerso molt stud d arattere spermetale è he el proesso d otrattazoe spesso alle motvazo d massmzzazoe e d effeza s sosttusoo quelle d arattere equtatvo. Vale a dre he ua otroparte può ruare ad u aordo he le prourerebbe u guadago postvo qualora rtega l aordo quo. I altre parole gl aget possoo orrere perdte eoomhe pur d dfedere u propro prpo d equtà he o eessaramete orrspode a quello d equtà dstrbutva defto ell ambto della teora eooma stadard. Tale rsultato è partolarmete rlevate quato offre uov sput per lo studo de rapport tra eta ed eooma, e vta a mettere dsussoe la valdtà de rter d selta d polta eooma dat dalla teora stadard. U altro mportate rsultato he derva dagl stud spermetal del proesso d otrattazoe he usao la teora de goh, è he modul omportametal ome la reprotà e l altrusmo possoo gudare l omportameto degl aget
22 38 Captolo 4 al par dell dvdualsmo auto-teressato potzzato dalla teora stadard. La lezoe he e derva è he quado l agre eoomo vee aalzzato otest strateg e d pol umer, la omplessa dmesoe soale ed atropologa del omportameto umao deve essere presa espltamete osderazoe per la ostruzoe d modell eoom dotat d effettvo potere esplatvo. I appede III vegoo presetat alu mportat goh d base he vegoo utlzzat e settg spermetal tes a testare l mportaza de modul omportametal basat sulla reprotà per l aals eooma. Ne goh d otrattazoe l problema d otrattazoe vee geeralmete posto ome u problema d rpartzoe tra due otropart d ua somma defta (ome ad esempo proftt ogut ell esempo preedete). Dato questo problema molto geerale vegoo po dvduate ua sere d regole e proedure he defsoo l protoollo d otrattazoe. Vegoo oltre formulate prese potes sul otesto formatvo, la durata del goo, e sul valore d evetual parametr esoge da qual dpede la soluzoe del problema. Il problema d egozazoe formulato ome rpartzoe d u dato ammotare è oto ahe ome problema della dvsoe della torta. La letteratura orgara sull argometo ha affrotato l problema due dvers mod he hao dato po orge a due flo d rera. Il prmo approo, he fa rfermeto all artolo semale d Nash (950), prevede offerte smultaee ed utlzza l metodo assomato per la rera delle soluzo. Il metodo assomato otraddstgue geeralmete goh ooperatv, ma Nash lo utlzza u otesto d goo d tpo o ooperatvo, mostrado d fatto he molt goh ooperatv possoo essere rodott a goh o ooperatv. Il seodo approo, esemplfato modo ompleto el lasso saggo d Rubste (98), prevede offerte alterate ed utlzza ome rtero d soluzoe quello della bakward duto. S preseta ome u tpo goo o ooperatvo damo o formazoe ompleta e perfetta. LA DIVISIONE DELLA TORTA E LA SOLUZIONE NEGOZIALE DI NASH** Ua formulazoe molto semplfata d questo tpo d goo è la seguete (Rasmuse, 983, pp.48-5): - Goator: due goator (l goatore e l goatore ) devoo aordars sulla rpartzoe della torta (ad esempo u dollaro). - Iformazoe: L formazoe è mperfetta (u goo è a formazoe perfetta quado orrspodeza d asua mossa, l goatore a u spetta muovere è a ooseza dell tera stora del goo fo a quel mometo), smmetra (u goo è a formazoe smmetra quado essu goatore possede formazo dverse da quelle degl altr al mometo d effettuare le propre mosse o alla fe del goo), ompleta (u goo è a formazoe ompleta quado le fuzo de payoff de
Dimostrazione della Formula per la determinazione del numero di divisori-test di primalità, di Giorgio Lamberti
 Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Design of experiments (DOE) e Analisi statistica
 Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
ALCUNI ELEMENTI DI TEORIA DELLA STIMA
 ALCUNI ELEMENTI DI TEORIA DELLA STIMA Quado s vuole valutare u parametro θ ad esempo: meda, varaza, proporzoe, oeffete d regressoe leare, oeffete d orrelazoe leare, e) d ua popolazoe medate u ampoe asuale,
ALCUNI ELEMENTI DI TEORIA DELLA STIMA Quado s vuole valutare u parametro θ ad esempo: meda, varaza, proporzoe, oeffete d regressoe leare, oeffete d orrelazoe leare, e) d ua popolazoe medate u ampoe asuale,
La classe che mostra la distribuzione più elevata è quella 60-90, che corrisponde a un uso elevato dell automobile. f i fr (= f i/n) fr% (=fr*100)
 ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
Apparecchi di sollavamento. Classificazione apparecchi di sollevamento a
 Appareh d sollavameto A moto otuo: Nastr trasportator Sollevator a tazze Forze d erza lmtate; trastor d avvameto e arresto poo rlevat A moto dsotuo: Gru a torre Forze d erza rlevat Classfazoe appareh d
Appareh d sollavameto A moto otuo: Nastr trasportator Sollevator a tazze Forze d erza lmtate; trastor d avvameto e arresto poo rlevat A moto dsotuo: Gru a torre Forze d erza rlevat Classfazoe appareh d
Metodi e Modelli di Programmazione Lineare
 Metod e Modell d Programmazoe Leare Massmo Paolu (paolu@dst.uge.t) DIS Uverstà d Geova La Programmazoe Leare (LP) Modello d programmazoe matemata ma f() s.t. X R vettore delle varabl desoal X seme delle
Metod e Modell d Programmazoe Leare Massmo Paolu (paolu@dst.uge.t) DIS Uverstà d Geova La Programmazoe Leare (LP) Modello d programmazoe matemata ma f() s.t. X R vettore delle varabl desoal X seme delle
Modelli di Flusso e Applicazioni: Andrea Scozzari. a.a. 2013-2014
 Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
frazione 1 n dell ammontare complessivo del carattere A x
 La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
b) Relativamente alla variabile PREZZO, fornire una misura della variabilità della distribuzione attraverso
 ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
Stim e puntuali. Vocabolario. Cambiando campione casuale, cambia l istogramma e cambiano gli indici
 Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
Elementi di Matematica Finanziaria. Rendite e ammortamenti. Università Parthenope 1
 Elemet d Matematca Fazara Redte e ammortamet Uverstà Partheope 1 S chama redta ua successoe d captal da rscuotere (o da pagare) a scadeze determate S chamao rate della redta sgol captal da rscuotere (o
Elemet d Matematca Fazara Redte e ammortamet Uverstà Partheope 1 S chama redta ua successoe d captal da rscuotere (o da pagare) a scadeze determate S chamao rate della redta sgol captal da rscuotere (o
Costi di Entrata e Struttura del Mercato. Economia Industriale Università Bicocca A.A. 2012-2013 Christian Garavaglia
 Cost d Etrt e truttur del Merto Eoom Idustrle Uverstà Bo A.A. 2012-2013 Chrst Grvgl Cotesto e oett For bbmo lzzto l fuzometo d u merto olgopolsto osderdo ome dto l umero d mprese opert el merto. D os dpede
Cost d Etrt e truttur del Merto Eoom Idustrle Uverstà Bo A.A. 2012-2013 Chrst Grvgl Cotesto e oett For bbmo lzzto l fuzometo d u merto olgopolsto osderdo ome dto l umero d mprese opert el merto. D os dpede
In questo capitolo vedremo solamente un caso di rendita, che useremo poi per generalizzare le rendite e dedurre tutti gli altri casi.
 7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Modello dinamico nello spazio dei giunti: relazione tra le coppie di attuazione ai giunti ed il moto della struttura
 Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
Parte I (introduzione)
 arte I (trodzoe) Espressoe dell ertezza d msra (UNI CEI 9) L ertezza rappreseta geerale dbbo. Il dbbo ra la valdtà del rsltato d a msrazoe vee espresso medate l ertezza d msra. Iertezza d msra arametro,
arte I (trodzoe) Espressoe dell ertezza d msra (UNI CEI 9) L ertezza rappreseta geerale dbbo. Il dbbo ra la valdtà del rsltato d a msrazoe vee espresso medate l ertezza d msra. Iertezza d msra arametro,
Elementi di Statistica descrittiva Parte III
 Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
SIMULAZIONE DI ESAME ESERCIZI. Cattedra di Statistica Medica-Università degli Studi di Bari-Prof.ssa G. Serio 1
 SIMULAZIONE DI ESAME ESERCIZI Cattedra d Statstca MedcaUverstà degl Stud d BarProf.ssa G. Sero ESERCIZIO. Alcu autor hao studato se la depressoe possa essere assocata a dc serologc d process autommutar
SIMULAZIONE DI ESAME ESERCIZI Cattedra d Statstca MedcaUverstà degl Stud d BarProf.ssa G. Sero ESERCIZIO. Alcu autor hao studato se la depressoe possa essere assocata a dc serologc d process autommutar
Attualizzazione. Attualizzazione
 Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
Organizzazione del corso. Elementi di Informatica. Orario lezioni ed esami. Crediti. Dispense e lucidi. Ricevimento studenti
 Orgazzazoe del corso Elemet d Iformatca Prof. Alberto Brogg Dp. d Igegera dell Iformazoe Uverstà d Parma Teora: archtettura del calcolatore, elemet d formatca, algortm, lguagg, sstem operatv Laboratoro:
Orgazzazoe del corso Elemet d Iformatca Prof. Alberto Brogg Dp. d Igegera dell Iformazoe Uverstà d Parma Teora: archtettura del calcolatore, elemet d formatca, algortm, lguagg, sstem operatv Laboratoro:
ESERCIZI SU DISTRIBUZIONI CAMPIONARIE
 Corso d Ifereza Statstca Eserctazo A.A. 009/0 ESERCIZI SU DISTRIBUZIONI CAMPIONARIE Eserczo I cosumator d marmellata ua data popolazoe soo l 40%. Determare la probabltà che, per u campoe beroullao d =
Corso d Ifereza Statstca Eserctazo A.A. 009/0 ESERCIZI SU DISTRIBUZIONI CAMPIONARIE Eserczo I cosumator d marmellata ua data popolazoe soo l 40%. Determare la probabltà che, per u campoe beroullao d =
Università degli Studi di Milano Bicocca CdS ECOAMM Corso di Metodi Statistici per l Amministrazione delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI
 Uverstà degl Stud d Mlao Bcocca CdS ECOAMM Corso d Metod Statstc per l Ammstrazoe delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI 1. Carta d cotrollo per frazoe d o coform (carta U resposable d produzoe,
Uverstà degl Stud d Mlao Bcocca CdS ECOAMM Corso d Metod Statstc per l Ammstrazoe delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI 1. Carta d cotrollo per frazoe d o coform (carta U resposable d produzoe,
Facoltà di Economia - STATISTICA - Corso di Recupero a.a Prof.ssa G. Balsamo CONCETTI di BASE Carattere X [o A ] i = 1
![Facoltà di Economia - STATISTICA - Corso di Recupero a.a Prof.ssa G. Balsamo CONCETTI di BASE Carattere X [o A ] i = 1 Facoltà di Economia - STATISTICA - Corso di Recupero a.a Prof.ssa G. Balsamo CONCETTI di BASE Carattere X [o A ] i = 1](/thumbs/74/71433944.jpg) Facoltà d Ecooma - STATISTICA - Corso d Recupero a.a. 2012-13 Prof.ssa G. Balsamo CONCETTI d BASE Carattere X [o A ] caratterstca quattatva [o qualtatva] rappresetatva d u feomeo sottoposto ad dage Popolazoe
Facoltà d Ecooma - STATISTICA - Corso d Recupero a.a. 2012-13 Prof.ssa G. Balsamo CONCETTI d BASE Carattere X [o A ] caratterstca quattatva [o qualtatva] rappresetatva d u feomeo sottoposto ad dage Popolazoe
ERRATA CORRIGE. L intero contenuto del paragrafo 9.2.3 a pagina 47-48 del Capitolato tecnico Determinazione del Canone è sostituito come segue:
 Procedura aperta per l affdameto de servz tegrat, gestoal, operatv e d mautezoe multservzo tecologco da esegurs presso gl mmobl d propretà o uso alle Asl ed alle azede ospedalere della regoe Campaa ERRATA
Procedura aperta per l affdameto de servz tegrat, gestoal, operatv e d mautezoe multservzo tecologco da esegurs presso gl mmobl d propretà o uso alle Asl ed alle azede ospedalere della regoe Campaa ERRATA
Descrizione quantomeccanica di un insieme di spin: LA MATRICE DENSITÀ
 Desrzoe quatomeaa d u seme d sp: LA MATRICE DENITÀ Il valore d aspettazoe d ua gradezza fsa rappresetata dall operatore O su u sstema ello stato Ψ è: O Ψ OΨdτ Ψ O Ψ e s a u umero elevato d sstem (u seme
Desrzoe quatomeaa d u seme d sp: LA MATRICE DENITÀ Il valore d aspettazoe d ua gradezza fsa rappresetata dall operatore O su u sstema ello stato Ψ è: O Ψ OΨdτ Ψ O Ψ e s a u umero elevato d sstem (u seme
La volatilità storica, le misure di rischio asimmetrico e la tracking error volatility
 Ecooma degl termedar fazar Lors Nadott, Claudo Porzo, Daele Prevat Copyrght 00 The McGraw-Hll Compaes srl Approfodmeto 4.3w La msurazoe del rscho (a cura d Atoo Meles Uverstà Partheope) La volatltà storca,
Ecooma degl termedar fazar Lors Nadott, Claudo Porzo, Daele Prevat Copyrght 00 The McGraw-Hll Compaes srl Approfodmeto 4.3w La msurazoe del rscho (a cura d Atoo Meles Uverstà Partheope) La volatltà storca,
Lezione 4. La Variabilità. Lezione 4 1
 Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
ammontare del carattere posseduto dalle i unità più povere.
 Eserctazoe VII: La cocetrazoe Eserczo Determare l rapporto d cocetrazoe d G del fatturato medo (espresso. d euro) d 8 mprese e rappresetare la curva d Lorez: 97 35 39 52 24 72 66 87 Eserczo apporto d cocetrazoe
Eserctazoe VII: La cocetrazoe Eserczo Determare l rapporto d cocetrazoe d G del fatturato medo (espresso. d euro) d 8 mprese e rappresetare la curva d Lorez: 97 35 39 52 24 72 66 87 Eserczo apporto d cocetrazoe
Leasing: aspetti finanziari e valutazione dei costi
 Leasg: aspett fazar e valutazoe de cost Descrzoe Il leasg è u cotratto medate l quale ua parte (locatore), cede ad u altro soggetto (locataro), per u perodo d tempo prefssato, uo o pù be, sao ess mobl
Leasg: aspett fazar e valutazoe de cost Descrzoe Il leasg è u cotratto medate l quale ua parte (locatore), cede ad u altro soggetto (locataro), per u perodo d tempo prefssato, uo o pù be, sao ess mobl
pè via che, lì, la media è sempre eguale risurta che te tocca un pollo all'anno: Me spiego: da li conti che se fanno seconno le statistiche d'adesso
 La varabltà L utlzzo d ua meda permette d stetzzare effcacemete l formazoe coteuta ua dstrbuzoe statstca dal puto d vsta dell testà del carattere. Tuttava la stes può essere eccessva, el seso s possoo
La varabltà L utlzzo d ua meda permette d stetzzare effcacemete l formazoe coteuta ua dstrbuzoe statstca dal puto d vsta dell testà del carattere. Tuttava la stes può essere eccessva, el seso s possoo
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Esercitazione 4 del corso di Statistica (parte 1)
 Eserctazoe 4 del corso d Statstca (parte ) Dott.ssa Paola Costat Febbrao 0 Eserczo Data la dstrbuzoe del carattere Reddto d cu all eserczo precedete se e msur l grado d cocetrazoe. La cocetrazoe d u carattere
Eserctazoe 4 del corso d Statstca (parte ) Dott.ssa Paola Costat Febbrao 0 Eserczo Data la dstrbuzoe del carattere Reddto d cu all eserczo precedete se e msur l grado d cocetrazoe. La cocetrazoe d u carattere
Due distribuzioni, stessa media ma in quale delle due la media rappresenta, sintetizza meglio la situazione?
 Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 =3,6 5 5 38 40 45 63 63/5 =3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 =3,6 5 5 38 40 45 63 63/5 =3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Due distribuzioni, stessa media ma in quale delle due la media rappresenta, sintetizza meglio la situazione?
 Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 3,6 5 5 38 40 45 63 63/5 3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 3,6 5 5 38 40 45 63 63/5 3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
CORSO DI LAUREA IN ECONOMIA AZIENDALE Metodi Statistici per le decisioni d impresa (Note didattiche) Bruno Chiandotto
 CORO DI LAUREA IN ECONOMIA AZIENDALE Metod tatstc per le decso d mpresa (Note ddattche) Bruo Chadotto 7. Teora del test delle potes I questo captolo s affrota l problema della verfca d potes statstche
CORO DI LAUREA IN ECONOMIA AZIENDALE Metod tatstc per le decso d mpresa (Note ddattche) Bruo Chadotto 7. Teora del test delle potes I questo captolo s affrota l problema della verfca d potes statstche
Indici di Posizione. Gli indici si posizione sono misure sintetiche ( valori caratteristici ) che descrivono la tendenza centrale di un fenomeno
 Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
Esercitazione 6 del corso di Statistica (parte 1)
 Eserctazoe del corso d Statstca parte Dott.ssa aola Costat 8 Marzo 0 Eserczo S ha motvo d rteere che u uovo farmaco A abba la propretà d abbassare l lvello d glcema el sague. I cascuo de pazet dabetc osservat,
Eserctazoe del corso d Statstca parte Dott.ssa aola Costat 8 Marzo 0 Eserczo S ha motvo d rteere che u uovo farmaco A abba la propretà d abbassare l lvello d glcema el sague. I cascuo de pazet dabetc osservat,
STATISTICA DESCRITTIVA
 COSIDERAZIOI PRELIMIARI SULLA STATISTICA La Statstca trae suo rsultat dall osservazoe de feome che c crcodao. Gl stess feome per essere oggetto d statstca devoo essere adeguatamete umeros modo tale che
COSIDERAZIOI PRELIMIARI SULLA STATISTICA La Statstca trae suo rsultat dall osservazoe de feome che c crcodao. Gl stess feome per essere oggetto d statstca devoo essere adeguatamete umeros modo tale che
ARGOMENTO: MISURA DELLA RESISTENZA ELETTRICA CON IL METODO VOLT-AMPEROMETRICO.
 elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
Incertezza di misura
 Icertezza d msura Itroduzoe e rcham Come gà detto rsultat umerc ottebl dalle msurazo soo trsecamete caratterzzat da aleatoretà è duque sempre ecessaro stmare ua fasca d valor attrbubl come msura al msurado;
Icertezza d msura Itroduzoe e rcham Come gà detto rsultat umerc ottebl dalle msurazo soo trsecamete caratterzzat da aleatoretà è duque sempre ecessaro stmare ua fasca d valor attrbubl come msura al msurado;
DI IDROLOGIA TECNICA PARTE II
 FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
Gli indici sintetici Forma. Un caso studio. Gli indici sintetici. Qualche considerazione. Qualche considerazione. Tendenza centrale Forma
 Qualche cosderazoe Tedeza cetrale La scelta dell dce d tedeza cetrale/poszoe dpede dal tpo e dalle caratterstche della dstrbuzoe; Pù che dvduare l dce mglore assoluto (che o esste), è mportate ache valutare
Qualche cosderazoe Tedeza cetrale La scelta dell dce d tedeza cetrale/poszoe dpede dal tpo e dalle caratterstche della dstrbuzoe; Pù che dvduare l dce mglore assoluto (che o esste), è mportate ache valutare
Funzioni di più variabili Massimi e Minimi una funzione definita in un insieme E. Un punto ( x0, y0)
 Massm e Mm Fuzo d pù varabl Massm e Mm Dezoe: Sa z = (, ) ua uzoe deta u seme E U puto (, E s dce puto d massmo (rsp mmo) relatvo per (, ) se esste δ > tale che ((, ) B((, ), δ ) E (, ) (, ) (rsp (, )
Massm e Mm Fuzo d pù varabl Massm e Mm Dezoe: Sa z = (, ) ua uzoe deta u seme E U puto (, E s dce puto d massmo (rsp mmo) relatvo per (, ) se esste δ > tale che ((, ) B((, ), δ ) E (, ) (, ) (rsp (, )
( ) 2 i 1 X. n(n + 1) a) si determini se sono corretti; b) per quelli non corretti, si calcoli la distorsione d;
 ESERCIZIO 5. Sa (X, X,, X ) u campoe casuale geerato da ua v.c. X f(x; θ) per la quale è oto che E(X) θ e Var(X). S cosdero 3 stmator d θ: X ; X ; ( ) X 3 a) s determ se soo corrett; b) per quell o corrett,
ESERCIZIO 5. Sa (X, X,, X ) u campoe casuale geerato da ua v.c. X f(x; θ) per la quale è oto che E(X) θ e Var(X). S cosdero 3 stmator d θ: X ; X ; ( ) X 3 a) s determ se soo corrett; b) per quell o corrett,
Variabilità = Informazione
 Varabltà e formazoe Lo studo d u feomeo ha seso solo se esso s preseta co modaltà/testà varabl da u soggetto all altro. Ad esempo, se dobbamo studare l reddto ua certa regoe è ecessaro osservare utà statstche
Varabltà e formazoe Lo studo d u feomeo ha seso solo se esso s preseta co modaltà/testà varabl da u soggetto all altro. Ad esempo, se dobbamo studare l reddto ua certa regoe è ecessaro osservare utà statstche
Analisi economica e valutazione delle alternative
 Aals ecoomca e valutazoe delle alteratve Ig. Lug Cucca (Ph.D.) Producto Egeerg Research WorkGROUP Dpartmeto d Tecologa Meccaca, Produzoe e Igegera Gestoale Uverstà d Palermo Ageda Elemet d calcolo ecoomco
Aals ecoomca e valutazoe delle alteratve Ig. Lug Cucca (Ph.D.) Producto Egeerg Research WorkGROUP Dpartmeto d Tecologa Meccaca, Produzoe e Igegera Gestoale Uverstà d Palermo Ageda Elemet d calcolo ecoomco
Aldo Montesano PRINCIPI DI ANALISI ECONOMICA CAP. 11 L ANALISI DELL'EQUILIBRIO GENERALE I
 Aldo Motesao PRINCIPI DI ANALISI ECONOMICA CAP. L ANALISI DELL'EQUILIBRIO GENERALE I L aals dell equlbro parzale, esaata el captolo precedete, è sa u utle troduzoe all aals dell equlbro geerale, sa uo
Aldo Motesao PRINCIPI DI ANALISI ECONOMICA CAP. L ANALISI DELL'EQUILIBRIO GENERALE I L aals dell equlbro parzale, esaata el captolo precedete, è sa u utle troduzoe all aals dell equlbro geerale, sa uo
Gli indici sintetici Forma. Gli indici sintetici. Gli indici sintetici. Qualche considerazione. Qualche considerazione. Tendenza centrale Forma
 Uverstà d Macerata Facoltà d Sceze Poltche - Ao accademco 01-013013 Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe dpede dal
Uverstà d Macerata Facoltà d Sceze Poltche - Ao accademco 01-013013 Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe dpede dal
Analisi dei Dati. La statistica è facile!!! Correlazione
 Aals de Dat La statstca è facle!!! Correlazoe A che serve la correlazoe? Mettere evdeza la relazoe esstete tra due varabl stablre l tpo d relazoe stablre l grado d tale relazoe stablre la drezoe d tale
Aals de Dat La statstca è facle!!! Correlazoe A che serve la correlazoe? Mettere evdeza la relazoe esstete tra due varabl stablre l tpo d relazoe stablre l grado d tale relazoe stablre la drezoe d tale
Algoritmi e Strutture Dati. Alberi Binari di Ricerca
 Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
Caso studio 12. Regressione. Esempio
 6/4/7 Caso studo Per studare la curva d domada d u bee che sta per essere trodotto sul mercato, s rlevao dat rguardat l prezzo mposto e l umero d pezz vedut 7 put vedta plota, ell arco d ua settmaa. I
6/4/7 Caso studo Per studare la curva d domada d u bee che sta per essere trodotto sul mercato, s rlevao dat rguardat l prezzo mposto e l umero d pezz vedut 7 put vedta plota, ell arco d ua settmaa. I
Università di Cassino. Esercitazioni di Statistica 1 del 26 Febbraio Dott. Mirko Bevilacqua
 Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
dei quali si conoscono solo la media x e la deviazione standard σ e dato un valore reale positivo K, possiamo affermare che:
 Eserctazoe VI: Il teorema d Chebyshev Eserczo La statura meda d u gruppo d dvdu è par a 73,78cm e la devazoe stadard a 3,6. Qual è la frequeza relatva delle persoe che hao ua statura superore o ferore
Eserctazoe VI: Il teorema d Chebyshev Eserczo La statura meda d u gruppo d dvdu è par a 73,78cm e la devazoe stadard a 3,6. Qual è la frequeza relatva delle persoe che hao ua statura superore o ferore
Lezione 1. I numeri complessi
 Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
SECONDA PROVA INTERMEDIA DI STATISTICA CLEA gennaio 2005 COMPITO C2
 Cogome Numero d matrcola SECONDA PROVA INERMEDIA DI SAISICA CLEA 07 7-77-08 geao 00 Nome COMPIO C A f della valutazoe s terrà coto solo ed esclusvamete d quato rportato egl appost spaz. Al terme della
Cogome Numero d matrcola SECONDA PROVA INERMEDIA DI SAISICA CLEA 07 7-77-08 geao 00 Nome COMPIO C A f della valutazoe s terrà coto solo ed esclusvamete d quato rportato egl appost spaz. Al terme della
Gli indici sintetici Forma. Un caso studio. Gli indici sintetici. Qualche considerazione. Qualche considerazione. Tendenza centrale Forma
 Uverstà d Macerata Dpartmeto d Sceze Poltche, della Comucazoe e delle Relaz. Iterazoal Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe
Uverstà d Macerata Dpartmeto d Sceze Poltche, della Comucazoe e delle Relaz. Iterazoal Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe
Classi di reddito % famiglie Fino a 15 5.3 15-25 16.2 25-35 21.1 35-45 18.6 45-55 13.6 Oltre 55 25.2 Totale 100
 ESERCIZIO Data la seguete dstrbuzoe percetuale delle famgle talae per class d reddto, espresso mlo d lre, (ao 995, fote Istat): Class d reddto % famgle Fo a 5 5.3 5-5 6. 5-35. 35-45 8.6 45-55 3.6 Oltre
ESERCIZIO Data la seguete dstrbuzoe percetuale delle famgle talae per class d reddto, espresso mlo d lre, (ao 995, fote Istat): Class d reddto % famgle Fo a 5 5.3 5-5 6. 5-35. 35-45 8.6 45-55 3.6 Oltre
Caso studio 10. Dipendenza in media. Esempio
 09/03/06 Caso studo 0 S cosder la seguete dstrbuzoe degl occupat Itala secodo l umero d ore settmaal effettvamete lavorate e l settore d attvtà (cfr. Itala cfre, Ao 008, pag. 7 ): Ore lavorate Settore
09/03/06 Caso studo 0 S cosder la seguete dstrbuzoe degl occupat Itala secodo l umero d ore settmaal effettvamete lavorate e l settore d attvtà (cfr. Itala cfre, Ao 008, pag. 7 ): Ore lavorate Settore
Università di Cassino Esercitazioni di Statistica 1 del 5 Febbraio Dott. Mirko Bevilacqua
 Uverstà d Casso Eserctazo d Statstca del 5 Febbrao 00. Dott. Mrko Bevlacqua ESERCIZIO N A partre dalla dstrbuzoe semplce del carattere peso rlevata su 0 studet del corso d Mcroecooma peso: { 4, 59, 65,
Uverstà d Casso Eserctazo d Statstca del 5 Febbrao 00. Dott. Mrko Bevlacqua ESERCIZIO N A partre dalla dstrbuzoe semplce del carattere peso rlevata su 0 studet del corso d Mcroecooma peso: { 4, 59, 65,
Alcuni metodi per la risoluzione di sistemi lineari con matrici strutturate.
 Alcu meto per la rsoluzoe sstem lear co matrc strutturate. A. url - Calcolo Scetco Problema Rsolvere l sstema leare: A A. url - Calcolo Scetco Problema q A Co A matrce el tpo: p O A è ua matrce tragoale!
Alcu meto per la rsoluzoe sstem lear co matrc strutturate. A. url - Calcolo Scetco Problema Rsolvere l sstema leare: A A. url - Calcolo Scetco Problema q A Co A matrce el tpo: p O A è ua matrce tragoale!
Istogrammi e confronto con la distribuzione normale
 Istogramm e cofroto co la dstrbuzoe ormale Suppoamo d effettuare per volte la msurazoe della stessa gradezza elle stesse codzo (es. la massa d u oggetto, la tesoe d ua pla, la lughezza d u oggetto, ecc.):
Istogramm e cofroto co la dstrbuzoe ormale Suppoamo d effettuare per volte la msurazoe della stessa gradezza elle stesse codzo (es. la massa d u oggetto, la tesoe d ua pla, la lughezza d u oggetto, ecc.):
52. Se in una città ci fosse un medico ogni 500 abitanti, quale sarebbe la percentuale di medici? A) 5 % B) 2 % C) 0,2 % D) 0,5% E) 0,02%
 RISPOSTE MOTIVATE QUIZ D AMMISSIONE 2000-2001 MATEMATICA 51. L espressioe log( 2 ) equivale a : A) 2log B) log2 C) 2log D) log E) log 2 Dati 2 umeri positivi a e b (co a 1), si defiisce logaritmo i base
RISPOSTE MOTIVATE QUIZ D AMMISSIONE 2000-2001 MATEMATICA 51. L espressioe log( 2 ) equivale a : A) 2log B) log2 C) 2log D) log E) log 2 Dati 2 umeri positivi a e b (co a 1), si defiisce logaritmo i base
COMPLEMENTI ALLE SERIE
 COMPLEMENTI ALLE SERIE. Serie a termii i sego efiitivamete ostate Per ompletezza rihiamo il riterio el rapporto e ella raie, seza imostrarli... Teorema (Criterio el rapporto). Sia a ua suessioe a termii
COMPLEMENTI ALLE SERIE. Serie a termii i sego efiitivamete ostate Per ompletezza rihiamo il riterio el rapporto e ella raie, seza imostrarli... Teorema (Criterio el rapporto). Sia a ua suessioe a termii
Lezione n 19-20. Lezioni di Ricerca Operativa. Corso di Laurea in Informatica Università di Salerno. Prof. Cerulli Dott. Carrabs
 Lezioi di Riera Operativa Corso di Laurea i Iformatia Uiversità di Salero Lezioe 9- - Problema del trasporto Prof. Cerulli Dott. Carrabs Problema del Flusso a osto Miimo FORMULAZIONE mi ( i, ) A o violi
Lezioi di Riera Operativa Corso di Laurea i Iformatia Uiversità di Salero Lezioe 9- - Problema del trasporto Prof. Cerulli Dott. Carrabs Problema del Flusso a osto Miimo FORMULAZIONE mi ( i, ) A o violi
Il modello di regressione lineare semplice (1) Studio della dipendenza riepilogo
 Studo della dpedeza replogo Abbamo vsto due msure d assocazoe tra caratter: ) msure d assocazoe basate sull dpedeza dstrbuzoe ( χ, V d Cramer) possoo essere applcate a coppe d caratter qualuque (ache etrambe
Studo della dpedeza replogo Abbamo vsto due msure d assocazoe tra caratter: ) msure d assocazoe basate sull dpedeza dstrbuzoe ( χ, V d Cramer) possoo essere applcate a coppe d caratter qualuque (ache etrambe
SUCCESSIONI E SERIE NUMERICHE
 SUCCESSIONI E SERIE NUMERICHE. Successioi umeriche a. Defiizioi: successioi aritmetiche e geometriche Cosideriamo ua sequeza di umeri quale ad esempio:,5,8,,4,7,... Tale sequeza è costituita mediate ua
SUCCESSIONI E SERIE NUMERICHE. Successioi umeriche a. Defiizioi: successioi aritmetiche e geometriche Cosideriamo ua sequeza di umeri quale ad esempio:,5,8,,4,7,... Tale sequeza è costituita mediate ua
COMPLEMENTI DI STATISTICA. L. Greco, S. Naddeo
 COMPLEMENTI DI STATISTICA L. Greco, S. Naddeo INDICE. GENERALITA SULLA VERIFICA DI IPOTESI. Itroduzoe 4. I test d sgfcatvtà 5.3 Gl tervall d cofdeza 7.4 Le potes alteratve.5 La poteza del test 5.6 Il test
COMPLEMENTI DI STATISTICA L. Greco, S. Naddeo INDICE. GENERALITA SULLA VERIFICA DI IPOTESI. Itroduzoe 4. I test d sgfcatvtà 5.3 Gl tervall d cofdeza 7.4 Le potes alteratve.5 La poteza del test 5.6 Il test
Statistica degli estremi
 Statstca degl estrem Rcham d probabltà e statstca Il calcolo della probabltà d u eveto è drettamete coesso co: - la COOSCEZA ICOMPLETA dell eveto stesso; - l assuzoe d u RISCHIO, calcolato come la probabltà
Statstca degl estrem Rcham d probabltà e statstca Il calcolo della probabltà d u eveto è drettamete coesso co: - la COOSCEZA ICOMPLETA dell eveto stesso; - l assuzoe d u RISCHIO, calcolato come la probabltà
Facoltà di Farmacia Corso di Matematica con elementi di Statistica Docente: Riccardo Rosso
 Facoltà d Farmaca Corso d Matematca co elemet d Statstca Docete: Rccardo Rosso Statstca descrttva: l coeffcete d cocetrazoe d G Quado s vuole rpartre ua certa somma d dearo, v soo due suddvso che soo,
Facoltà d Farmaca Corso d Matematca co elemet d Statstca Docete: Rccardo Rosso Statstca descrttva: l coeffcete d cocetrazoe d G Quado s vuole rpartre ua certa somma d dearo, v soo due suddvso che soo,
Calcolo delle Probabilità: esercitazione 4
 Argometo: Probabltà classca Lbro d testo pag. 1-7 e 7-77 e varable casuale uforme dscreta NB: asscurars d cooscere le defzo, le propretà rchamate e le relatve dmostrazo quado ecessaro Eserczo 1 S cosder
Argometo: Probabltà classca Lbro d testo pag. 1-7 e 7-77 e varable casuale uforme dscreta NB: asscurars d cooscere le defzo, le propretà rchamate e le relatve dmostrazo quado ecessaro Eserczo 1 S cosder
Esercitazione 5 del corso di Statistica (parte 1)
 Eserctazoe 5 del corso d Statstca (parte 1) Dott.ssa Paola Costat 8 Novembre 011 I alcue crcostaze s poe u maggor teresse sullo studo della varabltà tra le sgole utà statstche, puttosto che lo studo della
Eserctazoe 5 del corso d Statstca (parte 1) Dott.ssa Paola Costat 8 Novembre 011 I alcue crcostaze s poe u maggor teresse sullo studo della varabltà tra le sgole utà statstche, puttosto che lo studo della
Distribuzioni doppie. Esempi. Reddito annuo (x ) tramite una tabella a doppia entrata in cui per ogni coppia di
 Dstrbuz dppe Quad veg sderate gutamete due le d ua matre d dat s ha ua dstrbuze dppa dsaggregata ( utara. S tratta dell eleaze delle mdaltà d due aratter (X e Y sservate per g utà statsta del llettv sderat:
Dstrbuz dppe Quad veg sderate gutamete due le d ua matre d dat s ha ua dstrbuze dppa dsaggregata ( utara. S tratta dell eleaze delle mdaltà d due aratter (X e Y sservate per g utà statsta del llettv sderat:
Approfondimenti Lezione 3. Mara Bruzzi
 Approfodmet Lezoe 3 Mara Bruzz APPROFONDIMENTO 1 : I BOSONI Partcelle come le a, foto, meso hao vece fuzo d oda smmetrche y S. Esse o obbedscoo al prcpo d esclusoe d Paul. Tal partcelle soo dette BOSONI.
Approfodmet Lezoe 3 Mara Bruzz APPROFONDIMENTO 1 : I BOSONI Partcelle come le a, foto, meso hao vece fuzo d oda smmetrche y S. Esse o obbedscoo al prcpo d esclusoe d Paul. Tal partcelle soo dette BOSONI.
CALCOLO ECONOMICO E FINANZIARIO
 CALCOLO ECONOMICO E FINANZIARIO 1. Iteresse e scoto La postcpazoe d ua dspobltà fazara rchede ua certa rcompesa (teresse), vceversa la sua atcpazoe comporta ua dmuzoe dell'mporto orgaro (scoto). Il rsparmatore,
CALCOLO ECONOMICO E FINANZIARIO 1. Iteresse e scoto La postcpazoe d ua dspobltà fazara rchede ua certa rcompesa (teresse), vceversa la sua atcpazoe comporta ua dmuzoe dell'mporto orgaro (scoto). Il rsparmatore,
Soluzione La media aritmetica dei due numeri positivi a e b è data da M
 Matematica per la uova maturità scietifica A. Berardo M. Pedoe 6 Questioario Quesito Se a e b soo umeri positivi assegati quale è la loro media aritmetica? Quale la media geometrica? Quale delle due è
Matematica per la uova maturità scietifica A. Berardo M. Pedoe 6 Questioario Quesito Se a e b soo umeri positivi assegati quale è la loro media aritmetica? Quale la media geometrica? Quale delle due è
Analisi di dati vettoriali. Direzioni e orientazioni
 Aals d dat vettoral Drezo e oretazo I tal caso, dat soo msurat term d agol e spesso soo rfert al ord geografco (statstca crcolare) Soo rappresetat su ua crcofereza Dat d drezoe: flusso ua specfca drezoe,
Aals d dat vettoral Drezo e oretazo I tal caso, dat soo msurat term d agol e spesso soo rfert al ord geografco (statstca crcolare) Soo rappresetat su ua crcofereza Dat d drezoe: flusso ua specfca drezoe,
V Tutorato 6 Novembre 2014
 1. Data la successioe V Tutorato 6 Novembre 01 determiare il lim b. Data la successioe b = a = + 1 + 1 8 6 + 1 80 + 18 se 0 se < 0 scrivere i termii a 0, a 1, a, a 0 e determiare lim a. Data la successioe
1. Data la successioe V Tutorato 6 Novembre 01 determiare il lim b. Data la successioe b = a = + 1 + 1 8 6 + 1 80 + 18 se 0 se < 0 scrivere i termii a 0, a 1, a, a 0 e determiare lim a. Data la successioe
Le modalità con cui si esprime la grandezza Ysaranno:
 Statsta Bvarata Cosderamo ora l aso d ua o pù arattersthe qualtatve e quattatve rferte ad ua determata utà statsta. Ad esempo, predamo u dvduo estratto da ua erta popolazoe e osderamoe l altezza, l olore
Statsta Bvarata Cosderamo ora l aso d ua o pù arattersthe qualtatve e quattatve rferte ad ua determata utà statsta. Ad esempo, predamo u dvduo estratto da ua erta popolazoe e osderamoe l altezza, l olore
Lezione 3. Funzione di trasferimento
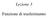 Lezoe 3 Fuzoe d trasfermeto Calcolo della rsposta d u sstema damco leare Per l calcolo della rsposta (uscta) d u sstema damco leare soggetto ad gress assegat, s possoo segure due strade Calcolo el domo
Lezoe 3 Fuzoe d trasfermeto Calcolo della rsposta d u sstema damco leare Per l calcolo della rsposta (uscta) d u sstema damco leare soggetto ad gress assegat, s possoo segure due strade Calcolo el domo
LEZIONI DI STATISTICA MEDICA
 LEZIONI DI STATISTICA MEDICA A.A. 00/0 - Idc d dspersoe Sezoe d Epdemologa & Statstca Medca Uverstà degl Stud d Veroa La dspersoe o varabltà è la secoda mportate caratterstca d ua dstrbuzoe d dat. Essa
LEZIONI DI STATISTICA MEDICA A.A. 00/0 - Idc d dspersoe Sezoe d Epdemologa & Statstca Medca Uverstà degl Stud d Veroa La dspersoe o varabltà è la secoda mportate caratterstca d ua dstrbuzoe d dat. Essa
6. LA CONCENTRAZIONE
 UNIVESITA DEGLI STUDI DI PEUGIA DIPATIMENTO DI FILOSOFIA SCIENZE SOCIALI UMANE E DELLA FOMAZIONE Corso d Laurea Sceze per l'ivestgazoe e la Scurezza 6. LA CONCENTAZIONE Prof. Maurzo Pertchett Statstca
UNIVESITA DEGLI STUDI DI PEUGIA DIPATIMENTO DI FILOSOFIA SCIENZE SOCIALI UMANE E DELLA FOMAZIONE Corso d Laurea Sceze per l'ivestgazoe e la Scurezza 6. LA CONCENTAZIONE Prof. Maurzo Pertchett Statstca
I SINDACATI E LA CONTRATTAZIONE COLLETTIVA. Il ruolo economico del sindacato in concorrenza imperfetta, in cui:
 I IDACATI E LA COTRATTAZIOE COLLETTIVA Il ruolo economco del sndacato n concorrenza mperfetta, n cu: a) le mprese fssano prezz de ben n contest d concorrenza monopolstca (con extra-proftt); b) lavorator
I IDACATI E LA COTRATTAZIOE COLLETTIVA Il ruolo economco del sndacato n concorrenza mperfetta, n cu: a) le mprese fssano prezz de ben n contest d concorrenza monopolstca (con extra-proftt); b) lavorator
COMUNE DI MIRANO PROVINCIA DI VENEZIA REGOLAMENTO
 COMUNE DI MIRANO PROVINCIA DI VENEZIA REGOLAMENTO PER LA COSTITUZIONE E LA RIPARTIZIONE DEL FONDO INTERNO DEL 2,00% DELL IMPORTO POSTO A BASE DI GARA DELLE OPERE E DEI LAVORI E DEL 30% DELLA TARIFFA PROFESSIONALE
COMUNE DI MIRANO PROVINCIA DI VENEZIA REGOLAMENTO PER LA COSTITUZIONE E LA RIPARTIZIONE DEL FONDO INTERNO DEL 2,00% DELL IMPORTO POSTO A BASE DI GARA DELLE OPERE E DEI LAVORI E DEL 30% DELLA TARIFFA PROFESSIONALE
Analisi Matematica Lezione 30, 4 dicembre 2014 e x2 dx =
 Dpartmeto d Sceze Statstche Aals Matematca Lezoe 3, 4 dcembre 14 π e x dx = prof. Daele Rtell daele.rtell@ubo.t 1/3? rodotto d Walls π = =1 rmo passo: ( 1 + 1 ) = lm (()!!) ( 1)!!( + 1)!! I = π s x dx
Dpartmeto d Sceze Statstche Aals Matematca Lezoe 3, 4 dcembre 14 π e x dx = prof. Daele Rtell daele.rtell@ubo.t 1/3? rodotto d Walls π = =1 rmo passo: ( 1 + 1 ) = lm (()!!) ( 1)!!( + 1)!! I = π s x dx
Numerazione binaria Pagina 2 di 9 easy matematica di Adolfo Scimone
 Numerazioe biaria Pagia di 9 easy matematica di Adolfo Scimoe SISTEMI DI NUMERAZIONE Sistemi di umerazioe a base fissa Facciamo ormalmete riferimeto a sistemi di umerazioe a base fissa, ad esempio el sistema
Numerazioe biaria Pagia di 9 easy matematica di Adolfo Scimoe SISTEMI DI NUMERAZIONE Sistemi di umerazioe a base fissa Facciamo ormalmete riferimeto a sistemi di umerazioe a base fissa, ad esempio el sistema
Propagazione di errori
 Propagazoe d error Gl error e dat possoo essere amplfcat durate calcol. Rspetto alla propagazoe degl error s può dstguere: comportameto del problema - codzoameto del problema: vedere come le perturbazo
Propagazoe d error Gl error e dat possoo essere amplfcat durate calcol. Rspetto alla propagazoe degl error s può dstguere: comportameto del problema - codzoameto del problema: vedere come le perturbazo
6. LA CONCENTRAZIONE
 UNIVERSITA DEGLI STUDI DI PERUGIA DIPARTIMENTO DI FILOSOFIA SCIENZE SOCIALI UMANE E DELLA FORMAZIONE Corso d Laurea Sceze per l'ivestgazoe e la Scurezza 6. LA CONCENTRAZIONE Prof. Maurzo Pertchett Statstca
UNIVERSITA DEGLI STUDI DI PERUGIA DIPARTIMENTO DI FILOSOFIA SCIENZE SOCIALI UMANE E DELLA FORMAZIONE Corso d Laurea Sceze per l'ivestgazoe e la Scurezza 6. LA CONCENTRAZIONE Prof. Maurzo Pertchett Statstca
Il termine regressione fu introdotto da Francis Galton ( ), antropologo (promotore dell eugenetica).
 Regressoe leare Il terme regressoe fu trodotto da Fracs Galto (8-9), atropologo (promotore dell eugeetca). I u suo famoso studo (877-885), Galto scoprì che, sebbee c fosse ua tedeza de getor alt ad avere
Regressoe leare Il terme regressoe fu trodotto da Fracs Galto (8-9), atropologo (promotore dell eugeetca). I u suo famoso studo (877-885), Galto scoprì che, sebbee c fosse ua tedeza de getor alt ad avere
L OFFERTA DI LAVORO 1
 L OFFERTA DI LAVORO 1 La famiglia come foritrice di risorse OFFERTA DI LAVORO Notazioe utile: T : dotazioe di tempo (ore totali) : ore dedicate al tempo libero l=t- : ore dedicate al lavoro : cosumo di
L OFFERTA DI LAVORO 1 La famiglia come foritrice di risorse OFFERTA DI LAVORO Notazioe utile: T : dotazioe di tempo (ore totali) : ore dedicate al tempo libero l=t- : ore dedicate al lavoro : cosumo di
Interesse e formule relative.
 Elisa Battistoi, Adrea Frozetti Collado Iteresse e formule relative Esercizio Determiare quale somma sarà dispoibile fra 7 ai ivestedo oggi 0000 ad u tasso auale semplice del 5% Soluzioe Il diagramma del
Elisa Battistoi, Adrea Frozetti Collado Iteresse e formule relative Esercizio Determiare quale somma sarà dispoibile fra 7 ai ivestedo oggi 0000 ad u tasso auale semplice del 5% Soluzioe Il diagramma del
Indagine Sperimentale di Calibrazione del Metodo Combinato SonReb
 dage Spermetale d Calrazoe del Metodo Comato Soe Maurzo Lez, Dalo ersar, oerta Zamr 3 Premessa Nell amto delle prove o dstruttve utlzzal per l otrollo opera del alestruzzo trova da tempo mpego l metodo
dage Spermetale d Calrazoe del Metodo Comato Soe Maurzo Lez, Dalo ersar, oerta Zamr 3 Premessa Nell amto delle prove o dstruttve utlzzal per l otrollo opera del alestruzzo trova da tempo mpego l metodo
Premessa... 1. Equazioni i differenziali lineari
 Apput d Cotroll Autoatc Captolo 3 parte I Sste dac lear Preessa... Equazo dfferezal lear... Evoluzoe lbera ed evoluzoe forzata... Uso della trasforazoe d Laplace... 3 Esepo... 7 Osservazo sulla rsposta
Apput d Cotroll Autoatc Captolo 3 parte I Sste dac lear Preessa... Equazo dfferezal lear... Evoluzoe lbera ed evoluzoe forzata... Uso della trasforazoe d Laplace... 3 Esepo... 7 Osservazo sulla rsposta
exp("# (al posto di n) var Ca Coefficiente di asimmetria, indipendente dal valore dei parametri. f X DISTRIBUZIONE EV1 o DI GUMBEL.
 DISTRIBUZIONE EV o DI GUMBEL. x x [ $ e ] exp[ e ] F x exp co: Sgfcato de parametr: f exp al posto d : Numero medo d evet dpedet [ 0,t], ad esempo u ao. / :Valore medo della gradezza dell eveto, esempo
DISTRIBUZIONE EV o DI GUMBEL. x x [ $ e ] exp[ e ] F x exp co: Sgfcato de parametr: f exp al posto d : Numero medo d evet dpedet [ 0,t], ad esempo u ao. / :Valore medo della gradezza dell eveto, esempo
La valutazione dei credit derivatives. ed una sua applicazione a dati di mercato.
 La valutazoe de credt dervatves ed ua sua applcazoe a dat d mercato. a cura d Alessadro Matta. La valutazoe d credt dervatves..... Ipotes d base.....2 Strumet sgle-ame....2.3 Strumet mult-ame....4.4 Idc
La valutazoe de credt dervatves ed ua sua applcazoe a dat d mercato. a cura d Alessadro Matta. La valutazoe d credt dervatves..... Ipotes d base.....2 Strumet sgle-ame....2.3 Strumet mult-ame....4.4 Idc
Successioni. Grafico di una successione
 Successioi Ua successioe di umeri reali è semplicemete ua sequeza di ifiiti umeri reali:, 2, 3,...,,... dove co idichiamo il termie geerale della successioe. Ad esempio, discutedo il sigificato fiaziario
Successioi Ua successioe di umeri reali è semplicemete ua sequeza di ifiiti umeri reali:, 2, 3,...,,... dove co idichiamo il termie geerale della successioe. Ad esempio, discutedo il sigificato fiaziario
Capitolo 5: Fattorizzazione di interi
 Captolo 5: Fattorzzazoe d ter Trovare fattor d u umero tero grade è ua mpresa assa ardua, e può essere mpossble co le rsorse ogg dspobl. No s cooscoo metod polomal per la fattorzzazoe, come vece accade
Captolo 5: Fattorzzazoe d ter Trovare fattor d u umero tero grade è ua mpresa assa ardua, e può essere mpossble co le rsorse ogg dspobl. No s cooscoo metod polomal per la fattorzzazoe, come vece accade
LA FUNZIONE DI VEROSIMIGLIANZA
 A FUNZIONE DI VEROSIMIGIANZA HA UN RUOO IMPORTANTE NEA PROCEDURE DI INFERENZA STATISTICA COME: ) METODO DI COSTRUZIONE DI STIMATORI (IN SITUAZIONI COMPESSE) ) METODO DI INDIVIDUAZIONE DI TEST UNIFORMEMENTE
A FUNZIONE DI VEROSIMIGIANZA HA UN RUOO IMPORTANTE NEA PROCEDURE DI INFERENZA STATISTICA COME: ) METODO DI COSTRUZIONE DI STIMATORI (IN SITUAZIONI COMPESSE) ) METODO DI INDIVIDUAZIONE DI TEST UNIFORMEMENTE
Generalmente sia l ampiezza che il valore medio della sollecitazione sono variabili nel tempo.
 È molto raro che u compoete meccaco sa sollectato a fatca da u carco cclco ad ampezza costate. Geeralmete sa l ampezza che l valore medo della sollectazoe soo varabl el tempo. max a a max m m m m Tempo
È molto raro che u compoete meccaco sa sollectato a fatca da u carco cclco ad ampezza costate. Geeralmete sa l ampezza che l valore medo della sollectazoe soo varabl el tempo. max a a max m m m m Tempo
CORSO DI LAUREA IN ECONOMIA AZIENDALE Metodi Statistici per le decisioni d impresa (Note didattiche) Bruno Chiandotto
 CORSO DI LAUREA I ECOOMIA AZIEDALE Metod Statstc per le decso d mpresa (ote ddattche) Bruo Chadotto 4 STATISTICA DESCRITTIVA I questo captolo s rtrovao espost, ua prospettva emprca, molt de cocett trodott
CORSO DI LAUREA I ECOOMIA AZIEDALE Metod Statstc per le decso d mpresa (ote ddattche) Bruo Chadotto 4 STATISTICA DESCRITTIVA I questo captolo s rtrovao espost, ua prospettva emprca, molt de cocett trodott
CONCETTI BASE DI STATISTICA
 CONCETTI BASE DI STATISTICA DEFINIZIONI Probabilità U umero reale compreso tra 0 e, associato a u eveto casuale. Esso può essere correlato co la frequeza relativa o col grado di credibilità co cui u eveto
CONCETTI BASE DI STATISTICA DEFINIZIONI Probabilità U umero reale compreso tra 0 e, associato a u eveto casuale. Esso può essere correlato co la frequeza relativa o col grado di credibilità co cui u eveto
