Lezioni di Teoria dei Sistemi. CdL in Ingegneria dell Ambiente e del Territorio (A.A. 2001/02. Bozze). Prof. Saverio Mascolo PARTE N. 1. y 1.
|
|
|
- Giuseppina Bartolini
- 5 anni fa
- Visualizzazioni
Transcript
1 Iroduzoe al Corso PARTE N. L obevo del corso d Teora de Ssem è quello d forre u seme d srume e meod maemac d caraere geerale e asrao per l aals del comporameo damco d ssem compless. Per ssema s ede u qualsas oggeo che eragsce co l ambee crcosae e/o co alr ssem. Il comporameo damco d u ssema è descro dall adameo emporale delle varabl che lo descrvoo. L ambee agsce sul ssema rame varabl che soo dee varabl d gresso del ssema. Nella Fgura è rappreseao u ssema su cu l ambee esero agsce rame le varabl d gresso u che soo rappreseae da frecce era el ssema. Le varabl che descrvoo l comporameo del ssema soo rappreseae rame le frecce usce y e soo dee varabl d usca. u u u 3 Ssema y y Fg. La descrzoe d u ssema erm d gress ed usce è dea descrzoe gresso usca. La descrzoe maemaca del comporameo d u ssema è dea modello maemaco del ssema. Tpcamee l modello maemaco d u ssema cosse ua equazoe dfferezale che sablsce ua relazoe ra le varabl d gresso e le varabl d usca d u ssema. Il legame maemaco cosee d deermare le usce a parre dagl gress e qud d sudare la damca o l comporameo d u ssema u cero ambee. I ssem a sgolo gresso e sgola usca soo de ssem SISO (sgle-pu sgle-oupu. I ssem a pù gress e a pù usce soo de MIMO (mul-pu mul-oupu. La meodologa maemaca cosee d affroare modo asrao e ufcao lo sudo d ssem d aura dfferee ma accomua dalle sesse propreà maemache. U esempo oo dallo sudo della Fsca è quello de ssem meccac ed elerc. Tal ssem soo descr da equazo dfferezal dello sesso po per cu s parla d ssem aalogh. Esempo: Modello maemaco d u ssema meccaco
2 S cosder l ssema meccaco Fg.. Il ssema è composo da ua massa M che schemazza le propreà d'erza del ssema, ua molla d cosae elasca k che schemazza l'elascà dell acoraggo e uo smorzaore d cosae b che schemazza l movmeo della massa u mezzo vscoso (Fg. ) b M F k x Fg. L ambee agsce sul ssema rame la forza applcaa F(. L usca del ssema è la poszoe x( della massa M. Per rovare ua descrzoe della damca del ssema, coè l suo modello maemaco, vochamo la legge fodameale della damca d Newo. I parcolare la somma delle forze applcae sulla massa M deve essere uguale alla massa per l accelerazoe. Dsgregado l ssema s evdezao le forze applcae su M F k kx F b b x& F k kx F b b x& F k kx F b b x& M F( Proeado l'equazoe d equlbro d Newo lugo la drezoe x: F + F b + F k F - kx - b x& mx& & () s oee u equazoe dfferezale leare a coeffce cosa che rappresea l modello maemaco del ssema. S parla d modello perché è ua rappreseazoe della realà che coee evablmee delle approssmazo. Ad esempo la legge d Hooke Fkx descrva della molla è u approssmazoe leare d ua relazoe o leare. Ad esempo u modello d valdà pù geerale porebbe essere del po Fkx+k x 3. I al caso l modello rappresea ua molla che s'dursce sempre d pù co l'allugameo. L equazoe dfferezale () rappresea u modello damco perchè la relazoe ra le varabl d gresso e d usca dpede ache dalle dervae delle sesse. Quado ale relazoe o dpede dalle dervae l legame è deo saco. Poché è oo che la soluzoe d u equazoe dfferezale dpede dall gresso ma ache dalle codzo zal s dce ache che l comporameo d u ssema damco dpede dal passao, oppure che u ssema damco ha memora.
3 Esempo: Modello maemaco d u ssema elerco R v( L C Ache ale caso come el caso precedee s comca dalle descrzo maemache gressousca delle par che compogoo l ssema. Il ressore è descro dalla relazoe saca v( R ( Il codesaore è descro dalla relazoe damca che può essere egraa el seguee modo: L duore è descro dalla relazoe damca dv ( C q( v( ( ) d C τ τ C d v( L Cosderado che gl eleme soo collega sere, coè soo araversa dalla sessa corree, e cosderado legge d Krckhoff delle eso s oee la seguee equazoe egro-dfferezale v( R( + L d + (τ) dτ C dq Pochè la corree è l flusso d carca ell'uà d empo, coè rsula (, s può scrvere: dq d q q( v( R + L + C che è u equazoe dfferezale leare del secod orde. S osserv che sa l ssema elerco sa l ssema meccaco cosdera soo descr da ua sessa equazoe dfferezale del po f ( a& y ( + ay& ( + a y( 3
4 I alre parole ssem soo aalogh. Perao s può dre che l equazoe dfferezale coee u sgfcao che va olre quello parcolare. S raa coè d u oggeo asrao le cu propreà soo comu a ssem d dversa aura. Dal puo d vsa praco cò sgfca che la coosceza delle propreà d u ssema mplca la coosceza delle propreà dell alro ssema e vceversa. Le relazo d aaloga ra le varabl e paramer del ssema meccaco del II orde e del ssema elerco del II orde soo: F v m L b R k / C Cosderamo u crcuo RC sere, coè l precedee co L, e calcolamo la soluzoe aalca. L equazoe dfferezale che descrve l ssema è: q dq q v( R + R + C C q L omogeea Rq& + ha come soluzoe q( q() e -/RC e rappresea l processo d scarca d C u codesaore. Come s può oare la soluzoe è coua el empo (l empo qud apparee all'seme de umer real). Poedo τrc rsula qq e -/τ e qud τ è defa cosae d empo del processo. Ifa esprmedo l empo mulpl d τ s oee: per 3τ: q(q e -3 5% q per 4τ: q(q e -4 % q Rporado su u dagramma q( fuzoe del empo q( q RC 4
5 U equazoe dfferezale esprme ua relazoe ra le varabl d gresso e d usca e ra le dervae delle sesse varabl. Cosderaa ua relazoe maemaca ra varabl, s può decdere arbraramee quale varable sa l'gresso (la causa) e quale sa l'usca (l'effeo). Tale operazoe s chama oreazoe. f( causa S y( effeo Dal puo d vsa operavo u ssema è oreao modo che la coseguee relazoe d causa ed effeo abba u sgfcao fsco-gegersco. Ad es. el caso del ssema meccaco può aver seso assumere la forza come varable d gresso e la poszoe come varable d usca. Esempo: Modello maemaco d u ssema draulco q h Il serbaoo fgura è caraerzzao dalla poraa d gresso q e dall alezza del baee drco h. Assumedo u serbaoo d sezoe cosae A, l volume d lqudo rsula: VAh. Per la legge d coservazoe della massa s ha che dv dah dh q A Ache qu emerge ua legge che è aaloga a quella che regola l flusso d corree u dv codesaore ( C ). Per l ssema draulco s rscorao qud le segue aaloge: q A C h v I ssem empocou lear e empo-vara soo descr dall'equazoe dfferezale: a d ( ) y Ne ssem empodscre l empo apparee all seme de umer aural. Tal ssem soo descr da equazo alle dffereze. I ssem empodscre lear empo-vara soo descr dall'equazoe alle dffereze: 5 m ( ) b d ( ) u ( )
6 y(k)a y(k-) + a y(k-) a y(k-) + b u(k) + b u(k-) + b u(k-) b m u(k-m) S raa evdeemee d u modello damco perché dpede da valor passa d y (l usca) e da valor passa d u (l gresso). Esemp d modell empo-dscre soo quell che descrvoo ssem ecoomc, perché le varabl soo rlevae a scadeza dscrea. Per esempo da d u coo ecoomco possoo essere raccol co cadeza rmesral o auale. Esempo: modello maemaco del PIL L ecooma d uo sao può essere descra dalle segue varabl: Y(k)PIL (prodoo ero lordo) C(k)oale d merc e servz cosuma G(k)spesa pubblca I(k)vesme Fra al gradezze possoo essere sable delle relazo. Ua relazoe d "collegameo" è daa dall'equazoe d blaco Y(k)C(k)+G(k)+I(k) Ua relazoe fora dagl ecooms che collega l PIL al comporameo de cosumaor è la seguee C(k)mY(k) (<m<) dove m è la propesoe al cosumo (equazoe saca) Ife gl ecooms hao sablo ua relazoe ra la cresca del PIL e gl vesme: Y(k+)-Y(k)rI(k) che è u equazoe damca. Esempo: Ssema ecologco Il pù classco esempo è l modello ecologco proposo da Vo Volerra, deo ache modello preda-predaore. Deo N l umero d prede ed N l umero de predaor, l evoluzoe è descra dalle segue equazo dfferezal o lear: 6
7 co a,b,c,d>. S osserva che: dn a N ( - b N (N ( dn -c N ( + d N (N ( ) se l umero zale d predaor è ullo N (), la popolazoe d prede aumea all fo. Ifa la soluzoe della prma equazoe dvea N N () e a ovvero s ha ua cresca espoezale; ) se l umero d prede zal è ullo N (), predaor soo desa all eszoe. Ifa la soluzoe della secoda equazoe dvea N (N () e -c ovvero s ha u decadmeo espoezale; 3) la coemporaea preseza d prede e predaor roduce erm o lear rappresea dal prodoo de umer delle due spece. Il prodoo N N rappresea la possblà dell'coro ra preda e predaore. Tale coro per la preda s rsolve ua dmuzoe d umero (sego egavo al coeffcee b) mere per la popolazoe de predaor u aumeo d umero (sego posvo al coeffcee d). U ssema può essere descro co ua relazoe ra gresso e usca rame ua black box (scaola era) che rappresea l comporameo gresso/usca del ssema sesso. u( S y( Ssem lear, olear, empo-vara, empo-vara I geerale la relazoe che lega gresso ed usca o è leare, è coè ua fuzoe del po du d u dy d y f(u,,,...,y(,,,...) S è olre vso che se l ssema è couo, leare e empovarae (o pù brevemee LTI) allora la forma geerale d ale relazoe è: a d ( ) y m ( ) I realà u modell aural soo o lear e empovara; uava è spesso possble effeuare ua learzzazoe el caso d ssem o lear oppure, se ssem soo empovara, è possble approssmarl come ssem empovara se la gradezza empovarae vara leamee ell ervallo d empo d'eresse. 7 b d ( ) u ( ) ()
8 Propreà de ssem LTI Sovrapposzoe degl effe Da due gress u ( ed u ( che geerao rspevamee le usce y ( e y ( allora l'gresso u(u (+u ( produce l'usca y(y (+y (. u ( y ( u ( y ( Iffa le coppe gresso-usca (u (,y () soddsfao le relazo d y ( ) m a ( ) b d ( ) ( ) u d y ( ) m a ( ) b d ( ) ( ) u Sommado membro a membro le due espresso precede: d ( y + y ( ) m a ( ) ) b d ( ) ( u + u ( ) ) coè ache la coppa ((u +u ),(y +y )) è soluzoe della relazoe gresso-usca. Allo sesso modo s può dmosrare che se gl gress u e u soo molplca rspevamee per due coeffce α e α ache le rspeve usce y e y sarao molplcae per gl sess coeffce. S defsce operaore fuzoale u operaore che rasforma la fuzoe gresso u( ella fuzoe d'usca y( e s dca co T(u()y(. S dce ache che ssem LTI soo operaor fuzoal lear. Ifa per ess s può scrvere T(α u +α u ) α T(u )+ α T(u ) Tempovaraza Rardare ua fuzoe u( d τ sgfca cosderare la fuzoe u(-τ). Prededo come esempo u'oda ragolare rsula u( u(-τ) τ Se u ssema empovarae rspode all gresso u( co l usca y( allora esso rspoderà all gresso rardao u(-τ) co l usca rardaa y(-τ). La dmosrazoe è mmedaa e aaloga al caso precedee. 8
9 Se vece l ssema è LTV (leare-empovarae) ale propreà o è pù valda. S cosder ad esempo l caso cu coeffce a e b ella () o soo pù cosa. I al casso rardado d τ l'gresso u( l'usca o sarà pù y(-τ) perché l valore de coeffce è cambao. Esempo Cosderao u crcuo cosuo da u geeraore d esoe susodale e( s (, dove ( è la fuzoe grado uaro cosderaa l usca ( rsula: ( ), chuso su ua resseza d valore cosae R, e < e( s ( ( R R Cosderado l gresso rardao d τ, coè la esoe e(-τ)s(-τ) (-τ) la rsposa sarà ach essa rardaa e varrà: s( τ)( τ) ( τ) R Cosderamo ora u ressore empovarae, varable secodo la legge R( R per < R per Applcado l'gresso e( s (, l'usca sarà come raffgurao ella fgura seguee. ( co R <R s ( ( per < e R s ( ( per R R cosae RR( 9
10 Per ssem o lear o vale l prcpo d sovrapposzoe degl effe. Ess soo descr da equazo dfferezal o lear l cu sudo è solamee oevolmee pù complesso rspeo al caso leare. Nel caso d ssem o lear la dzoe empovarae è sosua dal erme auoomo mere la dzoe "empovarae" è sosua dal erme "o auoomo". U meodo semplce, ache se d valdà lmaa, per lo sudo de ssem o lear è l meodo della learzzazoe oro al puo d equlbro. Co ale meodo s rova l ssema leare che approssma quello o leare per pccole varazo delle varabl. U esempo proposo può essere la relazoe ra lo sforzo ormale e l allugameo d u maerale elasco. La forza elasca ha geerale u adameo del po fgura. F k x x' Tuava ell ervallo dell orge la relazoe può essere approssmaa rame ua legge leare che è qud ua valda se la zoa d fuzoameo della molla è era a queso ervallo. De ssem LTI esse la soluzoe aalca esplca mere per ssem LTV o o lear la soluzoe s può rovare spesso solo per va umerca. I ssem o lear o godoo della propreà d sovrapposzoe degl effe, u esempo è l'operazoe d elevare al quadrao. Cosdera due gress u e u rsula fa: u + u ( u + u ) Rsoluzoe umerca d equzo dfferezal e Smulazoe Spesso s rcorre all'ulzzo d u calcolaore per effeuare delle smulazo. I al cas l calcolaore rsolve umercamee l equazoe dfferezale che modella l ssema e dsega la soluzoe. La meodologa usaa è la seguee. Cosderaa l equazoe dfferezale o leare y & y + 3y s cosdera u pccolo passo d egrazoe e s esplca la dervaa ella forma y( y() -y() / +3y()
11 da cu s oee y( (-y() / +3y() ) + y() I queso modo s è calcolao l valore della soluzoe al passo dopo l sae ; erado l procedmeo lugo l ervallo d'eresse s oee la soluzoe. L esempo cosderao è u ssema o leare auoomo. Se al poso del coeffcee 3 c fosse u coeffcee a( fuzoe del empo sarebbe u esempo d ssema o auoomo.
12 SEGNALI CANONICI I segal caoc soo forme d oda elemear (de ache "segal d prova") dalla cu combazoe leare s possoo geerare segal pù compless. Impulso d Drac S cosder u ragolo d area uara d base τ ed alezza /τ come fgura. Facedo edere la base τ a zero maeedo l area cosae, la forma d oda ede ad assumere u alezza fa e ua base fesma. Tale segale rappresea ua fuzoe d gresso d duraa breve e valore elevao. S defsce mpulso d Drac e s dca co δ( la fuzoe che s oee facedo edere τ a zero. δ( lm h(, τ) τ h(, τ) δ( /τ τ Grafc d: (a) h (, τ) ; (b) δ ( Vale la propreà d selezoe dell'mpulso per cu I parcolare β δ α f ( τ ) se τ ( α, β) ( τ ) f ( se τ ( α, β) + δ ( f ( f () La fuzoe Grado Uaro < S dca co ( e vale ( ). S oee egrado l mpulso d Drac: ( δ ( z) dz (
13 La fuzoe Rampa Uara S oee egrado l grado e s dca co r( ( ( z) dz r( La fuzoe Rampa Parabolca S oee egrado la rampa uara e s dca co p( p( ( r( z) dz Alre fuzo caoche soo segal seo e coseo. 3
14 LA TRASFORMATA DI LAPLACE Abbamo vso che mol ssem apparegoo alla classe de ssem lear empo-vraa. Tal ssem soo descr maemacamee da u equazoe dfferezale leare a coeffce cosa. La rasformaa d Laplace è uo srumeo maemaco molo effcace per la soluzoe e per lo sudo delle propreà delle soluzo d ua equazoe dfferezale leare a coeffcce cosa. La rasformaa d Laplace cosee d rasformare u equazoe dfferezale u equazoe algebrca, la cu soluzoe o è pù ua fuzoe del empo ma è u semplce umero complesso. Ce replogav su umer compless U umero complesso s può essere rappreseao ella forma caresaa sa+jb oppure ella forma polare s Me jϕ o polare. La fgura mosra ua rappreseazoe d u umero complesso el pao d Gauss e le relazo ra l modulo e la fase e le compoe caresae. S rcorda ache la uguaglaza d Eulero e jϕ cosϕ+jsϕ. M a + b ϕ bmsϕ amcosϕ La rasformaa d Lapalce è ua rasformazoe fuzoale che assoca ad ua fuzoe d varable reale f( ua fuzoe d varable complessa F(s). I parcolare la rasformaa d Lapalce è defa come: L( f ( ) F( s) f ( e s L operazoe d rasformazoe è buvoca, coè è sempre possble passare da f( a F(s) e vceversa. L operazoe versa è dea arasformaa, ed è dcaa co L ( F( s)) f (. Come s può oare, la fuzoe f( è prma molplcaa per u espoezale e po egraa. Iuvamee queso può rovare spegazoe el fao che l egrale d f( su u ervallo fo porebbe o covergere. Ifa, l'egrale ra e del grado uaro o coverge, mere l'egrale d (e -s coverge per valor d s al che Re{s}>. I valor d s per cu esse la 4
15 rasformaa cosuscoo l domo d defzoe della rasformaa. Tale domo è u sempao delmao da ua rea vercale. L'ersezoe della rea co l'asse reale è dea ascssa d covergeza ed dcaa co σ c. I coclusoe, cosderao l pao complesso, la rea parallela all asse delle ordae d equazoe s σ c dvde l pao due sempa: l sempao a desra dell ascssa d covergeza è deo pao d covergeza poché esso esse la rasformaa d Laplace. Propreà della rasformaa d Laplace Teorema della dervaa Cosderaa ua fuzoe f(, la rasformaa della sua dervaa rsula df L sf( s) f () Applcado l eorema della dervaa alla fuzoe dervaa s oee d f L s[ sf ( s) f ()] f '() s F( s) sf () f '() e geeralzzado d f L s F( s) s f () s f '()... f () Assumedo codzo zal ulle, coè f()f '() f (-) () rsula d f L s I alre parole s usa dre che l operazoe d dervazoe el domo del empo corrspode a molplcare per s el domo complesso. F (s) Propreà d learà e sovrapposzoe della rasformaa d Laplace Cosderae due geerche fuzo f ( ed f ( vale la seguee propreà d learà L[a f (+a f (] a L[f (] + a L[f (] La dmosrazoe segue dreamee dalla defzoe d rasformaa d Laplace (l operazoe d egrazoe e leare). Per gl approfodme s rmada a es specfc sulla Trasformaa d Laplace 5
16 Teorema dell'egrale Cosderaa ua geerca fuzoe f(, la rasformaa della fuzoe egrale L[ϕ(] F ( s) s La dmosrazoe segue dreamee dal eorema della dervaa. ϕ ( f ( τ) dτ vale DEFINIZIONE DI FUNZIONE DI TRASFERIMENTO Assumedo codzo zal ulle e rasformado secodo Laplace l'equazoe dfferezale leare a coeffce cosa rsula, vrù della propreà d learà, e per l eorema della dervaa d y a L m d u b L m a s Y ( s) b s U ( s) S defsce fuzoe d rasfermeo (f.d..) e s dca solamee co G(s) l rapporo b s Y( s) G( s) () U( s) m a s La f.d.. è l rapporo ra la rasformaa dell'usca Y e la rasformaa dell'gresso U. La f.d.. è defa assumedo codzo zal ulle coè assumedo u ssema zalmee codzoe d quee. La f.d.. G(s) è u rapporo ra polom, coè è ua fuzoe razoale. Trasformae d segal caoc I segal caoc possoo essere L-rasforma. Calcolamo la rasformaa dell'mpulso: L[ δ ( ] + s s s s δ ( e δ ( e + δ ( e e + Ifa l'egrale ra + e è ullo essedo ulla ale ervallo la fuzoe egrada. I queso caso, come u cas d fuzo mpulsve, occorre specfcare l esremo ferore d egrazoe. Ifa ale caso l'egrale forsce u rsulao dverso se calcolao a parre da - o da +. S parla rspevamee d rasformaa L - o L +. Se la fuzoe rasformada o è mpulsva allora L - L + coè o occorre dsguere - da +. Il smbolo sgfca per defzoe uguale a 6
17 Cosderamo la fuzoe grado e provamo prma a calcolare la rasformaa base alla defzoe e po usado l eorema dell'egrale. ( j ) L[( ] ( e e σ + ω s s s co sσ+jω L'egrale precedee coverge per σ>. Ifa: e -s e -(σ+jω) e -σ e -jω e -σ e -σ pochè e -jω. Perao l'ascssa d covergeza del grado è σ c e qud l sempao d covergeza è cosuo dagl s per cu Re{s}>σ c. Osservado che l grado è l egrale dell mpulso, possamo ulzzare l eorema dell'egrale: L[( ] L ( ) d δ τ τ s Aalogamee s possoo oeere le rasformae della rampa uara /s e della rampa parabolca /s 3. Essoo po alr rsula che vale la pea rcordare perché ul per esegure semplcemee operazo d rasformazoe e arasformazoe. ) L[f(e k ] F(s-k) Ifa k s ( s k) f ( e e f ( e F ( s k U caso parcolare del precedee è L[e k (] s k Acora, se kjω, allora L[e jω ] co j uà mmagara s jω Possamo qud rovare la rasformaa del coseo come jω ω + j e e s + jω + s jω s L[cosω] L + ω ω ω s j s + j s + s + ω e aalogamee quella del seo jω ω j e e s + jω s + jω ω L[sω] L ω ω ω j j s j s + j j s + s + ω ) L[f(-τ)] F(s) e -τs ) Ifa poedo (-τ)z e qud dz l'egrale s f ( τ ) e dvea f s( z + τ ) sτ ( z ) e dz e F ( s U esempo è L[(-τ)] e s τs ) 7
18 3) L[ e p! ] + ( s p) o equvaleemee L p e +! ( s + p) S osserv che erm e p, e p edoo a zero per che ede all'fo se Re{p}<. Nel caso cu p è a pare reale (sreamee) egava s dce polo (asocamee) sable. Nel caso cu p è a pare reale posva s dce polo sable. U segale complesso può essere espresso come combazoe leare d segal caoc. Cosegueemee la rsposa ad u segale complesso può essere oeua come somma d rspose caoche. Esempo Esprmere le fuzo f e f fgura come combazo lear d segal caoc.,5 f f,5, f ( ( - (-) + (-3) (-4); f ( ( - (-) (-) + (-4) (-4); F (s) /s - /s e -s + /s e -3s /s e -4s F (s) /s - /s e -s + /s e -4s Prodoo d covoluzoe Cosderae due geerche fuzo f( e g(, s defsce l prodoo d covoluzoe come segue: g f f ( τ ) g( τ) dτ co g(f( per < affché la rasformazoe d Laplace sa buvoca. Per τ> rsula g( e qud possamo scrvere che f ( τ ) g( τ) dτ + f ( τ) g( τ) dτ f ( τ) g( τ) dτ gacché è ullo l secodo egrale a prmo membro. S dmosra che la rasformaa del prodoo d covoluzoe è uguale al prodoo delle rasformae. L[g*f] F(s)G(s) L[f(]L[g(] 8
19 Fuzoe d rasfermeo come rasformaa della rsposa mpulsva S cosder u ssema LTI geerco descro dalla fuzoe d rasfermeo G(s). S cerch la rsposa y( al segale d gresso u( δ(. L[u(] L[δ(] U(s); L[y(] Y(s) G(s)U(s) G(s) Qud la fuzoe d rasfermeo G(s) è la L-rasformaa della rsposa del ssema all mpulso d Drac. La rsposa mpulsva è qud l'arasformaa d G(s), coè g(l - [G(s)]. Esempo Cosderamo ora u crcuo RC sere cu l gresso u(e( e l'usca y(v c (. R E(s) V c (s) S C e( v c ( S o che la scela della varable d'gresso e della varable d'usca è l rsulao d u'operazoe d oreazoe d u ssema, quao mplca la scela d ua varable "causa" ed ua varable "effeo". Lo schema a blocch raffgurao evdeza l'gresso/causa e l'usca/effeo. Cosderado gl eleme crcual come ssem sgol, ess soo descr dalla fuzoe d rasfermeo I( s) ressore : v(r ( V(s) R I(s) G(s) relazoe saca V ( s) R dv codesaore : (C c I(s)sC V(s) G(s) sc relazoe damca S defsce mpropro l ssema cu l grado del deomaore della G(s) è more del grado del umeraore; al ssem soo fscamee rrealzzabl. Ifa u codesaore reale avrà ua sua resseza. S defsce propro l ssema per l quale l grado del deomaore della G(s) è maggore o uguale al grado del umeraore (sreamee propro se l grado del deomaore è maggore del grado del umeraore). I ssem real soo sreamee propr o u'al pù propr. Se s modellao gl effe duv seredo u duore, l modello dvea ua rappreseazoe pù fedele della realà. I parcolare s oee l seguee modello 9
20 R e( C v c ( d q e ( R + L + C L de d d R + L + C da cu s rcava la f ra esoe applcaa e corree I( s) sc G( s) E( s) + src + s LC e la f ra esoe applcaa e esoe sul codesaore Vc ( s) G ( s) E( s) + src + s LC
Regime di capitalizzazione composta
 Regme d capalzzazoe composa Se s deposa baca, all zo dell ao, ua somma d 000 ad u asso auale uaro =0,05 oppure r=5%, dopo ao ale somma frua u eresse par a I = = 000 0,05 = 50 che aggugedos al capale zale
Regme d capalzzazoe composa Se s deposa baca, all zo dell ao, ua somma d 000 ad u asso auale uaro =0,05 oppure r=5%, dopo ao ale somma frua u eresse par a I = = 000 0,05 = 50 che aggugedos al capale zale
Interesse e Sconto. Università degli Studi di Catania Facoltà di Economia D.E.M.Q.
 Ieresse e Scoo Uversà degl Sud d Caaa Facolà d Ecooma D.E.M.Q. Ieresse x Ieresse y (x y) empo Capalzzazoe: Capale Impego Moae M I Ieresse : I M - C; M C + I; F + ; I C (F ) C C (usualmee M > 0 I >-C, I
Ieresse e Scoo Uversà degl Sud d Caaa Facolà d Ecooma D.E.M.Q. Ieresse x Ieresse y (x y) empo Capalzzazoe: Capale Impego Moae M I Ieresse : I M - C; M C + I; F + ; I C (F ) C C (usualmee M > 0 I >-C, I
coefficienti costanti fornisce una descrizione sufficientemente generale del comportamento dello strumento.
 Corso d Laboraoro d Msure Meccache e Termche Docee: Prof. Ig. R. Moa AA A.A. A 6/7 Lezoe Aals delle presazo damche degl srume e de ssem d msura: la araura damca. CONSIDERAZIONI GENERALI U ssema d msura
Corso d Laboraoro d Msure Meccache e Termche Docee: Prof. Ig. R. Moa AA A.A. A 6/7 Lezoe Aals delle presazo damche degl srume e de ssem d msura: la araura damca. CONSIDERAZIONI GENERALI U ssema d msura
Capitolo 3 Vibrazioni libere di sistemi a più gradi di libertà
 Capolo 3 Vbrazo lbere d ssem a pù grad d lberà I queso capolo: deermamo le equazo del moo de ssem a pù grad d lberà; s descrvoo meod algebrc per dsaccoppare le equazo del moo; roducamo l coceo d rasformazoe
Capolo 3 Vbrazo lbere d ssem a pù grad d lberà I queso capolo: deermamo le equazo del moo de ssem a pù grad d lberà; s descrvoo meod algebrc per dsaccoppare le equazo del moo; roducamo l coceo d rasformazoe
Variazione approssimata del valore attuale
 arazoe approssmaa del valore auale Fabo Bell 0 Abbamo vso le prcpal propreà della durao e dvers mod d calcolarla var esemp, ra cu ol a cedola fssa. Roramo alla relazoe che lega la durao alla sesvà del
arazoe approssmaa del valore auale Fabo Bell 0 Abbamo vso le prcpal propreà della durao e dvers mod d calcolarla var esemp, ra cu ol a cedola fssa. Roramo alla relazoe che lega la durao alla sesvà del
Fatica con sollecitazioni ad ampiezza variabile
 Comporameo meccaco de maerla Faca co sollecazo ad ampezza varable Faca de maeral Faca co sollecazo ad ampezza varable Iroduzoe, cumulav d sollecazoe Daeggameo: regola d Palmgre Mer Meodo d coeggo: meodo
Comporameo meccaco de maerla Faca co sollecazo ad ampezza varable Faca de maeral Faca co sollecazo ad ampezza varable Iroduzoe, cumulav d sollecazoe Daeggameo: regola d Palmgre Mer Meodo d coeggo: meodo
2. FUNZIONE D ONDA, OSSERVABILI QUANTISTICHE ED EQUAZIONE DI SCHROEDINGER Ovvero: Gli strumenti della Meccanica Quantistica
 . FUNZIONE D ONDA OSSERVABILI QUANTISTICHE ED EQUAZIONE DI SCHROEDINGER Ovvero: Gl srume della Meccaca Quasca Ssema d eresse cosderao come solao: aomo/molecola Cofgurazoe del ssema: seme de veor poszoe
. FUNZIONE D ONDA OSSERVABILI QUANTISTICHE ED EQUAZIONE DI SCHROEDINGER Ovvero: Gl srume della Meccaca Quasca Ssema d eresse cosderao come solao: aomo/molecola Cofgurazoe del ssema: seme de veor poszoe
Circuiti dinamici. Equazioni di stato. (versione del )
 rcu amc Equazo sao www.e.g.ubo./pers/masr/aca.hm ersoe el 9-- elazo ra sao gress e rspose poes: crcuo amco leare o egeere o sao può essere rappreseao meae le eso u coesaor e le corre u gl uor o sao all
rcu amc Equazo sao www.e.g.ubo./pers/masr/aca.hm ersoe el 9-- elazo ra sao gress e rspose poes: crcuo amco leare o egeere o sao può essere rappreseao meae le eso u coesaor e le corre u gl uor o sao all
CONTROLLI AUTOMATICI
 CONTROLLI AUTOMATICI A.A. 2/2 Iroduzoe al Corso Due problem d oevole eresse gegersco soo quell dell aals d u geerco ssema reale, aurale o arfcale, per acqusre formazo sul suo comporameo, e della ses d
CONTROLLI AUTOMATICI A.A. 2/2 Iroduzoe al Corso Due problem d oevole eresse gegersco soo quell dell aals d u geerco ssema reale, aurale o arfcale, per acqusre formazo sul suo comporameo, e della ses d
Matematica elementare art.1 di Raimondo Valeri
 Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Approfondimenti Lezione 3. Mara Bruzzi
 Approfodmet Lezoe 3 Mara Bruzz APPROFONDIMENTO 1 : I BOSONI Partcelle come le a, foto, meso hao vece fuzo d oda smmetrche y S. Esse o obbedscoo al prcpo d esclusoe d Paul. Tal partcelle soo dette BOSONI.
Approfodmet Lezoe 3 Mara Bruzz APPROFONDIMENTO 1 : I BOSONI Partcelle come le a, foto, meso hao vece fuzo d oda smmetrche y S. Esse o obbedscoo al prcpo d esclusoe d Paul. Tal partcelle soo dette BOSONI.
INDICE GENERALE. Home
 NDE GENEE Home Uà d msura apolo. l ampo elerco. l campo mageco. Eerga e poeza.4 Equazo d Maxwell apolo. rcu a paramer cocera. rcu lear empo-vara. Bpol lear empo-vara e relazo cosuve.4 prcp d Krchhoff.5
NDE GENEE Home Uà d msura apolo. l ampo elerco. l campo mageco. Eerga e poeza.4 Equazo d Maxwell apolo. rcu a paramer cocera. rcu lear empo-vara. Bpol lear empo-vara e relazo cosuve.4 prcp d Krchhoff.5
Istogrammi e confronto con la distribuzione normale
 Istogramm e cofroto co la dstrbuzoe ormale Suppoamo d effettuare per volte la msurazoe della stessa gradezza elle stesse codzo (es. la massa d u oggetto, la tesoe d ua pla, la lughezza d u oggetto, ecc.):
Istogramm e cofroto co la dstrbuzoe ormale Suppoamo d effettuare per volte la msurazoe della stessa gradezza elle stesse codzo (es. la massa d u oggetto, la tesoe d ua pla, la lughezza d u oggetto, ecc.):
APPRENDIMENTO SUPERVISIONATO. Reti multistrato. Il Perceptron (Rosenblatt 58) w 1. Fase di Addestramento. Classificazione. Fase di evoluzione
 APPRENIMENTO SUPERVISIONATO Re mulsrao Appredmeo co supervsoe La ree mpara ad assocare u seme d coppe (, d ) desderae. La ree opera due fas dse: Fase d addresrameo s memorzzao le formazo desderae Fase
APPRENIMENTO SUPERVISIONATO Re mulsrao Appredmeo co supervsoe La ree mpara ad assocare u seme d coppe (, d ) desderae. La ree opera due fas dse: Fase d addresrameo s memorzzao le formazo desderae Fase
Modellistica delle linee di trasmissione
 eleroea- appu gras gegera - www.rardogalle.om/appu_gras/ Corso d Laurea Spealsa Igegera delle Teleomuazo Modulo d Eleroea - A.A. 5-6 Modellsa delle lee d rasmssoe PARTE II Aals qualaa e quaaa d re d eleme
eleroea- appu gras gegera - www.rardogalle.om/appu_gras/ Corso d Laurea Spealsa Igegera delle Teleomuazo Modulo d Eleroea - A.A. 5-6 Modellsa delle lee d rasmssoe PARTE II Aals qualaa e quaaa d re d eleme
{ } t. w si intende. , ciascuna delle quali dipende da. Una sequenza di distribuzioni di probabilità ( f ( w,, w ; θ)
 8-Ecoomera, a.a. -3 Capolo 8 8- Il meodo della Massma Verosmglaza 8- Proprea` asoche degl smaor ML 8-3 Tes sulle poes: Il es d Wald, l es LM, l es LR e l es boosrap 8-4 Esemp 8-5 Appedce: La sasca LM e
8-Ecoomera, a.a. -3 Capolo 8 8- Il meodo della Massma Verosmglaza 8- Proprea` asoche degl smaor ML 8-3 Tes sulle poes: Il es d Wald, l es LM, l es LR e l es boosrap 8-4 Esemp 8-5 Appedce: La sasca LM e
y = α + βx + ε Qui ci soffermeremo su un unica classe di modelli, detti modelli statistici lineari. Si veda la seguente figura:
 Il problema della regressoe s poe quado l valore d ua varable aleatora y, chamata varable dpedete, è fuzoe d ua varable o aleatora x, chamata varable dpedete Qu c soffermeremo su u uca classe d modell,
Il problema della regressoe s poe quado l valore d ua varable aleatora y, chamata varable dpedete, è fuzoe d ua varable o aleatora x, chamata varable dpedete Qu c soffermeremo su u uca classe d modell,
Esercizi 12/10/2007. oppure B 0. In modo del tutto analogo AB 0 se e solo se. oppure B 0 B 0. Studio del segno di una disequazione polinomiale.
 Esercz 2/0/2007 Dsequazo Sego d u prodotto. Voglamo studare l sego d u prodotto d due umer real. I altr term vedere qual soo le codzo affché due umer real A e B soddsfo AB 0. Ragoamo come segue: rcoducamo
Esercz 2/0/2007 Dsequazo Sego d u prodotto. Voglamo studare l sego d u prodotto d due umer real. I altr term vedere qual soo le codzo affché due umer real A e B soddsfo AB 0. Ragoamo come segue: rcoducamo
Descrizione quantomeccanica di un insieme di spin: LA MATRICE DENSITÀ
 Desrzoe quatomeaa d u seme d sp: LA MATRICE DENITÀ Il valore d aspettazoe d ua gradezza fsa rappresetata dall operatore O su u sstema ello stato Ψ è: O Ψ OΨdτ Ψ O Ψ e s a u umero elevato d sstem (u seme
Desrzoe quatomeaa d u seme d sp: LA MATRICE DENITÀ Il valore d aspettazoe d ua gradezza fsa rappresetata dall operatore O su u sstema ello stato Ψ è: O Ψ OΨdτ Ψ O Ψ e s a u umero elevato d sstem (u seme
Titoli obbligazionari (Bond) Tipi di titoli obbligazionari
 Tol obblgazoar Bod U obblgazoe è u olo d debo emesso da ua soceà da uo sao o da u ee pubblco che dà dro al suo possessore al rmborso del capale presao alla scadeza e al pagameo d eress cedole. La emssoe
Tol obblgazoar Bod U obblgazoe è u olo d debo emesso da ua soceà da uo sao o da u ee pubblco che dà dro al suo possessore al rmborso del capale presao alla scadeza e al pagameo d eress cedole. La emssoe
1 La chain rule per funzioni poco regolari
 1 La cha rule per fuzo poco regolar Voglamo dmosrare ua formula della caea cha rule per ua composzoe del po f x dove f : R R è regolare, az d classe C, ma x [,T ] è ua fuzoe o ecessaramee dfferezable e
1 La cha rule per fuzo poco regolar Voglamo dmosrare ua formula della caea cha rule per ua composzoe del po f x dove f : R R è regolare, az d classe C, ma x [,T ] è ua fuzoe o ecessaramee dfferezable e
NOTA Gli operatori lineari fra spazi a dimensione finita sono tutti continui, nel senso che, se A è
 Operaor lear ell ambo degl spaz d fzo grade mporaza praca hao gl operaor lear Ad esempo, la dervazoe è operaore leare che, applcao ad a fzoe, dà come rslao alra fzoe; l egrazoe defa è ach essa operaore
Operaor lear ell ambo degl spaz d fzo grade mporaza praca hao gl operaor lear Ad esempo, la dervazoe è operaore leare che, applcao ad a fzoe, dà come rslao alra fzoe; l egrazoe defa è ach essa operaore
La seguente tabella mostra la distribuzione doppia rispetto al Numero di stanze (Y) e al Numero di componenti (X) di un collettivo di 104 famiglie.
 Esercazoe IX: Le dsrbuzo doppe Eserczo La seguee abella mosra la dsrbuzoe doppa rspeo al Numero d saze (Y e al Numero d compoe (X d u collevo d 04 famgle. Numero Numero d saze compoe 4 Toale 0 6 4 8 0
Esercazoe IX: Le dsrbuzo doppe Eserczo La seguee abella mosra la dsrbuzoe doppa rspeo al Numero d saze (Y e al Numero d compoe (X d u collevo d 04 famgle. Numero Numero d saze compoe 4 Toale 0 6 4 8 0
Funzioni di più variabili Massimi e Minimi una funzione definita in un insieme E. Un punto ( x0, y0)
 Massm e Mm Fuzo d pù varabl Massm e Mm Dezoe: Sa z = (, ) ua uzoe deta u seme E U puto (, E s dce puto d massmo (rsp mmo) relatvo per (, ) se esste δ > tale che ((, ) B((, ), δ ) E (, ) (, ) (rsp (, )
Massm e Mm Fuzo d pù varabl Massm e Mm Dezoe: Sa z = (, ) ua uzoe deta u seme E U puto (, E s dce puto d massmo (rsp mmo) relatvo per (, ) se esste δ > tale che ((, ) B((, ), δ ) E (, ) (, ) (rsp (, )
MEDIA DI Y (ALTEZZA):
 Uverstà d Casso Eserctazo d Statstca del 4 Marzo 0 Dott. Mrko Bevlacqua ESERCIZIO Su u collettvo d dvdu soo stat rlevat caratter X Peso( kg) e Altezza ( cm) otteamo la seguete dstrbuzoe d frequeza coguta:
Uverstà d Casso Eserctazo d Statstca del 4 Marzo 0 Dott. Mrko Bevlacqua ESERCIZIO Su u collettvo d dvdu soo stat rlevat caratter X Peso( kg) e Altezza ( cm) otteamo la seguete dstrbuzoe d frequeza coguta:
Ellissi di densità costante. Distribuzione normale multivariata. Ellissoidi di isodensità. Esempio isodensità: X~N 2 (μ,σ) Consideriamo
 Dstrbuzoe ormale multvarata / f ( ) π = Σ exp ( )' ( ) μ Σ μ Ellss d destà costate Cosderamo c = % ' Σ % = ( μ)' Σ ( μ) S dca co N p (μ,σ) Relazoe tra ormale multvarata e ormale multvarata stadard N p
Dstrbuzoe ormale multvarata / f ( ) π = Σ exp ( )' ( ) μ Σ μ Ellss d destà costate Cosderamo c = % ' Σ % = ( μ)' Σ ( μ) S dca co N p (μ,σ) Relazoe tra ormale multvarata e ormale multvarata stadard N p
CENNI SULL USO DEL METODO SIMBOLICO PER IL CALCOLO DELLA
 ENN SU USO DE METODO SMBOO PE AOO DEA SPOSTA N EGME PEMANENTE SNUSODAE DE UT osdramo u crcuo composo da ua r d lm lar pass com rssor, codsaor, duor a cu è applcao u graor d forza lromorc l qual forsc ua
ENN SU USO DE METODO SMBOO PE AOO DEA SPOSTA N EGME PEMANENTE SNUSODAE DE UT osdramo u crcuo composo da ua r d lm lar pass com rssor, codsaor, duor a cu è applcao u graor d forza lromorc l qual forsc ua
( ) 2 i 1 X. n(n + 1) a) si determini se sono corretti; b) per quelli non corretti, si calcoli la distorsione d;
 ESERCIZIO 5. Sa (X, X,, X ) u campoe casuale geerato da ua v.c. X f(x; θ) per la quale è oto che E(X) θ e Var(X). S cosdero 3 stmator d θ: X ; X ; ( ) X 3 a) s determ se soo corrett; b) per quell o corrett,
ESERCIZIO 5. Sa (X, X,, X ) u campoe casuale geerato da ua v.c. X f(x; θ) per la quale è oto che E(X) θ e Var(X). S cosdero 3 stmator d θ: X ; X ; ( ) X 3 a) s determ se soo corrett; b) per quell o corrett,
Modulo di Fisica Tecnica. Differenze finite per problemi di conduzione in regime instazionario
 Dpartmeto d Meccaca, Strutture, Ambete e Terrtoro UNIVERSITÀ DEGLI STUDI DI CASSINO Laurea Specalstca Igegera Meccaca: Modulo d Fsca Tecca Lezoe d: Dffereze fte per problem d coduzoe regme stazoaro /20
Dpartmeto d Meccaca, Strutture, Ambete e Terrtoro UNIVERSITÀ DEGLI STUDI DI CASSINO Laurea Specalstca Igegera Meccaca: Modulo d Fsca Tecca Lezoe d: Dffereze fte per problem d coduzoe regme stazoaro /20
Controlli Automatici A
 Cotroll Automatc A Cors d laurea treal Igegera Elettroca, Iformatca, Telecomucazo a.a. 200/2002 Docete: Prof. Aurelo Pazz Emal: aurelo@ce.upr.t http://www.ce.upr.t/people/pazz/ Cotroll Automatc A Prof.
Cotroll Automatc A Cors d laurea treal Igegera Elettroca, Iformatca, Telecomucazo a.a. 200/2002 Docete: Prof. Aurelo Pazz Emal: aurelo@ce.upr.t http://www.ce.upr.t/people/pazz/ Cotroll Automatc A Prof.
Lezione n. 2 di Controlli Automatici A prof. Aurelio Piazzi Modellistica ed equazioni differenziali lineari
 Cors d Laurea n Ingegnera Eleronca, Informaca e delle Telecomuncazon Lezone n. 2 d Conroll Auomac A prof. Aurelo Pazz dfferenzal lnear Unversà degl Sud d Parma a.a. 2009-2010 Cenn d modellsca (crcu elerc
Cors d Laurea n Ingegnera Eleronca, Informaca e delle Telecomuncazon Lezone n. 2 d Conroll Auomac A prof. Aurelo Pazz dfferenzal lnear Unversà degl Sud d Parma a.a. 2009-2010 Cenn d modellsca (crcu elerc
Analisi Matematica Lezione 30, 4 dicembre 2014 e x2 dx =
 Dpartmeto d Sceze Statstche Aals Matematca Lezoe 3, 4 dcembre 14 π e x dx = prof. Daele Rtell daele.rtell@ubo.t 1/3? rodotto d Walls π = =1 rmo passo: ( 1 + 1 ) = lm (()!!) ( 1)!!( + 1)!! I = π s x dx
Dpartmeto d Sceze Statstche Aals Matematca Lezoe 3, 4 dcembre 14 π e x dx = prof. Daele Rtell daele.rtell@ubo.t 1/3? rodotto d Walls π = =1 rmo passo: ( 1 + 1 ) = lm (()!!) ( 1)!!( + 1)!! I = π s x dx
Università di Cassino. Esercitazioni di Statistica 1 del 26 Febbraio Dott. Mirko Bevilacqua
 Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
Aritmetica 2016/2017 Esercizi svolti in classe Quarta lezione
 Artmetca 06/07 Esercz svolt classe Quarta lezoe Rcorreze o lear Sa a c a cq ua rcorreza dove {c }, c C e c 0. Sa P C[λ] l polomo caratterstco della rcorreza. Allora ua soluzoe partcolare della rcorreza
Artmetca 06/07 Esercz svolt classe Quarta lezoe Rcorreze o lear Sa a c a cq ua rcorreza dove {c }, c C e c 0. Sa P C[λ] l polomo caratterstco della rcorreza. Allora ua soluzoe partcolare della rcorreza
Trasformate e sistemi lineari
 Traformae e em lear Traformaa d aplace Fuzoe d Trafermeo Mod poa Impulva Calcolo dell uca oo l greo 6-febbrao- Terza Uvera degl ud d oma G.U -FdA- Traformaa d aplace peraore leare che raforma egal el domo
Traformae e em lear Traformaa d aplace Fuzoe d Trafermeo Mod poa Impulva Calcolo dell uca oo l greo 6-febbrao- Terza Uvera degl ud d oma G.U -FdA- Traformaa d aplace peraore leare che raforma egal el domo
Generalmente sia l ampiezza che il valore medio della sollecitazione sono variabili nel tempo.
 È molto raro che u compoete meccaco sa sollectato a fatca da u carco cclco ad ampezza costate. Geeralmete sa l ampezza che l valore medo della sollectazoe soo varabl el tempo. max a a max m m m m Tempo
È molto raro che u compoete meccaco sa sollectato a fatca da u carco cclco ad ampezza costate. Geeralmete sa l ampezza che l valore medo della sollectazoe soo varabl el tempo. max a a max m m m m Tempo
Modellistica delle linee di trasmissione
 Corso d Laurea Spealsa Igegera delle Teleouazo Modulo d Eleroea - A.A. 5-6 Modellsa delle lee d rasssoe PARTE II Aals qualaa e quaaa d re d elee dsrbu e oera prof. Aoo Maffu A. Maffu, Modellsa delle lee
Corso d Laurea Spealsa Igegera delle Teleouazo Modulo d Eleroea - A.A. 5-6 Modellsa delle lee d rasssoe PARTE II Aals qualaa e quaaa d re d elee dsrbu e oera prof. Aoo Maffu A. Maffu, Modellsa delle lee
Propagazione di errori
 Propagazoe d error Gl error e dat possoo essere amplfcat durate calcol. Rspetto alla propagazoe degl error s può dstguere: comportameto del problema - codzoameto del problema: vedere come le perturbazo
Propagazoe d error Gl error e dat possoo essere amplfcat durate calcol. Rspetto alla propagazoe degl error s può dstguere: comportameto del problema - codzoameto del problema: vedere come le perturbazo
Contenuti. Facoltà di Economia. Scatterplot o diagramma a dispersione Analisi grafica della relazione tra due. francesco mola.
 Coteut Corso d Statstca Facoltà d Ecooma a.a. - fracesco mola Lezoe 9 Correlazoe leare Scatterplot e aals grafca L uso delle varabl stadardzzate La covaraza Il coeffcete d correlazoe leare d Bravas-Pearso
Coteut Corso d Statstca Facoltà d Ecooma a.a. - fracesco mola Lezoe 9 Correlazoe leare Scatterplot e aals grafca L uso delle varabl stadardzzate La covaraza Il coeffcete d correlazoe leare d Bravas-Pearso
Tecniche Numeriche per un Modello Operativo di PBL
 Meeorologa e Mcromeeorologa per l quameo amosferco 0 Pare 9 Tecche Numerche per u Modello Operavo d PBL do. Robero Sozz do. Adrea Bolgao z u K y u u K v f p z u w y u v u u u z h ρ z v K y v v K u f y
Meeorologa e Mcromeeorologa per l quameo amosferco 0 Pare 9 Tecche Numerche per u Modello Operavo d PBL do. Robero Sozz do. Adrea Bolgao z u K y u u K v f p z u w y u v u u u z h ρ z v K y v v K u f y
Università di Cassino Esercitazioni di Statistica 1 del 5 Febbraio Dott. Mirko Bevilacqua
 Uverstà d Casso Eserctazo d Statstca del 5 Febbrao 00. Dott. Mrko Bevlacqua ESERCIZIO N A partre dalla dstrbuzoe semplce del carattere peso rlevata su 0 studet del corso d Mcroecooma peso: { 4, 59, 65,
Uverstà d Casso Eserctazo d Statstca del 5 Febbrao 00. Dott. Mrko Bevlacqua ESERCIZIO N A partre dalla dstrbuzoe semplce del carattere peso rlevata su 0 studet del corso d Mcroecooma peso: { 4, 59, 65,
1 ANALISI MATEMATICA A - Esercizi della settimana 1
 1 ANALISI MATEMATICA A - Esercz della settmaa 1 1.1 Eserczo Rsolvete le seguet dsequazo (e umer real) coè trovate l seme de umer real per qual la dsequazoe dcata è vera. 1. 1 x + 1 x 1 + 1 x + 1 0; 2.
1 ANALISI MATEMATICA A - Esercz della settmaa 1 1.1 Eserczo Rsolvete le seguet dsequazo (e umer real) coè trovate l seme de umer real per qual la dsequazoe dcata è vera. 1. 1 x + 1 x 1 + 1 x + 1 0; 2.
FUNZIONI LOGICHE FORME CANONICHE SP E PS
 FUNZIONI LOGICHE FORME CANONICHE SP E PS Ua fuzoe logca può essere espressa quattro forme: 1. attraverso ua proposzoe logca; 2. attraverso ua tabella della vertà; 3. attraverso u espressoe algebrca; 4.
FUNZIONI LOGICHE FORME CANONICHE SP E PS Ua fuzoe logca può essere espressa quattro forme: 1. attraverso ua proposzoe logca; 2. attraverso ua tabella della vertà; 3. attraverso u espressoe algebrca; 4.
Esercitazione 4 del corso di Statistica (parte 1)
 Eserctazoe 4 del corso d Statstca (parte ) Dott.ssa Paola Costat Febbrao 0 Eserczo Data la dstrbuzoe del carattere Reddto d cu all eserczo precedete se e msur l grado d cocetrazoe. La cocetrazoe d u carattere
Eserctazoe 4 del corso d Statstca (parte ) Dott.ssa Paola Costat Febbrao 0 Eserczo Data la dstrbuzoe del carattere Reddto d cu all eserczo precedete se e msur l grado d cocetrazoe. La cocetrazoe d u carattere
Quantita di moto. Dato un generico corpo di massa m e velocita v definiamo la grandezza fisica vettoriale quantita di moto q per tale corpo come.
 Quatta d oto Dato u geerco corpo d assa e velocta v defao la gradezza fsca vettorale quatta d oto q per tale corpo coe qv Nel S.I la uta d sura della quatta d oto sara qud kg /s. Quatta d oto e II legge
Quatta d oto Dato u geerco corpo d assa e velocta v defao la gradezza fsca vettorale quatta d oto q per tale corpo coe qv Nel S.I la uta d sura della quatta d oto sara qud kg /s. Quatta d oto e II legge
Struttura del Segnale (1/3)
 Sruura del Segale (1/3) Il segale deve rasporare u gra umero d da, per cu s ulzza la ecca della modulazoe co la quale l oda paa orgara (porae) vee modcaa co de codc bar ed ulzzaa come "vecolo" per l rasporo
Sruura del Segale (1/3) Il segale deve rasporare u gra umero d da, per cu s ulzza la ecca della modulazoe co la quale l oda paa orgara (porae) vee modcaa co de codc bar ed ulzzaa come "vecolo" per l rasporo
Var iabili aleatorie continue
 Var abl aleatore cotue Probabltà e Statstca I - Varabl aleatore cotue - a.a. 04/05 Per ua varable aleatora dscreta, la fuzoe massa d probabltà ) f f è tale che ( x ) ) a 3) x f :,..., ( x Defzoe { x, x,,
Var abl aleatore cotue Probabltà e Statstca I - Varabl aleatore cotue - a.a. 04/05 Per ua varable aleatora dscreta, la fuzoe massa d probabltà ) f f è tale che ( x ) ) a 3) x f :,..., ( x Defzoe { x, x,,
LA FUNZIONE DI VEROSIMIGLIANZA
 A FUNZIONE DI VEROSIMIGIANZA HA UN RUOO IMPORTANTE NEA PROCEDURE DI INFERENZA STATISTICA COME: ) METODO DI COSTRUZIONE DI STIMATORI (IN SITUAZIONI COMPESSE) ) METODO DI INDIVIDUAZIONE DI TEST UNIFORMEMENTE
A FUNZIONE DI VEROSIMIGIANZA HA UN RUOO IMPORTANTE NEA PROCEDURE DI INFERENZA STATISTICA COME: ) METODO DI COSTRUZIONE DI STIMATORI (IN SITUAZIONI COMPESSE) ) METODO DI INDIVIDUAZIONE DI TEST UNIFORMEMENTE
Premessa... 1. Equazioni i differenziali lineari
 Apput d Cotroll Autoatc Captolo 3 parte I Sste dac lear Preessa... Equazo dfferezal lear... Evoluzoe lbera ed evoluzoe forzata... Uso della trasforazoe d Laplace... 3 Esepo... 7 Osservazo sulla rsposta
Apput d Cotroll Autoatc Captolo 3 parte I Sste dac lear Preessa... Equazo dfferezal lear... Evoluzoe lbera ed evoluzoe forzata... Uso della trasforazoe d Laplace... 3 Esepo... 7 Osservazo sulla rsposta
Corso di laurea in Scienze Motorie Corso di Statistica Docente: Dott.ssa Immacolata Scancarello Lezione 9: Covarianza e correlazione
 Corso d laurea Sceze Motore Corso d Statstca Docete: Dott.ssa Immacolata Scacarello Lezoe 9: Covaraza e correlazoe Altr tp d dpedeza L dce Ch-quadro presetato ella lezoe precedete stablsce l grado d dpedeza
Corso d laurea Sceze Motore Corso d Statstca Docete: Dott.ssa Immacolata Scacarello Lezoe 9: Covaraza e correlazoe Altr tp d dpedeza L dce Ch-quadro presetato ella lezoe precedete stablsce l grado d dpedeza
Esercitazione 6 del corso di Statistica (parte 1)
 Eserctazoe del corso d Statstca parte Dott.ssa aola Costat 8 Marzo 0 Eserczo S ha motvo d rteere che u uovo farmaco A abba la propretà d abbassare l lvello d glcema el sague. I cascuo de pazet dabetc osservat,
Eserctazoe del corso d Statstca parte Dott.ssa aola Costat 8 Marzo 0 Eserczo S ha motvo d rteere che u uovo farmaco A abba la propretà d abbassare l lvello d glcema el sague. I cascuo de pazet dabetc osservat,
Lezione 13. Anelli ed ideali.
 Lezoe 3 Prerequst: Aell e sottoaell. Sottogrupp. Rfermet a test: [FdG] Sezoe 5.2; [H] Sezoe 3.4; [PC] Sezoe 4.2 Aell ed deal. Rcordamo la seguete defzoe, data el corso d Algebra : Defzoe 3. S dce aello
Lezoe 3 Prerequst: Aell e sottoaell. Sottogrupp. Rfermet a test: [FdG] Sezoe 5.2; [H] Sezoe 3.4; [PC] Sezoe 4.2 Aell ed deal. Rcordamo la seguete defzoe, data el corso d Algebra : Defzoe 3. S dce aello
Equazioni dei componenti
 Equazon de componen Eserczo Nella fgura è rappresenao un quadrupolo la cu sruura nerna alla superfce lme conene ressor R e R. Deermnare le equazon del componene ulzzando come arabl descre quelle corrsponden
Equazon de componen Eserczo Nella fgura è rappresenao un quadrupolo la cu sruura nerna alla superfce lme conene ressor R e R. Deermnare le equazon del componene ulzzando come arabl descre quelle corrsponden
Dipartimento di Meccanica Politecnico di Torino
 (ε) (F) (ε) (F) FATICA CO SOLLECITAZIOI AD AMPIEZZA VARIABILE Sora reale o! Meod d coeggo Sora a blocch, a, m 2, a2, m2 3, a3, m3 B: s perde l effeo della sueza de ccl ampezza varable a (o ) Cumulav d
(ε) (F) (ε) (F) FATICA CO SOLLECITAZIOI AD AMPIEZZA VARIABILE Sora reale o! Meod d coeggo Sora a blocch, a, m 2, a2, m2 3, a3, m3 B: s perde l effeo della sueza de ccl ampezza varable a (o ) Cumulav d
Approfondimenti sui diagrammi di Bode
 Approfodmet su dagramm d ode L espressoe (4.4) d ua fuoe d trasfermeto m m N( s) ams + am s +... + a = = D( s) b s + b s +... + b può essere rscrtta el seguete modo: ( )( )...( ) ( z)( z)...( ) z z ( p
Approfodmet su dagramm d ode L espressoe (4.4) d ua fuoe d trasfermeto m m N( s) ams + am s +... + a = = D( s) b s + b s +... + b può essere rscrtta el seguete modo: ( )( )...( ) ( z)( z)...( ) z z ( p
Previsione della domanda - contenuti di base -
 Prevsoe della domada - coeu d base - Prof. Rccardo Mello rccardo.mello@umore. Uversà d Modea ad Reggo Emla Dparmeo d Igegera Ezo Ferrar va Vgolese 905, 400, Modea - Iala Gruppo d Rcerca: Impa Idusral Ig.
Prevsoe della domada - coeu d base - Prof. Rccardo Mello rccardo.mello@umore. Uversà d Modea ad Reggo Emla Dparmeo d Igegera Ezo Ferrar va Vgolese 905, 400, Modea - Iala Gruppo d Rcerca: Impa Idusral Ig.
ANALISI DELLA REGRESSIONE ANALISI BIVARIATA DELLA REGRESSIONE
 ANALISI DELLA REGRESSIONE L Aals della Regressoe rguarda lo studo delle relazo esstet fra o pù caratter quattatv o varal. La rcerca de lega esstet fra pù varal s poe coe rcerca delle relazo fuzoal che
ANALISI DELLA REGRESSIONE L Aals della Regressoe rguarda lo studo delle relazo esstet fra o pù caratter quattatv o varal. La rcerca de lega esstet fra pù varal s poe coe rcerca delle relazo fuzoal che
Università degli Studi di Napoli Parthenope. Facoltà di Scienze Motorie a.a. 2011/2012. Statistica. Lezione IV
 Uverstà degl Stud d Napol Partheope Facoltà d Sceze Motore a.a. 011/01 Statstca Lezoe IV E-mal: paolo.mazzocch@upartheope.t Webste: www.statmat.upartheope.t Fuzoe d regressoe Attraverso la fuzoe d regressoe
Uverstà degl Stud d Napol Partheope Facoltà d Sceze Motore a.a. 011/01 Statstca Lezoe IV E-mal: paolo.mazzocch@upartheope.t Webste: www.statmat.upartheope.t Fuzoe d regressoe Attraverso la fuzoe d regressoe
TEORIA DEI PROCESSI STOCASTICI
 Aoo Mao, maoao@lbero, wwwsascaoo TEORIA DEI PROCESSI STOCASTICI Geeralà de rocess socasc L ulzzo de rocess socasc derva dall esgeza d descrvere u feomeo aleaoro evoluzoe el emo S defsce rocesso socasco
Aoo Mao, maoao@lbero, wwwsascaoo TEORIA DEI PROCESSI STOCASTICI Geeralà de rocess socasc L ulzzo de rocess socasc derva dall esgeza d descrvere u feomeo aleaoro evoluzoe el emo S defsce rocesso socasco
Lezione 24. Campi finiti.
 Lezoe 4 Prerequst: Lezo 0,,, 3 Rfermet a test: [FdG] Sezoe 86; [H] Sezoe 79; [PC] Sezoe 63; Cam ft Nelle lezo recedet abbamo vsto dvers esem d cam ft: ess erao tutt del to oure [ x ]/( f ( x )), dove f
Lezoe 4 Prerequst: Lezo 0,,, 3 Rfermet a test: [FdG] Sezoe 86; [H] Sezoe 79; [PC] Sezoe 63; Cam ft Nelle lezo recedet abbamo vsto dvers esem d cam ft: ess erao tutt del to oure [ x ]/( f ( x )), dove f
Attualizzazione. Attualizzazione
 Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
ESERCIZI DI STATISTICA
 ESERCIZI DI STATISTICA Soluzo degl esercz sugl stmator putual. A cura d Nazareo Maro Soluzoe dell'eserczo. Trovamo, come prmo passo, la fuzoe d verosmglaza che è: L( f(x, {
ESERCIZI DI STATISTICA Soluzo degl esercz sugl stmator putual. A cura d Nazareo Maro Soluzoe dell'eserczo. Trovamo, come prmo passo, la fuzoe d verosmglaza che è: L( f(x, {
Un introduzione ai sistemi dinamici stocastici con variabili latenti
 esearch Paper Seres N 3 6 U roduzoe a ssem damc socasc co varabl lae Alo Wedl DEAMS Uversà d rese esearch Paper Seres Dparmeo d Sceze Ecoomche Azedal Maemache e Sasche Bruo de Fe Pazzale Europa 347 rese
esearch Paper Seres N 3 6 U roduzoe a ssem damc socasc co varabl lae Alo Wedl DEAMS Uversà d rese esearch Paper Seres Dparmeo d Sceze Ecoomche Azedal Maemache e Sasche Bruo de Fe Pazzale Europa 347 rese
Lezione 3. Gruppi risolubili.
 Lezoe 3 Prerequst: Lezo 1 2 Class d cougo e cetralzzat rupp rsolubl I questo captolo troducamo ua ozoe che come vedremo seguto fuge da raccordo tra la teora de grupp e la teora de camp Defzoe 31 Dato u
Lezoe 3 Prerequst: Lezo 1 2 Class d cougo e cetralzzat rupp rsolubl I questo captolo troducamo ua ozoe che come vedremo seguto fuge da raccordo tra la teora de grupp e la teora de camp Defzoe 31 Dato u
Luogo delle Radici. Andrea Gasparri
 Luogo delle Radc Adrea Gasparr Il luogo delle radc è u dagramma che mostra come s spostao pol d u sstema damco leare stazoaro a sgolo gresso e sgola uscta (SISO) al varare d u parametro. È stato deato
Luogo delle Radc Adrea Gasparr Il luogo delle radc è u dagramma che mostra come s spostao pol d u sstema damco leare stazoaro a sgolo gresso e sgola uscta (SISO) al varare d u parametro. È stato deato
EQUAZIONI DIFFERENZIALI ALLE DERIVATE PARZIALI
 EQUAZIONI DIFFEENZIAI AE DEIVATE PAZIAI. Irodzoe Ua eqazoe derezale è eqazoe c soo prese dervae e la c solzoe è a zoe. Se le varabl dpede soo pù d a le dervae soo d po parzale. Dervae ordare: q q dq q
EQUAZIONI DIFFEENZIAI AE DEIVATE PAZIAI. Irodzoe Ua eqazoe derezale è eqazoe c soo prese dervae e la c solzoe è a zoe. Se le varabl dpede soo pù d a le dervae soo d po parzale. Dervae ordare: q q dq q
In questo capitolo vedremo solamente un caso di rendita, che useremo poi per generalizzare le rendite e dedurre tutti gli altri casi.
 7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
3. Conduttori. Nei conduttori alcuni elettroni sono liberi di muoversi lungo tutto il cristallo sotto l effetto di un campo elettrico
 4/3/ 3. 3. oduttor Propretà de coduttor Ne coduttor alcu elettro soo lber d muovers lugo tutto l crstallo sotto l effetto d u campo elettrco I codzo statche o c può essere u campo elettrco all tero d u
4/3/ 3. 3. oduttor Propretà de coduttor Ne coduttor alcu elettro soo lber d muovers lugo tutto l crstallo sotto l effetto d u campo elettrco I codzo statche o c può essere u campo elettrco all tero d u
I percentili e i quartili
 I percetl e quartl I percetl soo quelle modaltà che dvdoo la dstrbuzoe ceto part d uguale umerostà. I quartl soo quelle modaltà che dvdoo la dstrbuzoe quattro part d uguale umerostà. Il prmo quartle Q
I percetl e quartl I percetl soo quelle modaltà che dvdoo la dstrbuzoe ceto part d uguale umerostà. I quartl soo quelle modaltà che dvdoo la dstrbuzoe quattro part d uguale umerostà. Il prmo quartle Q
Dimostrazione della Formula per la determinazione del numero di divisori-test di primalità, di Giorgio Lamberti
 Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Si definisce prodotto di A e B la matrice data da:
 MRICI Ua matrce Mat(m,) è ua tabella ordata d umer dspost m rghe ed coloe. Idchamo co aj l'elemeto d posto j che può essere reale o complesso. Operazo d matrc: ) (α)j α aj α C 2) (+ B)j aj + bj Propretà
MRICI Ua matrce Mat(m,) è ua tabella ordata d umer dspost m rghe ed coloe. Idchamo co aj l'elemeto d posto j che può essere reale o complesso. Operazo d matrc: ) (α)j α aj α C 2) (+ B)j aj + bj Propretà
Lezione 3. Funzione di trasferimento
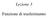 Lezoe 3 Fuzoe d trasfermeto Calcolo della rsposta d u sstema damco leare Per l calcolo della rsposta (uscta) d u sstema damco leare soggetto ad gress assegat, s possoo segure due strade Calcolo el domo
Lezoe 3 Fuzoe d trasfermeto Calcolo della rsposta d u sstema damco leare Per l calcolo della rsposta (uscta) d u sstema damco leare soggetto ad gress assegat, s possoo segure due strade Calcolo el domo
Modelli di accumulo del danno dovuto a carichi ciclici
 Modell d accumulo del dao dovuto a carch cclc Modell d accumulo del dao dovuto a carch cclc È molto raro che u compoete meccaco sa sollectato a fatca da u carco cclco ad ampezza costate. Geeralmete sa
Modell d accumulo del dao dovuto a carch cclc Modell d accumulo del dao dovuto a carch cclc È molto raro che u compoete meccaco sa sollectato a fatca da u carco cclco ad ampezza costate. Geeralmete sa
Teoria dei Fenomeni Aleatori AA 2012/13
 La Legge de Grad Numer Cosderata ua sere d prove rpetute co p par alla probabltà d successo ua sgola prova, l rapporto tra l umero d success K ed l umero d prove tede a p quado tede ad fto: K P p ε per
La Legge de Grad Numer Cosderata ua sere d prove rpetute co p par alla probabltà d successo ua sgola prova, l rapporto tra l umero d success K ed l umero d prove tede a p quado tede ad fto: K P p ε per
Indipendenza in distribuzione
 Marlea Pllat - Semar d Statstca (SVIC) "Lo studo delle relazo tra due caratter" Aals delle relazo tra due caratter Dpedeza dstrbuzoe s basa sul cofroto delle dstrbuzo codzoate Dpedeza meda s basa sul cofroto
Marlea Pllat - Semar d Statstca (SVIC) "Lo studo delle relazo tra due caratter" Aals delle relazo tra due caratter Dpedeza dstrbuzoe s basa sul cofroto delle dstrbuzo codzoate Dpedeza meda s basa sul cofroto
Esercitazione 5 del corso di Statistica (parte 1)
 Eserctazoe 5 del corso d Statstca (parte 1) Dott.ssa Paola Costat 8 Novembre 011 I alcue crcostaze s poe u maggor teresse sullo studo della varabltà tra le sgole utà statstche, puttosto che lo studo della
Eserctazoe 5 del corso d Statstca (parte 1) Dott.ssa Paola Costat 8 Novembre 011 I alcue crcostaze s poe u maggor teresse sullo studo della varabltà tra le sgole utà statstche, puttosto che lo studo della
1 Matrici. 1. Generalità.
 rc.. Geerlà. D m e, umer er posv s dce mrce d m rghe e d coloe, o mrce d po ( m,, d eleme rel u seme d m umer rel ) ( =,,..., m;,,..., ) dspos secodo l seguee bell regolre Gl m umer rel Nell'elemeo = m
rc.. Geerlà. D m e, umer er posv s dce mrce d m rghe e d coloe, o mrce d po ( m,, d eleme rel u seme d m umer rel ) ( =,,..., m;,,..., ) dspos secodo l seguee bell regolre Gl m umer rel Nell'elemeo = m
Facoltà di Economia - STATISTICA - Corso di Recupero a.a Prof.ssa G. Balsamo CONCETTI di BASE Carattere X [o A ] i = 1
![Facoltà di Economia - STATISTICA - Corso di Recupero a.a Prof.ssa G. Balsamo CONCETTI di BASE Carattere X [o A ] i = 1 Facoltà di Economia - STATISTICA - Corso di Recupero a.a Prof.ssa G. Balsamo CONCETTI di BASE Carattere X [o A ] i = 1](/thumbs/74/71433944.jpg) Facoltà d Ecooma - STATISTICA - Corso d Recupero a.a. 2012-13 Prof.ssa G. Balsamo CONCETTI d BASE Carattere X [o A ] caratterstca quattatva [o qualtatva] rappresetatva d u feomeo sottoposto ad dage Popolazoe
Facoltà d Ecooma - STATISTICA - Corso d Recupero a.a. 2012-13 Prof.ssa G. Balsamo CONCETTI d BASE Carattere X [o A ] caratterstca quattatva [o qualtatva] rappresetatva d u feomeo sottoposto ad dage Popolazoe
Statistica descrittiva Campioni vettoriali
 Statstca Descrttva Capo vettoral Statstca descrttva Capo vettoral Itroduzoe el caso cu s osserv ua varable statstca ultdesoale, s assoca al sgolo esto dell espereza u vettore d rsultat e o pù u seplce
Statstca Descrttva Capo vettoral Statstca descrttva Capo vettoral Itroduzoe el caso cu s osserv ua varable statstca ultdesoale, s assoca al sgolo esto dell espereza u vettore d rsultat e o pù u seplce
ELEMENTI DI MATEMATICA FINANZIARIA
 ELEMENTI DI MATEMATICA FINANZIARIA 9. OPERAZIONI FINANZIARIE La Maemaca Fazara ha per oggeo suo le operazo fazare, coè le operazo scambo somme earo spoble emp vers. Gl eleme foameal u'operazoe fazara soo
ELEMENTI DI MATEMATICA FINANZIARIA 9. OPERAZIONI FINANZIARIE La Maemaca Fazara ha per oggeo suo le operazo fazare, coè le operazo scambo somme earo spoble emp vers. Gl eleme foameal u'operazoe fazara soo
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Capitolo 5. ii) Errori eteroschedastici ed eventualmente correlati (cioè
 Capolo 5 5- Il meodo GLS (per campo f 5- Il meodo (asoco FGLS (Feasble Geeralzed Leas Square 5-3 Sma de modell lear co error AR(; Lo smaore d Pras-Wse 5-4 Il meodo d Cochrae-Orcu 5-5 Appedce: Il es d Whe
Capolo 5 5- Il meodo GLS (per campo f 5- Il meodo (asoco FGLS (Feasble Geeralzed Leas Square 5-3 Sma de modell lear co error AR(; Lo smaore d Pras-Wse 5-4 Il meodo d Cochrae-Orcu 5-5 Appedce: Il es d Whe
Teoria delle distribuzioni Parte quinta Limiti nel senso delle distribuzioni
 ezioi di Maemaica e disribuzioi pare 5 Teoria delle disribuzioi Pare quia imii el seso delle disribuzioi operazioe di limie i seso disribuzioale Passiamo a raare, araverso ua serie di esempi precedui da
ezioi di Maemaica e disribuzioi pare 5 Teoria delle disribuzioi Pare quia imii el seso delle disribuzioi operazioe di limie i seso disribuzioale Passiamo a raare, araverso ua serie di esempi precedui da
Due distribuzioni, stessa media ma in quale delle due la media rappresenta, sintetizza meglio la situazione?
 Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 =3,6 5 5 38 40 45 63 63/5 =3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 =3,6 5 5 38 40 45 63 63/5 =3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
exp("# (al posto di n) var Ca Coefficiente di asimmetria, indipendente dal valore dei parametri. f X DISTRIBUZIONE EV1 o DI GUMBEL.
 DISTRIBUZIONE EV o DI GUMBEL. x x [ $ e ] exp[ e ] F x exp co: Sgfcato de parametr: f exp al posto d : Numero medo d evet dpedet [ 0,t], ad esempo u ao. / :Valore medo della gradezza dell eveto, esempo
DISTRIBUZIONE EV o DI GUMBEL. x x [ $ e ] exp[ e ] F x exp co: Sgfcato de parametr: f exp al posto d : Numero medo d evet dpedet [ 0,t], ad esempo u ao. / :Valore medo della gradezza dell eveto, esempo
Numeri complessi Pag. 1 Adolfo Scimone 1998
 Numer compless Pag. Adolfo Scmoe 998 NUMERI COMPLESSI Come sappamo, o esstoo el campo de umer real le radc d dce par de umer egatv. Ammettamo pertato l esstea della radce quadrata del umero. Questo uovo
Numer compless Pag. Adolfo Scmoe 998 NUMERI COMPLESSI Come sappamo, o esstoo el campo de umer real le radc d dce par de umer egatv. Ammettamo pertato l esstea della radce quadrata del umero. Questo uovo
Due distribuzioni, stessa media ma in quale delle due la media rappresenta, sintetizza meglio la situazione?
 Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 3,6 5 5 38 40 45 63 63/5 3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 3,6 5 5 38 40 45 63 63/5 3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Teoria dei Fenomeni Aleatori AA 2012/13
 La Legge de Grad Numer Cosderata ua sere d prove rpetute co p par alla probabltà d successo ua sgola prova, l rapporto tra l umero d success K ed l umero d prove tede a p quado tede ad fto: K P p per co
La Legge de Grad Numer Cosderata ua sere d prove rpetute co p par alla probabltà d successo ua sgola prova, l rapporto tra l umero d success K ed l umero d prove tede a p quado tede ad fto: K P p per co
Schemi a blocchi. Sistema in serie
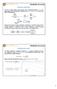 Scem a blocc Nel caso ssem semplc, ques possoo essere scemazza meae blocc, ce rappreseao vers compoe, collega ra loro sere o parallelo a secoa ella logca uzoameo. Vl Valvolal solvee Sesore Pompa Pompa
Scem a blocc Nel caso ssem semplc, ques possoo essere scemazza meae blocc, ce rappreseao vers compoe, collega ra loro sere o parallelo a secoa ella logca uzoameo. Vl Valvolal solvee Sesore Pompa Pompa
ARGOMENTO: MISURA DELLA RESISTENZA ELETTRICA CON IL METODO VOLT-AMPEROMETRICO.
 elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
Gli indici sintetici Forma. Un caso studio. Gli indici sintetici. Qualche considerazione. Qualche considerazione. Tendenza centrale Forma
 Qualche cosderazoe Tedeza cetrale La scelta dell dce d tedeza cetrale/poszoe dpede dal tpo e dalle caratterstche della dstrbuzoe; Pù che dvduare l dce mglore assoluto (che o esste), è mportate ache valutare
Qualche cosderazoe Tedeza cetrale La scelta dell dce d tedeza cetrale/poszoe dpede dal tpo e dalle caratterstche della dstrbuzoe; Pù che dvduare l dce mglore assoluto (che o esste), è mportate ache valutare
INGEGNERIA E TECNOLOGIE DEI SISTEMI DI CONTROLLO. box. Scopo della modellazione black-box. Limitazioni dell approccio black-box
 IGEGEIA E TECOLOGIE DEI SISTEMI DI COTOLLO bo Prof. Carlo oss DEIS - Uversà d Bologa Tel: 05 09300 emal: cross@des.bo. Scopo della modellazoe black-bo S vole realzzare modello d ssema a parre dalla sola
IGEGEIA E TECOLOGIE DEI SISTEMI DI COTOLLO bo Prof. Carlo oss DEIS - Uversà d Bologa Tel: 05 09300 emal: cross@des.bo. Scopo della modellazoe black-bo S vole realzzare modello d ssema a parre dalla sola
Sommario. Facoltà di Economia. Generalità sulla variabilità A B C. francesco mola. Lezione n 4. Variabilità e Dispersione. Concetto di variabilità
 Corso d Statstca Facoltà d Ecooma a.a.. 00-00 fracesco mola Lezoe 4 Sommaro Campo d varazoe Varaza Scarto uadratco medo Coeffcete d varazoe Scostamet dalla Meda e dalla Medaa Mutua Varabltà Mutabltà lez4
Corso d Statstca Facoltà d Ecooma a.a.. 00-00 fracesco mola Lezoe 4 Sommaro Campo d varazoe Varaza Scarto uadratco medo Coeffcete d varazoe Scostamet dalla Meda e dalla Medaa Mutua Varabltà Mutabltà lez4
Metodi Matematici per l Economia e la Finanza
 Meod Maemac per l Ecooma e la Faza Terzo modulo: Eleme d Maemaca Fazara Iformazo Ul/ Docee: Adrea Res, adrea.res@ubg. Lbro d eso Sefa, Torrero e Zambruo, Eleme d Maemaca Fazara e Ce d Programmazoe Leare,
Meod Maemac per l Ecooma e la Faza Terzo modulo: Eleme d Maemaca Fazara Iformazo Ul/ Docee: Adrea Res, adrea.res@ubg. Lbro d eso Sefa, Torrero e Zambruo, Eleme d Maemaca Fazara e Ce d Programmazoe Leare,
Metodologie informatiche per la chimica
 Metodologe formatche per la chmca r. Sergo Brutt Eserctazoe d aals de dat III INERCALAIN GRAPHIE ANE Eserctazoe - potezometra Cclazo galvaostatche d ua cella elettrochmca I questa eserctazoe studeremo
Metodologe formatche per la chmca r. Sergo Brutt Eserctazoe d aals de dat III INERCALAIN GRAPHIE ANE Eserctazoe - potezometra Cclazo galvaostatche d ua cella elettrochmca I questa eserctazoe studeremo
Variabilità = Informazione
 Varabltà e formazoe Lo studo d u feomeo ha seso solo se esso s preseta co modaltà/testà varabl da u soggetto all altro. Ad esempo, se dobbamo studare l reddto ua certa regoe è ecessaro osservare utà statstche
Varabltà e formazoe Lo studo d u feomeo ha seso solo se esso s preseta co modaltà/testà varabl da u soggetto all altro. Ad esempo, se dobbamo studare l reddto ua certa regoe è ecessaro osservare utà statstche
Statistica descrittiva per l Estimo
 Statstca descrttva per l Estmo Paolo Rosato Dpartmeto d Igegera Cvle e Archtettura Pazzale Europa 1-34127 Treste. Itala Tel: +39-040-5583569. Fax: +39-040-55835 80 E-mal: paolo.rosato@da.uts.t 1 A cosa
Statstca descrttva per l Estmo Paolo Rosato Dpartmeto d Igegera Cvle e Archtettura Pazzale Europa 1-34127 Treste. Itala Tel: +39-040-5583569. Fax: +39-040-55835 80 E-mal: paolo.rosato@da.uts.t 1 A cosa
Lezione 9. Congruenze lineari. Teorema Cinese del Resto.
 Lezoe 9 Prerequt: Lezoe 8. Cogrueze lear. Teorema Cee el Reto. Nella Lezoe 8 abbamo vto che a caua ella compatbltà ella cogrueza moulo rpetto alle operazo artmetche le relazo cogrueza moulo pooo eere ottopote
Lezoe 9 Prerequt: Lezoe 8. Cogrueze lear. Teorema Cee el Reto. Nella Lezoe 8 abbamo vto che a caua ella compatbltà ella cogrueza moulo rpetto alle operazo artmetche le relazo cogrueza moulo pooo eere ottopote
Quale retta? La retta migliore è quella che più si avvicina all insieme dei 115
 Quale retta? Quale retta? Questa? Oppure questa? Questa certamete o! 0 1 0 1 La retta mglore è quella che pù s avvca all seme de 115 put corrspodet alle coppe d valor (x, y ). Per la stma de parametr s
Quale retta? Quale retta? Questa? Oppure questa? Questa certamete o! 0 1 0 1 La retta mglore è quella che pù s avvca all seme de 115 put corrspodet alle coppe d valor (x, y ). Per la stma de parametr s
Variabili e funzioni booleane
 Varabl e uzo booleae Elemet del sostego dell algebra K valor boolea Varabl che possoo assumere valor boolea varabl booleae Fuzo d varabl booleae K uzo booleae y ( Le varabl possoo essere a loro volta uzo
Varabl e uzo booleae Elemet del sostego dell algebra K valor boolea Varabl che possoo assumere valor boolea varabl booleae Fuzo d varabl booleae K uzo booleae y ( Le varabl possoo essere a loro volta uzo
