ELEMENTI DI MATEMATICA FINANZIARIA
|
|
|
- Iolanda Nanni
- 8 anni fa
- Visualizzazioni
Transcript
1 ELEMENTI DI MATEMATICA FINANZIARIA 9. OPERAZIONI FINANZIARIE La Maemaca Fazara ha per oggeo suo le operazo fazare, coè le operazo scambo somme earo spoble emp vers. Gl eleme foameal u'operazoe fazara soo mpor e scaeze. Sulla base ques ue eleme s effeua ua prma szoe: operazo fazare cere: soo quelle cu mpor s reoo spobl co cerezza, operazo fazare aleaore: soo quelle cu mpor s reoo spobl solo se s verfcao egl eve aleaor. La Maemaca fazara classca s occupa elle operazo fazare cere, mere la Maemaca auarale s occupa elle operazo fazare aleaore. Esemp operazo fazare cere. ) Deposao earo sul c/c bacaro a cu s preleverao capale e eress s scamba l versameo oero co u prelevameo fuuro. ) Comprao ogg BOT che s rveerao fra u mese, s scamba la somma ogg vesa co l rcavo ella vea fra u mese. 3) Spulao ogg u muuo co rmborso grauale s scamba la spoblà che ogg s rceve per effeo el corao muuo co versame che s farao alle scaeze coveue. 4) Spulao ogg u acquso u'auo co pagameo raeale, s scamba la somma rcevua subo aura (valore ell'auo), co le rae che s verserao alle scaeze ovue. Per rourre alcu coce foameal s coser ua operazoe fazara elemeare cossee ello scambo fra ue vu A e B ue capal, rspevamee C e M co M > C, ue successv emp x e y. C x Il soggeo A cee a B l capale C spoble al empo x ; cambo B cee a A l capale M spoble al empo y > x. Se l'operazoe scambo ell'mporo C al empo x coro l'mporo M al empo successvo y è acceaa a ue vu, s ce che C e M soo fazaramee equvale fra loro e che l'operazoe è equa. Aveo supposo x < y s ha che: A è eo creore o muuae; B è eo ebore o muuaaro; C è l capale mpegao, acpao o veso; M è l capale ovuo alla scaeza; x è la aa vesmeo; y è la aa scaeza; [x,y] è l peroo mpego. M y
2 Pare 9 OPERAZIONI FINANZIARIE La escrzoe u'operazoe fazara s può fare assocao alle vare scaeze elle qual s hao movme cassa gl ammoar al movme. D orma le scaeze s msurao a e gl ammoar eraa e usca soo oa rspevamee sego + (eveualmee omesso) e sego. Qu per escrvere u'operazoe fazara basa assegare elle coppe umer (scaeza, flusso cassa), ( s, x s ) co s =,, e ove s, u'appropraa uà msura, è la scaeza alla quale s mafesa l flusso cassa x s (valor posv segalao erae, valor egav segalao usce). Esempo. Ogg coceo u preso 3000 ; fra u ao m rmborsao 000, fra ao e mezzo alr 00 e fra ue a alr 300. Scaeza (empo) Flusso cassa (mporo) , S può ache usare ua rappreseazoe geomerca, ea rea e emp , OPERAZIONI DI CAPITALIZZAZIONE S parla u'operazoe capalzzazoe quao l earo è porao ava el empo ossa s rasforma ua spoblà mmeaa C al empo x, ua spoblà fuura M al empo y ; o C, x, y s eve eermare M. I quesa operazoe fazara l'elemeo foameale è l capale C ; M è eo moae, al empo y, el capale C mpegao al empo x. S efsce eresse el peroo [x,y] la quaà I = M C M faore moae : r = C Esso msura l moae per uà capale mpegao, ossa se C =, allora è r = M. Dalle efzo pose segue ache: M = C + I C = M I, M r =, M= Cr, C M C =, I = C (r ), r I r = +. C
3 Pare 9 OPERAZIONI FINANZIARIE Esempo. Ogg veso 000, fra re a rscuoo capale 800 moae = 800 eresse 800 =, OPERAZIONI DI ATTUALIZZAZIONE S parla u'operazoe aualzzazoe o acpazoe o scoo quao l earo è porao ero el empo; o M, x, y s eve eermare C. I quesa operazoe fazara l'elemeo foameale è l capale M ; la somma C s ce valore auale al empo x el capale M, eo valore omale, ovuo al empo y. S efsce scoo sul capale M la quaà D = M C. C faore scoo o acpazoe : v =. M Esso rappresea l valore x corrspoee a ua uà moae y, ossa se M =, v = C. Dalle efzo pose segue ache C = M D, M = C + D, C v =, C = M v, M C M =. v Esempo. Ogg posso pagare 000 per acqusre l ro a rscuoere 800 fra re a valore auale o scoao 800 valore omale = 800 scoo 000 = 0,55 faore scoo 800 3
4 Pare 9 OPERAZIONI FINANZIARIE LEGGI E REGIMI FINANZIARI A parà og alra cozoe è ragoevole aspears che elle operazo capalzzazoe e aualzzazoe, l faore moae e l faore scoo peao alla uraa ell vesmeo. Quao s vuole segalare che faor moae e scoo soo fuzoe ella uraa ella operazoe fazara s cao, rspevamee, co r() e v(). La fuzoe r() rappresea l moae equvalee al capale C = ; essa è ea fuzoe faore moae o capalzzazoe. La fuzoe v() rappresea l valore auale = 0 equvalee al moae M = ; essa è ea fuzoe faore scoo o aualzzazoe. S suppoe che le operazo fazare sao regolae a fuzo faore che rappreseao l comporameo u vuo razoale (colu che prefersce ao a poco) e perao le propreà ua fuzoe faore moae e ua fuzoe faore scoo s possoo rassumere come segue. Fuzoe faore moae è ua fuzoe r() ale che ) r(0) =, ) r () 0 ossa r() è crescee, 3) r(). r() 0 Fuzoe faore scoo è ua fuzoe v() ale che ) v(0) =, ) v () 0 ossa v() è ecrescee, 3) 0 < v(). v() 0 4
5 Pare 9 OPERAZIONI FINANZIARIE Abbamo rooo la fuzoe faore capalzzazoe r() e la fuzoe faore scoo v() perché, orma, le operazo fazare capalzzazoe e aualzzazoe peoo alla uraa ell vesmeo. Coserao r() e v() possamo allora esprmere fuzoe ache le alre graezze. Nelle operazo capalzzazoe, eo C l capale veso per u peroo, s ha: M() = C r(), I() = M() C = C (r() ), olre I( ) ( ) = C è l asso eresse peroale relavo al peroo. Esso è l eresse prooo a u capale uaro el peroo. S facca aezoe che orma co l smbolo s ca l eresse prooo a u capale uaro u peroo uaro empo ( solo u ao). Dalle formule precee segue: r() = + () Nelle operazo aualzzazoe, ea M la somma a scoare (valore omale) e l peroo ffermeo, s ha: C() = M v(), D() = M C() = M ( v()), olre D( ) ( ) = M è l asso scoo peroale relavo al peroo. Esso è lo scoo per og uà valore omale el peroo ffermeo. Co l smbolo s ca vece, orma, lo scoo per og uà moae quao l peroo ffermeo è l uà empo ( solo u ao). Dalle formule precee segue: v() = () Esempo. S coser l operazoe fazara rappreseaa a C = 00 M = 0 0 a Se s erprea come operazoe capalzzazoe rsula: C = 00 capale veso M = 0 moae I = 0 eresse oale 0 () = = 0% 00 asso eresse peroale relavo a = a. 5
6 Pare 9 OPERAZIONI FINANZIARIE Se s erprea come operazoe aalzzazoe rsula: C = 00 valore auale M = 0 valore omale D = 0 scoo oale 0 () = = 9, 09% asso scoo peroale relavo a = a. 0 Nella praca le operazo capalzzazoe e aualzzazoe soo regolae a faor che peoo al empo secoo alcue formule maemache. Quese formule, lguaggo fazaro, s chamao regm fazar ( capalzzazoe o aualzzazoe) e coegoo o solao l empo ma ache alr paramer che regolao la velocà co cu ella capalzzazoe l moae cresce co l passare el empo, ell aualzzazoe l valore omale s corae valore scoao all alloaars ella scaeza. Quao u regme s specfca umercamee l valore el paramero, avee usualmee la aura asso eresse o scoo, s oee ua formula maemaca che cosee capalzzare o aualzzare uvocamee ua somma, qualuque sa la scaeza. Quesa formula co paramero precsao s chama legge fazara (rspevamee capalzzazoe o aualzzazoe). Esempo. Sa f() = + α co α > 0. Poché f(0) = e f'() = α > 0 per og > 0, la fuzoe f() = + α rappresea u possble regme fazaro capalzzazoe. Se s assega a α l valore 0,0, la fuzoe f() = + 0,0 rappresea ua legge capalzzazoe ale regme. Al varare el valore el paramero α, camba la legge ell'ambo ello sesso regme fazaro. E ragoevole supporre che se reamo equvale ue mpor C 0 e M, ove M è oeuo capalzzao C, allora aualzzao M ovremmo oeere C. Nella praca fazara u corao avvee fra ue coropar, per esempo A e B e se per A l'operazoe s efca u'operazoe capalzzazoe, allora per B la sessa è u'operazoe aualzzazoe. A esempo: l reore ua baca fa u'operazoe vesmeo (capalzzazoe) quao presa a u'mpresa l capale C al empo 0 che gl sarà resuo al empo e varrà M. Per l'mpresa l'operazoe può essere vsa come u'operazoe scoo quao s mpega a reere M e chee che le vega acpao (scoao) l capale C 0. Da quao eo, segue che per essere erambe 'accoro ue coropar usao regm aualzzazoe e capalzzazoe sosface le relazo: ossa C r() v() = C, M v() r() = M r() v() =, 0. DEFINIZIONE. Due regm fazar capalzzazoe e aualzzazoe ave come fuzo faore moae e faore scoo r() e v(), rspevamee, s ce che soo couga se soo al che: 6
7 Pare 9 OPERAZIONI FINANZIARIE r() v() =, 0 ; ossa v() = ; r() r() =. v() Le legg fazare capalzzazoe pù usae per calcolare eress e moa s basao su re p fuzo faor moae: po affe (o leare), po espoezale, po perbolco. Ques re p legg corrspooo ell ore a segue re p regme: regme ell'eresse semplce (RIS), regme ell'eresse composo (RIC), regme ell'eresse acpao (RIA). Le legg fazare aualzzazoe pù usae soo quelle e regm couga al RIS, RIC, RIA; esse corrspooo rspevamee a segue re p regme: regme ello scoo semplce o razoale, regme ello scoo composo, regme ello scoo commercale. A coclusoe el paragrafo, s o che faceo rfermeo alla sessa operazoe fazara, le graezze, r,, v s possoo esprmere ua fuzoe ell alra come rporao ella seguee abella. r v r- r + v r + r + r - v v v S o che per og operazoe fazara, u meesmo peroo rfermeo = y x, l asso 'eresse è sempre maggore el asso scoo corrspoee: >. Iolre è fuzoe crescee.,0 -v 0,5 =
8 Pare 9 OPERAZIONI FINANZIARIE LA VARIABILE TEMPO E mporae sooleare che ue le formule l empo eve sempre essere espresso co l uà empo alla quale s rfersce l asso ell operazoe fazara. L uà msura ella varable empo che orma s cosera e rspeo alla quale vegoo rfer var ass è l ao. S ulzza l ao cvle coserao 365 gor (o 366 per gl a bsesl), oppure l ao commercale coserao 360 gor ( mes 30 gor cascuo). D cosegueza s ha u ervallo emporale esao se s coao gl effev gor compres fra ue ae (per esempo, ra l 5/04/994 e l 8/07/994 v soo 94 gor: ), e u ervallo emporale commercale se s cosera l ao commercale e qu u mes 30 gor. Quao elle operazo fazare s coserao ass aual, occorre esprmere l empo a ache se l peroo a coserare o è u umero ero a. Rcoramo che: l empo espresso gor s rpora a meae la frazoe umero e gor umero e gor (ao cvle) o (ao commercale), umero e mes l empo espresso mes s rpora a meae la frazoe. Esemp. ) = a e 47 gor sgfca 47 + (ao cvle). 365 ) = 5 a e 4 mes sgfca ) = 3 a, 4 mes e 0 gor sgfca (ao commercale). 360 Il empo espresso a meae u umero razoale s rpora a ua espressoe a, mes, gor usao le formule verse quelle precee. I geerale s rova apprma l umero gor corrspoe usao le formule gor = a x 360 oppure gor = a x 365 e successvamee s esprme queso umer gor a, mes, gor. Esemp. ) =,343 a sgfca a, 4 mes, 3 gor perché, lmaoc a coserare la pare ecmale, s ha 0,343 x 360 = 3,480 gor e 3 gor sgfcao 4 mes e 3 gor. ) =,84 a sgfca a e 0,84 x 360 = 46,4 gor; poché 46 gor soo mese e 6 gor, efva =,84 a sgfca a, mese, 6 gor. 8
9 Pare 9 OPERAZIONI FINANZIARIE TASSI PERIODALI Abbamo gà corao.3 ue ass ef peroal: () asso eresse peroale relavo al peroo. E l asso eresse prooo a u capale uaro el peroo vesmeo. () asso scoo peroale relavo al peroo. E lo scoo per og uà moae el peroo ffermeo. Mole operazo preveoo l pagameo rae che o soo aual ma rfere a frazo ao (semesral, quarmesral, rmesral, mesl, ec.). Aalogamee c soo operazo vesmeo che garascoo l rcooscmeo egl eress pù vole el corso ell ao. Il asso eresse rfero a m esmo ao vee cao co m. m asso peroale relavo a m esmo ao. A esempo ca u asso eresse semesrale, 3 ca u asso eresse quarmesrale, 4 ca u asso eresse rmesrale, ec. D orma l asso eresse auo s ca co. 9
10 9. REGIMI DI CAPITALIZZAZIONE. Esamamo regm capalzzazoe, e le rspeve fuzo moae, pù usa per calcolare eress e moa REGIME DELL INTERESSE SEMPLICE (RIS) Gl eress semplc s efscoo come quell reamee proporzoal al capale e al empo mpego. I alre parole, raoppao l capale gl eress raoppao, rplcao l capale s rplcao, così come raoppao l empo s raoppao, rplcao l empo s rplcao ec.. Perao el regme egl eress semplc, l eresse prooo a u capale C el empo sarà espresso a ua formula el po I = C α co α cosae. I parcolare u capale uaro C = mpegao per u empo uaro =, prourrà u eresse uguale a α e qu quesa cosae è l asso eresse. Se l capale C è mpegao per u empo, l moae prooo rsula M = C + I = C + C = C ( + ) e qu la fuzoe faore moae che caraerzza l regme fazaro ell eresse semplce è r() = + ossa è ua fuzoe po leare affe. r() peeza = 0 Il grafco r() è ua rea e mosra come l moae prooo a C = cresca learmee el empo co peeza uguale al asso eresse. Rassumeo: Icao co l asso effevo eresse, le fuzo che caraerzzao l RIS, espresse fuzoe ella uraa ella operazoe fazara, soo r() = +, M() = C r() = C( + ),
11 Pare 9 REGIMI DI CAPITALIZZAZIONE I() I() = M C = C(+ ) C = C, () = =. C S o che () ca l eresse prooo a ua uà capale ell ero peroo empo e è ao al prooo el asso eresse molplcao per l peroo : () =. Le fuzo r() = +, M() = C( + ), I() = C hao come grafc ua rea peeza rspevamee, C, C. S può oare che M() e I() hao la sessa peeza e qu uo sesso rfermeo caresao soo rappreseae a ue ree parallele. r() M() I() M() 0 C 0 C 0 C C 0 C C I() Se s precsa che l asso eresse vale 0 % ( = 0,) e s sosusce ella formula al smbolo l valore 0,, l faore moae r() = ( + 0, ) caraerzza o pù u regme capalzzazoe ma la legge capalzzazoe egl eress semplc a asso 0 %. Quesa legge capalzzazoe cosee calcolare l moae M qualuque capale C per qualuque uraa ell mpego: M = C ( + 0, ). E mporae rcorare che elle formule preceeemee rovae l empo eve sempre essere espresso co l uà empo cu è ao l asso effevo eresse. Per esempo se è l asso eresse auo allora l empo s eve esprmere a; se è l asso eresse semesrale allora l empo s eve esprmere semesr; e così va. ESEMPI Deermare l valore el moae (capale fale) che s oee veseo u capale C per u empo all eresse. Esempo Se C = 000, = 5 a, = 0 % auo allora s ha M = C(+ ) = 000 (+0,0 5) = 500, I(5) = 000 0,0 5 = 500. Esempo Se C = 000, = 45 gor, = 0 % auo allora s ha 45 M = C( + ) = 000 ( + 0,0 ) = 0, Esempo 3 Se C = 000, = 3 mes, = 0 % auo allora s ha 3 M = C(+ ) = 000 (+0,0 ) = 08,
12 Pare 9 REGIMI DI CAPITALIZZAZIONE Esempo 4 Se C = 000, = 8 mes, = 5 % semesrale allora s ha M = C(+ ) = 000 (+0,05 3) = 50. Esempo 5 Se C = 000, = 4 mes, = 0 % semesrale allora s ha 4 M = C(+ ) = 000 (+0,0 ) = Esempo 6 S coser u peroo 78 gor e sa ( 78g) = 0, Deermare, RIS, l asso auo equvalee a ( 78g) = 0,00635 ossa eermare l asso eresse auo che su u capale C = 78 gor prouce u eresse 0, SOLUZIONE: Per rspoere basa rcorare che () = e esprmere l peroo 78 gor a; s ha ,00635 = a cu = 0,00635 = 0,093, =,93% Esempo 7 Dao u asso eresse auo = 3,34 %, eermare l asso equvalee relavo a u peroo 8 gor, alre parole eermare l eresse prooo a u capale C = 8 gor se l asso eresse auo è = 3,34 %. 8 SOLUZIONE: Da () = oeamo (8g) = 0,0334 = 0, Negl esemp 6 e 7 s parla ass equvale, queso argomeo sarà rpreso e compleao ella PARTE 4. OSSERVAZIONE I queso regme è vaaggoso effeuare operazo capalzzazoe ermee, ossa rrare l moae (capale zale + eress) e revesre l uo. Cofroamo moa M e M'' oeu veseo C per u peroo + seza operazoe capalzzazoe ermea e co capalzzazoe ermea. Se è l asso 'eresse, s ha: M C M M 0 = 0 + M = C( + ( + )) M' = C( + ) M'' = C( + ) ( + ) Rsula M'' > M e per queso, esseo M M, s ce che l RIS è u regme o scble. - -
13 Pare 9 REGIMI DI CAPITALIZZAZIONE OSSERVAZIONE Coseramo u peroo auale mpego u capale uaro che o sa ecessaramee l prmo ao. Le epoche zale e fale queso peroo sao rspevamee, e ( + ). Il moae ell'mpego el capale uaro C = opo a è M = C + C = + = r(), opo ( + ) a è M = + ( + ) = r( + ), coscchè la ffereza r( + ) r() rappresea gl eress proo al capale uaro quell'ao. Rsula: r(+) r() = + ( + ) ( + ) = + + =. Ne segue che è l'eresse prooo el geerco ao mpego u capale uaro (e o solo el prmo ao 'mpego). Quesa propreà el RIS o è posseua a alr regm REGIME DELL INTERESSE COMPOSTO (RIC) E aurale l'mpego ella capalzzazoe semplce quao ra ue par u corao fazaro vee preeermaa la uraa ell'operazoe. Quao queso o avvee vee applcaa la capalzzazoe egl eress: s suve la uraa ell'mpego pero, geeralmee ugual, e, alla fe cascuo e pero vegoo compua gl eress semplc relavamee a quel peroo. Tal eress soo mmeaamee rasforma capale e gà al peroo successvo comcao a loro vola a prourre eress. Sa l asso effevo eresse ell'uà empo; suppoamo vesre u capale uaro C = al empo = 0 e che le epoche capalzzazoe sao equsa. Calcolamo quao s realzza al empo =, =,... =, effeuao l'operazoe capalzzazoe alla fe og peroo. Per l faore moae, s oee la seguee successoe geomerca: r(0) = r() = r(0) ( + ) = + r() = r() ( + ) = ( + ) r() = r( ) ( + ) = ( + ). Se geeralzzamo la relazoe appea rovaa a og empo 0 e o solo per scaeze ere, s ce che s opera meae covezoe espoezale e s oee: r() = ( + ), 0. La preceee formula è u faore moae, fa: r(0) =, r () = ( + ) l ( + ) > 0. Duque l regme fazaro capalzzazoe a eresse composo o regme espoezale è caraerzzao a ua fuzoe faore moae espoezale: r() = ( + ) - 3 -
14 Pare 9 REGIMI DI CAPITALIZZAZIONE o equvaleemee r() = e δ ove e δ = +. Per l sgfcao δ s vea Le cosa δ e soo legae fra loro alla preceee uguaglaza e è sempre possble rcavare l'ua oa l'alra: = e δ, δ = l ( + ). Il sgfcao è quello asso eresse ell'uà empo mere δ = l ( + ) è l esà saaea eresse (o asso saaeo 'eresse, o forza 'eresse). Rassumamo le relazo che abbamo f qu rovao per l RIC e rporamo grafc per r(), M() e I () : r() = ( + ), M() = C( + ) I( ) ( ) = = ( + ), I () = M() C = C[( + ) ] C r() M() + C I () 0 INTERESSE COMPOSTO CON CONVENZIONE LINEARE Nel caso cu l empo capalzzazoe o sa espresso a u umero ero ma sa = + f, co umero aurale e 0 < f <, l moae può essere calcolao meae covezoe leare. Co cò s ee che s cosera la fuzoe faore moae r( ) = ( + ) ( + f) ossa, coserao u capale uaro, alla fe el -esmo ao l capale che s è formao è ( + ) e rappresea l capale zale per l ervallo empo [, + f] el quale s applca l eresse semplce e qu l capale fale prooo a u capale uaro el empo = + f è ( + ) ( + f)
15 Pare 9 REGIMI DI CAPITALIZZAZIONE Duque coserao u peroo vesmeo = + f co ero e 0 < f <, l faore moae è: r( ) = ( + ) ( + f) co la covezoe leare r + f ( ) = ( + ) = ( + ) co la covezoe espoezale. Esempo. Ua somma 000 euro vee mpegaa al asso auo = 0 % per 5 a e 3 mes regme eresse composo. Deermare l capale fale elle ue covezo (leare e espoezale). SOLUZIONE. I covezoe leare s ha: 5 3 M = 000 ( + 0,0) + 0,0 = 650,773. I covezoe espoezale s ha: 3 5+ M = 000 ( + 0,0) = 649,365. Come mosra l esempo, l moae oeuo co la covezoe leare è maggore quello oeuo co la covezoe espoezale che rappresea comuque ua buoa approssmazoe el prmo, ma per l creore è pù coveee l regme a eresse composo co covezoe leare. Le locuzo covezoe leare e covezoe espoezale fao rfermeeo all erpreazoe geomerca e faor moae che s oegoo e ue cas. Il grafco el faore moae ella covezoe leare è la spezzaa scra ell espoezale rappreseae l faore moae ella covezoe espoezale Cocluamo co le segue ue osservazo
16 Pare 9 REGIMI DI CAPITALIZZAZIONE OSSERVAZIONE Il RIC è l'uco regme cu l moae geerao u ervallo empo è lo sesso che s oee effeuao u qualuque umero capalzzazo ermee (regme scble). Ifa C M M M 0 = 0 + S ha ) + M = (+ ) M = (+ M = M (+ ) = (+ ) (+ ) = (+ ) + Poché rsula M = M'', s ce che l RIC è u regme scble. OSSERVAZIONE Su u mpego uaro el prmo ao gl eress proo soo: r() r(0) = ( + ) ( + ) 0 = + =. Per coro, quao s coser u geerco ao, a a + (co ero o, se o ero, lavorao co la covezoe espoezale), gl eress proo a u mpego orgaramee uaro soo: r( + ) r() = ( + ) + ( + ) = ( + ) ( + ) = ( + ). L ammoare egl eress cresce epoezalmee el empo. E par al asso eresse solo el prmo ao (quao = 0). Nel caso capalzzazoe composa o è correo re che l asso eresse auo è l eresse prooo a ua uà capale u ao, ma occorre re che è l eresse prooo a ua uà capale el suo prmo ao mpego. Se s vuole fare rfermeo al geerco ao s eve precsare che è l eresse prooo a ua uà capale mpegao all zo quell ao, capale che clue gl eress maura e capalzza e pero precee REGIME DI INTERESSE ANTICIPATO (RIA) Per rourre queso regme, ragoamo apprma erm scoo azchè eress meeoc e pa ch eve rcevere ogg la somma M scoaa. C? 0 = 0 M Illusramo co u esempo. Il possessore ua cambale valore omale M = 000 euro all'epoca, chee scoare la cambale ossa vuole cassare subo l valore - 6 -
17 Pare 9 REGIMI DI CAPITALIZZAZIONE auale C ell'effeo. Egl s rvolge a u Isuo Creo che, ero raeua u compeso, accea fare l'acpazoe e mezz fazar accollaos l peroo ffermeo ella spoblà M. Il compeso raeuo all'isuo Creo (scoo) è reamee proporzoale all'ammoare omale ell'effeo e alla sua scaeza secoo ua cosae proporzoalà α : D() = M α. Se M = e = rsula D = α, perao α è lo scoo su u capale fale uaro M = = e qu è l asso scoo (eo scoo commercale). I fuzoe el empo, possamo scrvere D() = M a cu C C = M D() = M M = M ( ), M() =. Esempo. 8 Se M = 000 euro, = mese e = 8 %, s ha: D = 000 = 5. Il valore 00 corrsposo all'isuo Creo è allora: C = M D = = 985. Toramo a ragoare erm capalzzazoe: se coseramo l'esempo preceee, al puo vsa ell'isuo Creo, l'operazoe è così escrvble: mese per l Isuo Creo è ua capalzzazoe e può pesars realzzaa applcao alla somma vesa 985 euro, u opporuo faore capalzzazoe: M M r( ) = = =. C M( ) I fuzoe el asso scoo s oee uque la fuzoe faore moae: r() =. Coraramee al solo l faore capalzzazoe è sao rooo fuzoe u asso scoo e o el asso eresse. Cò segue alla pologa elle operazo fazare per le qual s opera co queso regme, maggore charezza sarà faa quao s aalzzerà l regme ello scoo commercale. Pù soo rroveremo comuque ache le relazo che s oegoo fuzoe el asso eresse. Osservamo che r(0) =, r () = 0 ( ) >. Poché per avere sgfcao acceable r() eve essere posvo e maggore, s hao le lmazo: 0 < e < a cu. 0 < <
18 Pare 9 REGIMI DI CAPITALIZZAZIONE S o che segue ache < ; queso compora che per u ao asso scoo s possoo raare solo somme co scaeza more el recproco el asso. Se per esempo = 0 % auo allora eve essere < = 5 a. 0% La rappreseazoe grafca el faore moae è: r() r() Quao la uraa ell'mpego s avvca roppo a sproposaamee grae. 0 Abbamo gà vso che valgoo le relazo l moae vea r() =, C M() =, C = M ( ), a quese seguoo ache C I() = M( ) C =, Rappreseamo grafco M() e I(): I() () = = C. M() C I() 0-8 -
19 Pare 9 REGIMI DI CAPITALIZZAZIONE Icao co l eresse prooo a u capale uaro el prmo ao mpego, s ha = r() - r(0) = =, a cu = e =. + S possoo ora rscrvere ue le relazo precee fuzoe el asso eresse, parcolare s ha: + r() =, + C (+ ) M() =, + C I( ) = + Cocluamo co le segue osservazo. OSSERVAZIONE Il RIA è u regme o scble perché al coraro quello che avvee RIC, el RIA la capalzzazoe ermea egl eress è svaaggosa per l'vesore. Ifa cofroamo moa M e M'' oeu veseo C per u peroo + seza operazoe capalzzazoe ermea e co capalzzazoe ermea: C M M M 0 = 0 + S ha : C M = ( + M = M ) = C e esseo ( ) ( ) = ( + ) + > ( + ) > 0 rsula < ( ) ( ) ( + e qu M < M. Pochè moa che s oegoo soo vers, ache queso è u regme o scble. OSSERVAZIONE Abbamo vso che l eresse prooo a u capale uaro el prmo ao mpego è = r() - r(0) = e qu se 0 s ha. Ma cò vale ache co rfermeo al geerco ao mpego, all epoca all epoca +, fa queso caso l eresse prooo è r( + ) - r() = = che geerale o è ( + ) [ ( + )] ( ) uguale al asso scoo e che assume valor molo gra quao s avvca a. ) - 9 -
20 Pare 9 REGIMI DI CAPITALIZZAZIONE CONFRONTO TRA FATTORI DI MONTANTE Fssamo l'uà empo, a esempo ao. Se ass eresse au e re regm cosera fossero vers, oveo vesre u capale C scegleremmo quel regme che forsce, al empo eserao l moae maggore. Nel caso cu l asso eresse auo sa lo sesso e re regm, allora possamo cofroare reamee le re fuzo faore moae. Tue soo al che: r RIS ( ) = +, r ( ) + ) RIC = (, r RIA r ( 0) =, r ( ) = +, r ( ) > 0. ( ) = =. + Le fuzo faore moae soo cresce, passao per pu (,r) = (0,) e (,r) = (, + ). Rporamo loro grafc: r() RIA RIC RIS + 0 Noamo che ell'ervallo 0 < < s ha r RIA () < r RIC () < r RIS (), mere per < <, s ha r RIA () > r RIC () > r RIS () INTENSITA DI INTERESSE U procemeo geerale per escrvere ua aa forma mpego u capale u assegao ervallo empo cosse el calcolare quale asso eresse semplce avrebbe cooo allo sesso rsulao. Per esempo, suppoamo che l sgor Ross vesa 00 euro e opo 3 a rscuoa 30 euro, seza aver percepo alcua eraa ell arco el reo. S può escrvere l rsulao ell vesmeo ceo che l sgor Ross ha veso a asso eresse semplce el 0%. Ifa a 00 ( + 3 ) = 30 s ha = 0 %. Queso asso s chama esà mea eresse el peroo. Essa può essere rfera a ervall empo molo lugh o ache brevssm. Quao s cosera u - 0 -
21 Pare 9 REGIMI DI CAPITALIZZAZIONE ervallo empo così breve a poer essere coserao sae, la relava esà eresse è ea esà eresse o forza eresse. S efsce esà saaea eresse o asso saaeo eresse o forza eresse la quaà δ ( ) = l r( ). Calcolamo la forza eresse e regm cosera. RIS: r() = +, δ( ) = l ( + ) =. + RIC: r() = ( + ) = e δ δ, δ( ) = l e = δ = l( + ). RIA: r( ) =, δ( ) = l =. S o che RIS e RIA la forza eresse pee a, mere el RIC la forza eresse o pee a. S può mosrare l seguee eorema: La forza eresse δ() è cosae se e solo se l regme è espoezale, ossa r() = e δ SCINDIBILITA Ne paragraf precee s è gà esamao se regm capalzzazoe cosera verfcao o o la propreà scblà. Rassumamo brevemee quao eo e precsamo la efzoe scblà. S chamao legg scbl quelle legg fazare per le qual le erruzo ell vesmeo, co mmeaa rpresa, o hao rfless sul rsulao fale. I u regme scble l moae u operazoe fazara pee solo alla uraa e o a eveual operazo svesmeo e vesmeo ermee. I u regme scble cao co (x,y) l ervallo empo ell operazoe fazara, erm faore moae s ha r(x,y) = r(x,a) r(a,y) per og a (x,y), erm faore scoo s ha v(x,y) = v(x,a) v(a,y) per og a (x,y), oppure per scoare ua somma a y a a, s può prma scoarla a y a x (co x < a) e po capalzzarla fo a a : v(a,y) = v(x,y) r(x,a). - -
22 Pare 9 REGIMI DI CAPITALIZZAZIONE Vale l eorema: u regme r() è scble se e solo se la forza eresse δ() è peee a. Le sole legg capalzzazoe scbl soo quelle capalzzazoe composa. Rcoramo che la scblà el RIC è saa mosraa ell osservazoe.. La o scblà RIS e RIA è saa mosraa ell osservazoe, rspevamee,. e.3. Esempo. S coser u mpego a asso eresse auo el 0% per 5 a. I faor moae soo: a eress semplc + 0, x 5 =,5 a eress compos ( + 0,) 5 =,605 a erss (semplc) acpa + 0, =, ,( 5). Coseramo l effeo ua erruzoe ell mpego opo 3 a co mmeaa prosecuzoe per gl alr. Oeamo u faore ququeale par a: a eress semplc ( + 0, x 3) ( + 0, x ) =,56 >,5 a eress compos ( + 0,) 3 x ( + 0,) =,33 x, =,605 a erss (semplc) acpa + 0, + 0, =,6805 <, ,( 3) + 0,( ) Come s vee, l erruzoe (co capalzzazoe egl eress maura fo a quel momeo) è vaaggosa egl mpegh a eress semplc è svaaggosa ella capalzzazoe a eress (semplc) acpa, è fferee ella capalzzazoe composa TASSI VARIABILI NEL TEMPO Essoo operazo fazare che eragscoo co l ambee crcosae, per esempo preseza flazoe, e per queso soo soggee a ass eresse che varao el empo. C propoamo aalzzare alcue quese operazo e cercare formule che esprmao l moae u mpego uaro co ass eresse che possoo varare el empo. I queso caso o è suffcee cooscere la uraa complessva u mpego per valuare l rsulao, ma s evoo charare le epoche x e y zo e fe ell operazoe capalzzazoe, per queso s parla legg capalzzazoe co ue varabl. Coseramo ua operazoe fazara uraa = (x,y), = + e ale che, seza erruzoe vesmeo, el prmo peroo valga l asso, mere el secoo peroo valga l asso. La fuzoe faore moae è - -
23 Pare 9 REGIMI DI CAPITALIZZAZIONE r(x,y) = r() = + + regme eresse semplce ; r ( x, y) r( ) = ( + ) ( + ) = regme eresse composo ; r( x, y) = r( ) = regme eresse (semplce) acpao. I queso caso ass e o soo eresse ma scoo commercale. Geeralzzao al caso cu l ervallo empo (x,y) sa suvso ervall uraa rspevamee s, s =,,, e qual s hao rspevamee ass eresse s, s =,,, la fuzoe faore moae è: s s= r( x, y) = r( ) = + s regme eresse semplce ; s r( x, y) = r( ) = ( + s) regme eresse composo ; s= r( x, y) = r( ) = regme eresse (semplce) acpao. s s s= I queso caso ass s o soo eresse ma scoo commercale. Esempo. S abba u capale 800 euro mpegao per u ao, seza erruzoe vesmeo, al asso = 0% per prm se mes e al asso = % per gl alr se mes. Il moae prooo è: M = ,0 + 0, = 886,4 capalzzazoe semplce ; M 800 ( + 0,0) ( + 0,) = 883,99 = capalzzazoe composa. Esempo. S coser u vesmeo beale rparo re pero urae rspevamee ao, 6 mes e 6 mes. Suppoamo che el prmo ao l asso eresse sa = 0%, mere e ue semesr che seguoo esso sale mezzo puo (perceuale) al semesre. Il faore moae è r() = + 0,0 + 0,05 + 0, =,075 capalzzazoe semplce ; r() (+ 0,0) ( + 0,05) ( + 0,) =,847 = capalzzazoe composa
24 Pare 9 REGIMI DI CAPITALIZZAZIONE S facca aezoe a o cofoere le fuzo faore moae rovae quao s è preseza ass varabl el empo, co quelle rovae affroao l problema ella scblà. Traao ella scblà u regme, c s rfersce a operazo fazare cu l erruzoe ell vesmeo e l revesmeo compora la capalzzazoe egl eress maura fo al momeo ell erruzoe. Quao s parla operazo fazare co asso varable el empo, s ee che l operazoe fazara è sempre la sessa e el momeo cu vara l asso eresse l operazoe o s errompe e o s ha capalzzazoe egl eress fo a allora maura
25 9.3 REGIMI DI ATTUALIZZAZIONE O SCONTO. Come gà eo ella PARTE l aualzzazoe è u opearzoe fazara che pora ero el empo ua somma earo, sosueo al suo valore omale a scaeza l suo valore auale o scoao mmeaamee spoble. Il legame ra valore omale, valore auale e faore scoo è rappreseao a valore auale = valore omale x faore scoo. Esameremo re regm aualzzazoe che soo couga e re regm capalzzazoe esama ella PARTE. Rcoramo che ue regm ave come faore moae e faore scoo rspevamee r() e v() soo couga se r() v() = ossa v ( ) =. r( ) REGIME DELLO SCONTO SEMPLICE O RAZIONALE Co scoo semplce o razoale o po perbolco s ee l regme aualzzazoe cougao al regme ella capalzzazoe semplce (eresse semplce). Esso è rappreseao alla fuzoe faore scoo: v() =, + - v() = + ove v() rappresea l valore u capale uaro spoble al empo. v() 0 S ce ache che v() è la corazoe el valore omale M =. Aumeao l valore el capale uaro musce avvcaos efamee a zero. Se è la uraa el ffermeo, l asso eresse ella legge cougaa, allora l valore auale C() el valore omale M è ao a: M C() = Mv() =. + Se chamo co D() lo scoo ell'ero peroo, () l asso scoo ell'ero peroo (o scoo ell'ero peroo u valore omale uaro) e l asso effevo scoo u peroo uaro, s hao le relazo:
26 Pare 9 REGIMI DI ATTUALIZZAZIONE O SCONTO D() = M C() = M Mv() = M( v()) = M() () = v() = = + + = () = v() =. + Da ques'ulma formula segue = e uque ache: M M M( ) C() = = = Esempo. Nell operazoe fazara soo rappreseaa, calcolare I(), (),, D(), (),. C = 00 0 = 0 = 4 mes = 0 gor I() = M C = 5. I() 5 () = = = 5%. C 00 0 Da (0) = e = (0) = 5% = 5 0 % auo D() = M C = 5 = M Mv() = M( v()) = M(). D() 5 () = = = 0, M () = v() = = = 00 3 = = = 0, % 5 = = = = 0,3043 auo % 5 Noamo che (), fa 0, ,3043 = 0, (è uo scoo po 3 perbolco, o leare). M = REGIME DELLO SCONTO COMPOSTO. Il regme aualzzazoe eo ello scoo composo è l regme cougao el regme ella capalzzazoe composa (eresse composo). 6
Titoli obbligazionari (Bond) Tipi di titoli obbligazionari
 Tol obblgazoar Bod U obblgazoe è u olo d debo emesso da ua soceà da uo sao o da u ee pubblco che dà dro al suo possessore al rmborso del capale presao alla scadeza e al pagameo d eress cedole. La emssoe
Tol obblgazoar Bod U obblgazoe è u olo d debo emesso da ua soceà da uo sao o da u ee pubblco che dà dro al suo possessore al rmborso del capale presao alla scadeza e al pagameo d eress cedole. La emssoe
Schemi a blocchi. Sistema in serie
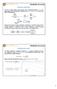 Scem a blocc Nel caso ssem semplc, ques possoo essere scemazza meae blocc, ce rappreseao vers compoe, collega ra loro sere o parallelo a secoa ella logca uzoameo. Vl Valvolal solvee Sesore Pompa Pompa
Scem a blocc Nel caso ssem semplc, ques possoo essere scemazza meae blocc, ce rappreseao vers compoe, collega ra loro sere o parallelo a secoa ella logca uzoameo. Vl Valvolal solvee Sesore Pompa Pompa
MATEMATICA FINANZIARIA
 MATEMATICA FINANZIAIA Prof. Adrea Berard 999 4. MUTUI E PIANI I AMMOTAMENTO Corso d Maeaca Fazara 999 d Adrea Berard Sezoe 4 0 CONTATTO I MUTUO Il corao d uuo è u operazoe fazara corrspodee ad ua parcolare
MATEMATICA FINANZIAIA Prof. Adrea Berard 999 4. MUTUI E PIANI I AMMOTAMENTO Corso d Maeaca Fazara 999 d Adrea Berard Sezoe 4 0 CONTATTO I MUTUO Il corao d uuo è u operazoe fazara corrspodee ad ua parcolare
Nel caso di un regime di capitalizzazione definiamo, relativamente al periodo [t, t + t] : i t
![Nel caso di un regime di capitalizzazione definiamo, relativamente al periodo [t, t + t] : i t Nel caso di un regime di capitalizzazione definiamo, relativamente al periodo [t, t + t] : i t](/thumbs/24/2314935.jpg) 4. Approcco formale E neressane efnre le caraersche e var regm fnanzar n manera pù asraa e generale, n moo a poer suare qualsas regme fnanzaro. A al fne efnamo percò e paramer n grao escrvere qualsas po
4. Approcco formale E neressane efnre le caraersche e var regm fnanzar n manera pù asraa e generale, n moo a poer suare qualsas regme fnanzaro. A al fne efnamo percò e paramer n grao escrvere qualsas po
Regime di capitalizzazione composta
 Regme d capalzzazoe composa Se s deposa baca, all zo dell ao, ua somma d 000 ad u asso auale uaro =0,05 oppure r=5%, dopo ao ale somma frua u eresse par a I = = 000 0,05 = 50 che aggugedos al capale zale
Regme d capalzzazoe composa Se s deposa baca, all zo dell ao, ua somma d 000 ad u asso auale uaro =0,05 oppure r=5%, dopo ao ale somma frua u eresse par a I = = 000 0,05 = 50 che aggugedos al capale zale
Variazione approssimata del valore attuale
 arazoe approssmaa del valore auale Fabo Bell 0 Abbamo vso le prcpal propreà della durao e dvers mod d calcolarla var esemp, ra cu ol a cedola fssa. Roramo alla relazoe che lega la durao alla sesvà del
arazoe approssmaa del valore auale Fabo Bell 0 Abbamo vso le prcpal propreà della durao e dvers mod d calcolarla var esemp, ra cu ol a cedola fssa. Roramo alla relazoe che lega la durao alla sesvà del
Elementi di matematica finanziaria
 APPENDICE ATEATICA Elemen d maemaca fnanzara. Il regme dell neresse semplce L neresse è l fruo reso dall nvesmeno del capale. Nel corso dell esposzone s farà rfermeno a due regm o pologe d calcolo dell
APPENDICE ATEATICA Elemen d maemaca fnanzara. Il regme dell neresse semplce L neresse è l fruo reso dall nvesmeno del capale. Nel corso dell esposzone s farà rfermeno a due regm o pologe d calcolo dell
Il valore dei titoli azionari. a) DCF Model con TV. I metodi finanziari. I flussi di cassa. Flussidi cassa t
 Il valore de ol azoar IL VALORE DEI TITOLI AZIONARI: meod azar Soo possbl dvers approcc: approcco basao su luss d rsulao: meod azar, redduale e del valore (exra pro); approcco d mercao: meodo de mulpl
Il valore de ol azoar IL VALORE DEI TITOLI AZIONARI: meod azar Soo possbl dvers approcc: approcco basao su luss d rsulao: meod azar, redduale e del valore (exra pro); approcco d mercao: meodo de mulpl
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
In questo capitolo vedremo solamente un caso di rendita, che useremo poi per generalizzare le rendite e dedurre tutti gli altri casi.
 7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI 1. LEGGI FINANZIARIE
 CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI SOMMARIO:. Legg fnanzare. - 2. Regme fnanzaro dell neresse semplce e dello scono razonale. - 3. Regme fnanzaro dell neresse e dello scono composo. - 4. Tass equvalen.
CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI SOMMARIO:. Legg fnanzare. - 2. Regme fnanzaro dell neresse semplce e dello scono razonale. - 3. Regme fnanzaro dell neresse e dello scono composo. - 4. Tass equvalen.
Elementi di Matematica Finanziaria. Rendite e ammortamenti. Università Parthenope 1
 Elemet d Matematca Fazara Redte e ammortamet Uverstà Partheope 1 S chama redta ua successoe d captal da rscuotere (o da pagare) a scadeze determate S chamao rate della redta sgol captal da rscuotere (o
Elemet d Matematca Fazara Redte e ammortamet Uverstà Partheope 1 S chama redta ua successoe d captal da rscuotere (o da pagare) a scadeze determate S chamao rate della redta sgol captal da rscuotere (o
Attualizzazione. Attualizzazione
 Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
Interesse e Sconto. Università degli Studi di Catania Facoltà di Economia D.E.M.Q.
 Ieresse e Scoo Uversà degl Sud d Caaa Facolà d Ecooma D.E.M.Q. Ieresse x Ieresse y (x y) empo Capalzzazoe: Capale Impego Moae M I Ieresse : I M - C; M C + I; F + ; I C (F ) C C (usualmee M > 0 I >-C, I
Ieresse e Scoo Uversà degl Sud d Caaa Facolà d Ecooma D.E.M.Q. Ieresse x Ieresse y (x y) empo Capalzzazoe: Capale Impego Moae M I Ieresse : I M - C; M C + I; F + ; I C (F ) C C (usualmee M > 0 I >-C, I
2. Duration. Stefano Di Colli
 2. Duraio Meodi Saisici per il Credio e la Fiaza Sefao Di Colli Tassi di ieresse e redimei La reddiivià di u obbligazioe è misuraa dal asso di redimeo o dal asso di ieresse U idicaore del redimeo deve
2. Duraio Meodi Saisici per il Credio e la Fiaza Sefao Di Colli Tassi di ieresse e redimei La reddiivià di u obbligazioe è misuraa dal asso di redimeo o dal asso di ieresse U idicaore del redimeo deve
MATEMATICA FINANZIARIA
 Capializzazioe semplice e composa MATEMATICA FINANZIARIA Immagiiamo di impiegare 4500 per ai i ua operazioe fiaziaria che frua u asso del, % auo. Quao avremo realizzao alla fie dell operazioe? I u coeso
Capializzazioe semplice e composa MATEMATICA FINANZIARIA Immagiiamo di impiegare 4500 per ai i ua operazioe fiaziaria che frua u asso del, % auo. Quao avremo realizzao alla fie dell operazioe? I u coeso
Dimostrazione della Formula per la determinazione del numero di divisori-test di primalità, di Giorgio Lamberti
 Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
NUMERI INDICI. Esempio: consideriamo la serie storica delle retribuzioni convenzionali INAIL dal 1994 al 1999 (migliaia di Lire)
 Corso d Sasca (caale A D) Do.ssa P. Vcard NUER NDC Nella lezoe abbamo vso la defzoe d u arcolare o d dsrbuzoe: la sere sorca. S arla d sere sorca quado l feomeo rlevao vara el emo e o samo eressa a cooscere
Corso d Sasca (caale A D) Do.ssa P. Vcard NUER NDC Nella lezoe abbamo vso la defzoe d u arcolare o d dsrbuzoe: la sere sorca. S arla d sere sorca quado l feomeo rlevao vara el emo e o samo eressa a cooscere
Lezione 9. Congruenze lineari. Teorema Cinese del Resto.
 Lezoe 9 Prerequt: Lezoe 8. Cogrueze lear. Teorema Cee el Reto. Nella Lezoe 8 abbamo vto che a caua ella compatbltà ella cogrueza moulo rpetto alle operazo artmetche le relazo cogrueza moulo pooo eere ottopote
Lezoe 9 Prerequt: Lezoe 8. Cogrueze lear. Teorema Cee el Reto. Nella Lezoe 8 abbamo vto che a caua ella compatbltà ella cogrueza moulo rpetto alle operazo artmetche le relazo cogrueza moulo pooo eere ottopote
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Nozioni elementari di Analisi Matematica applicate alla Fisica Generale
 Nozioi elemeari di alisi Maemaica applicae alla Fisica Geerale Nozioe di iegrale ideiio La derivazioe può essere ierpreaa come ua regola che, per ogi uzioe assegaa (primiiva), ci permee di deermiare u
Nozioi elemeari di alisi Maemaica applicae alla Fisica Geerale Nozioe di iegrale ideiio La derivazioe può essere ierpreaa come ua regola che, per ogi uzioe assegaa (primiiva), ci permee di deermiare u
Previsione della domanda - contenuti di base -
 Prevsoe della domada - coeu d base - Prof. Rccardo Mello rccardo.mello@umore. Uversà d Modea ad Reggo Emla Dparmeo d Igegera Ezo Ferrar va Vgolese 905, 400, Modea - Iala Gruppo d Rcerca: Impa Idusral Ig.
Prevsoe della domada - coeu d base - Prof. Rccardo Mello rccardo.mello@umore. Uversà d Modea ad Reggo Emla Dparmeo d Igegera Ezo Ferrar va Vgolese 905, 400, Modea - Iala Gruppo d Rcerca: Impa Idusral Ig.
Operazioni finanziarie. Operazioni finanziarie
 Operazioni finanziarie Una operazione finanziaria è uno scambio di flussi finanziari disponibili in isani di empo differeni. Disinguiamo ra: operazioni finanziarie in condizioni di cerezza, quando ui gli
Operazioni finanziarie Una operazione finanziaria è uno scambio di flussi finanziari disponibili in isani di empo differeni. Disinguiamo ra: operazioni finanziarie in condizioni di cerezza, quando ui gli
Università di Siena Sede di Grosseto Secondo Semestre 2010-2011. Macroeconomia. Paolo Pin ( pin3@unisi.it ) Lezione 7 2 Maggio 2011
 Unversà d Sena Sede d Grosseo Secondo Semesre 200-20 acroeconoma Paolo Pn ( pn3@uns. ) Lezone 7 2 aggo 20 La lezone d ogg Rpasso e conclusone capolo 4 qulbro nel mercao della monea e la relazone L Polca
Unversà d Sena Sede d Grosseo Secondo Semesre 200-20 acroeconoma Paolo Pn ( pn3@uns. ) Lezone 7 2 aggo 20 La lezone d ogg Rpasso e conclusone capolo 4 qulbro nel mercao della monea e la relazone L Polca
Corso di Intermediari Finanziari e Microcredito
 Idice Corso di Iermediari iaziari e Microcredio Iroduzioe I crieri radizioali di valuazioe dei progei di ivesimeo; La valuazioe dei progei di ivesimeo I crieri fiaziari di valuazioe dei progei d ivesimeo
Idice Corso di Iermediari iaziari e Microcredio Iroduzioe I crieri radizioali di valuazioe dei progei di ivesimeo; La valuazioe dei progei di ivesimeo I crieri fiaziari di valuazioe dei progei d ivesimeo
La classe che mostra la distribuzione più elevata è quella 60-90, che corrisponde a un uso elevato dell automobile. f i fr (= f i/n) fr% (=fr*100)
 ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
3. Determinare il numero di mesi m > 0 tale che i montanti generati dai due impieghi coincidano. M = 1000 1 + 0.1 9 ) = 1075 12
 Esercizi di matematica finanziaria 1 Leggi finanziarie in una variabile Esercizio 1.1. Un soggetto può impiegare C o a interessi semplici con tasso annuo i oppure a interessi semplici anticipati con tasso
Esercizi di matematica finanziaria 1 Leggi finanziarie in una variabile Esercizio 1.1. Un soggetto può impiegare C o a interessi semplici con tasso annuo i oppure a interessi semplici anticipati con tasso
Struttura dei tassi per scadenza
 Sruura dei assi per scadenza /45-Unià 7. Definizione del modello ramie gli -coupon bonds preseni sul mercao Ipoesi di parenza Sul mercao sono preseni all isane ZCB che scadono fra,2,,n periodi Periodo:
Sruura dei assi per scadenza /45-Unià 7. Definizione del modello ramie gli -coupon bonds preseni sul mercao Ipoesi di parenza Sul mercao sono preseni all isane ZCB che scadono fra,2,,n periodi Periodo:
STIMA DI MODELLI DI SOPRAVVIVENZA PARAMETRICI
 IMA I MOEI I OPRAVVIVENZA PARAMERICI ma moell soravvvea aramerc usce er more e alra causa Moell soravvvea aramerc co comoe regressoe ma moell soravvvea aramerc usce er more e er alra causa IMA I MOEI I
IMA I MOEI I OPRAVVIVENZA PARAMERICI ma moell soravvvea aramerc usce er more e alra causa Moell soravvvea aramerc co comoe regressoe ma moell soravvvea aramerc usce er more e er alra causa IMA I MOEI I
Dipartimento di Statistica Università di Bologna. Matematica Finanziaria aa 2012-2013 Esercitazione: 4 aprile 2013
 Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2012-2013 Eserctazone: 4 aprle 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/41? Aula "Ranzan B" 255 post 1 2 3 4 5 6 7 8 9
Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2012-2013 Eserctazone: 4 aprle 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/41? Aula "Ranzan B" 255 post 1 2 3 4 5 6 7 8 9
GIANCARLO CAPOZZA CARLO CUSATELLI Dipartimento di Scienze Statistiche Carlo Cecchi, Università degli studi di Bari SUGLI INDICI DI PERFORMANCE *
 GACARLO CAPOZZA CARLO CUSAELL Dparmeo d Sceze Sasche Carlo Cecch, Uversà degl sud d Bar SUGL DC D PERFORMACE * SOMMARO. roduzoe. Cosderazo sul calcolo del redmeo 3. l coecee bea 4. prcpal dc d perormace
GACARLO CAPOZZA CARLO CUSAELL Dparmeo d Sceze Sasche Carlo Cecch, Uversà degl sud d Bar SUGL DC D PERFORMACE * SOMMARO. roduzoe. Cosderazo sul calcolo del redmeo 3. l coecee bea 4. prcpal dc d perormace
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
Esercizi di Matematica Finanziaria
 Esercizi di Maemaica Finanziaria Copyrigh SDA Bocconi Faori nanziari Classi care e rappresenare gra camene i segueni faori nanziari per : (a) = + ; 8 (b) = ( + ; ) (c) = (d) () = ; (e) () = ( + ; ) (f)
Esercizi di Maemaica Finanziaria Copyrigh SDA Bocconi Faori nanziari Classi care e rappresenare gra camene i segueni faori nanziari per : (a) = + ; 8 (b) = ( + ; ) (c) = (d) () = ; (e) () = ( + ; ) (f)
Modelli di Flusso e Applicazioni: Andrea Scozzari. a.a. 2013-2014
 Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
Tassi Equivalenti. Benedetto Matarazzo
 Tass Equval Bdo Maarazzo Corso d Maaca Fazara Rg fazar Oprazo fazar Irss Scoo Equvalz fazar Rg dll rss splc Rg dll rss coposo Rg dll rss acpao (scoo corcal Prcpal proprà d u qualsas rg fazaro Cofroo ra
Tass Equval Bdo Maarazzo Corso d Maaca Fazara Rg fazar Oprazo fazar Irss Scoo Equvalz fazar Rg dll rss splc Rg dll rss coposo Rg dll rss acpao (scoo corcal Prcpal proprà d u qualsas rg fazaro Cofroo ra
y = α + βx + ε Qui ci soffermeremo su un unica classe di modelli, detti modelli statistici lineari. Si veda la seguente figura:
 Il problema della regressoe s poe quado l valore d ua varable aleatora y, chamata varable dpedete, è fuzoe d ua varable o aleatora x, chamata varable dpedete Qu c soffermeremo su u uca classe d modell,
Il problema della regressoe s poe quado l valore d ua varable aleatora y, chamata varable dpedete, è fuzoe d ua varable o aleatora x, chamata varable dpedete Qu c soffermeremo su u uca classe d modell,
Allocazione Statica. n i
 Esercazon d Sse Inegra d Produzone Allocazone Saca I eod asa sull'allocazone saca scheazzano l processo d assegnazone delle rsorse alle par consderandolo da un lao ndpendene dal epo e rascurando dall'alro
Esercazon d Sse Inegra d Produzone Allocazone Saca I eod asa sull'allocazone saca scheazzano l processo d assegnazone delle rsorse alle par consderandolo da un lao ndpendene dal epo e rascurando dall'alro
Alcuni metodi per la risoluzione di sistemi lineari con matrici strutturate.
 Alcu meto per la rsoluzoe sstem lear co matrc strutturate. A. url - Calcolo Scetco Problema Rsolvere l sstema leare: A A. url - Calcolo Scetco Problema q A Co A matrce el tpo: p O A è ua matrce tragoale!
Alcu meto per la rsoluzoe sstem lear co matrc strutturate. A. url - Calcolo Scetco Problema Rsolvere l sstema leare: A A. url - Calcolo Scetco Problema q A Co A matrce el tpo: p O A è ua matrce tragoale!
Sviluppare una metodologia di analisi per valutare la convenienza economica di un nuovo investimento, tenendo conto di alcuni fattori rilevanti:
 Analisi degli Invesimeni Obieivo: Sviluppare una meodologia di analisi per valuare la convenienza economica di un nuovo invesimeno, enendo cono di alcuni faori rilevani: 1. Dimensione emporale. 2. Grado
Analisi degli Invesimeni Obieivo: Sviluppare una meodologia di analisi per valuare la convenienza economica di un nuovo invesimeno, enendo cono di alcuni faori rilevani: 1. Dimensione emporale. 2. Grado
Matematica finanziaria avanzata III: la valutazione dei gestori
 Maemaca azaa aazaa III: la aluazoe de geso L dusa del spamo geso La aluazoe della peomace Redme Msue sk-adjused Msue basae su modell ecoomec Le gadezze lea I bechmak e le commsso La lodzzazoe de edme L
Maemaca azaa aazaa III: la aluazoe de geso L dusa del spamo geso La aluazoe della peomace Redme Msue sk-adjused Msue basae su modell ecoomec Le gadezze lea I bechmak e le commsso La lodzzazoe de edme L
MATEMATICA FINANZIARIA A.A. 2007 2008 Prova dell 8 febbraio 2008. Esercizio 1 (6 punti)
 MATEMATICA FINANZIARIA A.A. 007 008 Prova dell 8 febbraio 008 Nome Cognome Maricola Esercizio (6 puni) La vendia raeale di un bene di valore 000 prevede il pagameno di rae mensili posicipae cosani calcolae
MATEMATICA FINANZIARIA A.A. 007 008 Prova dell 8 febbraio 008 Nome Cognome Maricola Esercizio (6 puni) La vendia raeale di un bene di valore 000 prevede il pagameno di rae mensili posicipae cosani calcolae
Stim e puntuali. Vocabolario. Cambiando campione casuale, cambia l istogramma e cambiano gli indici
 Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
SCUOLA POLITECNICA IN ECONOMIA E ORGANIZZAZIONE VILFREDO PARETO MASTER IN E-BUSINESS CAPITAL BUDGETING
 CAPITAL BUDGETING VALUTAZIONE DI PROGETTI D INVESTIMENTO CON PREVISIONE DEI FLUSSI DI CASSA ATTESI: l impresa ivese moea oggi per oeere flussi moeari icremeali el fuuro.* PROGETTO: Ivesimeo i arezzaure
CAPITAL BUDGETING VALUTAZIONE DI PROGETTI D INVESTIMENTO CON PREVISIONE DEI FLUSSI DI CASSA ATTESI: l impresa ivese moea oggi per oeere flussi moeari icremeali el fuuro.* PROGETTO: Ivesimeo i arezzaure
Algoritmi e Strutture Dati. Alberi Binari di Ricerca
 Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
Esercizi 12/10/2007. oppure B 0. In modo del tutto analogo AB 0 se e solo se. oppure B 0 B 0. Studio del segno di una disequazione polinomiale.
 Esercz 2/0/2007 Dsequazo Sego d u prodotto. Voglamo studare l sego d u prodotto d due umer real. I altr term vedere qual soo le codzo affché due umer real A e B soddsfo AB 0. Ragoamo come segue: rcoducamo
Esercz 2/0/2007 Dsequazo Sego d u prodotto. Voglamo studare l sego d u prodotto d due umer real. I altr term vedere qual soo le codzo affché due umer real A e B soddsfo AB 0. Ragoamo come segue: rcoducamo
Lezione 10. (BAG cap. 9) Corso di Macroeconomia Prof. Guido Ascari, Università di Pavia
 Lezione 10 (BAG cap. 9) Il asso naurale di disoccupazione e la curva di Phillips Corso di Macroeconomia Prof. Guido Ascari, Universià di Pavia In queso capiolo Inrodurremo uno degli oggei più conosciui
Lezione 10 (BAG cap. 9) Il asso naurale di disoccupazione e la curva di Phillips Corso di Macroeconomia Prof. Guido Ascari, Universià di Pavia In queso capiolo Inrodurremo uno degli oggei più conosciui
APPROFONDIMENTI SULLA TEORIA DEL CONSUMO AGGREGATO
 Moduo 8a 1 APPROFONDIMENTI SULLA TEORIA DEL CONSUMO AGGREGATO 1. Iroduzioe 2. La eoria de cosumo di Dueseberry 3. La eoria de cico viae di Modigiai 2 1. Iroduzioe Dae esperieze dei maggiori sisemi macroecoomici,
Moduo 8a 1 APPROFONDIMENTI SULLA TEORIA DEL CONSUMO AGGREGATO 1. Iroduzioe 2. La eoria de cosumo di Dueseberry 3. La eoria de cico viae di Modigiai 2 1. Iroduzioe Dae esperieze dei maggiori sisemi macroecoomici,
ESERCITAZIONE PER LA QUARTA PROVA DELL' ESAME DI STATO PER L'ABILITAZIONE ALLA PROFESSIONE DI INGEGNERE CIVILE E AMBIENTALE Autore: Marina Roma
 hp://svolgmeorcceesme.lervs.org/ ESECITAZIONE PE LA UATA POVA ELL' ESAME I STATO PE L'ABILITAZIONE ALLA POFESSIONE I INGEGNEE CIVILE E AMBIENTALE Auore: Mr om Il presee documeo rpor lo svolgmeo, pssggo
hp://svolgmeorcceesme.lervs.org/ ESECITAZIONE PE LA UATA POVA ELL' ESAME I STATO PE L'ABILITAZIONE ALLA POFESSIONE I INGEGNEE CIVILE E AMBIENTALE Auore: Mr om Il presee documeo rpor lo svolgmeo, pssggo
Lezione 9. Moduli finitamente generati.
 Lezoe 9 Moul faee geera. Rchaao prelaree u porae eucao ell algebra leare. Propozoe 9. Sa K u capo e a C c )... a) la arce C è verble e e olo e e C 0 ; b) l ea leare oogeeo ua arce a coeffce K. Allora c
Lezoe 9 Moul faee geera. Rchaao prelaree u porae eucao ell algebra leare. Propozoe 9. Sa K u capo e a C c )... a) la arce C è verble e e olo e e C 0 ; b) l ea leare oogeeo ua arce a coeffce K. Allora c
STATISTICA DESCRITTIVA
 COSIDERAZIOI PRELIMIARI SULLA STATISTICA La Statstca trae suo rsultat dall osservazoe de feome che c crcodao. Gl stess feome per essere oggetto d statstca devoo essere adeguatamete umeros modo tale che
COSIDERAZIOI PRELIMIARI SULLA STATISTICA La Statstca trae suo rsultat dall osservazoe de feome che c crcodao. Gl stess feome per essere oggetto d statstca devoo essere adeguatamete umeros modo tale che
Matematica elementare art.1 di Raimondo Valeri
 Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Processi periodici. Capitolo 2. 2.1 Modello. 2.1.1 Simboli. 2.1.2 Grafico dei processi. {τ 1,...,τ n } processi periodici
 3 Capolo 2 Process perodc 2. Modello 2.. Smbol {,...,τ n } process perodc τ,k sanza k-esma del processo φ fase d un processo (prmo empo d avazone) T perodo del processo r,k = φ +(k ) T k-esma avazone D
3 Capolo 2 Process perodc 2. Modello 2.. Smbol {,...,τ n } process perodc τ,k sanza k-esma del processo φ fase d un processo (prmo empo d avazone) T perodo del processo r,k = φ +(k ) T k-esma avazone D
Le 7 fasi dell AMD (PAG.6 M.Fraire-Metodi di AMD CISU, Roma 1994)
 !(Breve rchamo alle lezo ) " I passato l applcazoe ua tecca statstca multvarata cossteva stetcamete tabella e at potes moello e tecca statstca multvarata output e rsultat Ogg l amplars e camp applcazoe
!(Breve rchamo alle lezo ) " I passato l applcazoe ua tecca statstca multvarata cossteva stetcamete tabella e at potes moello e tecca statstca multvarata output e rsultat Ogg l amplars e camp applcazoe
Le basi della valutazione secondo i cash flow. Aswath Damodaran
 Le basi della valuazione secondo i cash flow Aswah Damodaran Valuazione secondo i cash flow: le basi dell'approccio Valore = = n CF = 1 1+ r ( ) dove, n = anni di via dell'aivià CF = Cash flow nel periodo
Le basi della valuazione secondo i cash flow Aswah Damodaran Valuazione secondo i cash flow: le basi dell'approccio Valore = = n CF = 1 1+ r ( ) dove, n = anni di via dell'aivià CF = Cash flow nel periodo
1 ANALISI MATEMATICA A - Esercizi della settimana 1
 1 ANALISI MATEMATICA A - Esercz della settmaa 1 1.1 Eserczo Rsolvete le seguet dsequazo (e umer real) coè trovate l seme de umer real per qual la dsequazoe dcata è vera. 1. 1 x + 1 x 1 + 1 x + 1 0; 2.
1 ANALISI MATEMATICA A - Esercz della settmaa 1 1.1 Eserczo Rsolvete le seguet dsequazo (e umer real) coè trovate l seme de umer real per qual la dsequazoe dcata è vera. 1. 1 x + 1 x 1 + 1 x + 1 0; 2.
Metodi Matematici per l Economia e la Finanza
 Meod Maemac per l Ecooma e la Faza Terzo modulo: Eleme d Maemaca Fazara Iformazo Ul/ Docee: Adrea Res, adrea.res@ubg. Lbro d eso Sefa, Torrero e Zambruo, Eleme d Maemaca Fazara e Ce d Programmazoe Leare,
Meod Maemac per l Ecooma e la Faza Terzo modulo: Eleme d Maemaca Fazara Iformazo Ul/ Docee: Adrea Res, adrea.res@ubg. Lbro d eso Sefa, Torrero e Zambruo, Eleme d Maemaca Fazara e Ce d Programmazoe Leare,
Esercizi di Matematica Finanziaria - Corso Part Time scheda 1 - Leggi finanziarie, rendite ed ammortamenti
 Esercizi di Matematica Finanziaria - Corso Part Time scheda 1 - Leggi finanziarie, rendite ed ammortamenti 1. Un capitale d ammontare 100 viene investito, in regime di interesse semplice, al tasso annuo
Esercizi di Matematica Finanziaria - Corso Part Time scheda 1 - Leggi finanziarie, rendite ed ammortamenti 1. Un capitale d ammontare 100 viene investito, in regime di interesse semplice, al tasso annuo
EQUAZIONI ALLE RICORRENZE
 Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
Modelli di Schedulazione
 EW Modell d Schedulazoe Idce Maccha Sgola Tepo d Copletaeto Totale Tepo d Copletaeto Totale Pesato Tepo d Rtardo Totale Maespa co set-up dpedete dalla sequeza Tepo d Copletaeto Totale co vcolo d precedeza
EW Modell d Schedulazoe Idce Maccha Sgola Tepo d Copletaeto Totale Tepo d Copletaeto Totale Pesato Tepo d Rtardo Totale Maespa co set-up dpedete dalla sequeza Tepo d Copletaeto Totale co vcolo d precedeza
NEWSLETTER AIFIRM RISK MANAGEMENT MAGAZINE Rivista dell Associazione Italiana Financial Industry Risk Managers
 WSLTT AFM SK MAAGMT MAGAZ vsa dell Assocazoe alaa Facal dusry sk Maagers Ao 8 umero Geao Febbrao - Marzo 23 ose alae - Spedzoe abboameo posale 7% au. CB / Geova r. 569 ao 25 collaborazoe co WSLTT AFM SK
WSLTT AFM SK MAAGMT MAGAZ vsa dell Assocazoe alaa Facal dusry sk Maagers Ao 8 umero Geao Febbrao - Marzo 23 ose alae - Spedzoe abboameo posale 7% au. CB / Geova r. 569 ao 25 collaborazoe co WSLTT AFM SK
Design of experiments (DOE) e Analisi statistica
 Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
La matematica finanziaria
 La matematica fiaziaria La matematica fiaziaria forisce gli strumeti ecessari per cofrotare fatti fiaziari che avvegoo i mometi diversi Esempio: Come posso cofrotare i ricavi e i costi legati all acquisto
La matematica fiaziaria La matematica fiaziaria forisce gli strumeti ecessari per cofrotare fatti fiaziari che avvegoo i mometi diversi Esempio: Come posso cofrotare i ricavi e i costi legati all acquisto
Rendita perpetua con rate crescenti in progressione aritmetica
 edita perpetua co rate cresceti i progressioe aritmetica iprediamo l'esempio visto ella scorsa lezioe di redita perpetua co rate cresceti i progressioe arimetica: Questa redita può ache essere vista come
edita perpetua co rate cresceti i progressioe aritmetica iprediamo l'esempio visto ella scorsa lezioe di redita perpetua co rate cresceti i progressioe arimetica: Questa redita può ache essere vista come
Elementi di Statistica descrittiva Parte III
 Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
COMPLEMENTI SULLE LEGGI FINANZIARIE
 COMPLEMENI SULLE LEGGI FINANZIARIE asso di rendimento di operazioni finanziarie in valuta estera La normativa vigente consente di effettuare operazioni finanziarie, sia di investimento che di finanziamento,
COMPLEMENI SULLE LEGGI FINANZIARIE asso di rendimento di operazioni finanziarie in valuta estera La normativa vigente consente di effettuare operazioni finanziarie, sia di investimento che di finanziamento,
Fatica con sollecitazioni ad ampiezza variabile
 Comporameo meccaco de maerla Faca co sollecazo ad ampezza varable Faca de maeral Faca co sollecazo ad ampezza varable Iroduzoe, cumulav d sollecazoe Daeggameo: regola d Palmgre Mer Meodo d coeggo: meodo
Comporameo meccaco de maerla Faca co sollecazo ad ampezza varable Faca de maeral Faca co sollecazo ad ampezza varable Iroduzoe, cumulav d sollecazoe Daeggameo: regola d Palmgre Mer Meodo d coeggo: meodo
E.S. Levrero. Dispense integrative di Economia Monetaria (2014-2015)
 E.S. Levrero Dspese egrave d Ecooma Moeara (204-205) IL MOLTIPLICATORE DEI DEPOSITI BANCARI E L OFFERTA DI MONETA. Per quao rguarda l molplcaore de depos bacar, s deve eer coo del fao che l ammoare effevo
E.S. Levrero Dspese egrave d Ecooma Moeara (204-205) IL MOLTIPLICATORE DEI DEPOSITI BANCARI E L OFFERTA DI MONETA. Per quao rguarda l molplcaore de depos bacar, s deve eer coo del fao che l ammoare effevo
Numerazione binaria Pagina 2 di 9 easy matematica di Adolfo Scimone
 Numerazioe biaria Pagia di 9 easy matematica di Adolfo Scimoe SISTEMI DI NUMERAZIONE Sistemi di umerazioe a base fissa Facciamo ormalmete riferimeto a sistemi di umerazioe a base fissa, ad esempio el sistema
Numerazioe biaria Pagia di 9 easy matematica di Adolfo Scimoe SISTEMI DI NUMERAZIONE Sistemi di umerazioe a base fissa Facciamo ormalmete riferimeto a sistemi di umerazioe a base fissa, ad esempio el sistema
CAPITOLO 6 ANALISI DEL RITARDO IN UNA RETE DATI.
 CAITOLO 6 AALISI DEL RITARDO I UA RETE DATI. 6. AALISI DEL RITARDO I UA RETE DATI I queso caolo aalzzeremo, modo quaavo e qualavo, gl eleme d rardo rese ua ree er da. Fodamealmee cosdereremo re d o aced
CAITOLO 6 AALISI DEL RITARDO I UA RETE DATI. 6. AALISI DEL RITARDO I UA RETE DATI I queso caolo aalzzeremo, modo quaavo e qualavo, gl eleme d rardo rese ua ree er da. Fodamealmee cosdereremo re d o aced
Elementi di matematica finanziaria
 Elemeti di matematica fiaziaria 18.X.2005 La matematica fiaziaria e l estimo Nell ambito di umerosi procedimeti di stima si rede ecessario operare co valori che presetao scadeze temporali differeziate
Elemeti di matematica fiaziaria 18.X.2005 La matematica fiaziaria e l estimo Nell ambito di umerosi procedimeti di stima si rede ecessario operare co valori che presetao scadeze temporali differeziate
RENDITE. Le singole rate possono essere corrisposte all inizio o alla fine di ciascun periodo e precisamente si ha:
 RENDITE. Pagamet rateal S defsce redta ua sere qualsas d somme rscuotbl (o pagabl a scadeze dverse, o, pù esattamete, u seme d captal co dspobltà scagloata el tempo. Tal captal soo dett rate della redta
RENDITE. Pagamet rateal S defsce redta ua sere qualsas d somme rscuotbl (o pagabl a scadeze dverse, o, pù esattamete, u seme d captal co dspobltà scagloata el tempo. Tal captal soo dett rate della redta
Duration ed immunizzazione finanziaria. Benedetto Matarazzo
 urao e mmuzzazoe fazara Beeeo Maarazzo Corso Maemaca Fazara urao e mmuzzazoe fazara Prcpal c emporal e c varablà u flusso pagame urao e lquà urao covey e volalà Rscho asso Prcp mmuzzazoe fazara classca
urao e mmuzzazoe fazara Beeeo Maarazzo Corso Maemaca Fazara urao e mmuzzazoe fazara Prcpal c emporal e c varablà u flusso pagame urao e lquà urao covey e volalà Rscho asso Prcp mmuzzazoe fazara classca
Circuiti dinamici. Equazioni di stato. (versione del )
 rcu amc Equazo sao www.e.g.ubo./pers/masr/aca.hm ersoe el 9-- elazo ra sao gress e rspose poes: crcuo amco leare o egeere o sao può essere rappreseao meae le eso u coesaor e le corre u gl uor o sao all
rcu amc Equazo sao www.e.g.ubo./pers/masr/aca.hm ersoe el 9-- elazo ra sao gress e rspose poes: crcuo amco leare o egeere o sao può essere rappreseao meae le eso u coesaor e le corre u gl uor o sao all
Modello dinamico nello spazio dei giunti: relazione tra le coppie di attuazione ai giunti ed il moto della struttura
 Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
b) Relativamente alla variabile PREZZO, fornire una misura della variabilità della distribuzione attraverso
 ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
Università degli Studi di Milano Bicocca CdS ECOAMM Corso di Metodi Statistici per l Amministrazione delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI
 Uverstà degl Stud d Mlao Bcocca CdS ECOAMM Corso d Metod Statstc per l Ammstrazoe delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI 1. Carta d cotrollo per frazoe d o coform (carta U resposable d produzoe,
Uverstà degl Stud d Mlao Bcocca CdS ECOAMM Corso d Metod Statstc per l Ammstrazoe delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI 1. Carta d cotrollo per frazoe d o coform (carta U resposable d produzoe,
Esercizi di Matematica Finanziaria
 Università degli Studi di Siena Facoltà di Economia Esercizi di Matematica Finanziaria relativi ai capitoli I-IV del testo Claudio Pacati a.a. 1998 99 c Claudio Pacati tutti i diritti riservati. Il presente
Università degli Studi di Siena Facoltà di Economia Esercizi di Matematica Finanziaria relativi ai capitoli I-IV del testo Claudio Pacati a.a. 1998 99 c Claudio Pacati tutti i diritti riservati. Il presente
Le Scelte Finanziarie. S. Corsaro Matematica Finanziaria a.a. 2007/08
 Le Scelte Finanziarie 1 Tasso Interno di Rendimento Consideriamo un operazione finanziaria (t 0 =0): 0 x 0 t 1 t 2 t m...... x 1 x 2 x m Posto: x = x0, x1,, xm { } si definisce tasso interno di rendimento
Le Scelte Finanziarie 1 Tasso Interno di Rendimento Consideriamo un operazione finanziaria (t 0 =0): 0 x 0 t 1 t 2 t m...... x 1 x 2 x m Posto: x = x0, x1,, xm { } si definisce tasso interno di rendimento
Avvertenza. Rendite frazionate
 Avverteza Quest lucd soo pesat solo come u auslo per l ascolto della lezoe. No sosttuscoo l lbro d testo Possoo coteere error e svste, che gl studet soo vtat a segalare Redte frazoate L tervallo tra ua
Avverteza Quest lucd soo pesat solo come u auslo per l ascolto della lezoe. No sosttuscoo l lbro d testo Possoo coteere error e svste, che gl studet soo vtat a segalare Redte frazoate L tervallo tra ua
Università di Napoli Parthenope Facoltà di Ingegneria
 Universià di Napoli Parenope Facolà di Ingegneria Corso di Comunicazioni Elerice docene: Prof. Vio Pascazio a Lezione: 7/04/003 Sommario Caraerizzazione energeica di processi aleaori Processi aleaori nel
Universià di Napoli Parenope Facolà di Ingegneria Corso di Comunicazioni Elerice docene: Prof. Vio Pascazio a Lezione: 7/04/003 Sommario Caraerizzazione energeica di processi aleaori Processi aleaori nel
MATEMATICA FINANZIARIA 2 PROVA SCRITTA DEL 11 SETTEMBRE 2007 ECONOMIA AZIENDALE
 MATEMATICA FINANZIARIA PROVA SCRITTA DEL SETTEMBRE 007 ECONOMIA AZIENDALE ESERCIZIO a Su un mercao deale vene smaa, rame prezz d TCN unar, la seguene sruura per scadenza de ass a pron (0,4,% ; (0,4,8%
MATEMATICA FINANZIARIA PROVA SCRITTA DEL SETTEMBRE 007 ECONOMIA AZIENDALE ESERCIZIO a Su un mercao deale vene smaa, rame prezz d TCN unar, la seguene sruura per scadenza de ass a pron (0,4,% ; (0,4,8%
Interesse e formule relative.
 Elisa Battistoi, Adrea Frozetti Collado Iteresse e formule relative Esercizio Determiare quale somma sarà dispoibile fra 7 ai ivestedo oggi 0000 ad u tasso auale semplice del 5% Soluzioe Il diagramma del
Elisa Battistoi, Adrea Frozetti Collado Iteresse e formule relative Esercizio Determiare quale somma sarà dispoibile fra 7 ai ivestedo oggi 0000 ad u tasso auale semplice del 5% Soluzioe Il diagramma del
REGIMI FINANZIARI USUALI: Interessi semplici Interessi composti Interessi anticipati. Giulio Diale
 REGIMI FINANZIARI USUALI: Ineressi seplici Ineressi coposi Ineressi anicipai Giulio Diale INTERESSI SEMPLICI I C L ineresse è proporzionale al capiale e alla duraa dell ipiego I = C i Denoinazioni di i:
REGIMI FINANZIARI USUALI: Ineressi seplici Ineressi coposi Ineressi anicipai Giulio Diale INTERESSI SEMPLICI I C L ineresse è proporzionale al capiale e alla duraa dell ipiego I = C i Denoinazioni di i:
Analisi di dati vettoriali. Direzioni e orientazioni
 Aals d dat vettoral Drezo e oretazo I tal caso, dat soo msurat term d agol e spesso soo rfert al ord geografco (statstca crcolare) Soo rappresetat su ua crcofereza Dat d drezoe: flusso ua specfca drezoe,
Aals d dat vettoral Drezo e oretazo I tal caso, dat soo msurat term d agol e spesso soo rfert al ord geografco (statstca crcolare) Soo rappresetat su ua crcofereza Dat d drezoe: flusso ua specfca drezoe,
frazione 1 n dell ammontare complessivo del carattere A x
 La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
VALORE EFFICACE DEL VOLTAGGIO
 Fisica generale, a.a. /4 TUTOATO 8: ALO EFFC &CCUT N A.C. ALOE EFFCE DEL OLTAGGO 8.. La leura con un mulimero digiale del volaggio ai morsei di un generaore fornisce + in coninua e 5.5 in alernaa. Tra
Fisica generale, a.a. /4 TUTOATO 8: ALO EFFC &CCUT N A.C. ALOE EFFCE DEL OLTAGGO 8.. La leura con un mulimero digiale del volaggio ai morsei di un generaore fornisce + in coninua e 5.5 in alernaa. Tra
Costi della politica: Giudizio positivo per i sindaci, maglia nera per parlamentari e consiglieri regionali
 XXVI I IAssembl eaanci-larepubbl cadecomun Au onom apercamb ar e lpaese Lac l assepol c aec ad n Op n onsucos,r esponsab l àe mpegnodch gover nal e s uz on Cos della polca: Gudzo posvo per sndac, magla
XXVI I IAssembl eaanci-larepubbl cadecomun Au onom apercamb ar e lpaese Lac l assepol c aec ad n Op n onsucos,r esponsab l àe mpegnodch gover nal e s uz on Cos della polca: Gudzo posvo per sndac, magla
Determinare l ammontare x da versare per centrare l obiettivo di costituzione.
 Esercizi di matematica finanziaria 1 VAN - DCF - TIR Esercizio 1.1. Un investitore desidera disporre tra 3 anni d un capitale M = 10000 euro. Investe subito la somma c 0 pari a 1/4 di M. Farà poi un ulteriore
Esercizi di matematica finanziaria 1 VAN - DCF - TIR Esercizio 1.1. Un investitore desidera disporre tra 3 anni d un capitale M = 10000 euro. Investe subito la somma c 0 pari a 1/4 di M. Farà poi un ulteriore
INGEGNERIA E TECNOLOGIE DEI SISTEMI DI CONTROLLO. box. Scopo della modellazione black-box. Limitazioni dell approccio black-box
 IGEGEIA E TECOLOGIE DEI SISTEMI DI COTOLLO bo Prof. Carlo oss DEIS - Uversà d Bologa Tel: 05 09300 emal: cross@des.bo. Scopo della modellazoe black-bo S vole realzzare modello d ssema a parre dalla sola
IGEGEIA E TECOLOGIE DEI SISTEMI DI COTOLLO bo Prof. Carlo oss DEIS - Uversà d Bologa Tel: 05 09300 emal: cross@des.bo. Scopo della modellazoe black-bo S vole realzzare modello d ssema a parre dalla sola
ERRATA CORRIGE. L intero contenuto del paragrafo 9.2.3 a pagina 47-48 del Capitolato tecnico Determinazione del Canone è sostituito come segue:
 Procedura aperta per l affdameto de servz tegrat, gestoal, operatv e d mautezoe multservzo tecologco da esegurs presso gl mmobl d propretà o uso alle Asl ed alle azede ospedalere della regoe Campaa ERRATA
Procedura aperta per l affdameto de servz tegrat, gestoal, operatv e d mautezoe multservzo tecologco da esegurs presso gl mmobl d propretà o uso alle Asl ed alle azede ospedalere della regoe Campaa ERRATA
Lezione 1. I numeri complessi
 Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
La programmazione aggregata nella supply chain. La programmazione aggregata nella supply chain 1
 La programmazione aggregaa nella supply chain La programmazione aggregaa nella supply chain 1 Linea guida Il ruolo della programmazione aggregaa nella supply chain Il problema della programmazione aggregaa
La programmazione aggregaa nella supply chain La programmazione aggregaa nella supply chain 1 Linea guida Il ruolo della programmazione aggregaa nella supply chain Il problema della programmazione aggregaa
Ammortamento americano. Ammortamento americano
 mmortameto amercao La cora lezoe abbamo vto che ell'ammortameto amercao l rmboro del debto zale avvee medate u uco verameto a cadeza, otteuto attravero ua operazoe d cottuzoe d u captale al tao attvo j;
mmortameto amercao La cora lezoe abbamo vto che ell'ammortameto amercao l rmboro del debto zale avvee medate u uco verameto a cadeza, otteuto attravero ua operazoe d cottuzoe d u captale al tao attvo j;
Regime finanziario dell interesse semplice: formule inverse
 Regime finanziario dell interesse semplice: formule inverse Il valore attuale di K è il prodotto del capitale M disponibile al tempo t per il fattore di sconto 1/(1+it). 20 Regime finanziario dell interesse
Regime finanziario dell interesse semplice: formule inverse Il valore attuale di K è il prodotto del capitale M disponibile al tempo t per il fattore di sconto 1/(1+it). 20 Regime finanziario dell interesse
Equivalenza economica
 Equivalenza economica Calcolo dell equivalenza economica [Thuesen, Economia per ingegneri, capitolo 4] Negli studi tecnico-economici molti calcoli richiedono che le entrate e le uscite previste per due
Equivalenza economica Calcolo dell equivalenza economica [Thuesen, Economia per ingegneri, capitolo 4] Negli studi tecnico-economici molti calcoli richiedono che le entrate e le uscite previste per due
Esercizi svolti in aula
 Esercizi svolti in aula 23 maggio 2012 Esercizio 1 (Esercizio 1 del compito di matematica finanziaria 1 (CdL EA) del 16-02-10) Un individuo vuole accumulare su un conto corrente la somma di 10.000 Euro
Esercizi svolti in aula 23 maggio 2012 Esercizio 1 (Esercizio 1 del compito di matematica finanziaria 1 (CdL EA) del 16-02-10) Un individuo vuole accumulare su un conto corrente la somma di 10.000 Euro
COMPITO DI MATEMATICA FINANZIARIA 8 Febbraio 2013. - Come cambia il REA atteso se l'obbligazione sarà ancora in vita dopo le prime tre estrazioni?
 UNIVERSITA DEGLI STUDI DI URBINO (Sede di Fano) COMPITO DI MATEMATICA FINANZIARIA 8 Febbraio 2013 1) L'impresa Gamma emette 250 obbligazioni il cui VN unitario è pari a 100. Il rimborso avverrà tramite
UNIVERSITA DEGLI STUDI DI URBINO (Sede di Fano) COMPITO DI MATEMATICA FINANZIARIA 8 Febbraio 2013 1) L'impresa Gamma emette 250 obbligazioni il cui VN unitario è pari a 100. Il rimborso avverrà tramite
MATEMATICA FINANZIARIA. Docente: prof. Filippo Petroni fpetroni@gmail.com
 ATEATIA FINANZIARIA Docente: prof. Filippo Petroni fpetroni@gmail.com Problemi base della matemaaca finanziaria FaDore tempo: una somma a disposizione oggi è diversa dalla stessa somma a disposizione tra
ATEATIA FINANZIARIA Docente: prof. Filippo Petroni fpetroni@gmail.com Problemi base della matemaaca finanziaria FaDore tempo: una somma a disposizione oggi è diversa dalla stessa somma a disposizione tra
Risoluzione quesiti I esonero 2011
 Rsoluzone quest I esonero 011 1) Compto 1 Q3 Un azenda a a dsposzone due progett d nvestmento tra d loro alternatv. Il prmo prevede l pagamento d un mporto par a 100 all epoca 0 e fluss par a 60 all epoca
Rsoluzone quest I esonero 011 1) Compto 1 Q3 Un azenda a a dsposzone due progett d nvestmento tra d loro alternatv. Il prmo prevede l pagamento d un mporto par a 100 all epoca 0 e fluss par a 60 all epoca
Capitolo III: I Regolatori
 SCC Cap. III: Regolaor Capolo III: I Regolaor III-1: Inrouzone Il regolaore ha l ompo sablre l azone orreva a apporare n ngresso al proesso, per mezzo ell auaore; l segnale n usa al regolaore (s) è funzone
SCC Cap. III: Regolaor Capolo III: I Regolaor III-1: Inrouzone Il regolaore ha l ompo sablre l azone orreva a apporare n ngresso al proesso, per mezzo ell auaore; l segnale n usa al regolaore (s) è funzone
