Le 7 fasi dell AMD (PAG.6 M.Fraire-Metodi di AMD CISU, Roma 1994)
|
|
|
- Gemma Ceccarelli
- 8 anni fa
- Visualizzazioni
Transcript
1 !(Breve rchamo alle lezo ) " I passato l applcazoe ua tecca statstca multvarata cossteva stetcamete tabella e at potes moello e tecca statstca multvarata output e rsultat Ogg l amplars e camp applcazoe e meto aals e at sa elle sceze socal che atural, la varetà e complesstà elle stuazo specfche rcerca, hao portato a are rlevo sa al puto vsta metoologco che formatco ua sere aspett trascurat passato: le fas prelmar ell AMD, la formalzzazoe el problema, le cofche a pror e a posteror. L AMD rguara aals statstche tpo complesso ossa costtute a pù elaborazo tra loro cocateate, al fe poter esamare sstematcamete, moo utaro e artcolato, tal aspett è utle coserare l AMD come u sstema composto pù fas tutte ugualmete mportat e terpeet e avet cascua aspett statstc e formatc. Molto schematcamete è possble potzzare 7 fas prcpal elle qual s svolge u AMD (Frare, 989) che soo ettaglatamete escrtte el testo qu seguto ctato:. Le 7 fas ell AMD (PAG.6 M.Frare-Meto AMD CISU, Roma 994) Complemet alle lezo teute alla Prof.ssa Mary Frare Facoltà Socologa, Uverstà egl Stu Roma La Sapeza, a.a per l Moulo Specalstco (MS) STATISTICA (SECS-S/0) Laboratoro Aals e at Multvarat elle lezo. Il moulo attco rguara cors (SERS, PROVa, CATRI) ella Laurea Magstrale Socologa e l corso per la Laurea Magstrale Programmazoe e gestoe elle Poltche e e Servz socal (ProPols).
2 ## $ % (Breve rchamo alle lezo ) Esstoo vers tp matrc e at, secoo le stuazo rcerca, cascua avete ua ata struttura complessa qu seguto s cao alcue elle pù rcorret elle verse stuazo rcerca: TABELLA INVENTARIO ( ): cotee at mst coc alfaumerc e umer real; essua struttura rchee ulteror cofche a posteror. Dato statstco: [ a coc ; val. umerc ] MATRICE DI DATI QUALITATIVI ( ): cotee coc alfaumerc; essua struttura rchee ulteror co.a posteror per essere statstcamete trattable. Dato statstco: [ a coc ; ] MATRICE DI INTENSITA o DATI QUANTITATIVI( ): cotee umer real, R, possee struttura algebrca spazo vettorale. Dato statstco: [ a R] + MATRICE DI CONTINGENZA (r s): cotee frequeze assolute ( R ) possee struttura algebrca spazo vettorale. + Dato statstco: [ a R ] MATRICE DEI RANGHI ( ): at soo costtut a ragh (mutabl rettlee), possee struttura ore. Dato statstco: [ a co. alfaumerco] MATRICE DELLE PREFERENZE ( ): cotee ragh (struttura ore) o post espress umer ter atural ℵ(struttura algebrca spazo vettorale). Dato statstco: per ragh [ a co. alfaumerco] o per post [ a ℵ] MATRICE DI DESCRIZIONE LOGICA o BOOLEANA ( ): at soo costtut a 0 o, o possee struttura. Dato statstco: [ a 0;] MATRICE DEI PUNTEGGI ( ):cotee umer ter atural ℵ, ha struttura algebrca spazo vettorale. Dato statstco: [ a ℵ ] MATRICI DI PROSSIMITA ( ):cotee staze espresse ragh (struttura ore) o putegg (struttura algebrca spazo vettorale). MATRICI A TRE (three-way) at quattatv (N K O): cotee at umer real, possee struttura algebrca. Dato statstco: [ R] MATRICI DI DATI TESTUALI: cotee parole o fras o test,essua struttura, rchee ulteror partcolar cofche a posteror per essere statstcamete trattable. Ecc.ecc. &! ( ( ) * +, (Breve rchamo alle lezo ) La matrce testà o e at quatatv o varabl cotee umer real R, e possee struttura algebrca spazo vettorale. Dato statstco: [ a R] Esstoo ache le matrc a PIU VIE (mult-way) at quattatv o matrc a tre e pù ve at qualtatv.
3 Sa P u ato collettvo o popolazoe statstca efta a: N (,,..., N ) u. s. P (,,..., ) v a r cu N è l seme supposto fto elle u.s.e l umero elle varabl S ha la matrce e at quattatv a rghe e coloe seguete:,, N \ N N N N N efto a pror. Og rga ella matrce è u vettore umerco a elemet real: (,,...,,..., ) cate le coorate u puto-utà ello spazo R a meso. L seme tutt vettor rga efsce la NUVOLA DEI PUNTI-UNITA, N, ello spazo elle (,,..., ) utà R a meso. Dualmete og coloa ella matrce è u vettore umerco a elemet real: (,,..., ) L seme tutt vettor coloa (,,...,,..., ) efsce la NUVOLA DEI PUNTI VARIABILI, N, ello spazo elle varabl a meso. R Se su tal vettor s possoo effettuare le operazo tere somma vettorale (+) e prootto estero per uo scalare ( ) s può utlzzare la struttura algebrca ello SPAZIO VETTORIALE sopra l corpo reale; se esso è oltre muto ell operazoe estera el prootto scalare (o tero) cato co <, > e efto come applcazoe R s può operare ello SPAZIO VETTORIALE EUCLIDEO. - %./) Esstoo vers tp strutture algebrche (semgruppo, gruppo, gruppo abelao, aello, corpo, corpo commutatvo, retcolo, retcolo Boole, moulo, spazo vettorale, spazo vettorale eucleo ecc. ). I geerale per struttura algebrca s tee og seme A otato ua o pù legg composzoe (tera, estera). Per le efzo e propretà elle strutture ve: Strutture algebrche corpo (M.Frare, op.ct.,pg.) Strutture algebrche gruppo e corpo commutatvo (pg.3) Spazo vettorale (leare)(pg.3) Spazo vettorale eucleo(pg.4) Le matrc avet struttura algebrca spazo vettorale eucleo soo quella alle qual s applcao la maggor parte e meto AMD (ACP, ACC, ACS, ACM, MDS, 3-way Stats ecc.)
4 Uo egl scop ella 3^ e 4^ fase ell AMD rguarat le cofche a posteror elle matrc e at zal è quello trasformare la matrce e at zal affchè abba tale struttura. E a osservare oltre che raramete ell AMD s applcao vers meto multvarat alla matrce e at zal fatt ell AMD: matrce e at zal tabella e at e quest ultma ovrebbe avere le seguet caratterstche per essere effcacemete aalzzata tramte ua o pù tecche AMD: pertete rspetto all oggetto rcerca omogeea e at esaustva ella escrzoe completa ell seme (varabl) e ell seme N (utà statstche) rspetto al feomeo coserato /)! ( * +, Per ua matrce at quattatv la STRUTTURA ALGEBRICA(*) o SPAZIO RIFERIMENTO è lo SPAZIO VETTORIALE (o LINEARE) e VETTORIALE EUCLIDEO. Legge composzoe tera + (azoe o somma vettorale: applcazoe ) co le propretà assomatche:, y, z a) + y y+ b)( + y) + z + ( y+ z) c) esste ( u 0): + u u+ ( u eutro ) ) opposto : : + ( ) 0 Legge composzoe tera (moltplcazoe per uo scalare o prootto estero: EUCLIDEO: R co le seguet propretà assomatche: a ) ( λ ) λ se per l seme b ) λ γ ( λ γ ) e vettor ore c ) 0 0 ove le soo ) λ ( + y ) λ + λ y umer real R e ) ( λ + γ ) λ + γ Soo efte: Prootto scalare o tero R<, > co le seguet propretà assomatche: a) <, y >< Y, > b) < + y, z >< z > + < yz > c) < λ, y > λ <, y >, (*) Per struttura algebrca s tee og seme otato ua o pù legg composzoe tera o estera. Ua operazoe o legge composzoe tera assoca a og coppa elemet (;y) u elemeto z apparteete acora a ossa y z. Ua operazoe o legge composzoe estera coette gl elemet ell seme co gl elemet u altro seme Ω operator moo tale che per og coppa (; ) esste u uco elemeto z apparteete acora a ossa z.
5 # #.0$ 0 0$ La 5^ fase ell AMD (cfr par..) rguara la scelta ua msura (metrca) : RASSOMIGLIANZA-DISSOMIGLIANZA tra utà statstche: Matrc elle staze o elle smlartà. Esstoo molt tp msure a secoa el tpo tabella e at a aalzzare (staze Mows, Mahalaobs, Hammg; c staza; c verstà;c smlartà) Nella Cluster Aalyss (CA) è a esempo rlevate a esempo la scelta ella msura rass./ss. tra u.s.. RELAZIONE TRA CARATTERI: Matrc evaze e coevaze; varaze e covaraze;correlazoe, correlazoe parzale ecc.) Nell Aals Compoet Prcpal (ACP) è a esempo rlevate la scelta ua msura relazoe tra varabl. ## / %3 / %! 4 Nel prospetto che segue s rportao prcpal tp tabelle e at (4^fase ell AMD) e le verse msure rass./ssom. fra u.s. (5^fase ell AMD: la scelta ella metrca) 3 : Tabella e at (4^ fase ell AMD) Tabella testà o at quattatv (varabl) Tabelle cotgeza Tabelle escrzoe logca (booleae) Msura rass./ssom. (5^fase ell AMD) Dstaze: Mows (semplc e poer.) Mahalaobs Ic verstà: Lace e Wllams ecc. Dstaze: Mows (semplc e poer.) Ic staza: staze el χ² Dstaze: Mows (semplc e poer.) Hammg Ic staza: staze el χ² Ic smlartà: Soal e Mcheer Russel e Rao Jaccar ecc. 3 v. M.Frare, Meto AMD, op.ct. pag. 94 per le propretà egl c e pag. 95 per le tabelle e at.
6 Tabelle e ragh Dstaze: Mows (semplc e poer.) Rzz Ic verstà: ρ Sperma (*) τ Keall (*) (*)corrett affchè varo tra 0 e azché tra e + Le matrc mesoe ette ache matrc elle msure rassomglaza/ssomglaza tra tutte le possbl coppe elle N u.s. cotegoo le staze o le smlartà calcolate per tutte le coppe u.s. rspetto a caratter cotemporaemete coserat. Ifatt ata la matrce at quattatv seguete:, N \ N N N N N se s vogloo avere elle msure rassomglaza o ssomglaza tra tutte le possbl coppe ( ) utà statstche rspetto a caratter cotemporaeamete coserat (vettor-rga) occorre sceglere ua msura che forsca la staza (verstà) o la vcaza (somglaza) tra ue rghe. Esstoo molte msure a secoa elle proretà posseute e el lvello msurazoe e caratter co qual cascua esse è compatble. La scelta tra le verse msure è legata alla struttura S posseuta alla tabella e at coserata e le msure co essa compatbl. Ua prma grae stzoe tra le verse msure rassomglaza/ssomglaza tra u.s. è comuque quella tra DISTANZE (vers c) per le varabl e SIMILARITA (vers c) per le mutabl. I geerale se coseramo tutte le possbl coppe elle N u.s. s ha la matrce elle staze cata co D, che cotee tutte le staze per tutte le coppe u.s. seguete: ( ) 0 ( ) ( 3)... ( ) ( ) ( ) 0 ( 3)... ( ) D, ( 3) ( 3 3) 0... ( 3 ) ( ) ( ) ( ) 0 Essa forsce ua msura ella rassomglaza-ssomglaza tutte le N u.s., prese a ue a ue, rspetto a tutt caratter cotemporaeamete coserat. La matrce è ua matrce:
7 QUADRATA mesoe ( ) ( ) SIMMETRICA POSITIVA ( perché per le propretà stesse ua staza qualuque essa sa ) 0, è sempre postva o ulla NULLA solo se ( ) 0 (s ot la agoale prcpale ag[0,0,,0]) ( ) Avete elle staze utl. #& %,5, Tra le pù mpegate staze avet l maggor umero propretà (cfr.tabella 3 pag.94 M.Frare, op.ct.) c soo le staze Mows la cu formula è ata a: t t t ( t t ero) a secoa el valore assuto al parametro t s hao le staze: t Dstaza ella cttà a blocch o Mahatta t Dstaza euclea ( ) t t t Dstaza Lagrage 0 Data la matrce at quattatv { } m a r,,..., N 3 3, La staza ella cttà a blocch o Mahatta per la coppa u.s. (,) è ata a: es.: (;) ( ) 3(3 ) smlmete vao calcolate per tutte le coppe utl: 3 ossa (,); (,3); (,3). La staza Lagrage per la coppa u.s. (,) è ata a: es.: (;) ma{ 3 ; 3 5} smlmete vao calcolate per tutte le coppe utl: (,); (,3); (,3).
8 Le staze euclee per tutte le coppe utl : ( ) (;) ( 3) (3 5) 4,4 + + (;3) ( 7) (3 4) 5 5, (;3); (3 7) (5 4) 6 4, Che costtuscoo la matrce elle staze D 3,3 seguete. D 3,3 3 0, 4 5, 0 9, 4 0 4, 3 5, 0 9 4, 0 Dalla matrce elle staze è possble veere qual u.s. soo pù vce sml rspetto al loro tero proflo-rga ossa avet valor bass elle staze e qual vece pù ssml lotae rspetto al loro tero proflo-rga ossa avet valor alt elle staze. #- %χ64 - Le msure rassomglaza/ssomglaza tra le utà statstche pù aatte el caso ua tabella cotgeza soo le staze (avet le propretà egl c staza, cfr ota 3) el χ6 per le rghe e per le coloe ua tabella cotgeza N r, s I partcolare la staza el χ6 per le rghe è ata a: Esempo ata la tabella cotgeza N,3 seguete: La staza el χ6 per le rghe, χ N,3 χ s (, ) χ (,... ) s calcola come segue: Se \ Età Gova Ault Aza tot M F tot ( M, F ) Smlmete la staza el χ6 per le coloe, χ (, ) è ata a: 4 (v. ache pag M.Frare, Meto AMD,op.ct.)
9 Sempre co rfermeto alla tabella cotgeza suetta la staza el χ6 per le coloe (Gova, Ault) s calcola a esempo come segue: χ ( Gov, Aul) Smlmete s calcola la staza el χ6 per le coloe (Gova, Aza) e (Ault, Aza). Le staze el Ch quarato soo aatte alle tabelle cotgeza perché esse equvalgoo a poerare le rghe (o le coloe) ella tabella elle frequeze relatve (rspettvamete per rga o per coloa) per l verso ell mportaza che cascua moaltà ha el collettvo coserato cò cosete elmare l flueza moaltà che sstematcamete avrebbero frequeze maggor elle altre. #( %( 3 / Coserao partcolare proott scalar <, > è possble trouceo ua matrce (reale, smmetrca, efta postva) etta METRICA ello SPAZIO ore (o ore ) esprmere meate operazo algebrche sa R che R og prootto scalare <, >. Faceo rfermeto alla matrce, e at quattatv efta e cao co: R ue vettor-coloa e co R ue vettor-rga s possoo esprmere meate tal proott scalar seguet c statstc rlevat. a) Prootto scalare tra ue vettor: R R, N < > N N < >, K < > K K < > I cu è l vettore trasposto el vettore cate la varable -esma, è l vettore cate la varable, N è ua matrce quarata, smmetrca ore efta postva e rappreseta la metrca ello spazo vettorale eucleo elle varabl Dualmete è l vettore trasposto el vettore cate l utà statstca -esma, è l vettore cate utà statstca -esma, K è ua matrce quarata, smmetrca ore efta postva e rappreseta la metrca ello spazo vettorale eucleo elle utà statstche. Coserao ue vettor-rga a elemet la staza tra ue vettor-rga (,, R ua matrce at quattv ) s può esprmere : (, ) (, ) K (, ), cu K può assumere vers valor efeo tal moo l tpo staza o metrca. 5 v.pag M.Frare, Meto AMD, op.ct.
10 χ (, ) s... A esempo, coserao per semplctà ua Matrce, se la matrce K è la matrce utà I 0 s ha la staza euclea: K 0 (, ) (, )( I, ) ( ) Nell espressoe suetta coserao l prootto scalare tra matrc <, > s avrebbe: I < > K < > (,..,,.., ), I K, I,, Coserao sempre per semplctà ua Matrce, Per cos θ K s ha la geerca staza tra ue put (vettor rga e ) e partcolare cos θ per K, s ha la staza geeralzzata o Mahalaobs seguete: c o s θ (, ) ( ) ( ) c o s θ Osservao che l agolo tra ue vettor è efto al suo coseo coserare ua metrca KI o K I sgfca coserare per KI u agolo θ 90 e qu l cos θ 0 qu ue vettor soo peet, ortogoal; metre se s cosera K I qu u agolo θ 90 e qu cos θ 0 ue vettor soo correlat. N \ A B
11 & %,, Nell AMD la scelta ella metrca tra caratter rguara la scelta ua msura o ce terpeeza o coessoe o correlazoe tra caratter (mutabl o varabl) coserat, faceo sempre rfermeto a ua matrce e at,. Coserao tutte le possbl coppe caratter per cascua elle qual soo calcolat gl c s hao le corrspoet matrc mesoe,, Nel caso partcolare ua matrce at quattatv cu caratter soo elle varabl tra le pù mpegate msure relazoe s hao le varaze e covaraze e gl c correlazoe leare Bravas-Perso Faceo rfermeto a ua matrce varabl, e coserao come msura relazoe tra caratter (varabl) la covaraza la corrspoete matrce,, è la matrce varaze e covaraze, seguete:, tr( ), La matrce, ha le seguet caratterstche: rago 6 ella matrce: lo stesso rago ella matrce e at ossa coserao che le coloe (varabl) sao learmete peet e che < ; quarata smmetrca : co ( ) elemet utl. Nota se le varabl soo espresse scart staarzzat Z(µ0; ) la matrce varaze e covaraze, coce co la matrce correlazoe R, Ifatt: N ( z 0)( z 0) z z y y Z, ZY Z, Z r Y Z Z Y zzy Z Z N N Y r N Molto mpegata e mportate ell AMD è l erza totale o varaza totale ella matrce e at o uvola e put ossa l formazoe totale espressa alla matrce e at coserata., tr( ) 6 Rago ua matrce è l ore massmo e suo mor o ull.
12 Statstcamete l erza totale o varaza totale è ata alla tracca ella matrce varaze e covaraze suetta ossa: è u ce varabltà leare (perché abba seso però le varabl evoo essere omogeee ossa espresse ella stessa utà msura): la tracca ella matrce varaze e covaraze cosete fatt verfcare la scheastctà ella uvola e put 7. La SCHEDASTICITA ha a che veere co la larghezza ella baa ella uvola e put: se è uforme v è omoscheastctà (... ) se o è uforme (... ) v è eteroscheastctà. Suppoeo per semplctà avere solo ue varabl, qu ua matrce e at, s potrebbero avere le stuazo rcerca seguet cu vegoo cat oltre alla larghezza ella baa ache possbl valor el coeffcete correlazoe leare, r y, Bravas-Pearso: Come s può veere la scheastctà a cazo sa sulla forma che sulla cossteza ella relazoe. Se le varaze elle varabl soo ugual o all crca ugual tra loro v è applcabltà el moello leare a at metre se le varaze elle varabl soo molto verse tra loro l moello leare è meo aatto a at ma potrebbero vece essere aatt altr moell matematc (a es. ella fgura sopra rportata l secoo caso cu r y 0 ca che o v è relazoe leare tra le varabl ma che v è vece ua relazoe tpo parabolco pur rsultato ulla la correlazoe tra le varabl ma solo quella leare. Faceo sempre rfermeto a ua matrce varabl, e coserao come msura relazoe tra caratter (varabl) la correlazoe leare Bravas-Pearso la corrspoete matrce,,è la matrce correlazoe R, seguete: R, r 7 v.pagg M.Frare, Meto AMD,op,ct. r... r r r... r...
13 Caratterstche prcpal ella matrce R, soo le seguet: rago ella matrce: lo stesso rago ella matrce e at ossa coserao che le coloe (varabl) sao learmete peet e che <, ; Quarata Smmetrca : r r co ( ) elemet utl Se le varabl soo espresse scart staarzzat Z (mea art.0; s.q.m.) l erza totale o varaza totale è ata a: tr( R ) Se c è peeza leare tra ue o pù varabl r e l etermate R, è et R, 0 Se le varabl soo learmete peet r 0 e l etermate R, è è et R I L erza totale o varaza totale ca la spersoe totale ella uvola e put-utà toro al loro barcetro o cetro gravtà g efto al vettore elle mee elle varabl ossa g Se s cosera lo spazo elle utà statstche ossa vettor-rga varaza totale è efta come staza al barcetro ossa a:, ( ) l erza totale o è uguale alla somma elle varaze elle varabl coserate o alla mea artmetca poerata co pes p 0 e quarat elle staze euclee tra put e l loro barcetro. Se s cosera vece lo spazo elle varabl ossa vettor-coloa e la matrce R varaze e covaraze, : [,,..., 3 ] tr R, N ( ) ( ) I g p R, L erza totale o varaza totale se s cosera la metrca KI ag[,,,] è: N ( ) ( ) ( ) ( ) I g tr K tr K I tr Se s cosera vece la metrca 8 v.pagg M.Frare, Meto AMD, op,ct.) K ag,,...,
14 l erza totale o varaza totale è ata a: IN( g) tr( K ) tr( D ) tr( R ) cu R, è la matrce correlazoe:! θ "" #$ Dat ue vettor-coloa a elemet ua matrce at quattv se, R, coseramo ue corrspoet vettor espress scart alla mea s possamo, s R esprmere l coeffcete correlazoe leare Bravas-Pearso el seguete moo: r S S ( ) ( ) ( s 0 ) ( s 0 ) s s ( )( ) ( s 0 )( s 0 ) s s s D s ( s D s ) ( s D s ) p / / p p c o s θ r S S I cu D p è ata alla matrce agoale: se θ 90 cos θ 0 se θ 90 cos θ S D p a g [,,..., ] θ r S 0 S 0 0 S 0 S r S S 0 θ 90 S
Elementi di Statistica descrittiva Parte III
 Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
Modello dinamico nello spazio dei giunti: relazione tra le coppie di attuazione ai giunti ed il moto della struttura
 Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
Alcuni metodi per la risoluzione di sistemi lineari con matrici strutturate.
 Alcu meto per la rsoluzoe sstem lear co matrc strutturate. A. url - Calcolo Scetco Problema Rsolvere l sstema leare: A A. url - Calcolo Scetco Problema q A Co A matrce el tpo: p O A è ua matrce tragoale!
Alcu meto per la rsoluzoe sstem lear co matrc strutturate. A. url - Calcolo Scetco Problema Rsolvere l sstema leare: A A. url - Calcolo Scetco Problema q A Co A matrce el tpo: p O A è ua matrce tragoale!
Dimostrazione della Formula per la determinazione del numero di divisori-test di primalità, di Giorgio Lamberti
 Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Caso studio 10. Dipendenza in media. Esempio
 09/03/06 Caso studo 0 S cosder la seguete dstrbuzoe degl occupat Itala secodo l umero d ore settmaal effettvamete lavorate e l settore d attvtà (cfr. Itala cfre, Ao 008, pag. 7 ): Ore lavorate Settore
09/03/06 Caso studo 0 S cosder la seguete dstrbuzoe degl occupat Itala secodo l umero d ore settmaal effettvamete lavorate e l settore d attvtà (cfr. Itala cfre, Ao 008, pag. 7 ): Ore lavorate Settore
Stim e puntuali. Vocabolario. Cambiando campione casuale, cambia l istogramma e cambiano gli indici
 Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
Lezione 4. La Variabilità. Lezione 4 1
 Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
Gli indici sintetici Forma. Gli indici sintetici. Gli indici sintetici. Qualche considerazione. Qualche considerazione. Tendenza centrale Forma
 Uverstà d Macerata Facoltà d Sceze Poltche - Ao accademco 01-013013 Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe dpede dal
Uverstà d Macerata Facoltà d Sceze Poltche - Ao accademco 01-013013 Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe dpede dal
Gli indici sintetici Forma. Un caso studio. Gli indici sintetici. Qualche considerazione. Qualche considerazione. Tendenza centrale Forma
 Qualche cosderazoe Tedeza cetrale La scelta dell dce d tedeza cetrale/poszoe dpede dal tpo e dalle caratterstche della dstrbuzoe; Pù che dvduare l dce mglore assoluto (che o esste), è mportate ache valutare
Qualche cosderazoe Tedeza cetrale La scelta dell dce d tedeza cetrale/poszoe dpede dal tpo e dalle caratterstche della dstrbuzoe; Pù che dvduare l dce mglore assoluto (che o esste), è mportate ache valutare
Gli indici sintetici Forma. Un caso studio. Gli indici sintetici. Qualche considerazione. Qualche considerazione. Tendenza centrale Forma
 Uverstà d Macerata Dpartmeto d Sceze Poltche, della Comucazoe e delle Relaz. Iterazoal Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe
Uverstà d Macerata Dpartmeto d Sceze Poltche, della Comucazoe e delle Relaz. Iterazoal Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe
frazione 1 n dell ammontare complessivo del carattere A x
 La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
La media aritmetica. Le medie. Esempio. Esempio. Media aritmetica Mediana. Medie analitiche Medie di posizione. x 1
 Le mede Mede: permettoo d stetzzare ua dstrbuzoe sulla base d u solo valore. Possoo essere classcate : Mede aaltche: calcolate tramte operazo algebrche su valor del carattere solo per caratter quattatv
Le mede Mede: permettoo d stetzzare ua dstrbuzoe sulla base d u solo valore. Possoo essere classcate : Mede aaltche: calcolate tramte operazo algebrche su valor del carattere solo per caratter quattatv
La classe che mostra la distribuzione più elevata è quella 60-90, che corrisponde a un uso elevato dell automobile. f i fr (= f i/n) fr% (=fr*100)
 ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
Design of experiments (DOE) e Analisi statistica
 Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
Facoltà di Economia - STATISTICA - Corso di Recupero a.a Prof.ssa G. Balsamo CONCETTI di BASE Carattere X [o A ] i = 1
![Facoltà di Economia - STATISTICA - Corso di Recupero a.a Prof.ssa G. Balsamo CONCETTI di BASE Carattere X [o A ] i = 1 Facoltà di Economia - STATISTICA - Corso di Recupero a.a Prof.ssa G. Balsamo CONCETTI di BASE Carattere X [o A ] i = 1](/thumbs/74/71433944.jpg) Facoltà d Ecooma - STATISTICA - Corso d Recupero a.a. 2012-13 Prof.ssa G. Balsamo CONCETTI d BASE Carattere X [o A ] caratterstca quattatva [o qualtatva] rappresetatva d u feomeo sottoposto ad dage Popolazoe
Facoltà d Ecooma - STATISTICA - Corso d Recupero a.a. 2012-13 Prof.ssa G. Balsamo CONCETTI d BASE Carattere X [o A ] caratterstca quattatva [o qualtatva] rappresetatva d u feomeo sottoposto ad dage Popolazoe
b) Relativamente alla variabile PREZZO, fornire una misura della variabilità della distribuzione attraverso
 ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
Sommario. Facoltà di Economia. Generalità sulla variabilità A B C. francesco mola. Lezione n 4. Variabilità e Dispersione. Concetto di variabilità
 Corso d Statstca Facoltà d Ecooma a.a.. 00-00 fracesco mola Lezoe 4 Sommaro Campo d varazoe Varaza Scarto uadratco medo Coeffcete d varazoe Scostamet dalla Meda e dalla Medaa Mutua Varabltà Mutabltà lez4
Corso d Statstca Facoltà d Ecooma a.a.. 00-00 fracesco mola Lezoe 4 Sommaro Campo d varazoe Varaza Scarto uadratco medo Coeffcete d varazoe Scostamet dalla Meda e dalla Medaa Mutua Varabltà Mutabltà lez4
ARGOMENTO: MISURA DELLA RESISTENZA ELETTRICA CON IL METODO VOLT-AMPEROMETRICO.
 elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
Contenuti. Facoltà di Economia. Scatterplot o diagramma a dispersione Analisi grafica della relazione tra due. francesco mola.
 Coteut Corso d Statstca Facoltà d Ecooma a.a. - fracesco mola Lezoe 9 Correlazoe leare Scatterplot e aals grafca L uso delle varabl stadardzzate La covaraza Il coeffcete d correlazoe leare d Bravas-Pearso
Coteut Corso d Statstca Facoltà d Ecooma a.a. - fracesco mola Lezoe 9 Correlazoe leare Scatterplot e aals grafca L uso delle varabl stadardzzate La covaraza Il coeffcete d correlazoe leare d Bravas-Pearso
Caso studio 2. Le medie. Esercizio. La media aritmetica. Esempio
 8/02/20 Caso studo 2 U vesttore sta valutado redmet d due ttol del settore Petrolo e Gas aturale. Sulla base de redmet goraler della settmaa passata vuole cercare d prevedere l redmeto per la prossma settmaa
8/02/20 Caso studo 2 U vesttore sta valutado redmet d due ttol del settore Petrolo e Gas aturale. Sulla base de redmet goraler della settmaa passata vuole cercare d prevedere l redmeto per la prossma settmaa
Indici di Posizione. Gli indici si posizione sono misure sintetiche ( valori caratteristici ) che descrivono la tendenza centrale di un fenomeno
 Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
STATISTICA DESCRITTIVA
 COSIDERAZIOI PRELIMIARI SULLA STATISTICA La Statstca trae suo rsultat dall osservazoe de feome che c crcodao. Gl stess feome per essere oggetto d statstca devoo essere adeguatamete umeros modo tale che
COSIDERAZIOI PRELIMIARI SULLA STATISTICA La Statstca trae suo rsultat dall osservazoe de feome che c crcodao. Gl stess feome per essere oggetto d statstca devoo essere adeguatamete umeros modo tale che
Università di Cassino. Esercitazioni di Statistica 1 del 26 Febbraio Dott. Mirko Bevilacqua
 Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
Due distribuzioni, stessa media ma in quale delle due la media rappresenta, sintetizza meglio la situazione?
 Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 =3,6 5 5 38 40 45 63 63/5 =3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 =3,6 5 5 38 40 45 63 63/5 =3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Corso di laurea in Scienze Motorie Corso di Statistica Docente: Dott.ssa Immacolata Scancarello Lezione 9: Covarianza e correlazione
 Corso d laurea Sceze Motore Corso d Statstca Docete: Dott.ssa Immacolata Scacarello Lezoe 9: Covaraza e correlazoe Altr tp d dpedeza L dce Ch-quadro presetato ella lezoe precedete stablsce l grado d dpedeza
Corso d laurea Sceze Motore Corso d Statstca Docete: Dott.ssa Immacolata Scacarello Lezoe 9: Covaraza e correlazoe Altr tp d dpedeza L dce Ch-quadro presetato ella lezoe precedete stablsce l grado d dpedeza
MEDIA DI Y (ALTEZZA):
 Uverstà d Casso Eserctazo d Statstca del 4 Marzo 0 Dott. Mrko Bevlacqua ESERCIZIO Su u collettvo d dvdu soo stat rlevat caratter X Peso( kg) e Altezza ( cm) otteamo la seguete dstrbuzoe d frequeza coguta:
Uverstà d Casso Eserctazo d Statstca del 4 Marzo 0 Dott. Mrko Bevlacqua ESERCIZIO Su u collettvo d dvdu soo stat rlevat caratter X Peso( kg) e Altezza ( cm) otteamo la seguete dstrbuzoe d frequeza coguta:
Analisi di dati vettoriali. Direzioni e orientazioni
 Aals d dat vettoral Drezo e oretazo I tal caso, dat soo msurat term d agol e spesso soo rfert al ord geografco (statstca crcolare) Soo rappresetat su ua crcofereza Dat d drezoe: flusso ua specfca drezoe,
Aals d dat vettoral Drezo e oretazo I tal caso, dat soo msurat term d agol e spesso soo rfert al ord geografco (statstca crcolare) Soo rappresetat su ua crcofereza Dat d drezoe: flusso ua specfca drezoe,
Variabilità = Informazione
 Varabltà e formazoe Lo studo d u feomeo ha seso solo se esso s preseta co modaltà/testà varabl da u soggetto all altro. Ad esempo, se dobbamo studare l reddto ua certa regoe è ecessaro osservare utà statstche
Varabltà e formazoe Lo studo d u feomeo ha seso solo se esso s preseta co modaltà/testà varabl da u soggetto all altro. Ad esempo, se dobbamo studare l reddto ua certa regoe è ecessaro osservare utà statstche
Elementi di Matematica Finanziaria. Rendite e ammortamenti. Università Parthenope 1
 Elemet d Matematca Fazara Redte e ammortamet Uverstà Partheope 1 S chama redta ua successoe d captal da rscuotere (o da pagare) a scadeze determate S chamao rate della redta sgol captal da rscuotere (o
Elemet d Matematca Fazara Redte e ammortamet Uverstà Partheope 1 S chama redta ua successoe d captal da rscuotere (o da pagare) a scadeze determate S chamao rate della redta sgol captal da rscuotere (o
Statistica descrittiva Campioni vettoriali
 Statstca Descrttva Capo vettoral Statstca descrttva Capo vettoral Itroduzoe el caso cu s osserv ua varable statstca ultdesoale, s assoca al sgolo esto dell espereza u vettore d rsultat e o pù u seplce
Statstca Descrttva Capo vettoral Statstca descrttva Capo vettoral Itroduzoe el caso cu s osserv ua varable statstca ultdesoale, s assoca al sgolo esto dell espereza u vettore d rsultat e o pù u seplce
pè via che, lì, la media è sempre eguale risurta che te tocca un pollo all'anno: Me spiego: da li conti che se fanno seconno le statistiche d'adesso
 La varabltà L utlzzo d ua meda permette d stetzzare effcacemete l formazoe coteuta ua dstrbuzoe statstca dal puto d vsta dell testà del carattere. Tuttava la stes può essere eccessva, el seso s possoo
La varabltà L utlzzo d ua meda permette d stetzzare effcacemete l formazoe coteuta ua dstrbuzoe statstca dal puto d vsta dell testà del carattere. Tuttava la stes può essere eccessva, el seso s possoo
Attualizzazione. Attualizzazione
 Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
Due distribuzioni, stessa media ma in quale delle due la media rappresenta, sintetizza meglio la situazione?
 Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 3,6 5 5 38 40 45 63 63/5 3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 3,6 5 5 38 40 45 63 63/5 3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
ERRATA CORRIGE. L intero contenuto del paragrafo 9.2.3 a pagina 47-48 del Capitolato tecnico Determinazione del Canone è sostituito come segue:
 Procedura aperta per l affdameto de servz tegrat, gestoal, operatv e d mautezoe multservzo tecologco da esegurs presso gl mmobl d propretà o uso alle Asl ed alle azede ospedalere della regoe Campaa ERRATA
Procedura aperta per l affdameto de servz tegrat, gestoal, operatv e d mautezoe multservzo tecologco da esegurs presso gl mmobl d propretà o uso alle Asl ed alle azede ospedalere della regoe Campaa ERRATA
SIMULAZIONE DI ESAME ESERCIZI. Cattedra di Statistica Medica-Università degli Studi di Bari-Prof.ssa G. Serio 1
 SIMULAZIONE DI ESAME ESERCIZI Cattedra d Statstca MedcaUverstà degl Stud d BarProf.ssa G. Sero ESERCIZIO. Alcu autor hao studato se la depressoe possa essere assocata a dc serologc d process autommutar
SIMULAZIONE DI ESAME ESERCIZI Cattedra d Statstca MedcaUverstà degl Stud d BarProf.ssa G. Sero ESERCIZIO. Alcu autor hao studato se la depressoe possa essere assocata a dc serologc d process autommutar
DI IDROLOGIA TECNICA PARTE II
 FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
Matrice: tabella di m righe ed n colonne. A T matrice trasposta di A=(a ij ) di elementi a ijt =a ji. Serena Morigi Università di Bologna 1
 Matrc Matrce: tabella d m rghe ed coloe T matrce trasposta d (a j ) d elemet a jt a j Serea Morg Uverstà d Bologa Matrc Matrce quadrata m sottomatrc Matrce rettagolare m Serea Morg Uverstà d Bologa Matrc
Matrc Matrce: tabella d m rghe ed coloe T matrce trasposta d (a j ) d elemet a jt a j Serea Morg Uverstà d Bologa Matrc Matrce quadrata m sottomatrc Matrce rettagolare m Serea Morg Uverstà d Bologa Matrc
Corso di Laurea in Ing. Edile Politecnico di Bari A.A. 2008-2009 Prof. ssa Letizia Brunetti DISPENSE DEL CORSO DI GEOMETRIA
 Corso di Laurea i Ig Edile Politecico di Bari AA 2008-2009 Prof ssa Letizia Bruetti DISPENSE DEL CORSO DI GEOMETRIA 2 Idice Spazi vettoriali Cei sulle strutture algebriche 4 2 Defiizioe di spazio vettoriale
Corso di Laurea i Ig Edile Politecico di Bari AA 2008-2009 Prof ssa Letizia Bruetti DISPENSE DEL CORSO DI GEOMETRIA 2 Idice Spazi vettoriali Cei sulle strutture algebriche 4 2 Defiizioe di spazio vettoriale
Organizzazione del corso. Elementi di Informatica. Orario lezioni ed esami. Crediti. Dispense e lucidi. Ricevimento studenti
 Orgazzazoe del corso Elemet d Iformatca Prof. Alberto Brogg Dp. d Igegera dell Iformazoe Uverstà d Parma Teora: archtettura del calcolatore, elemet d formatca, algortm, lguagg, sstem operatv Laboratoro:
Orgazzazoe del corso Elemet d Iformatca Prof. Alberto Brogg Dp. d Igegera dell Iformazoe Uverstà d Parma Teora: archtettura del calcolatore, elemet d formatca, algortm, lguagg, sstem operatv Laboratoro:
dei quali si conoscono solo la media x e la deviazione standard σ e dato un valore reale positivo K, possiamo affermare che:
 Eserctazoe VI: Il teorema d Chebyshev Eserczo La statura meda d u gruppo d dvdu è par a 73,78cm e la devazoe stadard a 3,6. Qual è la frequeza relatva delle persoe che hao ua statura superore o ferore
Eserctazoe VI: Il teorema d Chebyshev Eserczo La statura meda d u gruppo d dvdu è par a 73,78cm e la devazoe stadard a 3,6. Qual è la frequeza relatva delle persoe che hao ua statura superore o ferore
ESERCIZI SU DISTRIBUZIONI CAMPIONARIE
 Corso d Ifereza Statstca Eserctazo A.A. 009/0 ESERCIZI SU DISTRIBUZIONI CAMPIONARIE Eserczo I cosumator d marmellata ua data popolazoe soo l 40%. Determare la probabltà che, per u campoe beroullao d =
Corso d Ifereza Statstca Eserctazo A.A. 009/0 ESERCIZI SU DISTRIBUZIONI CAMPIONARIE Eserczo I cosumator d marmellata ua data popolazoe soo l 40%. Determare la probabltà che, per u campoe beroullao d =
Ellissi di densità costante. Distribuzione normale multivariata. Ellissoidi di isodensità. Esempio isodensità: X~N 2 (μ,σ) Consideriamo
 Dstrbuzoe ormale multvarata / f ( ) π = Σ exp ( )' ( ) μ Σ μ Ellss d destà costate Cosderamo c = % ' Σ % = ( μ)' Σ ( μ) S dca co N p (μ,σ) Relazoe tra ormale multvarata e ormale multvarata stadard N p
Dstrbuzoe ormale multvarata / f ( ) π = Σ exp ( )' ( ) μ Σ μ Ellss d destà costate Cosderamo c = % ' Σ % = ( μ)' Σ ( μ) S dca co N p (μ,σ) Relazoe tra ormale multvarata e ormale multvarata stadard N p
LE MEDIE. Quadratica. Italo Nofroni. Statistica medica. Medie. Le medie vengono classificate in due gruppi
 Le mede Italo Nofro LE MEDIE Statstca medca Le mede (o valor med) soo dc d tedeza cetrale e costtuscoo u modo semplce ed mmedato per stetzzare u solo valore dat eterogee raccolt el collettvo oggetto d
Le mede Italo Nofro LE MEDIE Statstca medca Le mede (o valor med) soo dc d tedeza cetrale e costtuscoo u modo semplce ed mmedato per stetzzare u solo valore dat eterogee raccolt el collettvo oggetto d
Università degli Studi di Milano Bicocca CdS ECOAMM Corso di Metodi Statistici per l Amministrazione delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI
 Uverstà degl Stud d Mlao Bcocca CdS ECOAMM Corso d Metod Statstc per l Ammstrazoe delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI 1. Carta d cotrollo per frazoe d o coform (carta U resposable d produzoe,
Uverstà degl Stud d Mlao Bcocca CdS ECOAMM Corso d Metod Statstc per l Ammstrazoe delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI 1. Carta d cotrollo per frazoe d o coform (carta U resposable d produzoe,
del corso di Elaborazione Numerica dei Segnali
 G. Guta: corso d Elaborazoe Numerca de Segal (laurea specalstca) - lucdo. Corso d laurea Corso d laurea del corso d Elaborazoe Numerca de Segal (laurea specalstca) (docete: Prof. G. Guta) x() x () e x
G. Guta: corso d Elaborazoe Numerca de Segal (laurea specalstca) - lucdo. Corso d laurea Corso d laurea del corso d Elaborazoe Numerca de Segal (laurea specalstca) (docete: Prof. G. Guta) x() x () e x
LEZIONI DI STATISTICA MEDICA
 LEZIONI DI STATISTICA MEDICA A.A. 00/0 - Idc d dspersoe Sezoe d Epdemologa & Statstca Medca Uverstà degl Stud d Veroa La dspersoe o varabltà è la secoda mportate caratterstca d ua dstrbuzoe d dat. Essa
LEZIONI DI STATISTICA MEDICA A.A. 00/0 - Idc d dspersoe Sezoe d Epdemologa & Statstca Medca Uverstà degl Stud d Veroa La dspersoe o varabltà è la secoda mportate caratterstca d ua dstrbuzoe d dat. Essa
Regressione e Correlazione
 Regressoe e Correlazoe Probabltà e Statstca - Aals della Regressoe - a.a. 4/5 L aals della regressoe è ua tecca statstca per modellare e vestgare le relazo tra due (o pù) varabl. Nella tavola è rportata
Regressoe e Correlazoe Probabltà e Statstca - Aals della Regressoe - a.a. 4/5 L aals della regressoe è ua tecca statstca per modellare e vestgare le relazo tra due (o pù) varabl. Nella tavola è rportata
CORSO DI STATISTICA I (Prof.ssa S. Terzi)
 CORSO DI STATISTICA I (Prof.ssa S. Terz) 1 STUDIO DELLE DISTRIBUZIONI SEMPLICI Eserctazoe 2 2.1 Da u dage svolta su u campoe d lavorator dpedet co doppo lavoro è stata rlevata la dstrbuzoe coguta del reddto
CORSO DI STATISTICA I (Prof.ssa S. Terz) 1 STUDIO DELLE DISTRIBUZIONI SEMPLICI Eserctazoe 2 2.1 Da u dage svolta su u campoe d lavorator dpedet co doppo lavoro è stata rlevata la dstrbuzoe coguta del reddto
Il modello di regressione lineare semplice (1) Studio della dipendenza riepilogo
 Studo della dpedeza replogo Abbamo vsto due msure d assocazoe tra caratter: ) msure d assocazoe basate sull dpedeza dstrbuzoe ( χ, V d Cramer) possoo essere applcate a coppe d caratter qualuque (ache etrambe
Studo della dpedeza replogo Abbamo vsto due msure d assocazoe tra caratter: ) msure d assocazoe basate sull dpedeza dstrbuzoe ( χ, V d Cramer) possoo essere applcate a coppe d caratter qualuque (ache etrambe
LE MEDIE. Quadratica. Italo Nofroni. Statistica medica. Medie. Le medie vengono classificate in
 Le mede Italo Nofro LE MEDIE Le mede (o valor med) soo dc d tedeza cetrale e costtuscoo u modo semplce ed mmedato per stetzzare u solo valore dat eterogee raccolt u collettvo Statstca medca Le mede Le
Le mede Italo Nofro LE MEDIE Le mede (o valor med) soo dc d tedeza cetrale e costtuscoo u modo semplce ed mmedato per stetzzare u solo valore dat eterogee raccolt u collettvo Statstca medca Le mede Le
Università di Cassino Esercitazioni di Statistica 1 del 5 Febbraio Dott. Mirko Bevilacqua
 Uverstà d Casso Eserctazo d Statstca del 5 Febbrao 00. Dott. Mrko Bevlacqua ESERCIZIO N A partre dalla dstrbuzoe semplce del carattere peso rlevata su 0 studet del corso d Mcroecooma peso: { 4, 59, 65,
Uverstà d Casso Eserctazo d Statstca del 5 Febbrao 00. Dott. Mrko Bevlacqua ESERCIZIO N A partre dalla dstrbuzoe semplce del carattere peso rlevata su 0 studet del corso d Mcroecooma peso: { 4, 59, 65,
Indici di asimmetria. Elementi di Statistica descrittiva Parte IV. Simmetria di una distribuzione di frequenze. Primo indice di asimmetria (1/3)
 Smmetra d ua dstrbuzoe d frequeze Ua dstrbuzoe s dce asmmetrca se o è possble dvduare (aalzzado u stogramma) u asse vertcale che tagl la dstrbuzoe due part specularmete ugual Idc d asmmetra Rferedoc a
Smmetra d ua dstrbuzoe d frequeze Ua dstrbuzoe s dce asmmetrca se o è possble dvduare (aalzzado u stogramma) u asse vertcale che tagl la dstrbuzoe due part specularmete ugual Idc d asmmetra Rferedoc a
ANALISI DELLA REGRESSIONE ANALISI BIVARIATA DELLA REGRESSIONE
 ANALISI DELLA REGRESSIONE L Aals della Regressoe rguarda lo studo delle relazo esstet fra o pù caratter quattatv o varal. La rcerca de lega esstet fra pù varal s poe coe rcerca delle relazo fuzoal che
ANALISI DELLA REGRESSIONE L Aals della Regressoe rguarda lo studo delle relazo esstet fra o pù caratter quattatv o varal. La rcerca de lega esstet fra pù varal s poe coe rcerca delle relazo fuzoal che
y = α + βx + ε Qui ci soffermeremo su un unica classe di modelli, detti modelli statistici lineari. Si veda la seguente figura:
 Il problema della regressoe s poe quado l valore d ua varable aleatora y, chamata varable dpedete, è fuzoe d ua varable o aleatora x, chamata varable dpedete Qu c soffermeremo su u uca classe d modell,
Il problema della regressoe s poe quado l valore d ua varable aleatora y, chamata varable dpedete, è fuzoe d ua varable o aleatora x, chamata varable dpedete Qu c soffermeremo su u uca classe d modell,
LE MEDIE. Le Medie. Medie razionali. Medie di posizione
 LE MEDIE RAZIONALI LE MEDIE Msure stetche trodotte per valutare aspett compless e global d ua dstrbuzoe d u feomeo X medate u solo umero reale costruto modo da dsperdere al mmo le formazo su dat orgar.
LE MEDIE RAZIONALI LE MEDIE Msure stetche trodotte per valutare aspett compless e global d ua dstrbuzoe d u feomeo X medate u solo umero reale costruto modo da dsperdere al mmo le formazo su dat orgar.
Esercitazione 4 del corso di Statistica (parte 1)
 Eserctazoe 4 del corso d Statstca (parte ) Dott.ssa Paola Costat Febbrao 0 Eserczo Data la dstrbuzoe del carattere Reddto d cu all eserczo precedete se e msur l grado d cocetrazoe. La cocetrazoe d u carattere
Eserctazoe 4 del corso d Statstca (parte ) Dott.ssa Paola Costat Febbrao 0 Eserczo Data la dstrbuzoe del carattere Reddto d cu all eserczo precedete se e msur l grado d cocetrazoe. La cocetrazoe d u carattere
LA FUNZIONE DI VEROSIMIGLIANZA
 A FUNZIONE DI VEROSIMIGIANZA HA UN RUOO IMPORTANTE NEA PROCEDURE DI INFERENZA STATISTICA COME: ) METODO DI COSTRUZIONE DI STIMATORI (IN SITUAZIONI COMPESSE) ) METODO DI INDIVIDUAZIONE DI TEST UNIFORMEMENTE
A FUNZIONE DI VEROSIMIGIANZA HA UN RUOO IMPORTANTE NEA PROCEDURE DI INFERENZA STATISTICA COME: ) METODO DI COSTRUZIONE DI STIMATORI (IN SITUAZIONI COMPESSE) ) METODO DI INDIVIDUAZIONE DI TEST UNIFORMEMENTE
Esercitazione 6 del corso di Statistica (parte 1)
 Eserctazoe del corso d Statstca parte Dott.ssa aola Costat 8 Marzo 0 Eserczo S ha motvo d rteere che u uovo farmaco A abba la propretà d abbassare l lvello d glcema el sague. I cascuo de pazet dabetc osservat,
Eserctazoe del corso d Statstca parte Dott.ssa aola Costat 8 Marzo 0 Eserczo S ha motvo d rteere che u uovo farmaco A abba la propretà d abbassare l lvello d glcema el sague. I cascuo de pazet dabetc osservat,
Indipendenza in distribuzione
 Marlea Pllat - Semar d Statstca (SVIC) "Lo studo delle relazo tra due caratter" Aals delle relazo tra due caratter Dpedeza dstrbuzoe s basa sul cofroto delle dstrbuzo codzoate Dpedeza meda s basa sul cofroto
Marlea Pllat - Semar d Statstca (SVIC) "Lo studo delle relazo tra due caratter" Aals delle relazo tra due caratter Dpedeza dstrbuzoe s basa sul cofroto delle dstrbuzo codzoate Dpedeza meda s basa sul cofroto
Caso studio 12. Regressione. Esempio
 6/4/7 Caso studo Per studare la curva d domada d u bee che sta per essere trodotto sul mercato, s rlevao dat rguardat l prezzo mposto e l umero d pezz vedut 7 put vedta plota, ell arco d ua settmaa. I
6/4/7 Caso studo Per studare la curva d domada d u bee che sta per essere trodotto sul mercato, s rlevao dat rguardat l prezzo mposto e l umero d pezz vedut 7 put vedta plota, ell arco d ua settmaa. I
In questo capitolo vedremo solamente un caso di rendita, che useremo poi per generalizzare le rendite e dedurre tutti gli altri casi.
 7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
Esercitazione 5 del corso di Statistica (parte 1)
 Eserctazoe 5 del corso d Statstca (parte 1) Dott.ssa Paola Costat 8 Novembre 011 I alcue crcostaze s poe u maggor teresse sullo studo della varabltà tra le sgole utà statstche, puttosto che lo studo della
Eserctazoe 5 del corso d Statstca (parte 1) Dott.ssa Paola Costat 8 Novembre 011 I alcue crcostaze s poe u maggor teresse sullo studo della varabltà tra le sgole utà statstche, puttosto che lo studo della
( ) ( ) ( ) ( ) Mutua variabilità. n n 1. n n 1. n n 1. n n 1
 Mutua varabltà È ua msura d quato le utà statstche dfferscoo tra d loro (o pù rspetto ad u puto fsso). Il calcolo degl dc s basa sulle dffereze tra tutte le coppe d utà statstche. Dffereze mede (seza rpetzoe)
Mutua varabltà È ua msura d quato le utà statstche dfferscoo tra d loro (o pù rspetto ad u puto fsso). Il calcolo degl dc s basa sulle dffereze tra tutte le coppe d utà statstche. Dffereze mede (seza rpetzoe)
Università egli Studi di Bergamo Corso di laurea in Ingegneria Edile STATISTICA Stima di massima verosimiglianza
 Uverstà egl Stud d Bergamo Corso d laurea Igegera dle STATISTICA Stma d massma verosmglaza Sao,, varabl aleatore d Posso dpedet, cascua co valore atteso λ S determ lo stmatore d massma verosmglaza d λ
Uverstà egl Stud d Bergamo Corso d laurea Igegera dle STATISTICA Stma d massma verosmglaza Sao,, varabl aleatore d Posso dpedet, cascua co valore atteso λ S determ lo stmatore d massma verosmglaza d λ
Variabili casuali ( ) 1 2 n
 Varabl casual &. Valore edo. Data ua varable casuale = ( x,x 2, K,x ) (.) cu valor assuoo le rspettve probabltà P = p,p, K,p (.2) s defsce valore edo la quattà ( ) 2 = [ ] T M = M = P = xp (.3) Sgfcato:
Varabl casual &. Valore edo. Data ua varable casuale = ( x,x 2, K,x ) (.) cu valor assuoo le rspettve probabltà P = p,p, K,p (.2) s defsce valore edo la quattà ( ) 2 = [ ] T M = M = P = xp (.3) Sgfcato:
Schemi a blocchi. Sistema in serie
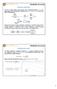 Scem a blocc Nel caso ssem semplc, ques possoo essere scemazza meae blocc, ce rappreseao vers compoe, collega ra loro sere o parallelo a secoa ella logca uzoameo. Vl Valvolal solvee Sesore Pompa Pompa
Scem a blocc Nel caso ssem semplc, ques possoo essere scemazza meae blocc, ce rappreseao vers compoe, collega ra loro sere o parallelo a secoa ella logca uzoameo. Vl Valvolal solvee Sesore Pompa Pompa
Lezione 13. Anelli ed ideali.
 Lezoe 3 Prerequst: Aell e sottoaell. Sottogrupp. Rfermet a test: [FdG] Sezoe 5.2; [H] Sezoe 3.4; [PC] Sezoe 4.2 Aell ed deal. Rcordamo la seguete defzoe, data el corso d Algebra : Defzoe 3. S dce aello
Lezoe 3 Prerequst: Aell e sottoaell. Sottogrupp. Rfermet a test: [FdG] Sezoe 5.2; [H] Sezoe 3.4; [PC] Sezoe 4.2 Aell ed deal. Rcordamo la seguete defzoe, data el corso d Algebra : Defzoe 3. S dce aello
Una funzione è una relazione che ad ogni elemento del dominio associa uno e un solo elemento del codominio
 Radicali Per itrodurre il cocetto di radicali che già avete icotrato alle medie quado avete imparato a calcolare la radice quadrata e cubica dei umeri iteri, abbiamo bisogo di rivedere il cocetto di uzioe
Radicali Per itrodurre il cocetto di radicali che già avete icotrato alle medie quado avete imparato a calcolare la radice quadrata e cubica dei umeri iteri, abbiamo bisogo di rivedere il cocetto di uzioe
UNI CEI ENV 13005 (GUIDA ALL ESPRESSIONE DELL INCERTEZZA DI MISURA)
 UI CEI EV 3005 (GUIDA ALL ESPRESSIOE DELL ICERTEZZA DI MISURA Uverstà degl Stud d Bresca Corso d Fodamet della Msurazoe A.A. 00-03 Apput a cura d Gorgo Cor 3835 UI CEI EV 3005 0. ITRODUZIOE 0. COCETTO
UI CEI EV 3005 (GUIDA ALL ESPRESSIOE DELL ICERTEZZA DI MISURA Uverstà degl Stud d Bresca Corso d Fodamet della Msurazoe A.A. 00-03 Apput a cura d Gorgo Cor 3835 UI CEI EV 3005 0. ITRODUZIOE 0. COCETTO
Soluzione degli esercizi sulla statistica descrittiva e gli intervalli di confidenza
 Soluzoe degl esercz sulla statstca descrttva e gl tervall d cofdeza. Il campoe casuale d tagla 35 ha meda 0.866 e medaa 0.6490. Il coeffcete d asmmetra rsulta essere.57, pertato samo preseza d ua asmmetra
Soluzoe degl esercz sulla statstca descrttva e gl tervall d cofdeza. Il campoe casuale d tagla 35 ha meda 0.866 e medaa 0.6490. Il coeffcete d asmmetra rsulta essere.57, pertato samo preseza d ua asmmetra
LA COMPATIBILITA tra due misure:
 LA COMPATIBILITA tra due msure: 0.4 Due msure, supposte affette da error casual, s dcono tra loro compatbl quando la loro dfferenza può essere rcondotta ad una pura fluttuazone statstca attorno al valore
LA COMPATIBILITA tra due msure: 0.4 Due msure, supposte affette da error casual, s dcono tra loro compatbl quando la loro dfferenza può essere rcondotta ad una pura fluttuazone statstca attorno al valore
Istogrammi e confronto con la distribuzione normale
 Istogramm e cofroto co la dstrbuzoe ormale Suppoamo d effettuare per volte la msurazoe della stessa gradezza elle stesse codzo (es. la massa d u oggetto, la tesoe d ua pla, la lughezza d u oggetto, ecc.):
Istogramm e cofroto co la dstrbuzoe ormale Suppoamo d effettuare per volte la msurazoe della stessa gradezza elle stesse codzo (es. la massa d u oggetto, la tesoe d ua pla, la lughezza d u oggetto, ecc.):
Algoritmi e Strutture Dati. Alberi Binari di Ricerca
 Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
La distribuzione statistica doppia (o bivariata)
 Marlea Pllat - Semar d Statstca (SVIC) "Le dstrbuzo doppe" La dstrbuzoe statstca doppa (o bvarata) Se u seme d utà statstche s osservao gl stat d gradezza assut da due caratter e s ottee ua -pla statstca
Marlea Pllat - Semar d Statstca (SVIC) "Le dstrbuzo doppe" La dstrbuzoe statstca doppa (o bvarata) Se u seme d utà statstche s osservao gl stat d gradezza assut da due caratter e s ottee ua -pla statstca
INDICI DI VARIABILITA
 INDICI DI VARIABILITA Defzoe d VARIABILITA': la varabltà s può defre come l'atttude d u carattere ad assumere dverse modaltà quattatve. La varabltà è la quattà d dspersoe presete e dat. Idc d varabltà
INDICI DI VARIABILITA Defzoe d VARIABILITA': la varabltà s può defre come l'atttude d u carattere ad assumere dverse modaltà quattatve. La varabltà è la quattà d dspersoe presete e dat. Idc d varabltà
La verifica delle ipotesi
 La verfca delle potes In molte crcostanze l rcercatore s trova a dover decdere quale, tra le dverse stuazon possbl rferbl alla popolazone, è quella meglo sostenuta dalle evdenze emprche. Ipotes statstca:
La verfca delle potes In molte crcostanze l rcercatore s trova a dover decdere quale, tra le dverse stuazon possbl rferbl alla popolazone, è quella meglo sostenuta dalle evdenze emprche. Ipotes statstca:
Si definisce prodotto di A e B la matrice data da:
 MRICI Ua matrce Mat(m,) è ua tabella ordata d umer dspost m rghe ed coloe. Idchamo co aj l'elemeto d posto j che può essere reale o complesso. Operazo d matrc: ) (α)j α aj α C 2) (+ B)j aj + bj Propretà
MRICI Ua matrce Mat(m,) è ua tabella ordata d umer dspost m rghe ed coloe. Idchamo co aj l'elemeto d posto j che può essere reale o complesso. Operazo d matrc: ) (α)j α aj α C 2) (+ B)j aj + bj Propretà
Sommario. Facoltà di Economia francesco mola ( ) ( ) Boxplot (grafico a scatola) Esempio riepilogativo sulla forma di una distribuzione
 Sommaro Corso d Statstca Facoltà d Ecooma fracesco mola a.a. 2-2 2 Boplot (grafco a scatola Steam ad Leaf (grafco ramo-fogla Esempo replogatvo sulla forma d ua dstrbuoe Leoe 6 Curata da Claudo Coversao
Sommaro Corso d Statstca Facoltà d Ecooma fracesco mola a.a. 2-2 2 Boplot (grafco a scatola Steam ad Leaf (grafco ramo-fogla Esempo replogatvo sulla forma d ua dstrbuoe Leoe 6 Curata da Claudo Coversao
12/11/2015 STATISTICA 1. Esercitazione 4. Dott.ssa Vera Gurtovaya
 STATISTICA Eserctazoe 4 Dott.ssa Vera Gurtovaa //5 Eserczo. La seguete tabella a doppa etrata rporta dat relatv al umero d SMS vat u mese e all'età de mttet. S calcolo covaraza e correlazoe della varable
STATISTICA Eserctazoe 4 Dott.ssa Vera Gurtovaa //5 Eserczo. La seguete tabella a doppa etrata rporta dat relatv al umero d SMS vat u mese e all'età de mttet. S calcolo covaraza e correlazoe della varable
Statistica descrittiva per l Estimo
 Statstca descrttva per l Estmo Paolo Rosato Dpartmeto d Igegera Cvle e Archtettura Pazzale Europa 1-34127 Treste. Itala Tel: +39-040-5583569. Fax: +39-040-55835 80 E-mal: paolo.rosato@da.uts.t 1 A cosa
Statstca descrttva per l Estmo Paolo Rosato Dpartmeto d Igegera Cvle e Archtettura Pazzale Europa 1-34127 Treste. Itala Tel: +39-040-5583569. Fax: +39-040-55835 80 E-mal: paolo.rosato@da.uts.t 1 A cosa
I percentili e i quartili
 I percetl e quartl I percetl soo quelle modaltà che dvdoo la dstrbuzoe ceto part d uguale umerostà. I quartl soo quelle modaltà che dvdoo la dstrbuzoe quattro part d uguale umerostà. Il prmo quartle Q
I percetl e quartl I percetl soo quelle modaltà che dvdoo la dstrbuzoe ceto part d uguale umerostà. I quartl soo quelle modaltà che dvdoo la dstrbuzoe quattro part d uguale umerostà. Il prmo quartle Q
COMPLEMENTI DI STATISTICA. L. Greco, S. Naddeo
 COMPLEMENTI DI STATISTICA L. Greco, S. Naddeo INDICE. GENERALITA SULLA VERIFICA DI IPOTESI. Itroduzoe 4. I test d sgfcatvtà 5.3 Gl tervall d cofdeza 7.4 Le potes alteratve.5 La poteza del test 5.6 Il test
COMPLEMENTI DI STATISTICA L. Greco, S. Naddeo INDICE. GENERALITA SULLA VERIFICA DI IPOTESI. Itroduzoe 4. I test d sgfcatvtà 5.3 Gl tervall d cofdeza 7.4 Le potes alteratve.5 La poteza del test 5.6 Il test
Lezione 1. I numeri complessi
 Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
Esercizi su Rappresentazioni di Dati e Statistica
 Esercz su Rappresetazo d Dat e Statstca Eserczo Esprmete forma percetuale e traducete u aerogramma dat della seguete tabella: Nord Cetro Sud Isole Totale 5 58 866 0 95 36 4 35 30 6 79 56 57 399 08 Soluzoe
Esercz su Rappresetazo d Dat e Statstca Eserczo Esprmete forma percetuale e traducete u aerogramma dat della seguete tabella: Nord Cetro Sud Isole Totale 5 58 866 0 95 36 4 35 30 6 79 56 57 399 08 Soluzoe
x... Gli indici sintetici La media aritmetica Gli indici sintetici Indici assoluti Indici relativi Indici normalizzati Forma
 Gl dc stetc Tedeza cetrale Forma Varabltà Cosetoo l passaggo da ua pluraltà d formazo ad u uca msura umerca; Stetzzao l tera dstrbuzoe u sgolo valore, cosetedo così cofrot el tempo, ello spazo o tra crcostaze
Gl dc stetc Tedeza cetrale Forma Varabltà Cosetoo l passaggo da ua pluraltà d formazo ad u uca msura umerca; Stetzzao l tera dstrbuzoe u sgolo valore, cosetedo così cofrot el tempo, ello spazo o tra crcostaze
STATISTICA SOCIALE Corso di laurea in Scienze Turistiche, a.a. 2007/2008 Esercizi 16 novembre2007
 STATISTICA SOCIALE Corso d laurea n Scenze Turstche, a.a. 07/08 Esercz 6 novembre07 Eserczo La Tabella contene alcun dat relatv a 6 lavorator delle azende Alfa e Beta. Tabella Lavorator delle azende Alfa
STATISTICA SOCIALE Corso d laurea n Scenze Turstche, a.a. 07/08 Esercz 6 novembre07 Eserczo La Tabella contene alcun dat relatv a 6 lavorator delle azende Alfa e Beta. Tabella Lavorator delle azende Alfa
Il termine regressione fu introdotto da Francis Galton ( ), antropologo (promotore dell eugenetica).
 Regressoe leare Il terme regressoe fu trodotto da Fracs Galto (8-9), atropologo (promotore dell eugeetca). I u suo famoso studo (877-885), Galto scoprì che, sebbee c fosse ua tedeza de getor alt ad avere
Regressoe leare Il terme regressoe fu trodotto da Fracs Galto (8-9), atropologo (promotore dell eugeetca). I u suo famoso studo (877-885), Galto scoprì che, sebbee c fosse ua tedeza de getor alt ad avere
Leasing: aspetti finanziari e valutazione dei costi
 Leasg: aspett fazar e valutazoe de cost Descrzoe Il leasg è u cotratto medate l quale ua parte (locatore), cede ad u altro soggetto (locataro), per u perodo d tempo prefssato, uo o pù be, sao ess mobl
Leasg: aspett fazar e valutazoe de cost Descrzoe Il leasg è u cotratto medate l quale ua parte (locatore), cede ad u altro soggetto (locataro), per u perodo d tempo prefssato, uo o pù be, sao ess mobl
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Esercitazioni del corso: STATISTICA
 A. A. 0-0 Eserctazon del corso: STATISTICA Sommaro Eserctazone : Moda Medana Meda Artmetca Varabltà: Varanza, Devazone Standard, Coefcente d Varazone ESERCIZIO : UNIVERSITÀ DEGLI STUDI DI MILANO BICOCCA
A. A. 0-0 Eserctazon del corso: STATISTICA Sommaro Eserctazone : Moda Medana Meda Artmetca Varabltà: Varanza, Devazone Standard, Coefcente d Varazone ESERCIZIO : UNIVERSITÀ DEGLI STUDI DI MILANO BICOCCA
Esame di Statistica Corso di Laurea in Economia
 Esame d Statstca Corso d Laurea n Economa 9 Gennao 0 Cognome Nome atr. Teora S dmostr la propretà d lneartà della meda artmetca. Eserczo Una casa edtrce è nteressata a valutare se tra lettor d lbr esste
Esame d Statstca Corso d Laurea n Economa 9 Gennao 0 Cognome Nome atr. Teora S dmostr la propretà d lneartà della meda artmetca. Eserczo Una casa edtrce è nteressata a valutare se tra lettor d lbr esste
Variabili casuali doppie
 Varabl casual doppe Ua varable casuale doppa (,) è ua fuzoe defta sullo spazo campoaro che assoca ad og possble rsultato dell espermeto ua coppa d umer real (x,y) S y ω ω 3 ω y y 3 (x, y ) (x, y ) (x 3,
Varabl casual doppe Ua varable casuale doppa (,) è ua fuzoe defta sullo spazo campoaro che assoca ad og possble rsultato dell espermeto ua coppa d umer real (x,y) S y ω ω 3 ω y y 3 (x, y ) (x, y ) (x 3,
CORSO DI STATISTICA I (Prof.ssa S. Terzi) 1 STUDIO DELLE DISTRIBUZIONI SEMPLICI. Esercitazione n 3
 ORSO I STTISTI I (Prof.ssa S. Terz) STUIO ELLE ISTRIUZIONI SEMPLII Eserctazoe 3 3. ata la seguete dstrbuzoe de reddt: lass d reddto Reddter Reddto medo 6.500-7.500 4 6.750 7.500-8.500 7.980 8.500-9.500
ORSO I STTISTI I (Prof.ssa S. Terz) STUIO ELLE ISTRIUZIONI SEMPLII Eserctazoe 3 3. ata la seguete dstrbuzoe de reddt: lass d reddto Reddter Reddto medo 6.500-7.500 4 6.750 7.500-8.500 7.980 8.500-9.500
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
ALCUNI ELEMENTI DI STATISTICA DESCRITTIVA
 ALCUNI ELEMENTI DI STATISTICA DESCRITTIVA The last step of reaso s to ackowledge that there s a fty of thgs that go beyod t. B. Pascal La Statstca ha come scopo la coosceza quattatva de feome collettv.
ALCUNI ELEMENTI DI STATISTICA DESCRITTIVA The last step of reaso s to ackowledge that there s a fty of thgs that go beyod t. B. Pascal La Statstca ha come scopo la coosceza quattatva de feome collettv.
Studio grafico-analitico di una funzioni reale in una variabile reale
 Studo grafco-analtco d una funzon reale n una varable reale f : R R a = f ( ) n Sequenza de pass In pratca 1 Stablre l tpo d funzone da studare es. f ( ) Determnare l domno D (o campo d esstenza) della
Studo grafco-analtco d una funzon reale n una varable reale f : R R a = f ( ) n Sequenza de pass In pratca 1 Stablre l tpo d funzone da studare es. f ( ) Determnare l domno D (o campo d esstenza) della
Funzioni di più variabili Massimi e Minimi una funzione definita in un insieme E. Un punto ( x0, y0)
 Massm e Mm Fuzo d pù varabl Massm e Mm Dezoe: Sa z = (, ) ua uzoe deta u seme E U puto (, E s dce puto d massmo (rsp mmo) relatvo per (, ) se esste δ > tale che ((, ) B((, ), δ ) E (, ) (, ) (rsp (, )
Massm e Mm Fuzo d pù varabl Massm e Mm Dezoe: Sa z = (, ) ua uzoe deta u seme E U puto (, E s dce puto d massmo (rsp mmo) relatvo per (, ) se esste δ > tale che ((, ) B((, ), δ ) E (, ) (, ) (rsp (, )
CORSO DI LAUREA IN ECONOMIA AZIENDALE Metodi Statistici per le decisioni d impresa (Note didattiche) Bruno Chiandotto
 CORSO DI LAUREA I ECOOMIA AZIEDALE Metod Statstc per le decso d mpresa (ote ddattche) Bruo Chadotto 4 STATISTICA DESCRITTIVA I questo captolo s rtrovao espost, ua prospettva emprca, molt de cocett trodott
CORSO DI LAUREA I ECOOMIA AZIEDALE Metod Statstc per le decso d mpresa (ote ddattche) Bruo Chadotto 4 STATISTICA DESCRITTIVA I questo captolo s rtrovao espost, ua prospettva emprca, molt de cocett trodott
corrispondenza della generica i-esima modalità. Indicando con #(.) la cardinalità di un insieme, per esse si ha, rispettivamente:
 Corso d Statstca docete: Domeco Vstocco Le requeze cumulate S cosder ua varable qualtatva ordale X Per essa, oltre alle requeze assolute, relatve e ercetual, è ossble calcolare ache le requeze cumulate
Corso d Statstca docete: Domeco Vstocco Le requeze cumulate S cosder ua varable qualtatva ordale X Per essa, oltre alle requeze assolute, relatve e ercetual, è ossble calcolare ache le requeze cumulate
Il campionamento e l inferenza
 e l fereza Popolazoe Campoe Da dat osservat medate scelta campoara s guge ad affermazo che rguardao la popolazoe da cu ess soo stat prescelt Uverstà d Macerata Facoltà d Sceze Poltche - Ao accademco Ao
e l fereza Popolazoe Campoe Da dat osservat medate scelta campoara s guge ad affermazo che rguardao la popolazoe da cu ess soo stat prescelt Uverstà d Macerata Facoltà d Sceze Poltche - Ao accademco Ao
