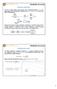
NUMERI INDICI. Esempio: consideriamo la serie storica delle retribuzioni convenzionali INAIL dal 1994 al 1999 (migliaia di Lire)
|
|
|
- Gemma Paoletti
- 8 anni fa
- Visualizzazioni
Transcript
1 Corso d Sasca (caale A D) Do.ssa P. Vcard NUER NDC Nella lezoe abbamo vso la defzoe d u arcolare o d dsrbuzoe: la sere sorca. S arla d sere sorca quado l feomeo rlevao vara el emo e o samo eressa a cooscere e sudare la sua evoluzoe emorale (PL, cosum, roduzoe, flazoe, vede, asce, cde sradal,...). queso caso er og refssao momeo emorale s rleva l eà (esà) del feomeo oggeo d sudo. Esemo: cosderamo la sere sorca delle rerbuzo covezoal NAL dal 994 al 999 (mglaa d Lre) Ao Rerbuzo NAL La rareseazoe grafca della sere sorca è la seguee Rerbuzo NAL dal 994 al Ao Alr esem: ossamo osservare l PL ao er ao oure l rezzo d u azoe goro er goro. Possamo osservare l umero d cde sradal, le asce, la oolazoe resdee secodo deermae cadeze emoral. oguo d ques d ques cas s arrva a defre ua sere sorca.
2 Corso d Sasca (caale A D) Do.ssa P. Vcard olo sesso è eressae sudare l evoluzoe d u feomeo o solo medae l grafco della sua sere sorca ma ache facedo cofro fra le esà del feomeo em dvers (coè calcolado le varazo dell esà da u erodo ad u alro). olre uò essere eressae aalzzare l adameo delle varazo del feomeo avveue ra erod d emo cogu. dchamo co,...,,..., ua sere sorca La varazoe avveua ra due em dvers (dchamol co e +) uò essere msuraa medae l raoro + 00 Queso dce è u raoro erceuale ed è deo asso erceuale d varazoe. arcolare queso è l asso erceuale d varazoe del feomeo del emo + rseo al emo recedee. Esemo: Cosderamo la sere sorca (vsa lezoe) relava all adameo del commerco co l esero, e arcolare alle esorazo, della Fraca ra l 984 e l 989. Calcolamo l asso erceuale d varazoe delle esorazo ra l 984 e l 989. Fare cò sgfca rsodere alla seguee domada: a quao ammoerebbero le esorazo el 989 se le esorazo el 984 fossero sae ar a 00? Rsosa: basa cosderare la seguee roorzoe Allora s rova A Esorazo ( mglaa d mlard) 984 8, , , ,6 989,4 x 989 : 984 x : Coè se el 984 le esorazo fossero sae ar a 00, el 989 sarebbero ar a 7.5 co u aumeo del 7.5%.
3 Corso d Sasca (caale A D) Do.ssa P. Vcard Osservazoe : l asso erceuale d varazoe è u umero che o dede dall uà d msura. Qud medae ques dc è ossble cofroare sere dverse (coè sere esresse uà d msura dverse). Osservazoe : se eressa, vece, calcolare la varazoe erceuale dell esà del feomeo ra l emo e l emo +, occorre calcolare l seguee raoro: + 00 che s caraerzza come ua dffereza relava. Ache queso raoro, come l asso erceuale d varazoe, o dede dall uà d msura. Queso raoro msura la varazoe del feomeo ra l emo e l emo +, faa uguale a 00 l esà del feomeo al emo. Qud, ell esemo recedee la varazoe erceuale delle esorazo ra l 984 e l 989 è saa del 7.5%. Quado s ha ua sere sorca e s è eressa a valuare l adameo delle varazo del feomeo, s ossoo cosrure umer dc. umer dc ossoo essere classfca : Numer dc semlc, che soo da dal raoro fra due esà d ua sessa sere Numer dc comless che s oegoo cofroado ù coe d umer rovee da sere dverse. umer dc semlc ossoo essere - a base fssa - a base moble Numer dc semlc Numer dc a base fssa. Quado s calcolao umer dce a base fssa, l erodo d rfermeo (coè l esà del feomeo da meere a deomaore del raoro) rmae semre lo sesso.
4 Corso d Sasca (caale A D) Do.ssa P. Vcard Cò sgfca che occorre dvduare la cosddea suazoe base. queso modo, le esà del feomeo e var em vegoo cofroae co l esà del feomeo ella suazoe base. Cosderamo la geerca sere sorca Temo esà del feomeo T Tabella Sceglamo come base l emo ; la sere de umer dce a base fssa co base è daa da Numer dc a base Temo fssa (base ) S o che umer dc a base fssa vegoo dca co la leera mauscola; l dce basso a ssra dca l emo base (e fa ella abella sora che rora umer dce co base, l umero è semre basso a ssra della leera ), l dce basso a desra dca l emo er l quale s calcola l dce. Geeralmee o umer dc calcola ella abella sora vegoo mollca er 00 modo ale da oeere ass erceual 4
5 Corso d Sasca (caale A D) Do.ssa P. Vcard Esemo: cosderamo uovamee la sere sorca delle rerbuzo covezoal NAL dal 994 al 999 (mglaa d Lre) Ao Rerbuzo NAL Numer dc a base fssa (base 994) / / / / / / Vedamo che le rerbuzo soo aumeae del 4% ra l 994 e l 995; mere soo aumeae del 4% crca ra l 994 e l 997. queso esemo è sao reso come ao base l 994. La scela del erodo base è u elemeo morae ella fase d cosruzoe d u dce a base fssa. Geeralmee covee redere come base u erodo cu l feomeo oggeo d sudo ha avuo ua esà ormale, coè o aleraa da crcosaze che orebbero avere erurbao l adameo del feomeo modo aomalo e/o eccezoale. geere l erodo base dovrebbe essere abbasaza lugo modo che s ossao comesare le cause accdeal che urbao l feomeo. La scela della base è acora ù dffcle se s vogloo cofroare umer dc calcola a arre da sere che s rferscoo a feome dvers che, quao al, ossoo avere erod o cocde d comorameo ormale. Cambameo d base Come abbamo vso, cosrure umer dc a base fssa comora la scela del erodo d rfermeo. Ua vola calcolaa la sere de umer dce a base fssa, è ossble effeuare u cambameo d base. alre arole, a arre da umer dce calcola co rfermeo alla veccha base, s ossoo cosrure umer dce co ua uova base fssa. S cosder la geerca sere sorca Tabella. dchamo co la veccha base fssa (quella, coè, che voglamo cambare). La sere d umer dc a dsoszoe è qud la seguee 5
6 Corso d Sasca (caale A D) Do.ssa P. Vcard,,...,,,..., + +, () Suoamo d o avere a dsoszoe la sere orgara Tabella e d dsorre solamee della sere () de umer dc co base fssa. Cambamo la base: sceglamo j come uovo emo base. Voglamo calcolare umer dc esress ella uova base ( j,,..., ) a arre da umer dc esress ella veccha base. j j j j j Coè umer dc esress ella uova base j s calcolao a arre da vecch dc come segue j j j,,..., () alre arole l umero dce a base fssa j relavo al emo s oee dvdedo l veccho umero dce a base fssa relavo al emo er l umero dce del erodo reso come uova base (j) calcolao rseo alla veccha base (). Esemo: rredamo l esemo delle rerbuzo NAL. Ao Numer dc a base fssa (base 994) 994 Numer dc a base fssa (base 997) / / / / / /.9.05 Usado la smbologa vsa sora, abbamo Veccha base 994 Nuova base j 997 Qud la uova sere d umer dc (esressa base 997) s oee dalla veccha sere ( base 994) dvdedo og dce della veccha sere ( 994 ) er Numer dc a base moble. 6
7 Corso d Sasca (caale A D) Do.ssa P. Vcard U alro modo er aalzzare l adameo d u feomeo è quello d cofroare la sua esà u erodo co la sua esà el erodo mmedaamee recedee. queso modo s vegoo a defre de umer dc er qual l valore d rfermeo o è semre lo sesso ma è l valore del erodo mmedaamee recedee. Gl dc che s oegoo s chamao umer dc a base moble. Cosderamo la sere sorca Tabella. azuo osservamo che l umero dce a base moble relavo al emo o uò essere calcolao quao o dsoamo dell esà del feomeo al emo recedee. Perao umer dc a base moble ossoo essere calcola a arre dal secodo emo della sere. umer dc a base moble vegoo dca co, coè s usa la leera muscola, e reseao solo u dce basso a desra che dca l emo a cu s rfersce l umero dce. (No è fa ecessaro dcare la base quao come elemeo d cofroo s rede semre l esà del feomeo el erodo recedee). La sere de umer dc a base moble è la seguee Temo Numer dc a base moble - Come umer dc a base fssa, geeralmee o ache umer dc calcola ella abella sora vegoo mollca er 00 modo ale da oeere ass erceual (vece che uar). Esemo: oramo a cosderare l esemo delle rerbuzo NAL. Calcolamo la sere de umer dc a base moble. (roramo ache la sere de umer dc a base fssa, base 994). 7
8 Corso d Sasca (caale A D) Do.ssa P. Vcard Ao Rerbuzo NAL Numer dc a base fssa (base 994) 994 Numer dc a base moble / / / / / Gl dc a base fssa colgoo l adameo d medo/lugo erodo del feomeo erché mosrao l adameo el emo della varable. Gl dc a base moble colgoo, vece, ase ù coguural ; fa ess aalzzao l adameo el emo delle varazo delle esà del caraere ra due erod d emo cogu. Quao deo rsula ù charo se s osserva l grafco seguee cu soo rareseae: la sere sorca e umer dce a base fssa (base 994) e la sere sorca de umer dc a base moble base 994 base moble Ao Dal grafco emerge charamee che gl dc a base fssa e quell a base moble colgoo e rareseao caraersche dverse dell evoluzoe del feomeo. Osservamo che l adameo de umer dc a base fssa è semre crescee (esaamee come avevamo rlevao guardado valor della sere). Cere vole le rerbuzo soo crescue d ù e cò è rareseao da ra ù cla della curva. Osservamo la curva raeggaa relava alla sere de umer dc a base moble. Noamo che o ha u adameo crescee. Essa, fa, mosra che doo l 996 8
9 Corso d Sasca (caale A D) Do.ssa P. Vcard gl creme delle rerbuzo soo rallea e ralleao fo al 998 quado segao ua leggera rresa. * * * * * * * E ossble assare dagl dc a base fssa agl dc a base moble e vceversa? Pù charamee, è ossble, a arre dalla sola sere d uo de due d dc, oeere l alra sere gorado la sere sorca d areza? Rsosa: ceramee sì! Vedamo come. Dagl dc a base fssa agl dc a base moble. Cosderamo l caso geerale cu s dsoe della sere de umer dc a base fssa (base ) Numer dc a base Numer dc a Temo fssa (base ) base moble - N Tabella Dsoamo della coloa de umer dc a base fssa (base ) e voglamo oeere la sere de umer dc a base moble. Alchamo roro la defzoe d ques umer dc, così come roraa ella abella sora. 9
10 Corso d Sasca (caale A D) Do.ssa P. Vcard Ne segue che er oeere umer dc a base moble a arre da umer dc a base fssa, basa dvdere og umero dce a base fssa della sere er quello mmedaamee recedee. Esemo: cosderamo semre le rerbuzo NAL e arcolare la sere de umer dc a base fssa (base 997). Cosruamo la sere de umer dc a base moble. Alchamo la regola 997,,..., 997 Ao Numer dc Numer dc a base a base fssa moble (base 997) / / / / / Dagl dc a base moble agl dc a base fssa (base ). Cosderamo d uovo la Tabella. La sere d areza è ora quella de umer dc a base moble (ella erza coloa della Tabella); a arre da quesa cosruamo la sere de umer dc a base fssa co base. 0
11 Corso d Sasca (caale A D) Do.ssa P. Vcard. Temo l umero dce er defzoe. Tem recede Dobbamo calcolare Aalogamee er l emo s ha Qud er calcolare umer dc a base fssa er u geerco emo h recedee, occorre fare l verso del rodoo d u gl dc a base moble dal emo h+ al emo cluso; coè geerale + + h h h h,...,, (). Tem successv a
12 Corso d Sasca (caale A D) Do.ssa P. Vcard + + Qud er calcolare umer dc a base fssa er u geerco emo g successvo a, occorre fare l rodoo d u gl dc a base moble dal emo + fo al emo g cluso; coè geerale g + + g, g +,..., (4) Esemo: cosderamo la seguee sere d umer dc a base moble relava alle varazo de rezz d u bee dal 99 al 995. Cosruamo la sere de umer dc a base fssa (base 99) a arre dalla sere de umer dc a base moble. Alchamo le regole vse a u, e. Ao Numer dc a base moble Numer dc a base fssa (base 99) /( ) / Per l calcolo d e abbamo usao la formula (). Per l calcolo d e abbamo usao la formula (4). Domada: qual è l cremeo medo auo del rezzo del bee dal 99 al 995? Per rsodere basa rcordare che u asso medo s calcola come meda geomerca de ass de sgol erod. alre arole, dobbamo calcolare la meda geomerca de umer dc a base moble er oeere l asso medo auo d varazoe. Doo cò er oeere l cremeo medo auo, occorre sorarre. Perao cremeo medo auo 4 ( ) 0. 8
13 Corso d Sasca (caale A D) Do.ssa P. Vcard Prcal roreà de umer dc Couamo a cosderare umer dc che msurao varazo su bas uare (coè o mollca er 00). geerco umero dce relavo al emo co base daa dal emo s. s deà Se s cofroa ua suazoe emorale co se sessa o se s cofroao due suazo emoral ugual, l umero dce è ar a. s s se s s s s allora s s s Reversblà delle bas Dao l umero dce s, allora s ha s s Vedamo erché: s, se s assume come base l emo vece del emo s s s s Proreà crcolare Cosderamo re em: r, s e. S ha s r s r o, modo equvalee, s r s r s Vedamo erché: r s rs r s r La roreà crcolare è la roreà che ermee d effeuare l cambameo d base. Suoamo d avere l umero dce a base fssa (base r) relavo al emo, r, e d voler cambare base rededo s come uova base. Allora, alcado la roreà d crcolarà, r esaamee come avevamo vso recedeza. s r s
14 Corso d Sasca (caale A D) Do.ssa P. Vcard Numer dc comless Suoamo d fare delle rlevazo su rezz. Se s vuole sudare l adameo del rezzo d u solo bee allora abbamo umer dc semlc. Se s vuole sudare l adameo del rezzo d ua classe d be, allora s hao umer dc comless che oerao ua ses delle sere sorche de rezz de sgol be della classe. Dal momeo che s sa cosruedo ua msura d ses delle varazo de rezz d be dvers, è ecessaro rodurre u ssema d es che msur l moraza d og sgolo bee ella classe cosderaa. l eso dovrà essere ao maggore quao maggore è l moraza del bee a cu s rfersce. Quado c s occua d sere rfere a rezz de be, come ssema d es s usao le quaà medamee cosumae de sgol be. Cosderamo u aere d be. Abbamo rezz e le quaà scambae degl be al emo 0 e al emo. Bee Prezzo al emo 0 Quaà al emo 0 0 q 0 Prezzo al emo Quaà al emo q 0 q 0 q m m0 q m0 m q m 0 q 0 q l umero dce de rezz d Laseyres è defo come L m m m0 m Queso dce s oee ulzzado er l calcolo del valore (rezzo mollcao er le quaà) de be scamba, semre le quaà al emo base. queso modo vee solaa la varazoe de rezz. L dce d Laseyres fssa le quaà al emo base (coè suoe che u cosumaore vogla lascare alerao l suo comorameo d cosumo) e cofroa l valore d quese quaà d be alcado rezz del emo, co l valore delle sesse quaà d be alcado rezz del emo 0. sosaza L msura d q q m0 m0 4
15 Corso d Sasca (caale A D) Do.ssa P. Vcard quao vara l valore della sesa del cosumaore ra l emo 0 e l emo ell oes che l cosumaore o modfch le sue abud. l umero dce de rezz d Paasche è defo come P m m m0 m Queso dce s oee ulzzado er l calcolo del valore de be scamba, le quaà al emo. Ache queso modo vee solaa la varazoe de rezz, ma l ssema de es o è cosae. q q m m Osservazoe: Usare L er ua sere d a equvale a cosrure ua sora d umer dc comless co ssema d es fsso (al emo 0). Qud er calcolare queso dce è suffcee deermare es al emo 0. Al coraro, l dce d Paasche o maee cosae l ssema d es erché usa quello dell ao corree. Cò sgfca che og ao adrebbero rlevae ache le quaà e rcalcola es. Queso è esremamee oeroso e comlesso. Per queso l suo d Sasca usa l dce d Laseyres. Vedamo che modo ossoo essere errea gl dc d Laseyres e d Paasche. Cosderamo due mod: ) Numer dc d mede oderae (es quaà) L dce d Laseyres uò essere scro come segue L m m q q m0 m m 0 m0 qm0 m q m m 0 meda oderaa del rezzo degl be al emo (es quaà al emo 0) meda oderaa del rezzo degl be al emo 0 (es quaà al emo 0) Coè l dce d Laeyres è erreable come u umero dce semlce cu rezz os a cofroo soo l rezzo medo degl be al emo e l rezzo medo degl be al emo 0. Nel calcolo de rezz med vegoo usae come ssema d es le quaà scambae al emo 0. 5
16 Corso d Sasca (caale A D) Do.ssa P. Vcard L dce d Paasche uò essere scro come segue P m qm m q m m q m0 m m q m m meda oderaa del rezzo degl be al emo (es quaà al emo ) meda oderaa del rezzo degl be al emo 0 (es quaà al emo ) Coè l dce d Paasche è erreable come u umero dce semlce cu rezz os a cofroo soo l rezzo medo degl be al emo e l rezzo medo degl be al emo 0. Nel calcolo de rezz med vegoo usae come ssema d es le quaà scambae al emo. ) ede oderae (es valore) de umer dc L dce d Laseyres uò essere scro ache così L m m m m0 m q m m0 m0 qm0 0 (5) Esso coè è oeuo facedo ua meda oderaa de umer dc semlc de rezz de sgol be usado come es l valore delle quaà scambae al emo 0 a rezz del emo 0. (Coè es m0 q m0 ) m0 L dce d Paasche uò essere scro ache così P m m m m0 m m0 qm 0 (6) q Esso coè è oeuo facedo ua meda oderaa de umer dc semlc de rezz de sgol be usado come es l valore delle quaà scambae al emo a rezz del emo 0. (Coè es q m m0 m ) Gl dc d Laseyres e d Paasche descrvoo modo dverso l adameo della varazoe de rezz. Cò è dovuo al fao che fao uso d ssem d es dvers. 6
17 Corso d Sasca (caale A D) Do.ssa P. Vcard Per comredere meglo quese cosderazo s osservo le formule (5) e (6) cu due dc comless soo calcola come meda oderaa d umer dc semlc. A causa della relazoe versa essee ra rezz e quaà, abbamo che ) L dce d Laseyres dà maggor eso agl aume d rezzo rseo all dce d Paasche. Se rezz aumeao allora q m < q m 0. D cosegueza m0 q m0 > m0 q m Pes dell dce d Laseyres Pes dell dce d Paasche ) L dce d Paasche dà maggor eso alle domuzo d rezzo rseo all dce d Laseyres. Se rezz dmuscoo allora q m > q m 0. D cosegueza m0 q m0 < m0 q m Pes dell dce d Laseyres Pes dell dce d Paasche U dce che sezza L e P è l dce d Fsher F che e fa la meda geomerca. L dce d Fsher è defo così F L P L, P e F godoo della roreà d deà. F gode ache della roreà d reversblà delle bas. Nessuo de re dc gode della roreà d crcolarà. 7
Variazione approssimata del valore attuale
arazoe approssmaa del valore auale Fabo Bell 0 Abbamo vso le prcpal propreà della durao e dvers mod d calcolarla var esemp, ra cu ol a cedola fssa. Roramo alla relazoe che lega la durao alla sesvà del
Dimostrazione della Formula per la determinazione del numero di divisori-test di primalità, di Giorgio Lamberti
Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Titoli obbligazionari (Bond) Tipi di titoli obbligazionari
Tol obblgazoar Bod U obblgazoe è u olo d debo emesso da ua soceà da uo sao o da u ee pubblco che dà dro al suo possessore al rmborso del capale presao alla scadeza e al pagameo d eress cedole. La emssoe
CAPITOLO 6 ANALISI DEL RITARDO IN UNA RETE DATI.
CAITOLO 6 AALISI DEL RITARDO I UA RETE DATI. 6. AALISI DEL RITARDO I UA RETE DATI I queso caolo aalzzeremo, modo quaavo e qualavo, gl eleme d rardo rese ua ree er da. Fodamealmee cosdereremo re d o aced
La classe che mostra la distribuzione più elevata è quella 60-90, che corrisponde a un uso elevato dell automobile. f i fr (= f i/n) fr% (=fr*100)
ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
UNIVERSITA DEGLI STUDI DI PADOVA
UNIVERSITA DEGLI STUDI DI PADOVA FACOLTA DI SCIENZE STATISTICHE CORSO DI LAUREA IN STATISTICA E GESTIONE IMPRESE RELAZIONE FINALE I NUMERI INDICI DI BORSA : UNA RASSEGNA RELATORE : CH.MO PROF. UGO TRIVELLATO
Regime di capitalizzazione composta
Regme d capalzzazoe composa Se s deposa baca, all zo dell ao, ua somma d 000 ad u asso auale uaro =0,05 oppure r=5%, dopo ao ale somma frua u eresse par a I = = 000 0,05 = 50 che aggugedos al capale zale
ELEMENTI DI MATEMATICA FINANZIARIA
ELEMENTI DI MATEMATICA FINANZIARIA 9. OPERAZIONI FINANZIARIE La Maemaca Fazara ha per oggeo suo le operazo fazare, coè le operazo scambo somme earo spoble emp vers. Gl eleme foameal u'operazoe fazara soo
( ) 2 i 1 X. n(n + 1) a) si determini se sono corretti; b) per quelli non corretti, si calcoli la distorsione d;
ESERCIZIO 5. Sa (X, X,, X ) u campoe casuale geerato da ua v.c. X f(x; θ) per la quale è oto che E(X) θ e Var(X). S cosdero 3 stmator d θ: X ; X ; ( ) X 3 a) s determ se soo corrett; b) per quell o corrett,
Università di Cassino Esercitazioni di Statistica 1 del 5 Febbraio Dott. Mirko Bevilacqua
Uverstà d Casso Eserctazo d Statstca del 5 Febbrao 00. Dott. Mrko Bevlacqua ESERCIZIO N A partre dalla dstrbuzoe semplce del carattere peso rlevata su 0 studet del corso d Mcroecooma peso: { 4, 59, 65,
Indici di Posizione. Gli indici si posizione sono misure sintetiche ( valori caratteristici ) che descrivono la tendenza centrale di un fenomeno
Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
Due distribuzioni, stessa media ma in quale delle due la media rappresenta, sintetizza meglio la situazione?
Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 =3,6 5 5 38 40 45 63 63/5 =3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Due distribuzioni, stessa media ma in quale delle due la media rappresenta, sintetizza meglio la situazione?
Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 3,6 5 5 38 40 45 63 63/5 3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Attualizzazione. Attualizzazione
Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
Schemi a blocchi. Sistema in serie
Scem a blocc Nel caso ssem semplc, ques possoo essere scemazza meae blocc, ce rappreseao vers compoe, collega ra loro sere o parallelo a secoa ella logca uzoameo. Vl Valvolal solvee Sesore Pompa Pompa
b) Relativamente alla variabile PREZZO, fornire una misura della variabilità della distribuzione attraverso
ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
Previsione della domanda - contenuti di base -
Prevsoe della domada - coeu d base - Prof. Rccardo Mello rccardo.mello@umore. Uversà d Modea ad Reggo Emla Dparmeo d Igegera Ezo Ferrar va Vgolese 905, 400, Modea - Iala Gruppo d Rcerca: Impa Idusral Ig.
frazione 1 n dell ammontare complessivo del carattere A x
La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
Variabilità = Informazione
Varabltà e formazoe Lo studo d u feomeo ha seso solo se esso s preseta co modaltà/testà varabl da u soggetto all altro. Ad esempo, se dobbamo studare l reddto ua certa regoe è ecessaro osservare utà statstche
Esercizi 12/10/2007. oppure B 0. In modo del tutto analogo AB 0 se e solo se. oppure B 0 B 0. Studio del segno di una disequazione polinomiale.
Esercz 2/0/2007 Dsequazo Sego d u prodotto. Voglamo studare l sego d u prodotto d due umer real. I altr term vedere qual soo le codzo affché due umer real A e B soddsfo AB 0. Ragoamo come segue: rcoducamo
I percentili e i quartili
I percetl e quartl I percetl soo quelle modaltà che dvdoo la dstrbuzoe ceto part d uguale umerostà. I quartl soo quelle modaltà che dvdoo la dstrbuzoe quattro part d uguale umerostà. Il prmo quartle Q
MATEMATICA FINANZIARIA
Capializzazioe semplice e composa MATEMATICA FINANZIARIA Immagiiamo di impiegare 4500 per ai i ua operazioe fiaziaria che frua u asso del, % auo. Quao avremo realizzao alla fie dell operazioe? I u coeso
pè via che, lì, la media è sempre eguale risurta che te tocca un pollo all'anno: Me spiego: da li conti che se fanno seconno le statistiche d'adesso
La varabltà L utlzzo d ua meda permette d stetzzare effcacemete l formazoe coteuta ua dstrbuzoe statstca dal puto d vsta dell testà del carattere. Tuttava la stes può essere eccessva, el seso s possoo
MATEMATICA FINANZIARIA
MATEMATICA FINANZIAIA Prof. Adrea Berard 999 4. MUTUI E PIANI I AMMOTAMENTO Corso d Maeaca Fazara 999 d Adrea Berard Sezoe 4 0 CONTATTO I MUTUO Il corao d uuo è u operazoe fazara corrspodee ad ua parcolare
STATISTICA DESCRITTIVA
COSIDERAZIOI PRELIMIARI SULLA STATISTICA La Statstca trae suo rsultat dall osservazoe de feome che c crcodao. Gl stess feome per essere oggetto d statstca devoo essere adeguatamete umeros modo tale che
SCHEDA DIDATTICA N 5
FACOLTA DI INGEGNEIA COSO DI LAUEA IN INGEGNEIA CIVILE COSO DI IDOLOGIA POF. PASQUALE VESACE SCHEDA DIDATTICA N 5 MOMENTI DELLE VAIABILI CASUALI E STIMA DEI PAAMETI A.A. 0-3 Momet delle varabl casual La
Nozioni elementari di Analisi Matematica applicate alla Fisica Generale
Nozioi elemeari di alisi Maemaica applicae alla Fisica Geerale Nozioe di iegrale ideiio La derivazioe può essere ierpreaa come ua regola che, per ogi uzioe assegaa (primiiva), ci permee di deermiare u
Modello dinamico nello spazio dei giunti: relazione tra le coppie di attuazione ai giunti ed il moto della struttura
Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
APPROFONDIMENTI SULLA TEORIA DEL CONSUMO AGGREGATO
Moduo 8a 1 APPROFONDIMENTI SULLA TEORIA DEL CONSUMO AGGREGATO 1. Iroduzioe 2. La eoria de cosumo di Dueseberry 3. La eoria de cico viae di Modigiai 2 1. Iroduzioe Dae esperieze dei maggiori sisemi macroecoomici,
In questo capitolo vedremo solamente un caso di rendita, che useremo poi per generalizzare le rendite e dedurre tutti gli altri casi.
7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
ammontare del carattere posseduto dalle i unità più povere.
Eserctazoe VII: La cocetrazoe Eserczo Determare l rapporto d cocetrazoe d G del fatturato medo (espresso. d euro) d 8 mprese e rappresetare la curva d Lorez: 97 35 39 52 24 72 66 87 Eserczo apporto d cocetrazoe
Esercitazione 4 del corso di Statistica (parte 1)
Eserctazoe 4 del corso d Statstca (parte ) Dott.ssa Paola Costat Febbrao 0 Eserczo Data la dstrbuzoe del carattere Reddto d cu all eserczo precedete se e msur l grado d cocetrazoe. La cocetrazoe d u carattere
Analisi dei Dati. La statistica è facile!!! Correlazione
Aals de Dat La statstca è facle!!! Correlazoe A che serve la correlazoe? Mettere evdeza la relazoe esstete tra due varabl stablre l tpo d relazoe stablre l grado d tale relazoe stablre la drezoe d tale
Corso di Intermediari Finanziari e Microcredito
Idice Corso di Iermediari iaziari e Microcredio Iroduzioe I crieri radizioali di valuazioe dei progei di ivesimeo; La valuazioe dei progei di ivesimeo I crieri fiaziari di valuazioe dei progei d ivesimeo
Matematica elementare art.1 di Raimondo Valeri
Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
2. Duration. Stefano Di Colli
2. Duraio Meodi Saisici per il Credio e la Fiaza Sefao Di Colli Tassi di ieresse e redimei La reddiivià di u obbligazioe è misuraa dal asso di redimeo o dal asso di ieresse U idicaore del redimeo deve
Lezione 24. Campi finiti.
Lezoe 4 Prerequst: Lezo 0,,, 3 Rfermet a test: [FdG] Sezoe 86; [H] Sezoe 79; [PC] Sezoe 63; Cam ft Nelle lezo recedet abbamo vsto dvers esem d cam ft: ess erao tutt del to oure [ x ]/( f ( x )), dove f
EQUAZIONI ALLE RICORRENZE
Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
Lezione 4. La Variabilità. Lezione 4 1
Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
Lezione 13. Anelli ed ideali.
Lezoe 3 Prerequst: Aell e sottoaell. Sottogrupp. Rfermet a test: [FdG] Sezoe 5.2; [H] Sezoe 3.4; [PC] Sezoe 4.2 Aell ed deal. Rcordamo la seguete defzoe, data el corso d Algebra : Defzoe 3. S dce aello
Esercitazione 5 del corso di Statistica (parte 1)
Eserctazoe 5 del corso d Statstca (parte 1) Dott.ssa Paola Costat 8 Novembre 011 I alcue crcostaze s poe u maggor teresse sullo studo della varabltà tra le sgole utà statstche, puttosto che lo studo della
Gli indici sintetici Forma. Gli indici sintetici. Gli indici sintetici. Qualche considerazione. Qualche considerazione. Tendenza centrale Forma
Uverstà d Macerata Facoltà d Sceze Poltche - Ao accademco 01-013013 Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe dpede dal
PARTE TERZA: L EQUILIBRIO PARAMETRICO
Aldo Motesao PRINCIPI DI ANALISI ECONOMICA PARTE TERZA: L EUILIBRIO PARAMETRICO Ca. 10 L ANALISI DELL EUILIBRIO PARZIALE Doo aver aalzzato le due otes fodametal della teora ecoomca, secodo cu le azo degl
Algoritmi e Strutture Dati. Alberi Binari di Ricerca
Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
Stim e puntuali. Vocabolario. Cambiando campione casuale, cambia l istogramma e cambiano gli indici
Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI 1. LEGGI FINANZIARIE
CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI SOMMARIO:. Legg fnanzare. - 2. Regme fnanzaro dell neresse semplce e dello scono razonale. - 3. Regme fnanzaro dell neresse e dello scono composo. - 4. Tass equvalen.
GIANCARLO CAPOZZA CARLO CUSATELLI Dipartimento di Scienze Statistiche Carlo Cecchi, Università degli studi di Bari SUGLI INDICI DI PERFORMANCE *
GACARLO CAPOZZA CARLO CUSAELL Dparmeo d Sceze Sasche Carlo Cecch, Uversà degl sud d Bar SUGL DC D PERFORMACE * SOMMARO. roduzoe. Cosderazo sul calcolo del redmeo 3. l coecee bea 4. prcpal dc d perormace
Esercizi su Rappresentazioni di Dati e Statistica
Esercz su Rappresetazo d Dat e Statstca Eserczo Esprmete forma percetuale e traducete u aerogramma dat della seguete tabella: Nord Cetro Sud Isole Totale 5 58 866 0 95 36 4 35 30 6 79 56 57 399 08 Soluzoe
Analisi Matematica Lezione 30, 4 dicembre 2014 e x2 dx =
Dpartmeto d Sceze Statstche Aals Matematca Lezoe 3, 4 dcembre 14 π e x dx = prof. Daele Rtell daele.rtell@ubo.t 1/3? rodotto d Walls π = =1 rmo passo: ( 1 + 1 ) = lm (()!!) ( 1)!!( + 1)!! I = π s x dx
Gli indici sintetici Forma. Un caso studio. Gli indici sintetici. Qualche considerazione. Qualche considerazione. Tendenza centrale Forma
Qualche cosderazoe Tedeza cetrale La scelta dell dce d tedeza cetrale/poszoe dpede dal tpo e dalle caratterstche della dstrbuzoe; Pù che dvduare l dce mglore assoluto (che o esste), è mportate ache valutare
L OCCHIO. L OCCHIO: Proprietà Ottiche
L OCCHIO La truttura dell cch può esser trvata svarat test, put fdametal per quat rguarda l str teresse: studad l spettr Elettr-Magetc s s trvat due ftrecettr c (per l rss, l blu ed l verde) bastcell (vse
Modelli di Flusso e Applicazioni: Andrea Scozzari. a.a. 2013-2014
Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
Università di Cassino. Esercitazioni di Statistica 1 del 26 Febbraio Dott. Mirko Bevilacqua
Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Modelli di Schedulazione
EW Modell d Schedulazoe Idce Maccha Sgola Tepo d Copletaeto Totale Tepo d Copletaeto Totale Pesato Tepo d Rtardo Totale Maespa co set-up dpedete dalla sequeza Tepo d Copletaeto Totale co vcolo d precedeza
Caso studio 10. Dipendenza in media. Esempio
09/03/06 Caso studo 0 S cosder la seguete dstrbuzoe degl occupat Itala secodo l umero d ore settmaal effettvamete lavorate e l settore d attvtà (cfr. Itala cfre, Ao 008, pag. 7 ): Ore lavorate Settore
corrispondenza della generica i-esima modalità. Indicando con #(.) la cardinalità di un insieme, per esse si ha, rispettivamente:
Corso d Statstca docete: Domeco Vstocco Le requeze cumulate S cosder ua varable qualtatva ordale X Per essa, oltre alle requeze assolute, relatve e ercetual, è ossble calcolare ache le requeze cumulate
Lezione 1. I numeri complessi
Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
ARGOMENTO: MISURA DELLA RESISTENZA ELETTRICA CON IL METODO VOLT-AMPEROMETRICO.
elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
Lezione di tutorato: Lunedì 26 marzo ore Aula 112 Blocco A (quello della biblioteca)
Lezoe d tutorato: Luedì 6 marzo ore -3 Aula Blocco A (quello della bbloteca) U lbro d massa kg cade ra le bracca d ua ersoa che s trova 0m ù basso. Poedo uguale a zero l'eerga otezale a lvello del suolo,
Elementi di Matematica Finanziaria. Rendite e ammortamenti. Università Parthenope 1
Elemet d Matematca Fazara Redte e ammortamet Uverstà Partheope 1 S chama redta ua successoe d captal da rscuotere (o da pagare) a scadeze determate S chamao rate della redta sgol captal da rscuotere (o
INGEGNERIA E TECNOLOGIE DEI SISTEMI DI CONTROLLO. box. Scopo della modellazione black-box. Limitazioni dell approccio black-box
IGEGEIA E TECOLOGIE DEI SISTEMI DI COTOLLO bo Prof. Carlo oss DEIS - Uversà d Bologa Tel: 05 09300 emal: cross@des.bo. Scopo della modellazoe black-bo S vole realzzare modello d ssema a parre dalla sola
Il valore dei titoli azionari. a) DCF Model con TV. I metodi finanziari. I flussi di cassa. Flussidi cassa t
Il valore de ol azoar IL VALORE DEI TITOLI AZIONARI: meod azar Soo possbl dvers approcc: approcco basao su luss d rsulao: meod azar, redduale e del valore (exra pro); approcco d mercao: meodo de mulpl
INDICI DI VARIABILITA
INDICI DI VARIABILITA Defzoe d VARIABILITA': la varabltà s può defre come l'atttude d u carattere ad assumere dverse modaltà quattatve. La varabltà è la quattà d dspersoe presete e dat. Idc d varabltà
1 ANALISI MATEMATICA A - Esercizi della settimana 1
1 ANALISI MATEMATICA A - Esercz della settmaa 1 1.1 Eserczo Rsolvete le seguet dsequazo (e umer real) coè trovate l seme de umer real per qual la dsequazoe dcata è vera. 1. 1 x + 1 x 1 + 1 x + 1 0; 2.
y = α + βx + ε Qui ci soffermeremo su un unica classe di modelli, detti modelli statistici lineari. Si veda la seguente figura:
Il problema della regressoe s poe quado l valore d ua varable aleatora y, chamata varable dpedete, è fuzoe d ua varable o aleatora x, chamata varable dpedete Qu c soffermeremo su u uca classe d modell,
MEDIA DI Y (ALTEZZA):
Uverstà d Casso Eserctazo d Statstca del 4 Marzo 0 Dott. Mrko Bevlacqua ESERCIZIO Su u collettvo d dvdu soo stat rlevat caratter X Peso( kg) e Altezza ( cm) otteamo la seguete dstrbuzoe d frequeza coguta:
Media Mobile di ampiezza k (k pari) Esempio: Vendite mensili di shampoo
Media Mobile di ampiezza k (k pari) Esempio: Vendie mensili di shampoo Mese y 1 266,0 2 145,9 3 183,1 4 119,3 5 180,3 6 168,5 7 231,8 8 224,5 9 192,8 10 122,9 11 336,5 12 185,9 1 194,3 2 149,5 3 210,1
Sommario. Facoltà di Economia. Generalità sulla variabilità A B C. francesco mola. Lezione n 4. Variabilità e Dispersione. Concetto di variabilità
Corso d Statstca Facoltà d Ecooma a.a.. 00-00 fracesco mola Lezoe 4 Sommaro Campo d varazoe Varaza Scarto uadratco medo Coeffcete d varazoe Scostamet dalla Meda e dalla Medaa Mutua Varabltà Mutabltà lez4
Apparecchi di sollavamento. Classificazione apparecchi di sollevamento a
Appareh d sollavameto A moto otuo: Nastr trasportator Sollevator a tazze Forze d erza lmtate; trastor d avvameto e arresto poo rlevat A moto dsotuo: Gru a torre Forze d erza rlevat Classfazoe appareh d
Se il libro viene preso a 1,5m l'energia posseduta in questo punto sarà U= 2x9.8x1.5= 29,4 J
U lbro d assa kg cade ra le bracca d ua ersoa che s trova 0 ù basso. Poedo uguale a zero l'eerga otezale a lvello del suolo, trovare ) l'eerga otezale del lbro all'state cu za la rora caduta; ) l'eerga
Elementi di Statistica descrittiva Parte III
Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
Voti Diploma Classico Scientifico Tecn. E Comm Altro
4 Data la seguete dstrbuzoe doppa de vot rportat ad u esame secodo l Dploma posseduto: Vot 8-3-5 6-8 9-30 Dploma Classco 8 4 5 Scetfco 5 7 7 5 Tec E Comm 8 0 0 Altro 3 a) s calcol la meda artmetca de vot
Analisi di dati vettoriali. Direzioni e orientazioni
Aals d dat vettoral Drezo e oretazo I tal caso, dat soo msurat term d agol e spesso soo rfert al ord geografco (statstca crcolare) Soo rappresetat su ua crcofereza Dat d drezoe: flusso ua specfca drezoe,
SUCCESSIONI E SERIE NUMERICHE
SUCCESSIONI E SERIE NUMERICHE. Successioi umeriche a. Defiizioi: successioi aritmetiche e geometriche Cosideriamo ua sequeza di umeri quale ad esempio:,5,8,,4,7,... Tale sequeza è costituita mediate ua
RENDITE. Le singole rate possono essere corrisposte all inizio o alla fine di ciascun periodo e precisamente si ha:
RENDITE. Pagamet rateal S defsce redta ua sere qualsas d somme rscuotbl (o pagabl a scadeze dverse, o, pù esattamete, u seme d captal co dspobltà scagloata el tempo. Tal captal soo dett rate della redta
Gli indici sintetici Forma. Un caso studio. Gli indici sintetici. Qualche considerazione. Qualche considerazione. Tendenza centrale Forma
Uverstà d Macerata Dpartmeto d Sceze Poltche, della Comucazoe e delle Relaz. Iterazoal Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe
Design of experiments (DOE) e Analisi statistica
Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
LE MEDIE. Quadratica. Italo Nofroni. Statistica medica. Medie. Le medie vengono classificate in
Le mede Italo Nofro LE MEDIE Le mede (o valor med) soo dc d tedeza cetrale e costtuscoo u modo semplce ed mmedato per stetzzare u solo valore dat eterogee raccolt u collettvo Statstca medca Le mede Le
INFLAZIONE (DEFLAZIONE)
COS SI INTENDE PER INFLZIONE (DEFLZIONE) E COME SI MISUR L'flazoe (deflazoe) è u rocesso geeralzzato d aumeto (dmuzoe) de rezz, che rguarda l seme de be e servz. L esgeza delle autortà d oltca ecoomca
ESERCITAZIONE PER LA QUARTA PROVA DELL' ESAME DI STATO PER L'ABILITAZIONE ALLA PROFESSIONE DI INGEGNERE CIVILE E AMBIENTALE Autore: Marina Roma
hp://svolgmeorcceesme.lervs.org/ ESECITAZIONE PE LA UATA POVA ELL' ESAME I STATO PE L'ABILITAZIONE ALLA POFESSIONE I INGEGNEE CIVILE E AMBIENTALE Auore: Mr om Il presee documeo rpor lo svolgmeo, pssggo
LA FUNZIONE DI VEROSIMIGLIANZA
A FUNZIONE DI VEROSIMIGIANZA HA UN RUOO IMPORTANTE NEA PROCEDURE DI INFERENZA STATISTICA COME: ) METODO DI COSTRUZIONE DI STIMATORI (IN SITUAZIONI COMPESSE) ) METODO DI INDIVIDUAZIONE DI TEST UNIFORMEMENTE
Esercitazione 6 del corso di Statistica (parte 1)
Eserctazoe del corso d Statstca parte Dott.ssa aola Costat 8 Marzo 0 Eserczo S ha motvo d rteere che u uovo farmaco A abba la propretà d abbassare l lvello d glcema el sague. I cascuo de pazet dabetc osservat,
Il confronto tra DUE campioni indipendenti
Il cofroto tra DUE camioi idiedeti Il cofroto tra DUE camioi idiedeti Cofroto tra due medie I questi casi siamo iteressati a cofrotare il valore medio di due camioi i cui i le osservazioi i u camioe soo
Lezione 3. Gruppi risolubili.
Lezoe 3 Prerequst: Lezo 1 2 Class d cougo e cetralzzat rupp rsolubl I questo captolo troducamo ua ozoe che come vedremo seguto fuge da raccordo tra la teora de grupp e la teora de camp Defzoe 31 Dato u
Aspetti Teorico-pratici per la Costruzione di Indici dei Prezzi al Consumo Franco Mostacci Servizio Prezzi, U.O. PRE/D
Asett Teorco-ratc er la Costruzoe d Idc de Prezz al Cosumo Fraco Mostacc Servzo Prezz U.O. PRE/D Abstract Il resete documeto orgaramete coceto a scoo ddattco-dvulgatvo s oe l obettvo d colmare la lacua
Allocazione Statica. n i
Esercazon d Sse Inegra d Produzone Allocazone Saca I eod asa sull'allocazone saca scheazzano l processo d assegnazone delle rsorse alle par consderandolo da un lao ndpendene dal epo e rascurando dall'alro
LE MEDIE. Quadratica. Italo Nofroni. Statistica medica. Medie. Le medie vengono classificate in due gruppi
Le mede Italo Nofro LE MEDIE Statstca medca Le mede (o valor med) soo dc d tedeza cetrale e costtuscoo u modo semplce ed mmedato per stetzzare u solo valore dat eterogee raccolt el collettvo oggetto d
Istogrammi e confronto con la distribuzione normale
Istogramm e cofroto co la dstrbuzoe ormale Suppoamo d effettuare per volte la msurazoe della stessa gradezza elle stesse codzo (es. la massa d u oggetto, la tesoe d ua pla, la lughezza d u oggetto, ecc.):
E.S. Levrero. Dispense integrative di Economia Monetaria (2014-2015)
E.S. Levrero Dspese egrave d Ecooma Moeara (204-205) IL MOLTIPLICATORE DEI DEPOSITI BANCARI E L OFFERTA DI MONETA. Per quao rguarda l molplcaore de depos bacar, s deve eer coo del fao che l ammoare effevo
STIME E LORO AFFIDABILITA
TIME E LORO AFFIDABILITA L idea chiave su cui si basa l aalisi statistica è che si ossoo eseguire osservaioi su u camioe di soggetti e che da questo si ossoo comiere iferee sulla oolaioe raresetata da
ANALISI DELLA REGRESSIONE ANALISI BIVARIATA DELLA REGRESSIONE
ANALISI DELLA REGRESSIONE L Aals della Regressoe rguarda lo studo delle relazo esstet fra o pù caratter quattatv o varal. La rcerca de lega esstet fra pù varal s poe coe rcerca delle relazo fuzoal che
COMPLEMENTI DI STATISTICA. L. Greco, S. Naddeo
COMPLEMENTI DI STATISTICA L. Greco, S. Naddeo INDICE. GENERALITA SULLA VERIFICA DI IPOTESI. Itroduzoe 4. I test d sgfcatvtà 5.3 Gl tervall d cofdeza 7.4 Le potes alteratve.5 La poteza del test 5.6 Il test
Soluzione degli esercizi del capitolo 11
Statstca - metodooge per e sceze ecoomche e soca /e S Borra, A D Cacco - McGraw H s Souzoe deg esercz de captoo a rsposta esatta è a c, fatt daa s ha: da cu rcavamo a corretto Ifatt,,,,,,,,,,,,,,, b Sì,
DI IDROLOGIA TECNICA PARTE II
FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
I PARTE: CALCOLO DELLE PROBABILITÀ
rof. Ig. Domzao Mostacc Apput d probabltà e statstca d coteggo I ARTE: CALCOLO DELLE ROBABILITÀ I. Evet ed Est Cosderamo l espermeto d gettare u dado. Gettamo l dado, aspettamo che s ferm e osservamo l
Fatica con sollecitazioni ad ampiezza variabile
Comporameo meccaco de maerla Faca co sollecazo ad ampezza varable Faca de maeral Faca co sollecazo ad ampezza varable Iroduzoe, cumulav d sollecazoe Daeggameo: regola d Palmgre Mer Meodo d coeggo: meodo
Corso di laurea in Scienze Motorie Corso di Statistica Docente: Dott.ssa Immacolata Scancarello Lezione 9: Covarianza e correlazione
Corso d laurea Sceze Motore Corso d Statstca Docete: Dott.ssa Immacolata Scacarello Lezoe 9: Covaraza e correlazoe Altr tp d dpedeza L dce Ch-quadro presetato ella lezoe precedete stablsce l grado d dpedeza
Tavola 1 - Popolazione italiana residente alle date dei censimenti generali, riportata ai confini attuali - Anni 1861-2001 (migliaia di unità)
4 Quai eravamo, quai siamo, quai saremo Che cosa si impara el capiolo 4 er cooscere le caraerisiche e l evoluzioe della popolazioe ialiaa araverso u lugo arco di empo uilizziamo il asso di icremeo medio