Componenti per l elaborazione binaria dell informazione. Sommario. Sommario. Approfondimento del corso di reti logiche. M. Favalli.
|
|
|
- Adelina Coco
- 8 anni fa
- Visualizzazioni
Transcript
1 Sommrio Componenti per l elorzione inri ell informzione Approfonimento el orso i reti logihe M. Fvlli Engineering Deprtment in Ferrr Porte logihe 2 Il livello swith 3 Aspetti tenologii 4 Reti logihe omintorie Anlisi Anlisi e sintesi ei iruiti igitli / Sommrio Porte logihe Anlisi e sintesi ei iruiti igitli 2 / Porte logihe Porte logihe Porte logihe 2 Il livello swith 3 Aspetti tenologii 4 Reti logihe omintorie Anlisi Si puó re un efinizione uplie elle porte logihe (gte): Visione inipenente ll tenologi Semplii funzioni ell lger i ommutzione on le quli ostruire reti logihe he relizzno funzioni piú omplesse Visione ipenente ll tenologi Ciruiti elementri i tipo igitle messi isposizione un t tenologi Anlisi e sintesi ei iruiti igitli 3 / Anlisi e sintesi ei iruiti igitli 4 /
2 Porte logihe Porte logihe Porte logihe numero i ingressi (fn-in) = 2 Porte logihe numero i ingressi (fn-in) > 2 NOT AND OR Le porte logihe possono essere estese l so in ui sino presenti piú ingressi = = =+ NAND NOR AND OR =() =(+) = =+ + EXOR = + EXNOR =+ NAND NOR =() =(++) Anlisi e sintesi ei iruiti igitli 5 / Aspetti tenologii Porte logihe Anlisi e sintesi ei iruiti igitli 6 / Sommrio Il livello swith Esistono iverse tenologie miroelettronihe he onsentono i relizzre gte (TTL, ECL, MOS, CMOS...) Cisun tenologi onsente i relizzre in mnier effiiente solo un erto numero i tipi i gte (gli ltri sono relizzili meinte opportune reti i gte elementri) Al livello tenologio i gte non sono rtterizzti solo lle funzioni he relizzno, m nhe ltri prmetri (osto, ritro, onsumo i potenz) Per pire questi spetti nlizzeremo un tenologi in ettglio Porte logihe 2 Il livello swith 3 Aspetti tenologii 4 Reti logihe omintorie Anlisi Anlisi e sintesi ei iruiti igitli 7 / Anlisi e sintesi ei iruiti igitli 8 /
3 Il livello swith Il livello swith Livello swith Livello swith L tenologi elettroni piú iffus é ttulmente quell CMOS In tle tenologi il omponente elementre piú semplie esriviile l livello logio non é il gte, m il trnsistore esriviile ome un interruttore (swith) Questo i onsente i veere il moo in ui un port logi é ostruit Supponimo he un segnle inrio () poss ontrollre lo stto (ON, OFF) ell interruttore Nell tenologi CMOS sono presenti ue tipi i trnsistori tipo n tipo p stto stto OFF ON ON OFF Anlisi e sintesi ei iruiti igitli 9 / Il livello swith Il livello swith Anlisi e sintesi ei iruiti igitli / Desrizione i reti i swith meinte l lger i ommutzione Connessioni serie e prllelo Connessione serie: Connessione prllelo: I sistemi fisii ostituiti swith interonnessi sono esriviili utilizzno l lger i ommutzione Bisogn oifire gli stti OFF e ON on un vlore inrio logi positiv logi negtiv OFF ON ON OFF Per esrizione ell rete, si intene un espressione he ssume il vlore se l rete é ON (logi positiv) s w s s serie OFF OFF OFF OFF ON OFF ON OFF OFF ON ON ON s s s w s s prllelo OFF OFF OFF OFF ON ON ON OFF ON ON ON ON Anlisi e sintesi ei iruiti igitli / Anlisi e sintesi ei iruiti igitli 2 /
4 Il livello swith Il livello swith Rppresentzione logi Prinipio i ulitá Logi positiv Logi negtiv s s serie AND s s serie s s prllelo OR s s prllelo Utilizzno lo stesso tipo i logi, le reti serie e prllelo relizzno funzioni uli (AND, OR) Cmino tipo i logi, l stess rete viene esritt un funzione ule Il prinipio i ulitá rigur il moello logio ei sistemi fisii Punto i vist el lolo elle proposizioni L serie é ON se entrmi gli swith sono ON. Il prllelo é ON se uno o l ltro egli swith é ON. L serie é OFF se uno egli swith é OFF. Il prllelo é OFF se entrmi gli swith sono OFF. OR AND Anlisi e sintesi ei iruiti igitli 3 / Anlisi e sintesi ei iruiti igitli 4 / Il livello swith Il livello swith Reti i swith Reti i swith (esempio i nlisi) Reti i swith in serie e in prllelo possono essere omposte in reti piú omplesse n n Tli reti possono essere nlizzte sostitueno iterttivmente: isun serie i ue o piú swith un singolo swith ontrollto l prootto logio egli ingressi egli swith sostituiti 2 isun prllelo i ue o piú swith un singolo swith ontrollto ll somm logi egli ingressi egli swith sostituiti +w w n w Si puó quini ffermre he l rete n é ON se é ver + w Anlisi e sintesi ei iruiti igitli 5 / Anlisi e sintesi ei iruiti igitli 6 /
5 Il livello swith Il livello swith Eserizi i nlisi Prolem Si nlizzino queste reti i swith nell ipotesi i utilizzre un logi positiv Le reti i swith sono piuttosto interessnti, m é un prolem i rttere elettrio. Gli swith non sono ieli m hnno un resistenz serie per ui l informzione si egr ttrversno serie i on troppi swith Come relizzre espressioni omplesse? Si frá riferimento ll logi positiv Anlisi e sintesi ei iruiti igitli 7 / Anlisi e sintesi ei iruiti igitli 8 / Il livello swith Il livello swith Gte (tenologi CMOS) NAND L soluzione onsiste nel fre in moo he un rete i swith poss ontrollre gli swith i un ltr rete (on un gugno in gro i "rinforzre" i segnli ) Veimo ome esempio il so ell tenologi CMOS Prourimoi le ostnti (v) e (gn) e utilizzimo swith i tipo p e n per relizzre ue reti on stti omplentri pull-own (n) pull-up (p) OFF ON ON OFF Nell tenologi CMOS non si puó relizzre irettmente un gte AND L relizzzione i un NAND é simile quell i un NOT: si ostruisono ue reti omplementri pull-up: he pilot un uno egli ingressi vle pull-own: he pilot uno quno entrmi gli ingressi vlgono pull-own (n) pull-up (p) OFF ON OFF ON OFF ON ON OFF Anlisi e sintesi ei iruiti igitli 9 / Anlisi e sintesi ei iruiti igitli 2 /
6 Il livello swith Aspetti tenologii Eserizi Sommrio Porte logihe Si relizzino porte logihe CMOS per le seguenti funzioni logihe: = ( + ) = ( (w + )) = + 2 Il livello swith 3 Aspetti tenologii 4 Reti logihe omintorie Anlisi Aspetti tenologii Anlisi e sintesi ei iruiti igitli 2 / Aspetti tenologii Anlisi e sintesi ei iruiti igitli 22 / Ciruiti integrti Costo Alune informzioni sulle porte logihe he possono essere eotte onsierno l loro struttur l livello swith Un ulteriore informzione rigur l tenologi: i iruiti sono relizzti integrno numerose porte logihe (> 6 ) in un iruito integrto relizzto on mterili semionuttori (es. siliio) l tenologi é plnre: i ispositivi (swith, gte) non possono essere sovrpposti (le interonnessioni invee possono oupre iversi livelli) il osto é proporzionle ll re utilizzt he ipene l numero i ispositivi e lle interonnessioni Nell tenologi CMOS un gte orrispone fisimente un re rettngolre le ui imensioni sono proporzionli l numero i trnsistori e quini i ingressi In un rete ompless, un primo ontriuto l osto é to un termine proporzionle ll somm ei gte pest sui loro ingressi Si verá in seguito il ontriuto elle interonnessioni Esempio i NAND 3 ingressi Anlisi e sintesi ei iruiti igitli 23 / Anlisi e sintesi ei iruiti igitli 24 /
7 Aspetti tenologii Reti logihe omintorie Ritro Sommrio I mimenti i vlore egli ingressi non si riflettono istntnemente sull usit Si h un ritro he é proporzionle l numero i trnsistori in serie he pilotno il nuovo vlore Porte logihe 2 Il livello swith NAND 3 Aspetti tenologii 4 Reti logihe omintorie Anlisi propgtion el Reti logihe omintorie Anlisi e sintesi ei iruiti igitli 25 / Reti logihe omintorie Anlisi e sintesi ei iruiti igitli 26 / Reti logihe omintorie Esempio Un rete logi onsiste i un insieme i porte logihe interonnesse seono opportune regole in moo un relizzre un funzione f : {, } n {, } m i i 2 Sino i, i 2,..., i n gli ingressi i tle rete e o, o 2,..., o m, le sue usite i 3 i 4 o Regole gli ingressi i un gte possono essere ti ingressi ell rete, un ostnte o usite i ltri gte l usit i un gte puó essere onness gli ingressi i un ltro gte o puó pilotre un usit le usite i ue gte non evono mi essere onnesse insieme non evono esistere mmini ilii nell rete i 5 i 6 i 7 fn o 2 Anlisi e sintesi ei iruiti igitli 27 / Anlisi e sintesi ei iruiti igitli 28 /
8 Reti logihe omintorie Reti logihe omintorie Anlisi Anlisi e sintesi i reti omintorie Algoritmo i nlisi Per nlisi i un rete omintori si intene il proesso on il qule prteno ll rete si ottiene l funzione orrisponente Per sintesi i un rete omintori si intene il proesso on il qule prteno un funzione e eventuli oiettivi i progetto (osto, ritro) si ottiene un rete In entrmi i si, le espressioni ell lger i ommutzione sono il moello mtemtio he onsente i gestire le trsformzioni he si hnno nei ue proessi Rete logi Espressione Funzione lgoritmo Si ssegn un nome isun ingresso vlutzione 2 Si proee in mnier iterttiv gli ingressi el iruito esprimeno l usit i isun gte ome un espressione egli ingressi ell rete isun psso vengono onsierti tutti i gte i ui ingressi sono giá stti lolti 3 Si proee fino quno non si h l espressione i tutte le usite ell rete Reti logihe omintorie Anlisi Anlisi e sintesi ei iruiti igitli 29 / Reti logihe omintorie Anlisi e sintesi ei iruiti igitli 3 / Esempio i nlisi Algoritmo i sintesi - I Funzione Espressione Rete logi? lgoritmo psso + =(+)(+e) Si inserisono nell espressione tutte le prentesi ompreso quelle rese non neessrie lle regole ell lger i ommutzione (senz onsierre le omplementzioni) e +e psso 2 psso 3 2 Si nlizz l espressione eterminno il livello i isun opertore inrio si inizilizz un inie i livello o (se tutt l espressione é rhius fr prentesi) 2 si inrement i tle inie tutte le volte he si inontr un prentesi pert e lo si erement i tutte le volte he si inontr un prentesi hius Anlisi e sintesi ei iruiti igitli 3 / Anlisi e sintesi ei iruiti igitli 32 /
9 Reti logihe omintorie Reti logihe omintorie Algoritmo i sintesi - II Esempi i sintesi 3 Si isegnno i segnli i ingresso orrisponenti lle iverse vriili ell espressione 4 Prteno l vlore piú lto ell inie i livello, si isegnno i simoli ei gte orrisponenti gli opertori onnetteno gli opportuni segnli i ingresso tle gte 5 Nel so un vriile i ingresso o un prentesi risultino omplementte si ggiunge un invertitore e = + ( + e + ) = ( ) + ( ( + e + ( )) ) = ( 2)+ ( 2(+ 3 e+ 3 ( 4)) ) livello 2 livello 3 livello livello 4 e e f = + ( + e)(f + g) = ( ) + ( ( + e) (f + g)) = ( 2)+ ( 2( + 3 e) 2(f + 3 g)) livello 2 Reti logihe omintorie Anlisi e sintesi ei iruiti igitli 33 / Reti logihe omintorie Anlisi e sintesi ei iruiti igitli 34 / Il ruolo el fn- in presenz i fn- É possiile he un port logi ne piloti piú i un (fn- > ) Questo onsente i riurre il numero i porte logihe e i onseguenz il osto i un rete L unio prolem é un umento el ritro ell rete Dl punto i vist egli lgoritmi i nlisi non mi null Dl punto i vist ell sintesi, invee, si hnno ei mimenti In prtiolre, prim el psso 3, si inseriese un ulteriore psso i rier i sottoespressioni omuni (si noti he l inie i livello puó essere iverso) Per il momento, quest operzione verrá svolt su si intuitive = ( + ) + (( + )e + f ) = (( + ())) + ((( + ())e) + f ) = (( + 3 ( 4 )) 2 ) + ((( + 4 ( 5 )) 3 e) + 2 f ) Nel isegnre l rete onviene onsierre l sottoespressione on i livelli mggiori f e liv. 4/5 liv. 3/4 liv. 3 liv. 2 liv. Anlisi e sintesi ei iruiti igitli 35 / liv. 2 Anlisi e sintesi ei iruiti igitli 36 /
10 Reti logihe omintorie Reti logihe omintorie Livelli Livelli: gli ingressi verso le usite Metoo per il lolo ei livelli Un rete puó essere ttrverst gli ingressi verso le usite o vievers (metoo preeente) ssegnno isun gte un inie i livello Entrmi i tipi i inie sono utili in iverse operzioni eseguiili sulle reti. Nel so i ttrversmento gli ingressi (livello ) verso le usite, il livello i isun gte é efinito univomente Nel so i ttrversmento lle usite (livello ) verso gli ingressi il livello non é efinito univomente i i 2 i 3 i 4 i 5 i 6 i o o 2 Reti logihe omintorie Anlisi e sintesi ei iruiti igitli 37 / Reti logihe omintorie Anlisi e sintesi ei iruiti igitli 38 / Livelli: lle usite verso gli ingressi Eserizi i i 2 i3 i o 2 i 5 i 6 3/2 i 7 o 2 Anlisi e sintesi ei iruiti igitli 39 / Anlisi e sintesi ei iruiti igitli 4 /
11 Reti logihe omintorie Conlusioni Si é visto ome si poss pssre un espressione un rete o un rete un espressione un funzione (trmite l vlutzione) Non sppimo nor ome pssre un funzione un espressione Questo psso é quello piú rilevnte l punto i vist ell sintesi Anlisi e sintesi ei iruiti igitli /
Componenti per l elaborazione binaria dell informazione. Sommario. Sommario. Approfondimento del corso di reti logiche. M. Favalli.
 Sommrio Componenti per l elorzione inri ell informzione Approfonimento el orso i reti logihe M. Fvlli Engineering Deprtment in Ferrr Porte logihe 2 3 Aspetti tenologii 4 Reti logihe omintorie Anlisi M.
Sommrio Componenti per l elorzione inri ell informzione Approfonimento el orso i reti logihe M. Fvlli Engineering Deprtment in Ferrr Porte logihe 2 3 Aspetti tenologii 4 Reti logihe omintorie Anlisi M.
La rappresentazione per elencazione consiste nell elencare tutte le coppie ordinate che verificano la relazione
 RELAZIONI E FUNZIONI Relzioni inrie Dti ue insiemi non vuoti e (he possono eventulmente oiniere), si ie relzione tr e un qulsisi legge he ssoi elementi elementi. L insieme A è etto insieme i prtenz. L
RELAZIONI E FUNZIONI Relzioni inrie Dti ue insiemi non vuoti e (he possono eventulmente oiniere), si ie relzione tr e un qulsisi legge he ssoi elementi elementi. L insieme A è etto insieme i prtenz. L
A.A.2009/10 Fisica 1 1
 Mhine termihe e frigoriferi Un mhin termi è un mhin he, grzie un sequenz i trsformzioni termoinmihe i un t sostnz, proue lvoro he può essere utilizzto. Un mhin solitmente lvor su i un ilo i trsformzioni
Mhine termihe e frigoriferi Un mhin termi è un mhin he, grzie un sequenz i trsformzioni termoinmihe i un t sostnz, proue lvoro he può essere utilizzto. Un mhin solitmente lvor su i un ilo i trsformzioni
Elettronica dei Sistemi Digitali Disegno del layout di porte logiche combinatorie CMOS
 Elettroni ei Sistemi Digitli Disegno el lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
Elettroni ei Sistemi Digitli Disegno el lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
Tecniche di Progettazione Digitale Progettazione e layout di porte logiche combinatorie CMOS p. 2
 Tenihe i Progettzione Digitle Progettzione e lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
Tenihe i Progettzione Digitle Progettzione e lout i porte logihe omintorie CMOS Vlentino Lierli Diprtimento i Tenologie ell Informzione Università i Milno, 26013 Crem e-mil: lierli@ti.unimi.it http://www.ti.unimi.it/
F (r(t)), d dt r(t) dt
 Cmpi vettorili Un cmpo vettorile è un funzione vlori vettorili F : A R, con A R n, ove in questo cso l imensione el ominio e el coominio è l stess. F ( 1, 2,..., n ) (f 1 ( 1, 2,..., n ), f 2 ( 1, 2,...,
Cmpi vettorili Un cmpo vettorile è un funzione vlori vettorili F : A R, con A R n, ove in questo cso l imensione el ominio e el coominio è l stess. F ( 1, 2,..., n ) (f 1 ( 1, 2,..., n ), f 2 ( 1, 2,...,
Componenti per l aritmetica binaria. Motivazioni. Sommario. Sommario. M. Favalli
 Sommrio Componenti per l ritmetic inri M. Fvlli Engineering Deprtment in Ferrr Introduzione 2 3 Appliczioni di n-it dder 4 Sommtore CLA Sommrio (ENDIF) Reti logiche / 27 Introduzione Motivzioni (ENDIF)
Sommrio Componenti per l ritmetic inri M. Fvlli Engineering Deprtment in Ferrr Introduzione 2 3 Appliczioni di n-it dder 4 Sommtore CLA Sommrio (ENDIF) Reti logiche / 27 Introduzione Motivzioni (ENDIF)
VERIFICA DI UN CIRCUITO RESISTIVO CONTENENTE PIÙ GENERATORI CON UN TERMINALE COMUNE E SENZA TERMINALE COMUNE.
 FCA D UN CCUTO SSTO CONTNNT PÙ GNATO CON UN TMNAL COMUN SNZA TMNAL COMUN. Si verifino quttro iruiti on due genertori: genertori on polrità onorde e un terminle omune genertori on polrità disorde e un terminle
FCA D UN CCUTO SSTO CONTNNT PÙ GNATO CON UN TMNAL COMUN SNZA TMNAL COMUN. Si verifino quttro iruiti on due genertori: genertori on polrità onorde e un terminle omune genertori on polrità disorde e un terminle
ESERCIZI IN PIÙ ESERCIZI DI FINE CAPITOLO
 L RLZIONI L FUNZIONI serizi in più SRIZI IN PIÙ SRIZI I FIN PITOLO TST Nell insieme ell figur, l relzione rppresentt goe ell o elle proprietà: TST L relzione «essere isenente i», efinit nell insieme egli
L RLZIONI L FUNZIONI serizi in più SRIZI IN PIÙ SRIZI I FIN PITOLO TST Nell insieme ell figur, l relzione rppresentt goe ell o elle proprietà: TST L relzione «essere isenente i», efinit nell insieme egli
Esercizi per il corso di Calcolatori Elettronici. svolti da Mauro IACOVIELLO & Fabio LAUDANI
 Eserizi per il orso i loltori Elettronii svolti Muro OVELLO & Fio LUDN Prte seon : Mhine stti finiti ESERZO : Mhin i Mely Si t l seguente mhin i Mely, sintetizzre un iruito he l implementi, utilizzno un
Eserizi per il orso i loltori Elettronii svolti Muro OVELLO & Fio LUDN Prte seon : Mhine stti finiti ESERZO : Mhin i Mely Si t l seguente mhin i Mely, sintetizzre un iruito he l implementi, utilizzno un
d coulomb d volt b trasformatore d alternatore b amperometro d reostato
 ppunti 7 TEST DI VERIFICA 1 Unità i misur ell ri elettri: henry weer volt oulom 2 Unità i misur ell pità elettri: oulom henry fr volt 3 Gener orrente lternt: umultore resistenz 4 Misur l tensione: resistometro
ppunti 7 TEST DI VERIFICA 1 Unità i misur ell ri elettri: henry weer volt oulom 2 Unità i misur ell pità elettri: oulom henry fr volt 3 Gener orrente lternt: umultore resistenz 4 Misur l tensione: resistometro
La parabola. Fuoco. Direttrice y
 L prol Definizione: si definise prol il luogo geometrio dei punti del pino equidistnti d un punto fisso detto fuoo e d un rett fiss dett direttrie. Un rppresentzione grfi inditiv dell prol nel pino rtesino
L prol Definizione: si definise prol il luogo geometrio dei punti del pino equidistnti d un punto fisso detto fuoo e d un rett fiss dett direttrie. Un rppresentzione grfi inditiv dell prol nel pino rtesino
Definizione. Si chiama similitudine una corrispondenza biunivoca dal piano in sé tale che,
 CAPITOLO 6 LE SIMILITUDINI 6 Rihimi i teori Definizione Si him similituine un orrisponenz iunivo l pino in sé tle he presi ue punti qulunque A B el pino e etti A B i loro orrisponenti si h he esiste un
CAPITOLO 6 LE SIMILITUDINI 6 Rihimi i teori Definizione Si him similituine un orrisponenz iunivo l pino in sé tle he presi ue punti qulunque A B el pino e etti A B i loro orrisponenti si h he esiste un
Esercitazione n. 2. Gian Carlo Bondi VERO/FALSO
 Eseritzioni svolte 2010 Suol Duemil 1 Eseritzione n. 2 Aspetti eonomii e lusole el ontrtto i omprvenit Risultti ttesi Spere: gli spetti tenii, giuriii e eonomii el ontrtto i omprvenit. Sper fre: eterminre
Eseritzioni svolte 2010 Suol Duemil 1 Eseritzione n. 2 Aspetti eonomii e lusole el ontrtto i omprvenit Risultti ttesi Spere: gli spetti tenii, giuriii e eonomii el ontrtto i omprvenit. Sper fre: eterminre
Esercizi per il corso di Calcolatori Elettronici
 Eserizi per il orso i loltori Elettronii svolti Muro IOVIELLO & io LUDNI Prte prim : mppe i Krnugh, metoo QM ESERIZIO : Mppe i Krnugh Minimizzre l rete rppresentt ll funzione: = {,,, 3, 4, 5,, } D = Ø
Eserizi per il orso i loltori Elettronii svolti Muro IOVIELLO & io LUDNI Prte prim : mppe i Krnugh, metoo QM ESERIZIO : Mppe i Krnugh Minimizzre l rete rppresentt ll funzione: = {,,, 3, 4, 5,, } D = Ø
Il modello relazionale. Il Modello Relazionale. Il modello relazionale. Relazione. Dominio. Esempio
 Il Moello elzionle Proposto E. F. o nel 1970 per vorire l inipenenz ei ti e reso isponiile ome moello logio in DM reli nel 1981 si s sul onetto mtemtio i relzione, questo ornise l moello un se teori he
Il Moello elzionle Proposto E. F. o nel 1970 per vorire l inipenenz ei ti e reso isponiile ome moello logio in DM reli nel 1981 si s sul onetto mtemtio i relzione, questo ornise l moello un se teori he
Il modello relazionale. Il Modello Relazionale. Il modello relazionale. Relazione. Dominio. Esempio
 Il Moello elzionle Proposto E. F. o nel 1970 per vorire l inipenenz ei ti e reso isponiile ome moello logio in DM reli nel 1981 si s sul onetto mtemtio i relzione, questo ornise l moello un se teori he
Il Moello elzionle Proposto E. F. o nel 1970 per vorire l inipenenz ei ti e reso isponiile ome moello logio in DM reli nel 1981 si s sul onetto mtemtio i relzione, questo ornise l moello un se teori he
Calcolo del costo unitario FASE 1
 ESERCIZIO Definizione el pino ei entri i osto e eterminzione el osto unitrio i prootto Clolo el osto unitrio FASE 1 Azien i prouzione: proue i eni,,, Il proesso prouttivo prevee 3 fsi o proessi prinipli:
ESERCIZIO Definizione el pino ei entri i osto e eterminzione el osto unitrio i prootto Clolo el osto unitrio FASE 1 Azien i prouzione: proue i eni,,, Il proesso prouttivo prevee 3 fsi o proessi prinipli:
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria di Primo Grado Classe Prima. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
Numeri razionali COGNOME... NOME... Classe... Data...
 I numeri rzionli Cpitolo Numeri rzionli Verifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
I numeri rzionli Cpitolo Numeri rzionli Verifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
! è l'insieme A degli attributi di ! $ B IL PROBLEMA DELLE VISTE MATERIALIZZATE: PROBLEMI IL PROBLEMA DELLE VISTE MATERIALIZZATE
 IL PROBLEMA DELLE VISTE MATERIALIZZATE IL PROBLEMA DELLE VISTE MATERIALIZZATE: PROBLEMI Le viste nei DBMS relzionli Utilità elle viste mterilizzte per l'eseuzione i interrogzioni Venite(ProutI, NegozioI,
IL PROBLEMA DELLE VISTE MATERIALIZZATE IL PROBLEMA DELLE VISTE MATERIALIZZATE: PROBLEMI Le viste nei DBMS relzionli Utilità elle viste mterilizzte per l'eseuzione i interrogzioni Venite(ProutI, NegozioI,
Sondaggio piace l eolico?
 Songgio pie l eolio? Durnte l inugurzione i Stell sono stti istriuiti ei questionri per vlutre l inie i grimento ell eolio prte ell popolzione Sono stti ompilti e quini nlizzti 50 questionri Quest presentzione
Songgio pie l eolio? Durnte l inugurzione i Stell sono stti istriuiti ei questionri per vlutre l inie i grimento ell eolio prte ell popolzione Sono stti ompilti e quini nlizzti 50 questionri Quest presentzione
Allegato 3 Elenco BAT ed esempio interventi efficientamento
 Allegto 3 Eleno BAT e esempio interventi effiientmento LINEE GUIDA per l onuzione ell ignosi energeti nel settore rtrio Pg. 1 i 6 Riepilogo BAT sul onsumo e sull effiienz energetii estrtte ll DECISIONE
Allegto 3 Eleno BAT e esempio interventi effiientmento LINEE GUIDA per l onuzione ell ignosi energeti nel settore rtrio Pg. 1 i 6 Riepilogo BAT sul onsumo e sull effiienz energetii estrtte ll DECISIONE
Disequazioni di primo grado
 Cpitolo Disequzioni i primo gro Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Cpitolo Disequzioni i primo gro Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
DAI POLIGONI ALLE SUPERFICI TOPOLOGICHE
 DAI POLIGONI ALLE SUPERFICI TOPOLOGICHE E1 Avete visto ome prteno un rettngolo si possno ostruire un ilinro, un nstro i Moeius e un toro, inollno i lti seono le inizioni ei olori. Or provte utilizzre l
DAI POLIGONI ALLE SUPERFICI TOPOLOGICHE E1 Avete visto ome prteno un rettngolo si possno ostruire un ilinro, un nstro i Moeius e un toro, inollno i lti seono le inizioni ei olori. Or provte utilizzre l
Equazioni di secondo grado Capitolo
 Equzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Equzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Corso di ELETTRONICA INDUSTRIALE
 0. Corso di LRONCA NDUSRAL 1 MODULAZON ORAL. CONROLLO D CORRN D NROR A NSON MPRSSA 0. 0. 4 Rppresentzione vettorile Rppresentzione vettorile rsformzioni dirett ed invers 0. 0. 5 6 Rppresentzione vettorile
0. Corso di LRONCA NDUSRAL 1 MODULAZON ORAL. CONROLLO D CORRN D NROR A NSON MPRSSA 0. 0. 4 Rppresentzione vettorile Rppresentzione vettorile rsformzioni dirett ed invers 0. 0. 5 6 Rppresentzione vettorile
3. 1. Capitolo 4. Reti logiche. Logica e Reti logiche. Il modello strutturale delle reti logiche. 4.1 Funzioni, espressioni e schemi logici
 Cpitolo 4 Reti logiche 4 - Funzioni, espressioni e schemi logici 42 - Alger di commutzione 43 - Fmiglie logiche 4 Funzioni, espressioni e schemi logici Tutti gli uomini sono mortli 2 Socrte è un uomo Logic
Cpitolo 4 Reti logiche 4 - Funzioni, espressioni e schemi logici 42 - Alger di commutzione 43 - Fmiglie logiche 4 Funzioni, espressioni e schemi logici Tutti gli uomini sono mortli 2 Socrte è un uomo Logic
L insieme Q+ Le frazioni Operazioni con le frazioni Problemi con le frazioni
 L insieme Q+ Le frzioni Operzioni on le frzioni Prolemi on le frzioni Le frzioni Ini l rispost estt. In un frzione il numertore ini SEZ. C in qunte prti si ivie l unità. qunti interi si onsierno. qunte
L insieme Q+ Le frzioni Operzioni on le frzioni Prolemi on le frzioni Le frzioni Ini l rispost estt. In un frzione il numertore ini SEZ. C in qunte prti si ivie l unità. qunti interi si onsierno. qunte
Analisi Matematica I per Ingegneria Gestionale, a.a Primo compitino, 18 novembre 2017 Testi 1
 Primo ompitino, 8 novemre 07 Testi Prim prte, gruppo. =, = ; r = α = = 0, = 4; r = α = r = 3, α = π/3; = =. Trovre le soluzioni ell isuguglinz tn( tli he 0 π. + log log(log ; lim + os(e ; lim 4. Clolre
Primo ompitino, 8 novemre 07 Testi Prim prte, gruppo. =, = ; r = α = = 0, = 4; r = α = r = 3, α = π/3; = =. Trovre le soluzioni ell isuguglinz tn( tli he 0 π. + log log(log ; lim + os(e ; lim 4. Clolre
Algebra Relazionale. Operazioni nel Modello Relazionale
 lger Relzionle lger Relzionle Operzioni nel Moello Relzionle Le operzioni sulle relzioni possono essere espresse in ue ormlismi i se: lger relzionle: le interrogzioni (query) sono espresse pplino opertori
lger Relzionle lger Relzionle Operzioni nel Moello Relzionle Le operzioni sulle relzioni possono essere espresse in ue ormlismi i se: lger relzionle: le interrogzioni (query) sono espresse pplino opertori
FUNZIONI MATEMATICHE. Una funzione lineare è del tipo:
 FUNZIONI MATEMATICHE Le relzioni mtemtihe utilizzte per desrivere fenomeni nturli, in iologi ome in ltre sienze, possono ovvimente essere le più svrite. Per lo più si trtt di equzioni lineri, qudrtihe,
FUNZIONI MATEMATICHE Le relzioni mtemtihe utilizzte per desrivere fenomeni nturli, in iologi ome in ltre sienze, possono ovvimente essere le più svrite. Per lo più si trtt di equzioni lineri, qudrtihe,
! Una gerarchia ricorsiva deriva dalla presenza di una ricorsione o ciclo (un anello nel caso più semplice) nello schema operazionale.
 Gerarhie Riorsive! Una gerarhia riorsiva eriva alla presenza i una riorsione o ilo (un anello nel aso più semplie) nello shema operazionale.! Esempio i shema operazionale on anello:! Rappresentazione sullo
Gerarhie Riorsive! Una gerarhia riorsiva eriva alla presenza i una riorsione o ilo (un anello nel aso più semplie) nello shema operazionale.! Esempio i shema operazionale on anello:! Rappresentazione sullo
Scomposizione di polinomi 1
 Somposizione i un polinomio Cpitolo Somposizione i polinomi 1 erifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Somposizione i un polinomio Cpitolo Somposizione i polinomi 1 erifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Circuiti Sequenziali Macchine Non Completamente Specificate
 CEFRIEL Consorzio pr l Formzion l Rir in Inggnri ll Informzion Politnio i Milno Ciruiti Squnzili Mhin Non Compltmnt Spifit Introuzion Comptiilità Riuzion l numro gli stti Mtoo gnrl FSM non ompltmnt spifit
CEFRIEL Consorzio pr l Formzion l Rir in Inggnri ll Informzion Politnio i Milno Ciruiti Squnzili Mhin Non Compltmnt Spifit Introuzion Comptiilità Riuzion l numro gli stti Mtoo gnrl FSM non ompltmnt spifit
ALGORITMI E COMPLESSITÀ CORSO DI LAUREA MAGISTRALE IN INFORMATICA UNIVERSITÀ DEGLI STUDI DI CATANIA ANNO ACCADEMICO 2014/15
 ANNO ACCADEMICO 01/15 Seon sessione i esmi (I ppello) - giugno 015 (B-trees) () Si efinis l struttur ti ei B-tree. () Si T l insieme ei vlori t N per i quli l lero T in figur poss essere onsierto un B-tree
ANNO ACCADEMICO 01/15 Seon sessione i esmi (I ppello) - giugno 015 (B-trees) () Si efinis l struttur ti ei B-tree. () Si T l insieme ei vlori t N per i quli l lero T in figur poss essere onsierto un B-tree
Le proprietà fondamentali del campo magnetico
 1) Ftti sperimentli. Le proprietà fonmentli el mpo mgnetio Riportimo ue ftti sperimentli: ) Un filo rettilineo infinito perorso orrente I gener un mpo mgnetio on le seguenti proprietà: l intensità ument
1) Ftti sperimentli. Le proprietà fonmentli el mpo mgnetio Riportimo ue ftti sperimentli: ) Un filo rettilineo infinito perorso orrente I gener un mpo mgnetio on le seguenti proprietà: l intensità ument
www.scuolaazienda.it MARIO FLORES L OPERATORE TURISTICO SOLUZIONI Vero o falso? Verifica le tue conoscenze Esercizi
 www.scuolaazienda.it MRIO FLORES L OPERTORE 4 TURISTIO SOLUZIONI Vero o falso? Verifica le tue conoscenze Esercizi VERO O FLSO? MOULO 1 1 V, 2 V, 3 F, 4 F 1 V, 2 V, 3 V, 4 F 1 V, 2 F, 3 F, 4 V 1 F, 2 F,
www.scuolaazienda.it MRIO FLORES L OPERTORE 4 TURISTIO SOLUZIONI Vero o falso? Verifica le tue conoscenze Esercizi VERO O FLSO? MOULO 1 1 V, 2 V, 3 F, 4 F 1 V, 2 V, 3 V, 4 F 1 V, 2 F, 3 F, 4 V 1 F, 2 F,
13. EQUAZIONI ALGEBRICHE
 G. Smmito, A. Bernrdo, Formulrio di mtemti Equzioni lgerihe F. Cimolin, L. Brlett, L. Lussrdi. EQUAZIONI ALGEBRICHE. Prinipi di equivlenz Si die identità un'uguglinz tr due espressioni ontenenti un o più
G. Smmito, A. Bernrdo, Formulrio di mtemti Equzioni lgerihe F. Cimolin, L. Brlett, L. Lussrdi. EQUAZIONI ALGEBRICHE. Prinipi di equivlenz Si die identità un'uguglinz tr due espressioni ontenenti un o più
Equazioni di primo grado
 Cpitolo Equzioni i primo gro Equzioni i primo gro erifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Cpitolo Equzioni i primo gro Equzioni i primo gro erifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Robotica industriale. Motori a magneti permanenti. Prof. Paolo Rocco (paolo.rocco@polimi.it)
 Rooti industrile Motori mgneti permnenti Prof. Polo Roo (polo.roo@polimi.it) Generzione di oppi L legge di Lorentz i die he un ri elettri q in moto on veloità v in un mpo mgnetio di intensità B è soggett
Rooti industrile Motori mgneti permnenti Prof. Polo Roo (polo.roo@polimi.it) Generzione di oppi L legge di Lorentz i die he un ri elettri q in moto on veloità v in un mpo mgnetio di intensità B è soggett
Politecnico di Milano Facoltà di Ingegneria dell Automazione INFORMATICA INDUSTRIALE Appello COGNOME E NOME. 11 febbraio 2008 RIGA COLONNA MATRICOLA
 Politecnico i Milno Fcoltà i Ingegneri ell Automzione INFORMATICA INDUSTRIALE Appello COGNOME E NOME ebbrio 2008 RIGA COLONNA MATRICOLA Il presente plico pinzto, composto i quttro ogli (ronte/retro)eve
Politecnico i Milno Fcoltà i Ingegneri ell Automzione INFORMATICA INDUSTRIALE Appello COGNOME E NOME ebbrio 2008 RIGA COLONNA MATRICOLA Il presente plico pinzto, composto i quttro ogli (ronte/retro)eve
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria Superiore Classe Terza. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse Terz Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse Terz Suol..........................................................................................................................................
Monomi e polinomi. Verifica per la classe prima COGNOME... NOME... Classe... Data...
 Cpitolo Monomi e polinomi Monomi Verifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Cpitolo Monomi e polinomi Monomi Verifi per l lsse prim COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Barriere all entrata e modello del Prezzo Limite Economia industriale Università Bicocca
 Brriere ll entrt e modello del Prezzo imite onomi industrile Università Bio Christin Grvgli - Giugno 006 Brriere ll entrt definizioni Condizioni he permettono lle imprese opernti in un industri di elevre
Brriere ll entrt e modello del Prezzo imite onomi industrile Università Bio Christin Grvgli - Giugno 006 Brriere ll entrt definizioni Condizioni he permettono lle imprese opernti in un industri di elevre
Piero Gallo Fabio Salerno. Task. Corso di informatica. Gli archivi sequenziali. il libro si estende sul web
 Piero Gllo Fio Slerno Tsk Corso i informti 2 il liro si estene sul we Gli rhivi sequenzili il liro si estene sul we LEZIONE L orgnizzzione sequenzile L orgnizzzione logi sequenzile Con rhivio logio sequenzile
Piero Gllo Fio Slerno Tsk Corso i informti 2 il liro si estene sul we Gli rhivi sequenzili il liro si estene sul we LEZIONE L orgnizzzione sequenzile L orgnizzzione logi sequenzile Con rhivio logio sequenzile
Unità D1.2 Selezione e proiezione
 (A) CONOSCENZA TEMINOLOGICA Dre un reve esrizione ei termini introotti: ienominzione Selezione Proiezione Composizione i operzioni (B) CONOSCENZA E COMPETENZA isponere lle seguenti omne proueno nhe qulhe
(A) CONOSCENZA TEMINOLOGICA Dre un reve esrizione ei termini introotti: ienominzione Selezione Proiezione Composizione i operzioni (B) CONOSCENZA E COMPETENZA isponere lle seguenti omne proueno nhe qulhe
Disequazioni di secondo grado
 Disequzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Disequzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
GT Definizione di grafo orientato e non
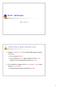 Grfi - efinizioni GT. 3.- Definizione i grfo orientto e non Un grfo orientto G = (V,E) è formto ll oppi i insiemi V e E oe: V è un insieme i ertii E è un insieme i rhi: oppie orinte i ertii (u,), elementi
Grfi - efinizioni GT. 3.- Definizione i grfo orientto e non Un grfo orientto G = (V,E) è formto ll oppi i insiemi V e E oe: V è un insieme i ertii E è un insieme i rhi: oppie orinte i ertii (u,), elementi
I S I E. Fermi - Lucca Istituto Tecnico settore Tecnologico
 I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
Componenti per l aritmetica binaria
 Componenti per l ritmetic inri Introduzione 2 Introduzione Motivzioni 3 Appliczioni di n-it dder 4 Sommtore CLA I itemi di clcolo neceitno di componenti che relizzino operzioni di tipo ritmetico (omme,
Componenti per l ritmetic inri Introduzione 2 Introduzione Motivzioni 3 Appliczioni di n-it dder 4 Sommtore CLA I itemi di clcolo neceitno di componenti che relizzino operzioni di tipo ritmetico (omme,
Lezione 7: Rette e piani nello spazio
 Lezione 7: Rette e pini nello spzio In quest lezione i metteremo in un riferimento rtesino ortonormle dello spzio. I primi oggetti geometrii he individuimo sono le rette e i pini. Per qunto rigurd le rette
Lezione 7: Rette e pini nello spzio In quest lezione i metteremo in un riferimento rtesino ortonormle dello spzio. I primi oggetti geometrii he individuimo sono le rette e i pini. Per qunto rigurd le rette
4 - TRASFORMAZIONI DI VARIABILI CASUALI
 4 - RASFORMAZIONI DI VARIABILI CASUALI 4 rsformzioni i vriili suli Cominimo un esempio Si l vriile sule lnio i un o non truto : / / / 4 / 5 / / e g() si l orrisponenz: pri test ispri roe Poihé g()g(4)g()test
4 - RASFORMAZIONI DI VARIABILI CASUALI 4 rsformzioni i vriili suli Cominimo un esempio Si l vriile sule lnio i un o non truto : / / / 4 / 5 / / e g() si l orrisponenz: pri test ispri roe Poihé g()g(4)g()test
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria di Primo Grado Classe Prima. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri i Primo Gro Clsse Prim Suol..........................................................................................................................................
Elettronica dei Sistemi Digitali Progetto di sottosistemi in tecnologia CMOS (parte II)
 Elettroni dei Sistemi Digitli Progetto di sottosistemi in tenologi CMOS (prte II) Vlentino Lierli Diprtimento di Tenologie dell Informzione Università di Milno, 2613 Crem e-mil: lierli@dti.unimi.it http://www.dti.unimi.it/
Elettroni dei Sistemi Digitli Progetto di sottosistemi in tenologi CMOS (prte II) Vlentino Lierli Diprtimento di Tenologie dell Informzione Università di Milno, 2613 Crem e-mil: lierli@dti.unimi.it http://www.dti.unimi.it/
Elettronica dei Sistemi Digitali Progetto di sottosistemi in tecnologia CMOS
 Elettroni dei Sistemi Digitli Progetto di sottosistemi in tenologi CMOS Vlentino Lierli Diprtimento di Tenologie dell Informzione Università di Milno, 2613 Crem e-mil: lierli@dti.unimi.it http://www.dti.unimi.it/
Elettroni dei Sistemi Digitli Progetto di sottosistemi in tenologi CMOS Vlentino Lierli Diprtimento di Tenologie dell Informzione Università di Milno, 2613 Crem e-mil: lierli@dti.unimi.it http://www.dti.unimi.it/
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del quinto appello, 3 luglio 2017 Testi 1
 nlisi Mtemti I per Ingegneri Gestionle,.. 6-7 Sritto el quinto ppello, 3 luglio 7 Testi Prim prte, gruppo.. Dire per quli R l funzione f() := sin( 3 ) + 3 è resente su tutto R.. Disporre le seguenti funzioni
nlisi Mtemti I per Ingegneri Gestionle,.. 6-7 Sritto el quinto ppello, 3 luglio 7 Testi Prim prte, gruppo.. Dire per quli R l funzione f() := sin( 3 ) + 3 è resente su tutto R.. Disporre le seguenti funzioni
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria Superiore Classe terza. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse terz Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse terz Suol..........................................................................................................................................
FEDERAZIONE ITALIANA GIUOCO CALCIO SETTORE TECNICO CORSO PER L ABILITAZIONE AD ALLENATORE PROFESSIONISTA DI 1^ CATEGORIA 2005 2006
 FEDERAZIONE ITALIANA GIUOCO CALCIO SETTORE TECNICO CORSO PER L ABILITAZIONE AD ALLENATORE PROFESSIONISTA DI 1^ CATEGORIA 2005 2006 L INSEGNAMENTO DEI FONDAMENTALI TATTICI: DALL UNO CONTRO UNO AL QUATTRO
FEDERAZIONE ITALIANA GIUOCO CALCIO SETTORE TECNICO CORSO PER L ABILITAZIONE AD ALLENATORE PROFESSIONISTA DI 1^ CATEGORIA 2005 2006 L INSEGNAMENTO DEI FONDAMENTALI TATTICI: DALL UNO CONTRO UNO AL QUATTRO
Architettura del calcolatore Esempi dettagliati di funzionamento interno di memoria e processore
 Corso i Cloltori Elettronii I Arhitettur el loltore Esempi ettgliti i funzionmento interno i memori e proessore ing. Alessnro Cilro Corso i Lure in Ingegneri Biomei Sommrio In quest presentzione verrnno
Corso i Cloltori Elettronii I Arhitettur el loltore Esempi ettgliti i funzionmento interno i memori e proessore ing. Alessnro Cilro Corso i Lure in Ingegneri Biomei Sommrio In quest presentzione verrnno
Il piano cartesiano e la retta
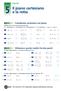 Cpitolo Eserizi Il pino rtesino e l rett Teori p. Coorinte rtesine nel pino Stilisi ove si trov isuno ei punti ti. (I I qurnte, II II qurnte, III III qurnte, IV IV qurnte, x sse x, y sse y) A(0, 8) B(,
Cpitolo Eserizi Il pino rtesino e l rett Teori p. Coorinte rtesine nel pino Stilisi ove si trov isuno ei punti ti. (I I qurnte, II II qurnte, III III qurnte, IV IV qurnte, x sse x, y sse y) A(0, 8) B(,
Icone, finestre e strutture dati
 u t o n e n i t à i m r e n i p p Ione, finestre e strutture ti Competenze speifihe Il signifito elle prinipli ione, il loro spostmento e orinmento sul esktop I prinipli elementi elle finestre elle pplizioni
u t o n e n i t à i m r e n i p p Ione, finestre e strutture ti Competenze speifihe Il signifito elle prinipli ione, il loro spostmento e orinmento sul esktop I prinipli elementi elle finestre elle pplizioni
Millenium 3 Interfaccia di comunicazione M3MOD Guida all'uso della Directory operativa 04/2006
 Millenium 3 Interfi i omunizione M3MOD Gui ll'uso ell Diretory opertiv 04/2006 160633105 Pnormi AGui ll'uso ell Diretory opertiv Introuzione L Diretory opertiv è un file i testo generto l softwre i progrmmzione
Millenium 3 Interfi i omunizione M3MOD Gui ll'uso ell Diretory opertiv 04/2006 160633105 Pnormi AGui ll'uso ell Diretory opertiv Introuzione L Diretory opertiv è un file i testo generto l softwre i progrmmzione
IL CONTRATTO RISTORATIVO
 IL CONTRATTO RISTORATIVO ATTIVITÀ E LABORATORIO i Pol LOBINA PREMESSA L rtiolo nlizz l ntur giurii el ontrtto i ristorzione osì ome viene elinet l Coie el onsumo e è orreto un primo test i verifi sui ontrtti.
IL CONTRATTO RISTORATIVO ATTIVITÀ E LABORATORIO i Pol LOBINA PREMESSA L rtiolo nlizz l ntur giurii el ontrtto i ristorzione osì ome viene elinet l Coie el onsumo e è orreto un primo test i verifi sui ontrtti.
Teorema di Sostituzione
 Teorema i Sostituzione Le Fiure (a) e (b) i seuito riportate, si riferiscono al Teorema i sostituzione che afferma: Una impeenza Z a percorsa a una corrente, può essere sostituita un eneratore i tensione
Teorema i Sostituzione Le Fiure (a) e (b) i seuito riportate, si riferiscono al Teorema i sostituzione che afferma: Una impeenza Z a percorsa a una corrente, può essere sostituita un eneratore i tensione
Cap. 8 Sistemi di controllo
 Cap. 8 Sistemi i ontrollo Come già etto, in generale, un sistema è solo potenialmente in grao i soisfare gli obiettivi per i quali è stato ostruito, e ioè i omportarsi nella maniera esierata. Per onseguire
Cap. 8 Sistemi i ontrollo Come già etto, in generale, un sistema è solo potenialmente in grao i soisfare gli obiettivi per i quali è stato ostruito, e ioè i omportarsi nella maniera esierata. Per onseguire
VERSO L ESAME DI STATO SCUOLA SECONDARIA DI PRIMO GRADO PROVA DI MATEMATICA
 VERSO L ESAME DI STATO SCUOLA SECONDARIA DI PRIMO GRADO PROVA DI MATEMATICA trtto Mtemti in zione, A. Arpinti, M. Musini Mettimoi ll prov! Suol..........................................................................................................................................
VERSO L ESAME DI STATO SCUOLA SECONDARIA DI PRIMO GRADO PROVA DI MATEMATICA trtto Mtemti in zione, A. Arpinti, M. Musini Mettimoi ll prov! Suol..........................................................................................................................................
01 Matematica Liceo \ Unità Didattica N 6 La retta 1
 Mtemti Lieo \ Unità Didtti N 6 L rett Unità didtti N 6 L rett rtesin ) Equzione vettorile dell rett 2) Equzioni prmetrihe dell rett 3) Equzione dell rett pssnte per due punti 4) Equzione dell rett pssnte
Mtemti Lieo \ Unità Didtti N 6 L rett Unità didtti N 6 L rett rtesin ) Equzione vettorile dell rett 2) Equzioni prmetrihe dell rett 3) Equzione dell rett pssnte per due punti 4) Equzione dell rett pssnte
Macchine non completamente specificate. Sintesi Sequenziale Sincrona Sintesi Comportamentale di Reti Sequenziali Sincrone
 Mhin non ompltmnt spifit Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spifit Comptiilità Vrsion l 5/12/02 Sono mhin in ui pr lun onfigurzioni
Mhin non ompltmnt spifit Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spifit Comptiilità Vrsion l 5/12/02 Sono mhin in ui pr lun onfigurzioni
Elettronica dei Sistemi Digitali Il test nei sistemi elettronici: guasti catastrofici e modelli di guasto (parte I)
 Elettronic dei Sistemi Digitli Il test nei sistemi elettronici: gusti ctstrofici e modelli di gusto (prte I) Vlentino Lierli Diprtimento di Tecnologie dell Informzione Università di Milno, 26013 Crem e-mil:
Elettronic dei Sistemi Digitli Il test nei sistemi elettronici: gusti ctstrofici e modelli di gusto (prte I) Vlentino Lierli Diprtimento di Tecnologie dell Informzione Università di Milno, 26013 Crem e-mil:
Technology Mapping. Librerie di celle
 Tehnology Mpping lusso i progetto Algoritmo Sintesi lto livello RTL Ottimizzzione logi Inipenente ll tenologi : stime pprossimte i osti e ritri Rete logi (teh. inepenent) Tehnology mpping Rete logi (teh.
Tehnology Mpping lusso i progetto Algoritmo Sintesi lto livello RTL Ottimizzzione logi Inipenente ll tenologi : stime pprossimte i osti e ritri Rete logi (teh. inepenent) Tehnology mpping Rete logi (teh.
Vettori - Definizione
 Vettori - Definizione z Verso Origine Modulo Direzione V y Form geometri x Form nliti Un vettore è un ente geometrio definito d: - Direzione: rett sull qule gie il vettore, he ne indi l orientmento nello
Vettori - Definizione z Verso Origine Modulo Direzione V y Form geometri x Form nliti Un vettore è un ente geometrio definito d: - Direzione: rett sull qule gie il vettore, he ne indi l orientmento nello
PARAMETRI DI VALUTAZIONE PER AUTOBUS INTERURBANI E CRITERI PER L'ASSEGNAZIONE DEI PUNTEGGI ALLEGATO 6/lotto 1
 PARAMETRI DI VALUTAZIONE PER AUTOBUS INTERURBANI E CRITERI PER L'ASSEGNAZIONE DEI PUNTEGGI ALLEGATO 6/lotto 1 PUNTEGGIO PARAMETRI INTERURBANO NORMALE Punteggio Vlutzioni 1 PREZZO DEL VEICOLO COMPLETO (vesi
PARAMETRI DI VALUTAZIONE PER AUTOBUS INTERURBANI E CRITERI PER L'ASSEGNAZIONE DEI PUNTEGGI ALLEGATO 6/lotto 1 PUNTEGGIO PARAMETRI INTERURBANO NORMALE Punteggio Vlutzioni 1 PREZZO DEL VEICOLO COMPLETO (vesi
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA. Scuola Secondaria Superiore Classe Prima. Scuola... Classe... Alunno...
 VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse Prim Suol..........................................................................................................................................
VALUTAZIONE DELLE CONOSCENZE E DELLE ABILITÀ DI BASE PROVA DI MATEMATICA Suol Seonri Superiore Clsse Prim Suol..........................................................................................................................................
COMBINAZIONI DI CARICO SOLAI
 COMBINAZIONI DI CARICO SOLAI (ppunti di Mrio Zfonte in fse di elorzione) Ai fini delle verifihe degli stti limite, seondo unto indito dll normtiv, in generle le ondizioni di rio d onsiderre, sono uelle
COMBINAZIONI DI CARICO SOLAI (ppunti di Mrio Zfonte in fse di elorzione) Ai fini delle verifihe degli stti limite, seondo unto indito dll normtiv, in generle le ondizioni di rio d onsiderre, sono uelle
La piattaforma Next Generation Guida rapida
 Gui rpi Quest gui rpi è stt ret on l oiettivo i iutrti fmilirizzre rpimente on le numerose rtteristihe e strumenti isponiili sull pittform Next Genertion. Sopri ove trovre i prootti isponiili e le notizie
Gui rpi Quest gui rpi è stt ret on l oiettivo i iutrti fmilirizzre rpimente on le numerose rtteristihe e strumenti isponiili sull pittform Next Genertion. Sopri ove trovre i prootti isponiili e le notizie
a a = 1, a a = 0; a a = 1, a a = 0; e quindi, = (a a ) (a a ) = (a a) a = 0 a = a
 Definizione 1. Si R un insieme otto i ue leggi i composizione interne e. Si ice che l struttur lgebric (R,, ) è un reticolo (lgebrico) se e verificno le proprietà: (1) x, y, z R, (x y) z = x (y z); (x
Definizione 1. Si R un insieme otto i ue leggi i composizione interne e. Si ice che l struttur lgebric (R,, ) è un reticolo (lgebrico) se e verificno le proprietà: (1) x, y, z R, (x y) z = x (y z); (x
Appunti di Matematica Computazionale Lezione 1. Equazioni non lineari. Consideriamo il problema della determinazione delle radici dell equazione
 Appunti di Mtemti Computzionle Lezione Equzioni non lineri Considerimo il prolem dell determinzione delle rdii dell equzione dove è un funzione definit in [,]. Teorem: Zeri di unzioni Continue Si un funzione
Appunti di Mtemti Computzionle Lezione Equzioni non lineri Considerimo il prolem dell determinzione delle rdii dell equzione dove è un funzione definit in [,]. Teorem: Zeri di unzioni Continue Si un funzione
] + [ ] [ ] def. ] e [ ], si ha subito:
![] + [ ] [ ] def. ] e [ ], si ha subito: ] + [ ] [ ] def. ] e [ ], si ha subito:](/thumbs/24/3548090.jpg) OPE OPERAZIONI BINARIE Definizione di operzione inri Dto un insieme A non vuoto, si him operzione (inri) su A ogni pplizione di A in A In generle, un'operzione su A viene indit on il simolo Se (x, y) è
OPE OPERAZIONI BINARIE Definizione di operzione inri Dto un insieme A non vuoto, si him operzione (inri) su A ogni pplizione di A in A In generle, un'operzione su A viene indit on il simolo Se (x, y) è
4.5 Il Parco dello Sport del Lambro e il PLIS della Media Valle del Lambro
 PGT Pino di Governo del Territorio 212 4.5 Il Pro dello Sport del Lmbro e il PLIS dell Medi Vlle del Lmbro Tngenile Est Nuovo pro Cresengo pro Vill Fini Nviglio dell Mrtesn pro Prdisi Lmbro pro dell Mrtesn
PGT Pino di Governo del Territorio 212 4.5 Il Pro dello Sport del Lmbro e il PLIS dell Medi Vlle del Lmbro Tngenile Est Nuovo pro Cresengo pro Vill Fini Nviglio dell Mrtesn pro Prdisi Lmbro pro dell Mrtesn
= det b, a, b, c R 3. In quest ottica, il determinante del terzo ordine e caratterizzato dalle seguenti proprieta : a a. c c
 Determinnti n = 3. Propriet Possimo rigurdre il determinnte di un mtrie del terzo ordine ome un funzione delle sue olonne: det b = det [, b,,, b, R 3. In quest otti, il determinnte del terzo ordine e rtterizzto
Determinnti n = 3. Propriet Possimo rigurdre il determinnte di un mtrie del terzo ordine ome un funzione delle sue olonne: det b = det [, b,,, b, R 3. In quest otti, il determinnte del terzo ordine e rtterizzto
ENEA - Dipartimento Biotecnologie, Agroindustria e Protezione della Salute Responsabile scientifico: Dott.ssa Paola CRINÒ
 UNITÀ OPERATIVA N ENEA - Diprtimento Biotenologie, Agroinustri e Protezione ell Slute Responsile sientifio: Dott.ss Pol CRINÒ Altri prteipnti: Dott. Sergio Luretti, Dott.ss Florin Fiohetti, Dott.ss Mriinoront
UNITÀ OPERATIVA N ENEA - Diprtimento Biotenologie, Agroinustri e Protezione ell Slute Responsile sientifio: Dott.ss Pol CRINÒ Altri prteipnti: Dott. Sergio Luretti, Dott.ss Florin Fiohetti, Dott.ss Mriinoront
3. Funzioni iniettive, suriettive e biiettive (Ref p.14)
 . Funzioni iniettive, suriettive e iiettive (Ref p.4) Dll definizione di funzione si ricv che, not un funzione y f( ), comunque preso un vlore di pprtenente l dominio di f( ) esiste un solo vlore di y
. Funzioni iniettive, suriettive e iiettive (Ref p.4) Dll definizione di funzione si ricv che, not un funzione y f( ), comunque preso un vlore di pprtenente l dominio di f( ) esiste un solo vlore di y
VERSO L ESAME DI STATO LA DERIVATA DI UNA FUNZIONE
 VERSO L ESAME DI STATO LA DERIVATA DI UNA FUNZIONE Soluzioni di quesiti e prolemi trtti dl Corso Bse Blu di Mtemti volume 5 [] (Es. n. 8 pg. 9 V) Dell prol f ( ) si hnno le seguenti informzioni, tutte
VERSO L ESAME DI STATO LA DERIVATA DI UNA FUNZIONE Soluzioni di quesiti e prolemi trtti dl Corso Bse Blu di Mtemti volume 5 [] (Es. n. 8 pg. 9 V) Dell prol f ( ) si hnno le seguenti informzioni, tutte
QUESITI DI PSICOLOGIA
 QUESITI DI PSICOLOGIA appunti 23 TEST DI VERIFICA 1 Che osa si intene on il onetto i atteniilità? a L effiaia he un test ha nel preveere i renimenti i un soggetto nelle ailità speifihe misurate Il grao
QUESITI DI PSICOLOGIA appunti 23 TEST DI VERIFICA 1 Che osa si intene on il onetto i atteniilità? a L effiaia he un test ha nel preveere i renimenti i un soggetto nelle ailità speifihe misurate Il grao
ISTITUTO TECNICO INDUSTRIALE "E. Fermi" LUCCA Anno Scolastico 2017/2018 Programma di MATEMATICA classe prima Sez. G Insegnante: MUSUMECI LUCIANA
 ISTITUTO TENIO INDUSTILE "E. Fermi" LU nno Solstio / Progrmm di MTEMTI lsse prim Sez. G Insegnnte MUSUMEI LUIN Gli insiemi ppresentzione di un insieme. I sottoinsiemi. Le operzioni on gli insiemi unione
ISTITUTO TENIO INDUSTILE "E. Fermi" LU nno Solstio / Progrmm di MTEMTI lsse prim Sez. G Insegnnte MUSUMEI LUIN Gli insiemi ppresentzione di un insieme. I sottoinsiemi. Le operzioni on gli insiemi unione
Capitolo 5 Reti combinatorie. 5.1 Il problema della sintesi. Progetto logico di circuiti combinatori. Obiettivi del progetto logico
 Cpitolo 5 Reti omintorie 5. - Il prolem dell sintesi 5.2 - Reti di osto minimo 5.3 - Il metodo delle mppe 5.4 - Reti Nnd ed Nor 5.5 - Reti progrmmili 5. Il prolem dell sintesi Funzione ssegnt Oiettivi
Cpitolo 5 Reti omintorie 5. - Il prolem dell sintesi 5.2 - Reti di osto minimo 5.3 - Il metodo delle mppe 5.4 - Reti Nnd ed Nor 5.5 - Reti progrmmili 5. Il prolem dell sintesi Funzione ssegnt Oiettivi
Geometria Analitica Domande, Risposte & Esercizi
 Geometri Anliti Domnde, Risposte & Eserizi L ellisse. Dre l definizione di ellisse ome luogo di punti. L ellisse è un luogo di punti, è ioè un insieme di punti del pino le ui distnze d due punti fissi
Geometri Anliti Domnde, Risposte & Eserizi L ellisse. Dre l definizione di ellisse ome luogo di punti. L ellisse è un luogo di punti, è ioè un insieme di punti del pino le ui distnze d due punti fissi
I S I E. Fermi - Lucca Istituto Tecnico settore Tecnologico
 I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
La statistica nei test Invalsi
 L sttisti nei test Invlsi 1) Osserv il grfio seguente he rppresent l distriuzione perentule di fmiglie per numero di omponenti, in se l ensimento 2001.. Qul è l perentule di fmiglie on 2 omponenti? Rispost:..%.
L sttisti nei test Invlsi 1) Osserv il grfio seguente he rppresent l distriuzione perentule di fmiglie per numero di omponenti, in se l ensimento 2001.. Qul è l perentule di fmiglie on 2 omponenti? Rispost:..%.
Capitolo 5 Reti combinatorie 5.1. Il problema della sintesi. Progetto logico di circuiti combinatori. Complessità e velocità. 5.2 Reti di costo minimo
 Cpitolo 5 Reti omintorie 5. Il prolem ell sintesi 5.2 Reti i osto minimo 5.3 Il metoo elle mppe 5.4 Reti progrmmili 5. Il prolem ell sintesi Funione ssegnt Il prolem ell sintesi Espressioni equivlenti
Cpitolo 5 Reti omintorie 5. Il prolem ell sintesi 5.2 Reti i osto minimo 5.3 Il metoo elle mppe 5.4 Reti progrmmili 5. Il prolem ell sintesi Funione ssegnt Il prolem ell sintesi Espressioni equivlenti
Capitolo 5 Reti combinatorie 5.1. Il problema della sintesi. Progetto logico di circuiti combinatori
 Cpitolo 5 Reti comintorie 5. - Il prolem dell sintesi 5.2 - Reti di costo minimo 5.3 Il metodo delle mppe 5.4 Reti progrmmili 5. Il prolem dell sintesi Funzione ssegnt Il prolem dell sintesi Espressioni
Cpitolo 5 Reti comintorie 5. - Il prolem dell sintesi 5.2 - Reti di costo minimo 5.3 Il metodo delle mppe 5.4 Reti progrmmili 5. Il prolem dell sintesi Funzione ssegnt Il prolem dell sintesi Espressioni
TIMER. Cliccando qui si può vedere il video del circuito su breadboard in cui si potrà notare:
 6 TIMER Il iruito proposto è un pproonimento personle sopo ittio per mettere in prti le nozioni ino or quisite (pssno nhe l mierto SUPERCAR qui rppresentto i CD07B), iò non tolie he non poss essere utile.
6 TIMER Il iruito proposto è un pproonimento personle sopo ittio per mettere in prti le nozioni ino or quisite (pssno nhe l mierto SUPERCAR qui rppresentto i CD07B), iò non tolie he non poss essere utile.
8 Equazioni parametriche di II grado
 Equzioni prmetrihe di II grdo Un equzione he oltre ll inognit (o lle inognite) ontiene ltre lettere (un o più) si die letterri o prmetri e le lettere sono himte, nhe, prmetri; si suppong he l equzione
Equzioni prmetrihe di II grdo Un equzione he oltre ll inognit (o lle inognite) ontiene ltre lettere (un o più) si die letterri o prmetri e le lettere sono himte, nhe, prmetri; si suppong he l equzione
Unità logico-aritmetica (ALU) Architetture dei Calcolatori (Lettere. Blocchi di base per costruire l ALUl. Passi per costruire l ALUl
 Unità logio-ritmeti (ALU) Arhitetture dei Cloltori (Lettere A-I) Unit Logio-Aritmeti (ALU) Prof. Frneso Lo Presti E l prte del proessore he svolge le operzioni ritmetio- logihe Rete omintori Operzioni
Unità logio-ritmeti (ALU) Arhitetture dei Cloltori (Lettere A-I) Unit Logio-Aritmeti (ALU) Prof. Frneso Lo Presti E l prte del proessore he svolge le operzioni ritmetio- logihe Rete omintori Operzioni
Capitolo 3. Modelli. Macchine combinatorie Macchine sequenziali asincrone sincrone
 Capitolo 3 Moelli Mahine ominatorie Mahine sequenziali asinrone sinrone Il moello el loo o satola nera i I: alfaeto i ingresso u U: alfaeto i usita ingresso ei ati i F u usita ei risultati F: relazione
Capitolo 3 Moelli Mahine ominatorie Mahine sequenziali asinrone sinrone Il moello el loo o satola nera i I: alfaeto i ingresso u U: alfaeto i usita ingresso ei ati i F u usita ei risultati F: relazione
PICCOLO LABORATORIO DI ELETTRONICA
 PICCOLO LORTORIO DI ELETTRONIC COME SI LVOR CON I CIRCUITI INTEGRTI cura di prof. Giandomenico ntonioli Slides realizzate con la collaborazione dello studente Emidio Elisii CIRCUITO INTEGRTO (I.C.) PIN
PICCOLO LORTORIO DI ELETTRONIC COME SI LVOR CON I CIRCUITI INTEGRTI cura di prof. Giandomenico ntonioli Slides realizzate con la collaborazione dello studente Emidio Elisii CIRCUITO INTEGRTO (I.C.) PIN
Unità logico-aritmetica (ALU) Unità logico-aritmetica. Passi per costruire l ALU. Blocchi di base per costruire l ALU
 Unità logio-ritmeti (ALU) Unità logio-ritmeti Arhitetture dei Cloltori (lettere A-I) E l prte del proessore he svolge le operzioni ritmetio-logihe Potenz di lolo del proessore Insieme di iruiti omintori
Unità logio-ritmeti (ALU) Unità logio-ritmeti Arhitetture dei Cloltori (lettere A-I) E l prte del proessore he svolge le operzioni ritmetio-logihe Potenz di lolo del proessore Insieme di iruiti omintori
Le molle. M. Guagliano
 Le molle M. Guagliano Introuzione Le molle sono organi meccanici che hanno la proprietà i eformarsi molto sotto carico, ma rimaneno nel campo elastico el materiale i cui sono costituite, ovvero non accumulano
Le molle M. Guagliano Introuzione Le molle sono organi meccanici che hanno la proprietà i eformarsi molto sotto carico, ma rimaneno nel campo elastico el materiale i cui sono costituite, ovvero non accumulano
operazioni con vettori
 omposizione e somposizione + = operzioni on vettori = + = + Se un vettore può essere dto dll omposizione di due o più vettori, questi vettori omponenti possono essere selti lungo direzioni ortogonli fr
omposizione e somposizione + = operzioni on vettori = + = + Se un vettore può essere dto dll omposizione di due o più vettori, questi vettori omponenti possono essere selti lungo direzioni ortogonli fr
