Analisi numerica. Richiami di teoria Zeri di una funzione, soluzione approssimata di un equazione. Teorema di esistenza degli zeri
|
|
|
- Roberta Catalano
- 7 anni fa
- Visualizzazioni
Transcript
1 6 - Alisi umeric 6 Alisi umeric. Richimi di teori Zeri di u fuzioe, soluzioe pprossimt di u equzioe Se o è possibile determire lgebricmete gli zeri dell fuzioe f(), rdici dell equzioe f() =, si possoo utilizzre i cosiddetti metodi umerici che coducoo vlori pprossimti delle soluzioi cercte. L ricerc delle rdici (soluzioi), vviee i due fsi:. ricerc degli itervlli i cui compre u e u sol rdice (isolmeto dell rdice);. determizioe, ll itero degli itervlli precedetemete determiti, dell soluzioe pprossimt. Teorem di esistez degli zeri teorem di uicità dell soluzioe teorem di uicità dell soluzioe grfico Fse Se u fuzioe y = f() è cotiu ell itervllo chiuso [; b] e ssume vlori discordi gli estremi di tle itervllo, cioè f() f(b) <, llor l equzioe f() =h lmeo u soluzioe iter ll itervllo: α ]; b[ f(α) =. Il teorem ssicur l esistez di lmeo u rdice dell equzioe, quidi è possibile che ve e si più di u, comuque sempre i umero dispri. Se u fuzioe y = f() è cotiu ell itervllo chiuso [; b], è derivbile ell itervllo perto ]; b[, f() f(b) < e f () ]; b[, llor l equzioe f() =h u e u sol soluzioe iter ll itervllo:! α ]; b[ f(α) =. Se u fuzioe y = f() è cotiu ell itervllo chiuso [; b], è derivbile volte ell itervllo perto ]; b[, f() f(b) < e f () si mtiee di sego costte ]; b[, llor l equzioe f() = h u e u sol soluzioe iter ll itervllo:! α ]; b[ f(α) =. Nel cso di fuzioi lgebriche complesse o trscedeti per le quli il clcolo delle derivte e del loro sego comporti prticolri difficoltà, è possibile cercre di isolre le rdici utilizzdo il metodo grfico. Tle metodo cosiste el riscrivere l equzioe f() = come ugugliz di ltre due fuzioi ell stess vribile, g() =h(), lmeo u di esse ot, per cui l ricerc delle soluzioi dell equzioe dt è ricodott quell delle soluzioi del sistem { y = g() y = h() 7
2 Richimi di teori Rppresette grficmete le fuzioi g() e h(), è possibile determire pprossimtivmete gli itervlli i cui cdoo le soluzioi d determire. di bisezioe Fse Determito l itervllo [; b] i cui l fuzioe y = f() mmette u e u sol rdice α (per cui è sicurmete f() f(b) < ), bisog ricercre il vlore pprossimto di tle soluzioe. Il metodo cosiste el suddividere ogi psso l itervllo [; b] i due prti uguli e determire i qule dei due sottoitervlli si trov l rdice (l soluzioe), cioè vlg sempre f() f(b) <. Proseguedo i questo modo si dimezz progressivmete l mpiezz dell itervllo che cotiee α. Posti = e b = b, si clcolo = + b e f( ): se f( )=, α = è lo zero cercto; se f( ) e f( ) soo cocordi, cioè f( ) f( ) >, si poe = e b = b ; se f( ) e f( ) soo discordi, cioè f( ) f( ) <, si poe = e b =. Si ripete il procedimeto pplicdolo ll itervllo [ ; b ] e così vi. Si form i tl modo u successioe di itervlli icpsulti di mpiezz ugule ll metà del precedete: b = b + b = b e, i geerle, b = b = b. L codizioe di rresto del procedimeto è dt d: b <ε, co ε R + errore idicto dl testo o scelto picere, cioè l itervllo cui pprtiee l soluzioe α è sufficietemete ristretto; f( ) <ε, cioè il vlore ssuto d f i è sufficietemete prossimo zero; etrmbe le codizioi. Si ssume llor che α = + b co u errore ssoluto che è o superiore b. L semplicità f di tle metodo uo dei più utilizzti, mlgrdo bbi u covergez d α bbstz let. Per l su ppliczioe ci si può vvlere del seguete schem. b f ( ) f (b ) f ( ) b delle corde Il metodo cosiste el cercre u successioe di pprossimzioi dello zero α di y = f() utilizzdo le fuzioi lieri dte dlle rette pssti per gli estremi dell fuzioe stess ell itervllo cosiderto. Se [; b] è l itervllo i cui l fuzioe y = f() mmette u e u sol rdice α (per cui è sicurmete f() f(b) < ), suppoimo che f () bbi sego costte [; b]. 73
3 6 - Alisi umeric Posto = b k = se f () f() >, = k = b se f () f(b) >, scrivedo l equzioe dell rett psste per ( ; f( )) e (k; f(k)) e itersecdol co l sse si ricv: k = f(k) f( ) f( ). Iterdo il procedimeto ( ; f( )) e puti successivi, si ottiee l formul geerle: + = k f(k) f( ) f( ). L codizioe di rresto del procedimeto è dt d: + <ε, cioè l differez tr due pprossimzioi successive di α è sufficietemete piccol; f( + ) <ε, cioè il vlore ssuto d f i + è sufficietemete prossimo zero; etrmbe le codizioi. Si ssume llor che α +. L formul itertiv, poco semplice, f di tle metodo uo dei meo utilizzti. Per l su ppliczioe ci si può vvlere del seguete schem. f ( ) k f (k) + ====== delle tgeti (o di Newto) Il metodo cosiste el cercre u successioe di pprossimzioi dello zero α di y = f() utilizzdo le fuzioi lieri dte dlle tgeti ll curv i u estremo dell itervllo cosiderto. Se [; b] è l itervllo i cui l fuzioe y = f() mmette u e u sol rdice α (per cui è sicurmete f() f(b) < ), suppoimo che f () bbi sego costte [; b]. Posto = se f () f() >, = b se f () f(b) >, scrivedo l equzioe dell tgete i e itersecdol co l sse si ricv: = f( ) f ( ). Iterdo il procedimeto e vlori successivi, si ottiee l formul geerle: + = f( ) f ( ). Le codizioi di rresto del procedimeto soo le stesse del metodo delle corde. Si ssume llor che α +. L velocità di covergez d α (il umero di cifre decimli estte rddoppi ogi iterzioe) f di tle metodo uo dei più utilizzti. Per l su ppliczioe ci si può vvlere del seguete schem. f ( ) f ( ) + ====== 74
4 Richimi di teori. Itegrzioe umeric Se o è possibile determire lgebricmete l itegrle defiito di u fuzioe f(), perché o soo pplicbili le regole di itegrzioe studite, o esse porto clcoli lboriosi, o perché l fuzioe è coosciut solo per lcui puti ( seguito d esempio di studi sttistici), si possoo utilizzre i cosiddetti metodi umerici, che coducoo u vlore pprossimto dell itegrle defiito richiesto. L itegrzioe umeric si bs sul sigificto geometrico di itegrle defiito: l itegrle defiito f()d rppreset l re dell prte di pio compres tr il grfico dell fuzioe, l sse e le rette di equzioe = e = b, suppoedo f() cotiu e o egtiv i [; b]. Tle prte di pio prede il ome di trpezoide. Per grtire l esistez dell itegrle f()d e poter effetture u stim dell errore commesso utilizzdo uo dei metodi umerici, suppoimo che l fuzioe ite- grd f() si cotiu, o egtiv e derivbile più volte sull itervllo chiuso e limitto [; b]. dei rettgoli Il metodo cosiste el suddividere l itervllo di itegrzioe [; b] i u umero fiito di prti uguli di mpiezz h = b medite gli +puti =, = + h, = +h = + h,..., = + h = + h = b, cui corrispodoo i vlori dell fuzioe y = f( ), y = f( ),..., y = f( ), y = f( ). Si cosiderio gli rettgoli veti per bse uo degli itervlli i cui è suddiviso [; b] (quidi tutti di bse h) e per ltezz il vlore ssuto dll fuzioe el primo estremo di tle itervllo (figur ); si clcoli l somm R delle loro ree: R = y h + y h y h. y FIG. O = b = L re del trpezoide di bse [; b] è pprossimt d R, per cui: f()d R = y h + y h y h = b (y + y + y y ) 3 Si cosiderio gli rettgoli veti per bse uo degli itervlli i cui è suddiviso [; b] (quidi tutti di bse h) e per ltezz il vlore ssuto dll fuzioe el secodo estremo di tle itervllo (figur ); si clcoli l somm R delle loro ree: R = y h + y h y h. y O = b = FIG. 75
5 6 - Alisi umeric L re del trpezoide di bse [; b] è pprossimt d R, per cui: dei trpezi f()d R = y h + y h y h = b (y + y y + y ) 4 Le formule 3 e 4 soo dette formule di qudrtur dei rettgoli. Si può evidezire che essedo l fuzioe f() itegrbile, le somme R e R covergoo llo stesso limite per tedete ifiito e quidi l loro differez può essere res piccol picere umetdo opportumete il umero degli itervlli di suddivisioe. Ioltre, se f() è mootò crescete i [; b], llor R rppreset u pprossimzioe per difetto e R u pprossimzioe per eccesso dell itegrle defiito dto, il vicevers se f() è mootò decrescete i [; b]. Se l fuzioe f() mmette derivt prim cotiu, idicto co ε l errore commesso e co M il vlore mssimo di f () i [; b] (M = m f () f () M [;b] [; b]), si h: (b ) ε M. 4 Si suddivide l itervllo [; b] i itervlli, ciscuo di mpiezz h = b, medite gli +puti =, = + h, = +h = + h,..., = + h = + h = b cui corrispodoo i vlori dell fuzioe y = f( ), y = f( ),..., y = f( ), y = f( ). Si cosiderio gli trpezi rettgoli veti per ltezz uo degli itervlli i cui è suddiviso [; b] (quidi tutti di ltezz h) e per bsi i vlori ssuti dll fuzioe egli estremi di tle itervllo (figur 3); si clcoli l somm T delle loro ree: T = y + y h + y + y h y FIG. 3 L re del trpezoide di bse [; b] è pprossimt d T, per cui: + y + y f()d T = y + y h. h + y + y O = b = h y + y h = = h y + y + y + y + y y + y + y = = b ( ) y + y + y + y y, 5 che esprime l formul di qudrtur dei trpezi. Se l fuzioe f() mmette derivt secod cotiu, idicto co ε l errore commesso e co M il vlore mssimo di f () i [; b] (M = m f () f () M [;b] [; b]), si h: (b )3 ε M. 5 76
6 Richimi di teori delle prbole o di Cvlieri- Simpso Si suddivide l itervllo [; b] i itervlli, ciscuo di mpiezz h = b, medite i +puti =, = + h, = +h = + h,..., = +h = + h = b cui corrispodoo i vlori dell fuzioe y = f( ), y = f( ),..., y = f( ), y = f( ). Si cosiderio gli itervlli [ i ; i+ ] i cui è suddiviso [; b] di puti,,..., (figur 4) e per ciscuo di essi si clcoli l re sottes ll prbol psste per i puti di sciss i, i+, i+ (co i+ puto medio di [ i ; i+ ] e i =,,..., ), il cui vlore è ugule y y = f () FIG. 4 S i = h 3 (y i +4y i+ + y i+ ). O = b = Si clcoli successivmete l somm S di tli ree: S = S i = i = h 3 (y +4y + y )+ h 3 (y +4y 3 + y 4 )+...+ h 3 (y +4y + y )= = h 3 (y +4y + y + y +4y 3 + y y +4y + y )= = h 3 [y + y +(y + y 4 + y y )+4(y + y 3 + y y )] = = b 6 [y + y +(y + y 4 + y y )+4(y + y 3 + y y )]. L re del trpezoide di bse [; b] è pprossimt d S, per cui: f()d S = b 6 [y + y +(y + y 4 + y y )+4(y + y 3 + y y )] 6 che esprime l formul di qudrtur delle prbole o di Cvlieri-Simpso. Se l fuzioe f() mmette derivt qurt cotiu, idicto co ε l errore com- e co M il vlore mssimo di f (IV) () i [; b] (M = m f (IV) () messo [;b] f (IV) () M [; b]), si h: ε (b ) M. 6 77
7 6 - Alisi umeric Esercizi svolti QUESITO 6 A.S. / Esme di Stto, s.o. Liceo Scietifico P.N.I. Quesito Co uo dei metodi di qudrtur studiti, si clcoli u pprossimzioe dell itegrle defiito π se d e si cofroti il risultto co il vlore estto dell itegrle. Risoluzioe guidt Clcolimo il vlore estto I dell itegrle: I = π se d =[ cos ] π = cos π ( cos ) = + = I metodo. Per il clcolo pprossimto dell itegrle si può utilizzre il metodo dei trpezi co u suddivisioe dell itervllo [; π] i =6prti uguli di mpiezz h = π 6 = π 6 medite i 7 puti =, = π 6, = π 3, 3 = π, 4 = 3 π, 5 = 5 6 π, 6 = π. Ricordt l 5, si h: f()d T 6 = b ( ) [ ] y + y 6 f( )+f( 6 ) + y y 5 = h + f( )+...+ f( 5 ) ed essedo: f( )=f() =, f( 3 )=f ( π ) =, f( )=f ( ) π 3 = 3, f( )=f ( π 6 ) =, f(4 )=f ( 3 π) = 3, f( 5)=f ( 5 6 π) =, f( 6)=f(π) = si ottiee: [ I T 6 = π ] 3 + = π 6 ( 3+), L errore compiuto è quidi ε 6 =, =, (b )3 Per l 5 si h che ε M, co f () M [; b], ed essedo f () = se M =, si ricv: ε 6 (π )3 = π3 6 36, , verificdo l disugugliz teoric 5. II metodo. Per il clcolo pprossimto dell itegrle si può utilizzre il metodo dei rettgoli co u suddivisioe dell itervllo [; π] i =6prti uguli di mpiezz h = π 6 = π 6 medite i 7 puti =, = π 6, = π 3, 3 = π, 4 = 3 π, 5 = 5 6 π, 6 = π. Ricordte l 3 e l 4, si h: f()d R 6 = b ( y + y + y y 5 ) f()d R 6 = b ( y + y + y y 6 ) 78
8 Esercizi svolti e utilizzdo i vlori già determiti per il metodo precedete: ( f()d R 6 = π ) 3 + = π 6 ( 3+ ), ( f()d R 6 = π ) = π 6 ( 3+ ), L errore compiuto è quidi ε 6 =, =, Nel cso prticolre i esme si è trovto R 6 = R 6 = T 6, metre i geerle il metodo dei rettgoli forisce u pprossimzioe meo precis di quello dei trpezi ed è: R R e T = R + R. (b ) Per l 4 si h che ε M, co f () M [; b], ed essedo f () = cos M =, si ricv: ε 6 (π ) 6 = π, , verificdo l disugugliz teoric 4. QUESITO 7 A.S. / Esme di Stto, s.o. Liceo Scietifico P.N.I. Quesito Verificto che l equzioe e =mmette u sol rdice positiv compres tr e se e clcoli u pprossimzioe pplicdo uo dei metodi umerici studiti. Risoluzioe Posto f() = e, l ricerc delle soluzioi dell equzioe dt è ricodott ll ricerc delle itersezioi dell fuzioe f co l sse delle scisse. L fuzioe f è defiit e cotiu su tutto R. Essedo: f() = e = < e f() = e = e >, f() ssume gli estremi dell itervllo chiuso I =[;] vlori discordi; perciò, per il teorem di esistez degli zeri pplicbile lle fuzioi cotiue i u itervllo chiuso, si deve ullre lmeo i u puto = α, α ]; [. Derivdo vremo: f () =+e. L fuzioe derivt prim risult sempre positiv, poiché f () > R, e quidi f sempre strettmete crescete su tutto R, i prticolre su I. Dll esistez dello zero = α e dll mootoi di f() si ricv che tle zero deve che essere uico ( teorem di uicità dell soluzioe). Applicdo f() il metodo delle tgeti, + = f( ) f ( ), dto che f () = e per cui f () < R e =(il metodo richiede che f ( ) f( ) > ), si ottiee, co u pprossimzioe di e utilizzdo 4 cifre decimli: f ( ) f ( ) + ======,5,65,665,5,5663,3,5676,663 3, ,8 79
9 6 - Alisi umeric Essedo il vlore ssoluto dell differez tr due pprossimzioi successive di α e il vlore f( ) miori del scelto, si ricv che α,567 (u vlore più preciso è α, ). QUESITO A.S. /3 Esme di Stto, s.o. Liceo Scietifico P.N.I. Quesito 3 Verificre che l equzioe 3 3 += mmette tre rdici reli. Di u di esse, quell compres tr e, si clcoli u pprossimzioe pplicdo uo dei metodi umerici studiti. Risoluzioe L fuzioe f() = 3 3 +è u fuzioe poliomile iter di terzo grdo cotiu R, co lim f() = lim f() =+, + per cui per il teorem di esistez degli zeri di u fuzioe ] ;+ [ tle che f() =; ioltre f è derivbile R co derivt prim f () =3 3. Dllo studio dei puti stziori e dl sego delle corrispodeti ordite si deduce il umero di itersezioi dell fuzioe f() co l sse delle scisse. Risult f () 3 3, co f( ) = 3 e f() =, per cui i puti stziori M( ; 3) e m(; ) soo rispettivmete mssimo e miimo reltivo co ordite di sego discorde. L fuzioe ssegt itersec quidi l sse delle scisse i tre puti, ovvero l equ- 3 FIG. M y zioe 3 3 += mmette tre rdici reli α, α, α 3. Il grfico i figur illustr l situzioe. Essedo f() = l soluzioe α ]; [ e per il clcolo del suo vlore pprossimto possimo usre il metodo di bisezioe. Co =, b =e u pprossimzioe di, utilizzdo 5 cifre decimli, si ottiee: α α α 3 O m b f ( ) f (b ) f ( ) b,5 3,5 4,35 5, ,34375,5,375,5,375,5,6563,5,5,6563,375,375,77,5,375,6563,77,35,93,5,375,93,77,34375,937,65,375,937,77,35938,37,35,35938,937,37,3557,6,563 7,34375,3557,937,6,34766,96,78 Essedo i vlori b e f( ) miori del scelto, si ricv che α,34766 (u vlore più preciso è α, ). 8
10 QUESITO 9 A.S. 3/4 Esme di Stto, s.o. Liceo Scietifico P.N.I. Liceo Scietifico (QUESITO 4) Quesito 4 Esercizi svolti Si dimostri che l equzioe e +3 =mmette u e u sol soluzioe rele, e se e clcoli u vlore pprossimto utilizzdo u metodo itertivo scelt. Risoluzioe guidt L equzioe dt, h() =e +3 =, può essere riscritt come e = 3, per cui l su rdice λ coicide co l soluzioe del sistem { f() = e g() = 3 cioè è il puto comue lle fuzioi elemetri f() = e e g() = 3 Essedo f() mootò strettmete crescete, g() mootò strettmete decrescete, lim +, lim f() = + +, lim g() = +, lim g() = +, le curve si icotrero i u solo puto, pprteete ll itervllo ] ; [, come risult che dll figur. FIG. y = g() λ y O y = f () Applicdo il metodo di bisezioe co =, b = e u pprossimzioe di, utilizzdo 4 cifre decimli, si ottiee: b h( ) h(b ) h( ) b,63,5,8935,5,8935,5,88,5,5,5,8935,88,375,4377,5 3,375,5,4377,88,35,59,5 4,35,5,59,88,83,89,65 Essedo i vlori b e h( ) miori del scelto, si ricv che λ,83 (u vlore più preciso è λ, ). QUESITO 3/4 Esme di Stto, s.s. Liceo Scietifico P.N.I. Quesito 5 Dopo ver spiegto perché l fuzioe f() = cos è positiv ell itervllo [; ], esplicitre u lgoritmo idoeo clcolre u vlore pprossimto dell re situt sotto il grfico dell fuzioe reltivmete ll itervllo cosiderto. 8
11 6 - Alisi umeric Risoluzioe Nell itervllo [; ] l fuzioe cos è decrescete e miore di, quidi risult >cos cos > f() = >, [; ]. cos I metodo. L re d clcolre è dt d: A = cos d per cui, per il clcolo pprossimto dell itegrle, si può utilizzre, d esempio, il metodo dei trpezi co u suddivisioe dell itervllo [; ] i =5prti uguli (o soo stte dte idiczioi sul grdo di precisioe) di mpiezz h = = 5 =, medite i 6 puti =, =,, =,4, 3 =,6, 4 =,8, 5 =. Ricordt l 5, utilizzdo 4 cifre decimli, si h: A T 5 = b ( ) [ y + y 5 f( )+f( 5 ) + y y 4 = h ed essedo ] + f( )+...+ f( 4 ) f( )=f() =,753, f( )=f(,) =,938, f( )=f(,4) =,83, f( 3 )=f(,6) =,638, f( 4 )=f(,8) =,4933, f( 5 )=f() =,439 si ottiee: A T 5 = 5 [ ],753+,439 +,938 +,83 +,638 +,4933 = 5 4,485 =,887 (u vlore più preciso è A,8554 e o è richiest l stim dell errore). II metodo. Co il metodo di Cvlieri-Simpso, per l 6, suddividedo l itervllo [; ] medite i = puti, sempre utilizzdo quttro cifre decimli, vremmo ivece otteuto: h = = =, =, =,, =,, 3 =,3,..., 9 =,9, =, A S 6 = b 6 [y + y +(y + y 4 + y 6 + y 8 )+4(y + y 3 + y 5 + y 7 + y 9 )] e y = f() =,753 y = f(,) =,547 y = f(,) =,938 y 3 = f(,3) =,9685 y 4 = f(,4) =,83 y 5 = f(,5) =,6997 y 6 = f(,6) =,638 y 7 = f(,7) =,5468 y 8 = f(,8) =,4933 y 9 = f(,9) =,4498 y = f() =,439 d cui: A S 6 = [,753 +,439 + (,938 +,83 +,638 +,4933) (,547 +,9685 +,6997 +,5468 +,4498)],8555 pprossimzioe migliore di quell otteut co il metodo dei trpezi. 8
Successioni. (0, a 0 ), (1, a 1 ), (2, a 2 ),...
 Successioi U successioe di umeri reli e u legge che ssoci ogi umero turle = 0, 1, 2, u umero rele, i breve: e u fuzioe N R, Puo essere rppresett co l isieme delle coppie ordite (0, 0 ), (1, 1 ), (2, 2
Successioi U successioe di umeri reli e u legge che ssoci ogi umero turle = 0, 1, 2, u umero rele, i breve: e u fuzioe N R, Puo essere rppresett co l isieme delle coppie ordite (0, 0 ), (1, 1 ), (2, 2
Corso di Calcolo Numerico
 Fcoltà di Igegeri - Lure Triele i Igegeri Meccic Corso di Clcolo Numerico Dott.ss M.C. De Bois Uiversità degli Studi dell Bsilict, Potez Fcoltà di Igegeri Corso di Lure i Igegeri Meccic Ao Accdemico 004/05
Fcoltà di Igegeri - Lure Triele i Igegeri Meccic Corso di Clcolo Numerico Dott.ss M.C. De Bois Uiversità degli Studi dell Bsilict, Potez Fcoltà di Igegeri Corso di Lure i Igegeri Meccic Ao Accdemico 004/05
Integrazione numerica.
 Itegrzioe umeric Autore: prof. RUGGIERO Domeico Itegrzioe umeric. Qui di seguito ci occupimo di metodi umerici volti l clcolo pprossimto di u itegrle defiito perveedo formule ce costituiscoo degli lgoritmi,
Itegrzioe umeric Autore: prof. RUGGIERO Domeico Itegrzioe umeric. Qui di seguito ci occupimo di metodi umerici volti l clcolo pprossimto di u itegrle defiito perveedo formule ce costituiscoo degli lgoritmi,
DERIVATE.. Si chiama rapporto incrementale della f (x) relativo al punto x
 DERIVATE Si f ( ; Se e soo due puti del suo domiio, si cim icremeto dell fuzioe il vlore f = f( f( Si cim rpporto icremetle dell f ( reltivo l puto e ll'icremeto il rpporto: y = u fuzioe rele defiit ell'itervllo
DERIVATE Si f ( ; Se e soo due puti del suo domiio, si cim icremeto dell fuzioe il vlore f = f( f( Si cim rpporto icremetle dell f ( reltivo l puto e ll'icremeto il rpporto: y = u fuzioe rele defiit ell'itervllo
Il problema è ricavare le radici (gli zeri) di una funzione f(x), cioè i valori z: f(z)=0
 Ricerc di zeri Equzioi o lieri Il prolem è ricvre le rdici (gli zeri di u fuzioe f(, cioè i vlori z: f(z0 qudo o si poss otteere l soluzioe i form chius (u formul Seprzioe delle rdici Per semplificre il
Ricerc di zeri Equzioi o lieri Il prolem è ricvre le rdici (gli zeri di u fuzioe f(, cioè i vlori z: f(z0 qudo o si poss otteere l soluzioe i form chius (u formul Seprzioe delle rdici Per semplificre il
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE Tema di: MATEMATICA E INFORMATICA
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE Tem di: MATEMATICA E INFORMATICA Il cdidto dopo ver dto u iustificzioe dell formul d iterzioe per prti: f d f f d dic cos c è di slito el riometo
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE Tem di: MATEMATICA E INFORMATICA Il cdidto dopo ver dto u iustificzioe dell formul d iterzioe per prti: f d f f d dic cos c è di slito el riometo
Successioni in R. n>a n+1
 Successioi i R U successioe è u fuzioe f : N R. Si preferisce deotre f() co e quidi u successioe co ( ). Il codomiio di u successioe ( ) è l'isieme dei vlori che ssume l successioe, cioè { } successioe
Successioi i R U successioe è u fuzioe f : N R. Si preferisce deotre f() co e quidi u successioe co ( ). Il codomiio di u successioe ( ) è l'isieme dei vlori che ssume l successioe, cioè { } successioe
punto di accumulazione per X. Valgono le seguenti
 4 I LIMITI Si f : X R R u fuzioe rele di vribile rele. Si puto di ccumulzioe per X. Vlgoo le segueti DEFINIZIONI ( ε ( ε ε ( ε ε. ( ε { } lim f( = l R : > I I ' X I : f( l I I ' X
4 I LIMITI Si f : X R R u fuzioe rele di vribile rele. Si puto di ccumulzioe per X. Vlgoo le segueti DEFINIZIONI ( ε ( ε ε ( ε ε. ( ε { } lim f( = l R : > I I ' X I : f( l I I ' X
Dove la suddivisione dell intervallo [a,b] è individuata dai punti
![Dove la suddivisione dell intervallo [a,b] è individuata dai punti Dove la suddivisione dell intervallo [a,b] è individuata dai punti](/thumbs/89/98520294.jpg) 04//205 Clcolo itegrle per fuzioi di u vriile Clcolo itegrle Itegrle defiito Si f:[,] R, limitt ξ ξ 2 ξ 3 ξ 4 ξ 5 0 = 2 3 4 5 = Costruimo l somm di Cuchy-Riem S f f Dove l suddivisioe dell itervllo [,]
04//205 Clcolo itegrle per fuzioi di u vriile Clcolo itegrle Itegrle defiito Si f:[,] R, limitt ξ ξ 2 ξ 3 ξ 4 ξ 5 0 = 2 3 4 5 = Costruimo l somm di Cuchy-Riem S f f Dove l suddivisioe dell itervllo [,]
LE SUCCESSIONI. ovvero: 1, 2, 1.5, 1., 1.6, 1.625,... I valori ottenuti si avvicinano alla sezione aurea: =
 LE SUCCESSIONI Si cosideri l seguete sequez di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fibocci. Ess rppreset il umero di coppie di coigli preseti ei primi mesi i u llevmeto! Si cosideri l sequez
LE SUCCESSIONI Si cosideri l seguete sequez di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fibocci. Ess rppreset il umero di coppie di coigli preseti ei primi mesi i u llevmeto! Si cosideri l sequez
Unità Didattica N 38. Calcolo approssimato delle radici dell equazione f(x) = 0. 01) La risoluzione approssimata delle equazioni f(x) = 0
 Uità Didttic N 8 Clcl pprssimt delle rdici dell'equzie ( Uità Didttic N 8 Clcl pprssimt delle rdici dell equzie ( L risluzie pprssimt delle equzii ( Metd gric per l seprzie delle rdici reli dell equzie
Uità Didttic N 8 Clcl pprssimt delle rdici dell'equzie ( Uità Didttic N 8 Clcl pprssimt delle rdici dell equzie ( L risluzie pprssimt delle equzii ( Metd gric per l seprzie delle rdici reli dell equzie
Scuole italiane all estero (Santiago del Cile) 2010 Quesiti QUESITO 1
 www.mtefili.it Scuole itlie ll estero (Stigo del Cile) 21 Quesiti QUESITO 1 Si f(x) = { x2 5, se x 3 x + 2, se x > 3 Si trovi: lim f(x) ; x 3 lim f(x) ; x 3 + lim f(x). x 3 lim f(x) = lim x 3 x 3 (x2 5)
www.mtefili.it Scuole itlie ll estero (Stigo del Cile) 21 Quesiti QUESITO 1 Si f(x) = { x2 5, se x 3 x + 2, se x > 3 Si trovi: lim f(x) ; x 3 lim f(x) ; x 3 + lim f(x). x 3 lim f(x) = lim x 3 x 3 (x2 5)
Argomento 9 Integrali definiti
 Argometo 9 Itegrli defiiti Premess. Si f u fuzioe cotiu ell itervllo [, b]. L regioe di pio compres tr l sse x, le due rette verticli di equzioe x = e x = b, ed il grfico di f è dett trpezoide reltivo
Argometo 9 Itegrli defiiti Premess. Si f u fuzioe cotiu ell itervllo [, b]. L regioe di pio compres tr l sse x, le due rette verticli di equzioe x = e x = b, ed il grfico di f è dett trpezoide reltivo
Argomento 9 Integrali definiti
 Argometo 9 Itegrli defiiti Premess. Si f u fuzioe cotiu ell itervllo [, ]. L regioe di pio compres tr l sse x, le due rette verticli di equzioe x = e x =, ed il grfico di f è dett trpezoide reltivo d f
Argometo 9 Itegrli defiiti Premess. Si f u fuzioe cotiu ell itervllo [, ]. L regioe di pio compres tr l sse x, le due rette verticli di equzioe x = e x =, ed il grfico di f è dett trpezoide reltivo d f
Gli integrali definiti
 Gli itegrli defiiti Si f : [, b] u fuzioe cotiu defiit i u itervllo chiuso e limitto e suppoimo che. Cosiderimo l regioe T delimitt dl grfico di f(x), dlle rette x=, x=b e dll sse delle scisse (regioe
Gli itegrli defiiti Si f : [, b] u fuzioe cotiu defiit i u itervllo chiuso e limitto e suppoimo che. Cosiderimo l regioe T delimitt dl grfico di f(x), dlle rette x=, x=b e dll sse delle scisse (regioe
Corso Integrato: Matematica e Statistica. Corso di Matematica (6 CFU)
 Corso di Lure i Scieze e Tecologie Agrrie Corso Itegrto: Mtemtic e Sttistic Modulo: Mtemtic (6 CFU) (4 CFU Lezioi CFU Esercitzioi) Corso di Lure i Tutel e Gestioe del territorio e del Pesggio Agro-Forestle
Corso di Lure i Scieze e Tecologie Agrrie Corso Itegrto: Mtemtic e Sttistic Modulo: Mtemtic (6 CFU) (4 CFU Lezioi CFU Esercitzioi) Corso di Lure i Tutel e Gestioe del territorio e del Pesggio Agro-Forestle
(labeling) si ottiene così l insieme a n ordinato (codominio della funzione f ) : Primo termine. Termine Generale
 Successioi umeriche / Def. Si chim successioe umeric ogi fuzioe f d N i R defiit i u isieme del tipo I= { N 0 }, co 0 umero turle e che ssoci d u itero di I u umero rele f(). I geerle però porremo f: N
Successioi umeriche / Def. Si chim successioe umeric ogi fuzioe f d N i R defiit i u isieme del tipo I= { N 0 }, co 0 umero turle e che ssoci d u itero di I u umero rele f(). I geerle però porremo f: N
RELAZIONE FRA LA STABILITA DEL SISTEMA E LA FUNZIONE DI TRASFERIMENTO
 RELAZIONE FRA LA STABILITA DEL SISTEMA E LA FUNZIONE DI TRASFERIMENTO L stbilità di u sistem liere, ivrite ed prmetri cocetrti può vlutrsi co due criteri diversi che fo rispettivmete riferimeto ll rispost
RELAZIONE FRA LA STABILITA DEL SISTEMA E LA FUNZIONE DI TRASFERIMENTO L stbilità di u sistem liere, ivrite ed prmetri cocetrti può vlutrsi co due criteri diversi che fo rispettivmete riferimeto ll rispost
dove il Sia p( x ) un polinomio di grado n. Si dimostri che la sua derivata n esima è coefficiente a è il coefficiente di
 Quesiti ord 010 Pgi 1 di 5 Si p( ) u poliomio di grdo. Si dimostri che l su derivt esim è coefficiete è il coefficiete di ( p ) ( ) =! dove il 1 Si p( ) = + 1 +... + 0 Applicdo l regol di derivzioe delle
Quesiti ord 010 Pgi 1 di 5 Si p( ) u poliomio di grdo. Si dimostri che l su derivt esim è coefficiete è il coefficiete di ( p ) ( ) =! dove il 1 Si p( ) = + 1 +... + 0 Applicdo l regol di derivzioe delle
Soluzione 1) è definita in tutto R e a ± ammette i seguenti valori:
 PROBLEMA E' ssegt l seguete equzioe i : -5. ) Dimostrre che mmette u e u sol soluzioe el cmpo rele. b) Determire il umero itero z tle che risulti: z < < z. c) Dopo ver riferito il pio u sistem di ssi crtesii
PROBLEMA E' ssegt l seguete equzioe i : -5. ) Dimostrre che mmette u e u sol soluzioe el cmpo rele. b) Determire il umero itero z tle che risulti: z < < z. c) Dopo ver riferito il pio u sistem di ssi crtesii
Polinomi, disuguaglianze e induzione.
 Allemeti Disid Mtemtic Geio 03 Poliomi, disuguglize e iduzioe. Qul è l mssim re di u rettgolo vete perimetro ugule 576? [Suggerimeto: utilizzre le medie e le loro disuguglize.] Svolgimeto. Predimo i cosiderzioe
Allemeti Disid Mtemtic Geio 03 Poliomi, disuguglize e iduzioe. Qul è l mssim re di u rettgolo vete perimetro ugule 576? [Suggerimeto: utilizzre le medie e le loro disuguglize.] Svolgimeto. Predimo i cosiderzioe
. La n a indica il valore assoluto della radice.
 RADICALI Defiizioe: U umero irrziole è u umero decimle illimitto o periodico. Esempio:, 0, π Per clcolre il vlore pprossimto di u espressioe coteete rdici coviee mipolre l espressioe per ridurre l mssimo
RADICALI Defiizioe: U umero irrziole è u umero decimle illimitto o periodico. Esempio:, 0, π Per clcolre il vlore pprossimto di u espressioe coteete rdici coviee mipolre l espressioe per ridurre l mssimo
2 Sistemi di equazioni lineari.
 Sistemi di equzioi lieri. efiizioe. Si dice equzioe liere elle icogite equzioe dell form () + +...+ = o che (') i= i i = ove,,..., R si chimo coefficieti e R termie oto.,,..., ogi efiizioe. Si dice soluzioe
Sistemi di equzioi lieri. efiizioe. Si dice equzioe liere elle icogite equzioe dell form () + +...+ = o che (') i= i i = ove,,..., R si chimo coefficieti e R termie oto.,,..., ogi efiizioe. Si dice soluzioe
ESAME DI STATO DI LICEO SCIENTIFICO a.s. 2002/2003 CORSO SPERIMENTALE PNI e Progetto Brocca SESSIONE SUPPLETIVA
 ESAME DI STATO DI LICEO SCIENTIFICO.s. / CORSO SPERIMENTALE PNI e Progetto Brocc SESSIONE SUPPLETIVA Il cdidto risolv uo dei due problemi e 5 dei quesiti i cui si rticol il questiorio. PROBLEMA. I u pio,
ESAME DI STATO DI LICEO SCIENTIFICO.s. / CORSO SPERIMENTALE PNI e Progetto Brocc SESSIONE SUPPLETIVA Il cdidto risolv uo dei due problemi e 5 dei quesiti i cui si rticol il questiorio. PROBLEMA. I u pio,
ANALISI MATEMATICA STUDIO DI FUNZIONI
 ANALISI MATEMATICA STUDIO DI FUNZIONI. RELAZIONI Le fuzioi soo prticolri relzioi; le relzioi (birie) soo sottoisiemi del prodotto crtesio tr due isiemi. L trttzioe prte quidi dl cocetto di prodotto crtesio.
ANALISI MATEMATICA STUDIO DI FUNZIONI. RELAZIONI Le fuzioi soo prticolri relzioi; le relzioi (birie) soo sottoisiemi del prodotto crtesio tr due isiemi. L trttzioe prte quidi dl cocetto di prodotto crtesio.
Approssimazione di funzioni mediante Interpolazione polinomiale
 Docete: Cludio Esttico esttico@uisubri.it Approssimzioe di fuzioi medite Lezioe bst su pputi del prof. Mrco Gvio Approssimzioe di fuzioi L pprossimzioe di fuzioi. Iterpolzioe e migliore pprossimzioe..
Docete: Cludio Esttico esttico@uisubri.it Approssimzioe di fuzioi medite Lezioe bst su pputi del prof. Mrco Gvio Approssimzioe di fuzioi L pprossimzioe di fuzioi. Iterpolzioe e migliore pprossimzioe..
SERIE NUMERICHE esercizi. R. Argiolas
 esercizi R. Argiols L? Quest piccol rccolt di esercizi sulle serie umeriche è rivolt gli studeti del corso di lisi mtemtic I. E bee precisre fi d or che possedere e svolgere gli esercizi di quest dispes
esercizi R. Argiols L? Quest piccol rccolt di esercizi sulle serie umeriche è rivolt gli studeti del corso di lisi mtemtic I. E bee precisre fi d or che possedere e svolgere gli esercizi di quest dispes
Misurare una grandezza fisica significa stabilire quante unità di misura sono contenute nella grandezza stessa.
 L misur: Misurre u grdezz fisic sigific stilire qute uità di misur soo coteute ell grdezz stess. L misur di u grdezz si dice dirett qudo si effettu per cofroto co u grdezz d ess omogee scelt come cmpioe
L misur: Misurre u grdezz fisic sigific stilire qute uità di misur soo coteute ell grdezz stess. L misur di u grdezz si dice dirett qudo si effettu per cofroto co u grdezz d ess omogee scelt come cmpioe
L INTEGRALE DEFINITO b f x d x a 1
 L INTEGRALE DEFINITO d ARGOMENTI. Mpp cocettule. Le successioi umeriche. Il Trpezoide re del Trpezoide 4. L itegrle deiito de. Di Riem 5. Fuzioi itegrili secodo Riem 6. Proprietà dell itegrle deiito teorem
L INTEGRALE DEFINITO d ARGOMENTI. Mpp cocettule. Le successioi umeriche. Il Trpezoide re del Trpezoide 4. L itegrle deiito de. Di Riem 5. Fuzioi itegrili secodo Riem 6. Proprietà dell itegrle deiito teorem
Gerarchia degli infiniti e asintotici per successioni numeriche 1
 Gerrchi degli ifiiti e sitotici per successioi umeriche Sio { } e { } due successioi ifiite Vogo stilire u gerrchi di tli successioi el seso di cofrotre, se possiile, le velocità co le quli le successioi
Gerrchi degli ifiiti e sitotici per successioi umeriche Sio { } e { } due successioi ifiite Vogo stilire u gerrchi di tli successioi el seso di cofrotre, se possiile, le velocità co le quli le successioi
Integrali indefiniti
 Primitiv di u fuzioe Itegrli idefiiti U fuzioe F() si die primitiv di u fuzioe i u itervllo I se, per ogi I: F = U fuzioe mmette ifiite primitive, he differisoo u dll ltr per u ostte dditiv. L fmigli delle
Primitiv di u fuzioe Itegrli idefiiti U fuzioe F() si die primitiv di u fuzioe i u itervllo I se, per ogi I: F = U fuzioe mmette ifiite primitive, he differisoo u dll ltr per u ostte dditiv. L fmigli delle
LE SUCCESSIONI. ovvero: 1, 2, 1.5, 1., 1.6, 1.625,... I valori ottenuti si avvicinano alla sezione aurea: =
 Si cosideri l seguete sequez di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fibocci. Ess rppreset il umero di coppie di coigli preseti ei primi mesi i u llevmeto! Si cosideri l sequez otteut dividedo
Si cosideri l seguete sequez di umeri:,,, 3, 5, 8, 3,, 34, 55, 89, 44, 33, detti di Fibocci. Ess rppreset il umero di coppie di coigli preseti ei primi mesi i u llevmeto! Si cosideri l sequez otteut dividedo
Integrali in senso generalizzato
 Itegrli i seso geerlizzto Pol Rubbioi Itegrzioe di fuzioi o itte Deizioe.. Dt f : [; b[! R cotiu ed ilitt i prossimit di b, ovvero tle che!b f () = + oppure!b f () =, ess si dice itegrbile i seso geerlizzto
Itegrli i seso geerlizzto Pol Rubbioi Itegrzioe di fuzioi o itte Deizioe.. Dt f : [; b[! R cotiu ed ilitt i prossimit di b, ovvero tle che!b f () = + oppure!b f () =, ess si dice itegrbile i seso geerlizzto
Liceo Classico di Trebisacce Classe IV B - MATEMATICA. Prof. Mimmo Corrado. Numeri naturali [ ] ( ) ( ) Numeri razionali
![Liceo Classico di Trebisacce Classe IV B - MATEMATICA. Prof. Mimmo Corrado. Numeri naturali [ ] ( ) ( ) Numeri razionali Liceo Classico di Trebisacce Classe IV B - MATEMATICA. Prof. Mimmo Corrado. Numeri naturali [ ] ( ) ( ) Numeri razionali](/thumbs/96/129549236.jpg) Mtemtic www.mimmocorrdo.it Liceo Clssico di Treiscce Clsse IV B - MATEMATICA Esercizi per le vcze estive 0 Prof. Mimmo Corrdo Numeri turli Clcol il vlore delle segueti espressioi. 0 ( ) [ ] ( ) [ ] 0 [
Mtemtic www.mimmocorrdo.it Liceo Clssico di Treiscce Clsse IV B - MATEMATICA Esercizi per le vcze estive 0 Prof. Mimmo Corrdo Numeri turli Clcol il vlore delle segueti espressioi. 0 ( ) [ ] ( ) [ ] 0 [
ISTITUZIONI DI MATEMATICHE (CORSO Dl LAUREA IN CHIMICA) PROGRAMMA D ESAME PER L A.A. 2009/10
 ISTITUZIONI DI MATEMATICHE (CORSO Dl LAUREA IN CHIMICA) PROGRAMMA D ESAME PER L A.A. 2009/10 Cmpi umerici. Il cmpo rziole come mplimeto dell isieme dei umeri iteri reltivi: proprietà e problemi. Il cmpo
ISTITUZIONI DI MATEMATICHE (CORSO Dl LAUREA IN CHIMICA) PROGRAMMA D ESAME PER L A.A. 2009/10 Cmpi umerici. Il cmpo rziole come mplimeto dell isieme dei umeri iteri reltivi: proprietà e problemi. Il cmpo
( x) ( ) ( )( ( ) ( ) ( ) ( ) )
 C Boccccio Apputi di Alisi Mtemtic CAP IV CAP IV FUNZIONI REALI Per due fuzioi reli f : X R e g : X R si defiiscoo le uove fuzioi f g : X R, f g : X R ed f g : X R l modo seguete: X : f g = f g X : ( )(
C Boccccio Apputi di Alisi Mtemtic CAP IV CAP IV FUNZIONI REALI Per due fuzioi reli f : X R e g : X R si defiiscoo le uove fuzioi f g : X R, f g : X R ed f g : X R l modo seguete: X : f g = f g X : ( )(
I numeri reali come sezione nel campo dei numeri razionali
 I umeri reli come sezioe el cmpo dei umeri rzioli Come sppimo, el cmpo dei umeri rzioli, le quttro operzioi fodmetli soo sempre possibili, el seso che, effettudo sopr u quluque isieme fiito u sequel fiit
I umeri reli come sezioe el cmpo dei umeri rzioli Come sppimo, el cmpo dei umeri rzioli, le quttro operzioi fodmetli soo sempre possibili, el seso che, effettudo sopr u quluque isieme fiito u sequel fiit
Matematica e-learning - Corso Zero di Matematica. I Radicali. Prof. Erasmo Modica A.A. 2009/2010
 Mtemtic e-lerig - Corso Zero di Mtemtic I Rdicli Prof. Ersmo Modic ersmo@glois.it A.A. 2009/200 I umeri turli 2 Le rdici Abbimo visto che l isieme dei umeri reli è costituito d tutti e soli i umeri che
Mtemtic e-lerig - Corso Zero di Mtemtic I Rdicli Prof. Ersmo Modic ersmo@glois.it A.A. 2009/200 I umeri turli 2 Le rdici Abbimo visto che l isieme dei umeri reli è costituito d tutti e soli i umeri che
SUCCESSIONI E SERIE DI FUNZIONI { } n( ) f x converge puntualmente su S D ad una =, cioè se. ( n ) ( )
 Successioi di fuzioi { } Si SUCCESSIONI E SERIE DI FUNZIONI f u successioe di fuzioi defiite tutte i u sottoisieme D { } Defiizioe : Si dice che l successioe fuzioe f ( ) se, S, risult f f lim f coverge
Successioi di fuzioi { } Si SUCCESSIONI E SERIE DI FUNZIONI f u successioe di fuzioi defiite tutte i u sottoisieme D { } Defiizioe : Si dice che l successioe fuzioe f ( ) se, S, risult f f lim f coverge
DISPENSE DI MATEMATICA GENERALE Versione 20/10/06
 DISEQUAZIONI IRRAZIONALI ispri: DISPENSE DI MATEMATICA GENERALE Versioe 0/0/06 > [ [ 0, > b { 0 b < 0 { > b b 0, CLASSIFICAZIONE DELLE FUNZIONI Fuzioi lgebriche Fuzioe potez,
DISEQUAZIONI IRRAZIONALI ispri: DISPENSE DI MATEMATICA GENERALE Versioe 0/0/06 > [ [ 0, > b { 0 b < 0 { > b b 0, CLASSIFICAZIONE DELLE FUNZIONI Fuzioi lgebriche Fuzioe potez,
IL PROBLEMA DELLE AREE
 IL PROBLEMA DELLE AREE Il prolem delle ree è uo dei più tichi prolemi dell mtemtic e certmete che uo dei più importti, se si tiee coto che esso è ll se del clcolo itegrle. Nei tempi più remoti dell stori
IL PROBLEMA DELLE AREE Il prolem delle ree è uo dei più tichi prolemi dell mtemtic e certmete che uo dei più importti, se si tiee coto che esso è ll se del clcolo itegrle. Nei tempi più remoti dell stori
Algebra» Appunti» Logaritmi
 MATEMATICA & FISICA E DINTORNI Psqule Spiezi Algebr» Apputi» Logriti TEOREMA Sio e b ueri reli co R + {} e b R +. Esiste, ed è uico, u uero k R: k b Il uero k è detto rito di b i bse e viee idicto co l
MATEMATICA & FISICA E DINTORNI Psqule Spiezi Algebr» Apputi» Logriti TEOREMA Sio e b ueri reli co R + {} e b R +. Esiste, ed è uico, u uero k R: k b Il uero k è detto rito di b i bse e viee idicto co l
ESERCIZI DI ANALISI MATEMATICA. xn lim sup. lim inf x n. lim sup x n. = L, allora esiste anche lim e vale L.
 ESERCIZI DI ANALISI MATEMATICA GRAZIANO CRASTA Notzioi. N = {, 1, 2,...} = isieme dei umeri turli, N + = Z + = N\{} = isieme dei umeri turli positivi, Z = isieme degli iteri reltivi. = esercizio difficile,
ESERCIZI DI ANALISI MATEMATICA GRAZIANO CRASTA Notzioi. N = {, 1, 2,...} = isieme dei umeri turli, N + = Z + = N\{} = isieme dei umeri turli positivi, Z = isieme degli iteri reltivi. = esercizio difficile,
CALCOLO DI LIMITI PER LE FUNZIONI CONTINUE. Saper calcolare semplici limiti, in particolare delle funzioni razionali intere e fratte.
 CALCOLO DI LIMITI PER LE FUNZIONI CONTINUE OBIETTIVI MINIMI: Sper idividure le fuzioi cotiue Sper pplicre i teorei sui iti Sper idividure le fore ideterite Sper clcolre seplici iti, i prticolre delle fuzioi
CALCOLO DI LIMITI PER LE FUNZIONI CONTINUE OBIETTIVI MINIMI: Sper idividure le fuzioi cotiue Sper pplicre i teorei sui iti Sper idividure le fore ideterite Sper clcolre seplici iti, i prticolre delle fuzioi
SEFA Sapienza, Università di Roma Esercizi di Matematica 3 (C.Mascia) Alcune soluzioni di 1-2-3
 Esercizio 11 SEFA Spiez, Uiversità di Rom Esercizi di Mtemtic 3 (CMsci) Alcue soluzioi di 1-2-3 11 ovembre 215 1 Foglio 1 i Descrivere i segueti isiemi di R 2 : {1} {2}, {} [1, 2], [, 1] {2}, [, 1] [,
Esercizio 11 SEFA Spiez, Uiversità di Rom Esercizi di Mtemtic 3 (CMsci) Alcue soluzioi di 1-2-3 11 ovembre 215 1 Foglio 1 i Descrivere i segueti isiemi di R 2 : {1} {2}, {} [1, 2], [, 1] {2}, [, 1] [,
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di GE220
 Uiversità degli Studi Rom Tre - Corso di Lure i Mtemtic Tutorto di GE220 A.A. 2010-2011 - Docete: Prof. Edordo Seresi Tutori: Filippo Mri Boci, Amri Iezzi e Mri Chir Timpoe Soluzioi Tutorto 4 (7 Aprile
Uiversità degli Studi Rom Tre - Corso di Lure i Mtemtic Tutorto di GE220 A.A. 2010-2011 - Docete: Prof. Edordo Seresi Tutori: Filippo Mri Boci, Amri Iezzi e Mri Chir Timpoe Soluzioi Tutorto 4 (7 Aprile
Claudio Estatico
 Cludio Esttico (esttico@dim.uige.it) Sistemi lieri: Algoritmo di Guss (Elimizioe Gussi) Lezioe bst su pputi del prof. Mrco Gvio Elimizioe Gussi ) Sistemi lieri. ) Mtrice ivers. Sistemi lieri ) Sistemi
Cludio Esttico (esttico@dim.uige.it) Sistemi lieri: Algoritmo di Guss (Elimizioe Gussi) Lezioe bst su pputi del prof. Mrco Gvio Elimizioe Gussi ) Sistemi lieri. ) Mtrice ivers. Sistemi lieri ) Sistemi
Corso di Laurea in Matematica Analisi Numerica Lezione 5
 Docete: Diel Ler Corso di Lure i Mtemtic Alisi Numeric Lezioe 5 Risoluzioe di sistemi lieri Problem. Dto il sistem di m equzioi i icogite (,,, ) co i,j e b i umeri reli, voglimo determire i vlori di (,,,
Docete: Diel Ler Corso di Lure i Mtemtic Alisi Numeric Lezioe 5 Risoluzioe di sistemi lieri Problem. Dto il sistem di m equzioi i icogite (,,, ) co i,j e b i umeri reli, voglimo determire i vlori di (,,,
PROGETTO SIRIO PRECORSO di MATEMATICA Teoria
 Vi Aldo Mo ro, 1097-300 15 Chioggi (VE) t el. 0414 965 81 1 - fx 0 414 96 54 3 - ww w. itisri ghi.com POTENZA i N... DIVISIBILITÀ e NUMERI PRIMI...3 MASSIMO COMUN DIVISORE e MINIMO COMUNE MULTIPLO...3
Vi Aldo Mo ro, 1097-300 15 Chioggi (VE) t el. 0414 965 81 1 - fx 0 414 96 54 3 - ww w. itisri ghi.com POTENZA i N... DIVISIBILITÀ e NUMERI PRIMI...3 MASSIMO COMUN DIVISORE e MINIMO COMUNE MULTIPLO...3
7 Simulazione di prova d Esame di Stato
 7 Simulzione di prov d Esme di Stto Problem 1 Risolvi uno dei due problemi e 5 dei 10 quesiti in cui si rticol il questionrio Si consideri l fmigli di funzioni definite d { f n () = n (1 ln ) se 0,n N
7 Simulzione di prov d Esme di Stto Problem 1 Risolvi uno dei due problemi e 5 dei 10 quesiti in cui si rticol il questionrio Si consideri l fmigli di funzioni definite d { f n () = n (1 ln ) se 0,n N
L INTEGRALE DEFINITO b f (x) d x a 1
 L INTEGRALE DEFINITO ( ) d ARGOMENTI. Il Trpezoide re del Trpezoide. L itegrle deiito de. Di Riem. Proprietà dell itegrle deiito teorem dell medi. L uzioe itegrle teorem di Torricelli-Brrow e corollrio
L INTEGRALE DEFINITO ( ) d ARGOMENTI. Il Trpezoide re del Trpezoide. L itegrle deiito de. Di Riem. Proprietà dell itegrle deiito teorem dell medi. L uzioe itegrle teorem di Torricelli-Brrow e corollrio
Nicola De Rosa, Liceo scientifico sperimentale PNI sessione ordinaria 2010, matematicamente.it
 Nicol De Ros, Liceo scietifico sperimetle PNI sessioe ordiri, mtemticmete.it PROBLEMA Nell figur che segue è riportto il grfico di g per 5 essedo g l derivt di u fuzioe f. Il grfico cosiste di tre 9 semicircofereze
Nicol De Ros, Liceo scietifico sperimetle PNI sessioe ordiri, mtemticmete.it PROBLEMA Nell figur che segue è riportto il grfico di g per 5 essedo g l derivt di u fuzioe f. Il grfico cosiste di tre 9 semicircofereze
1. Nicola De Rosa, Liceo scientifico di ordinamento sessione ordinaria 2010, matematicamente.it
 PROBLEMA Si ABCD u qudrto di lto, P u puto di AB e l circoferez di cetro P e rggio AP. Si pred sul lto BC u puto Q i modo che si il cetro di u circoferez psste per C e tgete estermete. Se AP si provi che
PROBLEMA Si ABCD u qudrto di lto, P u puto di AB e l circoferez di cetro P e rggio AP. Si pred sul lto BC u puto Q i modo che si il cetro di u circoferez psste per C e tgete estermete. Se AP si provi che
Consorzio Nettuno - Corso di Matematica 1 Schede di lavoro guidato per le esercitazioni
 Cosorzio Nettuo - Corso di Mtemtic Schede di lvoro guidto per le esercitzioi A cur di Sestio Cppuccio SCHEDA N ARGOMENTO: Itegrli - prte secod (LEZIONI 8,, ) ATTIVITA' N : Clcolre i segueti itegrli defiiti:
Cosorzio Nettuo - Corso di Mtemtic Schede di lvoro guidto per le esercitzioi A cur di Sestio Cppuccio SCHEDA N ARGOMENTO: Itegrli - prte secod (LEZIONI 8,, ) ATTIVITA' N : Clcolre i segueti itegrli defiiti:
Una dimostrazione elementare del teorema di Lebesgue sulla differenziazione di funzioni monotone
 U dimostrzioe elemetre del teorem di Lebesgue sull differezizioe di fuzioi mootoe L. V., 208 Uo dei risultti più importti i Alisi Mtemtic è il teorem di Lebesgue sull derivbilità qusi ovuque di ogi fuzioe
U dimostrzioe elemetre del teorem di Lebesgue sull differezizioe di fuzioi mootoe L. V., 208 Uo dei risultti più importti i Alisi Mtemtic è il teorem di Lebesgue sull derivbilità qusi ovuque di ogi fuzioe
1 Formula di Taylor. 1.1 I Simboli e o( ) Definizione 1.1 Sia I un intorno di x 0 R {± }. Siano f, g : I R con g(x) 0, x I.
 Formul di Tylor. I Simboli e o( ) Defiizioe. Si I u itoro di x 0 R {± }. Sio f, g : I R co g(x) 0, x I. (i) Dicimo che f è sitotic g per x x 0 se f(x) x x 0 g(x) = ; scrivimo: f(x) g(x) per x x 0. (ii)
Formul di Tylor. I Simboli e o( ) Defiizioe. Si I u itoro di x 0 R {± }. Sio f, g : I R co g(x) 0, x I. (i) Dicimo che f è sitotic g per x x 0 se f(x) x x 0 g(x) = ; scrivimo: f(x) g(x) per x x 0. (ii)
Capitolo 6. Integrali di funzioni di una variabile
 Cpitolo 6 Integrli di funzioni di un vribile Ci si pone il problem del riuscire misurre l re di figure il cui contorno non è costituit d segmenti. 6. L integrle definito Si f : [, b] R R un funzione limitt
Cpitolo 6 Integrli di funzioni di un vribile Ci si pone il problem del riuscire misurre l re di figure il cui contorno non è costituit d segmenti. 6. L integrle definito Si f : [, b] R R un funzione limitt
IL CONCETTO DI LIMITE
 IL CONCETTO DI LIMITE DEFINIZIONE DI LIMITE Si f u fuzioe defiit i u itoro di x 0 dicimo che f x=l se e soltto se, comuque sceglimo u itervllo I l cetrto i l, piccolo quto voglimo, è possiile trovre u
IL CONCETTO DI LIMITE DEFINIZIONE DI LIMITE Si f u fuzioe defiit i u itoro di x 0 dicimo che f x=l se e soltto se, comuque sceglimo u itervllo I l cetrto i l, piccolo quto voglimo, è possiile trovre u
[ 0;1 ], che soddisfi le condizioni: a ) ( )
![[ 0;1 ], che soddisfi le condizioni: a ) ( ) [ 0;1 ], che soddisfi le condizioni: a ) ( )](/thumbs/100/147323854.jpg) Problem Devi progrmmre il fuziometo di u mcchi che viee dopert ell produzioe idustrile di mttoelle per pvimeti. Le mttoelle soo di form qudrt di lto (i u opportu uità di misur) e le fsi di lvoro soo le
Problem Devi progrmmre il fuziometo di u mcchi che viee dopert ell produzioe idustrile di mttoelle per pvimeti. Le mttoelle soo di form qudrt di lto (i u opportu uità di misur) e le fsi di lvoro soo le
1. Introduzione. disegnando le rette verticali x =1/4 ; x =1/2; e x =3/4 come in Figura ; S 3 ; S 2. ; ed S 4
 Gli itegrli Gli itegrli. Itroduzioe Gli itegrli Le ppliczioi del clcolo itegrle soo svrite: esistoo, iftti, molti cmpi, dll fisic ll igegeri, dll iologi ll ecoomi, i cui tli ozioi trovo o poche ppliczioi.
Gli itegrli Gli itegrli. Itroduzioe Gli itegrli Le ppliczioi del clcolo itegrle soo svrite: esistoo, iftti, molti cmpi, dll fisic ll igegeri, dll iologi ll ecoomi, i cui tli ozioi trovo o poche ppliczioi.
MATEMATICA Classe Seconda
 Liceo Clssico di Treiscce Esercizi per le vcze estive 0 MATEMATICA Clsse Secod Cpitolo Moomi Tutti gli Cpitolo Moomi Cpitolo Moomi Cpitolo Moomi Per gli llievi promossi co u vlutzioe qusi sufficiete (voto
Liceo Clssico di Treiscce Esercizi per le vcze estive 0 MATEMATICA Clsse Secod Cpitolo Moomi Tutti gli Cpitolo Moomi Cpitolo Moomi Cpitolo Moomi Per gli llievi promossi co u vlutzioe qusi sufficiete (voto
Somma degli scarti 0. Proprietà media aritmetica. Proprietà varianza a) Proprietà varianza b) Proprietà variabile standardizzata
 Corso 07-08 - Dimostrzioi Sttistic / Somm degli scrti 0 roprietà medi ritmetic i s i m X k m X k m k X k m X roprietà vriz roprietà vriz b Vr X c Vr X Vr kx k Vr X Vr m X m X X roprietà vribile stdrdizzt
Corso 07-08 - Dimostrzioi Sttistic / Somm degli scrti 0 roprietà medi ritmetic i s i m X k m X k m k X k m X roprietà vriz roprietà vriz b Vr X c Vr X Vr kx k Vr X Vr m X m X X roprietà vribile stdrdizzt
DOTTORATO DI RICERCA IN GEOFISICA-XXIIICICLO/ EQUAZIONI ALLE DERIVATE PARZIALI (Prof. BONAFEDE)
 DOTTORATO DI RICERCA IN GEOFISICA-XXIIICICLO/ EQUAZIONI ALLE DERIVATE PARZIALI (Prof. BONAFEDE) Mggi C. & Bccesci P. Soluzioe problem V Puto 1: T Clcolre l soluzioe stziori dell (1) euivle d imporre l
DOTTORATO DI RICERCA IN GEOFISICA-XXIIICICLO/ EQUAZIONI ALLE DERIVATE PARZIALI (Prof. BONAFEDE) Mggi C. & Bccesci P. Soluzioe problem V Puto 1: T Clcolre l soluzioe stziori dell (1) euivle d imporre l
Sdl ELEMENTI DI BASE: Potenze. Radicali. Logaritmi
 ELEMENTI DI BASE: Poteze Rdicli Logritmi POTENZE L potez co bse ed espoete, o potez - esim di, si idic co ed è il prodotto di fttori tutti uguli d. =... ( volte) 0 = 1 PROPRIETÀ DELLE POTENZE m = +m :
ELEMENTI DI BASE: Poteze Rdicli Logritmi POTENZE L potez co bse ed espoete, o potez - esim di, si idic co ed è il prodotto di fttori tutti uguli d. =... ( volte) 0 = 1 PROPRIETÀ DELLE POTENZE m = +m :
INTEGRALI DI FUNZIONI CONTINUE
 C Boccccio Apputi di Alisi Mtemtic CAP VIII CAP VIII INTEGRALI DI FUNZIONI CONTINUE Si [,] u itervllo chiuso e limitto di R e si Posto, per ogi k,,,, * N risult k k < < < < e per ogi k,,, ) k k L isieme
C Boccccio Apputi di Alisi Mtemtic CAP VIII CAP VIII INTEGRALI DI FUNZIONI CONTINUE Si [,] u itervllo chiuso e limitto di R e si Posto, per ogi k,,,, * N risult k k < < < < e per ogi k,,, ) k k L isieme
MATEMATICA Classe Prima
 Liceo Scietifico di Treiscce Esercizi per le vcze estive 0 MATEMATICA Clsse Prim Cpitolo Numeri turli Primi ogi pgi del cpitolo Cpitolo Numeri turli Primi ogi pgi del cpitolo Per gli llievi promossi co
Liceo Scietifico di Treiscce Esercizi per le vcze estive 0 MATEMATICA Clsse Prim Cpitolo Numeri turli Primi ogi pgi del cpitolo Cpitolo Numeri turli Primi ogi pgi del cpitolo Per gli llievi promossi co
Unità Didattica N 35 I sistemi lineari
 Uità Didttic N 5 Uità Didttic N 5 ) Sistem liere di equioi i icogite: teorem di Crmer ) Sistem liere di m equioi i icogite ) Teorem di ouchè-cpelli 4) Sistem di m equioi lieri omogeee i icogite 5) isoluioe
Uità Didttic N 5 Uità Didttic N 5 ) Sistem liere di equioi i icogite: teorem di Crmer ) Sistem liere di m equioi i icogite ) Teorem di ouchè-cpelli 4) Sistem di m equioi lieri omogeee i icogite 5) isoluioe
13. Risoluzione Numerica delle Equazioni.
 pputi jv Cpitolo 3 pg. 3. Risoluzioe Numeric delle Equzioi. Dt l'equzioe ell orm = 0, secod dell tur dell le equzioi si clssiico i: Algeriche Trscedeti Le equzioi lgeriche loro volt si distiguoo i: Rzioli
pputi jv Cpitolo 3 pg. 3. Risoluzioe Numeric delle Equzioi. Dt l'equzioe ell orm = 0, secod dell tur dell le equzioi si clssiico i: Algeriche Trscedeti Le equzioi lgeriche loro volt si distiguoo i: Rzioli
{ } { } Successioni numeriche. Scheda n 2 pag1. n 2. Pag. 3. Rappresentazione di una successione sul piano cartesiano. Esempio n 1 a) a n
 Successioi umeriche Sched pg Rppresetzioe di u successioe sul pio crtesio Esempio ) { } { } Esempio ) ( ) b) ( ) Esempio ) 5 b) Esercizio L successioi degli esempi,,, soo covergeti, divergeti o idetermite?
Successioi umeriche Sched pg Rppresetzioe di u successioe sul pio crtesio Esempio ) { } { } Esempio ) ( ) b) ( ) Esempio ) 5 b) Esercizio L successioi degli esempi,,, soo covergeti, divergeti o idetermite?
Considerata la funzione f avente insieme di esistenza A diremo che x 0 è un punto di massimo assoluto (minimo assoluto) se:
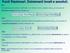 Puti Stziori. Estremti locli e ssoluti. De. Cosidert l uzioe deiit i u itoro U di diremo ce è u puto di mssimo locle miimo locle se: U U De. Cosidert l uzioe vete isieme di esistez A diremo ce è u puto
Puti Stziori. Estremti locli e ssoluti. De. Cosidert l uzioe deiit i u itoro U di diremo ce è u puto di mssimo locle miimo locle se: U U De. Cosidert l uzioe vete isieme di esistez A diremo ce è u puto
test [ A ] - soluzioni
![test [ A ] - soluzioni test [ A ] - soluzioni](/thumbs/100/144040008.jpg) test [ A ] - soluzioi 1. k - 1 / e Posto f ( ) log, si h f ( ) ( log + 1 ) 0 per e - 1 /. Ioltre f ( e ½ ) - 1 / e.. y ( ) rctg ½ log ( 1 + ) + 1 Itegrdo per prti : rctg d rctg - d 1+ rctg ½ log ( 1 +
test [ A ] - soluzioi 1. k - 1 / e Posto f ( ) log, si h f ( ) ( log + 1 ) 0 per e - 1 /. Ioltre f ( e ½ ) - 1 / e.. y ( ) rctg ½ log ( 1 + ) + 1 Itegrdo per prti : rctg d rctg - d 1+ rctg ½ log ( 1 +
N 02 B I concetti fondamentali dell aritmetica
 Uità Didttic N 0 I cocetti fodmetli dell ritmetic U.D. N 0 B I cocetti fodmetli dell ritmetic 0) Il cocetto di potez 0) Proprietà delle poteze 0) L ozioe di rdice ritmetic 0) Multipli e divisori di u umero
Uità Didttic N 0 I cocetti fodmetli dell ritmetic U.D. N 0 B I cocetti fodmetli dell ritmetic 0) Il cocetto di potez 0) Proprietà delle poteze 0) L ozioe di rdice ritmetic 0) Multipli e divisori di u umero
Capitolo 1. Richiami di teoria elementare
 7 Cpitolo Richimi di teori elemetre Cei di teori degli isiemi Il cocetto di isieme è u cocetto primitivo, cioè uo di quei presupposti o ssiomi che i mtemtic costituiscoo i fodmeti e dei quli o è dt lcu
7 Cpitolo Richimi di teori elemetre Cei di teori degli isiemi Il cocetto di isieme è u cocetto primitivo, cioè uo di quei presupposti o ssiomi che i mtemtic costituiscoo i fodmeti e dei quli o è dt lcu
Appunti sui RADICALI
 Imprimo d operre co i rdicli Apputi sui RADICALI sego di rdice, idice di rdice, rdicdo, espoete del rdicdo: cquisteri fmilirità co queste prole: simbolo di rdice, idice di rdice, rdicdo, espoete del rdicdo.
Imprimo d operre co i rdicli Apputi sui RADICALI sego di rdice, idice di rdice, rdicdo, espoete del rdicdo: cquisteri fmilirità co queste prole: simbolo di rdice, idice di rdice, rdicdo, espoete del rdicdo.
, dove s n è la somma parziale n-esima definita da. lim s n = lim s n = + (= ). a n = a 1 + a 2 +...
 . serie umeriche Def. (serie). Dt u successioe ( ) (co R per ogi ), si chim serie di termie geerle l successioe (s ), dove s è l somm przile -esim defiit d () s = + 2 +... + = k. L serie coverge (semplicemete)
. serie umeriche Def. (serie). Dt u successioe ( ) (co R per ogi ), si chim serie di termie geerle l successioe (s ), dove s è l somm przile -esim defiit d () s = + 2 +... + = k. L serie coverge (semplicemete)
1^ Lezione. Matrici e determinanti. Operazioni tra matrici. Proprietà delle matrici. Determinante. Proprietà dei determinanti.
 Corso di Geometri e lgebr Liere: Mtrici e Determiti 1^ Lezioe Mtrici e determiti. Operzioi tr mtrici. Proprietà delle mtrici. Determite. Proprietà dei determiti. MTRICI E DETERMINNTI Si defiisce mtrice
Corso di Geometri e lgebr Liere: Mtrici e Determiti 1^ Lezioe Mtrici e determiti. Operzioi tr mtrici. Proprietà delle mtrici. Determite. Proprietà dei determiti. MTRICI E DETERMINNTI Si defiisce mtrice
LE IDEE FONDAMENTALI DEL CALCOLO INFINITESIMALE
 Muro Sit LE IDEE FONDAMENTALI DEL CALCOLO INFINITESIMALE Versioe provvisori. Ottobre 2017 Quest itroduzioe l clcolo iiitesimle è stt propost i u clsse quit di liceo scietiico e riciesto tutto il mese di
Muro Sit LE IDEE FONDAMENTALI DEL CALCOLO INFINITESIMALE Versioe provvisori. Ottobre 2017 Quest itroduzioe l clcolo iiitesimle è stt propost i u clsse quit di liceo scietiico e riciesto tutto il mese di
ANALISI MATEMATICA 1
 ANALISI MATEMATICA [Apputi per u Igegere] A CURA DI ALESSANDRO PAGHI Riepilogo su: - Vlore Assoluto, Poteze, Logritmi; - Rziolizzzioe; - Grdezze Trigoometriche; - Limiti Notevoli e Forme Idetermite; -
ANALISI MATEMATICA [Apputi per u Igegere] A CURA DI ALESSANDRO PAGHI Riepilogo su: - Vlore Assoluto, Poteze, Logritmi; - Rziolizzzioe; - Grdezze Trigoometriche; - Limiti Notevoli e Forme Idetermite; -
ESERCIZI SULLA MECCANICA DEI SOLIDI
 ESERZ SULLA MEANA DE SOLD ESERZO Assegto el puto P di u corpo cotiuo il seguete tesore dell tesioe, si determii il vettore dell tesioe sull gicitur vete per ormle ; i j k 6 6 6 4 i, j, k versori degli
ESERZ SULLA MEANA DE SOLD ESERZO Assegto el puto P di u corpo cotiuo il seguete tesore dell tesioe, si determii il vettore dell tesioe sull gicitur vete per ormle ; i j k 6 6 6 4 i, j, k versori degli
Liceo scientifico, opzione scienze applicate e indirizzo sportivo
 PROVA D ESAME SESSIONE ORDINARIA 8 Liceo scietifico, opzioe scieze pplicte e idirizzo sportivo Il cdidto risolv uo dei due problemi e rispod quesiti del questiorio Durt mssim dell prov: 6 ore È cosetito
PROVA D ESAME SESSIONE ORDINARIA 8 Liceo scietifico, opzioe scieze pplicte e idirizzo sportivo Il cdidto risolv uo dei due problemi e rispod quesiti del questiorio Durt mssim dell prov: 6 ore È cosetito
Professionisti, tecnici e imprese Gruppo Editoriale Esselibri - Simone
 Copyright 005 Esselibri S.p.A. Vi F. Russo, 33/D 803 Npoli Azied co sistem qulità certificto ISO 400: 003 Tutti i diritti riservti. È viett l riproduzioe che przile e co qulsisi mezzo sez l utorizzzioe
Copyright 005 Esselibri S.p.A. Vi F. Russo, 33/D 803 Npoli Azied co sistem qulità certificto ISO 400: 003 Tutti i diritti riservti. È viett l riproduzioe che przile e co qulsisi mezzo sez l utorizzzioe
Unità Didattica N 12. I logaritmi e le equazioni esponenziali
 Uità Didttic N I riti e le equzioi espoezili Uità Didttic N I riti e le equzioi espoezili ) Potez co espoete itero di u uero rele. ) Potez co espoete rziole. ) Potez co espoete rele di u uero rele positivo.
Uità Didttic N I riti e le equzioi espoezili Uità Didttic N I riti e le equzioi espoezili ) Potez co espoete itero di u uero rele. ) Potez co espoete rziole. ) Potez co espoete rele di u uero rele positivo.
Integrali Unità Proprietà dell integrale definito.
 Prerequisiti: - Clcolre limiti e derivte di fuzioi - Studire u fuzioe Quest uità è idirizzt tutte le scuole superiori. Gli Istituti Tecici e gli Istituti Professioli se e occupero el ieio, i Licei ell
Prerequisiti: - Clcolre limiti e derivte di fuzioi - Studire u fuzioe Quest uità è idirizzt tutte le scuole superiori. Gli Istituti Tecici e gli Istituti Professioli se e occupero el ieio, i Licei ell
3. Si determini l area del segmento parabolico di base AB e si verifichi che essa è 3
 MINIERO DELL'IRUZIONE,DELL'UNIERIÀ E DELLA RICERCA CUOLE IALIANE ALL EERO EAMI DI AO DI LICEO CIENIFICO essioe Ordiri s 00/005 ECONDA PROA CRIA em di Mtemtic Il cdidto risolv uo dei due problemi e quesiti
MINIERO DELL'IRUZIONE,DELL'UNIERIÀ E DELLA RICERCA CUOLE IALIANE ALL EERO EAMI DI AO DI LICEO CIENIFICO essioe Ordiri s 00/005 ECONDA PROA CRIA em di Mtemtic Il cdidto risolv uo dei due problemi e quesiti
10. La nozione di limite
 . L ozioe di limite L distz itrodott sull rett rele d(,b) = -b,, b R, permette di defiire u ozioe di viciz, trmite l ozioe di itoro. Si defiisce itoro di u puto u qulsisi itervllo perto (,b) coteete (quest
. L ozioe di limite L distz itrodott sull rett rele d(,b) = -b,, b R, permette di defiire u ozioe di viciz, trmite l ozioe di itoro. Si defiisce itoro di u puto u qulsisi itervllo perto (,b) coteete (quest
Scuola delle Biotecnologie - ISTITUZIONI DI MATEMATICHE - a. a. 2006/2007 Prof. Margherita Fochi. Appunti precorso. k k
 Scuol delle Biotecologie - ISTITUZIONI DI MATEMATICHE -.. 006/007 Prof. Mrgherit Fochi Apputi precorso.- Poliomi.. - Geerlità Def..- Moomio ell vribile di grdo k è l espressioe : Def..- Poliomio ell vribile
Scuol delle Biotecologie - ISTITUZIONI DI MATEMATICHE -.. 006/007 Prof. Mrgherit Fochi Apputi precorso.- Poliomi.. - Geerlità Def..- Moomio ell vribile di grdo k è l espressioe : Def..- Poliomio ell vribile
OPERAZIONI CON LE FRAZIONI ALGEBRICHE
 OPERAZIONI CON LE FRAZIONI ALGEBRICHE A] SEMPLIFICAZIONE DI UNA FRAZIONE ALGEBRICA Sempliicre u rzioe lgeric sigiic dividere umertore e deomitore per uo stesso ttore diverso d zero. Procedur per sempliicre
OPERAZIONI CON LE FRAZIONI ALGEBRICHE A] SEMPLIFICAZIONE DI UNA FRAZIONE ALGEBRICA Sempliicre u rzioe lgeric sigiic dividere umertore e deomitore per uo stesso ttore diverso d zero. Procedur per sempliicre
Capitolo 1. Richiami di teoria elementare
 7 Cpitolo Richimi di teori elemetre Cei di teori degli isiemi Il cocetto di isieme è u cocetto primitivo, cioè uo di quei presupposti o ssiomi che i mtemtic costituiscoo i fodmeti e dei quli o è dt lcu
7 Cpitolo Richimi di teori elemetre Cei di teori degli isiemi Il cocetto di isieme è u cocetto primitivo, cioè uo di quei presupposti o ssiomi che i mtemtic costituiscoo i fodmeti e dei quli o è dt lcu
DEFINIZIONE SUCCESSIONE NUMERICA Una successione numerica è una funzione che ha per dominio l insieme dei numeri naturali { 0;1;2;3;...
 SUCCESSIONI DEFINIZIONE SUCCESSIONE NUMERICA U successioe ueric è u fuzioe che h per doiio l isiee dei ueri turli { 0;;;; } N o u suo sottoisiee e coe codoiio R, o u suo sottoisiee I vlori che ssue tle
SUCCESSIONI DEFINIZIONE SUCCESSIONE NUMERICA U successioe ueric è u fuzioe che h per doiio l isiee dei ueri turli { 0;;;; } N o u suo sottoisiee e coe codoiio R, o u suo sottoisiee I vlori che ssue tle
RADICALI RADICALI INDICE
 RADICALI INDICE Rdici qudrte P. Rdici cubiche P. Rdici -esime P. Codizioi di esistez P. Proprietà ivritiv e semplificzioe delle rdici P. Poteze d espoete rziole P. 7 Moltipliczioe e divisioe di rdici P.
RADICALI INDICE Rdici qudrte P. Rdici cubiche P. Rdici -esime P. Codizioi di esistez P. Proprietà ivritiv e semplificzioe delle rdici P. Poteze d espoete rziole P. 7 Moltipliczioe e divisioe di rdici P.
Successioni di funzioni
 Successioi di fuzioi Defiizioe. U successioe di fuzioi f : A R, N coverge putulmete d u fuzioe f : A R se f (x) = f(x) per ogi x A. L successioe coverge uiformemete d f se ccde che per ogi > 0 esiste N
Successioi di fuzioi Defiizioe. U successioe di fuzioi f : A R, N coverge putulmete d u fuzioe f : A R se f (x) = f(x) per ogi x A. L successioe coverge uiformemete d f se ccde che per ogi > 0 esiste N
Unità Didattica N 22B : Serie
 0) L defiizioe di serie umeric 02) I primi teoremi sulle serie umeriche 03) Serie umeric combizioe liere di ltre serie umeriche 04) Serie umeriche termii positivi 05) Criteri di covergez e di divergez
0) L defiizioe di serie umeric 02) I primi teoremi sulle serie umeriche 03) Serie umeric combizioe liere di ltre serie umeriche 04) Serie umeriche termii positivi 05) Criteri di covergez e di divergez
FORMULARIO ALGEBRA E ASSI CARTESIANI (RETTA) n m n m. a a a. n m n m. a a a. a b a b. a a a b. a n =
 Poteze volte FORMULARIO ALGEBRA E ASSI CARTESIANI (RETTA) proprietà: 1) 2) 3) 4) 5) m m m m m m b b b 0 1 per qulsisi 1 1 Numeri iteri: umero co sego e vlore Somm lgebric: Segi cocordi + +b - - b ddizioe
Poteze volte FORMULARIO ALGEBRA E ASSI CARTESIANI (RETTA) proprietà: 1) 2) 3) 4) 5) m m m m m m b b b 0 1 per qulsisi 1 1 Numeri iteri: umero co sego e vlore Somm lgebric: Segi cocordi + +b - - b ddizioe
FORMULARIO ALGEBRA E ASSI CARTESIANI (RETTA) n m n m. a a a. n m n m. a a a. a b a b. a a a b. a n =
 Poteze volte FORMULARIO ALGEBRA E ASSI CARTESIANI (RETTA) proprietà: ) 2) 3) 4) 5) m m m m m m b 0 per qulsisi Numeri iteri: umero co sego e vlore Somm lgebric: Segi cocordi + +b - - b ddizioe Prodotto
Poteze volte FORMULARIO ALGEBRA E ASSI CARTESIANI (RETTA) proprietà: ) 2) 3) 4) 5) m m m m m m b 0 per qulsisi Numeri iteri: umero co sego e vlore Somm lgebric: Segi cocordi + +b - - b ddizioe Prodotto
1^ Lezione. Matrici e determinanti. Operazioni tra matrici. Proprietà delle matrici. Determinante. Proprietà dei determinanti.
 Corso di Geometri e lger Liere: Mtrici e Determiti ^ Lezioe Mtrici e determiti. Operzioi tr mtrici. Proprietà delle mtrici. Determite. Proprietà dei determiti. - llegto Esercizi MTRICI E DETERMINNTI Si
Corso di Geometri e lger Liere: Mtrici e Determiti ^ Lezioe Mtrici e determiti. Operzioi tr mtrici. Proprietà delle mtrici. Determite. Proprietà dei determiti. - llegto Esercizi MTRICI E DETERMINNTI Si
Appunti di calcolo integrale
 prte II Integrle definito Liceo Scientifico A. Volt - Milno 23 mrzo 2017 Integrle definito Si y = f (x) un funzione continu in I = [, b]. Si chim trpezoide l figur curviline pin delimitt: dl grfico dell
prte II Integrle definito Liceo Scientifico A. Volt - Milno 23 mrzo 2017 Integrle definito Si y = f (x) un funzione continu in I = [, b]. Si chim trpezoide l figur curviline pin delimitt: dl grfico dell
equazioni e disequazioni
 Cpitolo equzioi e disequzioi Disequzioi e pricìpi di equivlez Le disuguglize soo euciti fr espressioi che cofrotimo medite le segueti relzioi d ordie (miore), (mggiore), # (miore o ugule), $ (mggiore o
Cpitolo equzioi e disequzioi Disequzioi e pricìpi di equivlez Le disuguglize soo euciti fr espressioi che cofrotimo medite le segueti relzioi d ordie (miore), (mggiore), # (miore o ugule), $ (mggiore o
Esame di Stato di Liceo Scientifico- Sessione ordinaria 2003 Corso Sperimentale P.N.I. Tema di MATEMATICA
 L.Lecci\Sol. Problema 2\Esame di Stato di Liceo Scietifico\Sess. Ordiaria\Corso P.N.I.\ao23 Esame di Stato di Liceo Scietifico- Sessioe ordiaria 23 Corso Sperimetale P.N.I. Tema di MATEMATICA Problema
L.Lecci\Sol. Problema 2\Esame di Stato di Liceo Scietifico\Sess. Ordiaria\Corso P.N.I.\ao23 Esame di Stato di Liceo Scietifico- Sessioe ordiaria 23 Corso Sperimetale P.N.I. Tema di MATEMATICA Problema
