Le conseguenze delle trasformazioni di Lorentz: la velocità limite e l addizione non galileiana delle velocità
|
|
|
- Angelo Paoletti
- 7 anni fa
- Visualizzazioni
Transcript
1 Le onseguenze delle trasformazioni di Lorentz: la eloità limite e l addizione non galileiana delle eloità L esistenza di una eloità massima possibile alida per ogni ente fisio (orpi materiali, onde, et. et. è sritta nelle trasformazioni di Lorentz. Si noti, infatti, he ompaiono denominatori on radii quadrate ( t t1 ( 1 ( 1 ( t t1 1 ; ( 1 ( 1 ; ( z z1 ( z z1 ; ( t t1 1 / 1 / le quali rihiedono (a meno he non si ogliano onsiderare quantità omplesse he il radiando sia positio 1- / 0 da ui Le trasformazioni di Lorentz rihiedono he, in ogni riferimento inerziale, la eloità di un qualunque ente fisio sia sempre minore o uguale a quella della lue, la quale, assume il ruolo di eloità limite. L esistenza di una eloità massima possibile ha ome onseguenza il fatto he le regole di omposizione delle eloità deono essere radialmente dierse da quelle galileiane altrimenti si arebbero palesi iolazioni del seondo postulato. Immaginiamo, ad esempio, he l osseratore O inii un raggio luminoso lungo le positie he, in irtù del seondo postulato, si propagherà on eloità rispetto a lui. Se fosse alida la legge galileiana di omposizione, la eloità del raggio luminoso osserata da O dorebbe essere + iolando ineitabilmente il seondo postulato. Quale è dunque la nuoa legge di omposizione delle eloità in aordo on l esistenza di una eloità limite? O O Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
2 Consideriamo ad esempio le trasformazioni degli interalli da O ad O. Eidentemente si ottengono le eloità sempliemente mettendo a rapporto gli interalli spaziali e temporali ( 1 + ( t t1 ( 1 ( 1 + ( t t1 1 / ( 1 + ( 1 + ( t t1 ( 1 ( 1 1 / 1+ t t ( t t1 1 / ( t t1 + ( 1 1+ ( 1 ( 1 ( 1 1 / ( 1 ( 1 1 / ( t t1 1 / ( z z1 ( z z1 ( t t1 ( t ( 1 t1 ( ( t t1 + ( 1 ( t t1 ( t t1 ( z z1 ( z z1 1 / 1 / 1 / ( z z1 z 1 / ( t t1 z ( t t1 + ( 1 ( t t1 1 z + ( 1 1+ ( t t1 da ui otteniamo le nuoe leggi della somma delle eloità he sostituisono quelle di Galileo alide nella fisia lassia, le leggi relatiistihe di omposizione delle eloità 1 / 1 / + z z La struttura delle nuoe leggi di omposizione è piuttosto omplessa, tuttaia, ome atteso, le leggi relatiistihe onduono a quelle galileiane nel aso di eloità piole rispetto a quella della lue. Infatti se << si ottiene failmente + z z Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
3 + 1 / 1 / z z Notiamo he dato un orpo materiale in moto on una erta eloità,, z rispetto ad O appare in moto anhe ad O, oiamente. Tuttaia le eloità trasersali al moto he egli ossera, non dipendono solamente dalle eloità trasersali he il orpo aea rispetto ad O, dipendono anhe da quella longitudinale lungo la direzione del moto. In un erto senso le omponenti della eloità si mesolano ontrariamente a quanto aiene on la omposizione galileiana delle eloità. Anora più sorprendente è la regola di addizione delle eloità lungo la direzione del moto. Ragionando on l esempio esaminato all inizio si ottiene O O Oero dato un riferimento O he si muoe on eloità rispetto ad O (lungo le positie, se un raggio luminoso si muoe on eloità rispetto ad O (lungo le positie, allora tale raggio si muoe on eloità anhe rispetto ad O. Dunque, seondo le leggi relatiistihe di omposizione delle eloità +, in aordo on l esistenza di una eloità limite (e on il seondo postulato ma in ompleto onflitto on le leggi galileiane. Per ompletezza analizziamo anhe il aso in ui il raggio luminoso ertialmente in O : 0, 1 / / ( (1 / he onferma le onlusioni già ommentate. O O Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
4 Le onseguenze delle trasformazioni di Lorentz: il prinipio di ausalità Esaminiamo, anora una olta, la trasformazione di Lorentz per l interallo temporale he risriiamo in una forma adatta per le onsiderazioni he faremo ( 1 ( t t1 + ( ( 1 ( 1 t t t t ( t t1 1 / 1 / ed immaginiamo he, nel riferimento O (per sempliità lungo l asse delle, abbiano luogo due eenti: il primo nel punto 1 al tempo t 1 ed il seondo nel punto al tempo t (on t quindi suessio a t 1. Osseriamo he se il numeratore dell ultima espressione è positio allora se t -t 1 >0 anhe t -t 1 >0 oero l ordine temporale degli eenti è lo stesso per tutti e due gli osseratori. Se inee il numeratore è negatio se t -t 1 <0 si ha t -t 1 <0 oero l osseratore O ede un ordine degli eenti inertito rispetto a quello osserato da O. Riassumendo abbiamo d altra parte abbiamo he ( 1 se 1+ > 0 allora ( t t1 > 0 ( t t1 > 0 ( t t1 ( 1 se 1+ < 0 allora ( t t1 > 0 ( t t1 < 0 ( t t1 ( ( ( ( 1+ > 0 > < dunque < ( t t ( t t ( t t ( t t ma 1 per ui possiamo risriere le nostre ondizioni nel modo seguente Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari e
5 ( 1 se < allora ( t t1 > 0 ( t t1 > 0 (1 ( t t1 ( 1 se > allora ( t t1 > 0 ( t t1 < 0 ( ( t t1 Quale è il signifiato di queste relazioni? Per apirlo, immaginiamo he nel riferimento O l eento A orrisponda allo sparo di un proiettile da un erto punto 1 ad un erto tempo t 1, mentre l eento B orrisponda all arrio del proiettile sul bersaglio nel punto al tempo t he, in seguito all impatto, a in frantumi. In questo aso l eento A ausa l eento B e, nel riferimento O, lo preede temporalmente. Ora se questo non fosse ero anhe in tutti gli altri riferimenti in aluni asi potrebbe aadere di osserare l eento B prima dell eento A e dunque una situazione assurda nella quale la frantumazione del bersaglio preede l arrio del proiettile! Il fatto he i due eenti possano essere onnessi da un proiettile i assiura, però, he dee essere erifiata la (1 poihé nessuna azione fisia può superare la eloità della lue. In questo aso le trasformazioni di Lorentz garantisono he ogni altro osseratore edrà gli eenti nello stesso ordine temporale songiurando la situazione assurda di ui sopra. L inersione degli eenti può aenire solo on la ondizione espressa dalla (. Oorre però sottolineare he in questo aso la distanza spaziale e temporale degli eenti è tale da non potere essere in nessun modo onnessi da una qualhe azione fisia per ui l inersione del prima on il dopo, in questo aso possibile, non può omunque produrre situazioni assurde. L esempio dorebbe allora hiarire il signifiato delle (1 e (: il quoziente R( - 1 /(t -t 1 è il rapporto tra la distanza spaziale e temporale tra i due eenti misurata da O. Riordando he seondo la TRR esiste una eloità limite per tutti gli enti fisii, R < signifia he i due eenti potrebbero essere onnessi da una qualhe azione fisia, mentre R > signifia he i due eenti non potrebbero in nessun modo essere onnessi da una qualhe azione fisia. Nel primo aso si die he gli eenti potrebbero essere in una relazione di ausa-effetto o sempliemente in una relazione ausale, mentre nel seondo aso si die he gli eenti non potrebbero essere in una relazione di ausa-effetto o in una relazione ausale. Le disequazioni di ui sopra allora affermano he se due eenti fisii possono essere in relazione ausale, l ordine temporale degli eenti è lo stesso per tutti gli osseratori inerziali, mentre, se due eenti fisii non possono essere in relazione ausale l ordine temporale degli eenti può essere sambiato per erti osseratori. Questa proprietà delle trasformazioni di Lorentz è di ruiale importanza in quanto afferma he nonostante la relatiità degli interalli spaziali e temporali nella teoria della relatiità ale il prinipio di ausalità (se due eenti sono in relazione ausale allora il primo dee preedere il seondo per iasun osseratore inerziale, un requisito irrinuniabile per una teoria fisia! Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
6 Le onseguenze delle trasformazioni di Lorentz: l assolutezza delle oinidenze spazio-temporali Abbiamo appreso, nelle pagine preedenti, he la distanza spaziale e temporale tra due eenti fisii è relatia dipendendo dall osseratore inerziale he la misura, osì ome relatia risulta essere la loro eentuale simultaneità. Seondo le trasformazioni di Galileo inee le distanze spaziali tra eenti simultanei sono assolute [ se t 0] osì ome le distanze temporali tra eenti non simultanei ( t t. L unia grandezza relatia risulta essere la distanza spaziale di eenti non simultanei he essendo data dalla espressione ( + t dipende hiaramente dall osseratore he la misura. Con le trasformazioni di Lorentz tutte queste grandezze dientano relatie per ui i si potrebbe hiedere se nella teoria della relatiità ristretta esistano grandezze assolute. Rihiamiamo allora le trasformazioni di Lorentz ed immaginiamo due eenti fisii tali he 0, 0, z 0 e t 0 oero tali da essere oinidenti sia spazialmente he temporalmente per l osseratore O : ( 1 0 ( t t1 ( 1 + ( 1 + ( t t1 ( ; ( 1 ( 1 ; ( 1 ( 1 ; ( 1 z z z z t t 1 / 1 / ( z z ( t t1 0 da ui otteniamo 0 0 z 0 z 0 t 0 t 0 se due eenti fisii oinidono spazialmente e temporalmente per un osseratore inerziale allora soddisfano questa ondizione per ogni altro osseratore inerziale dunque la oinidenza spaziale e temporale di due eenti è assoluta. Come edremo questa proprietà delle trasformazioni di Lorentz è di grande rileanza. Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
7 Le onseguenze delle trasformazioni di Lorentz: l assolutezza delle distanze spazio-temporali Rihiamiamo anora le trasformazioni di Lorentz, risriiamole in una forma più ompatta sostituendo le espressioni ( - 1 on et. et, eleiamo al quadrato gli interalli e, infine, sommiamo i quadrati dei tre interalli spaziali sottraendo il quadrato di quello temporale moltipliato per. Eo qua sotto i aloli ( 1 + ( t t1 ( / t t t 1 / (1 / ( 1 ( 1 ( z z1 ( z z1 z z z z ( 1 + ( 1 t t t + ( 1 t t + + t 4 t t 1 / 1 / t (1 / t + + t 4 + t + t + + z t + + z (1 / (1 / + + t t t (1 / (1 / (1 / (1 / t + + z t + + z + + z t Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
8 oero Vale la pena siluppare alune onsiderazioni in merito alla espressione appena ista. Per ominiare pensiamo a due punti nello spazio ordinario tridimensionale: la loro distanza, per un erto osseratore O, è data dal teorema di Pitagora Ora se assumiamo un riferimento O ruotato rispetto ad O il nuoo osseratore misurerà dierse oordinate dei punti e quindi diersi alori degli interalli,, z ma, quando a a alolare la distanza tra i due punti, troa lo stesso alore misurato da O. Dunque d ( + + z da ui ( + + z t ( + + z t Si noti he la somma dei termini tra parentesi rappresenta il quadrato della distanza spaziale tra due eenti e he questa, ome atteso non è la stessa per tutti gli osseratori inerziali. Tuttaia se gli osseratori inerziali sottraggono alla distanza spaziale tra due eenti il prodotto della eloità della lue on la loro distanza temporale (oero la quantità t he ha le dimensioni di una lunghezza eleata al quadrato troeranno tutti lo stesso alore. Nella TRR questo tipo di distanza prende il nome di distanza spaziotemporale tra due eenti per ui possiamo affermare he la distanza spazio-temporale tra gli eenti è la stessa per tutti gli osseratori inerziali oero he la distanza spaziotemporale tra due eenti è una grandezza assoluta (in questa forma, l assolutezza delle oinidenze spaziotemporali iste nella pagina preedente si deria immediatamente. d ( + + z ( + + z ( + + z (1 la distanza tra due punti dello spazio ordinario è la stessa per tutti gli osseratori ruotati tra loro. Ora gli eenti fisii possiedono, oltre ad una posizione nello spazio, anhe una posizione nel tempo per ui potremmo pensare di rappresentarli in un riferimento on quattro assi artesiani: tre dediati alla posizione spaziale (,,z ed uno dediato a quella temporale t. Per rappresentare lunghezze anhe su questo quarto asse, potrebbe poi essere oneniente posizionare l eento non in t ma in t. In questo modo, due eenti fisii in questo spazio sarebbero aratterizzati dagli interalli spaziali,, z e temporali t e la distanza potrebbe essere alolata attraerso il teorema di Pitagora in quattro dimensioni d ( + + z + t Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
9 Pensando poi di assimilare un ambiamento di riferimento inerziale ad una rotazione del sistema d assi quadridimensionale si otterrebbe, in analogia on il aso tridimensionale, e quindi d ( + + z + t ( + + z + t ( + + z + t ( he assomiglia molto alla relazione soddisfatta dalle trasformazioni di Lorentz troata nella pagina preedente ( + + z t ( + + z t (3 Seguendo questa idea si potrebbe pensare di interpretare il passaggio fisio da un riferimento all altro ome una rotazione ordinaria di un riferimento a quattro dimensioni (tre spaziali ed una temporale nel quale però il teorema di Pitagora ale per le dimensioni spaziali ma non per quella temporale dato he è un segno meno nella (3. Se si è però disposti ad introdurre un asse dei tempi immaginario, la (3 può essere sritta ome ( + + z + ( i t ( + + z + ( i t (4 oero identia alla (. Dunque, una olta introdotti tre assi spaziali ordinari ed un asse dei tempi immaginario, il passaggio da un riferimento inerziale ad un altro è assimilabile ad una rotazione dell intero sistema d assi, doe, pur ariando gli interalli, engono onserate le distanze alolate on il teorema di Pitagora in quattro dimensioni. Questa interpretazione geometria delle trasformazioni di Lorentz, basata sul onetto di rotazione, fu suggerita nel 1908 dal matematio tedeso Hermann Minkowsk (ira tre anni dopo la formulazione della TRR da parte di A. Einstein. In suo onore, il riferimento a quattro assi ortogonali di ui tre ordinari ed uno temporale immaginario, iene detto riferimento spaziotemporale o spazio-tempo di Minkowsk. Assumendo questa definizione i risulta i appena disussi si riassumono affermando he il passaggio fisio da un riferimento inerziale all altro è assimilabile ad una rotazione del riferimento di Minkowsk (o ad una rotazione nello spazio-tempo di Minkowsk. Lo spazio tempo di Minkowsk è, in ultima analisi, una elegante ostruzione formale apae di desriere in modo sintetio il ontenuto fisio della teoria della relatiità ristretta. Quando i fisii deono stabilire se una data nuoa teoria rispetti o meno la TRR, oppure ogliono ostruire una nuoa teoria in aordo on la TRR, lo spazio-tempo di Minkowsk rappresenta la ia più rapida per raggiungere lo sopo. Nonostante questo fondamentale antaggio, sotto il profilo fisio non aggiunge nulla di nuoo a quanto già affermato dalle stesse trasformazioni di Lorentz. Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
10 Rotazioni del riferimento di Minkowsk: deduzione degli effetti relatiistii In quel he segue, erheremo di dedurre gli effetti relatiistii per ia geometria, ruotando il riferimento di Minkowsk. Per ominiare analizziamo una rotazione ordinaria, di un erto angoloα, della oppia di assi rappresentata in figura. Con tutta eidenza il punto P possiede oordinate e rispetto al sistema iniziale (in rosso e oordinate e rispetto a quello finale ruotato (in blu. Dalla figura sottostante troiamo failmente os α sin os α sinα os α + sin os α + sin os α + sinα os α + sin le quale si può anhe sriere ome α α α α OO P Y t g α 1 + t g α + t g α 1 + t g α Tali espressioni mostrano una noteole somiglianza on le trasformazioni di Lorentz! OO P Y Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
11 Riordiamo ora he le trasformazioni di Lorentz sono rotazioni nello spazio-tempo di Minkowsk he preede un asse dei tempi immaginario he assumiamo lungo l asse delle it it Notiamo, inoltre, he nelle espressioni della pagina preedente ompare la radie 1+ tg α alla quale orrisponde, nelle trasformazioni di Lorentz, la radie 1 OO P Y Le due radii quadrate saranno uguali se tg α tgα i Sostituendo ora,, e tg α nelle formule della rotazione ordinaria della pagina preedente otteniamo le espressioni it ( i + t tgα ( i 1 tg α + + tgα t + it + ( i 1 tg α t it ( i 1 perfettamente oinidenti on le trasformazioni di Lorentz per le oordinate e t! OO P Y Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
12 Giungiamo allora alla seguente onlusione: ostruendo lo spazio di Minkowsk on la ariabile lungo l asissa e la ariabile it lungo l ordinata, la trasformazione di Lorentz on eloità (oero il passaggio da un riferimento inerziale O in moto on eloità al riferimento inerziale O fisso è formalmente identia ad una rotazione oraria del riferimento di un angoloαtale he tgα i doe eidentemente l angolo è tanto più grande quanto maggiore è la eloità. NOTA: data una erta eloità di traslazione, si alolerà l angolo tale he tgα/ e gli si aggiungerà l unità immaginaria i. OO P it Distanza spaziotemporale Dati due eenti fisii P e Q, la trasformazione di Lorentz (rotazione lasia inariata la distanza degli eenti sostituendo otteniamo + + i t i t + ( i t + ( i t t t la quale mostra he l inarianza della distanza spaziotemporale tra due eenti in seguito ad una trasformazione di Lorentz iene interpretata ome inarianza della distanza pitagoria nello spazio di Minkowsk a seguito della rotazione orrispondente. Si noti he, ome aso partiolare, si ottiene immediatamente he se P e Q oinidono per O allora oinidono anhe per O da ui l affermazione he se due eenti oinidono spazialmente e temporalmente per un osseratore inerziale allora deono oinidere per ogni altro. OO 1 P it 1 Q it Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
13 Dilatazione del tempo Consideriamo l orologio luminoso on il ammino di andata e ritorno del raggio lungo l asse del riferimento O analizzato a suo tempo. La partenza e l arrio del raggio luminoso in O orrispondono a due eenti on la stessa asissa e diersa ordinata it (edi figura. La trasformazione di Lorentz (rotazione del riferimento fa si he l osseratore O eda inee due eenti on un erto interallo spaziale - 1 (he O non ossera e soprattutto un dierso interallo temporale t -t 1 (dilatazione del tempo. Per quanto riguarda quest ultimo si ha os α tgα i i t i t osα 1/ 1+ tg α 1 1 t i t i t i t t 1+ tg α 1 / 1 / Dalla trigonometria si ha dilatazione del tempo e quindi sostituendo la formula della Q it P it 1 OO 1 Relatiità della simultaneità Gli eenti P e Q, in posizioni dierse, appaiono simultanei a O ma non ad O (relatiità della simultaneità. Dalla geometria si ha failmente he sinα tgα i i t sin α tgα / 1+ tg α Dalla trigonometria si ha da ui sostituendo la formula della desinronizzazione tgα i t 1+ tg α i 1 Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari t 1 OO P Q
14 Contrazione delle lunghezze Data una lunghezza in quiete nel riferimento O, l osseratore in moto O misura una lunghezza pari alla distanza di due suoi osseratori he edono gli estremi nello stesso istante, dunque la distanza dei punti P e Q. L osseratore O inee misura la distanza dei punti P e Q. Abbiamo allora os α tgα i P P Q Dalla trigonometria si ha della ontrazione della lunghezza osα 1/ 1+ tg α 1 / e quindi sostituendo la formula OO Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
15 Dai raggi luminosi alle proprietà intrinsehe dello spazio e del tempo Tutti gli esempi ed i ommenti preedenti hanno riguardato sistemi fisii relatiamente semplii nei quali era sempre oinolta la propagazione di raggi luminosi. Questo fatto è in erto senso ineitabile poihé i postulati della TRR preisano in he modo si propaga la lue e quindi qualunque esempio he oglia sfruttarli direttamente dee neessariamente preedere eenti fisii on raggi luminosi. Questo fatto potrebbe fare sorgere il dubbio he le trasformazioni di Lorentz desriano il omportamento dei raggi luminosi e di tutti i fenomeni ad essi onnessi e non proprietà intrinsehe dello spazio e del tempo. h Ad esempio onsideriamo il semplie dispositio utilizzato per illustrare il fenomeno della dilatazione dei tempi. Come sappiamo qualhe si dimostra failmente he t L interallo temporale tra gli eenti t 0, misurato dall osseratore in quiete O, è più orto di quello t M misurato dall osseratore in moto O. In questa situazione si potrebbe pensare he non è l interallo temporale a dilatarsi ma piuttosto il modo in ui lo misuriamo. In altre parole, si potrebbe pensare he usando un orologio, diiamo osì, luminoso, si troa l effetto alolato mentre usando, ad esempio, un orologio a uù, si potrebbe troare una diersa entità dell effetto o, addirittura, la sua ompleta assenza. Se le ose stessero osì, non saremmo in presenza di proprietà autentihe (oero intrinsehe degli interalli temporali, ma piuttosto di proprietà dipendenti dal modo in ui questi engono misurati. Come edremo la TRR non lasia aperta questa possibilità! Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari M t 0 1 / O O t t h h O
16 Per omprendere questo fatto, immaginiamo di aggiungere al dispositio di prima un pendolo di lunghezza tale da osillare, nel riferimento O, on lo stesso tempo he impiega il raggio luminoso a ompiere il ammino di andata e ritorno. Possiamo poi sistemare il pendolo in modo tale he, quando il raggio luminoso parte dal punto A, il pendolo parta dallo stesso punto. Siome il pendolo ha la lunghezza giusta, quando torna nel punto A, inontra nuoamente, in quel punto, il raggio luminoso. Notiamo subito he in A la posizione del pendolo e del raggio luminoso oinidono sia spazialmente he temporalmente e he, dopo un erto tempo, il raggio luminoso ed il pendolo tornano nello stesso punto A oero tornano a oinidere sia spazialmente he temporalmente. Siome le oinidenze spaziotemporali sono assolute, queste aengono per tutti gli osseratori inerziali per ui ogni altro osseratore inerziale O troerà tali oinidenze. Questo però rihiede he l osillazione del pendolo e l osillazione dell orologio luminoso abbiano la stessa durata non solo per l osseratore O ma per ogni altro osseratore O. Questo a sua olta equiale ad affermare he se si dilata il tempo misurato dall orologio luminoso dee dilatarsi, nello stesso modo, anhe il tempo misurato dal pendolo. Dato he questo stesso ragionamento può essere ripetuto on qualunque dispositio si oglia misurare gli interalli temporali, è hiaro he i troiamo innanzi ad una proprietà del tempo indipendente dal modo in ui iene misurato ale a dire ad una sua proprietà intrinsea. Questi ragionamenti possono essere failmente estesi anhe agli altri effetti relatiistii quali la relatiità della simultaneità e la ontrazione delle lunghezze. Possiamo allora affermare in generale he: L assolutezza delle oinidenze spazio-temporali rihiede he le proprietà dello spazio e del tempo, misurate on i raggi luminosi, debbano essere ere per qualunque altro metodo di misura, oero, he siano proprietà intrinsehe dello spazio e del tempo. Dunque qualunque interallo temporale dura più a lungo se osserato i moimento osì ome qualunque distanza spaziale si aoria. Sono lo spazio ed il tempo in se ad essere oinolti e non sempliemente la loro operazione di misura. O O A t t h h h O Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
17 Aluni ommenti sulle Trasformazione di Lorentz : nella TRR è tutto relatio? Spesso si die he on la teoria della relatiità tutto dienta relatio. Nulla di più sbagliato! La teoria della relatiità afferma he erte grandezze he nella fisia lassia si pensaa fossero assolute sono in realtà relatie ma he esistono nuoe grandezze fisihe ignote alla fisia lassia he inee sono assolute. In un erto senso la teoria della relatiità rende relatie le ehie grandezze fisihe ma ne introdue nuoe he sono assolute. Questo fatto è in se eidente se riassumiamo le prinipali onlusioni ui siamo giunti analizzando le trasformazioni di Lorentz i Gli interalli temporali dipendono dall osseratore inerziale, sono dunque relatii ed aumentano on la eloità dell osseratore (fenomeno della dilatazione dei tempi; ii La simultaneità tra due eenti separati nello spazio dipende dall osseratore inerziale, è dunque relatia ed il grado di dissinronia aumenta on la eloità dell osseratore e on la distanza spaziale degli eenti stessi (relatiità della simultaneità; iii Le distanze spaziali dipendono dall osseratore inerziale, sono dunque relatie e diminuisono on la eloità dell osseratore (fenomeno della ontrazione delle lunghezze; i La eloità della lue è la stessa per tutti gli osseratori inerziali ed è dunque una grandezza assoluta; Le distanza spaziotemporali e le oinidenze spaziotemporali sono le stesse per tutti gli osseratori inerziali e sono dunque grandezze assolute; i L ordine temporale di eenti he possono essere onnessi ausalmente è lo stesso per tutti gli osseratori inerziali ed è dunque assoluto; In estrema sintesi la TRR afferma he le distanze spaziali e temporali sono relatie ma quelle spaziotemporali sono assolute. Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
18 La ostruzione della meania relatiistia Quale sia la meania nel aso in ui le eloità dei orpi materiali siano piole rispetto alla eloità della lue lo sappiamo: questa non può he essere la meania newtoniana. Nel suo ambito, i suessi la apaità di spiegare i fatti sperimentali sono tali da non lasiare spazio a dubbi. Immaginiamo allora he O sia un osseratore inerziale he ede, ad un erto istante, il orpo materiale fermo (dato he il orpo materiale in generale può aelerare il riferimento O soddisfa questa ondizione solo all istante t e quindi erifia la alidità della meania newtoniana. Chiameremo O il riferimento proprio (oppure osseratore proprio del orpo materiale. Per apire quali siano, inee, le leggi meanihe nel aso in ui la eloità del orpo materiale sia rileante rispetto a quella della lue, si potrebbe pensare di assumere il punto di ista di un osseratore inerziale O he ede il riferimento O in rapido moto. Chiameremo O riferimento relatiistio (oppure osseratore relatiistio. Si potrebbe poi pensare di ottenere le leggi meanihe alide per l osseratore relatiistio (meania relatiistia sempliemente effettuando una trasformazione di Lorentz su ognuna delle grandezze he ompaiono nelle leggi meanihe note (oero le leggi newtoniane dell osseratore proprio. Si può fare, ma sorgono aluni problemi he deono essere superati. Per ominiare a ragionare in termini onreti, immaginiamo he l osseratore proprio, newtoniano O, applihi il seondo prinipio della dinamia ad un erto orpo materiale di massa m soggetto ad una forza F. Lungo l asse delle, ad esempio, srierà d d F m dt dt doe gli apii riordano he si tratta di grandezze fisihe misurate da O. Sulla base di quanto detto la meania relatiistia si potrebbe ottenere effettuando una trasformazione di Lorentz sulle grandezze F, m, dt, e. Premesso he non sappiamo ome si trasformano F ed m, è omunque hiaro he il numero di trasformazioni di Lorentz da effettuare nei due membri della equazione è differente. Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
19 Come è faile intuire, se effettuiamo un dierso numero di trasformazioni di Lorentz nei due membri della equazione si determina ambiamento di forma della equazione per l osseratore relatiistio O e dunque una iolazione del primo postulato he uole he tutti gli osseratori inerziali erifihino le stesse leggi della fisia. Comprendiamo allora he il ontenuto fisio del prinipio di relatiità può essere soddisfatto rihiedendo he i due membri della equazione di una erta legge fisia, qualora si ambi riferimento inerziale, si trasformino on lo stesso numero di trasformazioni di Lorentz (oero si trasformino nello stesso modo. Giungiamo allora alla formulazione matematia del prinipio di relatiità spesso detto prinipio di oarianza il quale afferma he affinhè una legge fisia soddisfi il prinipio di relatiità è suffiiente he, qualora si ambi il riferimento inerziale, i suoi membri si trasformino nello stesso modo rispetto alle trasformazioni di Lorentz. Riprendiamo allora l equazione meania d d F m dt dt e osseriamo subito he abbiamo buoni motii per rihiedere he la forza F si trasformi, nel passaggio da un riferimento all altro, ome. Riordiamo infatti he la forza altro non è he l azione siluppata da un dinamometro ompresso o allungato disposto, ad un erto istante, tra due punti dello spazio P e Q. Questo signifia he nel passaggio da un riferimento all altro la forza F dee trasformarsi ome il segmento he ongiunge i punti P a Q nello stesso istante t oero ome le grandezze, e z on t 0 (si riordi he abbiamo già sfruttato questo fatto all inizio introduendo la meania newtoniana. Rihiamiamo allora la legge di trasformazione degli interalli nel passaggio da O ad O ( t + ( t + 1 / 1 / 1 / z z z z z z ( t + ( t + t t 1 / t 1 / 1 / F F 1 / F F Fz Fz F F t 1 / NOTA: Si osseri he nel riferimento relatiistio O, oltre alla forza opportunamente trasformata he omunque si ossera anhe nel riferimento proprio O, ompare una grandezza he abbiamo indiata on F t e he dipende da F. Pur non oupandoi ora del suo signifiato, tale grandezza è una onseguenza ineitabile delle trasformazioni di Lorentz e dunque della TRR. Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
20 Qualora ambiassimo riferimento, sulla base del prinipio di oarianza (oero del prinipio di relatiità, doremmo aere nella equazione d d F m dt dt lo stesso numero di trasformazioni di Lorentz. Trasformandosi la forza ome il membro di sinistra porta on se una trasformazione di Lorentz per ui la stessa osa dee fare il membro di destra. Dato he la posizione del orpo materiale porta on se una trasformazione di Lorentz dobbiamo onludere he le grandezze m e dt non deono essere trasformate rimanendo quelle del riferimento proprio per ogni osseratore inerziale O. Dunque affinhè sia soddisfatto il prinipio di oarianza (prinipio di relatiità è neessario he la massa del orpo materiale e l interallo temporale engano misurate nel riferimento proprio. Dato he la massa e il tempo nel riferimento proprio si hiamano solitamente massa a riposo e tempo proprio e si indiano on m 0 eτ, il seondo prinipio della dinamia nel riferimento proprio O prende allora la forma seguente d d F m0 dτ dτ Usando le trasformazioni di Lorentz, possiamo affermare, senza fare aloli, he nel riferimento relatiistio il seondo prinipio della dinamia arà la stessa forma ma on la forza e la posizione senza apii. Dunque, l espressione relatiistia del seondo prinipio della dinamia dee essere la seguente d d F m0 dτ dτ Dunque, nella espressione delle leggi meanihe alide per un erto osseratore inerziale O non ompaiono la massa la eloità e l aelerazione misurate da O nel modo onsueto oero diidendo (nel aso della eloità e della aelerazione la ariazione di posizione e eloità misurate da O per l interallo temporale pure misurato da O. Compaiono inee la massa misurata nel riferimento proprio (massa a riposo ed un nuoo tipo di eloità ed aelerazione, alolate diidendo la ariazione di posizione misurata da O per l interallo temporale misurato dall osseratore proprio (dunque quantità misurate da differenti osseratori. Tali eloità ed aelerazione engono dette eloità ed aelerazione di Minkowsk d d d la forza eguaglia la deriata rispetto al V A dτ dτ dτ tempo proprio della massa a riposo per la eloità di Minkowsk (quantità di moto per ui una formulazione equialente del seondo prinipio è F d di Minkowsk oppure il prodotto della m0v F m0 A massa a riposo per l aelerazione di Minkowsk Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari dτ la forza eguaglia il prodotto della massa a riposo per la deriata seonda rispetto al tempo proprio della posizione
21 Fine della lezione V Lezioni sulla Teoria della Relatiità - Niola Semprini Cesari
L invarianza della velocità della luce. Dai postulati della teoria della relatività alle equazioni di Lorentz. (2) R
 L inarianza della eloità della lue. Dai postulati della teoria della relatiità alle equazioni di Lorentz. Conferma sperimentale dell inarianza della eloità della lue. Relazioni tra spostamenti e eloità
L inarianza della eloità della lue. Dai postulati della teoria della relatiità alle equazioni di Lorentz. Conferma sperimentale dell inarianza della eloità della lue. Relazioni tra spostamenti e eloità
Domande. E = mc 1! v / c. La massa delle particelle riportate nelle tabelle corrisponde all energia che esse possiedono quando sono ferme (v = 0 m/s).
 Cutnell, Johnson Fisia olume 3 Capitolo 5 La relatiità ristretta Domande. Il postulato sulla eloità della lue stabilise he la eloità della lue nel uoto, misurata in un qualsioglia sistema di riferimento
Cutnell, Johnson Fisia olume 3 Capitolo 5 La relatiità ristretta Domande. Il postulato sulla eloità della lue stabilise he la eloità della lue nel uoto, misurata in un qualsioglia sistema di riferimento
ARGOMENTI DI RELATIVITÀ
 A0 6 Armando Tielli ARGOMENTI DI RELATIVITÀ TEORIA E ESERCIZI Copyright MMX ARACNE editrie S.r.l. www.araneeditrie.it info@araneeditrie.it ia Raffaele Garofalo, 33/A B 0073 Roma (06) 9378065 ISBN 978
A0 6 Armando Tielli ARGOMENTI DI RELATIVITÀ TEORIA E ESERCIZI Copyright MMX ARACNE editrie S.r.l. www.araneeditrie.it info@araneeditrie.it ia Raffaele Garofalo, 33/A B 0073 Roma (06) 9378065 ISBN 978
(2) v (1 ' Δx) = γ ( Δx (2 '
 La ontrazione degli spazi. La oordinata temporale ome dimensione spaziale, l inariante relatiistio e la distanza spazio temporale. L eetto doppler nella relatiità. Dalla simmetria delle trasormazioni all
La ontrazione degli spazi. La oordinata temporale ome dimensione spaziale, l inariante relatiistio e la distanza spazio temporale. L eetto doppler nella relatiità. Dalla simmetria delle trasormazioni all
LEZIONE II LA RELATIVITA' RISTRETTA DI EINSTEIN
 LEZIONE II LA RELATIVITA' RISTRETTA DI EINSTEIN Nel suo famoso artiolo del 905. Einstein propose un punto di ista del tutto rioluzionario. Partendo da un numero estremamente limitato di Postulati egli
LEZIONE II LA RELATIVITA' RISTRETTA DI EINSTEIN Nel suo famoso artiolo del 905. Einstein propose un punto di ista del tutto rioluzionario. Partendo da un numero estremamente limitato di Postulati egli
Enrico Borghi PARADOSSO DEI GEMELLI
 Enrio Borghi PARADOSSO DEI GEMELLI Premessa. In questo studio le definizioni di: - punto-evento; - linea di universo; - tempo proprio; - metria pseudoeulidea oltre he la legge relativistia di omposizione
Enrio Borghi PARADOSSO DEI GEMELLI Premessa. In questo studio le definizioni di: - punto-evento; - linea di universo; - tempo proprio; - metria pseudoeulidea oltre he la legge relativistia di omposizione
Proprietà delle operazioni sui numeri naturali. Introduzione geometrica alle proprietà delle operazioni = 11 = 8 + 3
 Proprietà delle operazioni sui numeri naturali 1. Le proprietà delle operazioni possono essere introdotte geometriamente in modo da fornirne una giustifiazione intuitiva e una visualizzazione : 2. Le proprietà
Proprietà delle operazioni sui numeri naturali 1. Le proprietà delle operazioni possono essere introdotte geometriamente in modo da fornirne una giustifiazione intuitiva e una visualizzazione : 2. Le proprietà
5. Dinamica relativistica
 5. Dinamica relatiistica Fino ad ora abbiamo solamente fornito una descrizione del moto, cioè uno studio di cinematica nell ambito della teoria relatiità ristretta. È ora necessario intraprendere un tipo
5. Dinamica relatiistica Fino ad ora abbiamo solamente fornito una descrizione del moto, cioè uno studio di cinematica nell ambito della teoria relatiità ristretta. È ora necessario intraprendere un tipo
GEOMETRIA ANALITICA 8 LE CONICHE
 GEOMETRIA ANALITICA 8 LE CONICHE Tra tutte le urve, ne esistono quattro partiolari he vengono hiamate onihe perhé sono ottenute tramite l intersezione di una superfiie i-onia on un piano. A seonda della
GEOMETRIA ANALITICA 8 LE CONICHE Tra tutte le urve, ne esistono quattro partiolari he vengono hiamate onihe perhé sono ottenute tramite l intersezione di una superfiie i-onia on un piano. A seonda della
2 Fisica dell equilibrio di un semiconduttore
 FISICA DELL EQUILIBRIO DI UN SEMICONDUTTORE 5 Fisia dell equilibrio di un semionduttore. Densità del numero di elettroni e laune È possibile desriere un insieme statistio di partielle in equilibrio mediante
FISICA DELL EQUILIBRIO DI UN SEMICONDUTTORE 5 Fisia dell equilibrio di un semionduttore. Densità del numero di elettroni e laune È possibile desriere un insieme statistio di partielle in equilibrio mediante
Università degli Studi di Teramo Facoltà di Scienze Politiche
 Università degli Studi di Teramo Faoltà di Sienze Politihe Corso di Laurea in Statistia Lezioni del Corso di Matematia a ura di D. Tondini a.a. 3/4 CAPITOLO II LE EQUAZIONI DIFFERENZIALI. GENERALITÀ È
Università degli Studi di Teramo Faoltà di Sienze Politihe Corso di Laurea in Statistia Lezioni del Corso di Matematia a ura di D. Tondini a.a. 3/4 CAPITOLO II LE EQUAZIONI DIFFERENZIALI. GENERALITÀ È
L'INERZIA DI UN CORPO È DIPENDENTE DAL SUO CONTENUTO DI ENERGIA? v 1 c
 LINERZIA DI UN CORPO È DIPENDENTE DAL SUO CONTENUTO DI ENERGIA? E oneniente a questo punto, prima di passare al ommento di questa prima memoria relatiistia di Einstein, edere il ontenuto dell altra sua
LINERZIA DI UN CORPO È DIPENDENTE DAL SUO CONTENUTO DI ENERGIA? E oneniente a questo punto, prima di passare al ommento di questa prima memoria relatiistia di Einstein, edere il ontenuto dell altra sua
Capitolo 1 Cinematica del punto materiale
 Capitolo Cinematia del punto materiale Introduzione La Cinematia si oupa della desrizione del moto. Utilizzeremo i ettori, le funzioni di una ariabile, la geometria, e... per desriere il moto di un punto
Capitolo Cinematia del punto materiale Introduzione La Cinematia si oupa della desrizione del moto. Utilizzeremo i ettori, le funzioni di una ariabile, la geometria, e... per desriere il moto di un punto
Esercitazioni di Elettrotecnica
 Eseritazioni di Elettrotenia a ura dell Ing ntonio Maffui Parte III: iruiti in eoluzione dinamia 00/003 Eseritazioni di Elettrotenia 00/003 Maffui ESEITZIONE N0: eti dinamihe del primo ordine ESEIZIO 0
Eseritazioni di Elettrotenia a ura dell Ing ntonio Maffui Parte III: iruiti in eoluzione dinamia 00/003 Eseritazioni di Elettrotenia 00/003 Maffui ESEITZIONE N0: eti dinamihe del primo ordine ESEIZIO 0
Spin. La hamiltoniana classica di una particella di massa m e carica q in presenza di un potenziale elettromagnetico (Φ, A) si scrive.
 Spin La hamiltoniana lassia di una partiella di massa m e aria q in presenza di un potenziale elettromagnetio Φ, A si srive Sviluppando il quadrato si ha H = H = p q A 2 + qφ p 2 + A 2 2q A p + qφ 2 Se
Spin La hamiltoniana lassia di una partiella di massa m e aria q in presenza di un potenziale elettromagnetio Φ, A si srive Sviluppando il quadrato si ha H = H = p q A 2 + qφ p 2 + A 2 2q A p + qφ 2 Se
INCERTEZZA NELLE MISURE ED ERRORI SPERIMENTALI 1. NON E POSSIBILE FARE MISURE INFINITAMENTE PRECISE : PRECISIONE ERRORE 0!
 Llab.1 INCERTEZZA NELLE MISURE ED ERRORI SPERIMENTALI 1. NON E POSSIBILE FARE MISURE INFINITAMENTE PRECISE : PRECISIONE ERRORE 0! FATTORI LIMITANTI LA PRECISIONE QUALITA DELLO STRUMENTO SENSIBILITA PORTATA
Llab.1 INCERTEZZA NELLE MISURE ED ERRORI SPERIMENTALI 1. NON E POSSIBILE FARE MISURE INFINITAMENTE PRECISE : PRECISIONE ERRORE 0! FATTORI LIMITANTI LA PRECISIONE QUALITA DELLO STRUMENTO SENSIBILITA PORTATA
Risolviamo un esercizio per illustrare il fenomeno in modo dettagliato anche se,in alcuni punti, semplificato.
 PARADOSSO DEI GEMELLI Il cosiddetto paradosso dei gemelli è forse una delle conseguenze più popolari della teoria della relatività di Einstein. In realtà non si tratta di un vero e proprio paradosso, bensì
PARADOSSO DEI GEMELLI Il cosiddetto paradosso dei gemelli è forse una delle conseguenze più popolari della teoria della relatività di Einstein. In realtà non si tratta di un vero e proprio paradosso, bensì
Espansione dell Universo e redshift
 Espansione dell Universo e redshift Primo Galletti Aldo Aluigi Roma, 21 Settembre 2002 In un Universo in ui avviene ontinuamente la nasita e la morte della materia 1 l ipotesi di una grande esplosione
Espansione dell Universo e redshift Primo Galletti Aldo Aluigi Roma, 21 Settembre 2002 In un Universo in ui avviene ontinuamente la nasita e la morte della materia 1 l ipotesi di una grande esplosione
UNIVERSITÀ DEGLI STUDI DI FERRARA
 UNIVERSITÀ DEGLI STUDI DI FERRARA SCUOLA DI SPECIALIZZAZIONE PER L INSEGNAMENTO SECONDARIO Classe di Speializzazione A049 Perorso Didattio Dalla teoria all'esperimento: postulati e siluppo della Relatiità
UNIVERSITÀ DEGLI STUDI DI FERRARA SCUOLA DI SPECIALIZZAZIONE PER L INSEGNAMENTO SECONDARIO Classe di Speializzazione A049 Perorso Didattio Dalla teoria all'esperimento: postulati e siluppo della Relatiità
Elettromagnetismo e Relatività dr.ing. Alberto Sacchi Sviluppo Progetti Avanzati srl- R&D Dept.
 Elettromagnetismo e Relatività dr.ing. Alberto Sahi Sviluppo Progetti Avanzati srl- R&D Dept. ing.sahi@alie.it SNTES (ABSTRACT) Analisi ritia dell esperimento di Feynman volto ad illustrare la orrelazione
Elettromagnetismo e Relatività dr.ing. Alberto Sahi Sviluppo Progetti Avanzati srl- R&D Dept. ing.sahi@alie.it SNTES (ABSTRACT) Analisi ritia dell esperimento di Feynman volto ad illustrare la orrelazione
Enrico Borghi LE VARIABILI DINAMICHE DEL CAMPO SCALARE REALE
 Enrio Borghi LE VARIABILI DINAMICHE DEL CAMPO SCALARE REALE E. Borghi - Variabili dinamihe del ampo salare reale Rihiami a studi presenti in fisiarivisitata Leggendo Le variabili dinamihe del ampo salare
Enrio Borghi LE VARIABILI DINAMICHE DEL CAMPO SCALARE REALE E. Borghi - Variabili dinamihe del ampo salare reale Rihiami a studi presenti in fisiarivisitata Leggendo Le variabili dinamihe del ampo salare
Pag. 1. Il tempo e lo spazio nella teoria della relatività
 Pag. 1 Il tempo e lo spazio nella teoria della relatività La fisica negli ultimi anni del 1800 si trovava a dover risolvere un dilemma inconciliabile con la teoria della meccanica classica. La relatività
Pag. 1 Il tempo e lo spazio nella teoria della relatività La fisica negli ultimi anni del 1800 si trovava a dover risolvere un dilemma inconciliabile con la teoria della meccanica classica. La relatività
Corso di MISURE E CONTROLLI IDRAULICI STRUMENTI PER LA MISURA DELLE VELOCITÀ CHE SI BASANO SULL EFFETTO DOPPLER
 Corso di MIUE E CONTOLLI IDAULICI TUMENTI E LA MIUA DELLE VELOCITÀ CHE I BAANO ULL EFFETTO DOLE a ura di Andrea DEFINA Lua CANIELLO EFFETTO DOLE 3 Eetto Doppler L eetto Doppler (J.C.A. Doppler 83-853)
Corso di MIUE E CONTOLLI IDAULICI TUMENTI E LA MIUA DELLE VELOCITÀ CHE I BAANO ULL EFFETTO DOLE a ura di Andrea DEFINA Lua CANIELLO EFFETTO DOLE 3 Eetto Doppler L eetto Doppler (J.C.A. Doppler 83-853)
NOTE SULLE EQUAZIONI DI MAXWELL E IL CORPO NERO
 NOTE SULLE EQUAZIONI DI MAXWELL E IL CORPO NERO G. Martinelli Abstrat Questi appunti ostituisono un sommario delle prinipali formule relative alla trattazione del orpo nero. 1 Le Equazioni di Maxwell Le
NOTE SULLE EQUAZIONI DI MAXWELL E IL CORPO NERO G. Martinelli Abstrat Questi appunti ostituisono un sommario delle prinipali formule relative alla trattazione del orpo nero. 1 Le Equazioni di Maxwell Le
L EFFETTO DOPPLER CLASSICO (1842)
 L EFFETTO DOPPLER CLAICO (84) Abbiamo già detto che l'effetto Doppler consiste in una ariazione apparente della frequenza delle onde emesse da. una sorgente per un moto relatio tra sorgente ed osseratore.
L EFFETTO DOPPLER CLAICO (84) Abbiamo già detto che l'effetto Doppler consiste in una ariazione apparente della frequenza delle onde emesse da. una sorgente per un moto relatio tra sorgente ed osseratore.
TEOREMA DEL CAMPIONAMENTO
 1 TEOREMA DEL CAMPIONAMENTO nota per il orso di Teleomuniazioni a ura di F. Benedetto G. Giunta 1. Introduzione Il proesso di ampionamento è di enorme importanza ai fini della realizzazione dei dispositivi
1 TEOREMA DEL CAMPIONAMENTO nota per il orso di Teleomuniazioni a ura di F. Benedetto G. Giunta 1. Introduzione Il proesso di ampionamento è di enorme importanza ai fini della realizzazione dei dispositivi
Elementi di calcolo vettoriale
 Mathit Elementi di calcolo ettoriale Nozione di ettore Grandezze ettoriali e grandezze scalari Segmenti orientati e ettori Definizioni Operazioni con i ettori Somma e differenza di ettori Moltiplicazione
Mathit Elementi di calcolo ettoriale Nozione di ettore Grandezze ettoriali e grandezze scalari Segmenti orientati e ettori Definizioni Operazioni con i ettori Somma e differenza di ettori Moltiplicazione
La Teoria della Relatività Ristretta. Prof. Michele Barcellona
 La Teoria della Relatività Ristretta Prof. Michele Barcellona I Postulati della Teoria della Relatività ristretta Per risolvere le contraddizioni tra Meccanica ed Elettromagnetismo Einstein propose una
La Teoria della Relatività Ristretta Prof. Michele Barcellona I Postulati della Teoria della Relatività ristretta Per risolvere le contraddizioni tra Meccanica ed Elettromagnetismo Einstein propose una
Analisi di segnali campionati
 Analisi nel dominio della frequenza Analisi di segnali ampionati - 1 Analisi di segnali ampionati 1 Analisi dei segnali nel dominio della frequenza I prinipali metodi di analisi dei segnali di misura possono
Analisi nel dominio della frequenza Analisi di segnali ampionati - 1 Analisi di segnali ampionati 1 Analisi dei segnali nel dominio della frequenza I prinipali metodi di analisi dei segnali di misura possono
Nella lezione precedente abbiamo visto che l'energia totale posseduta da un corpo di massa a riposo m 0 che viaggia con velocità v è pari a
 LEZIONE VI Il quadriettore Energia - quantità di moto. Nella lezione preedente abbiamo isto he l'energia totale posseduta da un orpo di massa a riposo m he iaggia on eloità è pari a m E = m = (1) D'altra
LEZIONE VI Il quadriettore Energia - quantità di moto. Nella lezione preedente abbiamo isto he l'energia totale posseduta da un orpo di massa a riposo m he iaggia on eloità è pari a m E = m = (1) D'altra
+ t v. v 3. x = p + tv, t R. + t. 3 2 e passante per il punto p =
 5. Rette e piani in R 3 ; sfere. In questo paragrafo studiamo le rette, i piani e le sfere in R 3. Ci sono due modi per desrivere piani e rette in R 3 : mediante equazioni artesiane oppure mediante equazioni
5. Rette e piani in R 3 ; sfere. In questo paragrafo studiamo le rette, i piani e le sfere in R 3. Ci sono due modi per desrivere piani e rette in R 3 : mediante equazioni artesiane oppure mediante equazioni
Considerazioni introduttive
 a linea elastica onsiderazioni introduttie In un elemento strutturale deformabile in cui una dimensione è prealente rispetto alle altre due, è possibile determinare la configurazione secondo la uale uesto
a linea elastica onsiderazioni introduttie In un elemento strutturale deformabile in cui una dimensione è prealente rispetto alle altre due, è possibile determinare la configurazione secondo la uale uesto
Lo spazio-tempo di Minkowski. prof.ssa Angela Donatiello
 Lo spazio-tempo di Minkowski Per meglio comprendere gli effetti relativistici dovuti all assunzione dei due postulati di Einstein, introduciamo un utile strumento geometrico noto con il nome di diagramma
Lo spazio-tempo di Minkowski Per meglio comprendere gli effetti relativistici dovuti all assunzione dei due postulati di Einstein, introduciamo un utile strumento geometrico noto con il nome di diagramma
MOTORI PER AEROMOBILI
 MOORI PER AEROMOBILI Cap. 2 CICLI DI URBINA A GAS PER LA PRODUZIONE DI POENZA (Shaft power yles) E opportuno suddividere i numerosi tipi di ili di turbina a gas in due ategorie: - ili di turbina a gas
MOORI PER AEROMOBILI Cap. 2 CICLI DI URBINA A GAS PER LA PRODUZIONE DI POENZA (Shaft power yles) E opportuno suddividere i numerosi tipi di ili di turbina a gas in due ategorie: - ili di turbina a gas
PROBLEMA. L EFFETTO GEMELLI Adattamento da P.A. Tipler Invito alla Fisica 3 E.F.Taylor-J.A.Wheeler Fisica dello Spazio-Tempo Zanichelli
 PROBLEMA. L EFFETTO GEMELLI Adattamento da P.A. Tipler Invito alla Fisica 3 E.F.Taylor-J.A.Wheeler Fisica dello Spazio-Tempo Zanichelli Obiettivi Presentare una soluzione semplificata del Paradosso dei
PROBLEMA. L EFFETTO GEMELLI Adattamento da P.A. Tipler Invito alla Fisica 3 E.F.Taylor-J.A.Wheeler Fisica dello Spazio-Tempo Zanichelli Obiettivi Presentare una soluzione semplificata del Paradosso dei
Introduzione. Istituzioni di Fisica Nucleare e Subnucleare. Prof. Francesco Ragusa Università degli Studi di Milano
 Istituzioni di Fisia Nuleare e Subnuleare Prof. Franeso Ragusa Università degli Studi di Milano Introduzione 30.09.014 Anno Aademio 014-015 Libro di testo A. Das T. Ferbel Introdution to Nulear and Partile
Istituzioni di Fisia Nuleare e Subnuleare Prof. Franeso Ragusa Università degli Studi di Milano Introduzione 30.09.014 Anno Aademio 014-015 Libro di testo A. Das T. Ferbel Introdution to Nulear and Partile
LEZIONE 7. k definiamo prodotto scalare di v e w il numero. = v x w x + v y w y + v z w z. w z
 LEZINE 7 7.1. Prodotto scalare. Fissiamo un sistema di riferimento ı j k in S 3. Dati i ettori geometrici = ı + y j + k e w = w ı + j + k definiamo prodotto scalare di e w il numero, w = ( y ) w = + y
LEZINE 7 7.1. Prodotto scalare. Fissiamo un sistema di riferimento ı j k in S 3. Dati i ettori geometrici = ı + y j + k e w = w ı + j + k definiamo prodotto scalare di e w il numero, w = ( y ) w = + y
Unità Didattica 1. Sistemi di Numerazione
 Unità Didattia Sistemi di Numerazione Sistemi di Numerazione Posizionali Criterio per la rappresentazione di un insieme infinito di numeri mediante un insieme limitato di simoli. Un sistema di numerazione
Unità Didattia Sistemi di Numerazione Sistemi di Numerazione Posizionali Criterio per la rappresentazione di un insieme infinito di numeri mediante un insieme limitato di simoli. Un sistema di numerazione
4. FORZE TRA CORRENTI
 19 IL CAMPO MAGNETICO Pael L Photo and Video/Shutterstock 4. FORZE TRA CORRENTI La definizione dell ampere Il alore della costante non è misurato con un esperimento, ma è stato scelto conenzionalmente
19 IL CAMPO MAGNETICO Pael L Photo and Video/Shutterstock 4. FORZE TRA CORRENTI La definizione dell ampere Il alore della costante non è misurato con un esperimento, ma è stato scelto conenzionalmente
16 L INTEGRALE INDEFINITO
 9. Integrali immediati 6 L INTEGRALE INDEFINITO Riassumiamo le puntate preedenti: si die INTEGRALE INDEFINITO di una funzione f ( ), la famiglia di tutte e sole quelle funzioni la ui derivata è uguale
9. Integrali immediati 6 L INTEGRALE INDEFINITO Riassumiamo le puntate preedenti: si die INTEGRALE INDEFINITO di una funzione f ( ), la famiglia di tutte e sole quelle funzioni la ui derivata è uguale
Trasformazioni di Lorentz
 Trasformazioni di Lorentz Regole di trasformazione fra un sistema inerziale S (descritto da x, y, z, t) ed uno S (descritto da x, y, z, t ) che viaggia a velocità V lungo x rispetto a S: x = γ(x V t) y
Trasformazioni di Lorentz Regole di trasformazione fra un sistema inerziale S (descritto da x, y, z, t) ed uno S (descritto da x, y, z, t ) che viaggia a velocità V lungo x rispetto a S: x = γ(x V t) y
1. Calcolo del Momento di plasticizzazione per una sezione tubolare in acciaio.
 1. Calolo del Momento di plastiizzazione per una sezione tubolare in aiaio. La sezione presa in onsiderazione è la seguente: Shema di riferimento per il alolo del momento di plastiizzazione della sezione
1. Calolo del Momento di plastiizzazione per una sezione tubolare in aiaio. La sezione presa in onsiderazione è la seguente: Shema di riferimento per il alolo del momento di plastiizzazione della sezione
Laboratorio di didattica Della matematica
 Didattia della matematia a.a. 004/00 Laboratorio di didattia Della matematia (La probabilita elementare ome strumento per un diverso approio ai numeri razionali) ANITA GARIBALDI Classe 9 Il onetto di frazione,
Didattia della matematia a.a. 004/00 Laboratorio di didattia Della matematia (La probabilita elementare ome strumento per un diverso approio ai numeri razionali) ANITA GARIBALDI Classe 9 Il onetto di frazione,
Laboratorio di Misure Fisiche per Scienze Biologiche
 Laboratorio di Misure Fisihe per Sienze Biologihe Nozioni di alorimetria e misura del alore speiio di una sostanza Rihiami di teoria (Ragozzino et al Fondamenti di Fisia) - Il onetto di temperatura. -
Laboratorio di Misure Fisihe per Sienze Biologihe Nozioni di alorimetria e misura del alore speiio di una sostanza Rihiami di teoria (Ragozzino et al Fondamenti di Fisia) - Il onetto di temperatura. -
PRIMITIVA DI UNA FUNZIONE. INTEGRALE INDEFINITO. INTEGRALI IMMEDIATI O RICONDUCIBILI AD IMMEDIATI. METODI DI INTEGRAZIONE.
 PRIMITIVA DI UNA FUNZIONE. INTEGRALE INDEFINITO. INTEGRALI IMMEDIATI O RICONDUCIBILI AD IMMEDIATI. METODI DI INTEGRAZIONE. DEF. Una funzione F() si die primitiva di una funzione y f() definita nell intervallo
PRIMITIVA DI UNA FUNZIONE. INTEGRALE INDEFINITO. INTEGRALI IMMEDIATI O RICONDUCIBILI AD IMMEDIATI. METODI DI INTEGRAZIONE. DEF. Una funzione F() si die primitiva di una funzione y f() definita nell intervallo
Esercizi sulla funzione integrale
 Eserizi sulla funzione integrale Versione del 8 marzo 27 In questo fasioletto propongo aluni eserizi sulla funzione integrale. I testi della prima parte sono presi dalle prove assegnate agli esami di stato
Eserizi sulla funzione integrale Versione del 8 marzo 27 In questo fasioletto propongo aluni eserizi sulla funzione integrale. I testi della prima parte sono presi dalle prove assegnate agli esami di stato
Modelli di base per la politica economica
 Modelli di base per la politia eonomia Capitolo Marella Mulino Modelli di base per la politia eonomia Corso di Politia eonomia a.a. 22-23 Modelli di base per la politia eonomia Capitolo Capitolo Modello
Modelli di base per la politia eonomia Capitolo Marella Mulino Modelli di base per la politia eonomia Corso di Politia eonomia a.a. 22-23 Modelli di base per la politia eonomia Capitolo Capitolo Modello
Problema (tratto dal 7.42 del Mazzoldi 2)
 Problema (tratto dal 7.4 del azzoldi Un disco di massa m D e raggio R ruota attorno all asse verticale passante per il centro con velocità angolare costante ω. ll istante t 0 viene delicatamente appoggiata
Problema (tratto dal 7.4 del azzoldi Un disco di massa m D e raggio R ruota attorno all asse verticale passante per il centro con velocità angolare costante ω. ll istante t 0 viene delicatamente appoggiata
Insegnare relatività. nel XXI secolo
 Insegnare relatività nel XXI secolo L ' o r o l o g i o a l u c e e i l t e m p o p r o p r i o L'orologio a luce serve a connettere l'invarianza della velocità della luce col carattere non più assoluto
Insegnare relatività nel XXI secolo L ' o r o l o g i o a l u c e e i l t e m p o p r o p r i o L'orologio a luce serve a connettere l'invarianza della velocità della luce col carattere non più assoluto
TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO
 TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO Si die he, per he tende a, la funzione y=f() ha per ite l e si srive: l = l I( ) ESEMPIO DI VERIFICA DI
TEORIA SUI LIMITI DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO Si die he, per he tende a, la funzione y=f() ha per ite l e si srive: l = l I( ) ESEMPIO DI VERIFICA DI
L unità di misura del lavoro è il Joule [L]=[F][ r]=n m=kg m 2 /s 2 Se lo spostamento non è rettilineo e/o la forza non è costante lungo il moto, si
![L unità di misura del lavoro è il Joule [L]=[F][ r]=n m=kg m 2 /s 2 Se lo spostamento non è rettilineo e/o la forza non è costante lungo il moto, si L unità di misura del lavoro è il Joule [L]=[F][ r]=n m=kg m 2 /s 2 Se lo spostamento non è rettilineo e/o la forza non è costante lungo il moto, si](/thumbs/50/26513150.jpg) Laoro di una forza Il laoro di una forza è definito come il prodotto scalare della forza F per lo spostamento r. Il laoro è una grandezza scalare Se lo spostamento è perpendicolare alla forza il laoro
Laoro di una forza Il laoro di una forza è definito come il prodotto scalare della forza F per lo spostamento r. Il laoro è una grandezza scalare Se lo spostamento è perpendicolare alla forza il laoro
8. Analisi delle principali configurazioni circuitali a BJT e FET
 8. Analisi delle principali configurazioni circuitali a BJT e FET 8. Concetti generali Esamineremo nel seguito i principali montaggi che si utilizzano per i circuiti a transistori, che differiscono tra
8. Analisi delle principali configurazioni circuitali a BJT e FET 8. Concetti generali Esamineremo nel seguito i principali montaggi che si utilizzano per i circuiti a transistori, che differiscono tra
Note sulla correttezza di RSA e sulla complessità degli attacchi
 Note sulla orrettezza di RSA e sulla omplessità degli attahi P. Bonatti 21 novembre 2016 1 Rihiami elementari di algebra Elevamento a potenza di binomi Riordiamo la definizione di oeffiiente binomiale:
Note sulla orrettezza di RSA e sulla omplessità degli attahi P. Bonatti 21 novembre 2016 1 Rihiami elementari di algebra Elevamento a potenza di binomi Riordiamo la definizione di oeffiiente binomiale:
II Simulazione Seconda prova Fisica
 II Simulazione Seonda proa Fisia MaturitàFisia_Simul_.indd 8/05/5 08:5 II Simulazione Seonda proa Fisia Problema n.. Channel-0 4MHz Channel-0 47MHz Channel-03 4MHz Channel-04 47MHz Channel-05 43MHz Channel-06
II Simulazione Seonda proa Fisia MaturitàFisia_Simul_.indd 8/05/5 08:5 II Simulazione Seonda proa Fisia Problema n.. Channel-0 4MHz Channel-0 47MHz Channel-03 4MHz Channel-04 47MHz Channel-05 43MHz Channel-06
FUNZIONI CONTINUE. funzioni di una variabile: def : Una funzione f(x) definita in un insieme D R si dice continua in un punto c D se risulta.
 FUNZIONI CONTINUE funzioni di una variabile: def : Una funzione f(x) definita in un insieme D R si die ontinua in un punto D se risulta Analizza bene la definizione: lim x f ( x) = f ( ) Il punto deve
FUNZIONI CONTINUE funzioni di una variabile: def : Una funzione f(x) definita in un insieme D R si die ontinua in un punto D se risulta Analizza bene la definizione: lim x f ( x) = f ( ) Il punto deve
UNITÀ DIDATTICA 5 LA RETTA
 UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
Stabilire se il punto di coordinate (1,1) appartiene alla circonferenza centrata nell origine e di raggio 1.
 Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Analisi del moto dei proietti
 Moto dei proietti E il moto di particelle che vengono lanciate con velocità iniziale v 0 e sono soggette alla sola accelerazione di gravità g supposta costante. La pallina rossa viene lasciata cadere da
Moto dei proietti E il moto di particelle che vengono lanciate con velocità iniziale v 0 e sono soggette alla sola accelerazione di gravità g supposta costante. La pallina rossa viene lasciata cadere da
Lezioni n.16. Trasformatore
 Lezione 6 Trasformatore Lezioni n.6 Trasformatore. Trasformatore ideale. Proprietà del trasporto di impedenza 3. Induttori accoppiati trasformatore reale 4. Schema circuitale equialente per accoppiamento
Lezione 6 Trasformatore Lezioni n.6 Trasformatore. Trasformatore ideale. Proprietà del trasporto di impedenza 3. Induttori accoppiati trasformatore reale 4. Schema circuitale equialente per accoppiamento
Incontri di introduzione alla Relatività Generale
 Incontri di introduzione alla Relatività Generale Prima parte La Torre del Sole - 11 Novembre 2015 Dr. Andrea Castelli, Ph.D. Università degli Studi di Bologna Struttura del corso PARTE PRIMA - 11 Novembre
Incontri di introduzione alla Relatività Generale Prima parte La Torre del Sole - 11 Novembre 2015 Dr. Andrea Castelli, Ph.D. Università degli Studi di Bologna Struttura del corso PARTE PRIMA - 11 Novembre
Le Derivate. Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri
 Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
Le Derivate Appunti delle lezioni di matematica di A. Pisani Liceo Classico Dante Alighieri Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato durante
4. I principi della meccanica
 1 Leggi del moto 4. I principi della meccanica Come si è visto la cinematica studia il moto dal punto di vista descrittivo, ma non si sofferma sulle cause di esso. Ciò è compito della dinamica. Alla base
1 Leggi del moto 4. I principi della meccanica Come si è visto la cinematica studia il moto dal punto di vista descrittivo, ma non si sofferma sulle cause di esso. Ciò è compito della dinamica. Alla base
Esercizio (tratto dal problema 7.36 del Mazzoldi 2)
 Esercizio (tratto dal problema 7.36 del Mazzoldi 2) Un disco di massa m D = 2.4 Kg e raggio R = 6 cm ruota attorno all asse verticale passante per il centro con velocità angolare costante ω = 0 s. ll istante
Esercizio (tratto dal problema 7.36 del Mazzoldi 2) Un disco di massa m D = 2.4 Kg e raggio R = 6 cm ruota attorno all asse verticale passante per il centro con velocità angolare costante ω = 0 s. ll istante
Capire la Fisica Livello intermedio.
 Capire la Fisica Livello intermedio. Quest opera è stata rilasciata con licenza Creative Commons ttribuzione - Non commerciale - Condividi allo stesso modo 3.0 Italia. Per leggere una copia della licenza
Capire la Fisica Livello intermedio. Quest opera è stata rilasciata con licenza Creative Commons ttribuzione - Non commerciale - Condividi allo stesso modo 3.0 Italia. Per leggere una copia della licenza
Controllo dell assetto variabile per Treni ETR-450
 UNIVESITÀ DEGLI STUDI DI OMA TO VEGATA FACOLTÀ DI INGEGNEIA Corso di Laurea in Ingegneria Informatica elazione per il corso di Misure per l Automazione Controllo dell assetto ariabile per Treni ET-450
UNIVESITÀ DEGLI STUDI DI OMA TO VEGATA FACOLTÀ DI INGEGNEIA Corso di Laurea in Ingegneria Informatica elazione per il corso di Misure per l Automazione Controllo dell assetto ariabile per Treni ET-450
Cenni di geometria differenziale delle superfici.
 Cenni di geometria differenziale delle superfici. 1. Superfici parametrizzate nello spazio. Definizione. Una superficie parametrizzata in IR 3 è un applicazione S: Ω IR 3, (u, S 1(u, S 2 (u,, S 3 (u, doe
Cenni di geometria differenziale delle superfici. 1. Superfici parametrizzate nello spazio. Definizione. Una superficie parametrizzata in IR 3 è un applicazione S: Ω IR 3, (u, S 1(u, S 2 (u,, S 3 (u, doe
Ottavio Serra Introduzione alla fisica quantistica Cap 1 Le difficoltà della fisica classica.
 Ottavio Serra Introduzione alla fisia quantistia Cap 1 Le diffioltà della fisia lassia. La fisia lassia, essenzialmente dovuta a Galileo e Newton per la meania, a Faraday e Maxwell per l'elettromagnetismo,
Ottavio Serra Introduzione alla fisia quantistia Cap 1 Le diffioltà della fisia lassia. La fisia lassia, essenzialmente dovuta a Galileo e Newton per la meania, a Faraday e Maxwell per l'elettromagnetismo,
e del guadagno percentuale in conto capitale, dato da e v
 Esame di Eonomia Politia - Istituzioni (A-K) Svolgimento della prova sritta del 8 aprile 2009 B questo è uno svolgimento ompleto, e potrebbe essere molto più sintetio FILA 3 1) (a) Si spieghi il signifiato
Esame di Eonomia Politia - Istituzioni (A-K) Svolgimento della prova sritta del 8 aprile 2009 B questo è uno svolgimento ompleto, e potrebbe essere molto più sintetio FILA 3 1) (a) Si spieghi il signifiato
Equazioni di secondo grado intere letterali
 Equazioni di seondo grado intere letterali Esempio. k ) x k + )x + k + 0 a k b k + ) k + Disussione. Se k 0 k l equazione si abbassa di grado. Disutiamo il aso a 0 aso in ui l equazione diventa di primo
Equazioni di seondo grado intere letterali Esempio. k ) x k + )x + k + 0 a k b k + ) k + Disussione. Se k 0 k l equazione si abbassa di grado. Disutiamo il aso a 0 aso in ui l equazione diventa di primo
1 L'esperimento di Michelson-Morley
 1 L'esperimento di Michelson-Morley La presentazione dell'esperimento di Michelson-Morley persegue il duplice scopo di: mostrare la metodologia seguita in sica nel suo processo di verica e estensione della
1 L'esperimento di Michelson-Morley La presentazione dell'esperimento di Michelson-Morley persegue il duplice scopo di: mostrare la metodologia seguita in sica nel suo processo di verica e estensione della
simmetria sferica. L intensità (potenza per unità di superficie) a distanza L vale allora I = P / 4π L
 Fisia Generale Modulo di Fisia II A.A. -5 seritaione OND LTTROMAGNTICH Gb. Si onsideri un onda elettromagnetia piana sinusoidale he si propaga nel vuoto nella direione positiva dell asse x. La lunghea
Fisia Generale Modulo di Fisia II A.A. -5 seritaione OND LTTROMAGNTICH Gb. Si onsideri un onda elettromagnetia piana sinusoidale he si propaga nel vuoto nella direione positiva dell asse x. La lunghea
TRASFORMATA DI HILBERT
 TRASFORMATA DI ILBERT La Trasformata di ilbert è una partiolare rappresentazione he, ontrariamente ad altre trasformate (Fourier, Laplae, Z, ) non realizza un ambiamento del dominio di definizione. In
TRASFORMATA DI ILBERT La Trasformata di ilbert è una partiolare rappresentazione he, ontrariamente ad altre trasformate (Fourier, Laplae, Z, ) non realizza un ambiamento del dominio di definizione. In
6. Moto in due dimensioni
 6. Moto in due dimensioni 1 Vettori er descriere il moto in un piano, in analogia con quanto abbiamo fatto per il caso del moto in una dimensione, è utile usare una coppia di assi cartesiani, come illustrato
6. Moto in due dimensioni 1 Vettori er descriere il moto in un piano, in analogia con quanto abbiamo fatto per il caso del moto in una dimensione, è utile usare una coppia di assi cartesiani, come illustrato
FORMARSI AGGIORNARSI CONDIVIDERE. I webinar per gli insegnanti di matematica e scienze
 FORMARSI AGGIORNARSI CONDIVIDERE I webinar per gli insegnanti di matematica e scienze Insegnare la relatività Parte I 17 febbraio 016 Vincenzo Barone (Università del Piemonte Orientale e INFN) Preparare
FORMARSI AGGIORNARSI CONDIVIDERE I webinar per gli insegnanti di matematica e scienze Insegnare la relatività Parte I 17 febbraio 016 Vincenzo Barone (Università del Piemonte Orientale e INFN) Preparare
TEORIA DEI SISTEMI SISTEMI LINEARI
 TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI SISTEMI LINEARI Ing. Cristian Secchi Tel.
TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI SISTEMI LINEARI Ing. Cristian Secchi Tel.
Appunti di Relatività Ristretta
 I.S.I.S.S. A. Sarpa Motta di Livenza (TV) Lieo Sientifio Classe V A Anno Solastio 007/008 Appunti di Relatività Ristretta Esher Relatività Tutto è relativo! L astuzia matematia di Lorentz Il pensiero innovativo
I.S.I.S.S. A. Sarpa Motta di Livenza (TV) Lieo Sientifio Classe V A Anno Solastio 007/008 Appunti di Relatività Ristretta Esher Relatività Tutto è relativo! L astuzia matematia di Lorentz Il pensiero innovativo
Test sull ellisse (vai alla soluzione) Quesiti
 Test sull ellisse (vai alla soluzione) Quesiti ) Considerata nel piano cartesiano l ellisse Γ : + y = 8 valutare il valore di verità delle seguenti affermazioni. I fuochi si trovano sull asse delle ordinate
Test sull ellisse (vai alla soluzione) Quesiti ) Considerata nel piano cartesiano l ellisse Γ : + y = 8 valutare il valore di verità delle seguenti affermazioni. I fuochi si trovano sull asse delle ordinate
Appunti di Logica Ternaria: Operatori Diadici
 Appunti di Logia Ternaria: Operatori Diadii Giuseppe Talario 27 Gennaio 2014 Nella logia ternaria, una taella di verità on due ingressi ha nove righe, per ui ne onsegue he il numero totale delle funzioni
Appunti di Logia Ternaria: Operatori Diadii Giuseppe Talario 27 Gennaio 2014 Nella logia ternaria, una taella di verità on due ingressi ha nove righe, per ui ne onsegue he il numero totale delle funzioni
L elettrodinamica dei corpi in movimento 1 A. Einstein
 L elettrodinamica dei corpi in moimento A Einstein È noto che l elettrodinamica di Maxwell - come la si interpreta attualmente - nella sua applicazione ai corpi in moimento porta a delle asimmetrie che
L elettrodinamica dei corpi in moimento A Einstein È noto che l elettrodinamica di Maxwell - come la si interpreta attualmente - nella sua applicazione ai corpi in moimento porta a delle asimmetrie che
7 Settimana 7-11 novembre
 7 Settimana 7-11 novembre 7.1 Topologia di R Definizione 7.1 Sia x R. Un insieme U R si die intorno di x se ontiene un intervallo aperto ontenente x. Equivalentemente, se esiste ɛ > 0 tale he ]x ɛ, x +
7 Settimana 7-11 novembre 7.1 Topologia di R Definizione 7.1 Sia x R. Un insieme U R si die intorno di x se ontiene un intervallo aperto ontenente x. Equivalentemente, se esiste ɛ > 0 tale he ]x ɛ, x +
edutecnica.it Circuiti in alternata -Esercizi 1 La tensione sinusoidale di frequenza f =1kHz è espressa in forma binomiale:
 edutecnica.it Circuiti in alternata -Esercizi Esercizio no. Soluzione a pag.7 Una corrente alternata sinusoidale è espressa in forma binomiale come I 7 j5 [ A] si risalga alla sua forma trigonometrica..[
edutecnica.it Circuiti in alternata -Esercizi Esercizio no. Soluzione a pag.7 Una corrente alternata sinusoidale è espressa in forma binomiale come I 7 j5 [ A] si risalga alla sua forma trigonometrica..[
L offerta della singola impresa: le curve di costo
 L offerta della singola impresa: le urve di osto La funzione di osto totale è di un impresa orrispondono alla somma dei osti fissi e dei osti variabili I osti fissi F sono quelli he sono sostenuti indipendentemente
L offerta della singola impresa: le urve di osto La funzione di osto totale è di un impresa orrispondono alla somma dei osti fissi e dei osti variabili I osti fissi F sono quelli he sono sostenuti indipendentemente
Geometria analitica del piano pag 32 Adolfo Scimone
 Geometria analitica del piano pag 32 Adolfo Scimone CAMBIAMENTI DI SISTEMA DI RIFERIMENTO Consideriamo il piano cartesiano R 2 con un sistema di riferimento (O,U). Se introduciamo in R 2 un secondo sistema
Geometria analitica del piano pag 32 Adolfo Scimone CAMBIAMENTI DI SISTEMA DI RIFERIMENTO Consideriamo il piano cartesiano R 2 con un sistema di riferimento (O,U). Se introduciamo in R 2 un secondo sistema
Fisica dei mezzi trasmissivi Prof. G. Macchiarella Prova del 28 Febbraio 2013
 Fisia dei mezzi trasmissivi Prof. G. Mahiarella Prova del 8 Febbraio 013 1 3 4 non srivere nella zona soprastante COGNOME E NOME MTRICO FIRM Eserizio 1 Un generatore, la ui tensione varia nel tempo ome
Fisia dei mezzi trasmissivi Prof. G. Mahiarella Prova del 8 Febbraio 013 1 3 4 non srivere nella zona soprastante COGNOME E NOME MTRICO FIRM Eserizio 1 Un generatore, la ui tensione varia nel tempo ome
CINEMATICA a.s.2007/08 Classe III C Scuola Media Sasso Marconi. SINTESI E APPUNTI Prof.ssa Elena Spera
 CINEMATICA a.s.2007/08 Classe III C Scuola Media Sasso Marconi SINTESI E APPUNTI Prof.ssa Elena Spera 1 SISTEMI DI RIFERIMENTO Il moto è relatio Ogni moto a studiato dopo aere fissato un sistema di riferimento,
CINEMATICA a.s.2007/08 Classe III C Scuola Media Sasso Marconi SINTESI E APPUNTI Prof.ssa Elena Spera 1 SISTEMI DI RIFERIMENTO Il moto è relatio Ogni moto a studiato dopo aere fissato un sistema di riferimento,
Convertitori da tensione a impulsi
 Misure basate sul conteggio di impulsi Conertitori da tensione a impulsi - Conertitori da tensione a impulsi - Conertitore tensione-frequenza Schema di principio Il conertitore tensione-frequenza consente
Misure basate sul conteggio di impulsi Conertitori da tensione a impulsi - Conertitori da tensione a impulsi - Conertitore tensione-frequenza Schema di principio Il conertitore tensione-frequenza consente
1.4 Geometria analitica
 1.4 Geometria analitica IL PIANO CARTESIANO Per definire un riferimento cartesiano nel piano euclideo prendiamo: Un punto detto origine i Due rette orientate passanti per. ii Due punti e per definire le
1.4 Geometria analitica IL PIANO CARTESIANO Per definire un riferimento cartesiano nel piano euclideo prendiamo: Un punto detto origine i Due rette orientate passanti per. ii Due punti e per definire le
Moto vario elastico: fenomeno del colpo d ariete
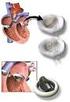 Moto vario elastio: fenomeno del olpo d ariete 1. Desrizione del fenomeno Si onsideri un semplie impianto ostituito da un serbatoio di grande ampiezza in modo tale he in esso il livello di ario rimanga
Moto vario elastio: fenomeno del olpo d ariete 1. Desrizione del fenomeno Si onsideri un semplie impianto ostituito da un serbatoio di grande ampiezza in modo tale he in esso il livello di ario rimanga
CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI. 1 Fondamenti Segnali e Trasmissione
 CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI Fondamenti Segnali e Trasmissione Numerizzazione dei segnali Nei moderni sistemi di memorizzazione e trasmissione i segnali in ingresso sono di tipo numerio, normalmente
CAMPIONAMENTO E RICOSTRUZIONE DI SEGNALI Fondamenti Segnali e Trasmissione Numerizzazione dei segnali Nei moderni sistemi di memorizzazione e trasmissione i segnali in ingresso sono di tipo numerio, normalmente
I VETTORI DELLO SPAZIO
 I VETTORI DELLO SPAZIO Riferimento cartesiano ortogonale nello spaio Bisogna assegnare nello spaio un punto O (detto origine e tre rette per esso a due a due perpendicolari e orientate in modo concorde
I VETTORI DELLO SPAZIO Riferimento cartesiano ortogonale nello spaio Bisogna assegnare nello spaio un punto O (detto origine e tre rette per esso a due a due perpendicolari e orientate in modo concorde
ISTITUTO DI MACCHINE COLLANA DIDATTICA
 FACOLTA DI INGEGNERIA ISTITUTO DI MACCHINE UNIVERSITA DI NAPOLI COLLANA DIDATTICA Eseritazione sull uso dei diagrammi termodinamii dei gas freshi e dei gas ombusti per motori a.i. ad aensione omandata.
FACOLTA DI INGEGNERIA ISTITUTO DI MACCHINE UNIVERSITA DI NAPOLI COLLANA DIDATTICA Eseritazione sull uso dei diagrammi termodinamii dei gas freshi e dei gas ombusti per motori a.i. ad aensione omandata.
La traduzione dei problemi: dal linguaggio naturale al linguaggio dell algebra
 Livello solare: 1 biennio La traduzione dei problemi: dal linguaggio naturale al linguaggio dell algebra Abilità Interessate In situazioni problematihe, individuare relazioni signifiative tra grandezze
Livello solare: 1 biennio La traduzione dei problemi: dal linguaggio naturale al linguaggio dell algebra Abilità Interessate In situazioni problematihe, individuare relazioni signifiative tra grandezze
Indirizzo : Scientifico Tecnologico. Corso sperimentale Progetto Brocca. Primo Quesito
 Indirizzo : Sientifio Tenologio Primo Quesito Corso sperimentale Progetto Broa Con la storia memoria dal titolo Teoria della legge di distribuzione dell energia dello spettro normale presentata all Aademia
Indirizzo : Sientifio Tenologio Primo Quesito Corso sperimentale Progetto Broa Con la storia memoria dal titolo Teoria della legge di distribuzione dell energia dello spettro normale presentata all Aademia
TRIGONOMETRIA. Un angolo si misura in gradi. Un grado è la novantesima parte di un angolo retto.
 TRIGONOMETRIA DA RICORDARE: Due angoli si dicono supplementari quando la loro somma è pari a 80 Due angoli si dicono complementari quando la loro somma è pari a 90 Due angoli si dicono opposti quando la
TRIGONOMETRIA DA RICORDARE: Due angoli si dicono supplementari quando la loro somma è pari a 80 Due angoli si dicono complementari quando la loro somma è pari a 90 Due angoli si dicono opposti quando la
PROFILI DI CORRENTE IN MOTO PERMANENTE
 PROFILI DI CORRENTE IN MOTO PERMANENTE I lassii approi relativi al dimensionamento ed alla verifia delle analizzazioni per fognatura e, più in generale, delle orrenti a pelo libero, muovono dall'ipotesi
PROFILI DI CORRENTE IN MOTO PERMANENTE I lassii approi relativi al dimensionamento ed alla verifia delle analizzazioni per fognatura e, più in generale, delle orrenti a pelo libero, muovono dall'ipotesi
Onde. la definizione di onda può essere data nel modo che segue: un onda è una perturbazione che si propaga nel vuoto o in un mezzo materiale.
 Onde 1. La definizione di onda Premesso che: un mezzo materiale è un mezzo dotato di massa ( acqua, tubo di acciaio, aria, legno ) una perturbazione è una ariazione di una o più grandezze fisiche, la definizione
Onde 1. La definizione di onda Premesso che: un mezzo materiale è un mezzo dotato di massa ( acqua, tubo di acciaio, aria, legno ) una perturbazione è una ariazione di una o più grandezze fisiche, la definizione
Politecnico di Torino Laurea a Distanza in Ingegneria Meccanica Corso di Macchine
 ESERCIZI SVOLTI Sono di seguito svolti due eserizi sulle turbine a vapore assiali, aggiuntivi rispetto a quelli svolti durante il tutorato (i ui testi e i risultati numerii sono riportati alla fine del
ESERCIZI SVOLTI Sono di seguito svolti due eserizi sulle turbine a vapore assiali, aggiuntivi rispetto a quelli svolti durante il tutorato (i ui testi e i risultati numerii sono riportati alla fine del
MATEMATICA CORSO A COMPITINO DI RECUPERO (Tema 2) 13 Febbraio 2014
 MATEMATICA CORSO A COMPITINO DI RECUPERO (Tema 2) 13 Febbraio 2014 Soluzioni 1. In un sahetto i sono 9 palline olorate: 2 rosse, 4 verdi e 3 gialle. Si fanno 3 estrazioni on rimessa. a) Calola la probabilità
MATEMATICA CORSO A COMPITINO DI RECUPERO (Tema 2) 13 Febbraio 2014 Soluzioni 1. In un sahetto i sono 9 palline olorate: 2 rosse, 4 verdi e 3 gialle. Si fanno 3 estrazioni on rimessa. a) Calola la probabilità
LEZIONE 27. C = { P = (x, y) x 2 /a 2 y 2 /b 2 = 1 }. C si dice iperbole di semiassi a e b (in forma canonica). L equazione
 LEZIONE 27 27.1. Ellisse, iperbole, parabola. Nelle prossime lezioni illustreremo come la teoria delle forme quadratiche e della riduzione ortogonale si applichi allo studio di alcuni oggetti geometrici
LEZIONE 27 27.1. Ellisse, iperbole, parabola. Nelle prossime lezioni illustreremo come la teoria delle forme quadratiche e della riduzione ortogonale si applichi allo studio di alcuni oggetti geometrici
Note per il corso di Geometria e algebra lineare 2009-10 Corso di laurea in Ing. Elettronica e delle Telecomunicazioni
 Note per il corso di Geometria e algebra lineare 009-0 Corso di laurea in Ing. Elettronica e delle Telecomunicazioni Spazi di n-uple e matrici. I prodotti cartesiani RR R e RRR R 3, costituiti dalle coppie
Note per il corso di Geometria e algebra lineare 009-0 Corso di laurea in Ing. Elettronica e delle Telecomunicazioni Spazi di n-uple e matrici. I prodotti cartesiani RR R e RRR R 3, costituiti dalle coppie
