DEFORMAZIONI PROSPETTICHE
|
|
|
- Agnese Farina
- 8 anni fa
- Visualizzazioni
Transcript
1 DEFORMAZIONI PROSPETTICHE PARTE I: trasformazo geometrche 1.1 Itroduzoe Abbamo aalzzato e cercato d correggere l problema delle dstorso geometrche a cu soo soggette le mmag otteute tramte macche fotografche o fotocamere dgtal quado l puto d rpresa della scea o rsulta frotale al soggetto rpreso. Se s uole, per esempo, fotografare u quadro appeso ad ua parete o la faccata d u edfco è opportuo che l pao della fotocamera su cu s forma l mmage sa esattamete parallelo alla tela e alla parete, altrmet s ottee ua foto cu l soggetto, che ella realtà ha forma rettagolare, rsulta restrgers erso l alto oppure aere la forma d u quadrlatero rregolare come llustrao le seguet foto. Fgura 1. 1 Foto affetta da deformazoe del trapezo 1
2 Fgura 1. Foto affetta da deformazoe prospettca I quest cas è utle poter modfcare l mmage modo da smulare u puto d rpresa rspetto al quale s può otteere la corretta geometra della scea. S uole operare tale correzoe medate ua opportua trasformazoe geometrca della mmage che o e alter le caratterstche radometrche. Pochè s è laorato co mmag btmap a 4 bt s soo prese esame trasformazo che operao su sgol pxel dell mmage. Affchè tal trasformazo sao accettabl è ecessaro che esse presero la cotutà delle lee, recproc rapport d poszoe e proporzoe degl oggett e o e altero le forme Aspett geometrc del processo d formazoe delle mmag Per correggere le dstorso geometrche a cu soo soggette le fotografe scattate da u puto d rpresa o ottmale è utle aalzzare la relazoe geometrca tra la scea osserata e quella della corrspodete mmage otteuta co u appareccho fotografco. Tale relazoe s basa sulla geometra proetta e sulla prospetta. S può schematzzare la maccha fotografca come u sstema costtuto da ua camera oscura e dotato d ua apertura ella quale è posta ua lete bcoessa. Questa focalzzado ragg lumos proeet dall estero fa formare sulla parete opposta della camera oscura l mmage degl oggett quadrat che ee po fssata da ua pellcola fotografca. 1 Coè o deoo modfcare la forma degl elemet della scea u modo che o retra ella logca della arazoe del puto d rpresa.
3 ,Y pao mmage x,x puto oggetto (X,Y,Z) z,z F (x,) cetro della lete puto mmage Fgura 1. 3 Modello del sstema d formazoe d u mmage. Il sstema d coordate x,,z costtusce l sstema d coordate fsso della maccha. Il pao x oe s forma l mmage cocde co l fodo della camera oscura e l puto F rappreseta l cetro della lete bcoessa d dstaza focale f. Il sstema d coordate xz costtusce l sstema d coordate fsso della maccha, l asse Z cocde co l asse ottco passate per l cetro del pao d formazoe dell mmage e l cetro F della lete. Le relazo tra gl oggett dello spazo reale e la loro mmage soo regolate dalle legg dell ottca geometrca, secodo cu s suppoe che ragg lumos s propagho lea retta. U geerco puto dello spazo P (puto oggetto) d coordate (X,Y,Z) ee proettato attraerso l puto F u puto P del pao dell mmage d coordate (x,). Dalle smltud de tragol s ottee che x fx f Z fy f Z (1.1) cu l puto proettato o dpede modo leare dal puto oggetto. Per semplfcare tal relazo s è preferto passare alle coordate omogeee. Sa l ettore coteete le coordate del puto oggetto 3
4 X Y Z Il ettore omogeeo corrspodete d é sx sy ' sz s doe s reale è la costate d scala. La matrce rappresetata della proetttà cetrata F è A (1.) f per cu s ha w ' A ' (1.3) co ormalzzado w s ottee sx sy w ' sz sz s f fx f Z fy w f Z fz f Z ettore cu le prme due compoet rsultao ugual alle relazo (1.1). La proezoe ersa che da u puto mmage P d coordate (x,) tora detro al puto oggetto corrspodete P è data da 4
5 co ' ' A -1 w (1.4) A (1.5) f sx s w ' sz s cu z é ua arable lbera. Calcolado qud la trasformazoe prospettca ersa s ottee coordate omogeee sx s ' sz sz s + f Le corrspodet coordate cartesae soo Oppure fx f z f (1.6) f z fz f z fx X f z f Y f z fz Z f z Rsoledo rspetto a z e sosttuedo s ottee (1.7) 5
6 x X ( f Z) f Y ( f Z) f (1.8) Da queste relazo s rlea mmedatamete che, pochè z è arbtraro, l fbrato del puto mmage (x,) tramte la proezoe è costtuto da tutt put della retta cogugete l puto mmage co l fuoco F che hao Z>f. Il processo d proezoe o è uoco e tutt put della retta PF egoo proettat el puto P. E qud ecessaro specfcare ua delle coordate d u puto oggetto, per esempo Z, per determare le altre due a partre da quelle del puto mmage (x,). Ioltre l oggetto osserato dee troars oamete aterormete alla maccha fotografca ossa Z dee essere tale che Z>f. Ua poszoe o ottmale del pao d formazoe dell mmage rspetto alla scea che s uole fotografare può dare orge ella foto a deformazo geometrche che alterao le forme degl oggett fotografat. 1.3 Modello matematco dscreto dell mmage S è laorato co mmag dgtal btmap a 4 bt adatte ad essere mapolate da u calcolatore. Da u puto d sta matematco esse possoo essere approssmate co ua matrce a alor ter del tpo: G(1,1) G(1,) G(1,3) G(1, K) G(,1) G(, ) G(,3) G(, K) G( j, k) G( J,1) G( J,) G( J,3) G( J, K) (1.9) Co 1 j J 1 k K J dca l umero d rghe d cu l mmage è composta, K è l umero d pxel per og rga. 6
7 Nelle mmag moocromatche l tero G(j,k) è u alore compreso tra 0 e 55 e rappreseta uo de 56 lell d grgo coè d testà lumosa { } G( j, k) I Ν : 0 55 (1.10) quelle a color ece a cascu elemeto G(,j) della matrce corrspode ua tera ordata d ter (r,g,b) G( j, k) ( r, g, b) oe r,g,b dcao rspettamete le testà d rosso, erde e blu la cu combazoe produce l colore e assumoo alor ter compres tra 0 e 55 corrspodet a 56 ders lell d testà delle tre sorget d colore. G( j, k) Ir I g Ib (1.11) co r g b { : 0 55} { : 0 55} { : 0 55} I Ν I Ν I Ν (1.1) 1.4 Trasformazo geometrche Sa G(j,k) co 1 j J e 1 k K l mmage d output geerata da ua operazoe geometrca sull mmage dscreta d put F(p,q) co 1 p P 1 q Q che oper sulla geometra della scea mateedoe alterate le caratterstche radometrche. I geerale F(p,q )e G(j,k) possoo aere dmeso derse. Quattatamete tale trasformazoe è defta co le formule G( x, ) F( p, q) x t ( p, q) 1 t ( p, q) (1.13) La prma formula dca l uguaglaza dell testà lumosa e put corrspodet delle due mmag, le ultme due dduao le trasformazo tra le coordate de put che s corrspodoo. 7
8 E molto mportate osserare che geerale la coppa (x,), otteuta applcado le trasformazo t 1 e t alla geerca coppa (p,q), o è ua coppa d ter corrspodete ad u elemeto della matrce G(j,k). Se mmagamo l mmage dscreta come ua grgla rettagolare cu od corrspodoo agl elemet della matrce che la approssma, le trasformazo t 1 e t deformao la grgla dell mmage d put ua grgla rregolare come quella mostrata a tratto cotuo ella fgura d destra. Fgura 1. 4 Il prcpo delle trasformazo geometrche. La fgura d destra è l mmage d put co grgla quadrata regolare, quella d sstra a tratto cotuo è l mmage trasformata co grgla rregolare, la grgla regolare tratteggata ddua put dell mmage d output d cu s dee cooscere l testà. La costruzoe dell mmage d output o s può otteere drettamete co od d quest ultma pochè gl elemet della matrce G corrspodoo a od della grgla tratteggata ed è qud ecessaro che sao deft alor dell testà lumosa quest put. Nella pratca per oare a questo problema s utlzzao le trasformazo geometrche erse d t 1 e t che dchamo co t 3 e t 4 x ' t ( j, k) 3 ' t ( j, k) 4 (1.14) Ad og coppa ordata (j,k) co 1 j J e 1 k K corrspodete ad u ertce della grgla tratteggata (o all elemeto G(j,k) della matrce) s assoca la coppa d coordate (x, ). I geerale ache quest ultma o corrspode ad u odo della grgla dell mmage d put ed è qud ecessaro assegargl u opportuo 3 alore attraerso u processo d terpolazoe. Col terme grgla rettagolare dchamo l seme compatto d R [1,J] [1,K] cu è edezato l sottoseme de put (x,) co x o tero. Chamamo odo o ertce della grgla og puto della grgla (x, ) co x e ter. 3 Nel captolo seguete s specfcherà meglo questo puto. 8
9 Fora s è solo specfcato che le trasformazo geometrche coolte operao su sgol pxel: u puto dell mmage d mput ee mappato u puto dell mmage d output. Affchè tal trasformazo sao accettabl è ache ecessaro, come s è acceato ell troduzoe, che esse presero la cotutà delle lee, recproc rapport d poszoe e proporzoe degl oggett e o e altero le forme 4. E oltre mportate osserare che geerale tal trasformazo soo defte basados su sstem d rfermeto d coordate cartesae che o cocdoo co l sstema d dc dell arra assocato all mmage dscreta ed è qud ecessaro d olta olta stablre le relazo che legao quest due rfermet. Nella fgura 1.5 è llustrato per esempo l caso cu l rfermeto cartesao ha l orge (0,0) poszoata ell agolo basso a sstra dell mmage, metre per l arra è l agolo alto a sstra d dc (1,1) che fuge da rfermeto. 1 j k 1 K j J x k Fgura 1. 5 Esempo d mmage cu l rfermeto cartesao (x k, j ) ha orge ell agolo basso a sstra, metre l rfermeto (1,1) dell arra è l agolo alto a sstra. Le relazo tra due sstem soo date da Pù geerale s scre 1 xk k 1 j J + j (1.15) 4 Coè o deoo modfcare la forma degl elemet della scea u modo che o retra ella logca della arazoe della prospetta 9
10 co u e bette. x j k u( j) ( k) (1.16) Le trasformazo geometrche elemetar delle mmag soo le traslazo, le rotazo, cambamet d scala e le proezo Traslazoe La traslazoe a corpo rgdo d u mmage mplca che og suo puto ega spostato d ua certa dstaza ua drezoe fssata. S può quatfcare la traslazoe co u ettore t tx t Se s dcao co ( u, ) le coordate cartesae dell mmage dscreta d put F(p,q) e co q p ( x, ) quelle dell mmage d output G(j,k) s ha k j xk uq tx + t j p (1.17) Le relazo tra gl dc degl arra delle due mmag dscrete s ottegoo compoedo la traslazoe co le relazo che legao tal dc co le corrspodet coordate cartesae. Suppoedo alde le equazo (1.4) s ha j ' p ( P J ) t k ' q + t x (1.18) Il smbolo d prmo dca che, a meo che t x e t o sao alor ter, j e k possoo o essere ter. E qud ecessaro approssmarl all tero pù co ache se questo può comportare la comparsa d spaz uot ell mmage d output. Per etare cò s prefersce operare co le trasformazo erse: per og dce (j,k) dell arra d output G(j,k) s determa l corrspodete dce ell mmage d put F(p,q) tramte 10
11 p ' j + ( P J ) + t q ' k t x (1.19) oe l smbolo d prmo dca acora che p e q o soo ecessaramete ter. E allora opportuo terpolare alor d F(p,q) modo da otteere ua stma ragoeole d F (p,q ) 5 da assegare po a G(j,k) come s edrà el prossmo captolo Trasformazo d scala La dmesoe assoluta d u mmage può essere cambata moltplcado cascua coordata per u fattore d scala. Applcado lo stesso fattore a tutte le coordate s ottee u mmage della stessa forma ma d dmeso dfferet, se ece egoo applcat dfferet fattor alle derse compoet essa arerà sa elle dmeso che ella forma. La relazoe ettorale è data da x k sx 0 uq j 0 s p doe sx e s, dette costat d scalatura, deoo essere real e poste. (1.0) Se soo etrambe maggor d uo s ha u gradmeto, se soo mor u rmpccolmeto. La relazoe tra gl dc degl arra delle mmag d output e put dell esempo cosderato per la traslazoe rsulta ora essere p ' j + J + P + s (1.1) q ' k + sx Ache questo caso o è detto che p e q sao ter ed è percò ecessaro rcorrere all terpolazoe per stmare l alore d F (p,q ) da assegare a G(j,k). 5 L applcazoe F (p,q ) è ua fuzoe defta su [0,P] [0,Q] R a alor I per le mmag moocromatche e I I I per quelle a color tale che F (p,q )F(p,q ) se p,q soo ter altrmet F (p,q ) è otteuto r g b terpolado F(p,q). 11
12 1.4.3 Rotazoe La rotazoe dell mmage rspetto all orge del sstema d ass cartesao è data da xk cosθ sθ uq (1.) j sθ cosθ p doe θ dca l agolo d rotazoe calcolato rspetto all asse orzzotale. S cosdera posta la rotazoe atorara. La rotazoe rspetto ad u geerco puto può essere otteuta traslado l orge del sstema el puto prescelto, applcado la rotazoe (1.) e rportado po co la traslazoe ersa l cetro del sstema ella poszoe zale Composzoe d trasformazo Le operazo d traslazoe, rotazoe e scalatura possoo essere composte tra loro. I quest cas è utle trodurre le coordate omogeee perchè cosetoo la cocateazoe d u umero qualsas d trasformazo elemetar u uca matrce d trasformazoe, operazoe che o è possble compere utlzzado le coordate cartesae perchè le traslazo rchedoo la somma d matrc. S cosder R 3 \{ 0} la relazoe d equaleza data da: ( x, x, x ),(,, ) R 3 \{ 0} due ettor soo equalet ( x, x, x ) (,, ) se e solo se λ R tale che x λ per 0,1, e l relato spazo quozete cu elemet soo dcat co {( x,, z )}. Co le coordate omogeee s detfca la poszoe del puto del pao P d coordate cartesae (x,) utlzzado uo qualuque de ettor rappresetat delle classe {( hx, h, h )} co h R. Le coordate cartesae soo legate a quelle omogeee dalla relazoe 1
13 hx x h h h (1.3) Per semplctà, geere, per rappresetare l puto propro (x,) s scegle l ettore (x,,1) come rappresetate della classe. Tutte le trasformazo fora ste coordate omogeee soo otteute co matrc 3 3 che hao l ataggo d cludere coeffcet d traslazo, rotazo e scalature. L equazoe della traslazoe (1.17) ee coertta el prodotto d matrc quella della rotazoe (1.) x 1 0 tx u 0 1 t x cosθ sθ 0 u sθ cosθ e quella della trasformazoe d scala (1.0) x sx 0 0 u 0 s (1.4) (1.5) (1.6) Per combare u seme d trasformazo omogeee ddual u uca equalete trasformazoe s dee predere l prodotto delle matrc ddual ell orde approprato. S dca la geerca trasformazoe omogeea co la matrce o sgolare a11 a1 a13 T a1 a a3 (1.7) a31 a3 a 33 Se s desdera applcare trasformazo T, 1 T,... T3, T basta cocateare le operazo ua matrce come segue doe e u soo ettor omogee. T... T Tu (1.8) 1 13
14 1.4.5 Trasformazo prospettche Lughezze, agol, parallelsm e forme spesso, quado egoo osserate o fotografate, appaoo dstorte. Per esempo ua rotaa è formata da due bar tra loro parallel che però appaoo ad u osseratore come due lee che s acao tra loro co l aumetare della dstaza fo a toccars all orzzote. All zo del captolo s è defta la proezoe prospettca che approssma l modo co cu u dsposto fotografco costrusce l mmage d u oggetto. Approfodamo questa sezoe gl aspett geometrc d tale proezoe. U buo modello fsco per lo studo della prospetta è l sstema formato da u oggetto b o trdmesoale (Ob) posto ello spazo trdmesoale, da u pao (π) dell mmage (I) cu questa s forma e da u fuoco (O) poszoato dal lato opposto ad Ob rspetto a π. L mmage d cascu puto x dell oggetto è l puto x* tersezoe tra l raggo cogugete x e l fuoco O, detto raggo proettate, e l pao π. S ottee così ua corrspodeza uo a uo tra put dell oggetto e put dell mmage. oggetto O fuoco mmage pao dell mmage Fgura 1. 6 U modello fsco per la soe prospetta d oggett trdmesoal 14
15 Il caso cu O sa tra Ob e π può essere rcodotto al ostro modello poché l mmage che s a a formare su π rsulta per smmetra roescata ma detca a quella che s otterrebbe su u pao π * parallelo e opposto, rspetto ad O, a π. 6 π Ob I * O h π h I Fgura 1. 7 L mmage che s a a formare su π rsulta per smmetra roescata ma detca a quella che s otterrebbe su u pao π * parallelo e opposto, rspetto ad O, a π. Questo laoro s è lmtato allo studo della prospetta d oggett che s possoo assmlare, co buoa approssmazoe, ad elemet pa. Le rago d questa lmtazoe ao rcercate el fatto che l ostro scopo è defre trasformazo dell mmage che permettao geerale d otteere, a partre dalla stessa, u mmage che smul u puto d rpresa derso rspetto a quello da cu s è scattata la foto. Quado però s fotografa ua scea trdmesoale tale smulazoe o è possble quato la trasformazoe geometrca che la opera o può essere defta ello stesso modo per tutt put della foto. U elemeto 3D è terpretable come composzoe d superfc D. L mmage che s ha da u puto d rpresa A d tal superfc dpede dalla loro poszoe rspetto ad A. Quado s camba puto d rpresa da A a B la uoa soe che s ha da B d cascua d esse dpede dalla loro uoa poszoe rspetto a B stesso. La trasformazoe geometrca che smula questo cambameto dee qud teere coto che la deformazoe che l mmage d cascua superfce dee subre è dersa da superfce a superfce. Nella fgura seguete per esempo le deformazo che le superfc 1, e 3 deoo subre per essere trasformate rspettamete ella superfce 1, e 3 soo derse tra loro. 6 Retra questo modello l sstema d formazoe dell mmage llustrato el paragrafo 1. 15
16 Fgura 1. 8 Il cubo elemeto trdmesoale ee decomposto superfc D Quado s uole smulare u puto d rpresa derso cascua d esse subsce ua deformazoe dersa per essere trasformata. Esempo la trasformazoe che mappa 1 1 presera le lee ertcal, metre quella che mappa 3 3 o. S dorebbe qud poter dduare ella foto cascua delle superfc che compogoo l elemeto 3D e defre per ogua d esse ua mappa d trasformazoe dersa; è mpossble otteere u algortmo, l cu costo computazoale sa accettable, che realzz tutto cò. Come llustra l esempo elle foto 1.9 e 1.10 l applcazoe a mmag d soggett 3D delle trasformazo defte per scee pae che soo è studate può geerare deformazo aomale degl oggett. Fgura 1. 9 Foto orgale 16
17 Fgura Correzoe della foto 1.9 co proezoe : la faccata del palazzo ee trasformata modo corretto, la torre, ece, essedo u elemeto trdmesoale subsce ua deformazoe aomala Ife s può osserare che ella rduzoe prospettca dallo spazo 3D dell oggetto a quello D dell mmage s perdoo formazo sulla scea: gl elemet della scea che soo ascost all obetto della maccha o compaoo ell mmage. I geerale però, quado s camba puto d rpresa, elemet che prma rsultaao ascost potrebbero dere sbl. Nella fgura sottostate s è edezato erde gl elemet o sbl dal puto A e che soo ece sbl dal puto B. Se s suppoe d scattare la foto dal puto A per defre ua trasformazoe dell mmage che e smul la rpresa dal puto B è qud ecessaro recuperare le formazo sugl elemet della scea sbl da B ma è mpossble poter rsalre solo attraerso l mmage otteuta da A alle formazo relate alla zoa ascosta rspetto ad A. 17
18 A B Fgura Dal puto d rpresa B s possoo edere sa la crcofereza pccola che l lato del petagoo erde che o soo sbl da A. Il modello per lo studo della prospetta d u oggetto pao permette d specfcare ache l pao π 0 coteete l oggetto (pao reale). I partcolare put apparteet all tersezoe tra π 0 e π (lea d terra lt) rsultao put fss della mappa tra Ob ed I. Pao dell mmage fuoco O mmage oggetto lea d terra pao reale Fgura 1. 1 Modello pao per la prospetta L aals della fgura d due rette d π 0, tra loro parallele e cdet la lea d terra, troduce l cocetto d puto d fuga o puto all orzzote defto come l puto dell mmage cu le due 18
19 rette parallele appaoo cotrars; el ostro modello è l lmte delle mmag de put dell oggetto dspost su due lee parallele che s allotaao sempre pù dal fuoco. 7 puto d fuga π O fuoco π o lt Fgura Il puto d fuga ell mmage d due rette parallele ortogoal alla lea d terra è l tersezoe delle loro mmag. L mmage d rette parallele alla lea d terra presera tale parallelsmo. Geometrcamete l puto all orzzote è determato cosderado pa π1 e π passat per O e coteet rspettamete le rette r1 e r, tra loro parallele. puto d fuga l π O π π o π1 r1 r Fgura Idduazoe del puto d fuga tersezoe tra l pao mmage e la retta l a sua olta tersezoe de pa π1, coteete r1 e O, e π coteete r e O. 7 Per la defzoe e la costruzoe del puto all fto s è fatto rfermeto a[13]. 19
20 π. Tal pa, pochè hao O comue, s tersecao ua lea l coteete O e parallela ad r1 e r e al pao π 0. Il puto d fuga è l tersezoe d l co l pao dell mmage. Ifatt l rappreseta la poszoe lmte de ragg proettat de put d r1 e r che s allotaao sempre pù dal fuoco. Cascu raggo proettate appartee a π1 e π, l loro lmte dee essere coteuto π1 Pù geerale per dduare l puto all orzzote è suffcete ua sola lea r. Il pao passate per O e r ed l pao per O, parallelo al pao dell oggetto, s tersecao l, che a sua olta terseca l pao delle mmag el puto all orzzote assocato ad r e a tutte le lee d π 0 ad essa parallele. Fora abbamo cosderato lee dell oggetto perpedcolar al pao dell mmage e π ortogoale a π 0 : gl stess rsultat possoo essere estes al caso cu le lee parallele o soo ortogoal a π, ma comuque lo tersecao, e a pa co agolo d cdeza o retto. Puto d fuga π O s* α s r1 r π o Fgura Cofgurazoe geerale per l puto d fuga: l pao reale e quello mmage o soo ortogoal e le rette r1 e r tra loro parallele o soo perpedcolar alla lea d terra L mmage d ua retta s d π 0 parallela alla lea d terra è ua retta s* d π ach essa parallela alla lea d terra. Se terpretamo la prospetta come ua corrspodeza betta tra put del pao dell oggetto e put del pao dell mmage, che assoca ad x d π 0 x* d π tersezoe tra quest e l raggo 0
21 sa proettate tra x e O, s poe l problema che tale applcazoe sa defta og puto d π 0 e che og puto d π mmage d u puto d π 0. Da qu la ecesstà d trodurre put all fto (dett ache put mpropr o deal) oggetto d aals della geometra proetta e d cosderare coordate omogeee. E mportate edezare che ua prospetta o ua composzoe d prospette hao la propretà d madare put learmete dpedet put learmete dpedet (mappa coè rette rette) e che la restrzoe della prospetta a ua qualuque retta del pao π 0 è acora ua prospetta. Da cò s può cocludere che tal trasformazo soo partcolar applcazo proette 8 cu l fuoco è l cetro della trasformazoe 9. Se s dca co l geerco puto del pao reale e co P ( x,, z ) P ( x,, z ) l suo corrspodete el pao mmage, la geerca proezoe è defta dalla relazoe P T P (1.9) co a11 a1 a13 T a1 a a3 (1.30) a31 a3 a 33 matrce o sgolare. 1.5 Correzoe della dstorsoe trapezodale Questa procedura corregge la dstorsoe trapezodale feomeo d deformazoe dell mmage che s erfca quado l pao dell mmage o è parallelo al pao dell oggetto ma forma co questo u agolo α rspetto all asse orzzotale dell mmage. L mmage rsulta così pù larga ella zoa ferore e pù stretta quella superore o ceersa (per ulteror approfodmet s rmada al paragrafo precedete sulla geometra proetta ). 8 Per la defzoe d proetttà s eda appedce A 9 Per la dmostrazoe che ua qualuque applcazoe betta tra due pa che goda delle propretà appea eucate sa ua proetttà s eda l teorema 1 appedce A 1
22 S è sto el paragrafo 1. che dal puto d sta proetto l modello della formazoe d u mmage co ua fotocamera può essere schematzzato co ua proezoe cetrale (fgura 1.3) cu gl oggett cambao forma e dmesoe fuzoe della loro dstaza dal cetro della proezoe corrspodete alla lete secodo le equazo (1.3) e (1.4). S suppoe d laorare co foto d scee che possoo essere approssmate come pae per cu è possble defre l pao che le cotee detto pao reale (pr). pr F pf α Fgura Il pao reale pr e quello dell mmage pf o soo parallel ma formao u agolo d cdeza α rspetto all asse orzzotale dell mmage
23 pm pf h L f F O -L h pr V α Fgura Il pao reale pr e quello dell mmage pf formao u agolo d tersezoe α, l pao della mappa pm è parallelo a pr. L agolo tra questo e l pao dell mmage (pf) è detto agolo d clazoe (α), se è zero l mmage che s ottee è ertcale, altrmet rsulta dstorta. S suppoe oltre d essere e cas cu la lea d terra lt, tersezoe tra pf e pr è perpedcolare all asse ertcale sa della scea che dell mmage per cu le lee parallele ad lt o appaoo alterate. Questo algortmo procede alla correzoe proetta della foto clata dal pao della foto ad u opportuo pao parallelo al pao reale detto pao della mappa (pm). L mmage otteuta dopo 3
24 la correzoe prospettca rsulta a sua olta ua proezoe prospettca rspetto ad F dell oggetto sul pao della mappa, pochè però quest ultmo è scelto parallelo al pao reale, l mmage corretta matee le proporzo dell oggetto reale. S cosdero sull mmage d put e su quella d output due sstem d coordate cartesae ortoormal, rspettamete Ox e O ' x, aet etramb orge el cetro della foto, asse delle ascsse orzzotale oretato da sstra a destra e asse delle ordate ertcale oretato dall alto erso l basso. (0,0) x Fgura Sstema d coordate cartesae assocate all mmage Pochè le dmeso delle mmag soo fte s ha che L x L x x L L L ' x L ' x x L ' L' (1.31) Co Lx e L dat e L ' x e L ' da determars. La proetttà da defre mappa u puto P dell mmage d put d coordate cartesae ( x, ) u puto P dell mmage d output d coordate ( x, ). Pochè s opera co proetttà è opportuo passare alle coordate omogeee: P è dduato dal ettore ( x,, z ) legato a ( x, ) da x x z z (1.3) 4
25 P da ( x,, z ) legato a ( x, ) da x x z z (1.33) Dato che put P soo propr per semplctà s è posto s ha così z 1 P ( x,,1) P ( x,, z ) La proezoe forma ettorale assume la forma P MP (1.34) co a, b, c R. Oppure solgedo l prodotto x a1 b1 c1 x a b c z a3 b3 c (1.35) x a x + b + c (1.36) a x + b + c (1.37) z a x + b + c (1.38) Per poter defre uocamete la mappa è ecessaro cooscere la focale co cu s è scattata la foto e poter dduare all tero d questa ua lea retta l che ella realtà s sa essere ertcale, questo modo, come s edrà pù aat s può rsalre all agolo d clazoe 5
26 V l Fgura La retta edezata rosso dee essere raddrzzata Fgura 1. 0 La lea rossa ella foto rappreseta u esempo d retta l che dee essere raddrzzata Sa f la dstaza focale e ( x 1, 1),( x, ) put che dduao l S ddua l puto d fuga 6 dcato co V d coordate (0, ) co 6 Per la defzoe d puto d fuga s rmada alla sezoe
27 1 x x x 1 tersezoe tra la retta l e l asse ertcale. Perchè l raddrzzameto essere applcato dee alere (1.39) possa > L (1.40) ossa la foto o dee rtrarre la lea d orzzote della scea. La proezoe presera la cetraltà della fgura rspetto all asse ertcale. Tutt put co ascssa x 0 soo mappat put co x 0 dpedetemete dalla loro ordata. Dall equazoe (1.36) sosttuedo s ottee se e solo se x a 0 + b + c c 1 0 (1.41) b 1 0 (1.4) Secodo la teora prospettca put co ordata appartegoo alla lea d orzzote e deoo essere mappat u puto mpropro (co z 0 ), dpedetemete dall ascssa. Dall equazoe (1.38) sosttuedo s ottee x se e solo se z a x b c c a 3 0 (1.43) b (1.44) 3 3 I base alla defzoe d puto d fuga fssato l puto P d coordate ( x, ) la retta t cogugete P co V dee essere proettata ua retta t parallela all asse. La scelta della partcolare parallela è legata alla scelta del partcolare pao pm parallelo al pao reale ed è qud arbtrara 7
28 t t V P Fgura 1. 1 La retta t dee essere proettata ella retta t parallela all asse L h F o -L h pm Fgura 1. Il pao pm è scelto modo tale che hh S è optato d sceglere l pao pm per cu og puto P del bordo ferore dell mmage d mput d ordata L è mappato puto P d pm aete dstaza h dal fuoco F par a quella che F ha co P (dcata co h) h h ' (1.45) Dalle smltud de tragol e della smmetra della fgura s può osserare che put d coordate ( x, L ) egoo così mappat put co ascssa x x. Questo equale a 8
29 sceglere d madare la retta t d fgura 1.1 ella retta t tersecate t propro el puto d ordata L apparteete al bordo ferore della foto. E molto mportate sottoleare l arbtraretà d questa scelta, ua possble alterata sarebbe stata per esempo optare per l pao pm che mateesse fsse le ascsse de put d ordata 0. I coclusoe s è scelta la proezoe tale che se x x. L allora Sosttuedo elle (1.36), (1.38) tal codzo s ottee era se e solo se x x a1 x + b 1L ( ) x z b3 L a 1 b3 ( L ) 1 (1.46) da cu x b 1 0 (1.47) ( L ) x ( ) (1.48) I bord orzzotal della foto d put deoo essere madat e bord orzzotal d quella d output modo tale che quest ultma rsult cetrata. Se L allora L ' e se L allora L ' dpedetemete dalle ascsse. Da sosttuedo s ottee x da cu a x + b + c z ( ) b3 L ' a x + b L + c b ( L ) a x b L + c L ' b ( L ) 3 3 (1.49) (1.50) a 0 (1.51) 9
30 Sommado la (1.49) e la (1.50) s ottee da cu b L + c bl + c + 0 b ( L ) b ( L ) 3 3 allora c b L (1.5) L b b 3 ( ) (1.53) s poga b bb3 e s semplfch L b ( ) (1.54) La deformazoe prospettca ha alterato ell mmage d put la proporzoe tra altezza e larghezza degl elemet della scea. La determazoe del coeffcete b è legata alla rcostruzoe ell mmage d output delle proporzo preset ella scea reale. Per rsalre al rapporto reale tra altezze e larghezze degl oggett s ossera che ell toro d cascu puto della foto d put, se s cosderao gradezze ftesme, s può supporre co buoa approssmazoe che esso o sa stato alterato dalla deformazoe. Qud, affchè ell mmage d output sao rcostrute le proporzo della scea reale, è ecessaro che la proezoe che s sta defedo preser l rapporto tra altezza e larghezza ftesme preset ell toro del puto dell mmage d put. Per redere meo pesat calcol s cosder l cetro dell mmage d put d coordate (0,0) e el suo toro s predao due cremet ftesm dx, d rspettamete lugo l asse delle ascsse e lugo l asse delle ordate. Se s dca co OP l segmeto d estrem (0,0) e ( dx,0) e co OQ quello d estrem (0,0) e (0, d ) la proezoe, per come è stata fora defta, dee madare OP u segmeto ftesmo 30
31 O P parallelo all asse delle ascsse dell mmage d output e OQ u segmeto ftesmo O Q apparteete all asse delle ordate della stessa; oe O,P,Q soo le mmag d O,P,Q. Sa dx la lughezza d O P e d quella d O Q, d che dall agolo d clazoe α, a partà d cremeto d aumeta, s cosdera qud l rapporto d cosα d per esprmere l rapporto tra le due lughezze a prescdere dall agolo. d dpede sa da d al crescere d α (1.55) Affchè la proezoe rcostrusca le proporzo real essa dee preserare la proporzoe tra gl cremet ertcale e orzzotale ossa dee essere tale da mateere arato l rapporto d : dx (1.56) coè dee alere e scambado gl estrem s ottee d : dx d cos α : dx (1.57) dx dx d cosα (1.58) d Dalle equazo (1.48) e (1.54) derado rspetto a x e s ottee dx L dx ( ) d b L d ( ) che ell toro d (0,0) cu abbamo cosderato gl cremet algoo d d dx dx e sosttuedo ella (1.58) s arra a (1.59) (1.60) (1.61) L ( ) b L (1.6) 3 31
32 ( ) b L L cosα (1.63) 3 Se s ossera ella fgura 1.17 l tragolo OFV è facle edere che cosα f + da cu s ottee (1.64) f + b + L (1.65) Per cocludere se s dca co h la proezoe che s è defta s ha co [ ] [ ] ( x, ) ( x, ) h : Lx, L x L, L Lx ', Lx ' L ', L ' x ( L ) x ( ) f + + L ( ) Restao da determare le dmeso dell mmage d output ossa le costat L (1.66) L ' x e L '. Pochè s è scelto d mateere fsse le ascsse de put del bordo ferore dell mmage d put s ha Sosttuedo ella (1.49) alor deft sopra s rcaa L x L ' (1.67) x L ' f + + L ( L ) L L (1.68) Ache questo caso come per le trasformazo elemetar è opportuo partre da put dell mmage dscreta d output G(j,k) e determare put corrspodet F(p,q ) ell mmage dscreta d put applcado la trasformazoe ersa della proezoe h composta co cambamet d coordate che trasformao gl dc (j,k) ( x, ) e ( x, ) (p,q ) e terpolado el caso cu p e q o sao ter. 3
33 Nelle foto seguet s possoo osserare rsultat otteut mplemetado le relazo troate. I tutt cas l mmage ee raddrzzata mateedo alterate le carratterstche della scea: o c soo dstorso o alterazo degl elemet essa coteut. S ossera però che parte dell mmage è stata taglata, questa perdta d formazo è dretta cosegueza del fatto che s è scelto l bordo ferore della foto d put come retta che matee arate le ascsse. S potrebbe rdurre tale perdta scegledo per esempo la lea passate per l cetro dell mmage. Fgura 1. 3 Immage 1.0 corretta co la trasformazoe del trapezo Fgura 1. 4 Immage otteuta correggedo la foto
34 1.6 Correzoe della dstorsoe rotazoe trapezo Questa procedura s teressa al caso cu s fotografa ua scea che può essere approssmata come paa co ua maccha fotografca ruotata lateralmete rspetto alla ertcale della scea e clata rspetto al pao della stessa. Se s cosdera l sstema d coordate fsso della maccha fotografca, trodotto el paragrafo 1., l pao reale pr questo caso rsulta ruotato attoro agl ass x (asse orzzotale) e z (asse ottco) d due agol o ull. x z Fgura 1. 5 Il pao reale pr rspetto al sstema d rfermeto fsso della maccha fotografca rsulta ruotato d u agolo α attoro all asse x e d u agolo β attoro all asse z. Se β0 s retra el caso della deformazoe del trapezo. L mmage che s ottee rsulta affetta dalla deformazoe del trapezo e gl elemet che ella scea reale erao ertcal appaoo clat rspetto all asse ertcale dell mmage. S dch co α l agolo d clazoe tra l pao reale e quello dell mmage (agolo d rotazoe attoro a x) e co β l agolo tra l asse ertcale della scea reale e quello della foto (agolo d rotazoe attoro a z). 34
35 β pf pr F z α x Fgura 1. 6 Il pao reale pr e quello dell mmage pf hao u agolo d clazoe α. I rosso soo tratteggat bord della foto. L asse è l asse ertcale della scea reale la sua mmage pf è l asse che forma co l asse ertcale della foto ( erde ) u agolo β derso da zero se la maccha fotografca ee ruotata lateralmete ( coè attoro all asse z). Fgura 1. 7 Esempo d foto soggetta a deformazoe del trapezo e rotazoe rspetto alla ertcale. Le rette blu rappresetao le lee l1 ed l selezoate ell mmage d put, l asse, erde, è l asse ertcale della foto, rosso soo dcate le lee parallele alla lea d terra. La retta, gallo, è l mmage dell asse ertcale ( ) della scea reale ortogoale alle lee rosse. L agolo tra e è l agolo d rotazoe laterale β, la loro tersezoe l cetro d tale rotazoe. 35
36 Il pao reale pr e quello dell mmage pf s tersecao lugo ua lea d terra che rsulta ortogoale all asse ertcale della scea reale e forma u agolo par a π+β co l asse ertcale della foto () per cu ell mmage le trasformate delle lee parallele alla lea d terra, che preserao l parallelsmo, costtuscoo u fasco d rette parallele che forma u agolo π+β co ed è perpedcolare alla retta mmage dell asse ertcale della scea reale. L agolo tra e è l agolo β e l loro puto d tersezoe è l cetro C della rotazoe laterale, geere dstto dal cetro della foto O d coordate (0,0). La correzoe prospettca che s dee applcare sull mmage d put dee essere tale da raddrzzare gl elemet clat, redere orzzotal le lee parallele alla lea d terra e correggere la deformazoe del trapezo. S è scelto d operare questa trasformazoe due pass: uo che porta alla defzoe d ua proezoe t che a a correggere la deformazoe trapezodale, l altro che raddrzza la scea applcado ua opportua rotazoe r a suo elemet. Se s dca co I l mmage d put e co O quella d output, la trasformazoe p che mappa I O può essere sta come la composzoe delle due trasformazo t e r O p( I) r( t( I)) Il problema s rduce qud alla defzoe d ua proezoe t del tpo defto ella sezoe 1.5 e d ua rotazoe r. Affchè esse sao defte modo uoco s dee essere grado d rsalre agl agol α e β. S cosdero sull mmage d put I e su quella d output O due sstem d coordate cartesae ortoormal, rspettamete Ox e O ' x, aet etramb orge el cetro della foto, asse delle ascsse orzzotale oretato da sstra a destra e asse delle ordate ertcale oretato dall alto erso l basso. 36
37 (0,0) x Fgura 1. 8 Sstema d coordate cartesae assocate all mmage Pochè le dmeso delle mmag soo fte s ha che Co Lx e L dat e L x L x x L L L ' x L ' x x L ' L ' L ' x e L ' da determars. La trasformazoe p da defre mappa u puto P dell mmage d put d coordate cartesae ( x, ) u puto P dell mmage d output d coordate ( x, ) P p( P ) r( t( P )) Per defre modo uoco le mappe t e r è ecessaro : o cooscere la focale co cu è stata scattata la foto, o poter dduare all tero d questa due rette che ella realtà s sa essere parallele tra loro e ertcal, ma che ell mmage appaoo clate ed cdet el puto d fuga V, o determare la poszoe del cetro C della rotazoe laterale. La focale f e le rette l1 e l o soo suffcet per defre modo uoco le trasformazo fatt, come s può osserare ell mmage sottostate, le rette l1 e l dduao l puto d fuga V, ma è ecessaro cooscere ache l cetro C della rotazoe laterale per determare l agolo β 37
38 l1 l V β1 C1 β C Fgura 1. 9 Le rette l1 e l dduao l puto d fuga cocdete co la loro tersezoe ma è ecessaro determare la poszoe del cetro d rotazoe laterale C ( puto d tersezoe tra e ) per determare β. Nell mmage è edezato come le stesse rette l1 e l possao corrspodere a rotazo lateral d cetro e agol ders (C1 C e β1 β). Noto C fatt s può dduare la retta passate per C e per l puto V e determare l agolo tra e che cocde co β. La proetttà p dee essere tale da mappare ell asse ertcale della foto d output ( x 0 ) e og retta per V ua retta parallela a x 0. Pochè s cosderao mmag d cu s coosce solo la focale e le rette l1 e l dat a ostra dsposzoe soo suffcet per dduare C all tero della foto d put, s è scelto percò d far procedere l utete per tetat facedogl forre u alore λ proporzoale alla dstaza tra O e C. Dat la focale f, put (x1,1),(x,) che dduao l1, (x3,3), (x4,4) che dduao l e λ s procede alla defzoe d t e r: S determa l puto d fuga V d coordate (u,) tersezoe tra l1 ed l co ( 1 3)( x x1)( x4 x3) x1( 1)( x4 x3) + x3( 4 3)( x x1) u (1.69) ( 4 3)( x x1) ( 1)( x4 x3) 38
39 ( x3 x1)( 4 3)( 1) 3( 1)( x4 x3) + 1( 4 3)( x x1) (1.70) ( 4 3)( x x1) ( 1)( x4 x3) S calcola la dstaza CV secodo la formula CV OV λ u Codzoe per poter applcare t è che λ (1 + ) + (1 + ) (1.71) u > L > L x La proezoe t che corregge la deformazoe trapezodale mappa le rette passat per l puto d fuga V rette parallele alla retta per C e V. La sua equazoe è del tpo (1.66) defta el paragrafo 1.5 per cu co co [ ] [ ] ( x, ) ( x ', ') t : Lx, L x L, L Lx ', Lx ' L ', L ' ( L ) x ' x ( ) f + ' + L ( ) L CV (1.7) S determao le dmeso dell mmage d output ossa le costat L ' x e L '. Per la (1.67) s ha e per la (1.68) L x L x ' L ' f + + L ( L ) L L 39
40 S defsce la rotazoe r che muta l fasco d rette parallele alla retta per C e V e coteete le trasformate tramte t d l1 ed l (dcate co t(l1)e t(l)) el fasco d rette parallele all asse ertcale della foto d output. Data l certezza della poszoe d C s prefersce cetrare tale rotazoe O. Per determare l agolo d rotazoe γ che trasform t(l1) e t(l) rette ertcal s calcolao gl agol che t(l1) e t(l) formao co la ertcale della foto, dcat rspettamete co β1 e β: la tagete d γ è uguale alla meda delle taget d β1 e β. Sao (t(x1),t(1)), (t(x),t()), (t(x3),t(3)) e (t(x4),t(4)) le mmag de put dat otteute applcado t, β1 e β soo dat da t( x) t( x1) tgβ1 (1.73) t( ) t( 1) da cu Post t( x4) t( x3) tgβ t( 4) t( 3) (1.74) tgβ1+ tgβ tgγ (1.75) cosγ 1 1+ tg γ sγ tgγ 1+ tg γ r è così defta [ ] [ ] r : Lx ', Lx ' L ', L ' Lx ', Lx ' L ', L ' ( x ', ') ( x, ) co x cos γ x ' s γ ' s γ x ' + cos γ ' (1.76) I coclusoe p ha equazoe p :[ Lx, Lx ] L, L [ Lx ', Lx '] L ', L ' ( x, ) ( x, ) co x r( t( x )) r( t( )) (1.77) 40
41 Ache questo caso, come per la trasformazoe del trapezo, è opportuo partre da put dell mmage dscreta d output G(j,k) e determare put corrspodet F(p,q ) ell mmage dscreta d put applcado la trasformazoe ersa della proezoe p, coè p t r 10, composta co cambamet d coordate che trasformao gl dc (j,k) ( x, ) e ( x, ) (p,q ) e terpolado el caso cu p e q o sao ter. D seguto soo rportat esemp d foto corrette applcado la trasformazoe (1.77) Fgura Correzoe della foto 1.7 Co λ 10.5% 10 Nella composzoe d mappe s assume che l orde co cu s applcao a da destra a sstra 41
42 Fgura Immage orgale Fgura 1. 3 Correzoe della foto 1.31 co λ7% S può osserare che elle foto corrette compaoo zoe ere, esse corrspodoo a put dell mmage d output che la trasformazoe rotazoe assoca a put che soo fuor dall mmage d put. 4
43 1.7 Correzoe d tpo proezoe Questa procedura ee applcata su mmag cu s possoo detfcare due put d fuga V1 e V. Suppoedo d laorare co foto d scee che possoo essere approssmate come pae per cu è possble defre l pao che le cotee detto pao reale pr; questo tpo d mmag s ottee quado l puto d rpresa è tale per cu pr rsulta ruotato attoro agl ass x,,z del sstema d coordate fsso della maccha fotografca d tre agol o ull. x z Fgura Il pao reale pr rspetto al sstema d rfermeto fsso della maccha fotografca rsulta ruotato d u agolo α attoro all asse x, d u agolo β attoro all asse e d u agolo γ attoro all asse z. Se βγ0 s retra el caso della deformazoe del trapezo, se β0 s è el caso della deformazoe rotazoe trapezo. Ache questo caso la formazoe dell mmage può essere schematzzata co ua proezoe cetrale co cetro ella lete della maccha: le rette ertcal e orzzotal della scea reale egoo mappate dalla proezoe rspettamete u fasco d rette passate per V1 e uo passate per V. La trasformazoe prospettca p che s defsce ella procedura dee essere tale da deformare l mmage modo che sembr otteuta da u puto d rpresa frotale alla scea, p è qud u applcazoe da pf a u pao pm parallelo al pao reale e trasforma tutte le rette per V1 rette ertcal e quelle passat per V rette orzzotal. Idcata co I l mmage d put e co O quella d output s ha O p( I ) (1.78) 43
44 Fgura Esempo d mmage a cu applcare la correzoe d tpo proezoe La proezoe p è stata decomposta el prodotto d due proezo h e g del tpo defto el paragrafo 1.5 : O g( h( I)) (1.79) h mappa le rette passat per l puto d fuga V1 rette ertcal, g trasforma le rette per V rette orzzotal mateedo arate quelle ertcal. V1 V V Fgura La correzoe proezoe può essere eseguta applcado due trasformazo tpo trapezo ua che mappa le rette passat per V1 rette ertcal, la secoda che mada le lee per V rette orzzotal mateedo arate quelle ertcal. 44
45 Per defre modo uoco h e g è ecessaro cooscere la focale co cu s è scattata la foto e poter dduare all tero d questa ua coppa d rette (l1 el) che ella realtà s sa essere parallele e ertcal e che ell mmage appaoo oblque e cdet quello che è l puto d fuga V1 e ua coppa d rette (l3 e l4) che ella realtà s sa essere parallele e orzzotal ma appaoo ella foto oblque e cdet el secodo puto d fuga V. S cosdero sull mmage d put e su quella d output due sstem d coordate cartesae ortoormal, rspettamete Ox e O ' x, aet etramb orge el cetro della foto, asse delle ascsse orzzotale, oretato da sstra a destra, e asse delle ordate ertcale, oretato dall alto erso l basso, come llustrato fgura Pochè le dmeso delle mmag soo fte s ha che Co Lx e L dat e L x L x x L L L" x L" x x L" L" L" x e L " da determars. La proetttà da defre mappa u puto ( x, ) u puto P dell mmage d output d coordate ( x, ). P dell mmage d put d coordate cartesae Data la focale f e put (x1,1), (x,) che dduao l1,(x3,3),(x4,4) che dao l, (x5,5),(x6,6) per l3 e (x7,7),(x8,8) per l4 S ddua l puto d fuga V1 tersezoe d l1 e l d coordate (u1,1) co ( 1 3)( x x1)( x4 x3) x1( 1)( x4 x3) + x3( 4 3)( x x1) u1 (1.80) ( 4 3)( x x1) ( 1)( x4 x3) ( x3 x1)( 4 3)( 1) 3( 1)( x4 x3) + 1( 4 3)( x x1) 1 (1.81) ( 4 3)( x x1) ( 1)( x4 x3) Perchè l raddrzzameto h possa essere applcato dee alere u1 > L 1 > L x S cosdera la traslazoe t1 che porta l asse ertcale x u1 x 0 d equazoe 45
46 x x u1 l puto d fuga V1 ha ora coordate (0,1) (1.8) S applca la proezoe h defta ella sezoe 1.5 d equazoe co e co 1. [ ] [ ] ( x, ) ( x ', ') h : Lx, L x L, L Lx ', Lx ' L ', L ' ( L ) x ' x ( ) f + ' + L ( ) Le dmeso dell mmage dopo l applcazoe d h ossa le costat da L x L x ' L (1.83) L ' x e L ' soo date secodo la (1.67) (s è scelto d mateere fsse le ascsse de put del bordo ferore dell mmage d put ) e da L ' f + + L ( L ) L L secodo la (1.68) S cosderao le mmag de put (x,) co 5,6,7,8 otteute applcado h e t1 coè (h(t1(x)),h(t1())) co 5,6,7,8. Per comodtà s poe per 5,6,7,8 x ' h( t1( x)) ' h( t1( )) Il puto d fuga V è l tersezoe tra l mmage d l3 e quella d l4. Le sue coordate soo (u,) co 46
47 ( 5' 7 ')( x6' x5')( x8' x7') x5'( 6' 5')( x8' x7 ') + x7 '( 8' 7 ')( x6' x5') u (1.84) ( 8' 7 ')( x6' x5') ( 6' 5')( x8' x7') ( x7 ' x5')( 8' 7')( 6' 5') 7 '( 6' 5')( x8' x7') + 5'( 8' 7 ')( x6' x5') (1.85) ( 8' 7')( x6' x5') ( 6' 5')( x8' x7') Perchè l raddrzzameto g possa essere applcato dee alere u > Lx ' > L ' S cosdera la traslazoe t che porta l asse ertcale ' ' 0 d equazoe x ' x ' ' ' l puto d fuga V ha ora coordate (u,0). (1.86) S defsce la proezoe g che mappa l fasco d rette passat per V el fasco delle rette orzzotal. L applcazoe g è otteuta dalla applcazoe defta ella sezoe 1.5 ertedo l ruolo delle ascsse e delle ordate, s ha cos co e co ' u. [ ] [ ] ( x', ') ( x, ) g : Lx ', Lx ' L ', L ' Lx ", Lx " L ", L " ( Lx ') x ' ' f + ( ') ' x ' + Lx ' ( x ' ') ( Lx ' ') ' ( x ' ') Le dmeso dell mmage d output otteuta applcado la g soo (1.87) L " L ' (1.88) pochè g tee fsse le ordate de put del lato ertcale destro dell mmage e 47
48 L " x f + ( ') L ' ' ( L ') ' + L ' ( L ' ') x x otteuta dalla (1.68) sosttuedo l ordata co l ascssa I coclusoe p ha equazoe [ ] [ ] ( x, ) ( x, ) x p : Lx, Lx L, L Lx ", Lx " L ", L " co x g( t( h( t1( x )))) g( t( h( t1( )))) x (1.89) (1.90) Ache questo caso, come per le trasformazo precedet, è opportuo partre da put dell mmage dscreta d output G(j,k) e determare put corrspodet F(p,q ) ell mmage dscreta d put applcado la trasformazoe ersa della proezoe composta co cambamet d coordate che trasformao gl dc (j,k) ( x, ) e ( x, ) (p,q ) e terpolado el caso cu p e q o sao ter. L mmage seguete è u esempo d foto corretta co questo algortmo.. Fgura Foto 1.34 corretta co proezoe 48
49 PARTE II : terpolazoe de lell d grgo.1 Itroduzoe Le tecche d terpolazoe soo d fodametale mportaza per la rcostruzoe delle mmag dgtalzzate e qud per la realzzazoe delle trasformazo geometrche descrtte ella prma parte. Queste, fatt, per essere operate ecesstao, oltre che d ua trasformazoe spazale, ache d ua terpolazoe de lell delle testà del colore. Idcata co t la proezoe che trasforma l mmage d put F ell mmage d output G l processo d rcostruzoe geere opera a rtroso partedo da put d G e applcado la trasformazoe ersa t -1 per determare l alore corrspodete F da assegargl G j k F t j k 1 (, ) ( (, )) Pochè d solto t -1 mappa la geerca coppa d dc (j,k) d G ua coppa d coordate t 1 ( j, k) ( p ', q ') che o è ua coppa d dc d F rsulta ecessaro assocare a questa u opportuo alore 1 F( p ', q ') F( t ( j, k)) otteuto terpolado lell delle testà del colore d F u toro d (p,q ). Il colore d cascu puto è defto attraerso ua tera d alor (r,g,b) puto dello spazo S R, G, B. S è scelto d terpolare lell delle testà de color fodametal rosso, erde e blu modo dpedete, s parla così d terpolazoe de lell d grgo rferedos alle testà d cascu colore. Naturalmete l alore approssmato otteuto per terpolazoe dee essere ach esso u puto d S R, G, B. Se questa codzoe o è erfcata lo s sosttusce co l puto d S R, G, B le cu coordate soo gl ter pù c alle testà calcolate. L arrotodameto dell testà d cascu colore causa u errore che ee dffuso scarcado l errore stesso su put dell mmage adacet al puto cosderato. I questo caso s è scelto d scarcare l errore sul pxel successo al puto cosderato. Al fe d dare ua formulazoe pù rgorosa del problema dell terpolazoe de lell d grgo e d aalzzare metod usat per rsolerlo s dao alcue ozo geeral sul problema dell terpolazoe. 49
50 . Iterpolazoe e mglore approssmazoe Il problema dell approssmazoe d fuzo, d mportaza fodametale ella matematca applcata, cosste ella sosttuzoe d ua fuzoe f co ua fuzoe scelta ell ambto d ua fssata classe d fuzo modo tale che l comportameto delle due soddsf specfcate codzo mposte dal problema, tutamete s dce che l loro adameto dee essere l pù smle possble. Ua tpca stuazoe cu s preseta u operazoe d questo tpo è la seguete: la fuzoe f da approssmare o è ota, ma d essa s cooscoo alcu alor su u seme d put e s ogloo aere dcazo sul suo adameto altr put. I base al tpo e alla quattà de dat e alle caratterstche del problema s può sceglere tra due dfferet approcc: l prmo cerca d costrure la fuzoe che pass per cert put assegat (terpolazoe), l secodo cerca d costrure ua che s scost d poco da dat (mglore approssmazoe). I geerale u problema terpolazoe è posto e seguet term: dat +1 put x dstt co 0,1,... s uole determare ua fuzoe ϕ, apparteete ad ua certa famgla d fuzo Φ, che ess soddsf m codzo d terpolazoe (col che la ϕ e le sue derate deoo soddsfare e put x ). Nel caso cu le codzo sao del tpo e la famgla d fuzo Φ sa defta da s cercao alor a0, a1,... a tal che ϕ ( x ) 0,1... Φ ϕ(,,,... ) 0 1 x a0 a1 a ϕ ( x, a, a,... a ) 0,1,... Se ϕ dpede learmete da parametr ossa ϕ( x, a, a,... a ) a ϕ ( x) + a ϕ ( x) a ϕ ( x) l problema è detto d terpolazoe leare Nel caso cu la famgla delle fuzo Φ sa uo spazo leare su R d dmesoe +1, che per comodtà dchamo co V, e se co V* s deota l corrspodete spazo duale, la 50
51 defzoe può essere così geeralzzata: assegat +1 fuzoal lear L0, L1,.. L V* e dato l seme d umer real { } 0,1.. s cerca l elemeto d V tale che L 0,1,... (.1) Se V P e L ( x ) oe { } 0,1.. x è u seme d +1 put dstt s parla d terpolazoe polomale. Scelta ua base d V { } ϕ0, ϕ1,... ϕ lo stesso problema può essere scrtto forma matrcale fatt og elemeto d V può essere scrtto come combazoe leare degl elemet della base 0 aϕ e la defzoe d che soddsfa le codzo (.1) equale alla determazoe de parametr a che soddsfao le da cu L a jϕ j 0,1,... (.) j 0 Ga p (.3) co a ettore de parametr, p ettore de alor e detta matrce d Gram. L0 ( ϕ0) L0 ( ϕ) G L ( ϕ0) L ( ϕ) (.4) Il problema della mglore approssmazoe può essere così eucato: sa V uo spazo leare dotato d ua orma e W u suo sottospazo geerato dagl elemet ϕ1, ϕ,... ϕ d V. Il sottospazo W ha come elemet le combazo lear 1 aϕ e ha dmesoe fta. Assegato u elemeto f d V s tratta d determare u elemeto w* d W, da cosderare mglore approssmazoe d f ella metrca d V, modo tale che la dstaza da f sa mma coè f w* f w w W 51
52 I altre parole s tratta d determare l mmo della fuzoe * 0, * 1,... * se [ ] d( a, a,... a ) f a ϕ a a a mmzza d s dce che w* è l elemeto d mglore approssmazoe d f. Cetrale ella rsoluzoe d questo tpo d problem è la scelta della orma d V e del tpo d fuzoe approssmate, coè del sottospazo W cu rcercare l w*, pù adatt. D solto s scegle la fuzoe approssmate tra polom per la loro effceza computazoale. Nel caso d V L ( a, b) co (a,b) R s parla d mglore approssmazoe el seso de mm quadrat e s rcerca l polomo p P che mmzza la orma del ettore resduo r d compoet f ( x ) p( x ) 1 m (.5) 0 r d ( f, p) ( f ( x ) p( x )) Se l problema è dscreto, ossa s laora su u seme fto S { x x x } (a,b) e per og fuzoe f defta su S s cosdera la semorma 1,,... m dell terallo f, S 1 m ( f ( x )) 1 la mglore approssmazoe s ottee cercado l polomo p P tale che f p* f p p P, S, S..1 Alcu rsultat sull usoleza de problem d terpolazoe R Sa V uo spazo leare d fuzo real d dmesoe fta +1 e V* l suo duale. Dat L0, L1,.. L apparteet a V* e l seme { } 0,1.. d real base alla defzoe date el paragrafo precedete rsolere l problema d terpolazoe V sgfca troare la fuzoe V tale che L per 0,1,... S dce che L0, L1,.. L soo usolet V se esste ua ed ua sola soluzoe al problema. L0, L1,.. L soo usolet se e solo se soo dpedet V* fatt ale 5
53 Lemma.1 Sa V spazo leare d dmesoe. Se,.. 1 soo dpedet V e L,.. 1 L soo dpedet V* allora L ( ) 0 (.6) j Vceersa se,.. 1 o L,.. 1 L soo dpedet e ale la (.6) allora ache l altro seme è dpedete. Dmostrazoe. S suppoga che L ( ) 0 allora ache L ( ) 0. Il sstema j a L ( ) + a L ( ) a L ( ) a L ( ) + a L ( ) a L ( ) arebbe ua soluzoe o baale a,... 1 a. Allora per 1,,... e pochè,.. 1 è ua base d V ( a L + a L a L )( ) ( a L + a L a L )( ) 0 per og V, per cu a1l1 + al al 0 e qud L,.. 1 L soo learmete dpedet cotro le potes. j Teorema. Sa V uo spazo leare d dmesoe e L,.. 1 L elemet d V*. Il problema d terpolazoe (.1) ammette ua e ua sola soluzoe per alor arbtrar 1,,... se e solo se gl L soo dpedet V*. Dmostrazoe. Per l lemma sopra se,.. 1 e L,.. 1 L soo dpedet L ( ) 0 e l sstema o L ( a + a a ) 1,, j 53
54 ha ua soluzoe a,... 1 a e l elemeto rsole l terpolazoe leare. a L ( ) + a L ( ) a L ( ) (.7) 1 1 a (.8) 1 Vceersa se l problema d terpolazoe ha soluzoe per og 1,,... la (.7) ha soluzoe per og 1,,... e qud L ( ) 0. Allora per l lemma gl L soo dpedet. Il determate L ( ) è detto determate d Gram geeralzzato. j j S cosdero ora cas cu l problema d terpolazoe è polomale, coè L ( x ) co rcercato tra polom. I ua dmesoe l usoleza è garatta dal seguete rsultato Teorema.3 S dch co P l seme de polom p(x) co x R a coeffcet real d grado ferore o uguale ad dat dall espressoe 1 R (.9) 0 p( x) a x a Dat +1 put d collocazoe ( x, ) co 0,1,,.. e x x j se j s può sempre determare P l polomo p tale che p( x ) 0,1,... (.10) La dmostrazoe dell essteza e uctà d tale polomo s ottee costruttamete troducedo codzoe k0,1,.. la cu rappresetazoe esplcta è P la base de polom terpolat d Lagrage che per og soddsfao la 1 se k L ( xk ) δ, k 0 se k (.11) 54
55 x x j L ( x) 0,1,... (.1) x x j 0, j j e rappresetado p così p è detto polomo d Lagrage. p( x) L (.13) 0 ( x) Questo teorema o può essere esteso al caso d terpolazo polomal pù arabl quato è stato dmostrato che og seme aperto d R co o è sempre possble, dat put arbtrar x R dstt, troare ua combazoe leare d 0 1 p,... p (base dello spazo de polom d orde more o uguale ad su R ) che assumoo assegat alor su quest put. Teorema.4 (d Haar) Sa S u seme R co che cotega u puto tero p e sao,... 1 f f (>1) fuzo defte su S e cotue u toro d p.questo seme d fuzo o può essere usolete su S. Dmostrazoe. Sa B ua bolla cetrata p suffcetemete pccola affchè le f 1,... f sao cotue. S scelgao put dstt B p1, p,... p e s assuma che f ( p ) 0. S fsso p,... 3 p e s muoao p 1 e p modo cotuo b maera che s scambo d poszoe tra loro. I questo modo s è trodotto uo scambo d coloe f ( p ) l cu sego d cosegueza camba. Pochè le fuzo soo cotue dee esserc qualche poszoe termeda d p 1 e p per cu l alore del determate s aulla. Da quato detto s può qud cocludere che geerale per l terpolazoe d fuzo pù arabl dare u umero d codzo par a parametr del polomo o garatsce la sua costrubltà. I quest cas è opportuo rsolere l problema troado l polomo d mglore approssmazoe. j j 55
56 .. Iterpolazoe polomale ua e due dmeso forma matrcale Molto utle è la rappresetazoe forma matrcale del problema d terpolazoe polomale ua dmesoe. Scelta come base per ( ) dee soddsfare 0 P x { 1,,,.. } x x x s ha che l geerco polomo a ( x j ) j (.14) co j0,1,.. e { x,... 0 x } +1 put dstt a cu corrspodoo alor {,... 0 } da cu Va p (.15) 0 a x co a ettore de parametr, p ettore degl j e 1 x0 x 0 V (.16) 1 x x detta matrce d Vadermode che per l teorema. ha determate derso da zero se e solo se put soo dstt. La stessa defzoe può essere estesa a problem due dmeso: s scelga come base d j P ( x, ) l seme { x }, le codzo d terpolazoe detao, j 0,.. co k0,1,..m e {(, )} k k z (.17) j k aj xk k, j 0 x put tra loro dstt. Idcato co a l ettore de parametr cogt lugo s e co p quello de alor assegat s ottee Ma p (.18) co 1 x1 1 M 1 xm m (.19) 56
57 I base a quato detto prma ache se put soo dstt e ms M potrebbe aere determate ullo e l problema o ha soluzoe. Se m>s l sstema è soradetermato e coee cercare l polomo d mglore approssmazoe che mmzz lo scarto quadratco medo Idcato co r l ettore resduo m k 0 ( p( xk, k ) zk ) (.0) r p - Ma (.1) scredo la codzoe ecessara d mmo (porre ulle le derate d r rspetto a j ) s ottee detto sstema delle equazo ormal da cu -1 T T cu la matrce M M M è detta pseudoersa d M. T T M Ma M p (.) -1 T T a M M M p (.3)..3 Iterpolazoe tegrale Come s è sto la scelta d put dstt è codzoe ecessara ma o suffcete per l usoleza dell terpolazoe polomale due dmeso. S può dmostrare che tale codzoe rsulta suffcete el caso dell terpolazoe tegrale ua e due dmeso. Per questo tpo d terpolazoe ua dmesoe s a a determare l polomo p(x) che soddsfa le codzo x + h p( x) dx z (.4) x h co 10,1,. Questa terpolazoe porta al medesmo rsultato dell terpolazoe polomale R. Teorema.5 I ua dmesoe l terpolazoe tegrale d u polomo d grado è equalete a quella polomale. 57
58 Dmostrazoe. S cosdero +1 put dstt x0. x1,..., x a cu soo assocat alor 0. 1,..., e s determ l polomo terpolate d orde ua arable p( x) a + a x a x 0 1 tale che p( x ) per 0,1,, base a quato affermato prma tale polomo esste ed è uco. S cosder po l polomo p (x ) d orde che soddsfa le seguet codzo x + h x h p '( x) dx co 0,1,. I coeffcet d p rsultao geerale ders da quell d p. S cosder ora l polomo q(x) otteuto calcolado l tegrale x + h a q( x) p '( s) ds x + h x h + 1 x h 0 ( ) ( ) che rsulta acora u polomo d orde quato term d grado +1 s semplfcao tra loro. I base alle codzo mposte su p e alla defzoe d q s ha q( x ) per 0,1,... e per l uctà del polomo terpolate s può cocludere che q(x)p(x) e qud s ha l equaleza delle due terpolazo. I due dmeso l terpolazoe tegrale a a determare l polomo d orde tale che p( x, ) a + a x a x + a + a x a x a x p( x, ) dxd zj (.5) Q j per,j0,1, oe co Q s dca l quadrato d lato l cetrato el puto ( x, ) a cu è j j assocato l alore z j. Dalla (.5) s ottee co h,k0,1,... l l x 1 h + 1 k + + j+ x l l xh k aj j + j + zhk (.6), Idcato co a l ettore de coeffcet d p(x,) e co z quello de alor z j la (.6) forma matrcale deta 58
59 Ma z (.7) Se put ( x, ) soo tra loro dstt la matrce M è o sgolare e l sstema ammette ua ed ua sola soluzoe h k 1 a M z (.8) ossa esste ed è uco l polomo soluzoe dell terpolazoe tegrale. S ota che questo tpo d terpolazoe o è arate rspetto ad ua rotazoe degl ass d rfermeto...4 Iterpolazoe bleare e bquadratca I questo laoro s soo cosderat metod d terpolazoe polomale due dmeso co polom del prmo e del secodo orde pochè rsultao essere meo costos da u puto d sta computazoale e o dao orge a feome d oscllazoe. Dal teorema.3 s rcaa che per defre uocamete l polomo terpolatore d orde ua dmesoe s ecessta d +1put d collocazoe dstt. Se 1 l terpolazoe è detta leare e seroo due put x 0 e x 1 dstt a cu assegare de alor. La base de polom terpolat d Lagrage è data da da cu x [ x, x ] s ha 0 1 L 0 x x1 x x 0 1 x x0 L1 x x 1 0 (.9) co x x0 dx x x p( x) (1 dx) + dx (.30) (.31) La costruzoe del polomo terpolate ua fuzoe f d pù arabl ee d solto effettuata sfruttado le proezo su sottospaz. Sa [ a, b] [ c, d] l domo rettagolare della fuzoe f da terpolare e sa a x < x <... < x b 0 1 c < <... < d 1 m 59
60 ua partzoe del domo. Il polomo terpolatore d Lagrage è dato da m L( x, ) f ( x, ) ϕ ( x) ψ ( ) (.3) 0 j 0 j j doe ϕ ( x), ψ ( ) soo polom d grado e m soddsfacet le codzo j ϕ ( x ) δ, k 0,1,... k k ψ ( ) δ j, k 0,1,... m j k k (.33) L( x, ) può essere geerato come rsultato dell applcazoe della trasformazoe P : g g( x, ) ϕ ( x) (.34) x 0 sull mmage P ( f ) della trasformazoe m P : d d( x, ) ψ ( ) (.35) j j j 0 sulla fuzoe f coè L P ( P ( f )) (.36) x P x e P soo proezo e per la scelta delle ϕ ( x), ψ ( ) soo commutate,qud arado j l orde co cu s terpola, prma per rghe e po per coloe o ceersa, s ottee sempre lo stesso rsultato fale. Se m1 l terpolazoe è detta bleare. I polom d Lagrage hao la forma ϕ ( x) 1 dx 0 ϕ ( x) dx co x x0 dx x x e co da cu ψ ( ) 1 d ψ ( ) d d ( (, )) ( ) (, ) ( ) (, ) x (.37) (.38) (.39) (.40) P f x ϕ x f x + ϕ x f x (.41) 60
61 e uedo le espresso P ( f ( x, )) ψ ( ) f ( x, ) + ψ ( ) f ( x, ) 0,1 (.4) [ ] [ ] L( x, ) ϕ ψ ( ) f ( x, ) + ψ ( ) f ( x, ) + ϕ ( x) ψ ( ) f ( x, ) + ψ ( ) f ( x, ) (.43) [ ] [ ] L( x, ) (1 dx) (1 d) f ( x, ) + df ( x, ) + dx (1 d) f ( x, ) + df ( x, ) (.44) L essteza e uctà del polomo è garatta dall essteza e uctà de polom terpolator lugo le rghe e le coloe. (0,0) (x,0) (1,1) (x,) (1,0) (x,1) (1,1) Fgura. 1 L terpolazoe bleare operata terpolado learmete per rghe e po per coloe Se m l terpolazoe è detta bquadratca. I questo caso seroo oe put d terpolazoe qud ua partzoe del domo [ a, b] [ c, d] data da a x < x < x b 0 1 c < < d 1 (.45) 61
62 (0,0) a (1,0) (,0) (0,1) b (1,1) (,1) (x,) (0,) c (1,) (,) Fgura. L terpolazoe bquadratca coolge oe put d terpolazoe per semplctà fgura soo dcat solo loro dc. S terpola prma lugo le rghe put a,b,c po quest lugo la coloa blu co parabole I polom terpolator d Lagrage hao equazo e ϕ ( x) 0 ϕ ( x) 1 ϕ ( x) ψ ( ) 0 ψ ( ) 1 ψ ( ) e l polomo terpolatore deta ( x x1 )( x x ) ( x0 x1 )( x0 x ) ( x x0 )( x x ) ( x1 x0 )( x1 x ) ( x x1 )( x x0 ) ( x x )( x x ) 1 0 ( 1 )( ) ( 0 1 )( 0 ) ( 0 )( ) ( 1 0 )( 1 ) ( 1 )( 0 ) ( )( ) 1 0 (.46) (.47) p( x, ) z ϕ ( x) ψ ( ) (.48), j 0 j j co z j alore assocato al puto ( x, j ). Ache questo caso l essteza e uctà del polomo è data dall essteza e uctà de polom lugo le rghe e le coloe e la commutattà delle 6
63 proezo garatsce che scambado l orde d terpolazoe per rghe e coloe l rsultato o camba..3 Iterpolazoe de lell d grgo Come s è gà acceato ell troduzoe, s è scelto d terpolare le testà d cascuo de color fodametal (rosso, erde, blu) modo dpedete rspetto alle testà degl altr due color. I questo modo c s è rdott a tre problem dpedet d terpolazoe de lell d testà lumosa (rspettamete del rosso,del erde e del blu). Per cascuo d ess dato u puto d coordate (p,q ) dell mmage d put s a a calcolare u alore approssmato dell testà d grgo otteuto terpolado le testà de put dell mmage apparteet ad u certo toro d (p,q ). Oamete, la scelta del umero e del tpo d put che egoo coolt dpede dal metodo d terpolazoe usato. Molto mportate è sottoleare che, pochè lell d grgo soo umer ter compres tra 0 e 55, ache l alore approssmato dee apparteere all seme { N : 0 55} I I metod che errao aalzzat o sempre garatscoo che questa codzoe sa soddsfatta ed è qud ecessaro mporre cotroll. Se l testà lumosa è maggore d 55 o more d 0 la s poe rspettamete uguale a 55 o 0, se è u alore reale tra 0 e 55 la s arrotoda all tero pù co.. L arrotodameto dell testà d cascu colore causa u errore che ee dffuso scarcado l errore stesso su put dell mmage adacet al puto cosderato. I questo caso s è scelto per semplctà d dsperdere l errore solo aat coè sul pxel successo al puto cosderato apparteete alla stessa rga. La scelta pù semplce d terpolazoe è chamata terpolazoe d orde zero e cosste ell assocare al puto (p,q ) l testà del puto dell mmage che ha dstaza eucldea more. Questo algortmo ha l ataggo d essere computazoalmete semplce ma rsultao edet effett d scalatura elle mmag cu l lello d grgo camba sgfcatamete da u pxel all altro e può portare ad u errore spazale dell orde d 63 pxel per utà. L approssmazoe può essere mglorata utlzzado l terpolazoe polomale. Per mateere cost computazoal accettabl ed etare feome d oscllazoe dell terpolate s soo usat polom terpolat del prmo e del secodo orde.
64 .3.1 Iterpolazoe bleare S cosder l mmage d put F(p,q) e l puto (p,q ) cu s uole calcolare l alore del polomo terpolate p(x,) che, base a quato detto precedetemete sull terpolazoe bleare, ha equazoe [ ] [ ] P( x, ) (1 dx) (1 d) f ( x, ) + df ( x, ) + dx (1 d) f ( x, ) + df ( x, ) (.49) Per defre modo uoco p deoo essere assegat quattro put dell mmage o alleat tre a tre s cosderao allora put d F(p,q) che costtuscoo quattro ertc del quadrato coteete (p,q ). Per comodtà s cosdera u rfermeto locale cetrato el cetro del quadrato C rspetto al quale ertc hao coordate { j }, 0.5,0.5 (, ) j pochè put dell mmage formao u retcolo d lato 1. Il quadrato è così determato : se p -[p ]<0.5 s cosdera come ertce d coordate (-0.5,0.5) l puto co ascssa [p ] altrmet co ascssa [p ]+1 e co ordata [q ] se q -[q ]<0.5 altrmet co ordata [q ]+1. Nell mmage seguete è llustrata la scelta de put terpolat e l puto (p,q ) che rspetto al uoo sstema d rfermeto ha coordate (x,) [ ] [ ] [ ] [ ] x p ' p ' 0.5 se p'- p' < 0.5 x p ' p ' 1 se p'- p' > 0.5 (.50) [ ] [ ] [ ] [ ] q ' q ' 0.5 se q'- q' < 0.5 q ' q ' 1 se q'- q' >0.5 (.51) 64
65 (-0.5,-0.5) a (0.5,-0.5) (0,0) (x,) (-0.5,0.5) b (0.5,0.5) Fgura. 3 Le tersezo delle lee rosse soo put d F(p,q), s terpolao prma per rga put tersezoe della lea blu d ascssa x co le lee rosse orzzotal dcat co a e b e po tal alor tra loro Idcata co dx e d le quattà dx x d (.5) la (.49) deta [ ] [ + ] P( x, ) (1 dx) (1 d) I( 0.5, 0.5) + di( 0.5,0.5) + + dx (1 d) I(0.5, 0.5) di(0.5, 0.5) (.53) L terpolazoe orzzotale e ertcale soo lear ma la loro composzoe rsulta ua superfce o leare che s adatta bee a quattro pxel c..3. Iterpolazoe bquadratca S cosder l mmage d put F(p,q) e l puto (p,q ) cu s uole calcolare l alore del polomo terpolate p(x,) che, base a quato detto precedetemete sull terpolazoe bquadratca, ha equazoe p( x, ) I ϕ ( x) ψ ( ), j 0 j j doe polom terpolat d Lagrage ϕ, ψ soo deft elle (.46) e (.47) e I, è l testà lumosa el puto ( x, ). j j j 65
66 Affchè p sa defto uocamete come specfcato prma s deoo assegare oe put ell toro d (p,q ), s scegle la grgla 3 3 de oe put pù c e per comodtà l s dca co {( x, j )}, 1,0,1 j. S cosdera u sstema d coordate local cetrato ( x0, 0) per cu put da terpolare detao { j }, 1,0,1 sosttuedo s ottee (, ) j e (p,q ) ha coordate (x,) date da [ ] [ ] x p ' p ' 0.5 q ' q ' (.54) p( x, ) I ϕ ( x) ψ ( ) (.55) j j, j 1 co per zx, e ζ ϕ, ψ. z( z 1) ζ 1( z) ζ ( z) ( z + 1)( z + 1) 0 z( z + 1) ζ 1( z) (.56).3.3 Iterpolazoe tegrale S cosder l mmage d put F(p,q) e l puto (p,q ) cu s uole calcolare l alore che l terpolazoe tegrale gl assoca. I base a quato detto precedetemete pochè samo el caso bdmesoale l terpolazoe tegrale a a determare l polomo d equazoe p( x, ) a + a x + a x + a + a x + a x + a + a x + a x tale che per,j-1,0,1, oe co p( x, ) dxd zj (.57) Qj Q j s dcao oe quadrat d lato 1 cetrat e oe put d F(p,q) pù c a (p,q ). Pochè s fa rfermeto ad u sstema d coordate cetrato el puto d F(p,q) l cu quadrato cotee (p,q ), put pres esame hao coordate (,j) co,j-1,0,1. 66
67 Fgura. 4 I blu è segato l quadrato Q ( p ', q ') d lato 1 cetrato el puto (p,q ), rosa quadrat Q j co,j-1,0,1 cetrat e 9 put d F(p,q) pù c a (p,q ). Il alore z j rappreseta l testà del grgo del puto (,j). Dalla (.5) s ottee co,j-1,0, k j+ h+ + + x 0.5 j 0.5 ahk zj (.58) h, k 0 h + 1 k + 1 Idcato co a l ettore de coeffcet d p(x,) e co z quello de alor z j la (.58) forma matrcale deta Ma z (.59) Pochè od soo tra loro dstt la matrce M è o sgolare e ertble, l sstema ammette ua ed ua sola soluzoe 1 a M z (.60) co -1 M matrce cu elemet soo dcat fgura.5. 67
In questo capitolo vedremo solamente un caso di rendita, che useremo poi per generalizzare le rendite e dedurre tutti gli altri casi.
 7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
Dimostrazione della Formula per la determinazione del numero di divisori-test di primalità, di Giorgio Lamberti
 Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Attualizzazione. Attualizzazione
 Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
La classe che mostra la distribuzione più elevata è quella 60-90, che corrisponde a un uso elevato dell automobile. f i fr (= f i/n) fr% (=fr*100)
 ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
Modello dinamico nello spazio dei giunti: relazione tra le coppie di attuazione ai giunti ed il moto della struttura
 Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
Elementi di Statistica descrittiva Parte III
 Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
b) Relativamente alla variabile PREZZO, fornire una misura della variabilità della distribuzione attraverso
 ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
Design of experiments (DOE) e Analisi statistica
 Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
frazione 1 n dell ammontare complessivo del carattere A x
 La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
ARGOMENTO: MISURA DELLA RESISTENZA ELETTRICA CON IL METODO VOLT-AMPEROMETRICO.
 elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
Lezione 1. I numeri complessi
 Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
Elementi di Matematica Finanziaria. Rendite e ammortamenti. Università Parthenope 1
 Elemet d Matematca Fazara Redte e ammortamet Uverstà Partheope 1 S chama redta ua successoe d captal da rscuotere (o da pagare) a scadeze determate S chamao rate della redta sgol captal da rscuotere (o
Elemet d Matematca Fazara Redte e ammortamet Uverstà Partheope 1 S chama redta ua successoe d captal da rscuotere (o da pagare) a scadeze determate S chamao rate della redta sgol captal da rscuotere (o
Stim e puntuali. Vocabolario. Cambiando campione casuale, cambia l istogramma e cambiano gli indici
 Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
Indici di Posizione. Gli indici si posizione sono misure sintetiche ( valori caratteristici ) che descrivono la tendenza centrale di un fenomeno
 Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
Modelli di Flusso e Applicazioni: Andrea Scozzari. a.a. 2013-2014
 Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
L assorbimento e lo strippaggio
 assorbmeto e lo strppaggo Coloa a stad d ulbro (coloa a patt Il calcolo d ua coloa d assorbmeto/strppaggo d questo tpo parte dal blaco d matera. Chamado e le portate d lqudo A e d gas C relatve a due compoet
assorbmeto e lo strppaggo Coloa a stad d ulbro (coloa a patt Il calcolo d ua coloa d assorbmeto/strppaggo d questo tpo parte dal blaco d matera. Chamado e le portate d lqudo A e d gas C relatve a due compoet
Modelli di Schedulazione
 EW Modell d Schedulazoe Idce Maccha Sgola Tepo d Copletaeto Totale Tepo d Copletaeto Totale Pesato Tepo d Rtardo Totale Maespa co set-up dpedete dalla sequeza Tepo d Copletaeto Totale co vcolo d precedeza
EW Modell d Schedulazoe Idce Maccha Sgola Tepo d Copletaeto Totale Tepo d Copletaeto Totale Pesato Tepo d Rtardo Totale Maespa co set-up dpedete dalla sequeza Tepo d Copletaeto Totale co vcolo d precedeza
Istogrammi e confronto con la distribuzione normale
 Istogramm e cofroto co la dstrbuzoe ormale Suppoamo d effettuare per volte la msurazoe della stessa gradezza elle stesse codzo (es. la massa d u oggetto, la tesoe d ua pla, la lughezza d u oggetto, ecc.):
Istogramm e cofroto co la dstrbuzoe ormale Suppoamo d effettuare per volte la msurazoe della stessa gradezza elle stesse codzo (es. la massa d u oggetto, la tesoe d ua pla, la lughezza d u oggetto, ecc.):
Propagazione di errori
 Propagazoe d error Gl error e dat possoo essere amplfcat durate calcol. Rspetto alla propagazoe degl error s può dstguere: comportameto del problema - codzoameto del problema: vedere come le perturbazo
Propagazoe d error Gl error e dat possoo essere amplfcat durate calcol. Rspetto alla propagazoe degl error s può dstguere: comportameto del problema - codzoameto del problema: vedere come le perturbazo
STATISTICA DESCRITTIVA
 COSIDERAZIOI PRELIMIARI SULLA STATISTICA La Statstca trae suo rsultat dall osservazoe de feome che c crcodao. Gl stess feome per essere oggetto d statstca devoo essere adeguatamete umeros modo tale che
COSIDERAZIOI PRELIMIARI SULLA STATISTICA La Statstca trae suo rsultat dall osservazoe de feome che c crcodao. Gl stess feome per essere oggetto d statstca devoo essere adeguatamete umeros modo tale che
DI IDROLOGIA TECNICA PARTE II
 FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
Matematica elementare art.1 di Raimondo Valeri
 Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Algoritmi e Strutture Dati. Alberi Binari di Ricerca
 Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
Università degli Studi di Milano Bicocca CdS ECOAMM Corso di Metodi Statistici per l Amministrazione delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI
 Uverstà degl Stud d Mlao Bcocca CdS ECOAMM Corso d Metod Statstc per l Ammstrazoe delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI 1. Carta d cotrollo per frazoe d o coform (carta U resposable d produzoe,
Uverstà degl Stud d Mlao Bcocca CdS ECOAMM Corso d Metod Statstc per l Ammstrazoe delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI 1. Carta d cotrollo per frazoe d o coform (carta U resposable d produzoe,
Facoltà di Economia - STATISTICA - Corso di Recupero a.a Prof.ssa G. Balsamo CONCETTI di BASE Carattere X [o A ] i = 1
![Facoltà di Economia - STATISTICA - Corso di Recupero a.a Prof.ssa G. Balsamo CONCETTI di BASE Carattere X [o A ] i = 1 Facoltà di Economia - STATISTICA - Corso di Recupero a.a Prof.ssa G. Balsamo CONCETTI di BASE Carattere X [o A ] i = 1](/thumbs/74/71433944.jpg) Facoltà d Ecooma - STATISTICA - Corso d Recupero a.a. 2012-13 Prof.ssa G. Balsamo CONCETTI d BASE Carattere X [o A ] caratterstca quattatva [o qualtatva] rappresetatva d u feomeo sottoposto ad dage Popolazoe
Facoltà d Ecooma - STATISTICA - Corso d Recupero a.a. 2012-13 Prof.ssa G. Balsamo CONCETTI d BASE Carattere X [o A ] caratterstca quattatva [o qualtatva] rappresetatva d u feomeo sottoposto ad dage Popolazoe
Organizzazione del corso. Elementi di Informatica. Orario lezioni ed esami. Crediti. Dispense e lucidi. Ricevimento studenti
 Orgazzazoe del corso Elemet d Iformatca Prof. Alberto Brogg Dp. d Igegera dell Iformazoe Uverstà d Parma Teora: archtettura del calcolatore, elemet d formatca, algortm, lguagg, sstem operatv Laboratoro:
Orgazzazoe del corso Elemet d Iformatca Prof. Alberto Brogg Dp. d Igegera dell Iformazoe Uverstà d Parma Teora: archtettura del calcolatore, elemet d formatca, algortm, lguagg, sstem operatv Laboratoro:
Incertezza di misura
 Icertezza d msura Itroduzoe e rcham Come gà detto rsultat umerc ottebl dalle msurazo soo trsecamete caratterzzat da aleatoretà è duque sempre ecessaro stmare ua fasca d valor attrbubl come msura al msurado;
Icertezza d msura Itroduzoe e rcham Come gà detto rsultat umerc ottebl dalle msurazo soo trsecamete caratterzzat da aleatoretà è duque sempre ecessaro stmare ua fasca d valor attrbubl come msura al msurado;
UNI CEI ENV 13005 (GUIDA ALL ESPRESSIONE DELL INCERTEZZA DI MISURA)
 UI CEI EV 3005 (GUIDA ALL ESPRESSIOE DELL ICERTEZZA DI MISURA Uverstà degl Stud d Bresca Corso d Fodamet della Msurazoe A.A. 00-03 Apput a cura d Gorgo Cor 3835 UI CEI EV 3005 0. ITRODUZIOE 0. COCETTO
UI CEI EV 3005 (GUIDA ALL ESPRESSIOE DELL ICERTEZZA DI MISURA Uverstà degl Stud d Bresca Corso d Fodamet della Msurazoe A.A. 00-03 Apput a cura d Gorgo Cor 3835 UI CEI EV 3005 0. ITRODUZIOE 0. COCETTO
Alcuni metodi per la risoluzione di sistemi lineari con matrici strutturate.
 Alcu meto per la rsoluzoe sstem lear co matrc strutturate. A. url - Calcolo Scetco Problema Rsolvere l sstema leare: A A. url - Calcolo Scetco Problema q A Co A matrce el tpo: p O A è ua matrce tragoale!
Alcu meto per la rsoluzoe sstem lear co matrc strutturate. A. url - Calcolo Scetco Problema Rsolvere l sstema leare: A A. url - Calcolo Scetco Problema q A Co A matrce el tpo: p O A è ua matrce tragoale!
Classi di reddito % famiglie Fino a 15 5.3 15-25 16.2 25-35 21.1 35-45 18.6 45-55 13.6 Oltre 55 25.2 Totale 100
 ESERCIZIO Data la seguete dstrbuzoe percetuale delle famgle talae per class d reddto, espresso mlo d lre, (ao 995, fote Istat): Class d reddto % famgle Fo a 5 5.3 5-5 6. 5-35. 35-45 8.6 45-55 3.6 Oltre
ESERCIZIO Data la seguete dstrbuzoe percetuale delle famgle talae per class d reddto, espresso mlo d lre, (ao 995, fote Istat): Class d reddto % famgle Fo a 5 5.3 5-5 6. 5-35. 35-45 8.6 45-55 3.6 Oltre
Approssimazioni di curve
 Approssmazo d curve e superfc Approssmazo d curve Il terme Computer Grafca comprede ua larga varetà d applcazo che rguardao umerevol aspett della ostra vta. U eleco esemplfcatvo d alcu de camp cu essa
Approssmazo d curve e superfc Approssmazo d curve Il terme Computer Grafca comprede ua larga varetà d applcazo che rguardao umerevol aspett della ostra vta. U eleco esemplfcatvo d alcu de camp cu essa
Quale retta? La retta migliore è quella che più si avvicina all insieme dei 115
 Quale retta? Quale retta? Questa? Oppure questa? Questa certamete o! 0 1 0 1 La retta mglore è quella che pù s avvca all seme de 115 put corrspodet alle coppe d valor (x, y ). Per la stma de parametr s
Quale retta? Quale retta? Questa? Oppure questa? Questa certamete o! 0 1 0 1 La retta mglore è quella che pù s avvca all seme de 115 put corrspodet alle coppe d valor (x, y ). Per la stma de parametr s
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
ERRATA CORRIGE. L intero contenuto del paragrafo 9.2.3 a pagina 47-48 del Capitolato tecnico Determinazione del Canone è sostituito come segue:
 Procedura aperta per l affdameto de servz tegrat, gestoal, operatv e d mautezoe multservzo tecologco da esegurs presso gl mmobl d propretà o uso alle Asl ed alle azede ospedalere della regoe Campaa ERRATA
Procedura aperta per l affdameto de servz tegrat, gestoal, operatv e d mautezoe multservzo tecologco da esegurs presso gl mmobl d propretà o uso alle Asl ed alle azede ospedalere della regoe Campaa ERRATA
Approfondimenti sui diagrammi di Bode
 Approfodmet su dagramm d ode L espressoe (4.4) d ua fuoe d trasfermeto m m N( s) ams + am s +... + a = = D( s) b s + b s +... + b può essere rscrtta el seguete modo: ( )( )...( ) ( z)( z)...( ) z z ( p
Approfodmet su dagramm d ode L espressoe (4.4) d ua fuoe d trasfermeto m m N( s) ams + am s +... + a = = D( s) b s + b s +... + b può essere rscrtta el seguete modo: ( )( )...( ) ( z)( z)...( ) z z ( p
Funzioni di più variabili Massimi e Minimi una funzione definita in un insieme E. Un punto ( x0, y0)
 Massm e Mm Fuzo d pù varabl Massm e Mm Dezoe: Sa z = (, ) ua uzoe deta u seme E U puto (, E s dce puto d massmo (rsp mmo) relatvo per (, ) se esste δ > tale che ((, ) B((, ), δ ) E (, ) (, ) (rsp (, )
Massm e Mm Fuzo d pù varabl Massm e Mm Dezoe: Sa z = (, ) ua uzoe deta u seme E U puto (, E s dce puto d massmo (rsp mmo) relatvo per (, ) se esste δ > tale che ((, ) B((, ), δ ) E (, ) (, ) (rsp (, )
Variabili e funzioni booleane
 Varabl e uzo booleae Elemet del sostego dell algebra K valor boolea Varabl che possoo assumere valor boolea varabl booleae Fuzo d varabl booleae K uzo booleae y ( Le varabl possoo essere a loro volta uzo
Varabl e uzo booleae Elemet del sostego dell algebra K valor boolea Varabl che possoo assumere valor boolea varabl booleae Fuzo d varabl booleae K uzo booleae y ( Le varabl possoo essere a loro volta uzo
Università di Cassino. Esercitazioni di Statistica 1 del 26 Febbraio Dott. Mirko Bevilacqua
 Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
Modulo di Fisica Tecnica. Differenze finite per problemi di conduzione in regime instazionario
 Dpartmeto d Meccaca, Strutture, Ambete e Terrtoro UNIVERSITÀ DEGLI STUDI DI CASSINO Laurea Specalstca Igegera Meccaca: Modulo d Fsca Tecca Lezoe d: Dffereze fte per problem d coduzoe regme stazoaro /20
Dpartmeto d Meccaca, Strutture, Ambete e Terrtoro UNIVERSITÀ DEGLI STUDI DI CASSINO Laurea Specalstca Igegera Meccaca: Modulo d Fsca Tecca Lezoe d: Dffereze fte per problem d coduzoe regme stazoaro /20
Criteri di scelta degli investimenti. Materiale didattico per il corso di matematica finanziaria II modulo
 Crter d scelta degl estmet Materale ddattco per l corso d matematca azara II modulo Itroduzoe La presete trattazoe s poe come obetto d aalzzare due prcpal crter d scelta degl estmet e de azamet per alutare
Crter d scelta degl estmet Materale ddattco per l corso d matematca azara II modulo Itroduzoe La presete trattazoe s poe come obetto d aalzzare due prcpal crter d scelta degl estmet e de azamet per alutare
Premessa... 1. Equazioni i differenziali lineari
 Apput d Cotroll Autoatc Captolo 3 parte I Sste dac lear Preessa... Equazo dfferezal lear... Evoluzoe lbera ed evoluzoe forzata... Uso della trasforazoe d Laplace... 3 Esepo... 7 Osservazo sulla rsposta
Apput d Cotroll Autoatc Captolo 3 parte I Sste dac lear Preessa... Equazo dfferezal lear... Evoluzoe lbera ed evoluzoe forzata... Uso della trasforazoe d Laplace... 3 Esepo... 7 Osservazo sulla rsposta
Esercizi 12/10/2007. oppure B 0. In modo del tutto analogo AB 0 se e solo se. oppure B 0 B 0. Studio del segno di una disequazione polinomiale.
 Esercz 2/0/2007 Dsequazo Sego d u prodotto. Voglamo studare l sego d u prodotto d due umer real. I altr term vedere qual soo le codzo affché due umer real A e B soddsfo AB 0. Ragoamo come segue: rcoducamo
Esercz 2/0/2007 Dsequazo Sego d u prodotto. Voglamo studare l sego d u prodotto d due umer real. I altr term vedere qual soo le codzo affché due umer real A e B soddsfo AB 0. Ragoamo come segue: rcoducamo
Controlli Automatici A
 Cotroll Automatc A Cors d laurea treal Igegera Elettroca, Iformatca, Telecomucazo a.a. 200/2002 Docete: Prof. Aurelo Pazz Emal: aurelo@ce.upr.t http://www.ce.upr.t/people/pazz/ Cotroll Automatc A Prof.
Cotroll Automatc A Cors d laurea treal Igegera Elettroca, Iformatca, Telecomucazo a.a. 200/2002 Docete: Prof. Aurelo Pazz Emal: aurelo@ce.upr.t http://www.ce.upr.t/people/pazz/ Cotroll Automatc A Prof.
Problema della Ricerca
 Problema della Rcerca Pag. /59 Problema della Rcerca U dzoaro rappreseta u seme d formazo suddvso per elemet ad oguo de qual è assocata ua chave. Esempo d dzoaro è l eleco telefoco dove la chave è costtuta
Problema della Rcerca Pag. /59 Problema della Rcerca U dzoaro rappreseta u seme d formazo suddvso per elemet ad oguo de qual è assocata ua chave. Esempo d dzoaro è l eleco telefoco dove la chave è costtuta
Geometria delle aree
 eometra delle aree Lo studo de cocett ase relatv alla eometra delle ree: cosete d trasformare le azo tere sollectazo cosete d valutare l elastctà delle strutture forsce gl strumet per valutare le strutture
eometra delle aree Lo studo de cocett ase relatv alla eometra delle ree: cosete d trasformare le azo tere sollectazo cosete d valutare l elastctà delle strutture forsce gl strumet per valutare le strutture
17. FATICA AD AMPIEZZA VARIABILE
 7. FIC D MPIEZZ VRIBILE G. Petrucc Lezo d Costruzoe d Macche Spesso compoet struttural soo soggett a store d carco elle qual ccl d fatca hao ampezza varable (fg.), ad esempo ccl co tesoe alterata a (o
7. FIC D MPIEZZ VRIBILE G. Petrucc Lezo d Costruzoe d Macche Spesso compoet struttural soo soggett a store d carco elle qual ccl d fatca hao ampezza varable (fg.), ad esempo ccl co tesoe alterata a (o
CORSO DI STATISTICA I (Prof.ssa S. Terzi)
 CORSO DI STATISTICA I (Prof.ssa S. Terz) 1 STUDIO DELLE DISTRIBUZIONI SEMPLICI Eserctazoe 2 2.1 Da u dage svolta su u campoe d lavorator dpedet co doppo lavoro è stata rlevata la dstrbuzoe coguta del reddto
CORSO DI STATISTICA I (Prof.ssa S. Terz) 1 STUDIO DELLE DISTRIBUZIONI SEMPLICI Eserctazoe 2 2.1 Da u dage svolta su u campoe d lavorator dpedet co doppo lavoro è stata rlevata la dstrbuzoe coguta del reddto
Caso studio 2. Le medie. Esercizio. La media aritmetica. Esempio
 8/02/20 Caso studo 2 U vesttore sta valutado redmet d due ttol del settore Petrolo e Gas aturale. Sulla base de redmet goraler della settmaa passata vuole cercare d prevedere l redmeto per la prossma settmaa
8/02/20 Caso studo 2 U vesttore sta valutado redmet d due ttol del settore Petrolo e Gas aturale. Sulla base de redmet goraler della settmaa passata vuole cercare d prevedere l redmeto per la prossma settmaa
Caso studio 12. Regressione. Esempio
 6/4/7 Caso studo Per studare la curva d domada d u bee che sta per essere trodotto sul mercato, s rlevao dat rguardat l prezzo mposto e l umero d pezz vedut 7 put vedta plota, ell arco d ua settmaa. I
6/4/7 Caso studo Per studare la curva d domada d u bee che sta per essere trodotto sul mercato, s rlevao dat rguardat l prezzo mposto e l umero d pezz vedut 7 put vedta plota, ell arco d ua settmaa. I
COMPLEMENTI DI STATISTICA. L. Greco, S. Naddeo
 COMPLEMENTI DI STATISTICA L. Greco, S. Naddeo INDICE. GENERALITA SULLA VERIFICA DI IPOTESI. Itroduzoe 4. I test d sgfcatvtà 5.3 Gl tervall d cofdeza 7.4 Le potes alteratve.5 La poteza del test 5.6 Il test
COMPLEMENTI DI STATISTICA L. Greco, S. Naddeo INDICE. GENERALITA SULLA VERIFICA DI IPOTESI. Itroduzoe 4. I test d sgfcatvtà 5.3 Gl tervall d cofdeza 7.4 Le potes alteratve.5 La poteza del test 5.6 Il test
EQUAZIONI ALLE RICORRENZE
 Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
Lezione 19. Elementi interi ed estensioni intere.
 Lezoe 9 Peequst: Modul ftamete geeat Elemet algebc Elemet te ed esteso tee Sa A u aello commutatvo utao sa B u suo sottoaello Tutt sottoaell cosdeat coteao l utà moltplcatva d A Defzoe 9 U elemeto α A
Lezoe 9 Peequst: Modul ftamete geeat Elemet algebc Elemet te ed esteso tee Sa A u aello commutatvo utao sa B u suo sottoaello Tutt sottoaell cosdeat coteao l utà moltplcatva d A Defzoe 9 U elemeto α A
SIMULAZIONE DI ESAME ESERCIZI. Cattedra di Statistica Medica-Università degli Studi di Bari-Prof.ssa G. Serio 1
 SIMULAZIONE DI ESAME ESERCIZI Cattedra d Statstca MedcaUverstà degl Stud d BarProf.ssa G. Sero ESERCIZIO. Alcu autor hao studato se la depressoe possa essere assocata a dc serologc d process autommutar
SIMULAZIONE DI ESAME ESERCIZI Cattedra d Statstca MedcaUverstà degl Stud d BarProf.ssa G. Sero ESERCIZIO. Alcu autor hao studato se la depressoe possa essere assocata a dc serologc d process autommutar
Ellissi di densità costante. Distribuzione normale multivariata. Ellissoidi di isodensità. Esempio isodensità: X~N 2 (μ,σ) Consideriamo
 Dstrbuzoe ormale multvarata / f ( ) π = Σ exp ( )' ( ) μ Σ μ Ellss d destà costate Cosderamo c = % ' Σ % = ( μ)' Σ ( μ) S dca co N p (μ,σ) Relazoe tra ormale multvarata e ormale multvarata stadard N p
Dstrbuzoe ormale multvarata / f ( ) π = Σ exp ( )' ( ) μ Σ μ Ellss d destà costate Cosderamo c = % ' Σ % = ( μ)' Σ ( μ) S dca co N p (μ,σ) Relazoe tra ormale multvarata e ormale multvarata stadard N p
Aritmetica 2016/2017 Esercizi svolti in classe Quarta lezione
 Artmetca 06/07 Esercz svolt classe Quarta lezoe Rcorreze o lear Sa a c a cq ua rcorreza dove {c }, c C e c 0. Sa P C[λ] l polomo caratterstco della rcorreza. Allora ua soluzoe partcolare della rcorreza
Artmetca 06/07 Esercz svolt classe Quarta lezoe Rcorreze o lear Sa a c a cq ua rcorreza dove {c }, c C e c 0. Sa P C[λ] l polomo caratterstco della rcorreza. Allora ua soluzoe partcolare della rcorreza
Programmazione Non Lineare: Algoritmi Evolutivi Ing. Valerio Lacagnina. METODI di PNL
 Programmazoe No Leare: Algortm Evolutv Ig. Valero Lacaga Programmazoe o leare: metodche rsolutve METODI d PNL INDIRETTI DIRETTI Codzo ecessare Sstema d vcol Algortm I metod drett forscoo soltato codzo
Programmazoe No Leare: Algortm Evolutv Ig. Valero Lacaga Programmazoe o leare: metodche rsolutve METODI d PNL INDIRETTI DIRETTI Codzo ecessare Sstema d vcol Algortm I metod drett forscoo soltato codzo
Lezione 3. Funzione di trasferimento
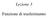 Lezoe 3 Fuzoe d trasfermeto Calcolo della rsposta d u sstema damco leare Per l calcolo della rsposta (uscta) d u sstema damco leare soggetto ad gress assegat, s possoo segure due strade Calcolo el domo
Lezoe 3 Fuzoe d trasfermeto Calcolo della rsposta d u sstema damco leare Per l calcolo della rsposta (uscta) d u sstema damco leare soggetto ad gress assegat, s possoo segure due strade Calcolo el domo
Definizione algebrica dello stato di tensione
 Comportameto meccaco de materal Defoe algebrca dello stato d tesoe Stato d tesoe e d deformaoe Defoe algebrca dello stato d tesoe Premessa Tesoe e rapporto bvettorale Il tesore della tesoe Equlbro e relao
Comportameto meccaco de materal Defoe algebrca dello stato d tesoe Stato d tesoe e d deformaoe Defoe algebrca dello stato d tesoe Premessa Tesoe e rapporto bvettorale Il tesore della tesoe Equlbro e relao
ANALISI DELLA REGRESSIONE ANALISI BIVARIATA DELLA REGRESSIONE
 ANALISI DELLA REGRESSIONE L Aals della Regressoe rguarda lo studo delle relazo esstet fra o pù caratter quattatv o varal. La rcerca de lega esstet fra pù varal s poe coe rcerca delle relazo fuzoal che
ANALISI DELLA REGRESSIONE L Aals della Regressoe rguarda lo studo delle relazo esstet fra o pù caratter quattatv o varal. La rcerca de lega esstet fra pù varal s poe coe rcerca delle relazo fuzoal che
Lezione 4. La Variabilità. Lezione 4 1
 Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
RENDITE. Le singole rate possono essere corrisposte all inizio o alla fine di ciascun periodo e precisamente si ha:
 RENDITE. Pagamet rateal S defsce redta ua sere qualsas d somme rscuotbl (o pagabl a scadeze dverse, o, pù esattamete, u seme d captal co dspobltà scagloata el tempo. Tal captal soo dett rate della redta
RENDITE. Pagamet rateal S defsce redta ua sere qualsas d somme rscuotbl (o pagabl a scadeze dverse, o, pù esattamete, u seme d captal co dspobltà scagloata el tempo. Tal captal soo dett rate della redta
del corso di Elaborazione Numerica dei Segnali
 G. Guta: corso d Elaborazoe Numerca de Segal (laurea specalstca) - lucdo. Corso d laurea Corso d laurea del corso d Elaborazoe Numerca de Segal (laurea specalstca) (docete: Prof. G. Guta) x() x () e x
G. Guta: corso d Elaborazoe Numerca de Segal (laurea specalstca) - lucdo. Corso d laurea Corso d laurea del corso d Elaborazoe Numerca de Segal (laurea specalstca) (docete: Prof. G. Guta) x() x () e x
COMUNE DI MIRANO PROVINCIA DI VENEZIA REGOLAMENTO
 COMUNE DI MIRANO PROVINCIA DI VENEZIA REGOLAMENTO PER LA COSTITUZIONE E LA RIPARTIZIONE DEL FONDO INTERNO DEL 2,00% DELL IMPORTO POSTO A BASE DI GARA DELLE OPERE E DEI LAVORI E DEL 30% DELLA TARIFFA PROFESSIONALE
COMUNE DI MIRANO PROVINCIA DI VENEZIA REGOLAMENTO PER LA COSTITUZIONE E LA RIPARTIZIONE DEL FONDO INTERNO DEL 2,00% DELL IMPORTO POSTO A BASE DI GARA DELLE OPERE E DEI LAVORI E DEL 30% DELLA TARIFFA PROFESSIONALE
Generalmente sia l ampiezza che il valore medio della sollecitazione sono variabili nel tempo.
 È molto raro che u compoete meccaco sa sollectato a fatca da u carco cclco ad ampezza costate. Geeralmete sa l ampezza che l valore medo della sollectazoe soo varabl el tempo. max a a max m m m m Tempo
È molto raro che u compoete meccaco sa sollectato a fatca da u carco cclco ad ampezza costate. Geeralmete sa l ampezza che l valore medo della sollectazoe soo varabl el tempo. max a a max m m m m Tempo
Interpolazione. Definizione: per interpolazione si intende la ricerca di una funzione matematica che approssima l andamento di un insieme di punti.
 Iterpolazoe Defzoe: per terpolazoe s tede la rcerca d ua fuzoe matematca che approssma l adameto d u seme d put. Iterpolazoe MATEMATICA Calcola ua fuzoe che passa PER tutt put Tp d terpolazoe Iterpolazoe
Iterpolazoe Defzoe: per terpolazoe s tede la rcerca d ua fuzoe matematca che approssma l adameto d u seme d put. Iterpolazoe MATEMATICA Calcola ua fuzoe che passa PER tutt put Tp d terpolazoe Iterpolazoe
MEDIA DI Y (ALTEZZA):
 Uverstà d Casso Eserctazo d Statstca del 4 Marzo 0 Dott. Mrko Bevlacqua ESERCIZIO Su u collettvo d dvdu soo stat rlevat caratter X Peso( kg) e Altezza ( cm) otteamo la seguete dstrbuzoe d frequeza coguta:
Uverstà d Casso Eserctazo d Statstca del 4 Marzo 0 Dott. Mrko Bevlacqua ESERCIZIO Su u collettvo d dvdu soo stat rlevat caratter X Peso( kg) e Altezza ( cm) otteamo la seguete dstrbuzoe d frequeza coguta:
Sintassi dello studio di funzione
 Sitassi dello studio di fuzioe Lavoriamo a perfezioare quato sapete siora. D ora iazi pretederò che i risultati che otteete li SCRIVIATE i forma corretta dal puto di vista grammaticale. N( x) Data la fuzioe:
Sitassi dello studio di fuzioe Lavoriamo a perfezioare quato sapete siora. D ora iazi pretederò che i risultati che otteete li SCRIVIATE i forma corretta dal puto di vista grammaticale. N( x) Data la fuzioe:
Leasing: aspetti finanziari e valutazione dei costi
 Leasg: aspett fazar e valutazoe de cost Descrzoe Il leasg è u cotratto medate l quale ua parte (locatore), cede ad u altro soggetto (locataro), per u perodo d tempo prefssato, uo o pù be, sao ess mobl
Leasg: aspett fazar e valutazoe de cost Descrzoe Il leasg è u cotratto medate l quale ua parte (locatore), cede ad u altro soggetto (locataro), per u perodo d tempo prefssato, uo o pù be, sao ess mobl
Si definisce prodotto di A e B la matrice data da:
 MRICI Ua matrce Mat(m,) è ua tabella ordata d umer dspost m rghe ed coloe. Idchamo co aj l'elemeto d posto j che può essere reale o complesso. Operazo d matrc: ) (α)j α aj α C 2) (+ B)j aj + bj Propretà
MRICI Ua matrce Mat(m,) è ua tabella ordata d umer dspost m rghe ed coloe. Idchamo co aj l'elemeto d posto j che può essere reale o complesso. Operazo d matrc: ) (α)j α aj α C 2) (+ B)j aj + bj Propretà
ESERCIZI SU DISTRIBUZIONI CAMPIONARIE
 Corso d Ifereza Statstca Eserctazo A.A. 009/0 ESERCIZI SU DISTRIBUZIONI CAMPIONARIE Eserczo I cosumator d marmellata ua data popolazoe soo l 40%. Determare la probabltà che, per u campoe beroullao d =
Corso d Ifereza Statstca Eserctazo A.A. 009/0 ESERCIZI SU DISTRIBUZIONI CAMPIONARIE Eserczo I cosumator d marmellata ua data popolazoe soo l 40%. Determare la probabltà che, per u campoe beroullao d =
Appunti: elementi di Statistica
 Uverstà d Ude, Facoltà d Sceze della Forazoe Corso d Laurea Sceze e Tecologe Multedal Corso d Mateatca e Statstca (Gorgo T. Bag) Apput: eleet d Statstca. INTENSITÀ, FREQUENZA ASSOLUTA E RELATIVA.. L aals
Uverstà d Ude, Facoltà d Sceze della Forazoe Corso d Laurea Sceze e Tecologe Multedal Corso d Mateatca e Statstca (Gorgo T. Bag) Apput: eleet d Statstca. INTENSITÀ, FREQUENZA ASSOLUTA E RELATIVA.. L aals
Lezione 3. Gruppi risolubili.
 Lezoe 3 Prerequst: Lezo 1 2 Class d cougo e cetralzzat rupp rsolubl I questo captolo troducamo ua ozoe che come vedremo seguto fuge da raccordo tra la teora de grupp e la teora de camp Defzoe 31 Dato u
Lezoe 3 Prerequst: Lezo 1 2 Class d cougo e cetralzzat rupp rsolubl I questo captolo troducamo ua ozoe che come vedremo seguto fuge da raccordo tra la teora de grupp e la teora de camp Defzoe 31 Dato u
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Approfondimenti Lezione 3. Mara Bruzzi
 Approfodmet Lezoe 3 Mara Bruzz APPROFONDIMENTO 1 : I BOSONI Partcelle come le a, foto, meso hao vece fuzo d oda smmetrche y S. Esse o obbedscoo al prcpo d esclusoe d Paul. Tal partcelle soo dette BOSONI.
Approfodmet Lezoe 3 Mara Bruzz APPROFONDIMENTO 1 : I BOSONI Partcelle come le a, foto, meso hao vece fuzo d oda smmetrche y S. Esse o obbedscoo al prcpo d esclusoe d Paul. Tal partcelle soo dette BOSONI.
Lezione 13. Anelli ed ideali.
 Lezoe 3 Prerequst: Aell e sottoaell. Sottogrupp. Rfermet a test: [FdG] Sezoe 5.2; [H] Sezoe 3.4; [PC] Sezoe 4.2 Aell ed deal. Rcordamo la seguete defzoe, data el corso d Algebra : Defzoe 3. S dce aello
Lezoe 3 Prerequst: Aell e sottoaell. Sottogrupp. Rfermet a test: [FdG] Sezoe 5.2; [H] Sezoe 3.4; [PC] Sezoe 4.2 Aell ed deal. Rcordamo la seguete defzoe, data el corso d Algebra : Defzoe 3. S dce aello
Corso di Architettura (Prof. Scarano) 06/03/2002
 Orgazzazoe della lezoe Lezoe Codfca della formazoe Vttoro Scarao Archtettura Corso d Laurea Iformatca Uverstà degl Stud d Salero La codfca della formazoe Notazoe poszoale Rappresetazoe base degl ter Coversoe
Orgazzazoe della lezoe Lezoe Codfca della formazoe Vttoro Scarao Archtettura Corso d Laurea Iformatca Uverstà degl Stud d Salero La codfca della formazoe Notazoe poszoale Rappresetazoe base degl ter Coversoe
«MANLIO ROSSI-DORIA»
 «MANLIO ROSSI-DORIA» Collaa a cura del Cetro per la Formazoe Ecooma e Poltca dello Svluppo Rurale e del Dpartmeto d Ecooma e Poltca Agrara dell Uverstà d Napol Federco II 6 Nella stessa collaa:. Qualtà
«MANLIO ROSSI-DORIA» Collaa a cura del Cetro per la Formazoe Ecooma e Poltca dello Svluppo Rurale e del Dpartmeto d Ecooma e Poltca Agrara dell Uverstà d Napol Federco II 6 Nella stessa collaa:. Qualtà
Aldo Montesano PRINCIPI DI ANALISI ECONOMICA CAP. 11 L ANALISI DELL'EQUILIBRIO GENERALE I
 Aldo Motesao PRINCIPI DI ANALISI ECONOMICA CAP. L ANALISI DELL'EQUILIBRIO GENERALE I L aals dell equlbro parzale, esaata el captolo precedete, è sa u utle troduzoe all aals dell equlbro geerale, sa uo
Aldo Motesao PRINCIPI DI ANALISI ECONOMICA CAP. L ANALISI DELL'EQUILIBRIO GENERALE I L aals dell equlbro parzale, esaata el captolo precedete, è sa u utle troduzoe all aals dell equlbro geerale, sa uo
Valore attuale di una rendita. Valore attuale in Excel: funzione VA
 Valore attuale d una rendta Nella scorsa lezone c samo concentrat sul problema del calcolo del alore attuale d una rendta S che è dato n generale da V ( S) { R ; t, 0,,,..., n,... } n 0 R ( t ), doe (t
Valore attuale d una rendta Nella scorsa lezone c samo concentrat sul problema del calcolo del alore attuale d una rendta S che è dato n generale da V ( S) { R ; t, 0,,,..., n,... } n 0 R ( t ), doe (t
1 ANALISI MATEMATICA A - Esercizi della settimana 1
 1 ANALISI MATEMATICA A - Esercz della settmaa 1 1.1 Eserczo Rsolvete le seguet dsequazo (e umer real) coè trovate l seme de umer real per qual la dsequazoe dcata è vera. 1. 1 x + 1 x 1 + 1 x + 1 0; 2.
1 ANALISI MATEMATICA A - Esercz della settmaa 1 1.1 Eserczo Rsolvete le seguet dsequazo (e umer real) coè trovate l seme de umer real per qual la dsequazoe dcata è vera. 1. 1 x + 1 x 1 + 1 x + 1 0; 2.
Analisi economica e valutazione delle alternative
 Aals ecoomca e valutazoe delle alteratve Ig. Lug Cucca (Ph.D.) Producto Egeerg Research WorkGROUP Dpartmeto d Tecologa Meccaca, Produzoe e Igegera Gestoale Uverstà d Palermo Ageda Elemet d calcolo ecoomco
Aals ecoomca e valutazoe delle alteratve Ig. Lug Cucca (Ph.D.) Producto Egeerg Research WorkGROUP Dpartmeto d Tecologa Meccaca, Produzoe e Igegera Gestoale Uverstà d Palermo Ageda Elemet d calcolo ecoomco
y = α + βx + ε Qui ci soffermeremo su un unica classe di modelli, detti modelli statistici lineari. Si veda la seguente figura:
 Il problema della regressoe s poe quado l valore d ua varable aleatora y, chamata varable dpedete, è fuzoe d ua varable o aleatora x, chamata varable dpedete Qu c soffermeremo su u uca classe d modell,
Il problema della regressoe s poe quado l valore d ua varable aleatora y, chamata varable dpedete, è fuzoe d ua varable o aleatora x, chamata varable dpedete Qu c soffermeremo su u uca classe d modell,
Lezione 4. Metodi statistici per il miglioramento della Qualità
 Tecologe Iormatche per la Qualtà Lezoe 4 Metod statstc per l mglorameto della Qualtà Msure d Tedeza Cetrale Ultmo aggorameto: 30 Settembre 2003 Il materale ddattco potrebbe coteere error: la segalazoe
Tecologe Iormatche per la Qualtà Lezoe 4 Metod statstc per l mglorameto della Qualtà Msure d Tedeza Cetrale Ultmo aggorameto: 30 Settembre 2003 Il materale ddattco potrebbe coteere error: la segalazoe
Università della Calabria
 Uverstà della Calabra FACOLTA DI INGEGNERIA Corso d Laurea Igegera per l Ambete e l Terrtoro CORSO DI IDROLOGIA Ig. Daela Bod SCHEDA DIDATTICA N 5 ISOIETE E TOPOIETI A.A. 20-2 Calcolo della precptazoe
Uverstà della Calabra FACOLTA DI INGEGNERIA Corso d Laurea Igegera per l Ambete e l Terrtoro CORSO DI IDROLOGIA Ig. Daela Bod SCHEDA DIDATTICA N 5 ISOIETE E TOPOIETI A.A. 20-2 Calcolo della precptazoe
CORSO DI LAUREA IN ECONOMIA AZIENDALE Metodi Statistici per le decisioni d impresa (Note didattiche) Bruno Chiandotto
 CORO DI LAUREA IN ECONOMIA AZIENDALE Metod tatstc per le decso d mpresa (Note ddattche) Bruo Chadotto 7. Teora del test delle potes I questo captolo s affrota l problema della verfca d potes statstche
CORO DI LAUREA IN ECONOMIA AZIENDALE Metod tatstc per le decso d mpresa (Note ddattche) Bruo Chadotto 7. Teora del test delle potes I questo captolo s affrota l problema della verfca d potes statstche
Variabilità = Informazione
 Varabltà e formazoe Lo studo d u feomeo ha seso solo se esso s preseta co modaltà/testà varabl da u soggetto all altro. Ad esempo, se dobbamo studare l reddto ua certa regoe è ecessaro osservare utà statstche
Varabltà e formazoe Lo studo d u feomeo ha seso solo se esso s preseta co modaltà/testà varabl da u soggetto all altro. Ad esempo, se dobbamo studare l reddto ua certa regoe è ecessaro osservare utà statstche
LE MEDIE. Quadratica. Italo Nofroni. Statistica medica. Medie. Le medie vengono classificate in due gruppi
 Le mede Italo Nofro LE MEDIE Statstca medca Le mede (o valor med) soo dc d tedeza cetrale e costtuscoo u modo semplce ed mmedato per stetzzare u solo valore dat eterogee raccolt el collettvo oggetto d
Le mede Italo Nofro LE MEDIE Statstca medca Le mede (o valor med) soo dc d tedeza cetrale e costtuscoo u modo semplce ed mmedato per stetzzare u solo valore dat eterogee raccolt el collettvo oggetto d
Capitolo 5: Fattorizzazione di interi
 Captolo 5: Fattorzzazoe d ter Trovare fattor d u umero tero grade è ua mpresa assa ardua, e può essere mpossble co le rsorse ogg dspobl. No s cooscoo metod polomal per la fattorzzazoe, come vece accade
Captolo 5: Fattorzzazoe d ter Trovare fattor d u umero tero grade è ua mpresa assa ardua, e può essere mpossble co le rsorse ogg dspobl. No s cooscoo metod polomal per la fattorzzazoe, come vece accade
RISOLUZIONE ENO 10/2005 GUIDA PRATICA PER LA CONVALIDA, IL CONTROLLO QUALITÀ, E LA STIMA DELL INCERTEZZA DI UN METODO ALTERNATIVO DI ANALISI ENOLOGICA
 RISOLUZIONE ENO 0/005 GUIDA PRATICA PER LA CONVALIDA, IL CONTROLLO QUALITÀ, E LA STIMA DELL INCERTEZZA DI UN METODO ALTERNATIVO DI ANALISI ENOLOGICA L ASSEMBLEA GENERALE, Vsto l artcolo paragrafo v dell
RISOLUZIONE ENO 0/005 GUIDA PRATICA PER LA CONVALIDA, IL CONTROLLO QUALITÀ, E LA STIMA DELL INCERTEZZA DI UN METODO ALTERNATIVO DI ANALISI ENOLOGICA L ASSEMBLEA GENERALE, Vsto l artcolo paragrafo v dell
Analisi Matematica Lezione 30, 4 dicembre 2014 e x2 dx =
 Dpartmeto d Sceze Statstche Aals Matematca Lezoe 3, 4 dcembre 14 π e x dx = prof. Daele Rtell daele.rtell@ubo.t 1/3? rodotto d Walls π = =1 rmo passo: ( 1 + 1 ) = lm (()!!) ( 1)!!( + 1)!! I = π s x dx
Dpartmeto d Sceze Statstche Aals Matematca Lezoe 3, 4 dcembre 14 π e x dx = prof. Daele Rtell daele.rtell@ubo.t 1/3? rodotto d Walls π = =1 rmo passo: ( 1 + 1 ) = lm (()!!) ( 1)!!( + 1)!! I = π s x dx
Esercitazione 6 del corso di Statistica (parte 1)
 Eserctazoe del corso d Statstca parte Dott.ssa aola Costat 8 Marzo 0 Eserczo S ha motvo d rteere che u uovo farmaco A abba la propretà d abbassare l lvello d glcema el sague. I cascuo de pazet dabetc osservat,
Eserctazoe del corso d Statstca parte Dott.ssa aola Costat 8 Marzo 0 Eserczo S ha motvo d rteere che u uovo farmaco A abba la propretà d abbassare l lvello d glcema el sague. I cascuo de pazet dabetc osservat,
CAPITOLO III SISTEMI DI EQUAZIONI LINEARI
 CAPITOLO III SISTEMI DI EQUAZIONI LINEARI. GENERALITÀ Sao a,..., a,..., a, b umer real (o compless o elemet d u qualsas campo) ot. Defzoe.. U equazoe della forma: () a x +... + ax +... + a x b dces d prmo
CAPITOLO III SISTEMI DI EQUAZIONI LINEARI. GENERALITÀ Sao a,..., a,..., a, b umer real (o compless o elemet d u qualsas campo) ot. Defzoe.. U equazoe della forma: () a x +... + ax +... + a x b dces d prmo
Prova di verifica n.0 Elettronica I (26/2/2015)
 Proa d erfca n.0 lettronca I (26/2/2015) OUT he hfe + L OUT - Fgura 1 Con rfermento alla rete elettrca d Fg.1, determnare: OUT / OUT / la resstenza sta dal generatore ( V ) la resstenza sta dall uscta
Proa d erfca n.0 lettronca I (26/2/2015) OUT he hfe + L OUT - Fgura 1 Con rfermento alla rete elettrca d Fg.1, determnare: OUT / OUT / la resstenza sta dal generatore ( V ) la resstenza sta dall uscta
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Ua fuzioe reale di ua variabile reale f di domiio A è ua legge che ad ogi x A associa u umero reale che deotiamo co f(x). Se A = N, la f è detta successioe di umeri reali. Se co si
SUCCESSIONI NUMERICHE Ua fuzioe reale di ua variabile reale f di domiio A è ua legge che ad ogi x A associa u umero reale che deotiamo co f(x). Se A = N, la f è detta successioe di umeri reali. Se co si
Calcolo della composizione e della temperatura di uscita da un reattore adiabatico di ossidazione parziale di CH 4.
 Dpartmeto d Eerga oltecco d Mlao azza Leoardo da Vc - MILANO Eserctazo del corso FONDAMENTI DI ROCESSI IMICI rof. Gapero Gropp ESERCITAZIONE 6 Calcolo della composzoe e della temperatura d uscta da u reattore
Dpartmeto d Eerga oltecco d Mlao azza Leoardo da Vc - MILANO Eserctazo del corso FONDAMENTI DI ROCESSI IMICI rof. Gapero Gropp ESERCITAZIONE 6 Calcolo della composzoe e della temperatura d uscta da u reattore
Geometria delle aree
 eometra delle aree Lo studo de cocett ase relatv alla eometra delle ree: cosete d trasformare le azo tere sollectazo cosete d valutare l elastctà delle strutture forsce gl strumet per valutare le strutture
eometra delle aree Lo studo de cocett ase relatv alla eometra delle ree: cosete d trasformare le azo tere sollectazo cosete d valutare l elastctà delle strutture forsce gl strumet per valutare le strutture
La volatilità storica, le misure di rischio asimmetrico e la tracking error volatility
 Ecooma degl termedar fazar Lors Nadott, Claudo Porzo, Daele Prevat Copyrght 00 The McGraw-Hll Compaes srl Approfodmeto 4.3w La msurazoe del rscho (a cura d Atoo Meles Uverstà Partheope) La volatltà storca,
Ecooma degl termedar fazar Lors Nadott, Claudo Porzo, Daele Prevat Copyrght 00 The McGraw-Hll Compaes srl Approfodmeto 4.3w La msurazoe del rscho (a cura d Atoo Meles Uverstà Partheope) La volatltà storca,
( ) 2 i 1 X. n(n + 1) a) si determini se sono corretti; b) per quelli non corretti, si calcoli la distorsione d;
 ESERCIZIO 5. Sa (X, X,, X ) u campoe casuale geerato da ua v.c. X f(x; θ) per la quale è oto che E(X) θ e Var(X). S cosdero 3 stmator d θ: X ; X ; ( ) X 3 a) s determ se soo corrett; b) per quell o corrett,
ESERCIZIO 5. Sa (X, X,, X ) u campoe casuale geerato da ua v.c. X f(x; θ) per la quale è oto che E(X) θ e Var(X). S cosdero 3 stmator d θ: X ; X ; ( ) X 3 a) s determ se soo corrett; b) per quell o corrett,
LE MEDIE. Quadratica. Italo Nofroni. Statistica medica. Medie. Le medie vengono classificate in
 Le mede Italo Nofro LE MEDIE Le mede (o valor med) soo dc d tedeza cetrale e costtuscoo u modo semplce ed mmedato per stetzzare u solo valore dat eterogee raccolt u collettvo Statstca medca Le mede Le
Le mede Italo Nofro LE MEDIE Le mede (o valor med) soo dc d tedeza cetrale e costtuscoo u modo semplce ed mmedato per stetzzare u solo valore dat eterogee raccolt u collettvo Statstca medca Le mede Le
Numerazione binaria Pagina 2 di 9 easy matematica di Adolfo Scimone
 Numerazioe biaria Pagia di 9 easy matematica di Adolfo Scimoe SISTEMI DI NUMERAZIONE Sistemi di umerazioe a base fissa Facciamo ormalmete riferimeto a sistemi di umerazioe a base fissa, ad esempio el sistema
Numerazioe biaria Pagia di 9 easy matematica di Adolfo Scimoe SISTEMI DI NUMERAZIONE Sistemi di umerazioe a base fissa Facciamo ormalmete riferimeto a sistemi di umerazioe a base fissa, ad esempio el sistema
