FORMULE DI AGGIUDICAZIONE
|
|
|
- Fabia Grillo
- 6 anni fa
- Visualizzazioni
Transcript
1 Mnule di supporto ll utilizzo di Sintel per stzione ppltnte FORMULE DI AGGIUDICAZIONE gin 1 di 18
2 Indice AZIENDA REGIONALE CENTRALE ACQUISTI - ARCA S.p.A. 1 INTRODUZIONE Mtrice modlità offert/modlità trtttiv FORMULE SINTEL Formul interpolzione linere Formul Bilinere Formul Servizi di pulizi Formule per gre di forniture Lvori Formul Lvori: interpolzione linere Formul Lvori: elemento tempo Formul del rezzo Minimo Formul del rezzo Mssimo - Minimo Formul Linere Formul Non linere SELEZIONE FORMULE SU SINTEL gin 2 di 18
3 1 INTRODUZIONE Il presente documento è volto d illustrre le crtteristiche delle principli formule di ggiudiczione comunemente utilizzte dlle stzioni ppltnti nei procedimenti di gr e presenti sull pittform Sintel. L scelt delle formul di ggiudiczione ssume un ruolo strtegico poiché può ndre d influenzre il comportmento dei fornitori, soprttutto qundo si opt per il criterio dell offert economicmente più vntggios. A tl proposito si precis l non tsstività di utilizzo delle formule descritte nel presente documento i fini dell ggiudiczione di gr e che l onere e l responsbilità di scelt di un determint formul sono in cpo ll singol Stzione Appltnte utilizztrice dell pittform Sintel. NOTA: è importnte evidenzire che ciscun stzione ppltnte oper su Sintel ed effettu le procedure sotto l propri direzione ed esclusiv responsbilità. Gli utenti si ssumono, in ogni cso, l pien ed esclusiv responsbilità circ l legittimità delle ttività d questi compiute sull pittform Sintel e l conformità delle medesime ll normtiv legisltiv e regolmentre vigente Aziend Regionle Centrle Acquisti S.p.A., pertnto, non ssume lcun responsbilità in relzione lle procedure di ffidmento effettute ttrverso Sintel ed lle scelte effettute nell impostzione delle discipline di gr. 1.1 Mtrice modlità offert/modlità trtttiv L mtrice di seguito riportt rissume le logiche che possono essere utilizzte e ricondotte ll strtegi di gr per le procedure che gli utenti delle stzioni ppltnti intendono gestire trmite l pittform di e-procurement Sintel. gin 3 di 18
4 2 FORMULE SINTEL Nell mbito di procedure rigurdnti contrtti reltivi Forniture e Servizi ed in prticolre con il criterio dell offert economicmente più vntggios, si possono utilizzre le formule che seguono per il clcolo del solo punteggio economico. 2.1 Formul interpolzione linere er clcolre il punteggio economico E di ciscun offert si può utilizzre l formul seguente; E E V = indice numerico di riferimento dell offert; V = coefficiente dell offert del concorrente ( 0< V 1); E = punteggio economico ssegnto ll offert del concorrente ; E = punteggio economico mssimo ssegnbile. er clcolre il coefficiente V per gli elementi di vlutzione di ntur quntittiv si pplic l seguente formul: ( ) = indice numerico di riferimento dell offert; V = coefficiente dell offert del concorrente ( 0< V 1); R = Vlore (ribsso/rilzo) offerto dl concorrente i-esimo; R best = Vlore (ribsso/rilzo) dell offert più conveniente. Nel dettglio: er vlore economico er vlore percentule Ribsso Rilzo Totle Unitri Totle Unitri BA = vlore riportto nel cmpo Bse d st lto SA: rocedure per vlore economico: vlore economico; rocedure per vlore percentule: vlore percentule %. = prezzo offerto dl concorrente i-esimo; gin 4 di 18
5 OT = offert totle del concorrente i-esimo, risultnte dll sommtori dei prezzi offerti per ogni prodotto pondert per le eventuli incidenze percentuli; = percentule di ribsso/rilzo offert dl concorrente i-esimo; = ribsso/rilzo complessivo offerto dl concorrente i-esimo, risultnte dll medi dei ribssi/rilzi offerti per ogni prodotto pondert per le eventuli incidenze percentuli. 2.2 Formul Bilinere er clcolre il punteggio economico E di ciscun offert si può utilizzre l formul seguente; E E V = indice numerico di riferimento dell offert; V = coefficiente dell offert del concorrente ( 0< V 1); E = punteggio economico ssegnto ll offert del concorrente ; E = punteggio economico mssimo ssegnbile. er clcolre il coefficiente V si pplic l seguente formul: - per A Asogli V A X A sogli - per A Asogli V X A (1,00 X ) A A A sogli sogli = indice numerico di riferimento dell offert; A = vlore dell offert del concorrente ; A sogli = medi ritmetic dei vlori delle offerte dei concorrenti; V = coefficiente dell offert del concorrente ( 0< V 1); X = coefficiente pri 0,80 oppure 0,85 oppure 0,90 (il vlore v indicto chirmente nei documenti di gr); A = vlore dell offert più conveniente per l stzione ppltnte. gin 5 di 18
6 N.B.: l utilizzo di quest formul penlizz le offerte che hnno vlori A x inferiori l vlore medio A sogli e f si che vri in mnier significtiv il punteggio economico (Δ~10) ttribuito d offerte che vrino poco tr loro livello di prezzo offerto (Δ~1). 2.3 Formul Servizi di pulizi er clcolre il punteggio economico E di ciscun offert si può utilizzre l formul seguente: E i E ( b ( b i ) m ) dove per le procedure per vlore economico l ribsso totli o unitrie : E i = punteggio economico (clcolto ed) ttribuito ll offert del concorrente i-esimo; E = punteggio economico mssimo ssegnbile; b = prezzo posto bse d st; i = prezzo offerto dl concorrente i-esimo; m = prezzo migliore offerto fr tutte le offerte pervenute. e per le procedure per vlore percentule l ribsso totli o unitrie : E i = punteggio economico (clcolto ed) ttribuito ll offert del concorrente i-esimo; E = punteggio economico mssimo ssegnbile; b = prezzo posto bse d st; i = prezzo offerto dl concorrente i-esimo; m = prezzo migliore offerto fr tutte le offerte pervenute. N.B.: nche nel cso di procedure per Vlore percentule i vlori che devono essere utilizzti nel clcolo del punteggio sono vlori economici espressi in Euro. In prticolre: i corrisponde l Bse d st Vlore percentule offerto dl concorrente i-esimo ; m corrisponde l Bse d st Vlore percentule mssimo offerto (fr tutte le offerte pervenute). N.B: l Formul Servizi di pulizi non può essere utilizzt per le procedure di gr con logic l rilzo su Sintel. gin 6 di 18
7 2.4 Formule per gre di forniture Lvori Formul Lvori: interpolzione linere Nell mbito di procedure rigurdnti contrtti reltivi Lvori in prticolre con il criterio dell offert economicmente più vntggios, si può utilizzre l formul che segue per il clcolo del solo punteggio economico. er clcolre il punteggio economico E di ciscun offert si può utilizzre l formul seguente; E E V = indice numerico di riferimento dell offert; V = coefficiente dell offert del concorrente ( 0< V 1); E = punteggio economico ssegnto ll offert del concorrente ; E = punteggio economico mssimo ssegnbile. er clcolre il coefficiente V per gli elementi di vlutzione di ntur quntittiv si pplic l seguente formul: R V 1 R worst R R best best = indice numerico di riferimento dell offert; V = coefficiente dell offert del concorrente ( 0< V 1) ; R = vlore dell offert del concorrente ; R best = vlore dell offert migliore(dell offert più conveniente); R worst = vlore dell offert peggiore. N.B.: l utilizzo di quest formul penlizz fortemente l offert meno conveniente nche se differisce di poco (Δ~1) livello di prezzo offerto d quell ppen migliore. gin 7 di 18
8 2.4.2 Formul Lvori: elemento tempo er clcolre il punteggio economico E di ciscun offert si può utilizzre l formul seguente: E i ( Ci c ) ( Di d ) dove per le procedure per vlore economico decrescente: vince il vlore più bsso offerto): l ribsso totli o unitrie (con offert migliortiv E i = punteggio economico (clcolto ed) ttribuito ll offert del concorrente i-esimo; c d = fttore ponderle che l utente deve inserire in pittform ( 0 30 ); = fttore ponderle che l utente deve inserire in pittform ( 0 10 ); c d C i = coefficiente elemento prezzo dell offert del concorrente i-esimo; D i = coefficiente elemento tempo dell offert del concorrente i-esimo. er il clcolo del coefficiente elemento prezzo C i si pplic un delle seguenti formule: per A A = X* ( / ) sogli per A A = X + (1,00 X) * [( )/( ) sogli = vlore dell offert del concorrente i-esimo = medi ritmetic dei vlori delle offerte dei concorrenti; X = coefficiente con vlore 0,80 oppure 0,85 oppure 0,90 che deve essere selezionto in pittform; = vlore dell offert più conveniente. er il clcolo di : = = prezzo posto bse d st; = prezzo offerto dl concorrente i-esimo. er il clcolo del coefficiente elemento tempo D si pplic l seguente formul: i gin 8 di 18
9 Dove: = riduzione percentule del tempo offert dl concorrente ì-esimo; = l medi ritmetic delle riduzioni percentuli del tempo offerte. dove per le procedure per vlore percentule l ribsso totli o unitrie (con offert migliortiv crescente: vince il vlore più lto offerto): E i = punteggio economico (clcolto ed) ttribuito ll offert del concorrente i-esimo; c d = fttore ponderle che l utente deve inserire in pittform ( 0 30 ); = fttore ponderle che l utente deve inserire in pittform ( 0 10 ); c d C i = coefficiente elemento prezzo dell offert del concorrente i-esimo; D i = coefficiente elemento tempo dell offert del concorrente i-esimo. er il clcolo del coefficiente elemento prezzo C i si pplic un delle seguenti formule: per A A = X* ( / ) sogli per A A = X + (1,00 X) * [( )/( )] sogli dove = vlore dell offert del concorrente i-esimo; = medi ritmetic dei vlori delle offerte dei concorrenti; X = coefficiente con vlore 0,80 oppure 0,85 oppure 0,90 che deve essere selezionto in pittform; = vlore dell offert più conveniente. er il clcolo di : = = vlore percentule posto bse d st; = vlore percentule offerto dl concorrente i-esimo er il clcolo del coefficiente elemento tempo D si pplic l seguente formul: i = riduzione percentule del tempo offert dl concorrente ì-esimo; gin 9 di 18
10 = l medi ritmetic delle riduzioni percentuli del tempo offerte. N.B: l Formul lvori: elemento tempo non può essere utilizzt per le procedure di gr con logic l rilzo su Sintel. 2.5 Formul del rezzo Minimo Quest formul h le seguenti crtteristiche: l offert migliore presentt, ottiene il totle dei punti economici ssegnti mentre le ltre offerte ottengono un frzione di tle punteggio; il punteggio economico E ssegnto d ogni prtecipnte dipende dll migliore offert presentt in gr. er le procedure totli e unitrie per vlore economico l ribsso l formul d pplicre è l seguente: E E o = rezzo offerto dl singolo concorrente; E = unteggio economico mssimo ssegnbile; min = rezzo più bsso offerto in gr. min o er le procedure totli e unitrie per vlore economico l rilzo (Formul l prezzo mssimo) l formul d pplicre è l seguente: E E o o = rezzo offerto dl singolo concorrente; E = unteggio economico mssimo ssegnbile; = rezzo più lto offerto in gr. gin 10 di 18
11 er le procedure totli e unitrie per vlore percentule l ribsso (Formul llo sconto mssimo) l formul d pplicre è l seguente: E E S S S o = ercentule offert dl singolo concorrente; E = unteggio economico mssimo ssegnbile; S = ercentule più lt offert in gr. o er le procedure totli e unitrie per vlore percentule l rilzo (Formul llo sconto minimo) l formul d pplicre è l seguente: E E S S o = ercentule offert dl singolo concorrente; min S o E = unteggio economico mssimo ssegnbile; S min = ercentule più bss offert in gr. gin 11 di 18
12 2.6 Formul del rezzo Mssimo - Minimo Quest formul h le seguenti crtteristiche: il punteggio economico E ssegnto d ogni prtecipnte dipende si dll migliore offert presentt in gr si dll peggiore offert presente in gr; l offert peggiore non viene premit. er le procedure totli e unitrie per vlore economico l ribsso l formul d pplicre è l seguente: E E E = unteggio economico mssimo ssegnbile; o = rezzo offerto dl singolo concorrente; = rezzo più lto presentto in gr; min = rezzo più bsso presentto in gr. o min er le procedure totli e unitrie per vlore economico l rilzo l formul d pplicre è l seguente: E E E = unteggio economico mssimo ssegnbile; o = rezzo offerto dl singolo concorrente; = rezzo più lto presentto in gr; min = rezzo più bsso presentto in gr. min min o gin 12 di 18
13 er le procedure totli e unitrie per vlore percentule l ribsso l formul d pplicre è l seguente: E E S S E = unteggio economico mssimo ssegnbile; S o = ercentule offert dl singolo concorrente; S = ercentule più lt offert in gr; S min = ercentule più bss offert in gr. min min S S o er le procedure totli e unitrie per vlore percentule l rilzo l formul d pplicre è l seguente: E E S S E = unteggio economico mssimo ssegnbile; S o = ercentule offert dl singolo concorrente; S = ercentule più lt offert in gr; S min = ercentule più bss offert in gr. S S o min gin 13 di 18
14 2.7 Formul Linere L formul d pplicre è l seguente: se, E E se, E E o = rezzo offerto dl singolo concorrente; = unteggio economico mssimo ssegnbile; b = rezzo bse d st; o o s s b b o s rim di nlizzre le crtteristiche di tle formul è importnte esplicre il ruolo ssunto dl rezzo sogli ( s ). Il seguente grfico (Figur 1) mostr i punti ottenuti d tre offerte ( o1, o2 e o3 ). Figur 1 Risult evidente che tutte le offerte incluse tr il prezzo sogli e zero ottengono il mssimo dei punti (in questo cso trttsi delle offerte o2 e o3 ), disincentivndo il fornitore d offrire prezzi inferiori l prezzo sogli. ertnto, l intervllo compreso tr il prezzo bse d st e il prezzo sogli concentr l competizione tr i prtecipnti (nel segmento compreso tr s e b ). Come condizione generle, l stzione ppltnte deve fissre il prezzo sogli d un livello NON RAGGIUNGIBILE d prte dei prtecipnti ll gr l fine di evitre il rischio che le imprese considerino il prezzo sogli come il prezzo che l stzione ppltnte si spett di ottenere dlle offerte dei fornitori. Tle condizione potrebbe essere rischios in qunto, se il prezzo sogli è troppo vicino ll bse d st, tutte le offerte economiche potrebbero convergere verso il prezzo sogli e quindi coincidere. gin 14 di 18
15 Il cso limite si verific con prezzo sogli pri zero e l formul ssume l seguente espressione: E E b o, b Nel seguente grfico (Figur 2) si evidenzi l differenz tr un formul linere con prezzo sogli ed un formul linere senz prezzo sogli ( s =0). E nn 80 Linere con sogli Linere senz sogli 0 s BA Figur 2 Il seguente grfico (Figur 3)mostr l effetto su un offert o presentt d un fornitore nel cso si stto fissto un prezzo sogli s e nel cso di formul linere senz prezzo di sogli. Figur 3 Il grfico (Figur 3) mostr che l offert o ottiene un punteggio economico differente in presenz o meno del prezzo sogli. Inftti, in cso di prezzo sogli s i punti economici E ottenuti d o sono pri 60, mentre l ridursi del prezzo sogli (fino l cso limite di s =0) si riduce conseguentemente nche il punteggio economico E ottenuto d s (nell esempio fino d un vlore E= 30 punti). gin 15 di 18
16 ertnto l scelt del vlore del prezzo sogli ssume un importnz strtegic, in qunto è in grdo di influenzre i comportmenti del fornitore. L esempio h dimostrto che in ssenz di prezzo sogli il fornitore, per ottenere un numero di punti equivlenti quelli generti dl prezzo sogli è costretto: ) d offrire uno sconto mggiore; ovvero, in lterntiv, b) competere sull prte qulittiv (quindi d ottenere un numero equivlente di T). iù in generle, l formul linere (con o senz prezzo sogli) present le seguenti crtteristiche: il punteggio ssegnto ciscun offert non dipende dlle offerte degli ltri prtecipnti; fcilit i fornitori nel presentre l loro miglior offert, in qunto questi non devono prevedere il comportmento degli ltri prtecipnti; riduce, rispetto quelle interdipendenti, il rischio di eventule collusione tr i prtecipnti ll gr; permette ll stzione ppltnte di spostre l competizione dll componente economic quell tecnic e vicevers; mntiene costnte il vlore economico del punto tecnico 1. 1 Il vlore economico di un punto tecnico corrisponde ll su conversione in vlut (euro), e corrisponde ll quntificzione di qunto cost d un fornitore offrire un prodotto con un punto tecnico ggiuntivo. gin 16 di 18
17 2.8 Formul Non linere L formul d pplicre è l seguente: ( ) = punteggio economico ttribuito ll offert del concorrente i-esimo; = punteggio economico mssimo ssegnbile; = Vlore (ribsso/rilzo) offerto dl concorrente i-esimo; = Vlore (ribsso/rilzo) dell offert più conveniente; α = coefficiente > 0. Nel dettglio: er vlore economico er vlore percentule Totle Ribsso Unitri BA = vlore riportto nel cmpo Bse d st lto SA: rocedure per vlore economico: vlore economico; rocedure per vlore percentule: vlore percentule %. = prezzo offerto dl concorrente i-esimo; OT = offert totle del concorrente i-esimo, risultnte dll medi dei prezzi offerti per ogni prodotto pondert per le eventuli incidenze percentuli; = percentule di ribsso/rilzo offert dl concorrente i-esimo; = ribsso/rilzo complessivo offerto dl concorrente i-esimo, risultnte dll medi dei ribssi/rilzi offerti per ogni prodotto pondert per le eventuli incidenze percentuli. gin 17 di 18
18 3 SELEZIONE FORMULE SU SINTEL Tutte le formule di ggiudiczione descritte nei cpitoli precedenti del documento sono presenti sull pittform Sintel e possono essere selezionte llo step Formule di ttribuzione del punteggio economico nel percorso di crezione del Modello dell procedur (Figur 4). Figur 4 gin 18 di 18
Manuale Generale Sintel Guida alle formule di aggiudicazione
 MANUALE DI SUPPOTO ALL UTILIZZO DELLA PIATTAFOMA SINTEL GUIDA ALLE FOMULE DI AGGIUDICAZIONE Pgin 1 di 21 AGENZIA EGIONALE CENTALE ACQUISTI Indice 1 INTODUZIONE... 3 1.1 Cso di studio... 4 2 FOMULE DI CUI
MANUALE DI SUPPOTO ALL UTILIZZO DELLA PIATTAFOMA SINTEL GUIDA ALLE FOMULE DI AGGIUDICAZIONE Pgin 1 di 21 AGENZIA EGIONALE CENTALE ACQUISTI Indice 1 INTODUZIONE... 3 1.1 Cso di studio... 4 2 FOMULE DI CUI
8 Controllo di un antenna
 8 Controllo di un ntenn L ntenn prbolic di un rdr mobile è montt in modo d consentire un elevzione compres tr e =2. Il momento d inerzi dell ntenn, Je, ed il coefficiente di ttrito viscoso, f e, che crtterizzno
8 Controllo di un ntenn L ntenn prbolic di un rdr mobile è montt in modo d consentire un elevzione compres tr e =2. Il momento d inerzi dell ntenn, Je, ed il coefficiente di ttrito viscoso, f e, che crtterizzno
" Osservazione. 6.1 Integrale indefinito. R Definizione (Primitiva) E Esempio 6.1 CAPITOLO 6
 CAPITOLO 6 Clcolo integrle 6. Integrle indefinito L nozione fondmentle del clcolo integrle è quell di funzione primitiv di un funzione f (). Tle nozione è in qulche modo speculre ll nozione di funzione
CAPITOLO 6 Clcolo integrle 6. Integrle indefinito L nozione fondmentle del clcolo integrle è quell di funzione primitiv di un funzione f (). Tle nozione è in qulche modo speculre ll nozione di funzione
Equazioni 1 grado. Definizioni Classificazione Risoluzione Esercizi
 Equzioni grdo Definizioni Clssificzione Risoluzione Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Prendimo in esme le due espressioni numeriche 8 entrmbe sono uguli 7, e l scrittur si chim uguglinz
Equzioni grdo Definizioni Clssificzione Risoluzione Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Prendimo in esme le due espressioni numeriche 8 entrmbe sono uguli 7, e l scrittur si chim uguglinz
Temi speciali di bilancio
 Università degli Studi di Prm Temi specili di bilncio Le imposte (3) Il consolidto fiscle nzionle RIFERIMENTI Normtiv Artt. 117 129 del TUIR Art. 96 del TUIR Prssi contbile Documento OIC n. 25 Documento
Università degli Studi di Prm Temi specili di bilncio Le imposte (3) Il consolidto fiscle nzionle RIFERIMENTI Normtiv Artt. 117 129 del TUIR Art. 96 del TUIR Prssi contbile Documento OIC n. 25 Documento
Anno 1. Numeri reali: proprietà e applicazioni di uso comune
 Anno Numeri reli: proprietà e ppliczioni di uso comune Introduzione L insieme dei numeri rzionli è composto d numeri che si ottengono dl rpporto tr due numeri interi. Tle rpporto, o frzione, è sempre ssociile
Anno Numeri reli: proprietà e ppliczioni di uso comune Introduzione L insieme dei numeri rzionli è composto d numeri che si ottengono dl rpporto tr due numeri interi. Tle rpporto, o frzione, è sempre ssociile
{ 3 x y=4. { x=2. Sistemi di equazioni
 Sistemi di equzioni Definizione Un sistem è un insieme di equzioni che devono essere verificte contempornemente, cioè devono vere contempornemente le stesse soluzioni. Definimo grdo di un sistem il prodotto
Sistemi di equzioni Definizione Un sistem è un insieme di equzioni che devono essere verificte contempornemente, cioè devono vere contempornemente le stesse soluzioni. Definimo grdo di un sistem il prodotto
Facoltà di Ingegneria
 UNIVERSITA DEGLI STUDI DI CAGLIARI Fcoltà di Ingegneri Corso di Lure Specilistic in Ingegneri per l Ambiente e il Territorio TESINA DI CALCOLO NUMERICO Anlisi dell errore nei metodi di risoluzione dei
UNIVERSITA DEGLI STUDI DI CAGLIARI Fcoltà di Ingegneri Corso di Lure Specilistic in Ingegneri per l Ambiente e il Territorio TESINA DI CALCOLO NUMERICO Anlisi dell errore nei metodi di risoluzione dei
b a 2. Il candidato spieghi, avvalendosi di un esempio, il teorema del valor medio.
 Domnde preprzione terz prov. Considert, come esempio, l funzione nell intervllo [,], il cndidto illustri il concetto di integrle definito. INTEGRALE DEFINITO, prendendo in esme un generic funzione f()
Domnde preprzione terz prov. Considert, come esempio, l funzione nell intervllo [,], il cndidto illustri il concetto di integrle definito. INTEGRALE DEFINITO, prendendo in esme un generic funzione f()
2 x = 64 (1) L esponente (x) a cui elevare la base (2) per ottenere il numero 64 è detto logaritmo (logaritmo in base 2 di 64), indicato così:
 Considerimo il seguente problem: si vuole trovre il numero rele tle che: = () L esponente () cui elevre l bse () per ottenere il numero è detto ritmo (ritmo in bse di ), indicto così: In prticolre in questo
Considerimo il seguente problem: si vuole trovre il numero rele tle che: = () L esponente () cui elevre l bse () per ottenere il numero è detto ritmo (ritmo in bse di ), indicto così: In prticolre in questo
AUTOVALORI ED AUTOVETTORI. Sia V uno spazio vettoriale di dimensione finita n.
 AUTOVALORI ED AUTOVETTORI Si V uno spzio vettorile di dimensione finit n. Dicesi endomorfismo di V ogni ppliczione linere f : V V dello spzio vettorile in sé. Se f è un endomorfismo di V in V, considert
AUTOVALORI ED AUTOVETTORI Si V uno spzio vettorile di dimensione finit n. Dicesi endomorfismo di V ogni ppliczione linere f : V V dello spzio vettorile in sé. Se f è un endomorfismo di V in V, considert
Catalogo Interregionale dell Alta Formazione Edizione 2013 Adeguamento monetario delle tabelle di riferimento per il calcolo dei costi forfettari
 Allegto B) Ctlogo Interregionle dell Alt Formzione Edizione 2013 Adegumento monetrio delle tbelle di riferimento per il clcolo dei costi forfettri Nell mbito del Ctlogo Interregionle Alt Formzione, per
Allegto B) Ctlogo Interregionle dell Alt Formzione Edizione 2013 Adegumento monetrio delle tbelle di riferimento per il clcolo dei costi forfettri Nell mbito del Ctlogo Interregionle Alt Formzione, per
DEBITI VERSO BANCHE 1 PREMESSA 2 CONTENUTO DELLA VOCE. Passivo SP D.4. Prassi Documento OIC n. 12; Documento OIC n. 19 2.
 Cp. 49 - Debiti verso bnche 49 DEBITI VERSO BANCHE Pssivo SP D.4 Prssi Documento OIC n. 12; Documento OIC n. 19 1 PREMESSA I debiti verso bnche ricomprendono tutti quei debiti in cui l controprte è un
Cp. 49 - Debiti verso bnche 49 DEBITI VERSO BANCHE Pssivo SP D.4 Prssi Documento OIC n. 12; Documento OIC n. 19 1 PREMESSA I debiti verso bnche ricomprendono tutti quei debiti in cui l controprte è un
Da 9.500,01 a 15.000,00 > 15.000,01 9.500,00 COSTO PASTO 1,15 2,30 3,45 4,60
 Per l Anno Scolstico 2015/2016 l Deliber di Giunt Comunle n.25 del 16.04.2015 d oggetto: Determinzione dei criteri e ppliczione delle triffe dei servizi comunli introitti dl Comune nno 2015. Ricognizione
Per l Anno Scolstico 2015/2016 l Deliber di Giunt Comunle n.25 del 16.04.2015 d oggetto: Determinzione dei criteri e ppliczione delle triffe dei servizi comunli introitti dl Comune nno 2015. Ricognizione
, x 2. , x 3. è un equazione nella quale le incognite appaiono solo con esponente 1, ossia del tipo:
 Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
COMUNE DI SUELLI. Settore Tecnico SETTORE : Cirina Sergio. Responsabile: 514 NUMERAZIONE SETTORIALE N. 268 NUMERAZIONE GENERALE N. 10/07/2015.
 COMUNE DI SUELLI SETTORE : Responsbile: Settore Tecnico NUMERAZIONE GENERALE N. 514 NUMERAZIONE SETTORIALE N. 68 in dt 10/07/015 OGGETTO: CIG: ZD514AB0B - AFFIDAMENTO SERVIZIO DI RIPARAZIONE AUTOVETTURA
COMUNE DI SUELLI SETTORE : Responsbile: Settore Tecnico NUMERAZIONE GENERALE N. 514 NUMERAZIONE SETTORIALE N. 68 in dt 10/07/015 OGGETTO: CIG: ZD514AB0B - AFFIDAMENTO SERVIZIO DI RIPARAZIONE AUTOVETTURA
COME SOPRAVVIVERE ALLA MATEMATICA. 1. La funzione matematica e la sua utilità in economia
 COME SOPRAVVIVERE ALLA MATEMATICA di Giuli Cnzin e Dominique Cppelletti Come potrete notre inoltrndovi nel corso di Introduzione ll economi, l interpretzione dell teori economic non presuppone conoscenze
COME SOPRAVVIVERE ALLA MATEMATICA di Giuli Cnzin e Dominique Cppelletti Come potrete notre inoltrndovi nel corso di Introduzione ll economi, l interpretzione dell teori economic non presuppone conoscenze
Titolazione Acido Debole Base Forte. La reazione che avviene nella titolazione di un acido debole HA con una base forte NaOH è:
 Titolzione Acido Debole Bse Forte L rezione che vviene nell titolzione di un cido debole HA con un bse forte NOH è: HA(q) NOH(q) N (q) A (q) HO Per quest rezione l costnte di equilibrio è: 1 = = >>1 w
Titolzione Acido Debole Bse Forte L rezione che vviene nell titolzione di un cido debole HA con un bse forte NOH è: HA(q) NOH(q) N (q) A (q) HO Per quest rezione l costnte di equilibrio è: 1 = = >>1 w
Integrali de niti. Il problema del calcolo di aree ci porterà alla de nizione di integrale de nito.
 Integrli de niti. Il problem di clcolre l re di un regione pin delimitt d gr ci di funzioni si può risolvere usndo l integrle de nito. L integrle de nito st l problem del clcolo di ree come l equzione
Integrli de niti. Il problem di clcolre l re di un regione pin delimitt d gr ci di funzioni si può risolvere usndo l integrle de nito. L integrle de nito st l problem del clcolo di ree come l equzione
Acidi Deboli. Si definisce acido debole un acido con K a < 1 che risulta perciò solo parzialmente dissociato in soluzione. Esempi di acidi deboli:
 Acidi Deboli Si definisce cido debole un cido con < 1 che risult perciò solo przilmente dissocito in soluzione. Esempi di cidi deboli: Acido cetico (H OOH) 1.75 1-5 Acido scorbico (vitmin ) 1 6.76 1-5.5
Acidi Deboli Si definisce cido debole un cido con < 1 che risult perciò solo przilmente dissocito in soluzione. Esempi di cidi deboli: Acido cetico (H OOH) 1.75 1-5 Acido scorbico (vitmin ) 1 6.76 1-5.5
IRRAGGIAMENTO: APPLICAZIONI ED ESERCIZI
 Elis Gonizzi N mtricol: 3886 Lezione del -- :3-:3 IRRAGGIAMENO: APPLICAZIONI ED EERCIZI E utile l fine di comprendere meglio le ppliczioni e gli esercizi ricordre cos si intend con i termini CORPI NERI
Elis Gonizzi N mtricol: 3886 Lezione del -- :3-:3 IRRAGGIAMENO: APPLICAZIONI ED EERCIZI E utile l fine di comprendere meglio le ppliczioni e gli esercizi ricordre cos si intend con i termini CORPI NERI
Teoria di Jourawski. 1. Sezione ad T. Lê2 L Lê2. à Soluzione
 eori di Jourwski ü [A.. 0-03 : ultim revisione 4 gennio 03] Si pplic l teori di Jourwski l fine di clcolre l distribuzione di tensioni tngenzili su lcune sezioni soggette sforzo di tglio.. Sezione d ê
eori di Jourwski ü [A.. 0-03 : ultim revisione 4 gennio 03] Si pplic l teori di Jourwski l fine di clcolre l distribuzione di tensioni tngenzili su lcune sezioni soggette sforzo di tglio.. Sezione d ê
Maturità scientifica, corso di ordinamento, sessione ordinaria 2000-2001
 Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone Mturità scientific, corso di ordinmento, sessione ordinri 000-001 PROBLEMA 1 Si consideri l seguente relzione tr le vribili reli x, y: 1 1 1 +
Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone Mturità scientific, corso di ordinmento, sessione ordinri 000-001 PROBLEMA 1 Si consideri l seguente relzione tr le vribili reli x, y: 1 1 1 +
Imparare: cosa, come, perché.
 GIOCO n. 1 Imprre: cos, come, perché. L pprendimento scolstico non è solo questione di metodo di studio, m di numerose situzioni di tipo personle e di gruppo, oppure legte l contesto in cui pprendimo.
GIOCO n. 1 Imprre: cos, come, perché. L pprendimento scolstico non è solo questione di metodo di studio, m di numerose situzioni di tipo personle e di gruppo, oppure legte l contesto in cui pprendimo.
PROGRAMMAZIONE DI FISICA PRIMO BIENNIO CLASSI SECONDE
 PROGRAMMAZIONE DI FISICA PRIMO BIENNIO CLASSI SECONDE Nel pino di lvoro sono indicte con i numeri d 1 5 le competenze di bse che ciscun unit' didttic concorre sviluppre, secondo l legend riportt di seguito.
PROGRAMMAZIONE DI FISICA PRIMO BIENNIO CLASSI SECONDE Nel pino di lvoro sono indicte con i numeri d 1 5 le competenze di bse che ciscun unit' didttic concorre sviluppre, secondo l legend riportt di seguito.
Il dominio della funzione, cioè l'insieme dei valori che si possono attribuire a x è tutto R ;
 CAPITOLO ESPONENZIALI E LOGARITMI ESPONENZIALI Teori in sintesi Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z. + Sono definite:
CAPITOLO ESPONENZIALI E LOGARITMI ESPONENZIALI Teori in sintesi Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z. + Sono definite:
Lezione 14. Risoluzione delle equazioni algebriche.
 Lezione Prerequisiti: Lezioni 8,. Risoluzione delle equzioni lgebriche. Si F un cmpo, e si K un chiusur lgebric di F. Si f ( ) F[ ] non costnte. Studimo i metodi di risoluzione per l equzione f ( ) = 0,
Lezione Prerequisiti: Lezioni 8,. Risoluzione delle equzioni lgebriche. Si F un cmpo, e si K un chiusur lgebric di F. Si f ( ) F[ ] non costnte. Studimo i metodi di risoluzione per l equzione f ( ) = 0,
( x) a) La simmetrica della parabola rispetto all origine è tale che: La parabola di equazione y = x + ax a ha vertice V = = mentre la parabola y S
 Sessione ordinri 996 Liceo di ordinmento Soluzione di De Ros Nicol ) In un pino, riferito d un sistem di ssi crtesini ortogonli (O), sono ssegnte le prbole di equzione:, dove è un numero rele positivo.
Sessione ordinri 996 Liceo di ordinmento Soluzione di De Ros Nicol ) In un pino, riferito d un sistem di ssi crtesini ortogonli (O), sono ssegnte le prbole di equzione:, dove è un numero rele positivo.
Oggetto: SOGGETTI IRES - LA RILEVAZIONE CONTABILE DELLE IMPOSTE DI ESERCIZIO
 Ai gentili Clienti Loro sedi Oggetto: SOGGETTI IRES - LA RILEVAZIONE CONTABILE DELLE IMPOSTE DI ESERCIZIO Al termine di ciscun periodo d impost, dopo ver effettuto le scritture di ssestmento e rettific,
Ai gentili Clienti Loro sedi Oggetto: SOGGETTI IRES - LA RILEVAZIONE CONTABILE DELLE IMPOSTE DI ESERCIZIO Al termine di ciscun periodo d impost, dopo ver effettuto le scritture di ssestmento e rettific,
Febbraio 2014. PROGETTO: Studio di Architettura e Urbanistica Dott. Arch. Guido Leoni Via Affò, 4 - Parma - tel. 0521.233423
 Comune di Poviglio Provinci di Reggio Emili Relzione illustrtiv dell Delierzione Consilire di pprovzione, dei coefficienti e prmetri di conversione che ssicurno l equivlenz tr le definizioni e le modlità
Comune di Poviglio Provinci di Reggio Emili Relzione illustrtiv dell Delierzione Consilire di pprovzione, dei coefficienti e prmetri di conversione che ssicurno l equivlenz tr le definizioni e le modlità
ESPONENZIALI E LOGARITMI
 ESPONENZIALI E LOGARITMI 1 se 0, per ogni R ; Teori in sintesi ESPONENZIALI Potenze con esponente rele L potenz è definit: se >0: Sono definite: se >0: Non sono definite: Csi prticolri: Le proprietà delle
ESPONENZIALI E LOGARITMI 1 se 0, per ogni R ; Teori in sintesi ESPONENZIALI Potenze con esponente rele L potenz è definit: se >0: Sono definite: se >0: Non sono definite: Csi prticolri: Le proprietà delle
Equazioni parametriche di primo grado
 Polo Sivigli Equzioni prmetriche di primo grdo Premess Come si s dll lgebr elementre, si chim equzione un uguglinz fr due espressioni letterli che si verific soltnto ttribuendo prticolri vlori lle lettere,
Polo Sivigli Equzioni prmetriche di primo grdo Premess Come si s dll lgebr elementre, si chim equzione un uguglinz fr due espressioni letterli che si verific soltnto ttribuendo prticolri vlori lle lettere,
Introduzione all algebra
 Introduzione ll lgebr E. Modic ersmo@glois.it Liceo Scientifico Sttle S. Cnnizzro Corso P.O.N. Modelli mtemtici e reltà A.S. 2010/2011 Premess Codificre e Decodificre Nell vit quotidin ci cpit spesso di
Introduzione ll lgebr E. Modic ersmo@glois.it Liceo Scientifico Sttle S. Cnnizzro Corso P.O.N. Modelli mtemtici e reltà A.S. 2010/2011 Premess Codificre e Decodificre Nell vit quotidin ci cpit spesso di
Il moto rettilineo uniformemente accelerato è un moto che avviene su una retta con accelerazione costante. a = costante
 Prof.. Di Muro Moto rettilineo uniformemente ccelerto ( m.r.u.. ) Il moto rettilineo uniformemente ccelerto è un moto che iene su un rett con ccelerzione costnte. Dll definizione di ccelerzione t t t t
Prof.. Di Muro Moto rettilineo uniformemente ccelerto ( m.r.u.. ) Il moto rettilineo uniformemente ccelerto è un moto che iene su un rett con ccelerzione costnte. Dll definizione di ccelerzione t t t t
ESPONENZIALI E LOGARITMI
 ESPONENZIALI E LOGARITMI RICHIAMI DI TEORIA dom f Im f grfico Funzioni esponenzili y=^ con > Funzioni esponenzili y=^ con
ESPONENZIALI E LOGARITMI RICHIAMI DI TEORIA dom f Im f grfico Funzioni esponenzili y=^ con > Funzioni esponenzili y=^ con
FOGLIO COMPARATIVO SULLE TIPOLOGIE DI MUTUO IPOTECARIO / FONDIARIO PER L ACQUISTO DELL ABITAZIONE PRINCIPALE
 FOGLIO COMPARATIVO SULLE TIPOLOGIE DI MUTUO IPOTECARIO / FONDIARIO PER L ACQUISTO DELL ABITAZIONE PRINCIPALE (disposizioni di trsprenz i sensi dell rt. 2 comm 5 D.L. 29.11.2008 n. 185) Per tutte le condizioni
FOGLIO COMPARATIVO SULLE TIPOLOGIE DI MUTUO IPOTECARIO / FONDIARIO PER L ACQUISTO DELL ABITAZIONE PRINCIPALE (disposizioni di trsprenz i sensi dell rt. 2 comm 5 D.L. 29.11.2008 n. 185) Per tutte le condizioni
ALLEGATO A) Disciplinare del Fondo per la Progettazione degli Interventi Strategici
 ALLEGATO A) Disciplinre del Fondo per l Progettzione degli Interventi Strtegici 1. Finlità del fondo Al fine di rzionlizzre e ccelerre l spes per investimenti pubblici, con prticolre rigurdo ll relizzzione
ALLEGATO A) Disciplinre del Fondo per l Progettzione degli Interventi Strtegici 1. Finlità del fondo Al fine di rzionlizzre e ccelerre l spes per investimenti pubblici, con prticolre rigurdo ll relizzzione
P8 Ponti radio terrestri e satellitari
 P8 Ponti rdio terrestri e stellitri P8.1 Un collegmento in ponte rdio 11 GHz impieg due ntenne prboliche uguli venti gudgno G 40 db ed efficienz η 0,5. Gli pprti di ricetrsmissione sono collegti lle rispettive
P8 Ponti rdio terrestri e stellitri P8.1 Un collegmento in ponte rdio 11 GHz impieg due ntenne prboliche uguli venti gudgno G 40 db ed efficienz η 0,5. Gli pprti di ricetrsmissione sono collegti lle rispettive
I costi dell impresa. Litri di benzene per unità di tempo. Linea di isocosto
 7 I costi dell impres 7.1. Per l combinzione di equilibrio dei due input, si ved il grfico successivo. L pendenz dell line di isocosto e` pri ll opposto del rpporto tr i prezzi dei fttori: -10 = 2 = -5.
7 I costi dell impres 7.1. Per l combinzione di equilibrio dei due input, si ved il grfico successivo. L pendenz dell line di isocosto e` pri ll opposto del rpporto tr i prezzi dei fttori: -10 = 2 = -5.
STUDIO COMMERCIALE TRIBUTARIO TOMASSETTI & PARTNERS Corso Trieste 88 00198 Roma Tel. 06/8848666 (RA) Fax 068844588 info@mt-partners.
 CIRCOLARE INFORMATIVA NR. 14 del 30/11/2012 ARGOMENTO: IMPOSTA SOSTITUIVA TFR 2013 Scde il prossimo 16 dicembre il termine per pgre l impost sostitutiv sul TFR. Tle impost rppresent l nticipo di tsse dovute
CIRCOLARE INFORMATIVA NR. 14 del 30/11/2012 ARGOMENTO: IMPOSTA SOSTITUIVA TFR 2013 Scde il prossimo 16 dicembre il termine per pgre l impost sostitutiv sul TFR. Tle impost rppresent l nticipo di tsse dovute
La metodologia di calcolo del costo medio ponderato del capitale (WACC) degli operatori di rete mobile
 Allegto C ll Deliber n. 509/10/CONS L metodologi di clcolo del costo medio ponderto del cpitle (WACC) degli opertori di rete mobile 1. Introduzione 1. In bse ll rt. 50 del Codice delle Comuniczioni, l
Allegto C ll Deliber n. 509/10/CONS L metodologi di clcolo del costo medio ponderto del cpitle (WACC) degli opertori di rete mobile 1. Introduzione 1. In bse ll rt. 50 del Codice delle Comuniczioni, l
Il volume del cilindro è dato dal prodotto della superficie di base per l altezza, quindi
 Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone 3 Questionrio Quesito 1 Provre che un sfer è equivlente i /3 del cilindro circoscritto. r 4 3 Il volume dell sfer è 3 r Il volume del cilindro
Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone 3 Questionrio Quesito 1 Provre che un sfer è equivlente i /3 del cilindro circoscritto. r 4 3 Il volume dell sfer è 3 r Il volume del cilindro
ASSENZE PER ASSISTENZA PORTATORI DI HANDICAP
 NORMATIVA ASSENZE PER ASSISTENZA PORTATORI DI HANDICAP A cur di Libero Tssell d Scuol&Scuol del 21/10/2003 Riferimenti normtivi: rt. 21 e 33 5.2.1992 n. 104 e successive modifiche ed integrzioni, Dlgs.
NORMATIVA ASSENZE PER ASSISTENZA PORTATORI DI HANDICAP A cur di Libero Tssell d Scuol&Scuol del 21/10/2003 Riferimenti normtivi: rt. 21 e 33 5.2.1992 n. 104 e successive modifiche ed integrzioni, Dlgs.
BANDO PUBBLICO PER IL SOSTEGNO AL REDDITO PER PERSONE E/O FAMIGLIE IN SITUAZIONE DI CRISI PER LA PERDITA DEL LAVORO - 2015
 BANDO PUBBLICO PER IL SOSTEGNO AL REDDITO PER PERSONE E/O FAMIGLIE IN SITUAZIONE DI CRISI PER LA PERDITA DEL LAVORO - 2015 Art. 1 - FINALITA E OGGETTO Il presente ndo disciplin le modlità per l'ssegnzione
BANDO PUBBLICO PER IL SOSTEGNO AL REDDITO PER PERSONE E/O FAMIGLIE IN SITUAZIONE DI CRISI PER LA PERDITA DEL LAVORO - 2015 Art. 1 - FINALITA E OGGETTO Il presente ndo disciplin le modlità per l'ssegnzione
Stabilità dei sistemi di controllo in retroazione
 Stbilità dei sistemi di controllo in retrozione Criterio di Nyquist Il criterio di Nyquist Estensione G (s) con gudgno vribile Appliczione sistemi con retrozione positiv 2 Criterio di Nyquist Stbilità
Stbilità dei sistemi di controllo in retrozione Criterio di Nyquist Il criterio di Nyquist Estensione G (s) con gudgno vribile Appliczione sistemi con retrozione positiv 2 Criterio di Nyquist Stbilità
Edizione dicembre 2010 - Rev 0. Manuale per l applicazione dell immagine coordinata
 Edizione dicembre 20 - Rev 0 Mnule per l ppliczione dell immgine coordint 1 Mnule per l ppliczione dell immgine coordint 1 Presentzione 2 Elementi bse Logotipo generico 3-4 Logotipo d personlizzre 5-8
Edizione dicembre 20 - Rev 0 Mnule per l ppliczione dell immgine coordint 1 Mnule per l ppliczione dell immgine coordint 1 Presentzione 2 Elementi bse Logotipo generico 3-4 Logotipo d personlizzre 5-8
Teoria in sintesi ESPONENZIALI. Potenze con esponente reale. La potenza. Sono definite: Non sono definite: Casi particolari :
 Teori in sintesi ESPONENZIALI Potenze con esponente rele L potenz è definit: se >, per ogni R se, per tutti e soli gli R se
Teori in sintesi ESPONENZIALI Potenze con esponente rele L potenz è definit: se >, per ogni R se, per tutti e soli gli R se
Prova n. 1 LEGER TEST
 Prov n. 1 LEGER TEST Descrizione L prov si svolge su un percorso delimitto d due coni, posti ll distnz di 20 mt l uno dll ltro. Il cndidto deve percorrere spol l distnz tr i due coni, pssndo dll velocità
Prov n. 1 LEGER TEST Descrizione L prov si svolge su un percorso delimitto d due coni, posti ll distnz di 20 mt l uno dll ltro. Il cndidto deve percorrere spol l distnz tr i due coni, pssndo dll velocità
Regime di sconto commerciale. S = sconto ; K = somma da scontare ; s = tasso di sconto unitario V a = valore attuale ; I = interesse ; C = capitale
 Regime di sconto commercile Formule d usre : S = sconto ; K = somm d scontre ; s = tsso di sconto unitrio V = vlore ttule ; I = interesse ; C = cpitle s t = st i t st = st S t Kst V K st () () ; () ( )
Regime di sconto commercile Formule d usre : S = sconto ; K = somm d scontre ; s = tsso di sconto unitrio V = vlore ttule ; I = interesse ; C = cpitle s t = st i t st = st S t Kst V K st () () ; () ( )
Gioco Interno Tipologie e Norme
 Gioco Interno Tipologie e Norme Per gioco interno si intende l misur complessiv di cui un nello si può spostre rispetto ll ltro in direzione oppost. E necessrio distinguere fr gioco rdile e gioco ssile.
Gioco Interno Tipologie e Norme Per gioco interno si intende l misur complessiv di cui un nello si può spostre rispetto ll ltro in direzione oppost. E necessrio distinguere fr gioco rdile e gioco ssile.
SIMULAZIONE CATASTO A VALORI
 SIMULAZIONE CATASTO A VALORI Nelle tbelle è presentt un simulzione di un Ctsto di vlori per lcuni Comuni, si grndi che medi, in vrie prti d Itli. I conteggi sono stti così impostti: per ogni Comune sono
SIMULAZIONE CATASTO A VALORI Nelle tbelle è presentt un simulzione di un Ctsto di vlori per lcuni Comuni, si grndi che medi, in vrie prti d Itli. I conteggi sono stti così impostti: per ogni Comune sono
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2002 Sessione straordinaria
 ESAME DI STAT DI LICE SCIENTIFIC CRS DI RDINAMENT 00 Sessione strordinri Il cndidto risolv uno dei due problemi e 5 dei 0 quesiti in cui si rticol il questionrio. PRBLEMA Con riferimento un sistem monometrico
ESAME DI STAT DI LICE SCIENTIFIC CRS DI RDINAMENT 00 Sessione strordinri Il cndidto risolv uno dei due problemi e 5 dei 0 quesiti in cui si rticol il questionrio. PRBLEMA Con riferimento un sistem monometrico
si definisce Funzione Integrale; si chiama funzione integrale in quanto il suo * x
 Appunti elorti dll prof.ss Biondin Gldi Funzione integrle Si y = f() un funzione continu in un intervllo [; ] e si 0 [; ]; l integrle 0 f()d si definisce Funzione Integrle; si chim funzione integrle in
Appunti elorti dll prof.ss Biondin Gldi Funzione integrle Si y = f() un funzione continu in un intervllo [; ] e si 0 [; ]; l integrle 0 f()d si definisce Funzione Integrle; si chim funzione integrle in
Macchine elettriche in corrente continua
 cchine elettriche in corrente continu Generlità Può essere definit mcchin un dispositivo che convert energi d un form un ltr. Le mcchine elettriche in prticolre convertono energi elettric in energi meccnic
cchine elettriche in corrente continu Generlità Può essere definit mcchin un dispositivo che convert energi d un form un ltr. Le mcchine elettriche in prticolre convertono energi elettric in energi meccnic
Problemi di collegamento delle strutture in acciaio
 1 Problemi di collegmento delle strutture in cciio Unioni con bulloni soggette tglio Le unioni tglio vengono generlmente utilizzte negli elementi compressi, quli esempio le unioni colonn-colonn soggette
1 Problemi di collegmento delle strutture in cciio Unioni con bulloni soggette tglio Le unioni tglio vengono generlmente utilizzte negli elementi compressi, quli esempio le unioni colonn-colonn soggette
Modulo 6. La raccolta bancaria e il rapporto di conto corrente. Unità didattiche che compongono il modulo. Tempo necessario
 58 Modulo 6 L rccolt bncri e il rpporto di conto corrente I destintri del Modulo sono gli studenti del quinto nno che, dopo ver nlizzto e ppreso le crtteristiche fondmentli dell ttività delle ziende di
58 Modulo 6 L rccolt bncri e il rpporto di conto corrente I destintri del Modulo sono gli studenti del quinto nno che, dopo ver nlizzto e ppreso le crtteristiche fondmentli dell ttività delle ziende di
Facoltà di Economia - Università di Sassari Anno Accademico 2004-2005. Dispense Corso di Econometria Docente: Luciano Gutierrez.
 Fcoltà di Economi - Università di Sssri Anno Accdemico 2004-2005 Dispense Corso di Econometri Docente: Lucino Gutierrez Algebr Linere Progrmm: 1.1 Definizione di mtrice e vettore 1.2 Addizione e sottrzione
Fcoltà di Economi - Università di Sssri Anno Accdemico 2004-2005 Dispense Corso di Econometri Docente: Lucino Gutierrez Algebr Linere Progrmm: 1.1 Definizione di mtrice e vettore 1.2 Addizione e sottrzione
8. MOVIMENTAZIONE DI MAGAZZINO: LE PRINCIPALI SCRITTURE CONTABILI
 8. MOVIMENTAZIONE DI MAGAZZINO: LE PRINCIPALI SCRITTURE CONTABILI Movimentzione di mgzzino: le principli scritture contbili 8. Le rilevzioni contbili 8.1. 8.1. LE RILEVAZIONI CONTABILI Le rilevzioni ttinenti
8. MOVIMENTAZIONE DI MAGAZZINO: LE PRINCIPALI SCRITTURE CONTABILI Movimentzione di mgzzino: le principli scritture contbili 8. Le rilevzioni contbili 8.1. 8.1. LE RILEVAZIONI CONTABILI Le rilevzioni ttinenti
FOGLIO COMPARATIVO SULLE TIPOLOGIE DI MUTUO IPOTECARIO / FONDIARIO PER L ACQUISTO DELL ABITAZIONE PRINCIPALE
 FOGLIO COMPARATIVO SULLE TIPOLOGIE DI MUTUO IPOTECARIO / FONDIARIO PER L ACQUISTO DELL ABITAZIONE PRINCIPALE (sposizioni trsprenz i sensi dell rt. 2 comm 5 D.L. 29.11.2008 n. 185) Per tutte le conzioni
FOGLIO COMPARATIVO SULLE TIPOLOGIE DI MUTUO IPOTECARIO / FONDIARIO PER L ACQUISTO DELL ABITAZIONE PRINCIPALE (sposizioni trsprenz i sensi dell rt. 2 comm 5 D.L. 29.11.2008 n. 185) Per tutte le conzioni
Salvatore Loris Pelella. Corso di. Matematica RCS LIBRI EDUCATION SPA
 Slvtore Loris Pelell Corso di Mtemtic RCS LIBRI EDUCATION SPA ISBN 88-45-084-3 004 RCS Libri S.p.A.- Milno Prim edizione: gennio 004 Ristmpe 004 005 006 3 4 5 Stmp: V. Bon, Torino Coordinmento editorile
Slvtore Loris Pelell Corso di Mtemtic RCS LIBRI EDUCATION SPA ISBN 88-45-084-3 004 RCS Libri S.p.A.- Milno Prim edizione: gennio 004 Ristmpe 004 005 006 3 4 5 Stmp: V. Bon, Torino Coordinmento editorile
T3 = Tempo di allacciamento contrattualmente previsto [standard specifico] ***** ***** ***** [misura in giorni solari]
![T3 = Tempo di allacciamento contrattualmente previsto [standard specifico] ***** ***** ***** [misura in giorni solari] T3 = Tempo di allacciamento contrattualmente previsto [standard specifico] ***** ***** ***** [misura in giorni solari]](/thumbs/40/21252056.jpg) 1 - Tempo di fornitur dell'llccimento inizile 2 - Tsso di mlfunzionmento per line di ccesso (servizio diretto con proprie strutture) (servizio indiretto in modlità CPS) tempo di fornitur t T1 M 07.00 13.00
1 - Tempo di fornitur dell'llccimento inizile 2 - Tsso di mlfunzionmento per line di ccesso (servizio diretto con proprie strutture) (servizio indiretto in modlità CPS) tempo di fornitur t T1 M 07.00 13.00
Esempio Data la matrice E estraiamo due minori di ordine 3 differenti:
 Minori di un mtrice Si A K m,n, si definisce minore di ordine p con p N, p
Minori di un mtrice Si A K m,n, si definisce minore di ordine p con p N, p
Nuovi criteri di deducibilità per le auto aziendali e professionali
 ACERBI & ASSOCIATI CONSULENZA TRIBUTARIA, AZIENDALE, SOCIETARIA E LEGALE NAZIONALE E INTERNAZIONALE CIRCOLARE N. 21 13 NOVEMBRE 2007 Nuovi criteri di deducibilità per le uto ziendli e professionli Copyright
ACERBI & ASSOCIATI CONSULENZA TRIBUTARIA, AZIENDALE, SOCIETARIA E LEGALE NAZIONALE E INTERNAZIONALE CIRCOLARE N. 21 13 NOVEMBRE 2007 Nuovi criteri di deducibilità per le uto ziendli e professionli Copyright
.TTESTATO DJ "ERGETiCA DEGLI EDIFI. Q Gruppo di unità immobiliari. Ventilazione meccanica. Prod. acqua calda sanitaria
 CODICE IDENTIHC DTI GENERLI.TTESTTO DJ "ERGETiC DEGLI EDIFI Destinzione d'uso y^ Residenzile PI Non residenzile Clssificzione D.P.it 41 2/93: il(l) bitzioni dibite o residenz con crotiere continutivo Oggetto
CODICE IDENTIHC DTI GENERLI.TTESTTO DJ "ERGETiC DEGLI EDIFI Destinzione d'uso y^ Residenzile PI Non residenzile Clssificzione D.P.it 41 2/93: il(l) bitzioni dibite o residenz con crotiere continutivo Oggetto
Protocollo di intesa tra :
 Protocollo di intes tr : o Comune di Correggio Servizio Socile Integrto AUSL di Reggio Emili Distretfo di Correggio Movimento per l Vit (ssocizione di Volontrito) Crits Croce Ross per lo sviluppo di un
Protocollo di intes tr : o Comune di Correggio Servizio Socile Integrto AUSL di Reggio Emili Distretfo di Correggio Movimento per l Vit (ssocizione di Volontrito) Crits Croce Ross per lo sviluppo di un
lim lim lim + Nome.Cognome Classe 4D 7 Aprile 2011 Verifica di matematica Problema (punti 3) Sono date le funzioni: f ( x)
 Nome.Cognome Clsse D 7 Aprile 0 Verific di mtemtic Problem (punti ) Sono dte le funzioni: f ( ) =, g ( ) = ( ) ) determinre il dominio di f() e di g() b) determinre, senz l uso dell clcoltrice f ( ) c)
Nome.Cognome Clsse D 7 Aprile 0 Verific di mtemtic Problem (punti ) Sono dte le funzioni: f ( ) =, g ( ) = ( ) ) determinre il dominio di f() e di g() b) determinre, senz l uso dell clcoltrice f ( ) c)
Scale con rampe diritte. Scala rettilinea a una rampa. Scala rettilinea a due rampe. Scala destra a una rampa a chiocciola (con un quarto di giro)
 0.0 Scle di legno 9 0.0 Scle di legno Le scle servono superre le differenze di ltezz. Nelle cse unifmiliri sono sovente costruite in legno. Un scl è definit tle se formt d lmeno tre sclini consecutivi,
0.0 Scle di legno 9 0.0 Scle di legno Le scle servono superre le differenze di ltezz. Nelle cse unifmiliri sono sovente costruite in legno. Un scl è definit tle se formt d lmeno tre sclini consecutivi,
Automobile Club d'italia
 Automobile Club d'itli SCHDA DI SINTSI MODALITA' DI AUTNTICA PRMSSA L'rt. 7 L. 24812006 non specific le modlit8 d seguire per I'utentic delle sottoscrizioni, né richim lcun disciplin già esistente, qule
Automobile Club d'itli SCHDA DI SINTSI MODALITA' DI AUTNTICA PRMSSA L'rt. 7 L. 24812006 non specific le modlit8 d seguire per I'utentic delle sottoscrizioni, né richim lcun disciplin già esistente, qule
Le spese di ricerca e sviluppo: gestione contabile ed iscrizione in bilancio *
 www.solmp.it Le : gestione contbile ed iscrizione in bilncio * Piero Pisoni, Fbrizio Bv, Dontell Busso e Alin Devlle ** 1. Premess Le sono esminte nei seguenti spetti: Il presente elborto è trtto d: definizione
www.solmp.it Le : gestione contbile ed iscrizione in bilncio * Piero Pisoni, Fbrizio Bv, Dontell Busso e Alin Devlle ** 1. Premess Le sono esminte nei seguenti spetti: Il presente elborto è trtto d: definizione
La costituzione d azienda
 L costituzione d ziend Esercizio1 In dt 15/01/X si costituisce, per volontà dei soci Alf e Bet, l Eridice S.p.A. Il cpitle socile, costituito d 40.000 zioni ordinrie d 10 euro nominli ciscun, viene sottoscritto
L costituzione d ziend Esercizio1 In dt 15/01/X si costituisce, per volontà dei soci Alf e Bet, l Eridice S.p.A. Il cpitle socile, costituito d 40.000 zioni ordinrie d 10 euro nominli ciscun, viene sottoscritto
1.134,23 24/03/2016 MERCATO LIBERO
 in cso di mncto recpito Koinè srl c/o Firenze CMP Accettzione G.C.50019 Sesto F.no Energetic Source Luce & Gs S.p.A. - Società soggett direzione e coordinmento d prte di Energetic Source S.p.A. Sede Legle
in cso di mncto recpito Koinè srl c/o Firenze CMP Accettzione G.C.50019 Sesto F.no Energetic Source Luce & Gs S.p.A. - Società soggett direzione e coordinmento d prte di Energetic Source S.p.A. Sede Legle
CORSO DI RAGIONERIA A.A. 2013/2014
 CORSO DI RAGIONERIA A.A. 2013/2014 MODULO A LEZIONE N. 10 LE SCRITTURE CONTABILI Il lesing IL CONTRATTO DI LEASING Il lesing è un contrtto tipico (non previsto dl Codice Civile) per mezzo del qule l ziend
CORSO DI RAGIONERIA A.A. 2013/2014 MODULO A LEZIONE N. 10 LE SCRITTURE CONTABILI Il lesing IL CONTRATTO DI LEASING Il lesing è un contrtto tipico (non previsto dl Codice Civile) per mezzo del qule l ziend
Conversione A/D e D/A. Quantizzazione
 Conversione A/D e D/A Per il trttmento dei segnli sempre più vengono preferite soluzioni di tipo digitle. È quindi necessrio, in fse di cquisizione, impiegre dispositivi che convertno i segnli nlogici
Conversione A/D e D/A Per il trttmento dei segnli sempre più vengono preferite soluzioni di tipo digitle. È quindi necessrio, in fse di cquisizione, impiegre dispositivi che convertno i segnli nlogici
SERVIZIO DISTRIBUZIONE GAS METANO PREZZARIO DELLE ATTIVITA' ACCESSORIE
 SERVIZIO DISTRIBUZIONE GAS METANO PREZZARIO DELLE ATTIVITA' ACCESSORIE PERIODO DI VALIDITA' I corrispettivi indicti nel presente prezzrio si intendono vlidi nel periodo dl 1 Gennio 2009 l 31 Dicemre 2009
SERVIZIO DISTRIBUZIONE GAS METANO PREZZARIO DELLE ATTIVITA' ACCESSORIE PERIODO DI VALIDITA' I corrispettivi indicti nel presente prezzrio si intendono vlidi nel periodo dl 1 Gennio 2009 l 31 Dicemre 2009
Il TFR nel Bilancio 2007 * Piero Pisoni, Fabrizio Bava, Donatella Busso e Alain Devalle **
 I temi MAP (Liber consultzione) Il TFR nel Bilncio 2007 * Piero Pisoni, Fbrizio Bv, Dontell Busso e Alin Devlle ** 1. Premess Il TFR è stto riformto con il D.Lgs. 05/12/2005, n. 252, concernente l disciplin
I temi MAP (Liber consultzione) Il TFR nel Bilncio 2007 * Piero Pisoni, Fbrizio Bv, Dontell Busso e Alin Devlle ** 1. Premess Il TFR è stto riformto con il D.Lgs. 05/12/2005, n. 252, concernente l disciplin
PROVVEDIMENTO del Funzionario delegato DAL DIRETTORE
 ISTITUZIONE SERVIZI EDUCATIVI SCOLASTICI CULTURALI E SPORTIVI DEL COMUNE DI CORREGGIO Vile dell Repubblic, 8 - Correggio (RE) 42015 tel. 0522/73.20.64-fx 0522/63.14.06 P.I. / C.F. n. 00341180354 PROVVEDIMENTO
ISTITUZIONE SERVIZI EDUCATIVI SCOLASTICI CULTURALI E SPORTIVI DEL COMUNE DI CORREGGIO Vile dell Repubblic, 8 - Correggio (RE) 42015 tel. 0522/73.20.64-fx 0522/63.14.06 P.I. / C.F. n. 00341180354 PROVVEDIMENTO
LEZIONE 20. è lineare. Per la commutatività del prodotto scalare segue anche la linearità dell applicazione
 LEZIONE 20 20.1. Prodotti sclri. Definizione 20.1.1. Si V uno spzio vettorile su R. Un prodotto sclre su V è un ppliczione tle che:, : V V R (v 1, v 2 ) v 1, v 2 (PS1) per ogni v 1, v 2 V si h v 1, v 2
LEZIONE 20 20.1. Prodotti sclri. Definizione 20.1.1. Si V uno spzio vettorile su R. Un prodotto sclre su V è un ppliczione tle che:, : V V R (v 1, v 2 ) v 1, v 2 (PS1) per ogni v 1, v 2 V si h v 1, v 2
Rapporti e proporzioni numeriche
 Rpporti e proporzioni numeriche Rpporti. Per rpporto tr due numeri e b, di cui il secondo diverso d zero, s intende il quoziente estto dell divisione dei due numeri dti, cioè :b oppure /b. Ad esempio dire
Rpporti e proporzioni numeriche Rpporti. Per rpporto tr due numeri e b, di cui il secondo diverso d zero, s intende il quoziente estto dell divisione dei due numeri dti, cioè :b oppure /b. Ad esempio dire
BOZZA. 1 2a S/2 S/2. Lezione n. 27. Le strutture in acciaio Le unioni bullonate Le unioni saldate
 Lezione n. 7 Le strutture in cciio Le unioni bullonte Le unioni sldte Unioni Le unioni nelle strutture in cciio devono grntire un buon funzionmento dell struttur e l derenz dell stess llo schem sttico
Lezione n. 7 Le strutture in cciio Le unioni bullonte Le unioni sldte Unioni Le unioni nelle strutture in cciio devono grntire un buon funzionmento dell struttur e l derenz dell stess llo schem sttico
- Ufficio Unico PIT2 - Progetto Integrato Territoriale NORD BARESE
 - Ufficio Unico PIT2 - Progetto Integrto Territorile NORD BARESE Andri Brlett Bisceglie Bitonto Cnos di Pugli Corto Giovinzzo Mrgherit di Svoi Molfett Ruvo di Pugli Sn Ferdinndo di Pugli Terlizzi Trni
- Ufficio Unico PIT2 - Progetto Integrto Territorile NORD BARESE Andri Brlett Bisceglie Bitonto Cnos di Pugli Corto Giovinzzo Mrgherit di Svoi Molfett Ruvo di Pugli Sn Ferdinndo di Pugli Terlizzi Trni
Page 1/6
 Edizione di sbto 14 novembre 2015 CONTABILITÀ L rilevzione dell impost sostitutiv sul trttmento di fine rpporto di Vivin Grippo Scde il prossimo 16 dicembre il termine per il versmento dell cconto dell
Edizione di sbto 14 novembre 2015 CONTABILITÀ L rilevzione dell impost sostitutiv sul trttmento di fine rpporto di Vivin Grippo Scde il prossimo 16 dicembre il termine per il versmento dell cconto dell
ISTITUTO TECNICO INDUSTRIALE STATALE "FERMI"
 ISTITUTO TECNICO INDUSTIALE STATALE "EMI" TEVISO GAA NAZIONALE DI MECCANICA 212 ropost di soluzione rim rov cur di Benetton rncesco (vincitore edizione 211 unzionmento: L gru bndier girevole sopr riportt
ISTITUTO TECNICO INDUSTIALE STATALE "EMI" TEVISO GAA NAZIONALE DI MECCANICA 212 ropost di soluzione rim rov cur di Benetton rncesco (vincitore edizione 211 unzionmento: L gru bndier girevole sopr riportt
UNITÀ DI GUIDA E SLITTE
 UNITÀ DI GUIDA E SLITTE TIPOLOGIE L gmm di unità di guid e di slitte proposte è molto mpi. Rggruppimo le guide in fmiglie: Unità di guid d ccoppire cilindri stndrd Si trtt di unità indipendenti, cui viene
UNITÀ DI GUIDA E SLITTE TIPOLOGIE L gmm di unità di guid e di slitte proposte è molto mpi. Rggruppimo le guide in fmiglie: Unità di guid d ccoppire cilindri stndrd Si trtt di unità indipendenti, cui viene
1 b a. f(x) dx. Osservazione 1.2. Se indichiamo con µ il valore medio di f su [a, b], abbiamo che. f(x) dx = µ(b a) =
![1 b a. f(x) dx. Osservazione 1.2. Se indichiamo con µ il valore medio di f su [a, b], abbiamo che. f(x) dx = µ(b a) = 1 b a. f(x) dx. Osservazione 1.2. Se indichiamo con µ il valore medio di f su [a, b], abbiamo che. f(x) dx = µ(b a) =](/thumbs/19/319521.jpg) Note ed esercizi di Anlisi Mtemtic - (Fosci) Ingegneri dell Informzione - 28-29. Lezione del 7 novembre 28. Questi esercizi sono reperibili dll pgin web del corso ttp://utenti.unife.it/dmino.fosci/didttic/mii89.tml
Note ed esercizi di Anlisi Mtemtic - (Fosci) Ingegneri dell Informzione - 28-29. Lezione del 7 novembre 28. Questi esercizi sono reperibili dll pgin web del corso ttp://utenti.unife.it/dmino.fosci/didttic/mii89.tml
Ing. Alessandro Pochì
 Dispense di Mtemtic clsse quint -Gli integrli Quest oper è distriuit con: Licenz Cretive Commons Attriuzione - Non commercile - Non opere derivte. Itli Ing. Alessndro Pochì Appunti di lezione svolti ll
Dispense di Mtemtic clsse quint -Gli integrli Quest oper è distriuit con: Licenz Cretive Commons Attriuzione - Non commercile - Non opere derivte. Itli Ing. Alessndro Pochì Appunti di lezione svolti ll
Esercizi sulle serie di Fourier
 Esercizi sulle serie di Fourier Corso di Fisic Mtemtic,.. 3- Diprtimento di Mtemtic, Università di Milno Novembre 3 Sviluppo in serie di Fourier (esponenzile) In questi esercizi, si richiede di sviluppre
Esercizi sulle serie di Fourier Corso di Fisic Mtemtic,.. 3- Diprtimento di Mtemtic, Università di Milno Novembre 3 Sviluppo in serie di Fourier (esponenzile) In questi esercizi, si richiede di sviluppre
PIANO di LAVORO A. S. 2013/ 2014
 Nome docente Borgn Giorgio Mteri insegnt Mtemtic Clsse Previsione numero ore di insegnmento IV G IPSIA ore complessive di insegnmento 33 settimne X 3 ore = 99 ore Nome Ins. Tecn. Prtico Testo in dozione
Nome docente Borgn Giorgio Mteri insegnt Mtemtic Clsse Previsione numero ore di insegnmento IV G IPSIA ore complessive di insegnmento 33 settimne X 3 ore = 99 ore Nome Ins. Tecn. Prtico Testo in dozione
-STRUTTURE DI LEWIS SIMBOLI DI LEWIS
 STRUTTURE DI LEWIS SIMBLI DI LEWIS ELETTRI DI VALEZA: sono gli elettroni del guscio esterno, i responsbili principli delle proprietà chimiche di un tomo e quindi dell ntur dei legmi chimici che vengono
STRUTTURE DI LEWIS SIMBLI DI LEWIS ELETTRI DI VALEZA: sono gli elettroni del guscio esterno, i responsbili principli delle proprietà chimiche di un tomo e quindi dell ntur dei legmi chimici che vengono
Equazioni e disequazioni
 Cpitolo Equzioni e disequzioni.1 Princìpi di equivlenz 1. Sommndo o sottrendo l stess quntità d entrmbi i membri di un equzione o di un disequzione ess non cmbi, ovvero: A(x) B(x) A(x) k(x) B(x) k(x).
Cpitolo Equzioni e disequzioni.1 Princìpi di equivlenz 1. Sommndo o sottrendo l stess quntità d entrmbi i membri di un equzione o di un disequzione ess non cmbi, ovvero: A(x) B(x) A(x) k(x) B(x) k(x).
ANALISI REALE E COMPLESSA a.a. 2007-2008
 ANALISI REALE E COMPLESSA.. 2007-2008 1 Successioni e serie di funzioni 1.1 Introduzione In questo cpitolo studimo l convergenz di successioni del tipo n f n, dove le f n sono tutte funzioni vlori reli
ANALISI REALE E COMPLESSA.. 2007-2008 1 Successioni e serie di funzioni 1.1 Introduzione In questo cpitolo studimo l convergenz di successioni del tipo n f n, dove le f n sono tutte funzioni vlori reli
Due classi dell Istituto Comprensivo Carano - Mazzini diretto dal professor Antonio Pavone - 5 e la 4. C, e nel corso della premiazione anche la 5
 Scritto d Dlil Bellcicco Lunedì 25 Mrzo 2013 07:15 Due clssi dell Istituto Comprensivo Crno - Mzzini diretto dl professor Antonio Pvone - 5 e l 4 C, e nel corso dell premizione nche l 5 C - hnno prtecipto
Scritto d Dlil Bellcicco Lunedì 25 Mrzo 2013 07:15 Due clssi dell Istituto Comprensivo Crno - Mzzini diretto dl professor Antonio Pvone - 5 e l 4 C, e nel corso dell premizione nche l 5 C - hnno prtecipto
MAURIZIO MARTINI ENZO DRAPELLI partners
 MAURIZIO MARTINI ENZO DRAPELLI prtners rgionieri commercilisti economisti d impres vldgno (vi) vi l. festri,15 tel. 0445/406758/408999 - fx 0445/408485 dueville (vi) - vi g. rossi, 26 tel. 0444/591846
MAURIZIO MARTINI ENZO DRAPELLI prtners rgionieri commercilisti economisti d impres vldgno (vi) vi l. festri,15 tel. 0445/406758/408999 - fx 0445/408485 dueville (vi) - vi g. rossi, 26 tel. 0444/591846
PROGRAMMA SVOLTO A. S. 2014/ 2015
 A. S. 4/ Nome docente Borgn Giorgio Mteri insegnt Mtemtic Clsse Previsione numero ore di insegnmento IV G mnutenzione e ssistenz tecnic ore complessive di insegnmento settimne X 4 ore = ore Nome Ins. Tecn.
A. S. 4/ Nome docente Borgn Giorgio Mteri insegnt Mtemtic Clsse Previsione numero ore di insegnmento IV G mnutenzione e ssistenz tecnic ore complessive di insegnmento settimne X 4 ore = ore Nome Ins. Tecn.
CORSO DI RAGIONERIA A.A. 2013/2014
 CORSO DI RAGIONERIA A.A. 2013/2014 MODULO A LEZIONE N. 12 LE SCRITTURE CONTABILI Ftture d emettere e ricevere e fondi rischi/oneri LE SCRITTURE AL Prim dell chiusur dell esercizio è necessrio operre le
CORSO DI RAGIONERIA A.A. 2013/2014 MODULO A LEZIONE N. 12 LE SCRITTURE CONTABILI Ftture d emettere e ricevere e fondi rischi/oneri LE SCRITTURE AL Prim dell chiusur dell esercizio è necessrio operre le
10. Completare la seguente tabella, in cui sono riportate le produzioni assolute e relative di tre colture altamente diffuse in Italia.
 ESERCIZI DI BASE 1. I soci proprietri di un piccol compgni gricol sono tre: i signori A, B, C. Mentre i signori A e C hnno l stess quot di prtecipzione ll ziend, il signor B h solo il 50% dell quot degli
ESERCIZI DI BASE 1. I soci proprietri di un piccol compgni gricol sono tre: i signori A, B, C. Mentre i signori A e C hnno l stess quot di prtecipzione ll ziend, il signor B h solo il 50% dell quot degli
Nome.Cognome. 18 Dicembre 2008 Classe 4G. VERIFICA di MATEMATICA
 Nome.Cognome. 8 Dicembre 008 Clsse G VERIFICA di MATEMATICA A) Risolvi le seguenti disequzioni goniometriche sin ) sin + ) 0 6 tn cos + sin ) 0 (punti:0,5) ) tn + tn > 0 sin 5) sin > cos (punti: ) 6) sin
Nome.Cognome. 8 Dicembre 008 Clsse G VERIFICA di MATEMATICA A) Risolvi le seguenti disequzioni goniometriche sin ) sin + ) 0 6 tn cos + sin ) 0 (punti:0,5) ) tn + tn > 0 sin 5) sin > cos (punti: ) 6) sin
Test di autovalutazione
 UNITÀ ELEMENTI DI CALCOLO ALGEBRICO Test di utovlutzione 0 0 0 0 0 0 60 0 80 90 00 n Il mio punteggio, in entesimi, è n Rispondi ogni quesito segnndo un sol delle lterntive. n Confront le tue risposte
UNITÀ ELEMENTI DI CALCOLO ALGEBRICO Test di utovlutzione 0 0 0 0 0 0 60 0 80 90 00 n Il mio punteggio, in entesimi, è n Rispondi ogni quesito segnndo un sol delle lterntive. n Confront le tue risposte
COMITATO REGIONALE CAMPANO SCACCHI c/o Circolo IncontrArci Via Arco 132 80043 S. Anastasia http://www.campaniascacchi.org
 COMITATO REGIONALE CAMPANO SCACCHI c/o Circolo IncontrArci Vi Arco 132 80043 S. Anstsi http://www.cmpnisccchi.org F.S.I. C.O.N.I. ORGANIZZA IL 19 CAMPIONATO REGIONALE A SQUADRE TORNEO OMOLOGABILE PER VARIAZIONI
COMITATO REGIONALE CAMPANO SCACCHI c/o Circolo IncontrArci Vi Arco 132 80043 S. Anstsi http://www.cmpnisccchi.org F.S.I. C.O.N.I. ORGANIZZA IL 19 CAMPIONATO REGIONALE A SQUADRE TORNEO OMOLOGABILE PER VARIAZIONI
Rilevazioni contabili caso Etiam (SAL rilevati come acconti) Criterio % di completamento: cost to cost
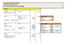 Rilevzioni contbili cso Etim (SAL rilevti come cconti) Criterio % di completmento: cost to cost nno n 01/01/n Bnc c/c Clienti 610,00 Incssto nticipo su commess 01/01/n Clienti Diversi 610,00 Fttur nticipo
Rilevzioni contbili cso Etim (SAL rilevti come cconti) Criterio % di completmento: cost to cost nno n 01/01/n Bnc c/c Clienti 610,00 Incssto nticipo su commess 01/01/n Clienti Diversi 610,00 Fttur nticipo
TABELLA DEGLI ONERI DI URBANIZZAZIONE ANNO 2010
 TABELLA DEGLI ANNO 00 criteri di ppliczione. Ai fini del clcolo degli oneri di urbnizzzione primri e secondri, i volumi sono clcolti secondo le norme degli strumenti urbnistici vigenti (rt. 7 c. 0 L.R./05);
TABELLA DEGLI ANNO 00 criteri di ppliczione. Ai fini del clcolo degli oneri di urbnizzzione primri e secondri, i volumi sono clcolti secondo le norme degli strumenti urbnistici vigenti (rt. 7 c. 0 L.R./05);
