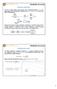
o in forma matriciale, con l evidente significato dei simboli,

Transcript

1 5-Ecoomeria, a.a. - Lezioe 5 Prorieà asioiche egli simaori OLS Ua caraerisica ei ai ecoomici è quella i essere (geeralmee) molo umerosi, erao i ecoomeria assumoo grae rilievo i risulai asioici e i quesi ci si occuerà er le rimaei lezioi. Le ioesi sul moello sarao irooe i vola i vola quao se e resea la ecessià; quella che segue e` saa gia` formulaa, la si riora solao er comleezza. OLS Il moello i regressioe lieare e le ioesi sugli errori: y = x β + u, E( u Ω ) =, x Ω er =,, o i forma mariciale, co l eviee sigificao ei simboli, y = Xβ + u, E( u Ω ) =, x Ω er =,,. Osservazioe: Ora e el seguio si assume semre, ache quao o è eo esliciamee, che i ai a isosizioe rovegoo a u D.G.P. (sruura) el moello, circosaza che si esrime iceo che il moello è correamee secificao. E` ooruo ricorare che er u fissao, lo simaore OLS (o equivaleemee lo simaore co il meoo ei momei) i β (quao auralmee esise) ha la seguee rareseazioe: xx y u ˆ x = β + xx = = x = = β =. XX ( Xy ) = β + XX ( Xu ) Ua imorae rorieà er gli simaori (alla quale come ra oco si vera` o si uò riuciare i reseza i grai camioi) è la cosiseza. Coizioi che assicurao la cosiseza ello simaore el aramero β si icoo coizioi i ieificabilià e quao soo ( ) resei il moello si ice ieificao. Da u veloce esame ella rima rareseazioe ello simaore ˆβ si oa immeiaamee che er la sua cosiseza e` richiesa la valiià` elle seguee rorieà: La marice xx è iveribile er ogi = sufficieemee grae (garaisce l esiseza ello simaore ˆβ ); L esressioe uilizzaa eriva al fao che er u umero i osservazioi che ee a, il DGP è uivocamee iiviuao.

2 5-Ecoomeria, a.a. - La sequeza xx = La sequeza u è limiaa i robabilià; x coverge a (i robabilià). ( ) = Si riorao qui i seguio alcue coizioi che assicurao la valiià elle receei i reseza i ai el io ime-series e el io cross-secio. OLS (er ime series) Il rocesso {( y, x )} a) sazioario e ergoico; ( 3) b) la marice E( xx )( = Σxx = Σ) i orie k è iveribile, è La sazioarieà e l ergoicià el rocesso assicurao la covergeza i robabilià elle ue successioi xx e = u x a Σ e riseivamee, mere all iveribilià i Σ segue la = covergeza i robabilià (e quii la limiaezza) i = xx, olre alla iveribilia` ella marice xx er = sufficieemee grae. OLS (er ai cross-secio) Poiché si sa assumeo imliciamee che il rocesso {( y, x )} e` muuamee iieee, alcue resrizioi sui momei (che o esseo molo resriive er queso geere i quesioi si assumerao semre valie) assicurao la valiià` ella legge ei grai umeri er i ue rocessi { xx } e { } u x, ( 4) e esseo E( xu ) = e` sufficiee richieere Ua sequeza i variabili aleaori Y si ice covergee a i robabilià e si scrive Y = o (), se er ogi ε >, δ > esise ν N ale che ( ν P( Y > ε) < δ ). Si ice ivece limiaa i robabilià (o igh) e si scrive Y = O () se er ogi δ > esise ε > ale che PY ( > ε ) < δ er ogi. 3 Defiizioe i ergoicià er rocessi sreamee sazioari: er ogi f e g misurabili e limiae si ha lime( f( x,, x ) g( x,, x )) = E( f( x,, x ))E( g( x,, x )); l + h + l + k+ l + h + l + k+ l si oi che er la sazioarieà el rocesso il secoo membro o iee a l. ( 4 ) Si segalao ue classici risulai che soo geeralmee iicai co l esressioe Legge ei grai umeri. Teorema: Sia ( X ) ua sequeza i v.a. muuamee iieei, co E( X ) σ si ha X i= i= μ. Teorema i Khichie: Sia ( X ) ua sequeza i v.a. ii... co E( X ) = μ, var( X ) = σ, = μ. Allora X μ. i= μ i= μ. Se

3 5-Ecoomeria, a.a. - che la marice ( Σ ) = lim xx sia iveribile. = Nel seguio si farà sesso uso ella ermiologia irooa ella seguee efiizioe. Defiizioe: Se isribuzioe (er ), ( 5) allora ˆβ è uo simaore el aramero β e la sequeza ( βˆ β) coverge i i) la variaza ella isribuzioe limie (e quii lim var( β ˆ) se esise) ( 6) icesi variaza asioica i ˆβ e si eoa co il simbolo Avar( βˆ ) ; ii) ˆβ si ice simaore cosisee i β. Si oi che, oiche` la covergeza i isribuzioe imlica la limiaezza i robabilià`, (uilizzao la oazioe irooa ella oa ), e` ( βˆ β) = O ( ) e quii ˆβ è ache simaore cosisee i β co ua velocia` ella covergeza ell`orie i /. Si segalao ora alcue versioi el eorema el limie cerale che sarao uilizzae i quese lezioi; il rimo e` uilizzao i reseza i ai el io cross-secio gli alri ue i reseza i ai el io ime series seza auocorrelazioe e co auocorrelazioe riseivamee. -Teorema el limie cerale er rocessi iieei Sia { x } ua sequeza i variabili aleaorie e si oe = x = x er ogi. i) Se { x } ii...( μσ, ). Allora ( x μ) N( ; Σ) (i aricolare si ha Avar( x) = Σ ). ii) Se le v.a. x soo iieei, i oorue ioesi sui momei (o aricolarmee resriive elle alicazioi ecoomeriche), oso μ = lim E( x ), si ha ( ) N( ;Avar( = Avar( x) = var( x = lim var( x ) x μ x)) co ( ) -Teorema (el limie cerale er iffereze marigale) Sia { x } ua sequeza i variabili aleaorie ale che, { } x è sreamee sazioaria co E( x ) e var( x ) Σ. = = = 5 La covergeza i isribuzioe i x a x equivale alla covergeza i isribuzioe i λ x a λ x er ogi λ. 6 Sussise il seguee risulao: Se X X e E( r r X ) m ( R ) allora si ha E( X ) = m r. r 3

4 5-Ecoomeria, a.a. - { x } è ergoica; { } Allora si ha x è ua iffereza marigala (cioè E( x x,, x) = er ogi ). x N(, Σ ). Le ioesi ell`ulimo eorema el limie cerale o soo rese eslicie, o solo erche` o soo semlici ma ache erche` elle alicazioi ecoomeriche o ci soo srumei che e assicurio la valiia`. 3-Teorema (el limie cerale er rocessi auocorrelai) Sia { x } u rocesso sazioario (sreamee) e ergoico co qualche forma iieeza (iù recisamee i ebole ieeza) er grui i variabili isai emoralmee (u esemio e` forio ai rocessi MA( q ), q, che sarao irooi iu` avai). Allora se μ = E( x ) si ha + esseo Avar( ) = j= j ( x μ) N(,Avar( x)), Γ j x x + j x μ x μ. x Γ co = cov(, ) = E ( )( ) Il seguee risulao forisce buoe rorieà asioiche er gli simaori OLS, i ioesi abbasaza geerali. Teorema (asioica ormalià egli simaori OLS) Per il moello i regressioe lieare y = x β + u, E( u Ω ) =, x Ω er =,, si assume la valiià elle ioesi OLS (vei sora la sua formulazioe er i vari ii i ai, qui è rioraa ua siesi) e OLS3 (che è rioraa qui i seguio). OLS È valia qualche versioe ella legge ei grai umeri er il rocesso { } esise lim xx ( = Σ ) ) e Σ è iveribile; = OLS3 Sussise ua versioe el eorema el limie cerale er il rocesso { u } xx (e quii x e quii Allora si ha: xu N(,Avar( )) x u. = ( βˆ β) N(,Avar( β ˆ)) e Avar( ˆ) Avar( ) β = Σ xu Σ. Dimosrazioe. Dalla rareseazioe 4

5 5-Ecoomeria, a.a. - β ˆ = β + u xx = x, = uilizzao la rorieà c) i roosizioe ell aeice, segue ovviamee l assero. Corollario Nelle receei ioesi, se è isoibile uo simaore cosisee er Avar( x u) (che, come e` solio, sarà eoao co Avar( x u) ), lo simaore ˆβ è uilizzabile ei roblemi i saisica ifereziale, auralmee i reseza i camioi sufficieemee grai. Osservazioe: Si reseao qui i seguio ue siuazioi frequei elle alicazioi i cui si ossoo rieere valie le ioesi el receee eorema: ) I reseza i ai cross-secio: E uso rieere ragioevole che il rocesso { y, x } muuamee iieee e quii (soo oorue ioesi sui momei che geeralmee si riegoo valie) sussise il eorema el limie cerale er il rocesso { u } umeri er il rocesso { } sia x e la legge ei grai xx, mere l iveribilià i Σ (limie i robabilià ella sequeza xx ), qui come el caso successivo, la si riiee cosegueza ell`ioesi i ieificazioe = el moello. ) I reseza i ai el io ime-series: La siuazioe è molo iversa a quella escria er i ai cross-secio. Ifai er la valiià el eorema el limie cerale si ovrao fare ioesi molo resriive. Per esemio richieere che il rocesso {, } y x sia sreamee sazioario e ergoico (ioesi geeralmee o verificae alle ime-series, che ra l alro assicura la valiià ella legge ei grai umeri er il rocesso { xx }) e che il rocesso { u } x sia ua iffereza marigala ( 7) o verifichi ua ioesi i ebole ieeza (vei il eorema el limie cerale 3). Come è sao già segalao lo simaore ˆβ, elle ioesi che lo reao asioicamee ormale, orà essere uilizzao ei roblemi i saisica ifereziale (cosruzioe i sime i iervallo e i es sulle ioesi) se è isoibile uo simaore cosisee ella sua variaza asioica. La sua cosruzioe, come si orà oare, o resea aricolari ifficolà. 7 Ua coizioe sufficiee, che ha il vaaggio i avere u semlice sigificao ecoomico, è la seguee E( u u, u,, x, x, ). = Si oi che qui o è richiesa la srea esogeeià elle variabili x, ma solao la o correlazioe i co ue le u iformazioi isoibili all isae. E ( ux ) ( u x ),( u x ), = E E(( ux ) u, u,, x, x, ) ( u x ),( u x ), = Dimosrazioe: [ ] [ ] (ci soo ifai iù iformazioi i ( u, u,, x, x, ) che i (( u x ),( u x ), ) = E[ x E( u u, u,, x, x, ) ( u x ),( u x ), ] =. 5

6 5-Ecoomeria, a.a. - Cosruzioe i uo simaore cosisee ella variaza asioica i ˆβ. Si esamiao searaamee i seguei re casi. I rimi ue casi soo iscussi i moo esauriee e i essi è assuo imliciamee le variabili el rocesso { u } x soo o correlae. a) Gli errori (coizioai) soo omoscheasici, cioè E( )( var( )) cui segue che E( u ) = σ ). b) Gli errori (coizioai) soo eeroscheasici. c) Gli errori (coizioai) soo eeroscheasici e auocorrelai. Caso a): Esseo E( u x ) = e E( u x ) = σ si ha u x = u x = σ (a x = x x = x x x = x x x = x x var( u ) E( u ) E E( u ) E E( u ) σ E( ) (i realà basa osservare che le varuiabili variabili el rocesso { u } u e xx soo o correlae) iolre esseo ache le x o correlae si ha Avar( ) lim var( ) lim E( ) lim x x. ux = u u σ x = x x = = = = = D alra are è richieso è: lim uˆ lim ˆ = u σ k = (cfr. oa i basso ( 8 ) ) e allora lo simarore = = ˆ Avar( β) = ˆ u = xx = k xx = = Caso b): Iao è ooruo segalare che l eeroscheasicià coizioale o esclue la omoscheasicia egli errori, che ceramee è resee quao si suoe che il rocesso { y, x } è sreamee sazioario. Iolre, esseo acora ua vola le variabili el rocesso { u } correlae, si ha: Avar( ux) = lim var( u ) lim E( u ) lim x = x x = u x x = = = = e (co argomei el uo simili a quelli resei ella oa 8 a iè i agia) lim ( uˆ ) lim u xx = xx =. = 8 Ifai all uguagliaza ( ) ( ) s x o uˆ ( ˆ ) (( ˆ ) ( ˆ ) ( ˆ ) ( ˆ = u u + u = u u + u u u u = u + u x β β x β β ), e ora sommao riseo a, ivieo er e assao al limie (i robabilià) er si ha lim uˆ = lim u = σ. = = 6

7 5-Ecoomeria, a.a. - Da uo ciò segue immeiaamee che uo simaore cosisee ella variaza asioica i ˆβ, eomiao simaore i Whie (oure robuso all eeroscheasicià o HCE), è Caso c): Le variabili el rocesso { x u } ˆ Avar( ) = ˆ u = = = β xx xx xx. soo ebolmee correlae e allora la variaza asioica i x u ha ua rareseazioe che coivolge ache le covariaze elle variabili el rocesso (vei eorema el limie cerale 3). U suo simaore cosisee (che qui o è riorao) è sao cosruio a Neey-Wes; ei sofare ecoomerici è iicao co il loro ome oure co la sigla HAC (heeroskeasiciy a auocorrelaio cosise). Osservazioe: Il caso b) o richiee alcua iformazioe su E( u x ). E aurale immagiare, e se e avrà coferma iù avai, che i reseza i oorue iformazioi su i essa, i meoi geerali ossao essere aaai er oeere simaori iù efficiei. A queso uo erò è ache abbasaza aurale orre il roblema ella ricerca i buoi moelli er ell ambio elle serie emorali. L argomeo, che i quese lezioi o sarà eure sfiorao, ha avuo aricolare aezioe a are egli ecoomerici orao a risulai ieressai al uo i visa sia eorico che alicaivo. Ω E( u ) Aeice Alcui risulai sulla covergeza i variabili aleaorie Proosizioe (Coservazioe ella covergeza soo rasformazioi coiue) Sia a () ua fuzioe a valori veoriali coiua. Allora ( ) ( ) a) z α a z a α ; b) z z a z a z. ( ) ( ) Ua immeiaa cosegueza ella a) ella receee roosizioe è la sabilià ella covergeza i robabilià soo le usuali oerazioi arimeiche. Più recisamee x + yβ + γ x β i) xβ, yγ urchè γ y γ x y β γ 7

8 5-Ecoomeria, a.a. - ii) Y Γ, Γ marice iveribile Y Γ. U risulao aalogo, uilizzao il uo b), si ha er la covergeza i isribuzioe; la seguee roosizioe, che sarà uilizzaa sesso, è oa come Teorema i Slusky. Proosizioe Qui α e A soo riseivamee u veore e ua marice i umeri reali. a) xx, yα x + yx + α ; b) x x y y x ', ; c) xx, AA AxAx, i aricolare quao è x N ( ; Σ) allora si ha N Ax ( AΣA ; '). ),, è iveribile ' x ; i aricolare se x x A A A x A x x A x N ( ; A) allora χk xa x esseo k la imesioe i x. Proosizioe Se x x e { z } è ua sequeza i variabili aleaorie ale che x z (si ice che le ue sequeze i variabili soo asioicamee equivalei) allora alla a) segue che ( ( ) ) z = z x + x x. Proosizioe (il ela meoo ) Sia z N ( I ) e { x } ali che e ( ) x β x β z ; ; K ua sequeza i veori aleaori i A( β) k r sia iolre a(): R R co r k, ua fuzioe coiua co le sue erivae e sia i rago massimo r. Allora si ha ( ( )) ( ax aβ ) A( β) z N A( β) A( β) ( ) ( ) ; '. I realà se ( x β) z è sosiuia a ( ) N(; ) sosaziale ella imosrazioe) si ha: ( ax ( ) aβ ( )) N( A ; ( β) ΣA( β) '). ( r K) K R a( β) = β x β Σ (seza alcua moifica 8

9 5-Ecoomeria, a.a. - Dimosrazioe. Iao al eorema i Lagrage er ogi esise y aareee al segmeo cogiugee Ora x e β ale che ( )( ) ax ( ) aβ ( ) = A y x β. ( 9) i) y β, (i quao { x } coverge i robabilia a β e aariee al segmeo cogiugee e β ); x ( ) ( ) ii) A y A β ; y iii) ( ( ) ( )) ax aβ A β z ( ) e quii l assero. Si assume che er il moello lieare Tes (asioici) sulle ioesi y = x β + u, E( u x ) = er ogi Soo valie ioesi che assicurao l asioica ormalià i ˆβ ; È isoibile uo simaore cosisee er Avar( β ˆ ) ; Si assa a cosruire u es (co valiià asioica) sulle seguei ioesi sul aramero β : ) (Ioesi lieari) { H : Rβ = b, H : Rβ b, esseo R ua marice i orie r k, co r k e i rago massimo. k r ) (Ioesi o lieari)) { H : a( β) =, H : a( β), esseo a: R R ( r k) c la marice a( β) A( β) = ( r k) β ha rago massimo. Caso Si cosruisce la saisica i Wal er l ioesi H (e er u camioe i lughezza ) Avar( βˆ ) R ( ˆ ) ( ˆ R W = Rβ b) Rβ b (ques ulima è ierreabile come ua saisica, i quao iee al camioe e misura la isaza esaa i Rβˆ a Rβ quao l ioesi H è vera). Ora esseo 9 I realà il eorema i Lagrage vale er fuzioi a valori reali e erao è ifferee er ciascua cooriaa ella fuzioe a(). Ma ciò è irrilevae, ciò che coa è che ciascu y aariee al segmeo cogiugee x e β. y 9

10 5-Ecoomeria, a.a. - ( Rβˆ Rβ) N ( R, Avar( βˆ) R ), Ava ˆ r( β) Avar( β ˆ ) e Rβ ha imesioe k, alla ) ella receee roosizioe segue che ell ioesi e i cosegueza il es, W χ r H si ha Si rifiua l ioesi H se W χr, α >, ha livello i sigificaivià α e e` valio er camioi sufficieemee grai, Caso Ache i queso caso si uò cosruire la saisica i Wal er l ioesi H Ora esseo ( ˆ ) β A β ( ˆ ) ˆ ˆ ˆ ( ˆ A( β)(avar( )) ( ) W = a( β) ) a( β). a( β) a( β ) N( Aβ, ( )Avar( βˆ ) A( β )) (er il eorema el ela meoo ); A( βˆ ) A( β ); ˆ Avar( β) Avar( β ˆ ) ; alla ) ella receee roosizioe segue che ell ioesi, W χ r H si ha che cosee, come rima, la cosruzioe el es. Osservazioe: E ooruo ricorare che i reseza i omoscheasicià er gli errori la saisica i Wal (er ioesi lieari) coicie co rf esseo F la saisica i Fisher. La saisica i Wal er ioesi o lieari resee il grosso icoveiee i o essere ivariae riseo alla rareseazioe ella ioesi ; i realà i valori ello sesso camioe ossoo essere molo iversi. Il seguee esemio mosra la o ivariaza ella saisica i Wal. Esemio: Si cosiera il seguee moello co errori omoscheasici H = β + β + β + y x x u e le ue ioesi olieari, che soo evieemee equivalei, A B H : ββ = e H : β =. β E facile verificare che le corrisoei saiiche i Wal soo ifferei.

11 5-Ecoomeria, a.a. -. Il meoo Boosra (Comlemei) Comlemei alla Lezioe 5 Il meoo el boosra (ella cosruzioe i es sulle ioesi) U elemeo esseziale ella cosruzioe ei es è: la isoibilia` ella isribuzioe i robabilià, ell ioesi, ella saisica che iiviua la classe ei es. H Si uò osservare che, i ui i es fiora cosruii, la saisica uilizzaa ha o solo la sessa isribuzioe (fiia o asioica) ell ioesi, quale che sia il DGP (Daa Geeraig Process) el moello, ma ale isribuzioe ha ua rareseazioe relaivamee semlice, erao o ci soo aricolari ifficola` er il calcolo ei quaili e el H valore. Nell`ioesi la rareseazioe ella isribuzioe si comlica, aaioo ifai le isribuzioi o cerae, ma essa ierviee solao se si è ieressai alla oeza el es. Comuque, i casi cosierai sebbee i grae ieresse soo molo aricolari; basi esare al caso (er la verià o uico e eure ra i iù ieressai) i cui si uilizza la isribuzioe asioica i ua saisica, seza esser ceri che il camioe ossa essere rieuo sufficieemee grae. Gli argomei che seguoo soo irouzioe a u meoo, eomiao boosra, che cosee i cosruire es i siuazioi iù geerali i quelle fiora cosierae (solo er reere l`esosizioe iu` semlice si fara` riferimeo ai moelli lieari). H Defiizioe: U es saisico su u moello si ice ivoale se, ell ioesi H, la isribuzioe ella saisica che lo efiisce è la sessa quale che sia il DGP (er ua fissaa lughezza el camioe e er assegai valori elle variabili esogee) el moello. Si ice asioicamee ivoale se a resare ivariaa è la isribuzioe asioica. Si oi che comuque o si richiee che sia oa la rareseazioe aaliica ella isribuzioe. Il Meoo i Moe Carlo Se u es saisico è ivoale, ma la isribuzioe ella saisica che lo efiisce o è oa (orebbe eveualmee ieere alle variabili esogee resei el moello), eciche i simulazioe saar (Meoo i Moe Carlo) coseoo i iiviuare ua sua isribuzioe emirica che uò essere uilizzaa er il calcolo el valore el camioe (i lughezza ), come sarà mosrao qui i seguio (oure, ma qui è sao omesso, er la cosruzioe ei valori criici). La Proceura: Si eoa co T la saisica che si uilizza er la cosruzioe el es e sia ˆ τ il suo valore el

12 5-Ecoomeria, a.a. -. Il meoo Boosra (Comlemei) camioe i lughezza l ioesi ( H ) a isosizioe. Si fissa u (qualuque) DGP el moello che verifica Cosruzioe ella isribuzioe emirica ella saisica T ell ioesi H : Si fissa u umero iero B (umero i simulazioi ella saisica che si voglioo realizzare). Ua simulazioe (elle B ) si cosruisce uilizzao simulazioe el DGP fissao e cosrueo il corrisoee valore * τ ella saisica T. ( ) * La sequeza ( τ j ) j=,, B cosee i cosruire la sua isribuzioe emirica. Calcolo el valore : Se il es è el io si rifiua H se è T c si ha value = P( T ˆ τ ), e * allora il suo valore emirico (frazioe i τ j che soo maggiori i ˆ τ ), uile er reere ecisioi, è ˆ = I > = I B B B * * ( τ ˆ j τ) ( τ j j= B j= τ ˆ), ove è I( τ ˆ τ) = quao τ ˆ τ, alrimei è uguale a. Il meoo Boosra I reseza i saisiche o ivoali (e quii eveualmee asioicamee ivoali) o si uò uilizzare il meoo i Moe Carlo. Quello che ora si va a escrivere, fializzao comuque alla cosruzioe i ua arossimazioe el valore e che uilizza semre eciche i simulazioe, è eomiao boosra. La iffereza sosaziale ra i ue meoi è che el rimo si simula u DGP el moello fissao arbirariamee e comuque comleamee oo, mere i queso caso si uilizza ua sima el DGP che ha geerao i ai a isosizioe (ale DGP simao icesi DGP-Boosra). Si ossoo researe i seguei ue casi: a) Il geerico DGP el moello è caraerizzao solao a arameri reali; i al caso il moello si ice comleamee secificao. b) Il geerico DGP el moello o è caraerizzao solao a arameri reali; i al caso il moello si ice arzialmee secificao. U esemio è u moello lieare co errori Descrizioe ella Proceura boosra ii...(, σ ). Per esemio, sia y = α + βx + γz + u il moello, co u N(, σ I ) e l`ioesi H : γ =. Per fissare u DGP che verifica l ioesi H, baserà cosierare la sruura che ha γ = e valori fissai (arbirariamee) er α, β e σ er esemio, e riseivamee. I realà, qualche recauzioe ella scela ei valori ei arameri va resa, er eviare roblemi i caraere umerico. Porebbe essere coveiee cosierare valori vicii alle sime OLS. Per l esemio cosierao i oa, al fie i cosierare ua simulazioe i T si cosierao simulazioi i ua ormale saar e uilizzao il camioe ( x,, x ) isoibile e il DGP fissao, si cosruiscoo ( y. Il,, y ) valore τ ella saisica si calcola uilizzao il moello origiario e il camioe ( y, x, z ) er =,,.

13 5-Ecoomeria, a.a. -. Il meoo Boosra (Comlemei) Caso a): Per reere iù chiara la escrizioe el meoo, si fa riferimeo al moello k k y x β z γ y u u i (co β R, γ R, k = k+ k ) e all ioesi saisica = + + δ +,.. (, σ ) H : γ =. Sia ifie { y, x, z } =,, Si oi che il moello è comleamee secificao; la ime-series elle osservazioi. la reseza i y ra le variabili iieei ree la saisica F o ivoale (è ivece asioicamee ivoale i quao si ha kf χ k ); ella roceura i sima la rima osservazioe (,, ) moello i ; si oe y = y ; y y x z è iuilizzabile er la reseza el il moello rioo è H y = + y + u u i : xβ δ,.. (, σ ). La cosruzioe el es boosra si realizza i iversi assi: Passo Si sima il moello origiario (co le ulime osservazioi) e si eoa co ˆ τ il ( RSSR USSR) / k valore ella saisica T = USSR /( ( + k)), che si iee uilizzare er la cosruzioe el es, el camioe a isosizioe. Passo Si simao i arameri el moello ell ioesi (che sarà uilizzao er la cosruzioe i y = x β + δ y + u, u i.. (, σ ), y, Passo 3 Si cosruiscoo B simulazioi ella saisica T. Prima Osservazioe: * Si simula u camioe ( u ) B =,, H, siao β,δ e σ. La sruura simulazioi ella saisica T ) è il DGP-Boosra. i lughezza a ua isribuzioe N(, σ ) e si cosruiscoo (er ricorreza) le osservazioi y = ( ),, y = x β + δ y + * * * * u, y ( y ) al DGP =. Il valore ella saisica T el camioe * y x z ( =,, ) è τ. * (,, ) La roceura ora escria si riee B vole e si oiee il camioe Boosra er la saisica T. Passo 4: Il calcolo el valore si effeua roceeo aalogamee a quao eo receeemee ella escrizioe el Meoo i Moe Carlo. Osservazioe: Il meoo boosra ora escrio si ice aramerico, i quao er la sua realizzazioe soo sae uilizzae solao sime arameriche. 3

14 5-Ecoomeria, a.a. -. Il meoo Boosra (Comlemei) Caso b): Si fa riferimeo semre al moello uilizzao ella iscussioe el caso a), assumeo erò che sia u ii...(, σ ). Si rocee esaamee allo sesso moo come el caso a) sosiueo, solao el Passo 3, l oerazioe * Si simula u camioe ( ) u i lughezza a ua isribuzioe =,, N(, σ ) co Si cosiera u camioe i lughezza alla oolazioe { u u },, esseo ( ) i resiui ella sima OLS revisa el Passo. u =,, Osservazioe: i) Ques`ulimo meoo boosra si ice o aramerico, i quao er la sua realizzazioe si uilizzao ache sime o arameriche. ii) Ua giusificazioe ella valiià ella roceura (iù recisamee ella sosiuzioe iicaa sora) segue alle seguei circosaze: Per ua variabile aleaoria la cui isribuzioe o è oa (el caso i esame la variabile errore (u )) e soo isoibili sue osservazioi, ua simulazioe ella sua isribuzioe emirica si oiee effeuao esrazioi co resiuzioe alle osservazioi; Esseo le sime OLS cosisei, le osservazioi ella variabile u che o soo isoibili ossoo essere sosiuie ai resiui. 4

15 5-Ecoomeria, a.a. -, Efficieza asioica egli simaori OLS U commeo sulla Lezioe 5 Efficieza asioica egli simaori OLS Lo scoo i queso aragrafo è quello i rovare l asioica efficieza (il cui sigificao sarà chiario el eorema che segue) egli simaori OLS ei moelli lieari co errori omoscheasici. La classe egli simaori cosruii co il meoo ei momei Il meoo ei momei escrio el caiolo suggerisce la seguee roceura er la cosruzioe i umerosi simaori i β, aramero el moello lieare (*) y = x β + u co E( u Ω ) = e x aariee a Sia ifai { } u rocesso i imesioe k ale che Ω, er =,,,. i) Ω er ogi (e quii E( u ) = ), ii) Il rocesso {,, } orie k, y x e` sreamee sazioario e ergoico e iolre la marice quaraa i ef Σ E( ) lim x = x = x, e` iveribile, ( k k) = iii) Il rocesso { u } e` ua iffereza marigala, allora cosierao la versioe emirica ell`uguagliaza i i) si oiee l`equazioe (veoriale) che er la ii) ha u`uica soluzioe (er eomiaa simaore i esogee. Prorieà e osservazioi: u ( y ) = xβ = =, = gae) ˆ β y = x u = β + = x =, = = β co il meoo ei momei corrisoee al veore i variabili ) Solao er ragioi i semlicià formale si fa riferimeo a rocessi el io ime.series. Quao qui eo e valio ache er ai el io cross secio, auralmee elle ioesi che siao valii (quao ecessario) la legge ei grai umeri e il eorema sel limie cerale. ) La cosruzioe i ˆ o richiee l esogeeià el rocesso β { x }, ma u qualche legame ra e x che assicuri l iveribilià i E( x ) ; 3) βˆ e` uo simaore cosisee i β ; 4) ( ˆ ) N(,Avar( ˆ β β β )) co ˆ = ( ) ( ) Avar( β) Σx Σu Σ x, 5

16 5-Ecoomeria, a.a. -, Efficieza asioica egli simaori OLS ove Σ = lim x x = e` saa efiia sora, Σ x e` la rasosa i Σ x e cioe` Σu lim var var( u) E( u ) lim u = = =. = Nelle seguei rorieà 5) e 6) si suoe che gli errori el moello soo omoscheasici, 5) Si ha E( u Ω ) = σ. ef Σu E( u ) σ E( = = ) = σ Σ co 6) Per ogi, eoaa co la marice elle osservazioi i elle osservazioi i ( x ) ( k) Σ lim =, W ( ), si ha WX WW Σ x = lim, = lim = e co X la marice Σ Avar( βˆ ) = σ lim ( WX ) ( WW )( XW ) 7) Per ogi si ha WX WW XW XX o equivaleemee assao alle marici ( ) ( )( ) ( ) iverse (vei il quaro uo ella roosizioe ell aeice i lezioe 3) ( ( k W ) ) ( )( ) ( ) ( ) ( I P ) XW WW WX XX X X. k W L ulima isuguagliaza, cioè che la marice X ( I P ) X è semiefiia osiiva, si rova immeiaamee. Ifai esseo ( I P W ) ua roiezioe orogoale si ha ( ) = ( ) k k quii er ogi z R, si ha z X Xz z X Xz Xz. ( I P ) = ( I P ) ( I P ) = ( I P ) Dalle receei segue il seguee k W k W k W k W k I P I P e W k W Teorema: Cosierao il moello lieare i (*) si suoe che er il rocesso { } siao verificae le receei coizioi i), ii) e iii), mere er il rocesso { } iveribile e il rocesso { u } omoscheasici (coizioai) si ha x si ha che la marrice è x è ua iffereza marigala. Allora se gli errori el moello soo ( ˆ OLS ) Avar( βˆ) = Avar( β ) Avar( ˆβ ). Il coeuo el eorema si uò riassumere brevemee el moo seguee: I reseza i omoscheasicià egli errori, lo simaore ra ui gli simaori cosruii co il meoo ei momei. Σ x OLS è il iù efficiee(asioicamee) 6