Analisi cinematica del PUMA
|
|
|
- Giacinto Calabrese
- 5 anni fa
- Visualizzazioni
Transcript
1 Unverstà d Bologna Faoltà d'ingegnera Meana de Robot Anals nemata del PUMA Equaon d husura La Fg. mostra la onvenone adottata per la selta de sstem d rfermento su asun membro. S adotta la notaone d Denavt-Hartenberg ponendo ( ): - φ : angolo d rotaone della -esma oppa rotodale; - : offset lungo l'asse della -esma oppa rotodale; - α : twst del membro -esmo; - a : offset del membro -esmo. Il segno de parametr geometr e d movmento è determnato utlando la onvenone d Morgan. Il sgnfato delle matr d trasformaone è anh esso llustrato n Fg.. Le matr d movmento M e d geometra G sono rspettvamente ugual a () M mentre la matre d trasformaone da () H osφ snφ a snφ osφ osα snα G snα osα S a S è osφ osα snφ snα snφ a osφ snφ osα osφ snα osφ a snφ M G snα osα La Fg. mostra l PUMA nella onfguraone ndvduata da φ ( ) (onfguraone d rfermento). In essa tutt gl ass sono tra loro parallel. Nella medesma fgura è rportata una tabella n u sono ompendate le arattersthe geometrhe del PUMA. Le matr d trasformaone valgono (3) ove s s s a 3 s3 s s as s3 3 H H H3 H s s s s s s H H snφ e osφ ( ). La matre E d trasformaone delle oordnate da a S espressa n funone degl angol φ ( ) è data da () E H3H on S
2 Unverstà d Bologna Faoltà d'ingegnera Meana de Robot () e () H H H H 3 s s 3 a + s s ss a s s3 3 as H H H H ove s sn ( φ + φ ) e os( φ φ ) 3 3 ss s s s s + s ss + ss s ss La matre E ha la seguente forma ER (7) E T n u l mnore ortogonale E R esprme l'orentamento d rspetto a S e l vettore [ y ] T la S S posone d n ( è l entro del polso sfero osttuto da membr e ). Anals d posone dretta Nell anals d posone dretta oorre determnare la postura della mano essendo note le varabl d gunto. Il problema s rsolve n manera mmedata sosttuendo valor not d φ ( ) nella matre a seondo membro dell Eq. () determnando osì la matre E. 3 Anals d posone nversa Nel problema nemato nverso è assegnata la postura della mano (oè la matre E) e oorre alolare l valore delle varabl d gunto. La ondone () rappresenta qund un sstema d equaon nelle nognte φ ( ). 3. Determnaone delle varabl d gunto φ φ e φ 3 Come s può notare osservando la Fg. la posone d n S dpende unamente da φ φ e φ 3. Se s estraggono dal sstema () le equaon d nd e 3 s ottene nfatt (8) ossa (9) s 3+ a + s ss 3 + as y 3+ as ( ) ( ) a s3+ s + a s3 s y 3+ as Le ondon (9) relatve a sol termn d traslaone della matre d trasformaone E rappresentano notoramente un set d tre equaon ndpendent all'nterno del sstema (). Nel aso ontngente esse onsentono d determnare drettamente φ φ e φ 3.
3 Unverstà d Bologna Faoltà d'ingegnera Meana de Robot Dalle prme due delle Eq. (9) s possono ravare e s n funone d φ e φ 3 : D D () s D D on () a s a s D D D a s y a s y S osserv he D non può annullars per valor real d φ e φ 3 essendo () ( ) D a s 3 + > Inoltre valor d e s fornt dall Eq. () non sono tra loro ndpendent n quanto oseno e seno dello stesso angolo φ. Deve però essere mposta l'equaone d ongruena (3) + s la quale espltata medante le Eq. () e () ondue a () ossa D + D D () ( a s ) y y( a s ) ( a s ) Espandendo l quadrato a prmo membro s ottene () ( y ) ( a s ) ( a s ) Nell Eq. () è leto dvdere entramb membr per D quanttà ertamente non nulla (v. Eq. ()); s ha pertanto (7) ( ) a s + y 3 La tera delle Eq. (9) e la stessa Eq. (7) rappresentano l rsultato dell'elmnaone dal sstema (9) dell'nognta φ. In altre parole la rsoluone del sstema (9) nelle nognte φ φ e φ 3 è stata rondotta alla rsoluone del sstema (8) + a s 3 ( ) 3 + a s y nelle sole nongte φ e φ 3 (ome s vedrà nel Par. le Eq. (8) possono essere ottenute pù spedtamente per va geometra). Se nelle Eq. (8) s sommano membro a membro la seonda on l quadrato della prma s ottene (9) e dunque + a s + a s + s + a a s + y () ( ) Con sempl passagg trgonometr s rava () + a + a s3 s3 + y + a s + y + a 3 3
4 Unverstà d Bologna Faoltà d'ingegnera Meana de Robot Tale ondone dpendendo lnearmente solo dalla seonda delle Eq. (8) può sostture unamente quest'ultma all'nterno del sstema medesmo. C s rdue qund a ravare φ e φ 3 dalla oppa d relaon osttute dall Eq. () e dalla prma delle Eq. (8) qu d seguto rportate per omodtà: () ( ) + + a + y + s3 a 3+ as In partolare la prma delle Eq. () fornse espltamente snφ 3 oè due soluon n φ 3 (sano φ 3a e φ 3b ) dstngubl dal valore d osφ 3 : (3) ± s 3 3 I valor d φ 3a e φ 3b sono entramb real se s3 [ ]. Supponendo ora noto l valore d φ 3 (sa esso φ 3a o φ 3b ) dalla seonda delle Eq. () s può ravare φ : () ( ) ( ) Utlando le note relaon trgonometrhe () ove t tan ( φ ) l Eq. () dvene + a s s 3 3 t t s + t + t () ( ) t ( a s ) t ( ) la quale porge (7) Pohé n vrtù dell Eq. () (8) l Eq. (7) può essere srtta nella forma (9) + + t a s ± a + a s a + a s + y 3 t a s ± + y + 3 L Eq. (9) fornse per φ le soluon: φ a e φ a per φ3 φ3a φ b e φ b per φ3 φ3b. Il radando a seondo membro dell Eq. (9) assume lo stesso valore per entrambe le rad d φ 3. Ne onsegue he valor d φ a φ a φ b e φ b sono o tutt real o tutt ompless. Per ognuna delle quattro possbl oppe d valor (φ φ 3 ) la sosttuone a rtroso nelle Eq. () e () ondue ad uno valore d φ. Il sstema (9) ammette pertanto quattro soluon n φ φ e φ Determnaone delle varabl d gunto φ φ e φ Per determnare le rmanent nognte φ φ e φ oorre onsderare le nove equaon relatve alle omponent d orentamento dell'equaone matrale () (omponent d nd 3). Indando on H R l mnore d rotaone (3 3) della matre d trasformaone H ( ) dall Eq. () 3
5 Unverstà d Bologna Faoltà d'ingegnera Meana de Robot s ottene (3) H H ER T R 3 R l u seondo membro è noto perhé tal sono gl angol φ φ e φ 3 da u H 3R dpende. T Indat on g ( 3) gl element d H E e tenendo persente l Eq. () l Eq. (3) può essere srtta nella forma (3) 3R R ss s s s g g g s s ss ss + + g g g s ss g g g Se s pota g33 le equaon del sstema (3) d nd e 3 onsentono d ravare φ φ e φ. Dall'equaone d posto 33 s ha nfatt (3) g3 3 la quale fornse due soluon per φ aratterate da (33) s ± Dalle relaon d nd 3 e 3 s dedue g g s 3 3 (3) s s Infne dalle equaon d posto 3 e 3 s ha 3 3 (3) s s g g s Ad ognuna delle quattro possbl terne (φ φ φ 3 ) preedentemente determnate sono però assoabl se g33 (e qund s ) due dstnte terne (φ φ φ ) per un totale d otto soluon d (). Nel aso sa g 33 (oè s ) le equaon avent posto e 3 nel sstema (3) sono dentamente soddsfatte. Rmangono da onsderare le rmanent quattro equaon le qual per ± dventano (3) on g g ( φ φ ) m sn ( φ φ ) ( φ φ ) os( φ φ ) ± os ± ± g g sn g g ± ± e g g e dove oorre prendere o segn superor o quell nferor. Le Eq. (3) s rduono alle due ondon sgnfatve (37) os ( φ φ ) g sn ( φ φ ) ± ± ± g A fronte de valor φ o π l Eq. (37) fornse un'nfntà d possbl oppe (φ φ ). 3.3 Shema del proesso rsolutvo [] Determnaone d φ 3 medante la prma delle Eq. () e l Eq. (3) ( soluon). [] Determnaone d φ medante l Eq. (9) ( soluon). [3] Determnaone d φ medante l Eq. (). [] Determnaone d φ medante le Eq. (3) e (33) ( soluon).
6 Unverstà d Bologna Faoltà d'ingegnera Meana de Robot [] Determnaone d φ medante l Eq. (3). [] Determnaone d φ medante l Eq. (3). Nel aso n u rsult g 33 pass []-[] sono sosttut da seguent: [ ] Determnaone d φ ( φ se g 33 φ π se g 33 ). [ ] Selta arbtrara d φ [ π[ ( soluon). [ ] Determnaone d φ medante l Eq. (37). Il passo [] può fornre per φ 3 due valor real dstnt o due valor real ondent (per 3 ) o due valor ompless onugat. Se due valor d φ 3 (sano φ 3a e φ 3b ) sono real s può passare alla suessva fase [] e verfare se l dsrmnante dell Eq. (9) (he assume lo stesso valore sa per φ 3a sa per φ 3b ) sa maggore mnore o uguale a ero. Se > s'ndvduano per φ le soluon real φ a e φ a on φ 3 φ 3a φ b e φ b on φ 3 φ 3b ; se nvee (e qund dall Eq. (8) a s3 ) rsulta φ a φ a e φ b φ b. In ogn aso se s può passare alla suessva fase [3] he ndvdua sempre un solo valore per φ. La ondone g 33 he dsrmna tra le sequene []-[] e [ ]-[ ] deve ora essere valutata n orrspondena ad ognuna delle quattro terne d valor (φ φ φ 3 ) preedentemente ndvduate. In ogn aso le soluon per φ sono real. Esse ondono se s dversamente sono dstnte. Se per ogn terna (φ φ φ 3 ) è g33 l anals d posone nversa ammette otto soluon. Altrment queste sono n numero nfnto. Spao d lavoro In questo paragrafo s determnerà lo spao d lavoro teoro del PUMA (assumendo ome punto d rfermento della mano). S presnderà oè da problem legat all nterferena tra membr e s assumerà he ogn oppa rotodale possa realare una rotaone relatva par a 3. Cò mpla he l polso sfero possa produrre n una qualunque posone un orentamento qualsas della mano e he soltanto la posone d sa soggetta a lmtaone. In queste ondon lo spao d lavoro destro onde on quello raggungble. S assumerà noltre a. La prma delle Eq. () ammette soluon real solo se l modulo del seondo membro è mnore o uguale a e dunque (38) + ( a ) + y + + ( a + ) Cò sgnfa he deve gaere nello spao ompreso tra due sfere entrate n e avent ragg ugual a + ( a ) e ( a ) + + rspettvamente. L Eq. (9) ammette soluon real solo se l suo dsrmnante è maggore o uguale a ero e dunque (39) + y Cò sgnfa he deve anhe gaere all esterno d un lndro d asse e raggo. Lo spao d lavoro teoro del PUMA è llustrato n Fg. 3. Le ondon (38) e (39) hanno la seguente nterpretaone geometra. nel pano y dalla Fg. rsulta Indando on r la proeone del vettore ( ) () as+ 3 r a s3 r + y
7 Unverstà d Bologna Faoltà d'ingegnera Meana de Robot e onseguentemente () ( ) a s + y 3 La prma delle Eq. () e l Eq. () ondono on le Eq. (8) ravate analtamente nel Par. 3.. È evdente he l brao osttuto da membr e raggunge la propra massma (rsp. mnma) elongaone quando φ 3 π (rsp. φ 3 π ). In questo aso rsulta () ( ) ( ) ( ) ( ) a + s a s (rsp. ) r a + r a Le Eq. () untamente alla tera delle Eq. () porgono (3) + y + + ( a + ) + y + + ( a ) (rsp. ) Le Eq. (3) fornsono le ondon (38). Inoltre pohé dalla seonda delle Eq. () rsulta () r a + la tera delle Eq. () porge () ( ) + y + a + Se sono soddsfatte le ondon (38) la dsuguaglana a destra è automatamente soddsfatta. La dsuguaglana a snstra fornse nvee la ondone (39). Anals d velotà La velotà del punto d rfermento () s può alolare dfferenando l Eq. (8) rspetto al tempo ss as + as & φ s 3 a s s 3 ass s & 3 φ + + & s + a s & φ mentre la velotà angolare della mano s può ottenere tenendo presente he (7) %ω EE & oppure n manera omputaonalmente pù omoda ome (8) ω & φ φ ( R R) & H LH ( & φi & φh & R φ3h RH R K & φh RH RH3 RH RH R) Le Eq. () e (8) espanse e srtte n forma matrale porgono l equaone d velotà del PUMA (9) dove la matre aobana è par a R T R & φ & J M & φ ω 7
8 Unverstà d Bologna Faoltà d'ingegnera Meana de Robot () ss 3 as + 3 as 3 s 3+ a + s s 3 ass s 3 s3+ a s3 J s s s3 3s + s ss s 3s s 3 ss3 s 3s ss s 3s ss 3 3 s3s s3s + 3 Indando on J e J mnor 3 3 post lungo la dagonale prnpale d J rsulta dopo qualhe passaggo () ( ) S not he () det det det a a s s J J J 3 3 ( ) as + s det J 3 3 φ φ3 φ dove le funon argomento delle dervate paral ondono on prm membr delle Eq. () e (3). La fattoraone dello aobano fornse ome noto delle valde ndaon per la srttura delle equaon d husura n forma trangolare. Confguraon sngolar Dall Eq. () rsulta he le ondon (3) a s3 () 3 () s ndvduano le onfguraon sngolar del PUMA. In asuna d esse due soluon real dell anals d posone nversa dventano ondent (v. Par. 3.3) e la mano del PUMA perde un grado d lbertà. Infatt quando le ondon (3) e () sono soddsfatte gae sulla frontera dello spao d lavoro: rspettvamente sul lndro espresso dall Eq. (39) oppure su una delle due sfere espresse dalle Eq. (38). Le Fg. e llustrano rspettvamente l grado d lbertà perso. Quando è soddsfatta la ondone () gl ass delle tre oppe rotodal del polso sfero dventano oplanar (n partolare l prmo ed l tero dventano ondent) e rsulta qund mpossble onferre alla mano una omponente d velotà angolare perpendolare a tale pano. 8
9 Unverstà d Bologna Faoltà d'ingegnera Meana de Robot S φ S S φ S φ + + α > a > > φ > φ a α α a S M S G S H M G Fg.. Convenone d Denavt-Hartenberg/Morgan. 9
10 Unverstà d Bologna Faoltà d'ingegnera Meana de Robot 3 a M M M 3 M M M α a a Fg.. Confguraone d rfermento e arattersthe geometrhe del PUMA.
11 Unverstà d Bologna Faoltà d'ingegnera Meana de Robot ( a ) + + ( a ) + Fg. 3. Spao d lavoro del PUMA.
12 Unverstà d Bologna Faoltà d'ingegnera Meana de Robot y φ +φ 3 y φ 3 r a φ 3 φ φ +φ 3 a φ y y φ φ r v Fg.. Determnaone delle equaon d posone del PUMA. Fg.. Confguraone d sngolartà ndvduata dall Eq. a s3. y φ 3 π v y φ 3 π v φ φ Fg.. Confguraon d sngolartà ndvduate dall Eq. 3.
Lezione 5 - Analisi cinematica
 eone 5 - nals cnematca [Ultmarevsone: revsone:25 25novembre 28] S consder ora una struttura bdmensonale, ossa un nseme d trav collegate tra loro ed al suolo da opportun vncol. In questa leone s voglono
eone 5 - nals cnematca [Ultmarevsone: revsone:25 25novembre 28] S consder ora una struttura bdmensonale, ossa un nseme d trav collegate tra loro ed al suolo da opportun vncol. In questa leone s voglono
asse fisso nel tempo in rotazione attorno ad un asse fisso dell asse di rotazione rimarranno fermi al passar del temporispetto al sistema inerziale
 Rotaon rgde attorno ad un asse fsso nel tempo un corpo rgdo n rotaone attorno ad un asse fsso ha un solo grado d lberta n quest cas per descrvere l moto converra rferrs ad un polo fsso se l asse d rotaone
Rotaon rgde attorno ad un asse fsso nel tempo un corpo rgdo n rotaone attorno ad un asse fsso ha un solo grado d lberta n quest cas per descrvere l moto converra rferrs ad un polo fsso se l asse d rotaone
5.3 LE TURBINE RADIALI
 5.3 LE TURBINE RADIALI 5.3. INTRODUZIONE Se la omponente d portata della velotà del fludo, nvee he parallela all asse d rotazone della mahna, è ad esso ortogonale, la turbna s de radale, entrfuga o entrpeta
5.3 LE TURBINE RADIALI 5.3. INTRODUZIONE Se la omponente d portata della velotà del fludo, nvee he parallela all asse d rotazone della mahna, è ad esso ortogonale, la turbna s de radale, entrfuga o entrpeta
Il modello del lot sizing
 Il modello del lot sng Dspensa per gl student del orso d Rera Operatva II Autore: Prof. Guseppe Bruno 009 Dspensa per l orso d Rera Operatva II - Prof. Guseppe Bruno IL MODELLO DEL LOT SIZIG Il modello
Il modello del lot sng Dspensa per gl student del orso d Rera Operatva II Autore: Prof. Guseppe Bruno 009 Dspensa per l orso d Rera Operatva II - Prof. Guseppe Bruno IL MODELLO DEL LOT SIZIG Il modello
Esercitazioni 2 - Analisi della deformazione
 Eserctaon - Anals della deformaone In questa eserctaone s studano alcun stat deformatv Infne, s danno alcune semplc funon Mathematca, che permettono l'automaone dello studo per qualsas stato deformatvo
Eserctaon - Anals della deformaone In questa eserctaone s studano alcun stat deformatv Infne, s danno alcune semplc funon Mathematca, che permettono l'automaone dello studo per qualsas stato deformatvo
Complementi 4 - Materiali non isotropi
 Complement 4 - Materal non sotrop [Ultmarevsone revsone9gennao gennao2009] In questo noteboo s parte dalla legge d Hooe per sold ansotrop, e s deducono le opportune restron sulle 21 costant elastche, potando
Complement 4 - Materal non sotrop [Ultmarevsone revsone9gennao gennao2009] In questo noteboo s parte dalla legge d Hooe per sold ansotrop, e s deducono le opportune restron sulle 21 costant elastche, potando
CINEMATICA DIRETTA. Paolo Fiorini Dipartimento di Informatica Università degli Studi di Verona
 CINEMATICA DIRETTA Paolo Forn Dpartmento d Informata Unvertà degl Stud d Verona Introduzone Manpolatore: atena nemata (aperta) d orp rgd (bra) e gunt (rotodal e prmat) Per poter manpolare un oggetto nello
CINEMATICA DIRETTA Paolo Forn Dpartmento d Informata Unvertà degl Stud d Verona Introduzone Manpolatore: atena nemata (aperta) d orp rgd (bra) e gunt (rotodal e prmat) Per poter manpolare un oggetto nello
Funzione di matrice. c i λ i. i=0. i=0. m 1. γ i A i. i=0. Moltiplicando entrambi i membri di questa equazione per A si ottiene. α i 1 A i α m 1 A m
 Captolo INTRODUZIONE Funzone d matrce Sa f(λ) una generca funzone del parametro λ svluppable n sere d potenze f(λ) Sa A una matrce quadrata d ordne n La funzone d matrce f(a) èdefnta nel modo seguente
Captolo INTRODUZIONE Funzone d matrce Sa f(λ) una generca funzone del parametro λ svluppable n sere d potenze f(λ) Sa A una matrce quadrata d ordne n La funzone d matrce f(a) èdefnta nel modo seguente
θ 2 i r 2 r La multifunzione f (z) = z z i
 1-19 1.4 1.4.1. La multfunone f () = + 1 3 è l prodotto d 2 multfunon Z Z e W 3 W. È qund ragonevole supporre che Z =, coè = 1 e W =, coè = sano punt d dramaone d f. Con rfermento alla fgura a lato, e
1-19 1.4 1.4.1. La multfunone f () = + 1 3 è l prodotto d 2 multfunon Z Z e W 3 W. È qund ragonevole supporre che Z =, coè = 1 e W =, coè = sano punt d dramaone d f. Con rfermento alla fgura a lato, e
7. METODO DELLE FORZE IMPOSTAZIONE GENERALE INFLUENZA DEGLI SPOSTAMENTI DEI VINCOLI
 aptolo7 ETODO DEE FORZE - IPOSTZIONE GENERE 7. ETODO DEE FORZE IPOSTZIONE GENERE INFUENZ DEGI SPOSTENTI DEI VINOI SPOSTENTI SSEGNTI DEI VINOI Supponamo he alun vnol abbano spostament / rotaon assegnat
aptolo7 ETODO DEE FORZE - IPOSTZIONE GENERE 7. ETODO DEE FORZE IPOSTZIONE GENERE INFUENZ DEGI SPOSTENTI DEI VINOI SPOSTENTI SSEGNTI DEI VINOI Supponamo he alun vnol abbano spostament / rotaon assegnat
Complementi 1 - Le trasformazioni lineari
 Complement 1 - Le trasformaon lnear [Ultmarevsone revsone20 20dcembre dcembre2008] In questa Leone s studano le propreta delle trasformaon lnear rappresentate da: ξ 1 = a 11 +a 12 +a 13 ξ 2 = a 21 +a 22
Complement 1 - Le trasformaon lnear [Ultmarevsone revsone20 20dcembre dcembre2008] In questa Leone s studano le propreta delle trasformaon lnear rappresentate da: ξ 1 = a 11 +a 12 +a 13 ξ 2 = a 21 +a 22
Meccanica Dinamica del corpo rigido
 Meccanca 8-9 6 Fora peso sul corpo rgdo Corpo sottoposto alla fora peso: Su ogn elemento nfntesmo d massa dm agsce la fora Rsultante delle fore: F peso V g dm Momento rsultante (polo ): M V Energa potenale:
Meccanca 8-9 6 Fora peso sul corpo rgdo Corpo sottoposto alla fora peso: Su ogn elemento nfntesmo d massa dm agsce la fora Rsultante delle fore: F peso V g dm Momento rsultante (polo ): M V Energa potenale:
Lezione 6 - Analisi statica
 eone 6 - nals statca [Ultmarevsone: revsone:5 5novembre 8] S consder la stessa struttura bdmensonale della leone precedente, ossa un nseme d trav collegate tra loro ed al suolo da opportun vncol. S vuole
eone 6 - nals statca [Ultmarevsone: revsone:5 5novembre 8] S consder la stessa struttura bdmensonale della leone precedente, ossa un nseme d trav collegate tra loro ed al suolo da opportun vncol. S vuole
di una delle versioni del compito di Geometria analitica e algebra lineare del 12 luglio 2013 distanza tra r ed r'. (punti 2 + 3)
 Esempo d soluzone d una delle verson del compto d Geometra analtca e algebra lneare del luglo 3 Stablre se la retta r, d equazon parametrche x =, y = + t, z = t (nel parametro reale t), è + y + z = sghemba
Esempo d soluzone d una delle verson del compto d Geometra analtca e algebra lneare del luglo 3 Stablre se la retta r, d equazon parametrche x =, y = + t, z = t (nel parametro reale t), è + y + z = sghemba
CINEMATICA DIRETTA. Introduzione. Giunti e Bracci. Paolo Fiorini Dipartimento di Informatica Università degli Studi di Verona
 CINEMATICA DIETTA Paolo Forn Dpartmento d Informata Unvertà degl Stud d Verona ALTAI -- Computer Sene Department Unverty of Verona Faoltá d Senze Motore, Coro d Bongegnera, Parte http://metropol..unvr.t
CINEMATICA DIETTA Paolo Forn Dpartmento d Informata Unvertà degl Stud d Verona ALTAI -- Computer Sene Department Unverty of Verona Faoltá d Senze Motore, Coro d Bongegnera, Parte http://metropol..unvr.t
Esercizi sui circuiti magnetici
 Esercz su crcut magnetc Eserczo a. Nel crcuto magnetco llustrato calcolare, trascurando la rluttanza del ferro, coeffcent d auto nduzone degl avvolgment e e l coeffcente d mutua nduzone tra due avvolgment
Esercz su crcut magnetc Eserczo a. Nel crcuto magnetco llustrato calcolare, trascurando la rluttanza del ferro, coeffcent d auto nduzone degl avvolgment e e l coeffcente d mutua nduzone tra due avvolgment
Sistemi Intelligenti Stimatori e sistemi lineari - III
 Sstem Intellgent Stmator e sstem lnear - III Alberto Borghese Unverstà degl Stud d Mlano Laboratory of Appled Intellgent Systems (AIS-Lab) Dpartmento d Informatca borghese@d.unm.t /6 http:\\borghese.d.unm.t\
Sstem Intellgent Stmator e sstem lnear - III Alberto Borghese Unverstà degl Stud d Mlano Laboratory of Appled Intellgent Systems (AIS-Lab) Dpartmento d Informatca borghese@d.unm.t /6 http:\\borghese.d.unm.t\
x 0 x 50 x 20 x 100 CASO 1 CASO 2 CASO 3 CASO 4 X n X n X n X n
 Corso d Statstca docente: Domenco Vstocco La msura della varabltà per varabl qualtatve ordnal Lo studo della varabltà per varabl qualtatve ordnal può essere condotto servendos degl ndc d omogenetà/eterogenetà
Corso d Statstca docente: Domenco Vstocco La msura della varabltà per varabl qualtatve ordnal Lo studo della varabltà per varabl qualtatve ordnal può essere condotto servendos degl ndc d omogenetà/eterogenetà
Esercizio 1. Esercitazione 14 Dicembre 2012 Sistemi trifase e potenze R 3 R 1 R 2. simmetrico L 1 L 3
 serctazone 4 Dcembre 0 Sstem trfase e potenze serczo L L L 00 f 50 Hz smmetrco Fg : Sstema trfase a stella S consder l crcuto d Fg e s calcolno le tre corrent d fase e le potenze attve, reattve ed apparent
serctazone 4 Dcembre 0 Sstem trfase e potenze serczo L L L 00 f 50 Hz smmetrco Fg : Sstema trfase a stella S consder l crcuto d Fg e s calcolno le tre corrent d fase e le potenze attve, reattve ed apparent
Lezione 15 - La teoria lineare
 Leone 5 - La teora lneare [Ultmarevsone revsone6 6gennao gennao009] In questa leone s esamnano le conseguene d una ragonevole potes sulla grandea d alcune quantta' d nteresse fsco. L'potes d pccole deformaon
Leone 5 - La teora lneare [Ultmarevsone revsone6 6gennao gennao009] In questa leone s esamnano le conseguene d una ragonevole potes sulla grandea d alcune quantta' d nteresse fsco. L'potes d pccole deformaon
Stabilità dei Sistemi Dinamici. Stabilità Semplice. Stabilità Asintotica. Stabilità: concetto intuitivo che può essere formalizzato in molti modi
 Gustavo Belforte Stabltà de Sstem Dnamc Gustavo Belforte Stabltà de Sstem Dnamc Stabltà de Sstem Dnamc Il Pendolo Stabltà: concetto ntutvo che può essere formalzzato n molt mod Intutvamente: Un oggetto
Gustavo Belforte Stabltà de Sstem Dnamc Gustavo Belforte Stabltà de Sstem Dnamc Stabltà de Sstem Dnamc Il Pendolo Stabltà: concetto ntutvo che può essere formalzzato n molt mod Intutvamente: Un oggetto
Pierpaolo De Filippi Dipartimento di Elettronica e Informazione Via Ponzio 34/ Ricevimento: solo su appuntamento
 Polteno d Mlano Cnemata Dretta e Invera Fondament d obota a.a. / Perpaolo De Flpp Fondament d obota Contatt Perpaolo De Flpp Dpartmento d Elettrona e Informazone Va Ponzo 34/5 39947 evmento: olo u appuntamento
Polteno d Mlano Cnemata Dretta e Invera Fondament d obota a.a. / Perpaolo De Flpp Fondament d obota Contatt Perpaolo De Flpp Dpartmento d Elettrona e Informazone Va Ponzo 34/5 39947 evmento: olo u appuntamento
Lezione 13 - Il gradiente di deformazione
 eone - Il gradente d deformaone [Ultmarevsone revsone dcembre dcembre008] In questa leone s comnca ad affrontare l'anals della deformaone, cu compto prncpale e' rspondere al seguente problema: - assegnate
eone - Il gradente d deformaone [Ultmarevsone revsone dcembre dcembre008] In questa leone s comnca ad affrontare l'anals della deformaone, cu compto prncpale e' rspondere al seguente problema: - assegnate
Esercizi numerici Parte A
 Polteno d Mlano Faoltà d Ingegnera dell Informazone Eserz numer Parte A Ret Radomobl Eserzo S onsder una rete ellulare d tpo multarrer-tdma he dspone d 24 portant, asuna on 3 anal a) Utlzzando l modello
Polteno d Mlano Faoltà d Ingegnera dell Informazone Eserz numer Parte A Ret Radomobl Eserzo S onsder una rete ellulare d tpo multarrer-tdma he dspone d 24 portant, asuna on 3 anal a) Utlzzando l modello
METODI PER L'ANALISI DEI CIRCUITI
 MTODI P 'NISI DI IUITI Nel seguto engono llustrat, medante esemp, alun tra metod pù utlzzat per l'anals de rut elettr. Il problema he s uole rsolere è l seguente: assegnato l ruto elettro e le grandezze
MTODI P 'NISI DI IUITI Nel seguto engono llustrat, medante esemp, alun tra metod pù utlzzat per l'anals de rut elettr. Il problema he s uole rsolere è l seguente: assegnato l ruto elettro e le grandezze
Esercitazioni di elettromagnetismo applicato
 A. affu: Esertazon Elettromagnetsmo Applato ver. 4.1 1/15 Unverstà egl tu Cassno e el Lazo eronale Esertazon elettromagnetsmo applato prof. Antono affu maffu@unas.t www.oente.unas.t/antono_maffu er.4.1
A. affu: Esertazon Elettromagnetsmo Applato ver. 4.1 1/15 Unverstà egl tu Cassno e el Lazo eronale Esertazon elettromagnetsmo applato prof. Antono affu maffu@unas.t www.oente.unas.t/antono_maffu er.4.1
LABORATORIO II. 1 La retta di regressione. NB create un nuovo foglio di lavoro
 LABORATORIO II B create un nuovo foglo d lavoro La retta d regressone Eserco. U PRIMO ESEMPIO DI RETTA DI REGRESSIOE LIEARE. Leggere attentamente paragraf.,. e. tutto Costrure la retta d regressone lneare
LABORATORIO II B create un nuovo foglo d lavoro La retta d regressone Eserco. U PRIMO ESEMPIO DI RETTA DI REGRESSIOE LIEARE. Leggere attentamente paragraf.,. e. tutto Costrure la retta d regressone lneare
5. Baricentro di sezioni composte
 5. Barcentro d sezon composte Barcentro del trapezo Il barcentro del trapezo ( FIURA ) s trova sull asse d smmetra oblqua (medana) della fgura; è suffcente, qund, determnare la sola ordnata. A tal fne,
5. Barcentro d sezon composte Barcentro del trapezo Il barcentro del trapezo ( FIURA ) s trova sull asse d smmetra oblqua (medana) della fgura; è suffcente, qund, determnare la sola ordnata. A tal fne,
Propagazione degli errori
 Propagaone degl error Voglamo rcavare le ncertee nelle msure ndrette. Abbamo gà vsto leone un prma stma degl error sulle grandee dervate valda n generale. Consderamo ora l caso specco d grandee aette da
Propagaone degl error Voglamo rcavare le ncertee nelle msure ndrette. Abbamo gà vsto leone un prma stma degl error sulle grandee dervate valda n generale. Consderamo ora l caso specco d grandee aette da
Principio di massima verosimiglianza
 Prncpo d massma verosmglana Sa data una grandea d cu s conosce la unone denstà d probabltà ; che dpende da un nseme de parametr ndcat con d valore sconoscuto. S vuole determnare la mglor stma de parametr.
Prncpo d massma verosmglana Sa data una grandea d cu s conosce la unone denstà d probabltà ; che dpende da un nseme de parametr ndcat con d valore sconoscuto. S vuole determnare la mglor stma de parametr.
Principio di massima verosimiglianza
 Prncpo d massma verosmglana Sa data una grandea d cu s conosce la unone denstà d probabltà ; che dpende da un nseme de parametr ndcat con d valore sconoscuto. S vuole determnare la mglor stma de parametr.
Prncpo d massma verosmglana Sa data una grandea d cu s conosce la unone denstà d probabltà ; che dpende da un nseme de parametr ndcat con d valore sconoscuto. S vuole determnare la mglor stma de parametr.
Esercitazione 12 ottobre 2011 Trasformazioni circuitali. v 3. v 1. Per entrambi i casi, i valori delle grandezze sono riportati in Tab. I.
 Eserctazone ottobre 0 Trasformazon crcutal Sere e parallelo S consderno crcut n Fg e che rappresentano rspettvamente un parttore d tensone e uno d corrente v v v v Fg : Parttore d tensone Fg : Parttore
Eserctazone ottobre 0 Trasformazon crcutal Sere e parallelo S consderno crcut n Fg e che rappresentano rspettvamente un parttore d tensone e uno d corrente v v v v Fg : Parttore d tensone Fg : Parttore
Esercizi sulle reti elettriche in corrente continua (parte 2)
 Esercz sulle ret elettrche n corrente contnua (parte ) Eserczo 3: etermnare gl equvalent d Thevenn e d Norton del bpolo complementare al resstore R 5 nel crcuto n fgura e calcolare la corrente che crcola
Esercz sulle ret elettrche n corrente contnua (parte ) Eserczo 3: etermnare gl equvalent d Thevenn e d Norton del bpolo complementare al resstore R 5 nel crcuto n fgura e calcolare la corrente che crcola
Determinare gli insiemi delle soluzioni dei seguenti sistemi lineari non omogenei e scriverli in forma di spazio affine ESERCIZIO 1.3.
 Deermnare gl nsem delle soluon de seguen ssem lnear non omogene e srverl n forma d spao affne ESERCIZIO ESERCIZIO ESERCIZIO ESERCIZIO ESERCIZIO ESERCIZIO 6 ESERCIZIO ESERCIZIO ESERCIZIO 9 ESERCIZIO SOLUZIONI
Deermnare gl nsem delle soluon de seguen ssem lnear non omogene e srverl n forma d spao affne ESERCIZIO ESERCIZIO ESERCIZIO ESERCIZIO ESERCIZIO ESERCIZIO 6 ESERCIZIO ESERCIZIO ESERCIZIO 9 ESERCIZIO SOLUZIONI
Metodi di analisi R 1 =15Ω R 2 =40Ω R 3 =16Ω
 Metod d anals Eserczo Anals alle magle n presenza d sol generator ndpendent d tensone R s J R Determnare le tenson sulle resstenze sapendo che: s s 0 R R 5.Ω s J R J R R 5Ω R 0Ω R 6Ω R 5 Dsegnamo l grafo,
Metod d anals Eserczo Anals alle magle n presenza d sol generator ndpendent d tensone R s J R Determnare le tenson sulle resstenze sapendo che: s s 0 R R 5.Ω s J R J R R 5Ω R 0Ω R 6Ω R 5 Dsegnamo l grafo,
Sistemi a più gradi di libertà: cinematica diretta
 Sstem a pù grad d lbertà: cnematca dretta Introduzone La poszone e l'orentamento d una terna soldale all ultmo elemento d un meccansmo a pù grad d lbertà (robot) dpende evdentemente dalle caratterstche
Sstem a pù grad d lbertà: cnematca dretta Introduzone La poszone e l'orentamento d una terna soldale all ultmo elemento d un meccansmo a pù grad d lbertà (robot) dpende evdentemente dalle caratterstche
* PROBABILITÀ - SCHEDA N. 2 LE VARIABILI ALEATORIE *
 * PROBABILITÀ - SCHEDA N. LE VARIABILI ALEATORIE *. Le varabl aleatore Nella scheda precedente abbamo defnto lo spazo camponaro come la totaltà degl est possbl d un espermento casuale; abbamo vsto che
* PROBABILITÀ - SCHEDA N. LE VARIABILI ALEATORIE *. Le varabl aleatore Nella scheda precedente abbamo defnto lo spazo camponaro come la totaltà degl est possbl d un espermento casuale; abbamo vsto che
Fisica dei semiconduttori: prova del
 6114.nb 1 Fsca de semconduttor: prova del 6 11 4 ü 1. 1. Un elettrone è descrtto da una funone d onda (n 1 dmensone) u(x) = a u 1 (x) + b u (x) dove u 1 (x) ed u (x) sono autofunon dell Hamltonana del
6114.nb 1 Fsca de semconduttor: prova del 6 11 4 ü 1. 1. Un elettrone è descrtto da una funone d onda (n 1 dmensone) u(x) = a u 1 (x) + b u (x) dove u 1 (x) ed u (x) sono autofunon dell Hamltonana del
Prova di verifica parziale N Dic 2008
 Corso d GEOTECNICA Ingegnera Edle-Arhtettura a.a. 8/9 Prova d verfa parzale N. 7 D 8 Eserzo q kpa SABBIA LIMOSA γ 8 kn/m φ' SABBIA E GHIAIA γ 9 kn/m φ' Con rfermento al muro d sostegno n fgura alolare:
Corso d GEOTECNICA Ingegnera Edle-Arhtettura a.a. 8/9 Prova d verfa parzale N. 7 D 8 Eserzo q kpa SABBIA LIMOSA γ 8 kn/m φ' SABBIA E GHIAIA γ 9 kn/m φ' Con rfermento al muro d sostegno n fgura alolare:
Dipartimento di Statistica Università di Bologna. Matematica Finanziaria aa lezione 17: 8 maggio 2012
 Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 17: 8 maggo 2012 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/20? Costture n regme semplce al tasso = 0, 025 l
Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 17: 8 maggo 2012 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/20? Costture n regme semplce al tasso = 0, 025 l
Corpi rigidi (prima parte)
 Corp rgd (prma parte) Corp rgd Un corpo rgdo è un corpo n cu le dstane tra le vare par che lo compongono rmangono costan3. r CM d CM È un po parcolare d sstema d N parcelle. Valgono ancora le legg dp dt
Corp rgd (prma parte) Corp rgd Un corpo rgdo è un corpo n cu le dstane tra le vare par che lo compongono rmangono costan3. r CM d CM È un po parcolare d sstema d N parcelle. Valgono ancora le legg dp dt
Il procedimento può essere pensato come una ricerca in un insieme ordinato, il peso incognito può essere cercato con il metodo della ricerca binaria.
 SCELTA OTTIMALE DEL PROCEDIMENTO PER PESARE Il procedmento può essere pensato come una rcerca n un nseme ordnato, l peso ncognto può essere cercato con l metodo della rcerca bnara. PESI CAMPIONE IN BASE
SCELTA OTTIMALE DEL PROCEDIMENTO PER PESARE Il procedmento può essere pensato come una rcerca n un nseme ordnato, l peso ncognto può essere cercato con l metodo della rcerca bnara. PESI CAMPIONE IN BASE
Rotazione rispetto ad asse fisso Asse z : asse di rotazione
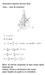 Rotaone rspetto ad asse fsso Asse : asse d rotaone 1 1 1 Ek= ω = ω= ω om. d nera: propreta d ogn corpo rgdo Dpende da: massa, forma e dmenson del corpo asse rspetto al quale lo s consdera Asta omogenea:
Rotaone rspetto ad asse fsso Asse : asse d rotaone 1 1 1 Ek= ω = ω= ω om. d nera: propreta d ogn corpo rgdo Dpende da: massa, forma e dmenson del corpo asse rspetto al quale lo s consdera Asta omogenea:
Dinamica del corpo rigido
 Anna Nobl 1 Defnzone e grad d lbertà S consder un corpo d massa totale M formato da N partcelle cascuna d massa m, = 1,..., N. Il corpo s dce rgdo se le dstanze mutue tra tutte le partcelle che lo compongono
Anna Nobl 1 Defnzone e grad d lbertà S consder un corpo d massa totale M formato da N partcelle cascuna d massa m, = 1,..., N. Il corpo s dce rgdo se le dstanze mutue tra tutte le partcelle che lo compongono
1 - SCELTA TIPOLOGICA DELLE OPERE DI FONDAZIONE
 1 - SCELTA TIPOLOGICA DELLE OPERE DI FODAZIOE La tpologa delle opere d fondazone sono onsone alle arattersthe meanhe del terreno defnte n ase a rsultat delle ndagn geognosthe. el aso n esame, la struttura
1 - SCELTA TIPOLOGICA DELLE OPERE DI FODAZIOE La tpologa delle opere d fondazone sono onsone alle arattersthe meanhe del terreno defnte n ase a rsultat delle ndagn geognosthe. el aso n esame, la struttura
Determinarelatranscaratteristicav out (v in ) del seguente circuito R. V out. V in V ٧ = 0.7V D Z D V R = 5V. R o V R V Z = -8V
 ESECZO SU DOD (Metodo degl Scatt) Determnarelatranscaratterstcav out (v n ) del seguente crcuto Dat del problema 5 o kω Ω 0 Ω Z -8 n ٧ 0.7 r D 0 Ω r Z 0 Ω r Ω D Z D o out Metodo degl scatt S determnano
ESECZO SU DOD (Metodo degl Scatt) Determnarelatranscaratterstcav out (v n ) del seguente crcuto Dat del problema 5 o kω Ω 0 Ω Z -8 n ٧ 0.7 r D 0 Ω r Z 0 Ω r Ω D Z D o out Metodo degl scatt S determnano
Progetto di travi in c.a.p isostatiche Il tracciato del cavi e il cavo risultante
 Unverstà degl Stud d Roma Tre - Facoltà d Ingegnera Laurea magstrale n Ingegnera Cvle n Protezone Corso d Cemento Armato Precompresso A/A 2015-16 Progetto d trav n c.a.p sostatche Il traccato del cav e
Unverstà degl Stud d Roma Tre - Facoltà d Ingegnera Laurea magstrale n Ingegnera Cvle n Protezone Corso d Cemento Armato Precompresso A/A 2015-16 Progetto d trav n c.a.p sostatche Il traccato del cav e
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO
 PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
ESERCIZIARIO SUI NUMERI COMPLESSI
 ESERCIZIARIO SUI NUMERI COMPLESSI I numer regnano sull unverso. PITAGORA Perché numer sono bell? È come chedere perché la Nona Snfona d Beethoven è bella. Se non ved perché, nessuno può spegartelo. Io
ESERCIZIARIO SUI NUMERI COMPLESSI I numer regnano sull unverso. PITAGORA Perché numer sono bell? È come chedere perché la Nona Snfona d Beethoven è bella. Se non ved perché, nessuno può spegartelo. Io
Le soluzioni della prova scritta di Matematica per il corso di laurea in Farmacia (raggruppamento M-Z)
 Le soluzon della prova scrtta d Matematca per l corso d laurea n Farmaca (raggruppamento M-Z). Data la funzone a. trova l domno d f f ( ) ln + b. scrv, esplctamente e per esteso, qual sono gl ntervall
Le soluzon della prova scrtta d Matematca per l corso d laurea n Farmaca (raggruppamento M-Z). Data la funzone a. trova l domno d f f ( ) ln + b. scrv, esplctamente e per esteso, qual sono gl ntervall
ESERCIZIO 4.1 Si consideri una popolazione consistente delle quattro misurazioni 0, 3, 12 e 20 descritta dalla seguente distribuzione di probabilità:
 ESERCIZIO. S consder una popolazone consstente delle quattro msurazon,, e descrtta dalla seguente dstrbuzone d probabltà: X P(X) ¼ ¼ ¼ ¼ S estrae casualmente usando uno schema d camponamento senza rpetzone
ESERCIZIO. S consder una popolazone consstente delle quattro msurazon,, e descrtta dalla seguente dstrbuzone d probabltà: X P(X) ¼ ¼ ¼ ¼ S estrae casualmente usando uno schema d camponamento senza rpetzone
Circuiti elettrici in regime stazionario
 rcut elettrc n regme stazonaro omponent www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del 3-9-0) Bpol resst Equazon caratterstca d un bpolo ressto f, 0 L equazone d un bpolo ressto defnsce una cura nel
rcut elettrc n regme stazonaro omponent www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del 3-9-0) Bpol resst Equazon caratterstca d un bpolo ressto f, 0 L equazone d un bpolo ressto defnsce una cura nel
CINEMATICA INVERSA. Paolo Fiorini Dipartimento di Informatica Università degli Studi di Verona
 CINEMATICA INVERSA Paolo Forn Dpartmento d Informata Unvertà degl Stud d Verona Introduzone Cnemata Dretta Dat: angol a gunt Calola: pozone e orentamento organo termnale Cnemata Invera Dat: pozone e orentamento
CINEMATICA INVERSA Paolo Forn Dpartmento d Informata Unvertà degl Stud d Verona Introduzone Cnemata Dretta Dat: angol a gunt Calola: pozone e orentamento organo termnale Cnemata Invera Dat: pozone e orentamento
Corsi di Laurea in Farmacia e CTF Prova di Matematica
 Cors d Laurea n Farmaca e CTF Prova d Matematca S O L U Z I O N I Effettua uno studo qualtatvo della funzone 4 f + con partcolare rfermento a seguent aspett: a trova l domno della funzone b trova gl ntervall
Cors d Laurea n Farmaca e CTF Prova d Matematca S O L U Z I O N I Effettua uno studo qualtatvo della funzone 4 f + con partcolare rfermento a seguent aspett: a trova l domno della funzone b trova gl ntervall
y x x 20 e gli assi delle ascisse e delle ordinate. Tracce assegnate durante l anno scolastico
 Tracce assegnate durante l anno scolastco. Dsegna nel pano cartesano la retta d equazone, dopo averla scrtta n orma esplcta. Stablsc, sa gracamente ce analtcamente, se l B ; 3 appartene alla retta. punto.
Tracce assegnate durante l anno scolastco. Dsegna nel pano cartesano la retta d equazone, dopo averla scrtta n orma esplcta. Stablsc, sa gracamente ce analtcamente, se l B ; 3 appartene alla retta. punto.
Geometria 1 a.a. 2011/12 Esonero del 23/01/12 Soluzioni (Compito A) sì determinarla, altrimenti dimostrare che ciò è impossibile.
 Geometra 1 a.a. 2011/12 Esonero del 23/01/12 Soluzon (Compto A) (1) S consder su C 2 l prodotto Hermtano, H assocato alla matrce ( ) 2 H =. 2 (a) Dmostrare che, H è defnto postvo e determnare una base
Geometra 1 a.a. 2011/12 Esonero del 23/01/12 Soluzon (Compto A) (1) S consder su C 2 l prodotto Hermtano, H assocato alla matrce ( ) 2 H =. 2 (a) Dmostrare che, H è defnto postvo e determnare una base
Lezione 2 a - Statistica descrittiva per variabili quantitative
 Lezone 2 a - Statstca descrttva per varabl quanttatve Esempo 5. Nella tabella seguente sono rportat valor del tasso glcemco rlevat su 10 pazent: Pazente Glcema (mg/100cc) 1 1 =103 2 2 =97 3 3 =90 4 4 =119
Lezone 2 a - Statstca descrttva per varabl quanttatve Esempo 5. Nella tabella seguente sono rportat valor del tasso glcemco rlevat su 10 pazent: Pazente Glcema (mg/100cc) 1 1 =103 2 2 =97 3 3 =90 4 4 =119
Controllo dei robot. (Prof. Rocco) Appello del 19 Luglio 2007
 Controllo de robot (Prof. Roo) Appello del 19 Luglo 27 Cognome:... Nome:... Matrola:... Frma:... Avvertenze: Il preente faolo ompone d 8 pagne (omprea la opertna). Tutte le pagne utlzzate vanno frmate.
Controllo de robot (Prof. Roo) Appello del 19 Luglo 27 Cognome:... Nome:... Matrola:... Frma:... Avvertenze: Il preente faolo ompone d 8 pagne (omprea la opertna). Tutte le pagne utlzzate vanno frmate.
Soluzioni 3.1. n(n 1) (n k + 1) z n k! k + 1 n k. lim k
 (1) La sere bnomale è B n (z) = k=0 Con l metodo del rapporto s ottene R = lm k Soluzon 3.1 n(n 1) (n k + 1) z n k! c k c k+1 = lm k k + 1 n k lm k c k z k. k=0 1 + 1 k 1 n k = 1 (2) La multfunzone f(z)
(1) La sere bnomale è B n (z) = k=0 Con l metodo del rapporto s ottene R = lm k Soluzon 3.1 n(n 1) (n k + 1) z n k! c k c k+1 = lm k k + 1 n k lm k c k z k. k=0 1 + 1 k 1 n k = 1 (2) La multfunzone f(z)
Problemi di Adattamento fra Generatore e Carico SOMMARIO
 SOMMRIO PROLMI I TTMNTO FR GNRTOR RIO... Introduzone... ondzon d adattamento d massma tensone... ondzon d adattamento d massma orrente... ondzon d adattamento d massma potenza...3 ondzon d adattamento
SOMMRIO PROLMI I TTMNTO FR GNRTOR RIO... Introduzone... ondzon d adattamento d massma tensone... ondzon d adattamento d massma orrente... ondzon d adattamento d massma potenza...3 ondzon d adattamento
Incidenza delle Onde sull interfaccia Dielettrico Conduttore
 Incdena delle Onde sull nterfacca Delettrco Conduttore Incdena su un nterfacca Generalmente quando un onda elettromagnetca o ncde una nterfacca che separa due me d natura dversa (e qund con mpedena ntrnseca
Incdena delle Onde sull nterfacca Delettrco Conduttore Incdena su un nterfacca Generalmente quando un onda elettromagnetca o ncde una nterfacca che separa due me d natura dversa (e qund con mpedena ntrnseca
Sorgenti Numeriche - Soluzioni
 Sorgent umerche - Soluzon *) L anals delle frequenze con cu compaono le vare lettere n un documento n talano, comprendente 5975 caratter, ha fornto seguent dat: Lettera umero Frequenza relatva A 666. B
Sorgent umerche - Soluzon *) L anals delle frequenze con cu compaono le vare lettere n un documento n talano, comprendente 5975 caratter, ha fornto seguent dat: Lettera umero Frequenza relatva A 666. B
3 CAMPIONAMENTO DI BERNOULLI E DI POISSON
 3 CAMPIOAMETO DI ROULLI E DI POISSO 3. ITRODUZIOE In questo captolo esamneremo due schem d camponamento che dversamente dal camponamento casuale semplce non producono campon d dmensone fssa ma varable.
3 CAMPIOAMETO DI ROULLI E DI POISSO 3. ITRODUZIOE In questo captolo esamneremo due schem d camponamento che dversamente dal camponamento casuale semplce non producono campon d dmensone fssa ma varable.
Esercitazione sulle Basi di di Definizione
 Eserctazone sulle as d d Defnzone ESERIZIO Un bpolo ressto (dodo) ha la seguente equazone: = k [ 0 + 00] con k 0 nella quale ed sono descrtt dalla conenzone degl utlzzator come n fgura. Stablre se l bpolo
Eserctazone sulle as d d Defnzone ESERIZIO Un bpolo ressto (dodo) ha la seguente equazone: = k [ 0 + 00] con k 0 nella quale ed sono descrtt dalla conenzone degl utlzzator come n fgura. Stablre se l bpolo
Formule principali per il calcolo delle caratteristiche geometriche
 Struttura dell aereo Gl aere ogg n attvtà sono osttut da vare omponent essenzal: la fusolera, le al o superf portant, l'apparato propulsore sstem d guda e d ontrollo; e.. La struttura tpa dell'ala onsste
Struttura dell aereo Gl aere ogg n attvtà sono osttut da vare omponent essenzal: la fusolera, le al o superf portant, l'apparato propulsore sstem d guda e d ontrollo; e.. La struttura tpa dell'ala onsste
2.1 Parabola nella forma canonica
 5 Clc per tutt gl appunt (AUTOMAZIONE TRATTAMENTI TERMICI ACCIAIO SCIENZA delle COSTRUZIONI ) e-mal per suggerment. Paraola nella forma canonca Studamo con metod general la conca nella espressone canonca
5 Clc per tutt gl appunt (AUTOMAZIONE TRATTAMENTI TERMICI ACCIAIO SCIENZA delle COSTRUZIONI ) e-mal per suggerment. Paraola nella forma canonca Studamo con metod general la conca nella espressone canonca
Corso di Fondamenti di Telecomunicazioni
 Corso d Fondament d Teleomunazon 6 - SEGNALI IN BANDA PASSANTE E MODULAZIONI Prof. Maro Barbera [parte 5] Modulazon dtal multlvello Modulazone multlvello: modulazone d un senale dtale on un numero d smbol
Corso d Fondament d Teleomunazon 6 - SEGNALI IN BANDA PASSANTE E MODULAZIONI Prof. Maro Barbera [parte 5] Modulazon dtal multlvello Modulazone multlvello: modulazone d un senale dtale on un numero d smbol
Equilibrio e stabilità di sistemi dinamici. Stabilità dell equilibrio di sistemi dinamici non lineari per linearizzazione
 Equlbro e stabltà d sstem dnamc Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem NL TC Crter d stabltà
Equlbro e stabltà d sstem dnamc Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem NL TC Crter d stabltà
Elemento Trave nel piano
 Il etodo degl Element Fnt Elemento Trave nel pano Dalle dpene del prof. Daro Amodo e dalle lezon del prof. Govann Santu.Cortee Progettazone eana agl Element Fnt (a.a. 11-1) Introduzone al alolo trutturale
Il etodo degl Element Fnt Elemento Trave nel pano Dalle dpene del prof. Daro Amodo e dalle lezon del prof. Govann Santu.Cortee Progettazone eana agl Element Fnt (a.a. 11-1) Introduzone al alolo trutturale
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa lezione 9: 3 marzo 2014
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2013-2014 lezone 9: 3 marzo 2014 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/25? Eserczo Consderamo una rendta perodca d 2n termn
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2013-2014 lezone 9: 3 marzo 2014 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/25? Eserczo Consderamo una rendta perodca d 2n termn
Predimensionamento reti chiuse
 Predmensonamento ret chuse Rspetto ad una rete aperta, ogn magla aggunge un grado d lbertà (una nfntà d soluzon) nella determnazone delle portate Q,Q 1, e Q 2, utlzzando le sole equazon d contnutà. La
Predmensonamento ret chuse Rspetto ad una rete aperta, ogn magla aggunge un grado d lbertà (una nfntà d soluzon) nella determnazone delle portate Q,Q 1, e Q 2, utlzzando le sole equazon d contnutà. La
Matematica Computazionale(6cfu) Ottimizzazione(8cfu)
 Docente: Marco Gavano (e-mal:gavano@unca.t) Corso d Laurea n Infomatca Corso d Laurea n Matematca Matematca Computazonale(6cfu) Ottmzzazone(8cfu) (a.a. 205-6, lez.8) Matematca Computazonale, Ottmzzazone,
Docente: Marco Gavano (e-mal:gavano@unca.t) Corso d Laurea n Infomatca Corso d Laurea n Matematca Matematca Computazonale(6cfu) Ottmzzazone(8cfu) (a.a. 205-6, lez.8) Matematca Computazonale, Ottmzzazone,
INTRODUZIONE ALL ESPERIENZA 4: STUDIO DELLA POLARIZZAZIONE MEDIANTE LAMINE DI RITARDO
 INTODUZION ALL SPINZA 4: STUDIO DLLA POLAIZZAZION DIANT LAIN DI ITADO Un utle rappresentazone su come agscono le lamne su fasc coerent è ottenuta utlzzando vettor e le matrc d Jones. Vettore d Jones e
INTODUZION ALL SPINZA 4: STUDIO DLLA POLAIZZAZION DIANT LAIN DI ITADO Un utle rappresentazone su come agscono le lamne su fasc coerent è ottenuta utlzzando vettor e le matrc d Jones. Vettore d Jones e
Predimensionamento reti chiuse
 Predmensonamento ret chuse Rspetto ad una rete aperta, ogn magla aggunge un grado d lbertà (una nfntà d soluzon) nella determnazone delle portate Q,Q 1, e Q 2, utlzzando le sole equazon d contnutà. a dfferenza
Predmensonamento ret chuse Rspetto ad una rete aperta, ogn magla aggunge un grado d lbertà (una nfntà d soluzon) nella determnazone delle portate Q,Q 1, e Q 2, utlzzando le sole equazon d contnutà. a dfferenza
Numeri complessi, polinomi - Risposte pagina 1 di 11 23
 Numer compless, polnom - Rsposte pagna d 0. a. I numer compless con Re () sono quell a destra della retta vertcale (retta compresa). Quell con modulo mnore d 4 sono all nterno della crconferena d centro
Numer compless, polnom - Rsposte pagna d 0. a. I numer compless con Re () sono quell a destra della retta vertcale (retta compresa). Quell con modulo mnore d 4 sono all nterno della crconferena d centro
Università di Cassino Corso di Statistica 1 Esercitazione del 17/10/2006 Dott. Alfonso Piscitelli. Esercizio 1
 Unverstà d Cassno Corso d Statstca Eserctazone del 7/0/006 Dott. Alfonso Psctell Eserczo Il seguente data set rporta la rlevazone d alcun caratter su un collettvo d 0 soggett. Soggetto Sesso Età Reddto
Unverstà d Cassno Corso d Statstca Eserctazone del 7/0/006 Dott. Alfonso Psctell Eserczo Il seguente data set rporta la rlevazone d alcun caratter su un collettvo d 0 soggett. Soggetto Sesso Età Reddto
PROVA SCRITTA DI MECCANICA RAZIONALE (13 gennaio 2017) (Prof. A. Muracchini)
 PRV SCRITT DI ECCNIC RZINLE (13 gennao 017) (Prof.. uracchn) Il sstema rappresentato n fgura è costtuto da: a) una lamna pesante, omogenea a forma d trangolo soscele (massa m, base l, altezza h) vncolata
PRV SCRITT DI ECCNIC RZINLE (13 gennao 017) (Prof.. uracchn) Il sstema rappresentato n fgura è costtuto da: a) una lamna pesante, omogenea a forma d trangolo soscele (massa m, base l, altezza h) vncolata
Lezione 2 a - Statistica descrittiva per variabili quantitative
 Lezone 2 a - Statstca descrttva per varabl quanttatve Esempo 5. Nella tabella seguente sono rportat valor del tasso glcemco rlevat su 10 pazent: Pazente Glcema (mg/100cc) 1 x 1 =103 2 x 2 =97 3 x 3 =90
Lezone 2 a - Statstca descrttva per varabl quanttatve Esempo 5. Nella tabella seguente sono rportat valor del tasso glcemco rlevat su 10 pazent: Pazente Glcema (mg/100cc) 1 x 1 =103 2 x 2 =97 3 x 3 =90
I.5. FORMULAZIONE DIFFERENZIALE DELL ELETTROSTATICA
 I.5. FORMULAZIONE DIFFERENZIALE DELL ELETTROTATICA I.5.. Propretà ntegral del campo elettrostatco Le propretà gà consderate del campo elettrostatco, descrtte dal teorema d Gauss e dal fatto che l campo
I.5. FORMULAZIONE DIFFERENZIALE DELL ELETTROTATICA I.5.. Propretà ntegral del campo elettrostatco Le propretà gà consderate del campo elettrostatco, descrtte dal teorema d Gauss e dal fatto che l campo
NATURA ATOMICA DELLA MATERIA
 NATURA ATOMICA DLLA MATRIA Un qualunque fludo è costtuto da un gran numero d partcelle (sa sngol atom che molecole) n un contnuo moto dsordnato defnto agtaone termca. Questo fenomeno sta alla base de cosddett
NATURA ATOMICA DLLA MATRIA Un qualunque fludo è costtuto da un gran numero d partcelle (sa sngol atom che molecole) n un contnuo moto dsordnato defnto agtaone termca. Questo fenomeno sta alla base de cosddett
UNIVERSITA DEGLI STUDI DI CASSINO FACOLTA DI INGEGNERIA
 UNIVERSITA DEGI STUDI DI CASSINO FACOTA DI INGEGNERIA ANTONIO RUSSO, ANGEO EOPARDI ANAISI DE ERRORE CONNESSO A APPROSSIMAZIONE DEE UNGHEZZE E DEE CEERITA NE METODO DI INTEGRAZIONE DEE CARATTERISTICHE (MOC)
UNIVERSITA DEGI STUDI DI CASSINO FACOTA DI INGEGNERIA ANTONIO RUSSO, ANGEO EOPARDI ANAISI DE ERRORE CONNESSO A APPROSSIMAZIONE DEE UNGHEZZE E DEE CEERITA NE METODO DI INTEGRAZIONE DEE CARATTERISTICHE (MOC)
Reti in fibra ottica. Prima Esercitazione Lunghezze d onda e potenze
 Ret n bra otta Prma Esertazone Lunghezze d onda e potenze Eserzo Un sstema d trasmssone otto è aratterzzato da una banda dsponble, mposta dalla urva d guadagno dell EDFA, par a 30 nm entrata attorno a
Ret n bra otta Prma Esertazone Lunghezze d onda e potenze Eserzo Un sstema d trasmssone otto è aratterzzato da una banda dsponble, mposta dalla urva d guadagno dell EDFA, par a 30 nm entrata attorno a
3 = 3 Ω. quindi se v g = 24 V, i = 1,89 A Dobbiamo studiare tre circuiti; in tutti e tre i casi si ottiene un partitore di corrente.
 5. Per la propretà d lneartà la tensone può essere espressa come = k g, doe g è la corrente del generatore. Utlzzando dat n Fgura a abbamo - = k 6, qund k = - ½. In Fgura b la corrente del generatore è
5. Per la propretà d lneartà la tensone può essere espressa come = k g, doe g è la corrente del generatore. Utlzzando dat n Fgura a abbamo - = k 6, qund k = - ½. In Fgura b la corrente del generatore è
Laboratorio 2B A.A. 2012/2013. Elaborazione Dati. Lab 2B CdL Fisica
 Laboratoro B A.A. 01/013 Elaborazone Dat Lab B CdL Fsca Lab B CdL Fsca Elaborazone dat spermental Prncpo della massma verosmglanza Quando eseguamo una sere d msure relatve ad una data grandezza fsca, quanto
Laboratoro B A.A. 01/013 Elaborazone Dat Lab B CdL Fsca Lab B CdL Fsca Elaborazone dat spermental Prncpo della massma verosmglanza Quando eseguamo una sere d msure relatve ad una data grandezza fsca, quanto
Esame di metodi matematici per le decisioni economiche e aziendali
 UNIVERSITÀ DEGLI STUDI ROMA TRE Esame d metod matematc per le decson economche e aendal 9-02-209 Canddato (cognome e nome)......... Matrcola...... ) Data la matrce 200 00 80 200 200 250 400 300 50 50 00
UNIVERSITÀ DEGLI STUDI ROMA TRE Esame d metod matematc per le decson economche e aendal 9-02-209 Canddato (cognome e nome)......... Matrcola...... ) Data la matrce 200 00 80 200 200 250 400 300 50 50 00
Circuiti elettrici in regime stazionario
 rcut elettrc n regme stazonaro Metod d anals www.de.ng.unbo.t/pers/mastr/ddattca.htm ersone del -0-00 Premessa Nel caso pù generale è possble ottenere la soluzone d un crcuto rsolendo un sstema formato
rcut elettrc n regme stazonaro Metod d anals www.de.ng.unbo.t/pers/mastr/ddattca.htm ersone del -0-00 Premessa Nel caso pù generale è possble ottenere la soluzone d un crcuto rsolendo un sstema formato
links utili:
 dspensa d Govann Bachelet Meccanca de Sstem, maggo 2003 lnks utl: http://scenceworld.wolfram.com/physcs/angularmomentum.html http://hyperphyscs.phy-astr.gsu.edu/hbase/necon.html Momento della quanttà d
dspensa d Govann Bachelet Meccanca de Sstem, maggo 2003 lnks utl: http://scenceworld.wolfram.com/physcs/angularmomentum.html http://hyperphyscs.phy-astr.gsu.edu/hbase/necon.html Momento della quanttà d
Dipartimento di Statistica Università di Bologna. Matematica Finanziaria aa lezione 7: 6 marzo 2012
 Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 7: 6 marzo 2012 professor Danele Rtell www.unbo.t/docdent/danele.rtell 1/29? Defnzone Se è un prestto se m {1, 2,..., n}
Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 7: 6 marzo 2012 professor Danele Rtell www.unbo.t/docdent/danele.rtell 1/29? Defnzone Se è un prestto se m {1, 2,..., n}
PROBLEMA 1. Soluzione. β = 64
 PROBLEMA alcolare l nclnazone β, rspetto al pano stradale, che deve avere un motocclsta per percorrere, alla veloctà v = 50 km/h, una curva pana d raggo r = 4 m ( Fg. ). Fg. Schema delle condzon d equlbro
PROBLEMA alcolare l nclnazone β, rspetto al pano stradale, che deve avere un motocclsta per percorrere, alla veloctà v = 50 km/h, una curva pana d raggo r = 4 m ( Fg. ). Fg. Schema delle condzon d equlbro
Propagazione degli errori
 Propagazone degl error Msure drette: la grandezza sca vene msurata drettamente (ad es. Spessore d una lastrna). Per questo tpo d msure, la teora dell errore svluppata nelle lezone precedent é sucente per
Propagazone degl error Msure drette: la grandezza sca vene msurata drettamente (ad es. Spessore d una lastrna). Per questo tpo d msure, la teora dell errore svluppata nelle lezone precedent é sucente per
4.6 Dualità in Programmazione Lineare
 4.6 Dualtà n Programmazone Lneare Ad ogn PL n forma d mn (max) s assoca un PL n forma d max (mn) Spaz e funzon obettvo dvers ma n genere stesso valore ottmo! Esempo: l valore massmo d un flusso ammssble
4.6 Dualtà n Programmazone Lneare Ad ogn PL n forma d mn (max) s assoca un PL n forma d max (mn) Spaz e funzon obettvo dvers ma n genere stesso valore ottmo! Esempo: l valore massmo d un flusso ammssble
Lezione 2 le misure di sintesi: le medie
 Lezone le msure d sntes: le mede Cattedra d Bostatstca Dpartmento d Scenze spermental e clnche, Unverstà degl Stud G. d Annunzo d Chet-Pescara Prof. Enzo Ballone Lezone a- Statstca descrttva per varabl
Lezone le msure d sntes: le mede Cattedra d Bostatstca Dpartmento d Scenze spermental e clnche, Unverstà degl Stud G. d Annunzo d Chet-Pescara Prof. Enzo Ballone Lezone a- Statstca descrttva per varabl
Metodi di analisi per circuiti resistivi
 Metod d anals per crcut resst www.de.ng.unbo.t/pers/mastr/ddattca.htm ersone del 7-0-07 Premessa Nel caso pù generale è possble ottenere la soluzone d un crcuto rsolendo un sstema formato dalle equazon
Metod d anals per crcut resst www.de.ng.unbo.t/pers/mastr/ddattca.htm ersone del 7-0-07 Premessa Nel caso pù generale è possble ottenere la soluzone d un crcuto rsolendo un sstema formato dalle equazon
Esercitazione I : Determinazione dei pesi
 Esertazone I : Il proget d un nuovo velvolo parte da una stma prelmnare de pes del velvolo stesso, ovvero dalla determnazone delle dverse alquote d peso he è le attenders he gl ompetano. Le alquote da
Esertazone I : Il proget d un nuovo velvolo parte da una stma prelmnare de pes del velvolo stesso, ovvero dalla determnazone delle dverse alquote d peso he è le attenders he gl ompetano. Le alquote da
Circuiti dinamici. Circuiti del secondo ordine. (versione del ) Circuiti del secondo ordine
 rcut dnamc rcut del secondo ordne www.de.ng.unbo.t/pers/mastr/ddattca.htm (versone del 9-6- rcut del secondo ordne rcut del secondo ordne: crcut l cu stato è defnto da due varabl x ( e x ( Per un crcuto
rcut dnamc rcut del secondo ordne www.de.ng.unbo.t/pers/mastr/ddattca.htm (versone del 9-6- rcut del secondo ordne rcut del secondo ordne: crcut l cu stato è defnto da due varabl x ( e x ( Per un crcuto
Dinamica dei sistemi particellari
 Dnamca de sstem partcellar Marco Favrett Aprl 11, 2010 1 Cnematca Sa dato un sstema d rfermento nerzale (O, e ), = 1, 2, 3 e consderamo un sstema d punt materal (sstema partcellare) S = {(OP, m )}, = 1,,
Dnamca de sstem partcellar Marco Favrett Aprl 11, 2010 1 Cnematca Sa dato un sstema d rfermento nerzale (O, e ), = 1, 2, 3 e consderamo un sstema d punt materal (sstema partcellare) S = {(OP, m )}, = 1,,
POLINOMIO MINIMO E FORMA CANONICA DI JORDAN NOTA AGGIUNTIVA PER IL CORSO DI GEOMETRIA ANALITICA E ALGEBRA LINEARE A.A DOCENTE: PAOLO LISCA
 POLINOMIO MINIMO E FORMA CANONICA DI JORDAN NOTA AGGIUNTIVA PER IL CORSO DI GEOMETRIA ANALITICA E ALGEBRA LINEARE AA 2009-2010 DOCENTE: PAOLO LISCA 1 Polnomo mnmo Avvertenza: con V ndcheremo uno spazo
POLINOMIO MINIMO E FORMA CANONICA DI JORDAN NOTA AGGIUNTIVA PER IL CORSO DI GEOMETRIA ANALITICA E ALGEBRA LINEARE AA 2009-2010 DOCENTE: PAOLO LISCA 1 Polnomo mnmo Avvertenza: con V ndcheremo uno spazo
Rappresentazione dei numeri PH. 3.1, 3.2, 3.3
 Rappresentazone de numer PH. 3.1, 3.2, 3.3 1 Tp d numer Numer nter, senza segno calcolo degl ndrzz numer che possono essere solo non negatv Numer con segno postv negatv Numer n vrgola moble calcol numerc
Rappresentazone de numer PH. 3.1, 3.2, 3.3 1 Tp d numer Numer nter, senza segno calcolo degl ndrzz numer che possono essere solo non negatv Numer con segno postv negatv Numer n vrgola moble calcol numerc
Teoremi dei circuiti
 Teorem de crcut www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del --04) Teorema d Tellegen potes: Crcuto con n nod e l lat ers d rfermento scelt per tutt lat secondo la conenzone dell utlzzatore {,...,
Teorem de crcut www.de.ng.unbo.t/pers/mastr/ddattca.htm (ersone del --04) Teorema d Tellegen potes: Crcuto con n nod e l lat ers d rfermento scelt per tutt lat secondo la conenzone dell utlzzatore {,...,
Integrazione numerica dell equazione del moto per un sistema lineare viscoso a un grado di libertà. Prof. Adolfo Santini - Dinamica delle Strutture 1
 Integrazone numerca dell equazone del moto per un sstema lneare vscoso a un grado d lbertà Prof. Adolfo Santn - Dnamca delle Strutture 1 Introduzone 1/2 L equazone del moto d un sstema vscoso a un grado
Integrazone numerca dell equazone del moto per un sstema lneare vscoso a un grado d lbertà Prof. Adolfo Santn - Dnamca delle Strutture 1 Introduzone 1/2 L equazone del moto d un sstema vscoso a un grado
