1. INTRODUZIONE TRAIETTORIA E LEGGE ORARIA ESEMPIO DI CALCOLO DELLA LEGGE ORARIA IN FORMA PARAMETRICA VARI TIPI DI MOTO
|
|
|
- Dorotea Scarpa
- 6 anni fa
- Visualizzazioni
Transcript
1 CINEMATICA 1. INTRODUZIONE TRAIETTORIA E LEGGE ORARIA ESEMPIO DI CALCOLO DELLA LEGGE ORARIA IN FORMA PARAMETRICA VARI TIPI DI MOTO IL MOTO DI UN GRAVE IL MOTO CIRCOLARE IL MOTO ARMONICO MOTI OSCILLATORI SMORZATI COMPOSIZIONE DEI MOVIMENTI RELATIVITA GALILEIANA ACCELERAZIONE APPARENTE DI CORIOLIS LE TRE LEGGI DI KEPLERO IL DIFFERENZIALE DI UNA FUNZIONE DI UNA SOLA VARIABILE DERIVATE IMPORTANTI E REGOLE DI DERIVAZIONE DERIVATE PARZIALI GLI INTEGRALI PRINCIPALI LE EQUAZIONI DIFFERENZIALI ALLE DERIVATE ORDINARIE LE EQUAZIONI DIFFERENZIALI LINEARI EQUAZIONI DIFFERENZIALI SEPARABILI APPLICAZIONI DELLE EQUAZIONI DIFFERENZIALI... 34
2 1.INTRODUZIONE La cinematica consiste nello studio dei movimenti dal punto di vista dei soli effetti misuabili, senza tenee in alcun conto le cause che tali effetti deteminano. Quest ultimo è il compito della dinamica. Noi consideeemo essenzialmente il moto di un punto mateiale, cioè di un punto matematico che è libeo di cambiae la sua posizione in funzione del tempo. Le due gandezze fisiche basilai della cinematica sono dunque la posizione ed il tempo. Con queste due gandezze è possibile costuie un ceto numeo di alte gandezze, dette gandezze deivate, come ad esempio la velocità, l acceleazione ecc. Mente la posizione e ovviamente un vettoe, il tempo invece è uno scalae. Infatti pe deteminae completamente la posizione di un punto nello spazio sono necessaie te misue (ad esempio te lunghezze cioè le te coodinate catesiane), mente pe deteminae completamente l istante di tempo in cui si veifica un fenomeno è necessaia una sola misua (ad esempio con un conometo). In geneale tutte le gandezze fisiche possono essee appesentate da un ente matematico del tipo seguente: a) un numeo (scalae) b) un vettoe (n componenti che dipendono da un solo indice) 1. v = [ v i ]= ( v 1,v 2,,v n ) c) una matice (piu componenti che dipendono da almeno due indici a 11 a a 1n a 21 a a 2n 2. M = = a ij a m1 a m2... a mn [ ], i = 1,...,m j =1,...,n Più in geneale si possono intodue i tensoi o gli spinoi (questi ultimi nella fisica micoscopica). Lo studio del moto di un copo complesso (sia esso solido o fluido) può sempe essee effettuato consideando il moto di un ceto numeo di punti mateiali che caatteizzano vaie pozioni anche piccolissime del copo stesso. 2
3 2.TRAIETTORIA E LEGGE ORARIA Studiamo il moto di un punto P nello spazio. Assumiamo che la geometia sia quella euclidea (cioè valga il teoema di Pitagoa pe espimee la distanza) e che lo spazio sia una funzione continua del tempo. Alloa possiamo palae di taiettoia Γ del punto nello spazio usuale a te dimensioni. Sia Γ la taiettoia di un punto mateiale, alloa è possibile scivee 3. P = f t la legge oaia in foma vettoiale. La (3) può essee espessa in foma catesiana, 4. ( ) x = f x ( t) y = f y () t z = f z () t dove il paameto libeo è il tempo t. Consideiamo pe semplicità un moto piano Y Γ P 0 dy θ P α dx ds O X fig.1 Figue 1 alloa se d s è il vettoe spostamento infinitesimo lungo la taiettoia del punto mobile (vettoe tangente alla taiettoia Γ) d s = dx,dy ( ) 3
4 il suo modulo è ds = dx cosα dove α è l'angolo ta la tangente alla taiettoia nel punto P e l'asse x. L'equazione della taiettoia Γ nel piano si iduce alla seguente equazione catesiana, dopo ave eliminato il paameto tempo t, y = f(x); deivando si ottiene: quadando si ottiene: cioè df dx = tg α = 1 cos2 α cosα 2 df cos 2 α = 1 cos 2 α dx cos 2 1 α = 1 + df 2 dx 5. ds = 1 + df 2 dx dx L'integale della fomula (5) pemette di ottenee la legge oaia in foma paametica: 6. s = st ( ) quando sia nota l'equazione della taiettoia; s è detta anche coodinata cuvilinea e appesenta la distanza misuata lungo la taiettoia Γ del punto P dall'oigine P 0. Z Γ P 0 P s O Y X fig.2 4
5 Nella fig.2 s s = Figue 2 è il vesoe tangente alla taiettoia Γ nel punto P s + ds P s ( ) ( ) = d P ds ds ed essendo s s = 1, alloa deivando d( s s ) = 2 s d s ds ds = 0 e dunque il vettoe d s ds è pependicolae al vesoe P cioè pependicolae alla taiettoia Γ. Possiamo alloa costuie il vesoe nomale alla taiettoia Γ. s y s s θ P θ O ρ x fig. 2a Figue 3 5
6 Si può dimostae che in un moto cicolae di aggio ρ ( fig. 3) si ha: Infatti: x = ρcosθ y = ρsen θ inolte s = ( senθ, cosθ) e icodando che ds = dx cosα dove α = π 2 +θ si ottiene ds = dx sen θ ma dx = ρsen θdθ dunque 7. d s ds = 1 ρ ds = ρsenθ dθ sen θ = ρdθ dunque deivando ilvesoe s ispetto al suo mod ulo si ottiene d s ds = 1 ρ d s d θ ed essendo d s dθ = senθ d dθ, d cosθ = ( cosθ,sen θ)= 1 dθ ρ è cioè un vesoe dietto in senso opposto al vesoe dietto come. In conclusione abbiamo dim ostato che d s ds = 1 ρ 6
7 da cui deiva l'equazione (7). Il vesoe pependicolae alla taiettoia è dunque τ = ρ d s ds dove ρ è il aggio di cuvatua della taiettoia nel punto P. 3.ESEMPIO DI CALCOLO DELLA LEGGE ORARIA IN FORMA PARAMETRICA Consideiamo la legge oaia in foma catesiana del moto ettilineo ed unifome: x = kt y = ht Eliminando il paameto tempo t si ottiene y = h k x che è l'equazione di una etta con coefficiente angolae tg α = h k cioè h = A sen α k = A cosα 7
8 Y y s α P O x X fig.2b Figua 4 In questo caso assai semplice si icava dalla fig. 4 s 2 = x 2 + y 2 = ( h 2 + k 2 )t 2 = A 2 t 2 cioè la legge oaia in foma paametica s = At Si può peò applicae l' equazione (5) sostituendo in essa: ottenendo cioè dy dx = h k ds = 1 + h k 2 dx ed integando s = h 2 + k 2 k x +B essendo B una costante di integazione, da cui s = A k x +B s = At+ B 8
9 4.VARI TIPI DI MOTO Velocità istantanea v = d P = d P ds = ds s = v dt ds dt dt 0 s, [ LT 1 ] da cui si deduce che v è sempe tangente alla taiettoia ed inolte si è definita la Velocità oaia Velocità angolae Acceleazione Acceleazione tangenziale v 0 = ds dt, [ ] LT 1 a = d v dt a T = dv 0 dt Acceleazione centipeta (nomale) a c = v 0 2 Acceleazione angolae ω = dθ,t [ 1 ] dt ρ = d2 P dt 2, LT 2 [ ],[ LT 2 ] [ ],LT 2 dω = d 2 θ dt dt 2, [ ] T 2 Odogafo è la descizione del moto nello spazio ( v x,v y,v z ) delle velocità. Moto Rettilineo Unifome Moto Acceleato Unifome Moto su di un piano v = C os tante a = C os tan te v P = C os tan te 9
10 5.IL MOTO DI UN GRAVE Come applicazione della legge di Newton, che vedemo nel capitolo seguente, studiamo il moto di un gave, cioè di un copo che si muove con acceleazione costante g. Y v0 y' Figua 5 YV y O g α V = ( x,y) v 0 = v 0x,v 0y a = g = 0, g tg α = v 0y ( ) ( ) v 0x l'acceleazione diventa: d 2 x d 2 dt 2 = g dt 2 = 0 cioè d 2 y dt 2 = d Figua 5 dy = g dt dt x XV ( angolo di alzo ), x' XG X dx = v dt 0x d dy = gdt dt, x = v 0x t dy = gt+ v 0y dt, x = v 0x t y = 1 2 gt2 +v 0y t moto a velocità cos tante moto ad acceleazione costan te Eliminando il paameto t si ottiene l'equazione catesiana della taiettoia: g y = 2 x2 + v 0y x v 0x 2v 0x che appesenta una paabola ivolta veso il basso. Si calcola facilmente la gittata XG, come intecetta con l'asse x: XG = 2v 0x v 0y g Si può calcolae anche l'angolo di alzo coispondente alla massima gittata, infatti si ha: 0
11 XG = 2v 0x v 0y g = v 0x v 0y + v 0x v 0y g = v 2 ( senα cosα +cosαsen α) g = v 2 g sen 2α che è massima pe α=π/4. Si calcolano facilmente anche le coodinate del vetica V: x V = v 0x v 0y g y V = v 0 2 2g sen 2 α da cui si icava che la massima altezza si aggiunge pe un angolo di alzo α=π/2. Si può ancoa opeae una taslazione di coodinate nel vetice V: x = x x V y = y y V alloa l'equazione della taiettoia diventa g y = 2 x 2 2v 0x 6.IL MOTO CIRCOLARE Il moto cicolae è un moto piano in cui la taiettoia è una ciconfeenza di aggio R, ( P = R). y v P ( x, y ) y θ -R O x R x fig.3 1
12 Figue 6 L'equazione oaia nella appesentazione catesiana è 8. ( ) () x = R cosθ t y = R senθ t deivando ispetto al tempo si ottiene la velocità puntuale cioè v x = Rsen θ() t dθ dt v y = Rcosθ() t d θ dt 9. v x = Rω sen θ( t) v y = Rω cosθ() t Nel pimo quadante l'equazione della taiettoia in foma catesiana è y = R 2 x 2, l'equazione (5) diventa alloa 2x ds = R 2 x 2 = 1 + = = = x 2 R 2 x 2 dx R 2 R 2 x 2 dx 1 1 x dx 2 R 1 1 cos 2 θ () t dx dx = sen θ t () 2 dx il segno meno deiva dal fatto che in figua ad un incemento di s coisponde un decemento di x. Si calcola il modulo della velocità istantanea 2
13 v = ds 1 dx = = dt sen θ() t dt sen θ() t sostituendo vx dalla pima equazione (1.5) si ottiene 10. v = ωr Veifichiamo oa che il vettoe posizione P èsempe otogonale al vettoe velocità v. Calcoliamo a questo scopo il podotto scalae P v = xv x + yv y = ωr 2 cos θ sen θ + ωr 2 senθ cos θ = 0 Deivando la velocità (eq. 9) ispetto al tempo si ottiene l'acceleazione a x = R dω dθ senθ Rω cosθ dt dt 11. a y = R dω dθ cosθ Rωsenθ dt dt a x = R dω dt senθ + ω2 cosθ a y = R dω dt cosθ ω2 senθ Si calcola il modulo dell'acceleazione a = a x 2 + a y 2 = R Nota 1 : se il moto è unifome d ω dt = 0 dω dt, alloa α = Rω ω 4 cioèa = ωv Nota 2 : dall eq. (11) si può decompoe l'acceleazione secondo due componenti essendo a = a centipeta + a tan genziale v x 12. a centipeta x = ω 2 R cosθ centipeta a y = ω 2 Rsenθ 13. da cui si calcolano i moduli tan a genziale x = dω dt R senθ tangenziale a y = dω dt R cosθ 3
14 a centipeta = Rω 2 tan genziale a = R dω dt Dimostiamo che l'acceleazione centipeta così definita è sempe pependicolae alla velocità, cioè è sempe dietta veso il cento della ciconfeenza v a centipeta = Rω senθ ω 2 R cosθ Rω cosθ ω 2 R senθ = 0 Dimostiamo che l'acceleazione tangenziale così definita è sempe pependicolae alla posizione P, cioè è sempe tangente alla taiettoia P a = R cosθ R dω dω senθ + R senθ R dt dt cosθ = 0 dω Nota 3 : nel caso di un moto cicolae unifome = 0 dt sopavvive soltanto l'acceleazione centipeta. 7.IL MOTO ARMONICO Una applicazione del moto cicolae unifome e il moto amonico. Il moto amonico e un moto oscillante attono ad un cento lungo una deteminata diezione. Figue 7 Esso è appesentato dal moto del punto H lungo il diameto quando il punto P si muove lungo la ciconfeenza di aggio R con moto cicolae unifome θ = ω t + θ 0. L equazione del moto amonico e dunque: 4
15 x = R cos(ω t + θ 0 ). θ 0 e la costante di fase e appesenta l angolo a cui si tova il punto P al tempo t=0, R si chiama ampiezza delle oscillazioni amoniche e appesenta il massimo valoe di x; la velocità angolae ω del punto P è detta pulsazione o fequenza angolae. Si chiama peiodo la duata di un'oscillazione completa; esso si indica con T e si misua ad esempio in secondi. Si chiama fequenza il numeo di oscillazioni compiuti nell'unità di tempo; essa si indica genealmente con il simbolo ν e si misua in hetz (Hz = numeo di oscillazioni al secondo). ν = 1 / T = ω / 2π Il valoe istantaneo della posizione (x), viene chiamato elongazione. Calcoliamo il tempo T (peiodo) al quale il punto H itona nella stessa posizione dopo un gio completo del punto P. da cui, cos(ω (t+t) + θ 0 )=cos(ω t + θ 0 +2π) T = 2π / ω. 5
16 Figua 8 L impotanza dei moti oscillanti è evidente quando si considei la loo diffusione nei fenomeni natuali: il pendolo, il taspoto del caloe nei mezzi mateiali, il moto sotto l effetto di una molla, la popagazione delle onde elettomagnetiche ecc. Figua 9 Nel paagafo successivo vedemo che un moto cicolae si puo consideae anche come la composizione di due moti amonici. Calcoliamo l acceleazione nel moto amonico: x = ω R sen( ωt) x = ω 2 Rcos( ωt) x = ω 2 x L acceleazione è dunque popozionale all elongazione. L impotanza di tale elazione saà evidente quando si intoduà la seconda legge di Newton, che dice che la foza è popozionale all acceleazione. L ultima delle equazioni pecedenti è chiamata equazione amonica. 6
17 8.MOTI OSCILLATORI SMORZATI La fomula dei moti oscillatoi smozati è: x = R cos(ω t + θ 0 ) exp(-t/t 0 ) questi moti sono l equivalente del moto amonico quando peò il aggio R diminuisce nel tempo con legge ad esempio esponenziale. Tali moti si pesentano ad esempio nelle oscillazioni in un mezzo mateiale eale cioè viscoso. Nei mezzi mateiali si manifestano delle foze di attito che si oppongono al moto. Il pendolo eale si compota come un oscillatoe smozato pe via dell attito con l aia che ne iduce l ampiezza di oscillazione al passae del tempo. Figue 10 Calcoliamo l acceleazione nel moto oscillatoio smozato. x = Rcos ωt ( )e αt x = R( ω sen(ωt)+α cos( ωt) )e αt da cui si icava ω R sen( ωt)e αt = x +αx deivando ancoa si ottiene x = R 2αωsen( ωt)+ α 2 ω 2 { ( ) cos ( ωt ) } in conclusione : x = ω 2 +α 2 x 2α x ( ) Il pimo temine del secondo membo appesenta l oscillazione amonica con pulsazione ω = sqt(ω 2 +α 2 ), mente il secondo temine appesenta lo smozamento popozionale alla velocità. 7
18 9.COMPOSIZIONE DEI MOVIMENTI Il poblema della composizione dei movimenti è così schematizzabile : noti il moto di un punto P e di un ossevatoe O ispetto ad un ossevatoe O consideato fisso, deteminae la taiettoia del punto P ispetto all'ossevatoe mobile O ( vedasi fig.11). P z ' y ' z ' V R o ' O y x ' x fig.4 Figua 11 Sia = f ( t) l'equazione oaia del punto P ispetto ad O, sia inolte R = F ( t) l'equazione oaia dell'ossevatoe O ispetto ad O. Alloa pe la composizione galileiana (vettoiale) dei moti, l'equazione del moto di P ispetto ad O è ' = R = f ( t) F ( t) cioè poiettando sugli assi catesiani ( pe semplicità su di un piano) x' = f x ( t) F x ( t) y' = f y () t F y () t ed eliminando il paameto tempo t si ottiene y' = Y( x' ) che appesenta l'equazione della taiettoia di P ispetto all'ossevatoe O. 8
19 1 Esecizio Il punto P sia in quiete ispetto ad O x = R y = 0 y y' O' θ P -R O R x' x fig.5 Figua 12 L'ossevatoe O' si muova ispetto ad O di moto cicolae ed unifome con velocità angolae ω = costante, dunque F x = R cos( ω t) F y = Rsen( ω t) L'equazione del moto di P ispetto ad Ò è dunque x' = f x F x = R( 1 cos( ω t) ) y' = f y F y = Rsen( ω t) che appesnta la taiettoia di fig.13, cioè la ciconfeenza di patenza taslata lungo l'asse x di un tatto pai al aggio R. 9
20 y' O R 2R x' fig.6 Figue 13 L ossevatoe O dunque vede il punto P muovesi di moto cicolae con taiettoia che passa pe l oigine e con la stessa velocità angolae. 2 Esecizio Studiamo la composizione di due moti amonici con la stessa fequenza. Il punto P si muova di moto amonico lungo y ispetto ad O y P y' O O' x' x fig.7 Figue 14 0
21 f x = 0 f y = R y cos ω t + φ y ( ) con ampiezza R, pulsazione ω e costante di fase φy. L'ossevatoe O si muova ispetto ad O di moto amonico lungo l'asse x F x F y = 0 = R x cos( ω t + φ x ) con ampiezza Rx, la stessa pulsazione ω e costante di fase φx. L'equazione del moto di P ispetto ad O è dunque F x = R x cos( ω t + φ x ) x'= f x y' = f y F y = R y cos ω t + φ y ( ) Nota 1 : Se la diffeenza di fase è nulla φx = φy, alloa la taiettoia si iduce ad una etta di equazione y' = R y R x x' con coefficiente angolae pai al appoto ta le ampiezze di oscillazione di P e di Ò ispetto ad O. Nota 2 : Se la diffeenza di fase è π 2 cioè φ x = φy - π alloa la 2 taiettoia diventa x' = R x cos( ω t) y' = R x sen( ω t) (dove pe semplicità si è posto φx = 0 ) una ellisse con semiassi ispettivamente Rx e Ry. La taiettoia poi si iduce ad una ciconfeenza se i due moti amonici hanno la stessa ampiezza. Nota 3 : Nel caso più geneale in cui siano divese sia le costanti di fase che le ampiezze, si ottengono le classiche Figue di Lissajous mostate in fig.15. 1
22 X X X O X Y O X Y O X Y O X Y O X Y O X Y O Y O Y O Y fig.8 Figue 15 2
23 10.RELATIVITA GALILEIANA Galileo pe pimo scopese un fenomeno che è intinseco a tutti i movimenti e che pende il nome di RELATIVITÀ dei moti. Galileo scopese che alcune caatteistiche del moto dipendono stettamente dall ossevatoe. In pimo luogo la taiettoia di un punto mobile cambia a secanda dell ossevatoe. Galileo, nel Dialogo sopa i due massimi sistemi del mondo, discute il famosissimo espeimento della nave: Rinseatevi con qualche amico nella maggio stanza che sia sotto coveta di alcun gan navilio, e quivi fate d'ave mosche, fafalle e simili animaletti volanti; siavi anche un gan vaso d'acqua e dentovi de' pescetti; sospendasi anche in alto qualche secchiello, che a goccia a goccia vada vesando dell'acqua in un alto vaso di angusta bocca, che sia posto a basso: e stando fema la nave, ossevate diligentemente come quelli animaletti volanti con pai velocità vanno veso tutte le pati della stanza: i pesci si vedanno anda notando indiffeentemente pe tutti i vesi; le stille cadenti enteanno tutte nel vaso sottoposto. [...] Ossevate che avete diligentemente tutte queste cose, peché niun dubbio ci sia che mente il vascello sta femo non debban succede così, fate muovee la nave con quanta si voglia velocità; che (pu che il moto sia unifome e non fluttuante in qua e in là) voi non iconosceete una minima mutazione in tutti li nominati effetti, né da alcuno di quelli potete compendee se la nave cammina o pue sta fema [...] le gocciole cadanno come pima nel vaso infeioe, senza cadene pu una veso poppa, benché mente la gocciola è pe aia, la nave scoa molti palmi; i pesci nella lo acqua non con più fatica noteanno veso la pecedente che veso la susseguente pate del vaso [...] e finalmente le fafalle e le mosche continueanno i loo voli indiffeentemente veso tutte le pati... Qui è messo in evidenza il fatto che un ossevatoe sulla nave in moto vede i movimenti degli oggetti in modo diveso da un ossevatoe sulla tea (vedasi figua). 3
24 Siano O ed O' due ossevatoi con gli stessi oologi e sia P il punto mateiale di cui essi studiano il moto. Sia V la velocità con cui l'ossevatoe O' si muove ispetto ad O, alloa V = d R dt Poichè vale la elazione di somma dei vettoi (ifeendosi alla fig. 11) 1. R + ' = 0 si ottiene la elazione notevole, deivando membo a membo ispetto al tempo: d ' = d dt dt d R dt cioè 2. v ' = v V dove v = velocità del punto P misuata dall'ossevatoe O v ' = velocità del punto P misuata dall'ossevatoe O'. Nel caso in cui il sistema di ifeimento O' si muova di moto ettilineo ed unifome V = costante, alloa l'equazione (1) diventa : 3. ' = t V L'equazione (2) è la legge di composizione delle velocità di Galileo, mente l'equazione (3) è la legge di tasfomazione di Galileo. Deivando ispetto al tempo l'equazione (2) si ottiene la legge di composizione delle acceleazioni : 4. a ' = a A dove A = d V è l'acceleazione con cui O' si muove ispetto ad O e dt si chiama acceleazione appaente. 11.ACCELERAZIONE APPARENTE DI CORIOLIS Consideiamo due ossevatoi: O (x,y,z) femo ed O (x,y,z ) che uota ispetto ad O attono all asse z =z con velocita angolae costante ω. Sia P un punto che si muova con velocita adiale costante ispetto ad O. Vogliamo dimostae che ispetto all ossevatoe uotante O il punto P si muove di moto acceleato. Tale acceleazione, che e appaente pechè indotta soltanto dal moto dell ossevatoe O, si chiama acceleazione di Coiolis ed è 4
25 popozionale alla velocità con cui P si muove ispetto ad O ed alla velocità angolae con cui O si muove sempe ispetto ad O. Questa acceleazione appaente si veifica ad esempio sulla Tea che e in moto otatoio attono al suo asse polae. Risulta dunque che il punto P, che si muove di moto ettilineo unifome ispetto all ossevatoe O, si muove di moto acceleato ispetto ad O, con acceleazione popozionale alla sua velocità ed alla velocità angolae con cui O uota. Il doppio di a O si chiama acceleazione di Coiolis. Si dimosta facilmente che l acceleazione di Coiolis è pependicolae al vettoe velocità v misuato da O, olte che al vettoe velocità angolae. Infatti: v '= R(θ) v = v x cosθ + v y senθ v x senθ + v y cosθ ed e' facile dimostae che : a o' v '= 0 Possiamo dunque concludee che: a o. = ω v ' 12.LE TRE LEGGI DI KEPLERO Le te leggi speimentali che egolano il moto planetaio sono state enunciate all inizio del XVII secolo dall astonomo tedesco Giovanni Kepleo. Le leggi fuono fomulate su base empiica a patie dai dati accolti dall astonomo danese Tycho Bahe, e solo con la teoia della gavitazione univesale di Isaac Newton tovaono una soddisfacente spiegazione teoica. Negando l antichissimo pincipio secondo cui i pianeti si muovevano attono al Sole su obite cicolai. La pima legge di Kepleo affema che essi obitano attono al Sole pecoendo taiettoie ellittiche delle quali il Sole occupa uno dei fuochi. La seconda legge stabilisce che la etta (il aggio vettoe) che congiunge un pianeta al Sole descive aee uguali in tempi uguali; ciò significa che ogni pianeta pecoe più apidamente i tatti di obita più vicini al Sole. 5
26 Infine, la teza legge affema che il appoto ta il cubo della distanza media, d, di un pianeta dal Sole e il quadato del suo peiodo di ivoluzione è costante; cioè il appoto d 3 /t 2 è lo stesso pe tutti i pianeti. Assumiamo in pima appossimazione che la taiettoia di un pianeta sia cicolae col sole nel cento e aggio R. Veifichiamo la seconda e la teza legge dalle popietà del moto cicolae. Seconda Legge. Poiche l aea descitta dal aggio vettoe dopo un angolo θ e : A = πr 2 θ 2π = 1 2 R2 θ e poiché il moto e cicolae unifome: θ = ω t con velocità angolae ω costante, alloa: A = ωr2 2 t, quindi il aggio vettoe del pianeta pecoe aee uguali in tempi uguali. Teza Legge. Poichè nell appossimazione del moto cicolae l unica acceleazione che agisce sul pianeta è quella centipeta a c : a c = R w 2, Pe la legge di Newton il l acceleazione e popozionale alla foza (in questo caso la foza di gavità) e dunque è invesamente popozionale al quadato del aggio: a c 1 R 2 si icava dunque: 6
27 Rω 2 1 R 2, R 3 1 ω 2 T 2 essendo ω invesamente popozionale al peiodo. E impotante notae che in ealtà Newton icavò la sua legge popio patendo dalle leggi di Kepleo, ipotizzando l esistenza di una foza gavitazionale che doveva essee invesamente popozionale al quadato della distanza. 13.IL DIFFERENZIALE DI UNA FUNZIONE DI UNA SOLA VARIABILE Figue 16 Consideiamo una funzione y = f(x) appesentata nel piano (x,y). Si ottiene: Δf = tgα Δx dunque passando al limite pe Δx 0 si ottiene: Δf df Δx dx tgα f ' essendo f la deivata della funzione f nel punto x. Dunque: df = f ' dx 7
28 df pende il nome di diffeenziale della funzione f nel punto x e appesenta di quanto vaia f al vaiae di una quantità infinitesima della vaiabile x. 14.DERIVATE IMPORTANTI E REGOLE DI DERIVAZIONE fomula notevole del diffeenziale: d(f g) = f dg + g df f (x) > 0 f (x) < 0 funzione cescente funzione decescente Fomula di integazione pe pati. Dalla fomula di deivazione del podotto di due funzioni f e g si ottiene (fg)'=f'g+fg' da cui 8
29 15.DERIVATE PARZIALI Consideiamo una funzione di due vaiabili f(x,y) Se fissiamo il valoe di una delle due vaiabili, ad esempio x=x o, la funzione viene a dipendee dalla sola vaiabile y e dunque ha senso calcolane la deivata odinaia ispetto a y: ( ) f x, y y x=xo df ( x 0, y ) dy il pimo membo si chiama deivata paziale di f ispetto a y nel punto x 0. 9
30 Figue 17 Si può alloa definie il diffeenziale di una funzione di due vaiabili nel modo seguente: e più in geneale: df = f f dx + x y dy f df ( x 1, x 2,..., x n )=Σ i=1,n dx i x i 16.GLI INTEGRALI PRINCIPALI adx= a x af() x dx = a f() x dx u + v dx = udx+ vdx ( ) 1 dx = ln x x x n dx = xn+1 n +1, n 1 0
31 e x dx = e x e ax dx = 1 a eax b ax dx = 1 a lnb bax,b > 0 sen( ax)dx cos( ax)dx tan( ax)dx = 1 cos( ax) a = 1 a xe ax dx = sen( ax) = ln[ cos( ax) ] ax 1 a 2 e ax xe x2 dx = 1 2 e x2 17.LE EQUAZIONI DIFFERENZIALI ALLE DERIVATE ORDINARIE Un equazione diffeenziale odinaia è sempe appesentabile nella foma: F(x,y,y,,y (n) ) = 0, dove y(x) è una funzione incognita della vaiabile indipendente x ed y (i) e la deivata odinaia di odine i-esimo. Un teoema fondamentale affema che esiste una funzione y(c 1,,c n ;x) che dipende da n costanti abitaie c i (i=1,,n) detta integale-geneale, che veifica identicamente l uguaglianza pecedente. Se si assume una n-pla di valoi ben definiti pe c i, alloa l integale geneale si chiama più popiamente integale paticolae dell equazione diffeenziale. Un modo pe deteminae le n costanti abitaie, cioè pe passae dall integale geneale all integale paticolae, consiste nel definie n equazioni di vincolo, cioè n condizioni iniziali: 1
32 y' ( x 0 )= y 1.. y (n) ( x 0 )= y n dove x 0 è detto valoe iniziale della vaiabile indipendente ed y i sono n paameti noti. Le condizioni iniziali pemettono di deteminae i valoi delle costanti abitaie. 18.LE EQUAZIONI DIFFERENZIALI LINEARI Le equazioni lineai del tipo: a n (x)y (n) (x)+a n-1 (x) y (n-1) (x)+... +a 1 (x)y (x)+a 0 (x)y(x) = Q(x) sono dette equazioni diffeenziali lineai. Dove a i (x) e Q(x) sono funzioni note. Se tutte le funzioni a i sono costanti, alloa si ottiene la seguente equazione diffeenziale lineae a coefficienti costanti: a n y (n) (x)+a n-1 y (n-1) (x)+... +a 1 y (x)+a 0 y(x) = Q(x) Esiste un teoema che affema che l integale geneale di tale equazione si può ottenee isolvendo l equazione algebica caatteistica, che si ottiene sostituendo alle deivate le potenze di una vaiabile complessa z con la convenzione che la funzione y sia la deivata di odine zeo della funzione stessa: a n z n +a n-1 z n a 1 z+a 0 = 0. L equazione caatteistica ammette sempe n soluzioni (zei) nel campo complesso z i (i=1,,n), pe il teoema fondamentale dell algeba. Alloa l integale geneale dell equazione diffeenziale lineae omogenea (Q=0) è: y O (c 1,,c n ;x) = c 1 exp(z 1 x) + c 2 exp(z 2 x) c n exp(z n x). Essendo c i (i=1,,n) le n costanti abitaie. 2
33 L integale geneale dell equazione non omogenea (Q(x) 0) è alloa y G (x) = y(c 1,,c n ;x) + f 0 (x), essendo f 0 (x) un qualsiasi integale paticolae dell equazione lineae a coefficienti costanti non omogenea. Esempio: Consideiamo l equazione diffeenziale lineae a coefficienti costanti omogenea: y +y = 0 L equazione caatteistica e : z 2 +1 = 0 e gli zei sono: z 1,2 = ± i dunque l integale geneale e : y = c 1 e ix + c 2 e -ix E facile veificae che l equazione di patenza ammette anche i seguenti integali paticolai: y = cos x y = sen x Ricodando che dalla fomula di Euleo si ha la seguente appesentazione complessa delle funzioni seno e coseno: cos x = eix + e ix Si ottiene che il coseno è l integale paticolae che coisponde alle seguenti costanti c 1 =c 2 =1/2 ed il seno coisponde invece alle seguenti costanti c 1 = i/2 ; c 2 = - i/2 2 senx = eix e ix 2i 3
34 19.EQUAZIONI DIFFERENZIALI SEPARABILI Le equazioni diffeenziali del tipo: dy/dx = h(x)g(y) si chiamano sepaabili (pechè si possono potae al pimo membo tutti i temini che dipendono solamente dalla vaiabile dipendente y ed al secondo membo tutti i temini che dipendono soltanto dalla vaiabile indipendente x) e sono facilmente integabili pechè diventano: g(y) = 0, che fonisce la soluzione costante e (1/g(y)) dy = h(x) dx in cui i due membi possono essee integati sepaatamente. Esempio: y - xy = 0 La soluzione y=0 e la soluzione costante e sepaando le vaiabili si ha: 1 y dy = xdx ln y = 1 2 x2 + ln y 0 1 y = y 0 e2 x2 20.APPLICAZIONI DELLE EQUAZIONI DIFFERENZIALI 1. Il decadimento degli atomi adioattivi. a. I nuclei degli atomi dei mateiali adioattivi decadono, cioe si tasfomano in alti nuclei, ad una fequenza che e popozionale al numeo totale di atomi di tale sostanza, cioe (essendo k una costante di decadimento positiva): dn(t)/dt = -k N(t) b. Tale equazione diffeenziale si può integae mediante la sepaazione delle vaiabili, 4
35 c. dn/n = -k dt d. dunque: ln N = -kt +lnn 0 essendo N 0 il numeo costante di atomi pesenti al tempo t=0. e. In definitiva: N=N 0 exp(-kt) 5
Il Problema di Keplero
 Il Poblema di Kepleo Il poblema di Kepleo nel campo gavitazionale Intoduzione Con Poblema di Kepleo viene indicato il poblema del moto di un copo in un campo di foze centali. Nel caso specifico gavitazionale
Il Poblema di Kepleo Il poblema di Kepleo nel campo gavitazionale Intoduzione Con Poblema di Kepleo viene indicato il poblema del moto di un copo in un campo di foze centali. Nel caso specifico gavitazionale
Gravitazione. Dati due corpi di massa m 1 e m 2, posti ad una distanza r, tra di essi si esercita una forza attrattiva data in modulo da
 Gavitazione Dati due copi di massa m 1 e m 2, posti ad una distanza, ta di essi si esecita una foza attattiva data in modulo da F = G m 1m 2 dove G è una costante univesale, avente lo stesso valoe pe tutte
Gavitazione Dati due copi di massa m 1 e m 2, posti ad una distanza, ta di essi si esecita una foza attattiva data in modulo da F = G m 1m 2 dove G è una costante univesale, avente lo stesso valoe pe tutte
Gravitazione universale
 INGEGNERIA GESTIONALE coso di Fisica Geneale Pof. E. Puddu LEZIONE DEL 22 OTTOBRE 2008 Gavitazione univesale 1 Legge della gavitazione univesale di Newton Ogni paticella attae ogni alta paticella con una
INGEGNERIA GESTIONALE coso di Fisica Geneale Pof. E. Puddu LEZIONE DEL 22 OTTOBRE 2008 Gavitazione univesale 1 Legge della gavitazione univesale di Newton Ogni paticella attae ogni alta paticella con una
Cinematica III. 11) Cinematica Rotazionale
 Cinematica III 11) Cinematica Rotazionale Abbiamo già tattato il moto cicolae unifome come moto piano (pa. 8) intoducendo la velocità lineae v e l acceleazione lineae a, ma se siamo inteessati solo al
Cinematica III 11) Cinematica Rotazionale Abbiamo già tattato il moto cicolae unifome come moto piano (pa. 8) intoducendo la velocità lineae v e l acceleazione lineae a, ma se siamo inteessati solo al
Fisica Generale II con Laboratorio. Lezione - 3
 Fisica Geneale II con Laboatoio Lezione - 3 Richiami - I Riassunto leggi della meccanica: Leggi di Newton 1) Pincipio di inezia Esistono sistemi di ifeimento ineziali (nei quali un copo non soggetto a
Fisica Geneale II con Laboatoio Lezione - 3 Richiami - I Riassunto leggi della meccanica: Leggi di Newton 1) Pincipio di inezia Esistono sistemi di ifeimento ineziali (nei quali un copo non soggetto a
Per migliorare la trasmissione tra satellite e Terra, emerge la necessità di portare il satellite ad un orbita circolare diversa.
 1 Esecizio (tatto dagli esempi 5.3 e 5.4 del cap. V del Mazzoldi-Nigo-Voci) Un satellite atificiale di massa m 10 3 Kg uota attono alla Tea descivendo un obita cicolae di aggio 1 6.6 10 3 Km. 1. Calcolae
1 Esecizio (tatto dagli esempi 5.3 e 5.4 del cap. V del Mazzoldi-Nigo-Voci) Un satellite atificiale di massa m 10 3 Kg uota attono alla Tea descivendo un obita cicolae di aggio 1 6.6 10 3 Km. 1. Calcolae
CASO 2 CASO 1. δ Lo. e N. δ Lo. e L. PROBLEMA A Corso di Fisica 1- Prima provetta- 22 maggio 2004 Facoltà di Ingegneria dell Università di Trento
 PROBEMA A Coso di Fisica 1- Pima povetta- maggio 004 Facoltà di Ingegneia dell Univesità di Tento Un anello di massa m= 70 g, assimilabile ad un copo puntifome, è infilato in una asta igida liscia di lunghezza
PROBEMA A Coso di Fisica 1- Pima povetta- maggio 004 Facoltà di Ingegneia dell Univesità di Tento Un anello di massa m= 70 g, assimilabile ad un copo puntifome, è infilato in una asta igida liscia di lunghezza
LIBRO DI TESTO S.Melone, F.Rustichelli Introduzione alla Fisica Biomedica Libreria Scientifica Ragni Ancona, 1998
 LIBRO DI TESTO S.Melone, F.Rustichelli Intoduzione alla Fisica Biomedica Libeia Scientifica Ragni Ancona, 1998 TESTO DI CONSULTAZIONE E WEB F.Bosa, D.Scannicchio Fisica con Applicazioni in Biologia e Medicina
LIBRO DI TESTO S.Melone, F.Rustichelli Intoduzione alla Fisica Biomedica Libeia Scientifica Ragni Ancona, 1998 TESTO DI CONSULTAZIONE E WEB F.Bosa, D.Scannicchio Fisica con Applicazioni in Biologia e Medicina
4. DINAMICA. I tre principi della dinamica per un corpo puntiforme (detto anche punto materiale o particella) sono:
 4.1 Pincipi della dinamica 4. DINAMICA I te pincipi della dinamica pe un copo puntifome (detto anche punto mateiale o paticella) sono: 1) pincipio di intezia di Galilei; 2) legge dinamica di Newton; 3)
4.1 Pincipi della dinamica 4. DINAMICA I te pincipi della dinamica pe un copo puntifome (detto anche punto mateiale o paticella) sono: 1) pincipio di intezia di Galilei; 2) legge dinamica di Newton; 3)
Moto su traiettorie curve: il moto circolare
 Moto su taiettoie cuve: il moto cicolae Così come il moto ettilineo è un moto che avviene lungo una linea etta, il moto cicolae è un moto la cui taiettoia è cicolae, cioè un moto che avviene lungo una
Moto su taiettoie cuve: il moto cicolae Così come il moto ettilineo è un moto che avviene lungo una linea etta, il moto cicolae è un moto la cui taiettoia è cicolae, cioè un moto che avviene lungo una
dove per i simboli si sono adottate le seguenti notazioni: 2 Corpo girevole attorno ad un asse fisso
 Il volano 1 Dinamica del copo igido Il poblema dello studio del moto di un copo igido libeo è il seguente: data una ceta sollecitazione F e del copo, cioè cete foze estene F i applicate nei punti del copo
Il volano 1 Dinamica del copo igido Il poblema dello studio del moto di un copo igido libeo è il seguente: data una ceta sollecitazione F e del copo, cioè cete foze estene F i applicate nei punti del copo
Massimi e minimi con le linee di livello
 Massimi e minimi con le linee di livello Pe affontae questo agomento è necessaio sape appesentae i fasci di cuve ed in paticolae: Fasci di paabole. Pe affontae questo agomento si consiglia di ivedee l
Massimi e minimi con le linee di livello Pe affontae questo agomento è necessaio sape appesentae i fasci di cuve ed in paticolae: Fasci di paabole. Pe affontae questo agomento si consiglia di ivedee l
v t V o cos t Re r v t
 Metodo Simbolico, o metodo dei Fasoi Questo metodo applicato a eti lineai pemanenti consente di deteminae la soluzione in egime sinusoidale solamente pe quanto attiene il egime stazionaio. idea di appesentae
Metodo Simbolico, o metodo dei Fasoi Questo metodo applicato a eti lineai pemanenti consente di deteminae la soluzione in egime sinusoidale solamente pe quanto attiene il egime stazionaio. idea di appesentae
Esercizi Scheda N Fisica II. Esercizi con soluzione
 Esecizio 9.1 Esecizi con soluzione Te divese onde sonoe hanno fequenza ν ispettivamente 1 Hz, 1 Hz e 5 Mhz. Deteminae le lunghezze d onda coispondenti ed i peiodi di oscillazione, sapendo che la velocità
Esecizio 9.1 Esecizi con soluzione Te divese onde sonoe hanno fequenza ν ispettivamente 1 Hz, 1 Hz e 5 Mhz. Deteminae le lunghezze d onda coispondenti ed i peiodi di oscillazione, sapendo che la velocità
Facoltà di Ingegneria Fisica II Compito A
 Facoltà di ngegneia Fisica 66 Compito A Esecizio n Un filo di mateiale isolante, con densità di caica lineae costante, viene piegato fino ad assumee la foma mostata in figua (la pate cicolae ha aggio e
Facoltà di ngegneia Fisica 66 Compito A Esecizio n Un filo di mateiale isolante, con densità di caica lineae costante, viene piegato fino ad assumee la foma mostata in figua (la pate cicolae ha aggio e
F 1 F 2 F 3 F 4 F 5 F 6. Cosa è necessario per avere una rotazione?
 Cosa è necessaio pe avee una otazione? Supponiamo di vole uotae il sistema in figua intono al bullone, ovveo intono all asse veticale passante pe, usando foze nel piano oizzontale aventi tutte lo stesso
Cosa è necessaio pe avee una otazione? Supponiamo di vole uotae il sistema in figua intono al bullone, ovveo intono all asse veticale passante pe, usando foze nel piano oizzontale aventi tutte lo stesso
9 GRAVITAZIONE UNIVERSALE
 9 GRAVIAZIONE UNIVERSAE e conoscenze elative alla foza di gavitazione si sono sviluppate a patie dalle ossevazioni astonomiche del moto dei pianeti del sistema solae Attaveso tali ossevazioni yco Bahe
9 GRAVIAZIONE UNIVERSAE e conoscenze elative alla foza di gavitazione si sono sviluppate a patie dalle ossevazioni astonomiche del moto dei pianeti del sistema solae Attaveso tali ossevazioni yco Bahe
GONIOMETRIA. MISURA DEGLI ANGOLI La misura di un angolo si può esprimere in diversi modi, a seconda dell unità di misura che si sceglie.
 of. Luigi Cai Anno scolastico 4-5 GONIOMETRIA MISURA DEGLI ANGOLI La misua di un angolo si può espimee in divesi modi, a seconda dell unità di misua che si sceglie. Sistema sessagesimale Si assume come
of. Luigi Cai Anno scolastico 4-5 GONIOMETRIA MISURA DEGLI ANGOLI La misua di un angolo si può espimee in divesi modi, a seconda dell unità di misua che si sceglie. Sistema sessagesimale Si assume come
AI VERTICI DI UN QUADRATO DI LATO 2L SONO POSTE 4 CARICHE UGUALI Q. DETERMINARE: A) IL CAMPO ELETTRICO IN UN PUNTO P DELL ASSE.
 ESERCIZIO 1 AI VERTICI DI UN UADRATO DI LATO SONO POSTE 4 CARICHE UGUALI. DETERMINARE: A) IL CAMPO ELETTRICO IN UN PUNTO P DELL ASSE. 4 caiche uguali sono poste ai vetiti di un quadato. L asse di un quadato
ESERCIZIO 1 AI VERTICI DI UN UADRATO DI LATO SONO POSTE 4 CARICHE UGUALI. DETERMINARE: A) IL CAMPO ELETTRICO IN UN PUNTO P DELL ASSE. 4 caiche uguali sono poste ai vetiti di un quadato. L asse di un quadato
int Schiusa Schiusa r r Φ = r r S o 1 Anno scolastico
 Anno scolastico 4 + ε ε int dt E d C dt d E C Q E S o S Schiusa Schiusa gandezza definizione fomula Foza di Loentz Foza agente su una caica q in moto con velocità v in una egione in cui è pesente un campo
Anno scolastico 4 + ε ε int dt E d C dt d E C Q E S o S Schiusa Schiusa gandezza definizione fomula Foza di Loentz Foza agente su una caica q in moto con velocità v in una egione in cui è pesente un campo
TEORIA DELLA GRAVITAZIONE
 LEGGI DI KEPLEO EOI DELL GVIZIONE Dopo la ivoluzionaia teoia eliocentica del monaco polacco Copenico, Giovanni Kepleo fomulò te leggi a coeggee e miglioae ulteiomente il modello copenicano. Egli è infatti
LEGGI DI KEPLEO EOI DELL GVIZIONE Dopo la ivoluzionaia teoia eliocentica del monaco polacco Copenico, Giovanni Kepleo fomulò te leggi a coeggee e miglioae ulteiomente il modello copenicano. Egli è infatti
( ) Energia potenziale U = GMm r. GMm r. GMm L AB. = r. r r. Definizione di energia potenziale
 Enegia potenziale Definizione di enegia potenziale Il lavoo, compiuto da una foza consevativa nello spostae il punto di applicazione da a, non dipende dal cammino seguito, ma esclusivamente dai punti e.
Enegia potenziale Definizione di enegia potenziale Il lavoo, compiuto da una foza consevativa nello spostae il punto di applicazione da a, non dipende dal cammino seguito, ma esclusivamente dai punti e.
Biomeccanica. Cinematica Dinamica Statica dei corpi rigidi Energia e principi di conservazione
 Biomeccanica Cinematica Dinamica Statica dei copi igidi Enegia e pincipi di consevazione Posizione: definita da : z modulo, diezione, veso vettoe s s z s s y unità di misua (S.I.) : meto x s x y Taiettoia:
Biomeccanica Cinematica Dinamica Statica dei copi igidi Enegia e pincipi di consevazione Posizione: definita da : z modulo, diezione, veso vettoe s s z s s y unità di misua (S.I.) : meto x s x y Taiettoia:
Meccanica Gravitazione
 Meccanica 016-017 Gavitazione 3 oza Mediatoe Gavitazione Intensità elativa Andaento asintotico Raggio d'azione Inteazione fote gluone 10 38 0 10-15 Inteazione elettoagnetica Inteazione debole fotone 10
Meccanica 016-017 Gavitazione 3 oza Mediatoe Gavitazione Intensità elativa Andaento asintotico Raggio d'azione Inteazione fote gluone 10 38 0 10-15 Inteazione elettoagnetica Inteazione debole fotone 10
Nome..Cognome. classe 5D 29 Novembre VERIFICA di FISICA: Elettrostatica Domande
 Nome..ognome. classe 5 9 Novembe 8 RIFI di FISI: lettostatica omande ) ai la definizione di flusso di un campo vettoiale attaveso una supeficie. nuncia il teoema di Gauss pe il campo elettico (senza dimostalo)
Nome..ognome. classe 5 9 Novembe 8 RIFI di FISI: lettostatica omande ) ai la definizione di flusso di un campo vettoiale attaveso una supeficie. nuncia il teoema di Gauss pe il campo elettico (senza dimostalo)
GEOMETRIA ELEMENTARE. h = 2 2 S. h =
 QUESITI 1 GEOMETRI ELEMENTRE 1. (Da Veteinaia 015) Le diagonali (ossia le linee che uniscono i vetici opposti) di un ombo misuano ispettivamente 4 cm e 8 cm. Qual è il peimeto del ombo in cm? a) 8 3 b)
QUESITI 1 GEOMETRI ELEMENTRE 1. (Da Veteinaia 015) Le diagonali (ossia le linee che uniscono i vetici opposti) di un ombo misuano ispettivamente 4 cm e 8 cm. Qual è il peimeto del ombo in cm? a) 8 3 b)
Fisica per Medicina. Lezione 22 - Campo magnetico. Dr. Cristiano Fontana
 Fisica pe Medicina Lezione 22 - Campo magnetico D. Cistiano Fontana Dipatimento di Fisica ed Astonomia Galileo Galilei Univesità degli Studi di Padova 1 dicembe 2017 ndice Elettomagnetismo Campo magnetico
Fisica pe Medicina Lezione 22 - Campo magnetico D. Cistiano Fontana Dipatimento di Fisica ed Astonomia Galileo Galilei Univesità degli Studi di Padova 1 dicembe 2017 ndice Elettomagnetismo Campo magnetico
Momenti. Momento di inerzia, momento di una forza, momento angolare
 Momenti Momento di inezia, momento di una foza, momento angolae Conce&o di Momento I momenti in fisica sono cose molto divese fa loo. Cetamente non hanno sempe la stessa unità di misua; ed avemo cua di
Momenti Momento di inezia, momento di una foza, momento angolae Conce&o di Momento I momenti in fisica sono cose molto divese fa loo. Cetamente non hanno sempe la stessa unità di misua; ed avemo cua di
Momenti. Momento di inerzia, momento di una forza, momento angolare
 Momenti Momento di inezia, momento di una foza, momento angolae Conce&o di Momento I momenti in fisica sono cose molto divese fa loo. Cetamente non hanno sempe la stessa unità di misua; ed avemo cua di
Momenti Momento di inezia, momento di una foza, momento angolae Conce&o di Momento I momenti in fisica sono cose molto divese fa loo. Cetamente non hanno sempe la stessa unità di misua; ed avemo cua di
Appunti su argomenti monografici per il corso di FM1 Prof. Pierluigi Contucci. Gravità e Teorema di Gauss
 1 Appunti su agomenti monogafici pe il coso di FM1 Pof. Pieluigi Contucci Gavità e Teoema di Gauss Vogliamo dimostae, a patie dalla legge di gavitazione univesale che il campo gavitazionale geneato da
1 Appunti su agomenti monogafici pe il coso di FM1 Pof. Pieluigi Contucci Gavità e Teoema di Gauss Vogliamo dimostae, a patie dalla legge di gavitazione univesale che il campo gavitazionale geneato da
Unità Didattica N 10 : I momenti delle forze
 Unità didattica N 10 I momenti delle foze 1 Unità Didattica N 10 : I momenti delle foze 01) omento di una foza ispetto ad un punto 02) omento isultante di un sistema di foze 03) omento di una coppia di
Unità didattica N 10 I momenti delle foze 1 Unità Didattica N 10 : I momenti delle foze 01) omento di una foza ispetto ad un punto 02) omento isultante di un sistema di foze 03) omento di una coppia di
Campi scalari e vettoriali (1)
 ampi scalai e vettoiali (1) 3 e ad ogni punto P = (x, y, z) di una egione di spazio Ω R è associato uno ed uno solo scalae φ diemo che un campo scalae è stato definito in Ω. In alti temini: φ 3 : P R φ(p)
ampi scalai e vettoiali (1) 3 e ad ogni punto P = (x, y, z) di una egione di spazio Ω R è associato uno ed uno solo scalae φ diemo che un campo scalae è stato definito in Ω. In alti temini: φ 3 : P R φ(p)
IL POTENZIALE. = d quindi: LAB
 1 IL POTENZIALE Sappiamo che il campo gavitazionale è un campo consevativo cioè nello spostamento di un copo ta due punti del campo gavitazionale teeste, le foze del campo compiono un lavoo che dipende
1 IL POTENZIALE Sappiamo che il campo gavitazionale è un campo consevativo cioè nello spostamento di un copo ta due punti del campo gavitazionale teeste, le foze del campo compiono un lavoo che dipende
Geometria analitica in sintesi
 punti distanza ta due punti coodinate del punto medio coodinate del baicento ta due punti di un tiangolo di vetici etta e foma implicita foma esplicita foma segmentaia equazione della etta m è il coefficiente
punti distanza ta due punti coodinate del punto medio coodinate del baicento ta due punti di un tiangolo di vetici etta e foma implicita foma esplicita foma segmentaia equazione della etta m è il coefficiente
7. LA DINAMICA Primo principio della dinamica Secondo principio della dinamica.
 7. LA DINAMICA Ta la foza applicata ad un copo e il moto che essa povoca esistono dei appoti molto stetti che sono studiati da una banca della fisica: la dinamica. Lo studio della dinamica si è ilevato
7. LA DINAMICA Ta la foza applicata ad un copo e il moto che essa povoca esistono dei appoti molto stetti che sono studiati da una banca della fisica: la dinamica. Lo studio della dinamica si è ilevato
Fisica Generale A. 9. Forze Inerziali. Cambiamento di Sistema di Riferimento. SdR in Moto Traslatorio Rettilineo Uniforme (II)
 isica Geneale A 9. oze Ineziali http://campus.cib.unibo.it/2429/ ctobe 21, 2010 ambiamento di istema di ifeimento ome cambia la descizione del moto passando da un d a un alto? In paticolae, come cambia
isica Geneale A 9. oze Ineziali http://campus.cib.unibo.it/2429/ ctobe 21, 2010 ambiamento di istema di ifeimento ome cambia la descizione del moto passando da un d a un alto? In paticolae, come cambia
LEZIONE 10. d(a, B) = AB = AB = (x A x B ) 2 + (y A y B ) 2 + (z A z B ) 2.
 LEZIONE 10 10.1. Distanze. Definizione 10.1.1. In S n sia fissata un unità di misua u. Se A, B S n, definiamo distanza fa A e B, e sciviamo d(a, B), la lunghezza del segmento AB ispetto ad u. Abbiamo già
LEZIONE 10 10.1. Distanze. Definizione 10.1.1. In S n sia fissata un unità di misua u. Se A, B S n, definiamo distanza fa A e B, e sciviamo d(a, B), la lunghezza del segmento AB ispetto ad u. Abbiamo già
La struttura stellare
 La stuttua stellae La stuttua stellae Una stella è una sfea di gas tenuta insieme dall auto gavità ed il cui collasso è impedito dalla pesenza di gadienti di pessione. Con ottima appossimazione una stella
La stuttua stellae La stuttua stellae Una stella è una sfea di gas tenuta insieme dall auto gavità ed il cui collasso è impedito dalla pesenza di gadienti di pessione. Con ottima appossimazione una stella
Vista dall alto. Vista laterale. a n. Centro della traiettoria
 I poblema Un ciclista pedala su una pista cicolae di aggio 5 m alla velocità costante di 3.4 km/h. La massa complessiva del ciclista e della bicicletta è 85.0 kg. Tascuando la esistenza dell aia calcolae
I poblema Un ciclista pedala su una pista cicolae di aggio 5 m alla velocità costante di 3.4 km/h. La massa complessiva del ciclista e della bicicletta è 85.0 kg. Tascuando la esistenza dell aia calcolae
MACCHINA ELEMENTARE A RILUTTANZA
 Sistemi magnetici con moto meccanico MACCHINA ELEMENTARE A RILUTTANZA Consiste in un nucleo magnetico con un avvolgimento a N spie e una pate mobile che uota con spostamento angolae θ e velocità angolae
Sistemi magnetici con moto meccanico MACCHINA ELEMENTARE A RILUTTANZA Consiste in un nucleo magnetico con un avvolgimento a N spie e una pate mobile che uota con spostamento angolae θ e velocità angolae
FISICA MATEMATICA 1 A.A. 2014/15 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 5
 8360 - FISICA MATEMATICA 1 A.A. 014/15 Poblemi dal libo di testo: D. Giancoli, Fisica, a ed., CEA Capitolo 5 Poblema 1 Un bimbo su una giosta si muove con una velocità di 1.5 m/s quando è a 1.10 m dal
8360 - FISICA MATEMATICA 1 A.A. 014/15 Poblemi dal libo di testo: D. Giancoli, Fisica, a ed., CEA Capitolo 5 Poblema 1 Un bimbo su una giosta si muove con una velocità di 1.5 m/s quando è a 1.10 m dal
Fondamenti di Gravitazione
 Fondamenti di Gavitazione Intoduzione all Astofisica AA 205/206 Pof. Alessando Maconi Dipatimento di Fisica e Astonomia Univesità di Fienze Dispense e pesentazioni disponibili all indiizzo http://www.aceti.asto.it/
Fondamenti di Gavitazione Intoduzione all Astofisica AA 205/206 Pof. Alessando Maconi Dipatimento di Fisica e Astonomia Univesità di Fienze Dispense e pesentazioni disponibili all indiizzo http://www.aceti.asto.it/
Lezione XV Cinghie. Organi di trasmissione. Normalmente gli assi di rotazione delle due pulegge sono paralleli.
 Ogani di tasmissione Ogani flessibili Nelle macchine tovano numeose applicazioni tanto ogani flessibili popiamente detti (cinghie e funi), quanto ogani costituiti da elementi igidi ta loo aticolati (catene).
Ogani di tasmissione Ogani flessibili Nelle macchine tovano numeose applicazioni tanto ogani flessibili popiamente detti (cinghie e funi), quanto ogani costituiti da elementi igidi ta loo aticolati (catene).
L = F s cosα = r F r s
 LVORO Se su un copo agisce una foza F, il lavoo compiuto dalla foza pe uno spostamento s è (podotto scalae di due vettoi): L = F s cosα = F s F α s LVORO L unità di misua del lavoo nel S.I. si chiama Joule:
LVORO Se su un copo agisce una foza F, il lavoo compiuto dalla foza pe uno spostamento s è (podotto scalae di due vettoi): L = F s cosα = F s F α s LVORO L unità di misua del lavoo nel S.I. si chiama Joule:
Q AB = Q AC + Q CB. liquido vapore. δq AB = δq AC + δq CB. δq = c x dt + r dx. Le 5 espressioni del δq nel campo dei vapori saturi
 Le 5 espessioni del Q nel campo dei vapoi satui A C K B Consideiamo la tasfomazione AB che si svolge tutta all inteno della campana dei vapoi satui di una sostanza qualsiasi. Supponiamo quindi di andae
Le 5 espessioni del Q nel campo dei vapoi satui A C K B Consideiamo la tasfomazione AB che si svolge tutta all inteno della campana dei vapoi satui di una sostanza qualsiasi. Supponiamo quindi di andae
Campo magnetico, forza magnetica, momenti meccanici sui circuiti piani
 Campo magnetico, foza magnetica, momenti meccanici sui cicuiti piani Esecizio 1 Un potone d enegia cinetica E k 6MeV enta in una egione di spazio in cui esiste un campo magnetico B1T otogonale al piano
Campo magnetico, foza magnetica, momenti meccanici sui cicuiti piani Esecizio 1 Un potone d enegia cinetica E k 6MeV enta in una egione di spazio in cui esiste un campo magnetico B1T otogonale al piano
I 0 Principio o legge d inerzia: un corpo non soggetto ad alcuna sollecitazione esterna mantiene il suo stato di quiete o di moto rettilineo uniforme
 Le leggi Newtoniane del moto Le foze sono vettoi I 0 Pincipio o legge d inezia: un copo non soggetto ad alcuna sollecitazione estena mantiene il suo stato di quiete o di moto ettilineo unifome Moto acceleato:
Le leggi Newtoniane del moto Le foze sono vettoi I 0 Pincipio o legge d inezia: un copo non soggetto ad alcuna sollecitazione estena mantiene il suo stato di quiete o di moto ettilineo unifome Moto acceleato:
IL POTENZIALE. Nello spostamento successivo B B, poiché la forza elettrica risulta perpendicolare allo spostamento, il lavoro L è nullo.
 1 I POTENZIAE Sappiamo che il campo gavitazionale è un campo consevativo cioè nello spostamento di un copo ta due punti del campo gavitazionale teeste, le foze del campo compiono un lavoo che dipende dalla
1 I POTENZIAE Sappiamo che il campo gavitazionale è un campo consevativo cioè nello spostamento di un copo ta due punti del campo gavitazionale teeste, le foze del campo compiono un lavoo che dipende dalla
Forza gravitazionale
 Foza gavitazionale Tea Mecuio Venee Mate Pianeti inteni Uano Nettuno Plutone atuno Giove istea solae Il oto dei pianeti descitto dalle 3 leggi di Kepleo Di qui Newton icavò la legge di gavitazione univesale:
Foza gavitazionale Tea Mecuio Venee Mate Pianeti inteni Uano Nettuno Plutone atuno Giove istea solae Il oto dei pianeti descitto dalle 3 leggi di Kepleo Di qui Newton icavò la legge di gavitazione univesale:
Dinamica. [studio delle cause del moto: forze] La forza è una grandezza vettoriale: una trazione o spinta ha sempre
![Dinamica. [studio delle cause del moto: forze] La forza è una grandezza vettoriale: una trazione o spinta ha sempre Dinamica. [studio delle cause del moto: forze] La forza è una grandezza vettoriale: una trazione o spinta ha sempre](/thumbs/56/38351749.jpg) Dinamica [studio delle cause del moto: foze] Il temine foza nel senso comune indica una tazione o una spinta La foza è una gandezza vettoiale: una tazione o spinta ha sempe una intensità (il modulo) una
Dinamica [studio delle cause del moto: foze] Il temine foza nel senso comune indica una tazione o una spinta La foza è una gandezza vettoiale: una tazione o spinta ha sempe una intensità (il modulo) una
Se i corpi 1 e 2 interagiscono solo fra loro e non con altri corpi si ha quindi l importante principio di conservazione della quantità di moto: dp r
 3. Dinamica Leggi di Newton Si intoduce il concetto di foza come misua della vaiazione dello stato di moto di un copo, ossevato in un sistema di ifeimento di pe se stesso non soggetto a foze (sistema ineziale).
3. Dinamica Leggi di Newton Si intoduce il concetto di foza come misua della vaiazione dello stato di moto di un copo, ossevato in un sistema di ifeimento di pe se stesso non soggetto a foze (sistema ineziale).
1 Potenziale elettrostatico e seconda equazione di Maxwell per E
 1 Potenziale elettostatico e seconda equazione di Maxwell pe E Consideiamo il campo elettico oiginato da una caica puntifome q che ipotizziamo fissa nell oigine degli assi: E( ) = q ˆ 2 = q 3 (1) Pe definizione,
1 Potenziale elettostatico e seconda equazione di Maxwell pe E Consideiamo il campo elettico oiginato da una caica puntifome q che ipotizziamo fissa nell oigine degli assi: E( ) = q ˆ 2 = q 3 (1) Pe definizione,
Si considerino le rette:
 Si consideino le ette: Eseciio (tipo tema d esame) : s : + () ) Si dica pe quali valoi del paameto eale le ette e s isultano sghembe, paallele o incidenti. ) Nel caso paallele si emino i paameti diettoi
Si consideino le ette: Eseciio (tipo tema d esame) : s : + () ) Si dica pe quali valoi del paameto eale le ette e s isultano sghembe, paallele o incidenti. ) Nel caso paallele si emino i paameti diettoi
Corso di Elettrotecnica 1 - Cod N Diploma Universitario Teledidattico in Ingegneria Informatica ed Automatica Polo Tecnologico di Alessandria
 Schede di Elettotecnica oso di Elettotecnica 1 - od. 9200 N Diploma Univesitaio Teledidattico in Ingegneia Infomatica ed Automatica Polo Tecnologico di Alessandia A cua di uca FEAIS Scheda N 8 icuiti in
Schede di Elettotecnica oso di Elettotecnica 1 - od. 9200 N Diploma Univesitaio Teledidattico in Ingegneia Infomatica ed Automatica Polo Tecnologico di Alessandia A cua di uca FEAIS Scheda N 8 icuiti in
Effetto Hall. flusso reale dei portatori se positivi. flusso reale dei portatori se negativi
 Appunti di Fisica II Effetto Hall L'effetto Hall è un fenomeno legato al passaggio di una coente I, attaveso ovviamente un conduttoe, in una zona in cui è pesente un campo magnetico dietto otogonalmente
Appunti di Fisica II Effetto Hall L'effetto Hall è un fenomeno legato al passaggio di una coente I, attaveso ovviamente un conduttoe, in una zona in cui è pesente un campo magnetico dietto otogonalmente
SESTA LEZIONE: campo magnetico, forza magnetica, momenti meccanici sui circuiti piani
 A. Chiodoni esecizi di Fisica II SESTA LEZIONE: campo magnetico, foza magnetica, momenti meccanici sui cicuiti piani Esecizio 1 Un potone d enegia cinetica E k 6MeV enta in una egione di spazio in cui
A. Chiodoni esecizi di Fisica II SESTA LEZIONE: campo magnetico, foza magnetica, momenti meccanici sui cicuiti piani Esecizio 1 Un potone d enegia cinetica E k 6MeV enta in una egione di spazio in cui
Lunghezza della circonferenza e area del cerchio
 Come possiamo deteminae la lunghezza di una ciconfeenza di aggio? Poviamo a consideae i poligoni egolai inscitti e cicoscitti alla ciconfeenza: è chiao che la lunghezza della ciconfeenza è maggioe del
Come possiamo deteminae la lunghezza di una ciconfeenza di aggio? Poviamo a consideae i poligoni egolai inscitti e cicoscitti alla ciconfeenza: è chiao che la lunghezza della ciconfeenza è maggioe del
Lo schema seguente spiega come passare da una equazione all altra e al grafico della circonferenza. Svolgere i calcoli.
 D4. Ciconfeenza D4.1 Definizione di ciconfeenza come luogo di punti Definizione: una ciconfeenza è fomata dai punti equidistanti da un punto detto cento. La distanza (costante) è detta aggio. Ci sono due
D4. Ciconfeenza D4.1 Definizione di ciconfeenza come luogo di punti Definizione: una ciconfeenza è fomata dai punti equidistanti da un punto detto cento. La distanza (costante) è detta aggio. Ci sono due
ed è pari a: 683 lumen/watt, pertanto:
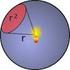 RICIAI GRADEZZE FOTOMETRICHE Fattoe di visibilità (o di sensibilità visiva) K ( λ) : funzione che appesenta la sensibilità media dell occhio umano a adiazioni di diffeente lunghezza d onda ma di eguale
RICIAI GRADEZZE FOTOMETRICHE Fattoe di visibilità (o di sensibilità visiva) K ( λ) : funzione che appesenta la sensibilità media dell occhio umano a adiazioni di diffeente lunghezza d onda ma di eguale
Moto di puro rotolamento
 oto-taslaione di un copo igido di seione cicolae (disco,cilindo,sfea) su di un piano, pe il quale il punto (o i punti) di contatto ta il copo ed il piano è femo ispetto a questo ( non vi è stisciamento
oto-taslaione di un copo igido di seione cicolae (disco,cilindo,sfea) su di un piano, pe il quale il punto (o i punti) di contatto ta il copo ed il piano è femo ispetto a questo ( non vi è stisciamento
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2009
 ESME DI STT DI LICE SCIENTIFIC CRS DI RDINMENT 009 Il candidato isolva uno dei due poblemi e 5 dei 0 quesiti in cui si aticola il questionaio. PRLEM È assegnato il settoe cicolae di aggio e ampiezza (
ESME DI STT DI LICE SCIENTIFIC CRS DI RDINMENT 009 Il candidato isolva uno dei due poblemi e 5 dei 0 quesiti in cui si aticola il questionaio. PRLEM È assegnato il settoe cicolae di aggio e ampiezza (
Il formalismo vettoriale della cinematica rotazionale
 Il fomalismo ettoiale della cinematica otaionale Le elaioni della cinematica otaionale assumono una foma semplice ed elegante, se sono iscitte in foma ettoiale. E questo l agomento dei paagafi che seguono.
Il fomalismo ettoiale della cinematica otaionale Le elaioni della cinematica otaionale assumono una foma semplice ed elegante, se sono iscitte in foma ettoiale. E questo l agomento dei paagafi che seguono.
Cambiamento del Sistema di Riferimento
 Cambiamento del Sistema di Rifeimento Il moto dipende dal sistema di ifeimento dal quale viene ossevato: Un viaggiatoe seduto sul sedile di una caozza feoviaia non si muove ispetto al vagone Se ossevato
Cambiamento del Sistema di Rifeimento Il moto dipende dal sistema di ifeimento dal quale viene ossevato: Un viaggiatoe seduto sul sedile di una caozza feoviaia non si muove ispetto al vagone Se ossevato
32. Significato geometrico della derivata. 32. Significato geometrico della derivata.
 32. Significato geometico della deivata. Deivata Definizione deivata di una funzione in un punto (30) Definizione deivata di una funzione (30) Significato della deivata Deivata in un punto (32) Deivata
32. Significato geometico della deivata. Deivata Definizione deivata di una funzione in un punto (30) Definizione deivata di una funzione (30) Significato della deivata Deivata in un punto (32) Deivata
( ) ( ) ( ) ( ) Esercizi 2 Legge di Gauss
 Esecizi Legge di Gauss. Un involuco sfeico isolante ha aggi inteno ed esteno a e b, ed e caicato con densita unifome ρ. Disegnae il diagamma di E in funzione di La geometia e mostata nella figua: Usiamo
Esecizi Legge di Gauss. Un involuco sfeico isolante ha aggi inteno ed esteno a e b, ed e caicato con densita unifome ρ. Disegnae il diagamma di E in funzione di La geometia e mostata nella figua: Usiamo
Sistemi di riferimento inerziali:
 La pima legge di Newton sul moto è anche chiamata pincipio di inezia. In fisica inezia significa esistenza ai cambiamenti di velocità. Es.: - la foza d attito ta la moneta e la tessea è molto piccola e
La pima legge di Newton sul moto è anche chiamata pincipio di inezia. In fisica inezia significa esistenza ai cambiamenti di velocità. Es.: - la foza d attito ta la moneta e la tessea è molto piccola e
Integrazione indefinita di funzioni irrazionali
 Esecizi di iepilogo e complemento Integazione indefinita di funzioni iazionali 0.5 setgay0 0.5 setgay Denotiamo con R(,,..., n ) una funzione azionale delle vaiabili indicate. Passiamo in assegna alcuni
Esecizi di iepilogo e complemento Integazione indefinita di funzioni iazionali 0.5 setgay0 0.5 setgay Denotiamo con R(,,..., n ) una funzione azionale delle vaiabili indicate. Passiamo in assegna alcuni
Attività didattica Determinazione della massa di Giove tramite le osservazioni dei satelliti galileiani
 Piazza. Ungaetti, 1 81100 Caseta tel. 08/44580 - www.planetaiodicaseta.it, info@planetaiodicaseta.it Attività didattica Deteminazione della massa di iove tamite le ossevazioni dei satelliti galileiani
Piazza. Ungaetti, 1 81100 Caseta tel. 08/44580 - www.planetaiodicaseta.it, info@planetaiodicaseta.it Attività didattica Deteminazione della massa di iove tamite le ossevazioni dei satelliti galileiani
CENTRO DI MASSA. Il centro di massa C divide il segmento AB in parti inversamente proporzionali alle masse: AC. x C = m A x A + m B x B.
 Due paticelle: CENTRO DI MASSA 0 A m A A C m B B B C Il cento di massa C divide il segmento AB in pati invesamente popozionali alle masse: AC CB = m B m A C A B C = m B m A m A C m A A = m B B m B C (
Due paticelle: CENTRO DI MASSA 0 A m A A C m B B B C Il cento di massa C divide il segmento AB in pati invesamente popozionali alle masse: AC CB = m B m A C A B C = m B m A m A C m A A = m B B m B C (
Energia cinetica di un corpo rigido in rotazione. ogni elemento del corpo ha la stessa velocità angolare m 2
 Enegia cinetica di un copo igido in otazione z Copo igido con asse di otazione fisso (Z) 1 1 ogni eleento del copo ha la stessa velocità angolae K un eleento a distanza K dall asse di otazione ha velocità
Enegia cinetica di un copo igido in otazione z Copo igido con asse di otazione fisso (Z) 1 1 ogni eleento del copo ha la stessa velocità angolae K un eleento a distanza K dall asse di otazione ha velocità
Università La Sapienza - Ingegneria Informatica e Automatica. Corso di Fisica Generale: MOTI RELATIVI. A. Bosco, F. Pettazzi ed E.
 Univesità La Sapienza - Ingegneia Infomatica e Automatica Coso i Fisica Geneale: MOTI RELATIVI A. Bosco, F. Pettazzi e E. Fazio Consieiamo un punto mateiale P che si muove i moto abitaio all inteno i un
Univesità La Sapienza - Ingegneia Infomatica e Automatica Coso i Fisica Geneale: MOTI RELATIVI A. Bosco, F. Pettazzi e E. Fazio Consieiamo un punto mateiale P che si muove i moto abitaio all inteno i un
ESERCIZIO n.2. y B. rispetto alle rette r e t indicate in Figura. GA#2 1
 ESERCZO n. Data la sezione a T ipotata in Figua, deteminae: a) gli assi pincipali centali di inezia; ) l ellisse pincipale centale di inezia; c) il nocciolo centale di inezia; d) i momenti di inezia e
ESERCZO n. Data la sezione a T ipotata in Figua, deteminae: a) gli assi pincipali centali di inezia; ) l ellisse pincipale centale di inezia; c) il nocciolo centale di inezia; d) i momenti di inezia e
MECCANICA. APPUNTI di. 1. Introduzione, leggi della dinamica
 APPUNTI di MECCANICA pe gli allievi del coso di TEORIA E PROGETTO DI COSTRUZIONI E STRUTTURE 1. Intoduzione, leggi della dinamica In Fisica si assumono come fondamentali le gandezze seguenti: lunghezza,
APPUNTI di MECCANICA pe gli allievi del coso di TEORIA E PROGETTO DI COSTRUZIONI E STRUTTURE 1. Intoduzione, leggi della dinamica In Fisica si assumono come fondamentali le gandezze seguenti: lunghezza,
Conduttori in equilibrio elettrostatico
 onduttoi in equilibio elettostatico In un conduttoe in equilibio, tutte le caiche di conduzione sono in equilibio Se una caica di conduzione è in equilibio, in quel punto il campo elettico è nullo caica
onduttoi in equilibio elettostatico In un conduttoe in equilibio, tutte le caiche di conduzione sono in equilibio Se una caica di conduzione è in equilibio, in quel punto il campo elettico è nullo caica
Momenti d'inerzia di figure geometriche semplici
 Appofondimento Momenti d'inezia di figue geometice semplici Pidatella, Feai Aggadi, Pidatella, Coso di meccanica, maccine ed enegia Zanicelli 1 Rettangolo Pe un ettangolo di ase e altezza (FGURA 1.a),
Appofondimento Momenti d'inezia di figue geometice semplici Pidatella, Feai Aggadi, Pidatella, Coso di meccanica, maccine ed enegia Zanicelli 1 Rettangolo Pe un ettangolo di ase e altezza (FGURA 1.a),
TEST PER RECUPERO OFA 25 marzo 2010
 TEST PER RECUPERO OFA mazo 010 A 1. Quale ta i seguenti numei, moltiplicato pe, dà come podotto un numeo azionale? A) 0 B) 1+ C) + D) 1 6 E).. Un esagono egolae è inscitto in una ciconfeenza di aggio.
TEST PER RECUPERO OFA mazo 010 A 1. Quale ta i seguenti numei, moltiplicato pe, dà come podotto un numeo azionale? A) 0 B) 1+ C) + D) 1 6 E).. Un esagono egolae è inscitto in una ciconfeenza di aggio.
di Enzo Zanghì pag 1 applichiamo il teorema di Pitagora e otteniamo:
 m@th_cone di Enzo Zanghì pag Distanza di due punti Pe deteminae la distanza ta i punti ( ; ) ( ; ) applichiamo il teoema di Pitagoa e otteniamo: = ( ) + ( ) Punto medio di un segmento M O M + Osseviamo
m@th_cone di Enzo Zanghì pag Distanza di due punti Pe deteminae la distanza ta i punti ( ; ) ( ; ) applichiamo il teoema di Pitagoa e otteniamo: = ( ) + ( ) Punto medio di un segmento M O M + Osseviamo
Moto in tre dimensioni. Legge oraria.
 Moto in te dimensioni. Legge oaia. Pe studiae il moto di un punto mateiale, muniamoci di un sistema di ifeimento, una tena catesiana, e di un oologio. La cuva descitta dal punto mateiale duante il moto
Moto in te dimensioni. Legge oaia. Pe studiae il moto di un punto mateiale, muniamoci di un sistema di ifeimento, una tena catesiana, e di un oologio. La cuva descitta dal punto mateiale duante il moto
ESERCIZIO n.1. rispetto alle rette r e t indicate in Figura. h t. d b GA#1 1
 Esecizi svolti di geometia delle aee Aliandi U., Fusci P., Pisano A., Sofi A. ESERCZO n.1 Data la sezione ettangolae ipotata in Figua, deteminae: a) gli assi pincipali centali di inezia; ) l ellisse pincipale
Esecizi svolti di geometia delle aee Aliandi U., Fusci P., Pisano A., Sofi A. ESERCZO n.1 Data la sezione ettangolae ipotata in Figua, deteminae: a) gli assi pincipali centali di inezia; ) l ellisse pincipale
13b. Reattore omogeneo con riflettore. Due gruppi di neutroni
 b. Reattoe omogeneo con iflettoe ue guppi di neutoni Assumiamo oa una appossimazione in teoia della diffusione consistente in due guppi enegetici: uno elativo ai neutoni temici (guppo temico) ed uno elativo
b. Reattoe omogeneo con iflettoe ue guppi di neutoni Assumiamo oa una appossimazione in teoia della diffusione consistente in due guppi enegetici: uno elativo ai neutoni temici (guppo temico) ed uno elativo
Momenti. Momento di una forza, momento di inerzia, momento angolare
 Momenti Momento di una foza, momento di inezia, momento angolae Momento di una foza Supponiamo di avee una pota vista dall alto e supponiamo che sia incadinata su un lato, diciamo in A. A Se applicassimo
Momenti Momento di una foza, momento di inezia, momento angolae Momento di una foza Supponiamo di avee una pota vista dall alto e supponiamo che sia incadinata su un lato, diciamo in A. A Se applicassimo
La legge di Lenz - Faraday Neumann
 1 La legge di Lenz - Faaday Neumann Il flusso del campo magnetico B Pe dae una veste matematica alle conclusioni delle espeienze viste nella lezione pecedente, abbiamo bisogno di definie una nuova gandezza
1 La legge di Lenz - Faaday Neumann Il flusso del campo magnetico B Pe dae una veste matematica alle conclusioni delle espeienze viste nella lezione pecedente, abbiamo bisogno di definie una nuova gandezza
Elementi di Dinamica
 Elementi di Dinamica ELEMENTI DI DINAMICA Mente la cinematica si limita allo studio delle possibilità di movimento di un ceto sistema ed alla elativa descizione matematica, la dinamica si occupa delle
Elementi di Dinamica ELEMENTI DI DINAMICA Mente la cinematica si limita allo studio delle possibilità di movimento di un ceto sistema ed alla elativa descizione matematica, la dinamica si occupa delle
Lezione 27 - Torsione nelle sezioni circolari ed ellittiche
 Lezione 7 - Tosione nelle sezioni cicolai ed ellittiche ü [A.a. 11-1 : ultima evisione 7 agosto 11] In questa lezione si applicano i isultati della lezione pecedente allo studio di alcune sezione di foma
Lezione 7 - Tosione nelle sezioni cicolai ed ellittiche ü [A.a. 11-1 : ultima evisione 7 agosto 11] In questa lezione si applicano i isultati della lezione pecedente allo studio di alcune sezione di foma
Esercizi Scheda N Fisica II. Esercizi con soluzione svolti
 Esecizi Scheda N. 45 Fisica II Esecizio. Esecizi con soluzione svolti Un filo ettilineo, indefinito, pecoso da una coente di intensità i=4 A, è immeso in un mezzo omogeneo, isotopo, indefinito e di pemeabilità
Esecizi Scheda N. 45 Fisica II Esecizio. Esecizi con soluzione svolti Un filo ettilineo, indefinito, pecoso da una coente di intensità i=4 A, è immeso in un mezzo omogeneo, isotopo, indefinito e di pemeabilità
L atomo. legge di Coulomb che da l attrazione elettrostatica tra protone ed elettrone.
 L atomo Secondo Rutefod l atomo è composto di un nucleo positivo, in cui è concentata tutta la massa, attono al quale uotano a notevole distanza gli elettoni. Gli elettoni eano in gado di vincee l attazione
L atomo Secondo Rutefod l atomo è composto di un nucleo positivo, in cui è concentata tutta la massa, attono al quale uotano a notevole distanza gli elettoni. Gli elettoni eano in gado di vincee l attazione
Corso di Progetto di Strutture. POTENZA, a.a Le piastre anulari
 Coso di Pogetto di Stuttue POTENZA, a.a. 3 Le piaste anulai Dott. aco VONA Scuola di Ingegneia, Univesità di Basilicata maco.vona@unibas.it http://www.unibas.it/utenti/vona/ LE PIASTE CICOLAI CAICATE ASSIALENTE
Coso di Pogetto di Stuttue POTENZA, a.a. 3 Le piaste anulai Dott. aco VONA Scuola di Ingegneia, Univesità di Basilicata maco.vona@unibas.it http://www.unibas.it/utenti/vona/ LE PIASTE CICOLAI CAICATE ASSIALENTE
OSCILLATORE ARMONICO SEMPLICE
 OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
OSCILLATORE ARMONICO SEMPLICE Un oscillatore è costituito da una particella che si muove periodicamente attorno ad una posizione di equilibrio. Compiono moti oscillatori: il pendolo, un peso attaccato
Utilizzando la forma complessa della legge di Ohm calcoliamo la corrente che scorre nel circuito r r
 Yui Geelli, uca Fontanesi, Riccado Campai ab. Elettomagnetismo INDUZIONE Scopo dell espeimento è duplice: dappima la misuazione dell induttanza di un solenoide, poi del coefficiente di mutua induzione
Yui Geelli, uca Fontanesi, Riccado Campai ab. Elettomagnetismo INDUZIONE Scopo dell espeimento è duplice: dappima la misuazione dell induttanza di un solenoide, poi del coefficiente di mutua induzione
Il campo magnetico. campo magnetico B (si misura in Telsa (T)) carica genera campo elettrico campo elettrico imprime forza su carica
 Il campo magnetico caica genea campo elettico campo elettico impime foza su caica e allo stesso modo caica in moto genea campo magnetico campo magnetico impime foza su caica in moto campo magnetico (si
Il campo magnetico caica genea campo elettico campo elettico impime foza su caica e allo stesso modo caica in moto genea campo magnetico campo magnetico impime foza su caica in moto campo magnetico (si
Facoltà di Ingegneria
 Facoltà di Ingegneia Poa in Itinee di Fisica I (a. a. 004-005) 6 Noebe 004 COPITO C Esecizio n. 1 Un copo di assa è appoggiato su di un piano oizzontale scabo, con coefficiente di attito dinaico µ d. Coe
Facoltà di Ingegneia Poa in Itinee di Fisica I (a. a. 004-005) 6 Noebe 004 COPITO C Esecizio n. 1 Un copo di assa è appoggiato su di un piano oizzontale scabo, con coefficiente di attito dinaico µ d. Coe
Legge di Ohm. La corrente elettrica dal punto di vista microscopico: modello di Drude
 Legge di Ohm. Obiettivi didattici: Veifica della elazione ta coente e d.d.p. pe un conduttoe metallico. Veifica della elazione ta la esistenza di un conduttoe e le sue dimensioni (lunghezza, sezione) Misua
Legge di Ohm. Obiettivi didattici: Veifica della elazione ta coente e d.d.p. pe un conduttoe metallico. Veifica della elazione ta la esistenza di un conduttoe e le sue dimensioni (lunghezza, sezione) Misua
1 Le funzioni reali di variabile reale
 1.1 Le funzioni Definizione 1 Le funzioni eali di vaiabile eale Una funzione f: A B è una elazione che associa a ciascuno degli elementi di un insieme A (il dominio) uno ed uno solo degli elementi di un
1.1 Le funzioni Definizione 1 Le funzioni eali di vaiabile eale Una funzione f: A B è una elazione che associa a ciascuno degli elementi di un insieme A (il dominio) uno ed uno solo degli elementi di un
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2009
 PRV RDINMENT 009 ESME DI STT DI LICE SCIENTIFIC CRS DI RDINMENT 009 Il candidato isolva uno dei due poblemi e 5 dei 0 quesiti in cui si aticola il questionaio. PRLEM È assegnato il settoe cicolae di aggio
PRV RDINMENT 009 ESME DI STT DI LICE SCIENTIFIC CRS DI RDINMENT 009 Il candidato isolva uno dei due poblemi e 5 dei 0 quesiti in cui si aticola il questionaio. PRLEM È assegnato il settoe cicolae di aggio
Applicazioni delle leggi della meccanica: moto armnico
 Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Applicazioni delle leggi della meccanica: moto armnico Discutiamo le caratteristiche del moto armonico utilizzando l esempio di una molla di costante k e massa trascurabile a cui è fissato un oggetto di
Lezione 21 - La geometria delle aree. Richiami
 Lezione 1 - La geometia delle aee. Riciami [Ultimaevisione: evisione: gennaio gennaio009] In questa Lezione si iciamano sinteticamente alcune nozioni di geometia delle aee, aicento di una figua piana,
Lezione 1 - La geometia delle aee. Riciami [Ultimaevisione: evisione: gennaio gennaio009] In questa Lezione si iciamano sinteticamente alcune nozioni di geometia delle aee, aicento di una figua piana,
LEZIONE 09 MOMENTO DI UNA FORZA Torque
 LEZIONE 09 OENO DI UNA ORZA oque Nella dinamica del punto mateiale, fissata la massa e la foa, si deduce una sola acceleaione lineae. Nelle otaioni, la stessa foa applicata sulla stessa massa, può invece
LEZIONE 09 OENO DI UNA ORZA oque Nella dinamica del punto mateiale, fissata la massa e la foa, si deduce una sola acceleaione lineae. Nelle otaioni, la stessa foa applicata sulla stessa massa, può invece
Equazioni e disequazioni irrazionali
 Equazioni e disequazioni iazionali 8 81 Equazioni iazionali con un solo adicale Definizione 81 Un equazione si dice iazionale quando l incognita compae sotto il segno di adice Analizziamo le seguenti equazioni:
Equazioni e disequazioni iazionali 8 81 Equazioni iazionali con un solo adicale Definizione 81 Un equazione si dice iazionale quando l incognita compae sotto il segno di adice Analizziamo le seguenti equazioni:
E, ds. - Flusso totale uscente dalla superficie chiusa S: è la somma di tutti i flussi elementari, al tendere a zero delle aree infinitesime: r )
 Flusso del campo elettico e legge di Gauss. - Si definisce supeficie gaussiana una ipotetica supeficie S chiusa, che contiene un volume V. - La legge di Gauss mette in elazione i valoi dei campi elettici
Flusso del campo elettico e legge di Gauss. - Si definisce supeficie gaussiana una ipotetica supeficie S chiusa, che contiene un volume V. - La legge di Gauss mette in elazione i valoi dei campi elettici
mm r r r r Si noti che: 1) F e centrale F F 3) e attrattiva soddisfa il principio di sovrapposizione:
 La legge univesale della gavitazione (dovuta ad Isaac Newton): Pe due punti ateiali,, sepaati da distanza, la foza di attazione gavitazionale e: = γ dove γ e la costante di gavitazione univesale: γ = 6.67
La legge univesale della gavitazione (dovuta ad Isaac Newton): Pe due punti ateiali,, sepaati da distanza, la foza di attazione gavitazionale e: = γ dove γ e la costante di gavitazione univesale: γ = 6.67
