ENERGIA CINETICA. T := 1 2 mv2. (1) T := N 1 2 m ivi 2. (2) i=1
|
|
|
- Romolo Locatelli
- 8 anni fa
- Visualizzazioni
Transcript
1 ENERGIA CINETICA Teorema de energa cnetca Defnzone Per un punto P dotato d massa m e veoctà v, s defnsce energa cnetca a seguente quanttà scaare non negatva T := mv. () Defnzone Per un sstema dscreto d punt P,dotatdmassam cascuno con veoctà v,sdefnsce energa cnetca a seguente quanttà scaare non negatva P T := N m v. () Defnzone 3 Dato un sstema contnuo, per ogn punto P de sstema, sa ρ (P ) a funzone denstà d massa, aora a quanttà scaare energa cnetca s defnsce come T := R C ρ (P ) v (P ) dc. (3) Defnzone 4 Per un punto P dotato d massa m e veoctà v, sdefnsce potenza dea forza F a seguente quanttà scaare π := F v. (4) Consderamo un sstema materae costtuto da N punt matera P n movmento rspetto ad un osservatore nerzae. Per ogn punto P vae equazone fondamentae dea dnamca dove F è rsutante dee forze esterne, f èrsutantedeeforzenterne, m a = F + f + Φ + φ =,...,N., (5) Φ è rsutante dee reazon vncoar esterne, φ è rsutante dee reazon vncoar nterne. Teorema (de Energa Cnetca) Consderamo un sstema materae costtuto da N punt matera P n movmento rspetto ad un osservatore nerzae. Per ogn punto P vaga equazone fondamentae dea dnamca 5 rstretta ae forze attve nterne ed esterne, aora vae a seguente equazone dt dt = Π est. + Π nt. (6) 5
2 6 Dmostrazone. Motpchamo scaarmente cascuna equazone de sstema 5 peraveoctàdognpunto v. S ottene Ma m a v = d dt m a v = F v + f v. =,...,N. (7) m v v = d dt m v = F v + f v. =,...,N. (8) S è rcavato da equazone fondamentae dea dnamca, scrtta per un sstema d N punt, che a potenza dee forze agent su sngoo punto eguaga a dervata dea sua energa cnetca rspetto a tempo t. SommamoeN equazon scaar membroamembroeottenamo NX d dt m v = NX F v + NX f v = dt dt = Π est. + Π nt., (9) dove Π est. è a rsutante dea potenza dee forze esterne e Π nt. è a rsutante dea potenza dee forze nterne. Osservazone Mentre e equazon cardna dea dnamca convogono soo e forze esterne e oro moment, pochè R nt. =0e M O nt. =0, teorema de energa cnetca convoge a potenza dee forze nterne che, n generae può non essere nua. Esempo Due punt dotat d massa m e m conness da una forza eastca (moa) avent veoctà v e v. Osservazone La potenza dee forze nterne ne C.R. è nua Dmostrazone. Per defnzone Π nt. = NX f v. (0) ne atto d moto rgdo, possamo scrvere v = v O + ω nea precedente equazone fornsce NX NX h NX NX Π nt. = f v = f v O + ω P O = f v O + P O, che sosttuta h f ω P O = R nt. v O + ω M O nt., () ma n un C.R. R nt. =0per prncpo d azone e reazone e M O nt. =0per a stessa ragone. Osservazone 3 Se corpo è vncoato con vncoo sco (esterno a corpo) e fsso, apotenzadeareazonevncoareènua. Sevncoononèfsso n generae a potenza è dversa da zero.
3 Osservazone 4 Secorpoèvncoatoconrotoamentosenzastrscamentoe vncoo è fsso, a potenza dea reazone vncoare è nua. 7 Se vncoo non è fssoedèesternoasstema,apotenzaèdversadazero. Osservazone 5 Se vncoo d rotoamento senza strscamento è nterno a sstema, a potenza dee reazon vncoar nterne è nua. Pochè c è rotoamento senza strscamento, e veoctà de punt d contatto sono ugua v H = v K () e a potenza dee reazon vncoar dventa Π = R 0 v H R 0 v K =0. (3) S osserv che non è nua a potenza su sngoo corpo.
4 8 Osservazone 6 Se vncoo è sco ed è nterno a sstema, a potenza dee reazon vncoar è nua. Infatt e component norma dee veoctà de punt d contatto sono ugua e a potenza dee reazon vncoar dventa pochè Φ H = Φ K per P.A.R. v H,n = v K,n (4) Π = Φ H v H Φ K v K = Φ H v H,n Φ K v K,n =0, (5) Teorema (d Köng) L energa cnetca d un sstema n moto è par a energa cnetca d trasazone de sstema come se tutta a massa fosse concentrata ne barcentro pù energa cnetca de sstema reatva ad un osservatore trasante con barcentro stesso. Dmostrazone. Consderamo un sstema d punt P,dotatdmassam cascuno con veoctà v. L energa cnetca d questo sstema è par a T = N P m v, (6) dove v è a veoctà assouta. S consder un rfermento mobe. Pochè egame tra rfermento mobe e queo assouto vene espresso da v = v S + v re., (7) dove v S è a veoctà d trascnamento e v re. è a veoctà reatva. Sosttuendo ne espressone de energa cnetca, ottenamo T = N P m v S + v re. NP v S + v re. = m h v S + v re. + v S v re. = NP m v S + NP m v re. NP + m v S v re.. (8)
5 Con una sceta opportuna de rfermento mobe s può emnare termne msto. Scegamo rfermento mobe con orgne ne barcentro G de sstema trasante, ovvero v S = v G. Aora termne msto dventa NP m v S v re. = NP m vg v re. = NP ma per defnzone Q re. =0.Indefntva T = NP m v re. vg = m v re. G 9 vg = Q re. v G, (9) m v re. + mv G = T re. + mv G. (0) Ne caso partcoare de Corpo Rgdo, T re. è energa cnetca d un atto d moto rotatoro attorno a barcentro G. Cacoamo espressone generae de energa cnetca per un atto d moto rotatoro ntorno ad O. T = R C h ρ (P ) ω Se ponamo a = ω P O dc = R C h ρ (P ) ω h P O ω P O, b = ω e c = P O, T dventa P O dc R n h o C ρ (P ) a b c dc. () h a b c è un prodotto msto. Usando e permutazon ccche, ottenamo h a b c = b [ c a] (3) e espressone s può scrvere come T = ω R ρ (P ) C nh h P O ω () o P O dc, (4) ma espressone sotto segno d ntegrae corrsponde a momento dea quanttà d moto con poo n O, per cu T = ω Γ O = ω I ω. (5) Usando una terna prncpae d nerza reatva ad O, Γ O dventa Γ O =(I xx ω x ) +(I yy ω y ) j +(I zz ω z ) k, (6) con, j e k versor dea terna prncpae d nerza e energa cnetca assume a forma T = h hω x + ω y j + ω z k (I xx ω x ) +(I yy ω y ) j +(I zz ω z ) k
6 0 = Ixx ω x + I yy ω y + I zz ω z. (7) possamo rscrvere T n un atro modo. Se ω = ω ω = ω u u versore d ω, (8) ω aora T = ω ( u I u) = I uω, (9) dove I u è momento d nerza rspetto a asse d stantanea rotazone u k ω.qund Per un atto d moto rototrasatoro T = I ωω. (30) T = mv G + I ωω. (3) Osservazone 7 Ne caso de Corpo Rgdo, teorema de energa cnetca dscende dae equazon cardna ½ d Q = R dt est. d. (3) Γ dt G = M (G)est. Dmostrazone. Motpchamo scaarmente a prma equazone per v G easeconda per ω ( d Q v dt G = m a G v G = R est. v G d h Γ dt G ω = d (I dt xx ω x ) +(I yy ω y ) j +(I zz ω z ) k ω = M (G)est. ω. (33) Sommamo e due equazon membro a membro m a G v G + d dt Γ G ω = R est. v G + M (G)est. ω = Π est., (34) ma m a G v G + d dt Γ G ω = d dt mv G " + I xx ω x + I yy ω y j + I zz ω z d k + Ixx ω x dt + I d j yyω y dt + I d zzω # k z ω = d dt dt mv G ³ ³ ³ + hi xx ω x + I yy ω y j + I zz ω z k + Ixx ω x ω + I yy ω y ω j + I zz ω z ω k ω = d dt mv G + I xx ω x ω x + I yy ω y ω y + I zz ω z ω z + h ω Γ G ω = d dt mv G +I xx ω x ω x +I yy ω y ω y +I zz ω z ω z = d dt mv G + Ixx ω x + I yy ω y + I zz ω z = d dt T = Π est. (35)
7 Lavoro e Camp conservatv Partamo da espressone 6 e supponamo d ncudere, otre ae forze attve esterne e nterne, anche e forze reattve esterne ed nterne. La forma espressa da equazone 6 è nota come prma forma de teorema de energa cnetca. C proponamo, ora d rcavare a seconda forma d tae teorema. Motpchamo ambo membr de espressone 6 per dt. Srcava dt = Π est. dt + Π nt. dt + Π 0 est.dt + Π 0 nt.dt = Πdt, (36) dove con Π abbamo ndcato sntetcamente tutt tp d forze (attve, reattve, nterne ed esterne). Per defnzone d potenza dt = Πdt = F vdt = F d P dt dt = F d P = δl, (37) dove con δl ndchamo avoro eementare computo da una forza F (P, v, t) (o rsutante d forze esterne, nterne,... ) agente su d un punto materae (o sstema) n un ntervao d tempo nfntesmo dt. Iavoroeementare non èundfferenzae esatto. In coordnate cartesane, avoro eementare s può rappresentare come δl = F x dx + F y dy + F z dz. (38) Se ntegramo n un ntervao d tempo [t 0,t ] a quanttà 36, s ottene avoro L computo daa forza F Z t t 0 Z t t 0 Z t dt = T = Πdt = δl = L Z t [Π est. + Π nt. + Π 0 est. + Π 0 nt.] dt = L est. + L nt. + L 0 est. + L 0 nt.. (39) t 0 L equazone scaare T = L est. + L nt. + L 0 est. + L 0 nt. (40) esprme teorema de energa cnetca nea II forma: a varazone d energa cnetca n un quasas ntervao d tempo è uguae aa somma agebrca de avor esegut da tutte e forze esterne, nterne, attve e reatttve agent su d un sstema materae. Consderamo ora, ntervao d tempo [t 0,t ] durante quae punto (sstema d punt, corpo rgdo,...) passa daa poszone P 0 aa poszone P descrvendo una curva. Se punto n un ntervao d tempo dt subsce o spostamento dp = v (t) dt, avorocomputodaaforzaf eperdefnzone o, pù n generae L = Z t t 0 δl = Z P P 0 t 0 h F d P Z Z h L = δl = F d P che rappresenta un ntegrae d nea. In coordnate cartesane possamo scrvere Z Z h Z Z x Z y Z z δl = F dp = [F x dx + F y dy + F z dz] = F x dx+ F y dy+ F z dz. x 0 y 0 z 0 (4) (4) (43)
8 Defnzone 5 S dce che F è un campo d forze conservatvo se ntegrae ungo a nea dpende soo dag estrem P 0 e P. Una seconda defnzone equvaente è a seguente Defnzone 6 S dce che F è un campo d forze conservatvo se ntegrae ungo una quasas nea chusa (senza buch a nterno dea nea chusa) è nuo. Una terza defnzone è data da Defnzone 7 S dce che F èuncampodforzeconservatvoseessteunafunzone scaare regoare U U (x, y, z), detta funzone potenzae tae che δl = du. Condzone Necessara e Suffcente affnché campo d forze F sa conservatvo è che rot F =0, (44) dove rot F è rotore dea forza F. In questo caso, F s dce rrotazonae. In component cartesane rot F s può rappresentare come rotf j k µ = x y z F x F y F = Fz y F µ y Fz j z x F µ x + z Fy k x F x. y z (45) Aora F èdeaforma F = gradu, (46) dove gradu è gradente de potenzae U e n termn cartesan possamo scrvere F x + F y j + F z U k = x + U y j + U z k. (47) Se esste potenzae aora daa 43, possamo scrvere Z Z Z U U U L = [F x dx + F y dy + F z dz] = dx + dy + x y z dz = du = U (P ) U (P 0 ). (48) Esempo (Forza costante) Per esempo, a forza peso. La forza F ècostante n moduo, drezone e verso. Prendamo una terna d ass cartesan, tae che asse x sa paraeo ad F = F. Daa 48, s rcava F x = F = U x F y =0= U y = U (x) =Fx+ costante. (49) F z =0= U z Ne caso dea forza peso, se y è asse vertcae ascendente vettore p = p j e potenzae vae U (y) = py + costante, (50) mentre se y è asse vertcae dscendente vettore p = p j e potenzae vae U (y) =py + costante. (5)
9 3 Esempo 3 (Forza d tpo centrae) Sa O un punto fsso e ½ f (r) u forza repusva F = f (r) u forza attrattva, f (r) 0 e u = P O. (5) P O Fssamo una terna con orgne n O esar = p x + y + z F x = ±f (r) x r F y = ±f (r) y r F z = ±f (r) z r = U (r) U (r 0 )= Z r r 0 f (t) dt. (53) Infatt U x U y U z = ±f (r) r x = ±f (r) x r = ±f (r) r y = ±f (r) y r = ±f (r) r z = ±f (r) z r. (54) Esempo 4 (Forza eastca) Sa F dea forma F = k P O = kr u, (55) aora Z r U (r) = ktdt = kr + costante. (56) Esempo 5 (Forza gravtazonae newtonana) Sa F dea forma F = G Mm u, (57) r aora Z r U (r) = G Mm dt = G Mm t r + costante. (58) TeoremdConservazone. Conservazone dea quanttà d moto secondo un asse Daa prma equazone cardnae dea dnamca d dt Q = R est. + R 0 est., (59) se r è un asse fsso d versore u e ³ R est. + R est. 0 u =0= d Q u dt = d ³ Q u dt = Q u = costante durante moto (60)
10 4 Esempo 6 Asta d unghezza emassam Nea drezone x non agscono forze. Qund ³ Rest. + R est. 0 =0 = Q = Q x = mv Gx = costante durante moto (6) Scrvamoacoordnata ungo assex de barcentro Pochè Q x è costante, anche x G = x + cos θ = ẋ G = ẋ sn θ θ. (6) mv Gx = m µ ẋ sn θ θ = costante. (63) Durante moto ẋ = sn θ θ. (64). Conservazone de momento dea quanttà d moto Daa seconda equazone cardnae dea dnamca d dt Γ O + v O Q = M (O)est. + M (O)est., 0 (65) consderamo due cas: a) Se rspetto ad un poo O M (O)est. + M (O)est. 0 =0e v O Q =0 = Γ O = costante durante moto. (66) Esempo 7 Corpo bero pesante. La rsutante de moment dee forze attve e reattve rspetto a barcentro è nuo M (G)est. + M (G)est. 0 e v G Q = 0, pochè v G k Q.Aora Γ G =costante.
11 b) Se rspetto ad un poo O eadunassefsso r d versore u, v O Q =0e ³ M (O)est. + M (O)est. 0 u =0 = Γ O u = costante durante moto. (67) Esempo 8 Corpo Rgdo con asse fsso. Supponamo che asse fsso sa orentato come asse z.prendamo ³ come poo O un punto de asse, aora v O Q =0pochè v O =0. M (O)est. + M (O)est. 0 k =0.Infatt M (O)est. è un vettore perpendcoare a k, pochè a forza peso p ha a stessa drezone d k. o stesso vae per M (O)est. 0, pochè poo è un punto de asse fsso e a reazone vncoare de asse è sempre perpendcoare a asse stesso. Aora Γ O,z =costante. 3. Conservazone de Energa Consderamo un stema materae soggetto a forze attve conservatve (nterne ed esterne), a vnco estern fss e a vnco (ntern ed estern) non dsspatv o perfett. Da teorema de energa cnetca nea prma forma, possamo scrvere dt dt = Π est. + Π nt. = dt =(Π est. + Π nt. ) dt. (68) Per potes, e forze che stamo consderando sono conservatve, per cu dt =(Π est. + Π nt. ) dt = dl est. + dl nt. = du est. + du nt. = d (U est. + U nt. ). (69) Scrtto n modo compatto, s ottene che, ntegrata fornsce 5 d (T U est. U nt. )=0 (70) T (U est. + U nt. )=E = costante durante moto. (7) La costante E s dce energa meccanca totae. Se vnco fossero scabr (dsspatv), per teorema de energa cnetca s può scrvere dt = du + dl 0, (7) dove abbamo ndcato sntetcamente con U potenzae dee forze attve nterne ed esterne e con dl 0 avoro dee forze d reazone. S not che dl 0 < 0. In forma ntegrata, a precedente reazone dventa E (t) =E 0 + L 0. (73) Usando energa potenzae V a posto de potenzae U, sottene T +(V est. + V nt. )=E = costante durante moto.
12 6 Esempo 9 Consderamo ancora esempo dea fgura a pagna 4 e scrvamo un atro ntegrae prmo: ntegrae de energa T U = E. (74) Usamo teorema d Köng per cacoo d T T = mv G + I ωω = m µ ẋ G + ẏg m + θ. (75) Dobbamo esprmere ẋ G e ẏ G n termn d e θ ½ xg = x + cos θ ½ ẋg = ẋ y G = sn θ = sn θ θ ẏ G = cos θ θ, (76) aora T = m ẋ G + ẏg + µ " m µ θ = m ẋ θ sn θ + µ cos θ θ #+ m 4 θ = m ẋ ẋ sn θ θ + θ + m 4 4 θ = mẋ + m 6 θ mẋ sn θ θ. (77) S not che vg può essere cacoato usando teorema d composzone dee veoctà v G =( v trasc. + v re. ) = v trasc. + v re. + v trasc. v re., (78) dove v trasc. = ẋ, v re. = θ/ e angoo compreso tra v trasc. e v re. vae π/+θ. S ottene à vg = ẋ + θ 4 + ẋ θ! ³ π θ cos + = ẋ + θ 4 ẋ θ sn θ. (79) I potenzae vae U = mgy G = mg sn θ (80) e energa totae dventa mẋ + m 6 θ mẋ sn θ θ mg sn θ = E. (8) Sappamo che questo sstema ha un secondo ntegrae prmo: a quanttà d moto ungo asse x, espresso daa 63. Se supponamo, per fssare e dee, che come condzone nzae, asta sa n quete n poszone orzzontae, aora energa totae E n quea confgurazone è nua, per cu ( mẋ + m θ ³ mẋ sn θ θ mg sn θ = E =0 6 m ẋ sn θ θ =0 = ẋ = sn θ θ. (8)
13 7 Emnando ẋ ne sstema precedente, s ottene µ m sn θ θ + m 6 θ µ m sn θ θ sn θ θ mg sn θ m µ sn θ θ + m 6 θ mg sn θ =0 4 sn θ θ + 3 θ = g sn θ = θ =3g sn θ +3 4 sn θ θ. (83) Cacoamo, per esempo, a veoctà angoare quando asta passa per a vertcae, coè θ = π/. La precedente espressone dventa r θ = g = θ 3g = ±. (84) Per tornando ndetro r θ = π/ = θ 3g =, (85) r 3g θ =. (86) Esempo 0 S consder sstema d fgura formato da un dsco d massa m eraggor che rotoa senza strscare su un pano ncnato d massa M. I pano ncnato è bero d muovers rspetto ad un sstema d rfermento fsso senza attrto. Determnare moto de dsco sapendo che, per t =0 sstema s trova n quete con dsco nea poszone pù ata. Consderamo sstema d rfermento d fgura e osservamo che e forze n goco, attve e reattve s rducono aa soa forza peso. Pochè vnco non sono dsspatv, energa meccanca s conserva, come pure s conserva a componente dea quanttà d moto ungo asse x. CacoamoQ x Q x = Mẋ + m (ẋ + ṡ cos α) =costante. (87)
14 8 Pochè sstema s trova n quete a tempo t =0 Q x (t) =Q x (0) = 0. (88) Cacoamo energa cnetca T = T dsco + T p.ncnato,dove ½ T p.ncnato = Mẋ T dsco = mv G + I Gω (teorema d Köng). (89) Le coordnate de barcentro d G eereatveveoctàsono e ½ xg = x + s cos α y G = s sn α = T dsco = m ẋ G + ẏg + ½ ẋg = ẋ + ṡ cos α ẏ G = ṡ sn α µ mr ω µ µṡ mr (90) = m (ẋ + ṡ cos α) +(ṡ sn α) + R = mẋ + mṡ + mẋṡ cos α + 4 mṡ = mẋ mṡ + mẋṡ cos α. (9) Per rotoamento senza strscamento ω = ṡ/r. Come ne esempo precedente v G può essere cacoato con a composzone dee veoctà v G =( v trasc. + v re. ) = v trasc. + v re. + v trasc. v re., (9) dove v trasc. = ẋ, v re. = ṡ e angoo compreso tra v trasc. e v re. vae α. Segue che vg = ẋ + ṡ +ẋṡ cos (α). (93) Compessvamente T = T dsco + T p.ncnato = mẋ mṡ + mẋṡ cos α + Mẋ. (94) I potenzae vae e energa totae dventa U = mgy G = mgs sn α (95) (m + M) ẋ mṡ + mẋṡ cos α mgs sn α = E. (96) Dae condzon nza deducamo che E =0. Sfruttando a conservazone dea quanttà d moto 87, possamo esprmere ẋ n funzone d ṡ ẋ = m cos α ṡ, (97) m + M per cu espressone 96 dventa µ (m + M) m cos α m + M ṡ + 3 µ 4 mṡ + m m cos α m + M ṡ ṡ cos α mgs sn α
15 m cos α m + M ṡ mṡ m cos α m + M ṡ mgs sn α =0. (98) Isoando ṡ, s ottene µ 3 4 m cos α m + M ṡ = gs sn α = ṡ = gs sn α Se ponamo 4(m + M) g sn α a = 3(m + M) m cos α equazone precedente dventa Possamo rsovera n due mod (a) Estraamo a radce quadrata e rcavamo ṡ = ds dt = ± as = varab separab Qund 9 µ 4(m + M) 3(m + M) m cos α (99) = costante, (00) ṡ = as. (0) ds s = ± adt = s = ± at. (0) s (t) s (0) = ± a 4 t = s (t) = a 4 t, (03) dove abbamo usato a condzone nzae s (0) = 0 e abbamo scartato segno pochè o spostamento non avvene spontaneamente n sata. (b) Dervamo rspetto a tempo t, equazone 0 e ottenamo ṡ s = aṡ = s = a = s = a. (04) Abbamo dvso per ṡ con potes che ṡ 6= 0. L equazone dfferenzae è de secondo ordne. Dobbamo ntegrare due vote. s = a = ṡ (t) ṡ (0) = a t = ṡ (t) =a t, (05) dove abbamo usato a condzone nzae d quete ṡ (0) = 0. Integrando una seconda vota s rcava ṡ (t) = a t = s (t) s (0) = a 4 t = s (t) = a 4 t. (06) I teorem d conservazone enuncat fornscono deg ntegra prm de moto. (Q x = costante, Γ O,z = costante). G ntegra prm de moto sono funzon dee coordnate bere e dee oro dervate prme rspetto a tempo, che s mantengono costant durante moto.
Elemento Finito (FE) per travi 2D
 Eemento Fnto (FE) per trav D Govann Formca corso d Cacoo Automatco dee Strutture AA. 9/1 Premesse a modeo modeo fsco prncp d banco e dsspazone { Pest P nt = { q u S u = P nt φ modeo smuato (dscretzzazone)
Eemento Fnto (FE) per trav D Govann Formca corso d Cacoo Automatco dee Strutture AA. 9/1 Premesse a modeo modeo fsco prncp d banco e dsspazone { Pest P nt = { q u S u = P nt φ modeo smuato (dscretzzazone)
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO
 PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
Macchine. 5 Esercitazione 5
 ESERCITAZIONE 5 Lavoro nterno d una turbomacchna. Il lavoro nterno massco d una turbomacchna può essere determnato not trangol d veloctà che s realzzano all'ngresso e all'uscta della macchna stessa. Infatt
ESERCITAZIONE 5 Lavoro nterno d una turbomacchna. Il lavoro nterno massco d una turbomacchna può essere determnato not trangol d veloctà che s realzzano all'ngresso e all'uscta della macchna stessa. Infatt
Dinamica dei sistemi particellari
 Dnamca de sstem partcellar Marco Favrett Aprl 11, 2010 1 Cnematca Sa dato un sstema d rfermento nerzale (O, e ), = 1, 2, 3 e consderamo un sstema d punt materal (sstema partcellare) S = {(OP, m )}, = 1,,
Dnamca de sstem partcellar Marco Favrett Aprl 11, 2010 1 Cnematca Sa dato un sstema d rfermento nerzale (O, e ), = 1, 2, 3 e consderamo un sstema d punt materal (sstema partcellare) S = {(OP, m )}, = 1,,
Dinamica del corpo rigido
 Anna Nobl 1 Defnzone e grad d lbertà S consder un corpo d massa totale M formato da N partcelle cascuna d massa m, = 1,..., N. Il corpo s dce rgdo se le dstanze mutue tra tutte le partcelle che lo compongono
Anna Nobl 1 Defnzone e grad d lbertà S consder un corpo d massa totale M formato da N partcelle cascuna d massa m, = 1,..., N. Il corpo s dce rgdo se le dstanze mutue tra tutte le partcelle che lo compongono
urto v 2f v 2i e forza impulsiva F r F dt = i t
 7. Urt Sstem a due partcelle Defnzone d urto elastco, urto anelastco e mpulso L urto è un nterazone fra corp che avvene n un ntervallo d tempo normalmente molto breve, al termne del quale le quanttà d
7. Urt Sstem a due partcelle Defnzone d urto elastco, urto anelastco e mpulso L urto è un nterazone fra corp che avvene n un ntervallo d tempo normalmente molto breve, al termne del quale le quanttà d
F E risultante t delle forze esterne agenti su P i. F forza esercitata t sul generico punto P ij del sistema da P : forza interna al sistema
 DINAMICA DEI SISTEMI Sstema costtuto da N punt materal P 1, P 2,, P N F E rsultante t delle forze esterne agent su P F E F forza eserctata t sul generco punto P j del sstema da P : forza nterna al sstema
DINAMICA DEI SISTEMI Sstema costtuto da N punt materal P 1, P 2,, P N F E rsultante t delle forze esterne agent su P F E F forza eserctata t sul generco punto P j del sstema da P : forza nterna al sstema
UNIVERSITÀ DEGLI STUDI DI TERAMO
 UIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA I TUTELA E BEESSERE AIMALE Corso d : FISICA MEDICA A.A. 015 /016 Docente: Dott. Chucch Rccardo mal:rchucch@unte.t Medcna Veternara: CFU 5 (corso ntegrato
UIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA I TUTELA E BEESSERE AIMALE Corso d : FISICA MEDICA A.A. 015 /016 Docente: Dott. Chucch Rccardo mal:rchucch@unte.t Medcna Veternara: CFU 5 (corso ntegrato
Progetto Lauree Scientifiche. La corrente elettrica
 Progetto Lauree Scentfche La corrente elettrca Conoscenze d base Forza elettromotrce Corrente Elettrca esstenza e resstvtà Legge d Ohm Crcut 2 Una spra d rame n equlbro elettrostatco In un crcuto semplce
Progetto Lauree Scentfche La corrente elettrca Conoscenze d base Forza elettromotrce Corrente Elettrca esstenza e resstvtà Legge d Ohm Crcut 2 Una spra d rame n equlbro elettrostatco In un crcuto semplce
Rotazione di un corpo rigido intorno ad un asse fisso
 INGEGNERIA GESTIONALE corso d Fsca Generale Prof. E. Puddu LEZIONE DEL 14 15 OTTOBRE 2008 Rotazone d un corpo rgdo ntorno ad un asse fsso 1 Cnematca rotazonale y Supponamo d osservare un corpo rgdo sul
INGEGNERIA GESTIONALE corso d Fsca Generale Prof. E. Puddu LEZIONE DEL 14 15 OTTOBRE 2008 Rotazone d un corpo rgdo ntorno ad un asse fsso 1 Cnematca rotazonale y Supponamo d osservare un corpo rgdo sul
Studio grafico-analitico di una funzioni reale in una variabile reale
 Studo grafco-analtco d una funzon reale n una varable reale f : R R a = f ( ) n Sequenza de pass In pratca 1 Stablre l tpo d funzone da studare es. f ( ) Determnare l domno D (o campo d esstenza) della
Studo grafco-analtco d una funzon reale n una varable reale f : R R a = f ( ) n Sequenza de pass In pratca 1 Stablre l tpo d funzone da studare es. f ( ) Determnare l domno D (o campo d esstenza) della
6.1- Sistemi punti, forze interne ed esterne
 1 CAP 6 - SISTEMI DI PUNTI MATERIALI Parte I 1 Cap 6 - Sstem d punt materal Cap 6 - Sstem d punt materal Il punto materale è un astrazone alla quale poch cas s possono assmlare. La maggor parte degl oggett
1 CAP 6 - SISTEMI DI PUNTI MATERIALI Parte I 1 Cap 6 - Sstem d punt materal Cap 6 - Sstem d punt materal Il punto materale è un astrazone alla quale poch cas s possono assmlare. La maggor parte degl oggett
Dipartimento di Statistica Università di Bologna. Matematica finanziaria aa 2012-2013 lezione 13: 24 aprile 2013
 Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 13: 24 aprle 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/23? reammortamento uò accadere che, dopo l erogazone
Dpartmento d Statstca Unverstà d Bologna Matematca fnanzara aa 2012-2013 lezone 13: 24 aprle 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/23? reammortamento uò accadere che, dopo l erogazone
Algebra 2. 6 4. Sia A un anello commutativo. Si ricorda che in un anello commutativo vale il teorema binomiale, cioè. (a + b) n = a i b n i i.
 Testo Fac-smle 2 Durata prova: 2 ore 8 1. Un gruppo G s dce semplce se suo unc sottogrupp normal sono 1 e G stesso. Sa G un gruppo d ordne pq con p e q numer prm tal che p < q. (a) Il gruppo G può essere
Testo Fac-smle 2 Durata prova: 2 ore 8 1. Un gruppo G s dce semplce se suo unc sottogrupp normal sono 1 e G stesso. Sa G un gruppo d ordne pq con p e q numer prm tal che p < q. (a) Il gruppo G può essere
Fondamenti di meccanica classica: simmetrie e leggi di conservazione
 Fondament d meccanca classca: smmetre e legg d conservazone d Marco Tulu A. A. 2005/2006 1 Introduzone Un corpo s dce omogeneo se ha n ogn suo punto ugual propretà fsche e chmche, ed è sotropo se n ogn
Fondament d meccanca classca: smmetre e legg d conservazone d Marco Tulu A. A. 2005/2006 1 Introduzone Un corpo s dce omogeneo se ha n ogn suo punto ugual propretà fsche e chmche, ed è sotropo se n ogn
Sistemi punti, forze interne ed esterne
 Ncola GglettoA.A. 2017/18 3 6.2- IL CENTRO DI MASSA Parte I 1 Cap 6 - Sstem d punt materal Cap 6 - Sstem d punt materal Il punto materale è un astrazone alla quale poch cas s possono assmlare. La maggor
Ncola GglettoA.A. 2017/18 3 6.2- IL CENTRO DI MASSA Parte I 1 Cap 6 - Sstem d punt materal Cap 6 - Sstem d punt materal Il punto materale è un astrazone alla quale poch cas s possono assmlare. La maggor
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energa e Lavoro Fnora abbamo descrtto l moto de corp (puntform) usando le legg d Newton, tramte le forze; abbamo scrtto l equazone del moto, determnato spostamento e veloctà n funzone del tempo. E possble
Energa e Lavoro Fnora abbamo descrtto l moto de corp (puntform) usando le legg d Newton, tramte le forze; abbamo scrtto l equazone del moto, determnato spostamento e veloctà n funzone del tempo. E possble
Dipartimento di Statistica Università di Bologna. Matematica Finanziaria aa 2012-2013 Esercitazione: 4 aprile 2013
 Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2012-2013 Eserctazone: 4 aprle 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/41? Aula "Ranzan B" 255 post 1 2 3 4 5 6 7 8 9
Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2012-2013 Eserctazone: 4 aprle 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/41? Aula "Ranzan B" 255 post 1 2 3 4 5 6 7 8 9
Elasticità nei mezzi continui
 Elastctà ne mezz contnu l tensore degl sforz o tensore d stress, σ j Consderamo un cubo d dmenson untare n un mezzo elastco deformato. l cubo è deformato dalle forze eserctate sulle sue facce dal resto
Elastctà ne mezz contnu l tensore degl sforz o tensore d stress, σ j Consderamo un cubo d dmenson untare n un mezzo elastco deformato. l cubo è deformato dalle forze eserctate sulle sue facce dal resto
Analisi ammortizzata. Illustriamo il metodo con due esempi. operazioni su di una pila Sia P una pila di interi con le solite operazioni:
 Anals ammortzzata Anals ammortzzata S consdera l tempo rchesto per esegure, nel caso pessmo, una ntera sequenza d operazon. Se le operazon costose sono relatvamente meno frequent allora l costo rchesto
Anals ammortzzata Anals ammortzzata S consdera l tempo rchesto per esegure, nel caso pessmo, una ntera sequenza d operazon. Se le operazon costose sono relatvamente meno frequent allora l costo rchesto
Il lavoro L svolto da una forza costante è il prodotto scalare della forza per lo spostamento del punto di applicazione della forza medesima
 avoro ed Energa F s Fs cos θ F// s F 0 0 se: s 0 θ 90 Il lavoro svolto da una orza costante è l prodotto scalare della orza per lo spostamento del punto d applcazone della orza medesma [] [M T - ] N m
avoro ed Energa F s Fs cos θ F// s F 0 0 se: s 0 θ 90 Il lavoro svolto da una orza costante è l prodotto scalare della orza per lo spostamento del punto d applcazone della orza medesma [] [M T - ] N m
Dipartimento di Matematica per le scienze economiche e sociali Università di Bologna. Matematica aa lezione marzo 2009
 Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2008-2009 lezone 25 17 marzo 2009 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/26? Convesstà Sa I un ntervallo
Dpartmento d Matematca per le scenze economche e socal Unverstà d Bologna Matematca aa 2008-2009 lezone 25 17 marzo 2009 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/26? Convesstà Sa I un ntervallo
Meccanica Dinamica del corpo rigido
 Meccanca 08-09 Dnamca del corpo rgdo 7 ω L Equaon del moto: Momento angolare: Energa cnetca: Sstem corpo rgdo E F K dp dt L L + L ω M otaone d un corpo rgdo L ω Momento d nera: r dm V dl dt r m L L ω L
Meccanca 08-09 Dnamca del corpo rgdo 7 ω L Equaon del moto: Momento angolare: Energa cnetca: Sstem corpo rgdo E F K dp dt L L + L ω M otaone d un corpo rgdo L ω Momento d nera: r dm V dl dt r m L L ω L
Lavoro, Energia e stabilità dell equilibrio II parte
 Lavoro, Energa e stabltà dell equlbro II parte orze conservatve e non conservatve Il concetto d Energa potenzale s aanca per mportanza a quello d Energa cnetca, perché c permette d passare dallo studo
Lavoro, Energa e stabltà dell equlbro II parte orze conservatve e non conservatve Il concetto d Energa potenzale s aanca per mportanza a quello d Energa cnetca, perché c permette d passare dallo studo
Stabilità dei Sistemi Dinamici. Stabilità Semplice. Stabilità Asintotica. Stabilità: concetto intuitivo che può essere formalizzato in molti modi
 Gustavo Belforte Stabltà de Sstem Dnamc Gustavo Belforte Stabltà de Sstem Dnamc Stabltà de Sstem Dnamc Il Pendolo Stabltà: concetto ntutvo che può essere formalzzato n molt mod Intutvamente: Un oggetto
Gustavo Belforte Stabltà de Sstem Dnamc Gustavo Belforte Stabltà de Sstem Dnamc Stabltà de Sstem Dnamc Il Pendolo Stabltà: concetto ntutvo che può essere formalzzato n molt mod Intutvamente: Un oggetto
FISICA per SCIENZE BIOLOGICHE, A.A. 2005/2006 Prova scritta del 21 Giugno 2006
 FISICA per SCIENZE BIOLOGICHE, A.A. 5/6 Prova scrtta del Gugno 6 ) Un corpo d massa m = 5 g scvola lungo un pano nclnato lsco d altezza h = m e nclnazone θ=3 rspetto all orzzontale. Il corpo parte da ermo
FISICA per SCIENZE BIOLOGICHE, A.A. 5/6 Prova scrtta del Gugno 6 ) Un corpo d massa m = 5 g scvola lungo un pano nclnato lsco d altezza h = m e nclnazone θ=3 rspetto all orzzontale. Il corpo parte da ermo
Valore attuale di una rendita. Valore attuale in Excel: funzione VA
 Valore attuale d una rendta Nella scorsa lezone c samo concentrat sul problema del calcolo del alore attuale d una rendta S che è dato n generale da V ( S) { R ; t, 0,,,..., n,... } n 0 R ( t ), doe (t
Valore attuale d una rendta Nella scorsa lezone c samo concentrat sul problema del calcolo del alore attuale d una rendta S che è dato n generale da V ( S) { R ; t, 0,,,..., n,... } n 0 R ( t ), doe (t
Corrente elettrica e circuiti
 Corrente elettrca e crcut Generator d forza elettromotrce Intenstà d corrente Legg d Ohm esstenza e resstvtà esstenze n sere e n parallelo Effetto termco della corrente Legg d Krchhoff Corrente elettrca
Corrente elettrca e crcut Generator d forza elettromotrce Intenstà d corrente Legg d Ohm esstenza e resstvtà esstenze n sere e n parallelo Effetto termco della corrente Legg d Krchhoff Corrente elettrca
Strutture deformabili torsionalmente: analisi in FaTA-E
 Strutture deformabl torsonalmente: anals n FaTA-E Il comportamento dsspatvo deale è negatvamente nfluenzato nel caso d strutture deformabl torsonalmente. Nelle Norme Tecnche cò vene consderato rducendo
Strutture deformabl torsonalmente: anals n FaTA-E Il comportamento dsspatvo deale è negatvamente nfluenzato nel caso d strutture deformabl torsonalmente. Nelle Norme Tecnche cò vene consderato rducendo
Meccanica Dinamica del corpo rigido
 eccanca 07-08 7 Denstà Defnamo denstà d un eemento nfntesmo d ρ d ρ d In geneae ρ ρ( ) ρ( x,, ) < ρ Tea > 5.5 g cm ρtea ρ( ) 3 Pofo d denstà dea Tea Costa:. -.9 g cm -3 anteo: 3.4-5.6 g cm -3 Se assa totae
eccanca 07-08 7 Denstà Defnamo denstà d un eemento nfntesmo d ρ d ρ d In geneae ρ ρ( ) ρ( x,, ) < ρ Tea > 5.5 g cm ρtea ρ( ) 3 Pofo d denstà dea Tea Costa:. -.9 g cm -3 anteo: 3.4-5.6 g cm -3 Se assa totae
ELEMENTI DI MECCANICA. 3 Meccanica del corpo rigido
 ELEMENT D MECCANCA 3 Meccanca del corpo rgdo Govann Buccoler Unverstà del Salento, Dpartmento Matematca e Fsca e-mal: govann.buccoler@unsalento.t 1 Sstem d punt Fnora abbamo consderato sstem format da
ELEMENT D MECCANCA 3 Meccanca del corpo rgdo Govann Buccoler Unverstà del Salento, Dpartmento Matematca e Fsca e-mal: govann.buccoler@unsalento.t 1 Sstem d punt Fnora abbamo consderato sstem format da
Statistica e calcolo delle Probabilità. Allievi INF
 Statstca e calcolo delle Probabltà. Allev INF Proff. L. Ladell e G. Posta 06.09.10 I drtt d autore sono rservat. Ogn sfruttamento commercale non autorzzato sarà perseguto. Cognome e Nome: Matrcola: Docente:
Statstca e calcolo delle Probabltà. Allev INF Proff. L. Ladell e G. Posta 06.09.10 I drtt d autore sono rservat. Ogn sfruttamento commercale non autorzzato sarà perseguto. Cognome e Nome: Matrcola: Docente:
Ministero della Salute D.G. della programmazione sanitaria --- GLI ACC - L ANALISI DELLA VARIABILITÀ METODOLOGIA
 Mnstero della Salute D.G. della programmazone santara --- GLI ACC - L ANALISI DELLA VARIABILITÀ METODOLOGIA La valutazone del coeffcente d varabltà dell mpatto economco consente d ndvduare gl ACC e DRG
Mnstero della Salute D.G. della programmazone santara --- GLI ACC - L ANALISI DELLA VARIABILITÀ METODOLOGIA La valutazone del coeffcente d varabltà dell mpatto economco consente d ndvduare gl ACC e DRG
Il lavoro in termodinamica
 Il lavoro n termodnamca Il lavoro esterno: W est =-F e Dl (-: orza e spos. dscord) Il lavoro atto dal sstema sarà: W=-W est = F e Dl La orza eserctata dall ambente può essere dervata dalla pressone esterna:
Il lavoro n termodnamca Il lavoro esterno: W est =-F e Dl (-: orza e spos. dscord) Il lavoro atto dal sstema sarà: W=-W est = F e Dl La orza eserctata dall ambente può essere dervata dalla pressone esterna:
3. Esercitazioni di Teoria delle code
 3. Eserctazon d Teora delle code Poltecnco d Torno Pagna d 33 Prevsone degl effett d una decsone S ndvduano due tpologe d problem: statc: l problema non vara nel breve perodo dnamc: l problema vara Come
3. Eserctazon d Teora delle code Poltecnco d Torno Pagna d 33 Prevsone degl effett d una decsone S ndvduano due tpologe d problem: statc: l problema non vara nel breve perodo dnamc: l problema vara Come
Le forze conservative e l energia potenziale
 S dcono conservatve quelle orze che s comportano n accordo alla seguente denzone: La orza F s dce conservatva se l lavoro eseguto da tale orza sul punto materale P mentre s sposta dalla poszone P 1 alla
S dcono conservatve quelle orze che s comportano n accordo alla seguente denzone: La orza F s dce conservatva se l lavoro eseguto da tale orza sul punto materale P mentre s sposta dalla poszone P 1 alla
Statistica di Bose-Einstein
 Statstca d Bose-Ensten Esstono sstem compost d partcelle dentche e ndstngubl che non sono soggette al prncpo d esclusone. In quest sstem non esste un lmte al numero d partcelle che possono essere osptate
Statstca d Bose-Ensten Esstono sstem compost d partcelle dentche e ndstngubl che non sono soggette al prncpo d esclusone. In quest sstem non esste un lmte al numero d partcelle che possono essere osptate
La retroazione negli amplificatori
 La retroazone negl amplfcator P etroazonare un amplfcatore () sgnfca sottrarre (o sommare) al segnale d ngresso (S ) l segnale d retroazone (S r ) ottenuto dal segnale d uscta (S u ) medante un quadrpolo
La retroazone negl amplfcator P etroazonare un amplfcatore () sgnfca sottrarre (o sommare) al segnale d ngresso (S ) l segnale d retroazone (S r ) ottenuto dal segnale d uscta (S u ) medante un quadrpolo
1.5 - Correnti indotte
 .5 - Corrent ndotte Generatà - S è vsto ne precedent paragraf che una corrente eettrca genera un campo magnetco concatenato con a sorgente dea corrente (un fo, una spra, un soenode). Non s verfca fenomeno
.5 - Corrent ndotte Generatà - S è vsto ne precedent paragraf che una corrente eettrca genera un campo magnetco concatenato con a sorgente dea corrente (un fo, una spra, un soenode). Non s verfca fenomeno
Ricordiamo che una trasformazione ortogonale di coordinate da una terna T (O, i, j, k) a una terna T 0 (O 0, i 0, j 0, k 0 ) e rappresentata da
 III Sstem rgd 1. Grado d lberta d un sstema rgdo lbero Dare la poszone d un sstema rgdo S rspetto ad una terna T e equvalente a dare la poszone d una terna T 0 rspetto a T. Infatt dat tre punt non allneat
III Sstem rgd 1. Grado d lberta d un sstema rgdo lbero Dare la poszone d un sstema rgdo S rspetto ad una terna T e equvalente a dare la poszone d una terna T 0 rspetto a T. Infatt dat tre punt non allneat
Fisica Generale LA N.1 Prova Scritta del 12 Febbraio 2018 Prof. Nicola Semprini Cesari
 Fsca Generale A N. Prova Scrtta del Febbrao 8 Prof. Ncola Semprn Cesar Meccanca: quest ) Al tempo t= una carrozza ferrovara comnca a muovers d moto rettlneo unformemente accelerato (a). Al tempo t=t, da
Fsca Generale A N. Prova Scrtta del Febbrao 8 Prof. Ncola Semprn Cesar Meccanca: quest ) Al tempo t= una carrozza ferrovara comnca a muovers d moto rettlneo unformemente accelerato (a). Al tempo t=t, da
Geometria 1 a.a. 2011/12 Esonero del 23/01/12 Soluzioni (Compito A) sì determinarla, altrimenti dimostrare che ciò è impossibile.
 Geometra 1 a.a. 2011/12 Esonero del 23/01/12 Soluzon (Compto A) (1) S consder su C 2 l prodotto Hermtano, H assocato alla matrce ( ) 2 H =. 2 (a) Dmostrare che, H è defnto postvo e determnare una base
Geometra 1 a.a. 2011/12 Esonero del 23/01/12 Soluzon (Compto A) (1) S consder su C 2 l prodotto Hermtano, H assocato alla matrce ( ) 2 H =. 2 (a) Dmostrare che, H è defnto postvo e determnare una base
Induzione elettromagnetica
 Induzone elettromagnetca L esperenza d Faraday L'effetto d produzone d corrente elettrca n un crcuto prvo d generatore d tensone fu scoperto dal fsco nglese Mchael Faraday nel 83. Egl studò la relazone
Induzone elettromagnetca L esperenza d Faraday L'effetto d produzone d corrente elettrca n un crcuto prvo d generatore d tensone fu scoperto dal fsco nglese Mchael Faraday nel 83. Egl studò la relazone
Rotazione rispetto ad asse fisso Asse z : asse di rotazione
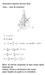 Rotaone rspetto ad asse fsso Asse : asse d rotaone 1 1 1 Ek= ω = ω= ω om. d nera: propreta d ogn corpo rgdo Dpende da: massa, forma e dmenson del corpo asse rspetto al quale lo s consdera Asta omogenea:
Rotaone rspetto ad asse fsso Asse : asse d rotaone 1 1 1 Ek= ω = ω= ω om. d nera: propreta d ogn corpo rgdo Dpende da: massa, forma e dmenson del corpo asse rspetto al quale lo s consdera Asta omogenea:
2. Le soluzioni elettrolitiche
 . Le soluzon elettroltche Classfcazone degl elettrolt: 1) soluzon elettroltche ) solvent onc: a) sal fus b) lqud onc 3) elettrolt sold Struttura del solvente Interazone one/solvente Interazone one/one
. Le soluzon elettroltche Classfcazone degl elettrolt: 1) soluzon elettroltche ) solvent onc: a) sal fus b) lqud onc 3) elettrolt sold Struttura del solvente Interazone one/solvente Interazone one/one
PROVA SCRITTA DI MECCANICA RAZIONALE (15 gennaio 2016) ( C.d.L. Ing. Energetica - Prof. A. Muracchini)
 PRV SRITT DI MENI RZINLE (15 gennao 2016) (.d.l. Ing. Energetca - Prof.. Muracchn) Il sstema n fgura, moble n un pano vertcale, è costtuto d un asta omogenea (massa m, lunghezza 2l) l cu estremo è vncolato
PRV SRITT DI MENI RZINLE (15 gennao 2016) (.d.l. Ing. Energetca - Prof.. Muracchn) Il sstema n fgura, moble n un pano vertcale, è costtuto d un asta omogenea (massa m, lunghezza 2l) l cu estremo è vncolato
LA COMPATIBILITA tra due misure:
 LA COMPATIBILITA tra due msure: 0.4 Due msure, supposte affette da error casual, s dcono tra loro compatbl quando la loro dfferenza può essere rcondotta ad una pura fluttuazone statstca attorno al valore
LA COMPATIBILITA tra due msure: 0.4 Due msure, supposte affette da error casual, s dcono tra loro compatbl quando la loro dfferenza può essere rcondotta ad una pura fluttuazone statstca attorno al valore
Dipartimento di Statistica Università di Bologna. Matematica Finanziaria aa 2011-2012 lezione 22: 30 maggio 2013
 Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 22: 30 maggo 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/27? Eserczo Dmostrare che l equazone della frontera
Dpartmento d Statstca Unverstà d Bologna Matematca Fnanzara aa 2011-2012 lezone 22: 30 maggo 2013 professor Danele Rtell www.unbo.t/docent/danele.rtell 1/27? Eserczo Dmostrare che l equazone della frontera
Intorduzione alla teoria delle Catene di Markov
 Intorduzone alla teora delle Catene d Markov Mchele Ganfelce a.a. 2014/2015 Defnzone 1 Sa ( Ω, F, {F n } n 0, P uno spazo d probabltà fltrato. Una successone d v.a. {ξ n } n 0 defnta su ( Ω, F, {F n }
Intorduzone alla teora delle Catene d Markov Mchele Ganfelce a.a. 2014/2015 Defnzone 1 Sa ( Ω, F, {F n } n 0, P uno spazo d probabltà fltrato. Una successone d v.a. {ξ n } n 0 defnta su ( Ω, F, {F n }
Calcolo della caduta di tensione con il metodo vettoriale
 Calcolo della caduta d tensone con l metodo vettorale Esempo d rete squlbrata ed effett del neutro nel calcolo. In Ampère le cadute d tensone sono calcolate vettoralmente. Per ogn utenza s calcola la caduta
Calcolo della caduta d tensone con l metodo vettorale Esempo d rete squlbrata ed effett del neutro nel calcolo. In Ampère le cadute d tensone sono calcolate vettoralmente. Per ogn utenza s calcola la caduta
Università di Napoli Parthenope Facoltà di Ingegneria
 Unverstà d Napol Parthenope acoltà d Ingegnera Corso d Metod Probablstc Statstc e Process Stocastc docente: Pro. Vto Pascazo 20 a Lezone: /2/2003 Sommaro Dstrbuzon condzonate: CD, pd, pm Teorema della
Unverstà d Napol Parthenope acoltà d Ingegnera Corso d Metod Probablstc Statstc e Process Stocastc docente: Pro. Vto Pascazo 20 a Lezone: /2/2003 Sommaro Dstrbuzon condzonate: CD, pd, pm Teorema della
MACROECONOMIA A.A. 2014/2015
 MACROECONOMIA A.A. 2014/2015 ESERCITAZIONE 2 MERCATO MONETARIO E MODELLO /LM ESERCIZIO 1 A) Un economa sta attraversando un perodo d profonda crs economca. Le banche decdono d aumentare la quota d depost
MACROECONOMIA A.A. 2014/2015 ESERCITAZIONE 2 MERCATO MONETARIO E MODELLO /LM ESERCIZIO 1 A) Un economa sta attraversando un perodo d profonda crs economca. Le banche decdono d aumentare la quota d depost
Unità Didattica N 5. Impulso e quantità di moto
 Imnpulso e quanttà d moto - - Impulso e quanttà d moto ) Sstema solato : orze nterne ed esterne...pag. 2 2) Impulso e quanttà d moto...pag. 3 3) Teorema d conservazone della quanttà d moto...pag. 6 4)
Imnpulso e quanttà d moto - - Impulso e quanttà d moto ) Sstema solato : orze nterne ed esterne...pag. 2 2) Impulso e quanttà d moto...pag. 3 3) Teorema d conservazone della quanttà d moto...pag. 6 4)
Esercizi di dinamica 2
 Esercizi di dinaica ) Un corpo di assa.0 kg si trova su un piano orizzontae scabro. I coefficiente di attrito statico tra corpo e piano è s 0.8. I corpo è sottoposto a azione di una forza orizzontae 7.0
Esercizi di dinaica ) Un corpo di assa.0 kg si trova su un piano orizzontae scabro. I coefficiente di attrito statico tra corpo e piano è s 0.8. I corpo è sottoposto a azione di una forza orizzontae 7.0
PROCEDURA INFORMATIZZATA PER LA COMPENSAZIONE DELLE RETI DI LIVELLAZIONE. (Metodo delle Osservazioni Indirette) - 1 -
 PROCEDURA INFORMATIZZATA PER LA COMPENSAZIONE DELLE RETI DI LIVELLAZIONE (Metodo delle Osservazon Indrette) - - SPECIFICHE DI CALCOLO Procedura software per la compensazone d una rete d lvellazone collegata
PROCEDURA INFORMATIZZATA PER LA COMPENSAZIONE DELLE RETI DI LIVELLAZIONE (Metodo delle Osservazon Indrette) - - SPECIFICHE DI CALCOLO Procedura software per la compensazone d una rete d lvellazone collegata
5. Limiti di funzione.
 Istituzioni di Matematiche - Appunti per e ezioni - Anno Accademico / 6 5. Limiti di funzione. 5.. Funzioni imitate. Una funzione y = f(x) definita in un intervao [ a b] imitata superiormente in tae intervao
Istituzioni di Matematiche - Appunti per e ezioni - Anno Accademico / 6 5. Limiti di funzione. 5.. Funzioni imitate. Una funzione y = f(x) definita in un intervao [ a b] imitata superiormente in tae intervao
Dai circuiti ai grafi
 Da crcut a graf Il grafo è una schematzzazone grafca semplfcata che rappresenta le propretà d nterconnessone del crcuto ad esso assocato Il grafo è costtuto da un nseme d nod e d lat Se lat sono orentat
Da crcut a graf Il grafo è una schematzzazone grafca semplfcata che rappresenta le propretà d nterconnessone del crcuto ad esso assocato Il grafo è costtuto da un nseme d nod e d lat Se lat sono orentat
CAMPI MAGNETICI E INDUZIONE ELETTROMAGNETICA
 CAMPI MAGETICI E IDUZIOE ELETTOMAGETICA Quando s para d camp magnetc, pù propramente s para d: B r IDUZIOE MAGETICA (o denstà d fusso magnetco) H r ITESITÀ DI CAMPO MAGETICO r r L equazone che ega queste
CAMPI MAGETICI E IDUZIOE ELETTOMAGETICA Quando s para d camp magnetc, pù propramente s para d: B r IDUZIOE MAGETICA (o denstà d fusso magnetco) H r ITESITÀ DI CAMPO MAGETICO r r L equazone che ega queste
Economie di scala, concorrenza imperfetta e commercio internazionale
 Sanna-Randacco Lezone n. 14 Econome d scala, concorrenza mperfetta e commerco nternazonale Non v è vantaggo comparato (e qund non v è commerco nter-ndustrale). S vuole dmostrare che la struttura d mercato
Sanna-Randacco Lezone n. 14 Econome d scala, concorrenza mperfetta e commerco nternazonale Non v è vantaggo comparato (e qund non v è commerco nter-ndustrale). S vuole dmostrare che la struttura d mercato
Elettricità e circuiti
 Elettrctà e crcut Generator d forza elettromotrce Intenstà d corrente Legg d Ohm esstenza e resstvtà Effetto termco della corrente esstenze n sere e n parallelo Legg d Krchoff P. Maestro Elettrctà e crcut
Elettrctà e crcut Generator d forza elettromotrce Intenstà d corrente Legg d Ohm esstenza e resstvtà Effetto termco della corrente esstenze n sere e n parallelo Legg d Krchoff P. Maestro Elettrctà e crcut
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Soluzioni 3.1. n(n 1) (n k + 1) z n k! k + 1 n k. lim k
 (1) La sere bnomale è B n (z) = k=0 Con l metodo del rapporto s ottene R = lm k Soluzon 3.1 n(n 1) (n k + 1) z n k! c k c k+1 = lm k k + 1 n k lm k c k z k. k=0 1 + 1 k 1 n k = 1 (2) La multfunzone f(z)
(1) La sere bnomale è B n (z) = k=0 Con l metodo del rapporto s ottene R = lm k Soluzon 3.1 n(n 1) (n k + 1) z n k! c k c k+1 = lm k k + 1 n k lm k c k z k. k=0 1 + 1 k 1 n k = 1 (2) La multfunzone f(z)
LE FREQUENZE CUMULATE
 LE FREQUENZE CUMULATE Dott.ssa P. Vcard Introducamo questo argomento con l seguente Esempo: consderamo la seguente dstrbuzone d un campone d 70 sttut d credto numero flal present nel terrtoro del comune
LE FREQUENZE CUMULATE Dott.ssa P. Vcard Introducamo questo argomento con l seguente Esempo: consderamo la seguente dstrbuzone d un campone d 70 sttut d credto numero flal present nel terrtoro del comune
INDICI STATISTICI MEDIA, MODA, MEDIANA, VARIANZA
 Lezone 7 - Indc statstc: meda, moda, medana, varanza INDICI STATISTICI MEDIA, MODA, MEDIANA, VARIANZA GRUPPO MAT06 Dp. Matematca, Unverstà d Mlano - Probabltà e Statstca per le Scuole Mede -SILSIS - 2007
Lezone 7 - Indc statstc: meda, moda, medana, varanza INDICI STATISTICI MEDIA, MODA, MEDIANA, VARIANZA GRUPPO MAT06 Dp. Matematca, Unverstà d Mlano - Probabltà e Statstca per le Scuole Mede -SILSIS - 2007
Metodi e Modelli per l Ottimizzazione Combinatoria Progetto: Metodo di soluzione basato su generazione di colonne
 Metod e Modell per l Ottmzzazone Combnatora Progetto: Metodo d soluzone basato su generazone d colonne Lug De Govann Vene presentato un modello alternatvo per l problema della turnazone delle farmace che
Metod e Modell per l Ottmzzazone Combnatora Progetto: Metodo d soluzone basato su generazone d colonne Lug De Govann Vene presentato un modello alternatvo per l problema della turnazone delle farmace che
F = 0 L = 0 se: s = 0 = 90 [L] = [ML 2 T -2 ] F // 1J = 10 7 erg
![F = 0 L = 0 se: s = 0 = 90 [L] = [ML 2 T -2 ] F // 1J = 10 7 erg F = 0 L = 0 se: s = 0 = 90 [L] = [ML 2 T -2 ] F // 1J = 10 7 erg](/thumbs/96/128573130.jpg) ) Un corpo d massa 5 kg è posto su un pano nclnato d 0. Una orza orzzontale d 00 N a rsalre l corpo lungo l pano nclnato con un accelerazone d 0.5 m/s. Qual è l coecente d attrto ra l corpo e l pano nclnato?
) Un corpo d massa 5 kg è posto su un pano nclnato d 0. Una orza orzzontale d 00 N a rsalre l corpo lungo l pano nclnato con un accelerazone d 0.5 m/s. Qual è l coecente d attrto ra l corpo e l pano nclnato?
Un montacarichi ha una potenza di 2x10 4 W quanto tempo impiega a sollevare a 20m di altezza un carico costituito da 40 sacchi da 85kg l'uno.
 Un montacarch ha una potenza d x0 4 W quanto tempo mpega a sollevare a 0m d altezza un carco costtuto da 40 sacch da 85kg l'uno. P t mgh ( 4085) 9.8 0 667000J 667000 t 33s P 0000 Calcolare l lavoro computo
Un montacarch ha una potenza d x0 4 W quanto tempo mpega a sollevare a 0m d altezza un carco costtuto da 40 sacch da 85kg l'uno. P t mgh ( 4085) 9.8 0 667000J 667000 t 33s P 0000 Calcolare l lavoro computo
Capitolo 7. La «sintesi neoclassica» e il modello IS-LM. 2. La curva IS
 Captolo 7 1. Il modello IS-LM La «sntes neoclassca» e l modello IS-LM Defnzone: ndvdua tutte le combnazon d reddto e saggo d nteresse per le qual l mercato de ben (curva IS) e l mercato della moneta (curva
Captolo 7 1. Il modello IS-LM La «sntes neoclassca» e l modello IS-LM Defnzone: ndvdua tutte le combnazon d reddto e saggo d nteresse per le qual l mercato de ben (curva IS) e l mercato della moneta (curva
Meccanica Dinamica del corpo rigido
 Meccanca 8-9 6 Fora peso sul corpo rgdo Corpo sottoposto alla fora peso: Su ogn elemento nfntesmo d massa dm agsce la fora Rsultante delle fore: F peso V g dm Momento rsultante (polo ): M V Energa potenale:
Meccanca 8-9 6 Fora peso sul corpo rgdo Corpo sottoposto alla fora peso: Su ogn elemento nfntesmo d massa dm agsce la fora Rsultante delle fore: F peso V g dm Momento rsultante (polo ): M V Energa potenale:
PROVA SCRITTA DI MECCANICA RAZIONALE (13 gennaio 2017) (Prof. A. Muracchini)
 PRV SCRITT DI ECCNIC RZINLE (13 gennao 017) (Prof.. uracchn) Il sstema rappresentato n fgura è costtuto da: a) una lamna pesante, omogenea a forma d trangolo soscele (massa m, base l, altezza h) vncolata
PRV SCRITT DI ECCNIC RZINLE (13 gennao 017) (Prof.. uracchn) Il sstema rappresentato n fgura è costtuto da: a) una lamna pesante, omogenea a forma d trangolo soscele (massa m, base l, altezza h) vncolata
Equilibrio e stabilità di sistemi dinamici. Stabilità dell equilibrio di sistemi dinamici non lineari per linearizzazione
 Equlbro e stabltà d sstem dnamc Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem NL TC Crter d stabltà
Equlbro e stabltà d sstem dnamc Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem NL TC Crter d stabltà
Risoluzione di travature reticolari iperstatiche col metodo delle forze. Complemento alla lezione 43/50: Il metodo delle forze II
 Risouzione di travature reticoari iperstatiche co metodo dee forze ompemento aa ezione 3/50: I metodo dee forze II sercizio. er a travatura reticoare sotto riportata, determinare gi sforzo nee aste che
Risouzione di travature reticoari iperstatiche co metodo dee forze ompemento aa ezione 3/50: I metodo dee forze II sercizio. er a travatura reticoare sotto riportata, determinare gi sforzo nee aste che
asse fisso nel tempo in rotazione attorno ad un asse fisso dell asse di rotazione rimarranno fermi al passar del temporispetto al sistema inerziale
 Rotaon rgde attorno ad un asse fsso nel tempo un corpo rgdo n rotaone attorno ad un asse fsso ha un solo grado d lberta n quest cas per descrvere l moto converra rferrs ad un polo fsso se l asse d rotaone
Rotaon rgde attorno ad un asse fsso nel tempo un corpo rgdo n rotaone attorno ad un asse fsso ha un solo grado d lberta n quest cas per descrvere l moto converra rferrs ad un polo fsso se l asse d rotaone
STATISTICA DESCRITTIVA - SCHEDA N. 5 REGRESSIONE LINEARE
 Matematca e statstca: da dat a modell alle scelte www.dma.unge/pls_statstca Responsabl scentfc M.P. Rogantn e E. Sasso (Dpartmento d Matematca Unverstà d Genova) STATISTICA DESCRITTIVA - SCHEDA N. REGRESSIONE
Matematca e statstca: da dat a modell alle scelte www.dma.unge/pls_statstca Responsabl scentfc M.P. Rogantn e E. Sasso (Dpartmento d Matematca Unverstà d Genova) STATISTICA DESCRITTIVA - SCHEDA N. REGRESSIONE
L = L E k 2 ENERGIA CINETICA DI ROTAZIONE. Espressione generica dell energia cinetica di rotazione: 1 ω
 NRGIA CINTICA DI ROTAZION k m R ) ( k R m R m spressone generca dell energa cnetca d rotazone: I k Se la rotazone aene ntorno ad un asse prncpale d nerza, allora: I L da cu: I L k NRGIA CINTICA DI ROTOTRASLAZION
NRGIA CINTICA DI ROTAZION k m R ) ( k R m R m spressone generca dell energa cnetca d rotazone: I k Se la rotazone aene ntorno ad un asse prncpale d nerza, allora: I L da cu: I L k NRGIA CINTICA DI ROTOTRASLAZION
MATEMATICA FINANZIARIA 1 ECONOMIA AZIENDALE. Cognome... Nome Matricola..
 MATEMATICA FINANZIARIA PROVA SCRITTA DEL 0 FEBBRAIO 009 ECONOMIA AZIENDALE Cognome... Nome Matrcola.. ESERCIZIO Un ndduo ha ogg a dsposzone una somma S0.000 che ha accumulato negl ultm ann tramte l ersamento
MATEMATICA FINANZIARIA PROVA SCRITTA DEL 0 FEBBRAIO 009 ECONOMIA AZIENDALE Cognome... Nome Matrcola.. ESERCIZIO Un ndduo ha ogg a dsposzone una somma S0.000 che ha accumulato negl ultm ann tramte l ersamento
Capitolo 3 Covarianza, correlazione, bestfit lineari e non lineari
 Captolo 3 Covaranza, correlazone, bestft lnear e non lnear ) Covaranza e correlazone Ad un problema s assoca spesso pù d una varable quanttatva (es.: d una persona possamo determnare peso e altezza, oppure
Captolo 3 Covaranza, correlazone, bestft lnear e non lnear ) Covaranza e correlazone Ad un problema s assoca spesso pù d una varable quanttatva (es.: d una persona possamo determnare peso e altezza, oppure
Esercitazione VIII - Lavoro ed energia II
 Esercitazione VIII - Lavoro ed energia II Forze conservative Esercizio Una pallina di massa m = 00g viene lanciata tramite una molla di costante elastica = 0N/m come in figura. Ammesso che ogni attrito
Esercitazione VIII - Lavoro ed energia II Forze conservative Esercizio Una pallina di massa m = 00g viene lanciata tramite una molla di costante elastica = 0N/m come in figura. Ammesso che ogni attrito
Il modello markoviano per la rappresentazione del Sistema Bonus Malus. Prof. Cerchiara Rocco Roberto. Materiale e Riferimenti
 Il modello marovano per la rappresentazone del Sstema Bonus Malus rof. Cercara Rocco Roberto Materale e Rferment. Lucd dstrbut n aula. Lemare 995 (pag.6- e pag. 74-78 3. Galatoto G. 4 (tt del VI Congresso
Il modello marovano per la rappresentazone del Sstema Bonus Malus rof. Cercara Rocco Roberto Materale e Rferment. Lucd dstrbut n aula. Lemare 995 (pag.6- e pag. 74-78 3. Galatoto G. 4 (tt del VI Congresso
Corpi rigidi (prima parte)
 Corp rgd (prma parte) Corp rgd Un corpo rgdo è un corpo n cu le dstane tra le vare par che lo compongono rmangono costan3. r CM d CM È un po parcolare d sstema d N parcelle. Valgono ancora le legg dp dt
Corp rgd (prma parte) Corp rgd Un corpo rgdo è un corpo n cu le dstane tra le vare par che lo compongono rmangono costan3. r CM d CM È un po parcolare d sstema d N parcelle. Valgono ancora le legg dp dt
Le soluzioni della prova scritta di Matematica per il corso di laurea in Farmacia (raggruppamento M-Z)
 Le soluzon della prova scrtta d Matematca per l corso d laurea n Farmaca (raggruppamento M-Z). Data la funzone a. trova l domno d f f ( ) ln + b. scrv, esplctamente e per esteso, qual sono gl ntervall
Le soluzon della prova scrtta d Matematca per l corso d laurea n Farmaca (raggruppamento M-Z). Data la funzone a. trova l domno d f f ( ) ln + b. scrv, esplctamente e per esteso, qual sono gl ntervall
FISICA per SCIENZE BIOLOGICHE, A.A. 2014/2015 Prova scritta del 24 Febbraio 2015
 FISICA per SCIENZE BIOLOGICHE, A.A. 04/05 Prova scrtta del 4 Febbrao 05 ) Un corpo d massa m = 300 g scvola lungo un pano nclnato lsco d altezza h = 3m e nclnazone θ=30 0 rspetto all orzzontale. Il corpo
FISICA per SCIENZE BIOLOGICHE, A.A. 04/05 Prova scrtta del 4 Febbrao 05 ) Un corpo d massa m = 300 g scvola lungo un pano nclnato lsco d altezza h = 3m e nclnazone θ=30 0 rspetto all orzzontale. Il corpo
SU UNA CLASSE DI EQUAZIONI CONSERVATIVE ED IPERBOLICHE COMPLETAMENTE ECCEZIONALI E COMPATIBILI CON UNA LEGGE DI CONSERVAZIONE SUPPLEMENTARE
 SU UNA CLASSE DI EQUAZIONI CONSERVATIVE ED IPERBOLICHE COMPLETAMENTE ECCEZIONALI E COMPATIBILI CON UNA LEGGE DI CONSERVAZIONE SUPPLEMENTARE GIOVANNI CRUPI, ANDREA DONATO SUMMARY. We characterze a set of
SU UNA CLASSE DI EQUAZIONI CONSERVATIVE ED IPERBOLICHE COMPLETAMENTE ECCEZIONALI E COMPATIBILI CON UNA LEGGE DI CONSERVAZIONE SUPPLEMENTARE GIOVANNI CRUPI, ANDREA DONATO SUMMARY. We characterze a set of
1 La domanda di moneta
 La domanda d moneta Eserczo.4 (a) Keynes elenca tre motv per detenere moneta: Scopo transattvo Scopo precauzonale Scopo speculatvo Il modello d domanda d moneta a scopo speculatvo d Keynes consdera la
La domanda d moneta Eserczo.4 (a) Keynes elenca tre motv per detenere moneta: Scopo transattvo Scopo precauzonale Scopo speculatvo Il modello d domanda d moneta a scopo speculatvo d Keynes consdera la
( F) Anello frenato Dati. M=2 kg massa dell anello R=2 m raggio dell anello rad ω= 10 (negativo perchè in senso orario) velocità iniziale dell'anello
 Anello renato Dat M= kg massa dell anello R= m raggo dell anello rad = 10 (negatvo perchè n senso oraro) veloctà nale dell'anello s = 0 veloctà nale dell'anello F= 10 ˆ 5ˆj ora applcata al dsco r = O=+
Anello renato Dat M= kg massa dell anello R= m raggo dell anello rad = 10 (negatvo perchè n senso oraro) veloctà nale dell'anello s = 0 veloctà nale dell'anello F= 10 ˆ 5ˆj ora applcata al dsco r = O=+
Premessa essa sulle soluzioni
 Appunt d Chmca La composzone delle soluzon Premessa sulle soluzon...1 Concentrazone...2 Frazone molare...2 Molartà...3 Normaltà...4 Molaltà...4 Percentuale n peso...4 Percentuale n volume...5 Massa per
Appunt d Chmca La composzone delle soluzon Premessa sulle soluzon...1 Concentrazone...2 Frazone molare...2 Molartà...3 Normaltà...4 Molaltà...4 Percentuale n peso...4 Percentuale n volume...5 Massa per
POLITECNICO DI BARI - DICATECh Corso di Laurea in Ingegneria Ambientale e del Territorio IDRAULICA AMBIENTALE - A.A. 2015/2016 ESONERO 15/01/2016
 POLITECNICO DI BARI - DICATECh Corso d Laurea n Ingegnera Ambentale e del Terrtoro IDRAULICA AMBIENTALE - A.A. 015/016 ESONERO 15/01/016 ESERCIZIO 1 S consder la rete aperta n fgura, nella quale le portate
POLITECNICO DI BARI - DICATECh Corso d Laurea n Ingegnera Ambentale e del Terrtoro IDRAULICA AMBIENTALE - A.A. 015/016 ESONERO 15/01/016 ESERCIZIO 1 S consder la rete aperta n fgura, nella quale le portate
links utili:
 dspensa d Govann Bachelet Meccanca de Sstem, maggo 2003 lnks utl: http://scenceworld.wolfram.com/physcs/angularmomentum.html http://hyperphyscs.phy-astr.gsu.edu/hbase/necon.html Momento della quanttà d
dspensa d Govann Bachelet Meccanca de Sstem, maggo 2003 lnks utl: http://scenceworld.wolfram.com/physcs/angularmomentum.html http://hyperphyscs.phy-astr.gsu.edu/hbase/necon.html Momento della quanttà d
Corso di laurea in Ingegneria Meccatronica. DINAMICI CA - 04 ModiStabilita
 Automaton Robotcs and System CONTROL Unverstà degl Stud d Modena e Reggo Emla Corso d laurea n Ingegnera Meccatronca MODI E STABILITA DEI SISTEMI DINAMICI CA - 04 ModStablta Cesare Fantuzz (cesare.fantuzz@unmore.t)
Automaton Robotcs and System CONTROL Unverstà degl Stud d Modena e Reggo Emla Corso d laurea n Ingegnera Meccatronca MODI E STABILITA DEI SISTEMI DINAMICI CA - 04 ModStablta Cesare Fantuzz (cesare.fantuzz@unmore.t)
Dipartimento di Economia Aziendale e Studi Giusprivatistici. Università degli Studi di Bari Aldo Moro. Corso di Macroeconomia 2014
 Dpartmento d Economa Azendale e Stud Gusprvatstc Unverstà degl Stud d Bar Aldo Moro Corso d Macroeconoma 2014 1.Consderate l seguente grafco: LM Partà de tass d nteresse LM B A IS IS Y E E E Immagnate
Dpartmento d Economa Azendale e Stud Gusprvatstc Unverstà degl Stud d Bar Aldo Moro Corso d Macroeconoma 2014 1.Consderate l seguente grafco: LM Partà de tass d nteresse LM B A IS IS Y E E E Immagnate
Principi di ingegneria elettrica. Lezione 6 a. Analisi delle reti resistive
 Prncp d ngegnera elettrca Lezone 6 a Anals delle ret resste Anals delle ret resste L anals d una rete elettrca (rsoluzone della rete) consste nel determnare tutte le corrent ncognte ne ram e tutt potenzal
Prncp d ngegnera elettrca Lezone 6 a Anals delle ret resste Anals delle ret resste L anals d una rete elettrca (rsoluzone della rete) consste nel determnare tutte le corrent ncognte ne ram e tutt potenzal
Lezione 10. L equilibrio del mercato finanziario: la struttura dei tassi d interesse
 Lezone 1. L equlbro del mercato fnanzaro: la struttura de tass d nteresse Ttol con scadenza dversa hanno prezz (e tass d nteresse) dfferent. Due ttol d durata dversa emess dallo stesso soggetto (stesso
Lezone 1. L equlbro del mercato fnanzaro: la struttura de tass d nteresse Ttol con scadenza dversa hanno prezz (e tass d nteresse) dfferent. Due ttol d durata dversa emess dallo stesso soggetto (stesso
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
Lezione n.13. Regime sinusoidale
 Lezone 3 Regme snusodale Lezone n.3 Regme snusodale. Rcham sulle funzon snusodal. etodo de fasor e fasor. mpedenza ed ammettenza. Dagramm fasoral 3. Potenza n regme snusodale 3. Potenza attva e reattva
Lezone 3 Regme snusodale Lezone n.3 Regme snusodale. Rcham sulle funzon snusodal. etodo de fasor e fasor. mpedenza ed ammettenza. Dagramm fasoral 3. Potenza n regme snusodale 3. Potenza attva e reattva
Circuiti di ingresso differenziali
 rcut d ngresso dfferenzal - rcut d ngresso dfferenzal - Il rfermento per potenzal Gl stad sngle-ended e dfferenzal I segnal elettrc prodott da trasduttor, oppure preleat da un crcuto o da un apparato elettrco,
rcut d ngresso dfferenzal - rcut d ngresso dfferenzal - Il rfermento per potenzal Gl stad sngle-ended e dfferenzal I segnal elettrc prodott da trasduttor, oppure preleat da un crcuto o da un apparato elettrco,
Il logaritmo discreto in Z p Il gruppo moltiplicativo Z p delle classi resto modulo un primo p è un gruppo ciclico.
 Il logartmo dscreto n Z p Il gruppo moltplcatvo Z p delle class resto modulo un prmo p è un gruppo cclco. Defnzone (Logartmo dscreto). Sa p un numero prmo e sa ā una radce prmtva n Z p. Sa ȳ Z p. Il logartmo
Il logartmo dscreto n Z p Il gruppo moltplcatvo Z p delle class resto modulo un prmo p è un gruppo cclco. Defnzone (Logartmo dscreto). Sa p un numero prmo e sa ā una radce prmtva n Z p. Sa ȳ Z p. Il logartmo
Determinazione del momento d inerzia di una massa puntiforme
 Determnazone del momento d nerza d una massa puntorme Materale utlzzato Set d accessor per mot rotator Sensore d rotazone Portamasse e masse agguntve Statvo con base Blanca elettronca Calbro nteracca GLX
Determnazone del momento d nerza d una massa puntorme Materale utlzzato Set d accessor per mot rotator Sensore d rotazone Portamasse e masse agguntve Statvo con base Blanca elettronca Calbro nteracca GLX
INDICE. Scaricabile su: Derivate TEORIA. Derivata in un punto. Significato geometrico della derivata
 P r o f Gu d of r a n c n Anteprma Anteprma Anteprma www l e z o n j md o c o m Scarcable su: ttp://lezonjmdocom/ INDICE TEORIA Dervata n un punto Sgnfcato geometrco della dervata Funzone dervata e dervate
P r o f Gu d of r a n c n Anteprma Anteprma Anteprma www l e z o n j md o c o m Scarcable su: ttp://lezonjmdocom/ INDICE TEORIA Dervata n un punto Sgnfcato geometrco della dervata Funzone dervata e dervate
Dinamica dei sistemi di punti materiali. Dott.ssa Elisabetta Bissaldi
 Dnamca de sstem d punt materal Dott.ssa Elsabetta Bssald Elsabetta Bssald (Poltecnco d Bar) A.A. 2018-2019 2 Sstem d punt materal Sno ad ora s è studato l moto d un sngolo punto materale. Nella dnamca
Dnamca de sstem d punt materal Dott.ssa Elsabetta Bssald Elsabetta Bssald (Poltecnco d Bar) A.A. 2018-2019 2 Sstem d punt materal Sno ad ora s è studato l moto d un sngolo punto materale. Nella dnamca
