I METODI DI DISCESA. Il teorema afferma quindi che risolvere il sistema (1) equivale a minimizzare la funzione (2).
|
|
|
- Cosima Buono
- 6 anni fa
- Visualizzazioni
Transcript
1 I MEODI DI DICE. Genealità sui metodi di discesa Pe la isoluzione di un sistema lineae b con matice eale simmetica e definita ositiva un alta famiglia di metodi iteativi è data dai così detti metodi di discesa. Il isultato teoico alla base di questi metodi è il seguente: eoema: ia R nn matice simmetica e definita ositiva alloa la soluzione del sistema lineae b coincide con il unto di minimo della seguente funzione quadatica n n n F b b aij i j bi i i j i ove la foma quadatica Q è ositiva e 0. Il teoema affema quindi che isolvee il sistema equivale a minimizzae la funzione. Dimostazione: e consideiamo il sistema e sostituiamo in esso al osto di un vettoe tentativo si otteà un vettoe esiduo di comonenti.... n - b La soluzione del sistema si otteà modificando successivamente il vettoe in modo tale che il vettoe diventi seme iù iccolo fino a scomaie; si ha cioè che il vettoe * coisonde a * - b 0.
2 Oa consideiamo la funzione quadatica: F b e cechiamo il suo unto di minimo. questo scoo deiviamo azialmente la funzione quadatica ed eguagliamo a zeo le deivate; e il fatto che la Q è ositiva il unto tovato saà oio il minimo della F. F i n j a ij j b i 0 i.. n ma questo equivale a scivee F * - b 0. Quindi il vettoe * che minimizza la funzione F coincide con la soluzione del sistema lineae ; vicevesa la soluzione del sistema con matice simmetica definita ositiva minimizza la coisondente funzione quadatica. Il isultato di questo teoema ci emette di affemae che e la isoluzione di sistemi lineai con matice simmetica definita ositiva in geneale ossono essee usati i metodi e deteminae il minimo di una funzione quadatica noti come metodi di discesa. Questi metodi consistono nel deteminae a atie da un vettoe iniziale una diezione ootuna e nel coeggee in questa diezione in modo che il valoe della funzione quadatica F nel nuovo unto t diminuisca cioè F t < F. Peché ciò avvenga il aameto t e la diezione devono essee scelti in modo ootuno. I diffeenti metodi di discesa sono caatteizzati dalla scelta della diezione di discesa fa le diezioni di discesa ammissibili.
3 La deteminazione del aameto t che emette di endee minima la F nella diezione è quello che diffeenzia i metodi suddetti quando vengono imiegati e la soluzione del sistema lineae b quindi in cui sia nota da quando vengono imiegati e deteminae il minimo di una funzione qualsiasi in cui quindi la matice è la matice delle deivate aziali seconde e quindi non è nota.. celta del aameto t Nel caso in cui la matice sia nota si vede infatti che F t t F t è una funzione quadatica in t. t t b t t Pe deteminane il minimo isetto a t basta consideae df dt t b t b t e uguaglialo a 0; si ottiene e il aameto t il valoe t b min 3 Questo significa che una volta deteminata la diezione ovveo scelto il metodo di minimizzazione la elazione 3 ci fonisce il valoe da assegnae al aameto t e ottenee il minimo valoe ossibile della F lungo la diezione. 3
4 Ossevazione: il valoe di t fonito dalla 3 ci fonisce un minimo e F in quanto se effettuiamo la deivata seconda in t otteniamo d dt F Che è una quantità ositiva e ogni diezione di. Nel caso in cui il metodo venga alicato e deteminae il minimo di una funzione e quindi la matice non sia nota il valoe di t ottimale si ottiene isolvendo un oblema di minimo monodimensionale e la funzione Ft. Nel unto di minimo ottenuto usando la fomula 3 e il valoe del aameto t abbiamo il seguente isultato: eoema: Nel unto di minimo t min ottenuto muovendosi lungo la diezione con t dato dalla 3 il vettoe esiduo b isulta otogonale alla diezione cioè ' 0 * Dimostazione: Essendo ' ' b t b t i ottiene ' t che isulta 0 scegliendo t secondo la 3. 4
5 3. Condizioni di ammissibilità e la diezione di discesa Pe quanto iguada la scelta delle diezioni di discesa se si considea la elazione t min si uò affemae che non deve essee otogonale al esiduo o in modo equivalente non deve essee otogonale al gadiente di F F eché questo oteebbe a t min 0. e inolte consideiamo lo sviluo in seie di aylo della F cioè F t F t F... e ichiediamo che nel unto t si abbia F t < F e t 0 4 alloa la diezione deve soddisfae la seguente condizione F < 0 che aesenta la condizione di diezione ammissibile. Questa condizione ci dice che l angolo fa la nuova diezione di discesa e il gadiente della F deve avee coseno negativo icodiamo che F F cosθ dove l angolo θ è l angolo fa i due vettoi cioè l angolo θ deve essee maggioe di π/. Poiché la condizione di ammissibilità e la diezione di discesa è data in funzione del gadiente della F i metodi di discesa vengono anche chiamati metodi del gadiente. Es: Inteetazione geometica dei metodi di discesa Nel caso n la funzione Fcost è aesentata da ellissi concentiche il cui cento coincide con il minimo della funzione quadatica F e costituisce la 5
6 soluzione del oblema. Il seguente gafico mosta quanto affemato dalla condizione di ammissibilità e la diezione di discesa. 4. Metodo della Discesa iù Riida teeest Descent Il metodo di Discesa iù Riida teeest Descent è caatteizzato dalla scelta ad ogni asso della diezione come l antigadiente della F calcolato nell iteato - -esimo ovveo F b. 5 Questo significa che ad ogni asso il vettoe coincide con la diezione di massima endenza e F. In questo caso la 6 diventa e t min t. min 6
7 5. Metodo del Gadiente Coniugato In questo metodo la scelta della diezione di discesa tiene conto non solo del gadiente della F - cioè di - ma anche della diezione di discesa -. In aticolae nel metodo del Gadiente Coniugato al geneico asso atendo dal unto - che è stato ottenuto muovendosi lungo la diezione - e in cui è stato calcolato il esiduo - otogonale a - si sceglie la nuova diezione di discesa come quella aatenente al iano π - assante e - e individuato dai due vettoi otogonali - e -. Più ecisamente si ha γ... 6 Il iano π - inteseca la funzione F con un ellisse assante e -. Poiché - ea stato scelto come unto di minimo nella diezione - in - l ellisse isulta tangente alla diezione di discesa -. Poiché il unto di minimo nel iano π - coincide con il cento dell ellisse il aameto γ - saà scelto in modo che la diezione unti veso il cento dell ellisse cioè sia il coniugato isetto all ellisse di -. Ciò significa che deve soddisfae la seguente elazione: 0. 7 ostituendo l esessione γ nella 7 si ottiene γ. * * Utilizzando tale valoe nella 6 si ottiene la nuova diezione e il nuovo unto viene calcolato come unto di minimo nella diezione cioè con 8 7
8 ... 9 i noti che in 8 gioca il uolo di t nelle fomule del aagafo ecedente e quindi la 9 aesenta il valoe che assume nel unto di minimo nella diezione. Le elazioni 6 ** 8 e 9 definiscono sostanzialmente il metodo del gadiente coniugato. Ci avvaliamo oa di alcuni isultati che emettono di semlificane le fomule iducendone la comlessità comutazionale. La ima semlificazione si ottiene ossevando che e il esiduo è ossibile definie una fomula icosiva che lo aggiona utilizzando una quantità che è necessaia anche e calcolae alte gandezze cioè cioè b b. 0 La seconda semlificazione segue dal seguente eoema: Nel metodo del gadiente coniugato le diezioni di discesa con.. fomano un sistema di diezioni coniugate mente i vettoi esidui con 0.. fomano un sistema otogonale cioè
9 Ossevazione: Poiché in R n non si ossono avee iù di n vettoi che costituiscono un sistema otogonale in linea teoica questa classe di metodi aatiene ai metodi dietti oiché viene costuita una successione { } 0.. di vettoi tali che * b quando n-. In atica eò a causa degli eoi di aotondamento il metodo non temina al asso n- e viene quindi utilizzato come metodo iteativo. In molti casi comunque si veifica che il numeo di iteazioni che occoono e aggiungee la ecisione ichiesta è di gan lunga infeioe alla dimensione del sistema e questo ende il metodo molto utile e oblemi di gosse dimensioni. Utilizziamo oa il fatto che i esidui in due assi successivi sono otogonali e ottenee un ulteioe oietà di otogonalità. Infatti sostituendo nella elazione che esime il isultato geneale l esessione di ottiene 0 data dalla e utilizzando la oietà di otogonalità 8 si 0 γ 0. Mediante questi isultati è ossibile tovae una nuova esessione e il aameto dato dalla 9. Infatti oiché si ottiene γ
10 .. 3 Da questa fomula si vede che se il esiduo non è nullo è seme ositivo. Utilizzando oa la fomula icoente 0 e il esiduo e la nuova esessione 3 di è ossibile tovae una fomula comutazionalmente iù efficiente e γ -. Dalla fomula icoente del esiduo si ottiene e quindi [ ] ostituendo oa la fomula di si ottiene e quindi l esessione di γ - diviene [ [? ]. 4 ]. 0
11 In definitiva l algoitmo del Gadiente Coniugato uò essee schematizzato come segue: celto 0 abitaio si calcola b si ende - 0 Pe If γ ε %test di convegenza non soddisfatto % Calcolo la nuova diezione di discesa γ else %ECI:test di convegenza soddisfatto etun Ossevazione: l algoitmo del gadiente coniugato così ottimizzato necessita di un unica moltilicazione matice e vettoe e ogni iteazione. Velocità di Convegenza La velocità di convegenza di un metodo iteativo si uò misuae consideando di quanto si è idotto l eoe iniziale alla -esima iteazione. Pe misuae l eoe si definisce la noma indotta dalla matice simmetica definita ositiva su come
12 . Pe il metodo del gadiente teeest Descent vale la seguente elazione K K * 0 * Petanto definendo l eoe al asso e * si ha 0 e K K e dove K è l indice di condizionamento di dato da K - ma / min. anto iù K è alto tanto iù il aoto K K e quindi tanto iù è lenta la convegenza. Pe il metodo del gadiente coniugato vale la seguente elazione K K * 0 * cioè 0 e K K e che mosta come la convegenza di questo metodo u imanendo seme legata all indice di condizionamento di sia iù veloce di quella del metodo di teeest Descent a aità di valoi di K. Comunque se la matice è molto mal condizionata uò accadee che siano necessai molti assi di iteazione e ottenee la convegenza.
13 Poiché l obiettivo dei metodi iteativi è quello di ottenee una buona aossimazione della soluzione del sistema b con mediamente oche iteazioni sono state studiate tecniche di econdizionamento che tasfomano il oblema oiginale in un oblema equivalente ma meglio condizionato. Ossevazione: Poiché la funzione quadatica F data dalla assegnata la Fcost aesenta l esessione di un ieellissoide con eccenticità legata dal aoto ma min ossiamo die che ad una matice mal condizionata coisonde un ieellissoide molto allungato mente ad un K iccolo coisonde un ieellissoide iù aotondato. Metodo del Gadiente Coniugato Pecondizionato i considei la tasfomazione detta asfomazione di Conguenza con non singolae e scelta in modo tale che K < K. i osseva che le tasfomazioni di conguenza in genee non mantengono gli auto valoi ma ne mantengono il segno. lloa il sistema oiginale b è equivalente al seguente sistema econdizionato con e b b. b Pe questo nuovo sistema l algoitmo del gadiente coniugato diventa 3
14 celto Pe abitaio si calcola b If si ende ε %test di convegenza non soddisfatto % Calcolo la nuova diezione di discesa γ γ 0 else %ECI:test di convegenza soddisfatto etun Patendo da ci si chiede come è ossibile esimee il nuovo algoitmo in temini delle gandezze oiginali. Il desideio di esimee l algoitmo in temini della matice di atenza è dovuto essenzialmente al fatto che la matice econdizionata  esenta una stuttua iù comlicata e in genee isulta iù densa isetto alla matice. Inolte si ceca di isamiae il costo della tasfomazione di conguenza. 4
15 5 Petanto si sostituiscono nell algoitmo dato le nuove gandezze con la loo definizione: Poiché b b si ha che b b b. Consideando oi i ottiene. 5 Pe calcolae il valoe bisogna calcolae i due odotti scalai. da cui onendo ~ 6 si ha ~. 7 Quindi
16 6 ~ ~. Oa è ossibile scivee il nuovo iteato del metodo econdizionato come ~ da cui moltilicando e si ha ~. nalogamente consideando il esiduo si ha ~ moltilicando e - e icodando che si ottiene ~ cioè ~. Pe calcolae γ utilizziamo la 7 e otteniamo ~ ~ ~ γ. Infine consideiamo ~ γ e moltilicando e si ha ~ γ da cui segue che ~ ~ γ.
17 utti questi calcoli ci hanno emesso di ottenee le fomule di base e il metodo del gadiente coniugato econdizionato scitto in temini delle gandezze oiginali iù un nuovo vettoe ~. e conoscessimo eslicitamente le matici e che comaiono nella tasfomazione di conguenza saebbe facile calcolae ~. In ealtà le matici e sono definite imlicitamente in quanto assegnata simmetica e definita ositiva e ottenee un buon econdizionatoe noi cechiamo una matice M simmetica definita ositiva che aossimi tale che M - I. Poiché M è simmetica e definita ositiva essa uò essee definita come in quanto è non singolae. Peciò si ottiene che cioè M ~ ~ M M. Questo significa che e calcolae il nuovo esiduo occoe isolvee questo sistema lineae con la matice M che aossima. L algoitmo del gadiente coniugato econdizionato diviene quindi: 7
18 celto 0 abitaio si calcola 0 0 b si calcola ~ 0 0 M e si ende Pe ~ ~ ~ 0 If ~ ~ Risolvi ~ M ~ ε %test di convegenza non soddisfatto % Calcolo la nuova diezione di discesa γ ~ ~ ~ ~ ~ γ else %ECI:test di convegenza soddisfatto etun i osseva che la diffeenza sostanziale dell algoitmo econdizionato sta nella isoluzione ad ogni asso di un sistema lineae; è evidente che e MI l algoitmo si iduce a quello non econdizionato. Oa quindi il oblema diviene quello di costuie una matice M che aossima e che sia facile da invetie. Pima eò vogliamo ci soffemiamo a caie eché dal oblema econdizionato b con 8
19 siamo assati al oblema di costuie la matice M con M matice che aossima. Questo è giustificato dal fatto che se consideo di emoltilicae  e avendo suosto invetibile ottengo M cioè è simile a M e quindi la tasfomazione di conguenza saà tanto miglioe quanto iù iduce l indice di condizionamento di cioè ma M cond cond M M min. Quindi tanto iù M aossima tanto iù c è la seanza che M l identità cioè sia con un indice di condizionamento ossimo ad. aossimi 9
20 Calcolo di ossibili econdizionatoi In letteatua esistono numeose ossibilità di econdizionatoi e il oblema è ancoa oggetto di amie iceche.. Pecondizionatoi Diagonali i definisce la matice M come la matice diagonale con gli elementi di sulla diagonale cioè e quindi M Diag a... a nn D M. Diag... D a ann Questa scelta coisonde a consideae la matice che comae in e che coisonde a M ai a Diag... D a a nn. Questa scelta è molto semlice in quanto ende il sistema M ~ isolvibile; utoo eò non seme ota a buoni isultati. facilmente. Pecondizionatoi basati sulla fattoizzazione di Cholesy incomleta Poiché la matice è simmetica e definita ositiva l idea è di consideae una matice tiangolae infeioe G che esenti una qualche stuttua sasa e aossimi al meglio ossibile il fattoe tiangolae infeioe L della fattoizzazione di Cholesy di LL e scegliee MGG. 0
21 Questa scelta ci assicua che M è simmetica definita ositiva e il sistema M ~ è facilmente isolvibile data la fattoizzazione MGG e la sasità dei fattoi tiangolai G e G. La matice che coisonde a questa scelta di M isulta essee Infatti G. M G G quanto iù G I. Il calcolo di G viene fatto in genee eseguendo una fattoizzazione aziale di che consiste nel oe a 0 i valoi di G che coisondono ai valoi a ij nulli e calcolando solo gli alti. Ossevazione finale: Il metodo del gadiente ichiede che la matice sia simmetica e definita ositiva. Esiste eò la ossibilità di estendelo a matici qualsiasi uchè non singolai. Dato il sistema lineae b lo si sostituisce con il sistema b In cui la matice è simmetica e definita ositiva. Oa è ossibile alicae il metodo del gadiente. Pe valutae l algoitmo occoe eò consideae sia il costo sueioe in temini di comlessità comutazionale dovuto all intoduzione dei odotti matice e vettoe sia la convegenza iù lenta oichè l indice di condizionamento è iù elevato dovuto al fatto che K K.
Algoritmo ricorsivo per il calcolo di π partendo da poligoni regolari
 CISTIANO TEODOO teodoocistiano@tiscali.it Algoitmo icosivo e il calcolo di π atendo da oligoni egolai Sommaio: viene illustato un algoitmo e il calcolo aossimato di π, con il quale, atendo da un oligono
CISTIANO TEODOO teodoocistiano@tiscali.it Algoitmo icosivo e il calcolo di π atendo da oligoni egolai Sommaio: viene illustato un algoitmo e il calcolo aossimato di π, con il quale, atendo da un oligono
( ) Energia potenziale U = GMm r. GMm r. GMm L AB. = r. r r. Definizione di energia potenziale
 Enegia potenziale Definizione di enegia potenziale Il lavoo, compiuto da una foza consevativa nello spostae il punto di applicazione da a, non dipende dal cammino seguito, ma esclusivamente dai punti e.
Enegia potenziale Definizione di enegia potenziale Il lavoo, compiuto da una foza consevativa nello spostae il punto di applicazione da a, non dipende dal cammino seguito, ma esclusivamente dai punti e.
Il Problema di Keplero
 Il Poblema di Kepleo Il poblema di Kepleo nel campo gavitazionale Intoduzione Con Poblema di Kepleo viene indicato il poblema del moto di un copo in un campo di foze centali. Nel caso specifico gavitazionale
Il Poblema di Kepleo Il poblema di Kepleo nel campo gavitazionale Intoduzione Con Poblema di Kepleo viene indicato il poblema del moto di un copo in un campo di foze centali. Nel caso specifico gavitazionale
AUTOVALORI ED AUTOVETTORI DI UNA MATRICE
 AUTOVALORI ED AUTOVETTORI DI UNA MATRICE TEOREMA: Un elemento di K è un autovaloe pe una matice A, di odine n, se e solo se, indicata con I la matice identità di odine n, isulta: det( A I) Il deteminante
AUTOVALORI ED AUTOVETTORI DI UNA MATRICE TEOREMA: Un elemento di K è un autovaloe pe una matice A, di odine n, se e solo se, indicata con I la matice identità di odine n, isulta: det( A I) Il deteminante
Regola di Ruffini - Wikipedia
 Pagina 1 di 7 Regola di Ruffini Da Wikipedia, l'enciclopedia libea. In matematica, la egola di Ruffini pemette la divisione veloce di un qualunque polinomio pe un binomio della foma x a. È stata descitta
Pagina 1 di 7 Regola di Ruffini Da Wikipedia, l'enciclopedia libea. In matematica, la egola di Ruffini pemette la divisione veloce di un qualunque polinomio pe un binomio della foma x a. È stata descitta
AI VERTICI DI UN QUADRATO DI LATO 2L SONO POSTE 4 CARICHE UGUALI Q. DETERMINARE: A) IL CAMPO ELETTRICO IN UN PUNTO P DELL ASSE.
 ESERCIZIO 1 AI VERTICI DI UN UADRATO DI LATO SONO POSTE 4 CARICHE UGUALI. DETERMINARE: A) IL CAMPO ELETTRICO IN UN PUNTO P DELL ASSE. 4 caiche uguali sono poste ai vetiti di un quadato. L asse di un quadato
ESERCIZIO 1 AI VERTICI DI UN UADRATO DI LATO SONO POSTE 4 CARICHE UGUALI. DETERMINARE: A) IL CAMPO ELETTRICO IN UN PUNTO P DELL ASSE. 4 caiche uguali sono poste ai vetiti di un quadato. L asse di un quadato
RANGO DI UNA MATRICE RAN. 1 Operazioni elementari di riga
 RN RNGO DI UN MTRICE Opeazioni elementai di iga Data una matice IR (mn) si dice opeazione elementae di iga ciascuna delle seguenti opeazioni: scambio della iesima iga con la jesima; moltiplicazione della
RN RNGO DI UN MTRICE Opeazioni elementai di iga Data una matice IR (mn) si dice opeazione elementae di iga ciascuna delle seguenti opeazioni: scambio della iesima iga con la jesima; moltiplicazione della
Lo schema seguente spiega come passare da una equazione all altra e al grafico della circonferenza. Svolgere i calcoli.
 D4. Ciconfeenza D4.1 Definizione di ciconfeenza come luogo di punti Definizione: una ciconfeenza è fomata dai punti equidistanti da un punto detto cento. La distanza (costante) è detta aggio. Ci sono due
D4. Ciconfeenza D4.1 Definizione di ciconfeenza come luogo di punti Definizione: una ciconfeenza è fomata dai punti equidistanti da un punto detto cento. La distanza (costante) è detta aggio. Ci sono due
Applicazioni del calcolo di erenziale: problemi di massimo e minimo
 Alicazioni del calcolo di eenziale: oblemi di massimo e minimo Maco Bamanti Decembe 1, 015 Abstact Vediamo alcuni esemi di come il calcolo di eenziale consenta di fomalizzae e isolvee oblemi geometici
Alicazioni del calcolo di eenziale: oblemi di massimo e minimo Maco Bamanti Decembe 1, 015 Abstact Vediamo alcuni esemi di come il calcolo di eenziale consenta di fomalizzae e isolvee oblemi geometici
Equazioni e disequazioni irrazionali
 Equazioni e disequazioni iazionali 8 81 Equazioni iazionali con un solo adicale Definizione 81 Un equazione si dice iazionale quando l incognita compae sotto il segno di adice Analizziamo le seguenti equazioni:
Equazioni e disequazioni iazionali 8 81 Equazioni iazionali con un solo adicale Definizione 81 Un equazione si dice iazionale quando l incognita compae sotto il segno di adice Analizziamo le seguenti equazioni:
Il criterio media varianza. Ordinamenti totali e parziali
 Il citeio media vaianza Il citeio media vaianza è un alto esemio di odinamento aziale ta lotteie definito da a M b se la lotteia b domina la lotteia a se ha media sueioe e vaianza infeioe a b eσ a σ b
Il citeio media vaianza Il citeio media vaianza è un alto esemio di odinamento aziale ta lotteie definito da a M b se la lotteia b domina la lotteia a se ha media sueioe e vaianza infeioe a b eσ a σ b
Effetto Hall. flusso reale dei portatori se positivi. flusso reale dei portatori se negativi
 Appunti di Fisica II Effetto Hall L'effetto Hall è un fenomeno legato al passaggio di una coente I, attaveso ovviamente un conduttoe, in una zona in cui è pesente un campo magnetico dietto otogonalmente
Appunti di Fisica II Effetto Hall L'effetto Hall è un fenomeno legato al passaggio di una coente I, attaveso ovviamente un conduttoe, in una zona in cui è pesente un campo magnetico dietto otogonalmente
IL POTENZIALE. = d quindi: LAB
 1 IL POTENZIALE Sappiamo che il campo gavitazionale è un campo consevativo cioè nello spostamento di un copo ta due punti del campo gavitazionale teeste, le foze del campo compiono un lavoo che dipende
1 IL POTENZIALE Sappiamo che il campo gavitazionale è un campo consevativo cioè nello spostamento di un copo ta due punti del campo gavitazionale teeste, le foze del campo compiono un lavoo che dipende
LEZIONE 10. d(a, B) = AB = AB = (x A x B ) 2 + (y A y B ) 2 + (z A z B ) 2.
 LEZIONE 10 10.1. Distanze. Definizione 10.1.1. In S n sia fissata un unità di misua u. Se A, B S n, definiamo distanza fa A e B, e sciviamo d(a, B), la lunghezza del segmento AB ispetto ad u. Abbiamo già
LEZIONE 10 10.1. Distanze. Definizione 10.1.1. In S n sia fissata un unità di misua u. Se A, B S n, definiamo distanza fa A e B, e sciviamo d(a, B), la lunghezza del segmento AB ispetto ad u. Abbiamo già
GEOMETRIA ELEMENTARE. h = 2 2 S. h =
 QUESITI 1 GEOMETRI ELEMENTRE 1. (Da Veteinaia 015) Le diagonali (ossia le linee che uniscono i vetici opposti) di un ombo misuano ispettivamente 4 cm e 8 cm. Qual è il peimeto del ombo in cm? a) 8 3 b)
QUESITI 1 GEOMETRI ELEMENTRE 1. (Da Veteinaia 015) Le diagonali (ossia le linee che uniscono i vetici opposti) di un ombo misuano ispettivamente 4 cm e 8 cm. Qual è il peimeto del ombo in cm? a) 8 3 b)
13b. Reattore omogeneo con riflettore. Due gruppi di neutroni
 b. Reattoe omogeneo con iflettoe ue guppi di neutoni Assumiamo oa una appossimazione in teoia della diffusione consistente in due guppi enegetici: uno elativo ai neutoni temici (guppo temico) ed uno elativo
b. Reattoe omogeneo con iflettoe ue guppi di neutoni Assumiamo oa una appossimazione in teoia della diffusione consistente in due guppi enegetici: uno elativo ai neutoni temici (guppo temico) ed uno elativo
Q AB = Q AC + Q CB. liquido vapore. δq AB = δq AC + δq CB. δq = c x dt + r dx. Le 5 espressioni del δq nel campo dei vapori saturi
 Le 5 espessioni del Q nel campo dei vapoi satui A C K B Consideiamo la tasfomazione AB che si svolge tutta all inteno della campana dei vapoi satui di una sostanza qualsiasi. Supponiamo quindi di andae
Le 5 espessioni del Q nel campo dei vapoi satui A C K B Consideiamo la tasfomazione AB che si svolge tutta all inteno della campana dei vapoi satui di una sostanza qualsiasi. Supponiamo quindi di andae
Giuseppe Accascina. Didattica della Matematica. Trasformazioni geometriche del piano
 SSIS A.A. 2 22 Indiizzo Fisico Infomatico Matematico Giusee Accascina Didattica della Matematica Tasfomazioni geometiche del iano. Pemessa 2. Il ogamma di Elangen 3. Isometie 4. Euazioni delle isometie
SSIS A.A. 2 22 Indiizzo Fisico Infomatico Matematico Giusee Accascina Didattica della Matematica Tasfomazioni geometiche del iano. Pemessa 2. Il ogamma di Elangen 3. Isometie 4. Euazioni delle isometie
GONIOMETRIA. MISURA DEGLI ANGOLI La misura di un angolo si può esprimere in diversi modi, a seconda dell unità di misura che si sceglie.
 of. Luigi Cai Anno scolastico 4-5 GONIOMETRIA MISURA DEGLI ANGOLI La misua di un angolo si può espimee in divesi modi, a seconda dell unità di misua che si sceglie. Sistema sessagesimale Si assume come
of. Luigi Cai Anno scolastico 4-5 GONIOMETRIA MISURA DEGLI ANGOLI La misua di un angolo si può espimee in divesi modi, a seconda dell unità di misua che si sceglie. Sistema sessagesimale Si assume come
! Un asta di peso p =! + 1 (vedi figura) è appoggiata su due. supporti A e B, distanti, dal baricentro G dell asta,
 isica eneale 5. Esecizi di Statica Esecizio Un asta di eso = + (vedi figua) è aoggiata su due 0 N suoti e, distanti, dal baicento dell asta, isettivamente a =. m e b = + 0. 000 m Calcolae la foza d aoggio
isica eneale 5. Esecizi di Statica Esecizio Un asta di eso = + (vedi figua) è aoggiata su due 0 N suoti e, distanti, dal baicento dell asta, isettivamente a =. m e b = + 0. 000 m Calcolae la foza d aoggio
RESISTENZE DI ATTRITO (Distillazione verticale)
 1 ESISTEZE DI ATTITO (Distillazione veticale) OBIETTIVI: Saee calcolae le esistenze d attito nelle iù comuni alicazioni meccaniche. Saee calcolae lavoo dissiato e otenza dissiata dalle foze d attito. esistenza
1 ESISTEZE DI ATTITO (Distillazione veticale) OBIETTIVI: Saee calcolae le esistenze d attito nelle iù comuni alicazioni meccaniche. Saee calcolae lavoo dissiato e otenza dissiata dalle foze d attito. esistenza
ESERCIZIO n.1. rispetto alle rette r e t indicate in Figura. h t. d b GA#1 1
 Esecizi svolti di geometia delle aee Aliandi U., Fusci P., Pisano A., Sofi A. ESERCZO n.1 Data la sezione ettangolae ipotata in Figua, deteminae: a) gli assi pincipali centali di inezia; ) l ellisse pincipale
Esecizi svolti di geometia delle aee Aliandi U., Fusci P., Pisano A., Sofi A. ESERCZO n.1 Data la sezione ettangolae ipotata in Figua, deteminae: a) gli assi pincipali centali di inezia; ) l ellisse pincipale
ESERCIZIO n.2. y B. rispetto alle rette r e t indicate in Figura. GA#2 1
 ESERCZO n. Data la sezione a T ipotata in Figua, deteminae: a) gli assi pincipali centali di inezia; ) l ellisse pincipale centale di inezia; c) il nocciolo centale di inezia; d) i momenti di inezia e
ESERCZO n. Data la sezione a T ipotata in Figua, deteminae: a) gli assi pincipali centali di inezia; ) l ellisse pincipale centale di inezia; c) il nocciolo centale di inezia; d) i momenti di inezia e
La struttura stellare
 La stuttua stellae La stuttua stellae Una stella è una sfea di gas tenuta insieme dall auto gavità ed il cui collasso è impedito dalla pesenza di gadienti di pessione. Con ottima appossimazione una stella
La stuttua stellae La stuttua stellae Una stella è una sfea di gas tenuta insieme dall auto gavità ed il cui collasso è impedito dalla pesenza di gadienti di pessione. Con ottima appossimazione una stella
Appunti su argomenti monografici per il corso di FM1 Prof. Pierluigi Contucci. Gravità e Teorema di Gauss
 1 Appunti su agomenti monogafici pe il coso di FM1 Pof. Pieluigi Contucci Gavità e Teoema di Gauss Vogliamo dimostae, a patie dalla legge di gavitazione univesale che il campo gavitazionale geneato da
1 Appunti su agomenti monogafici pe il coso di FM1 Pof. Pieluigi Contucci Gavità e Teoema di Gauss Vogliamo dimostae, a patie dalla legge di gavitazione univesale che il campo gavitazionale geneato da
Nome..Cognome. classe 5D 29 Novembre VERIFICA di FISICA: Elettrostatica Domande
 Nome..ognome. classe 5 9 Novembe 8 RIFI di FISI: lettostatica omande ) ai la definizione di flusso di un campo vettoiale attaveso una supeficie. nuncia il teoema di Gauss pe il campo elettico (senza dimostalo)
Nome..ognome. classe 5 9 Novembe 8 RIFI di FISI: lettostatica omande ) ai la definizione di flusso di un campo vettoiale attaveso una supeficie. nuncia il teoema di Gauss pe il campo elettico (senza dimostalo)
Si considerino le rette:
 Si consideino le ette: Eseciio (tipo tema d esame) : s : + () ) Si dica pe quali valoi del paameto eale le ette e s isultano sghembe, paallele o incidenti. ) Nel caso paallele si emino i paameti diettoi
Si consideino le ette: Eseciio (tipo tema d esame) : s : + () ) Si dica pe quali valoi del paameto eale le ette e s isultano sghembe, paallele o incidenti. ) Nel caso paallele si emino i paameti diettoi
Massimi e minimi con le linee di livello
 Massimi e minimi con le linee di livello Pe affontae questo agomento è necessaio sape appesentae i fasci di cuve ed in paticolae: Fasci di paabole. Pe affontae questo agomento si consiglia di ivedee l
Massimi e minimi con le linee di livello Pe affontae questo agomento è necessaio sape appesentae i fasci di cuve ed in paticolae: Fasci di paabole. Pe affontae questo agomento si consiglia di ivedee l
Momenti. Momento di inerzia, momento di una forza, momento angolare
 Momenti Momento di inezia, momento di una foza, momento angolae Conce&o di Momento I momenti in fisica sono cose molto divese fa loo. Cetamente non hanno sempe la stessa unità di misua; ed avemo cua di
Momenti Momento di inezia, momento di una foza, momento angolae Conce&o di Momento I momenti in fisica sono cose molto divese fa loo. Cetamente non hanno sempe la stessa unità di misua; ed avemo cua di
Lunghezza della circonferenza e area del cerchio
 Come possiamo deteminae la lunghezza di una ciconfeenza di aggio? Poviamo a consideae i poligoni egolai inscitti e cicoscitti alla ciconfeenza: è chiao che la lunghezza della ciconfeenza è maggioe del
Come possiamo deteminae la lunghezza di una ciconfeenza di aggio? Poviamo a consideae i poligoni egolai inscitti e cicoscitti alla ciconfeenza: è chiao che la lunghezza della ciconfeenza è maggioe del
dove per i simboli si sono adottate le seguenti notazioni: 2 Corpo girevole attorno ad un asse fisso
 Il volano 1 Dinamica del copo igido Il poblema dello studio del moto di un copo igido libeo è il seguente: data una ceta sollecitazione F e del copo, cioè cete foze estene F i applicate nei punti del copo
Il volano 1 Dinamica del copo igido Il poblema dello studio del moto di un copo igido libeo è il seguente: data una ceta sollecitazione F e del copo, cioè cete foze estene F i applicate nei punti del copo
Facoltà di Ingegneria Fisica II Compito A
 Facoltà di ngegneia Fisica 66 Compito A Esecizio n Un filo di mateiale isolante, con densità di caica lineae costante, viene piegato fino ad assumee la foma mostata in figua (la pate cicolae ha aggio e
Facoltà di ngegneia Fisica 66 Compito A Esecizio n Un filo di mateiale isolante, con densità di caica lineae costante, viene piegato fino ad assumee la foma mostata in figua (la pate cicolae ha aggio e
SIMULAZIONE DELLA PROVA D ESAME DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I.
 SIMULAZINE DELLA PRVA D ESAME DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. Risolvi uno dei due poblemi e 5 dei quesiti del questionaio. PRBLEMA In un piano è data la ciconfeenza di cento e aggio A ; conduci
SIMULAZINE DELLA PRVA D ESAME DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. Risolvi uno dei due poblemi e 5 dei quesiti del questionaio. PRBLEMA In un piano è data la ciconfeenza di cento e aggio A ; conduci
Conduttori in equilibrio elettrostatico
 onduttoi in equilibio elettostatico In un conduttoe in equilibio, tutte le caiche di conduzione sono in equilibio Se una caica di conduzione è in equilibio, in quel punto il campo elettico è nullo caica
onduttoi in equilibio elettostatico In un conduttoe in equilibio, tutte le caiche di conduzione sono in equilibio Se una caica di conduzione è in equilibio, in quel punto il campo elettico è nullo caica
Momenti. Momento di inerzia, momento di una forza, momento angolare
 Momenti Momento di inezia, momento di una foza, momento angolae Conce&o di Momento I momenti in fisica sono cose molto divese fa loo. Cetamente non hanno sempe la stessa unità di misua; ed avemo cua di
Momenti Momento di inezia, momento di una foza, momento angolae Conce&o di Momento I momenti in fisica sono cose molto divese fa loo. Cetamente non hanno sempe la stessa unità di misua; ed avemo cua di
Docente Francesco Benzi
 MACCHINE ELETTRICHE Coso di Lauea in Ingegneia Industiale Anno Accademico 015-016 MACCHINE ELEMENTARI Docente Fancesco Benzi Univesità di Pavia e-mail: fbenzi@unipv.it Dispense in collaboazione con Giovanni
MACCHINE ELETTRICHE Coso di Lauea in Ingegneia Industiale Anno Accademico 015-016 MACCHINE ELEMENTARI Docente Fancesco Benzi Univesità di Pavia e-mail: fbenzi@unipv.it Dispense in collaboazione con Giovanni
STUDIO DELLA RESISTENZA DI UN DISCO A SPESSORE COSTANTE UTILIZZANDO IL METODO DEGLI ELEMENTI FINITI
 POLITECNICO DI TORINO Facoltà di Ingegneia I Anno accademico xxxx/xxxx Coso di COSTRUZIONE DI MACCHINE Elettix1 STUDIO DELLA RESISTENZA DI UN DISCO A SPESSORE COSTANTE UTILIZZANDO IL METODO DEGLI ELEMENTI
POLITECNICO DI TORINO Facoltà di Ingegneia I Anno accademico xxxx/xxxx Coso di COSTRUZIONE DI MACCHINE Elettix1 STUDIO DELLA RESISTENZA DI UN DISCO A SPESSORE COSTANTE UTILIZZANDO IL METODO DEGLI ELEMENTI
1. SATELLITI ARTIFICIALI
 Calo Sintini Satelliti atificiali www.matematicamente.it. SATELLITI ARTIFICIALI Calo Sintini. IL MOTO DEI SATELLITI Il 4 ottobe 957 venne lanciato il imo satellite atificiale intono alla tea, ebbe inizio
Calo Sintini Satelliti atificiali www.matematicamente.it. SATELLITI ARTIFICIALI Calo Sintini. IL MOTO DEI SATELLITI Il 4 ottobe 957 venne lanciato il imo satellite atificiale intono alla tea, ebbe inizio
Corso di Elettrotecnica 1 - Cod N Diploma Universitario Teledidattico in Ingegneria Informatica ed Automatica Polo Tecnologico di Alessandria
 Schede di Elettotecnica oso di Elettotecnica 1 - od. 9200 N Diploma Univesitaio Teledidattico in Ingegneia Infomatica ed Automatica Polo Tecnologico di Alessandia A cua di uca FEAIS Scheda N 8 icuiti in
Schede di Elettotecnica oso di Elettotecnica 1 - od. 9200 N Diploma Univesitaio Teledidattico in Ingegneia Infomatica ed Automatica Polo Tecnologico di Alessandia A cua di uca FEAIS Scheda N 8 icuiti in
v t V o cos t Re r v t
 Metodo Simbolico, o metodo dei Fasoi Questo metodo applicato a eti lineai pemanenti consente di deteminae la soluzione in egime sinusoidale solamente pe quanto attiene il egime stazionaio. idea di appesentae
Metodo Simbolico, o metodo dei Fasoi Questo metodo applicato a eti lineai pemanenti consente di deteminae la soluzione in egime sinusoidale solamente pe quanto attiene il egime stazionaio. idea di appesentae
Esercizi Scheda N Fisica II. Esercizi con soluzione
 Esecizio 9.1 Esecizi con soluzione Te divese onde sonoe hanno fequenza ν ispettivamente 1 Hz, 1 Hz e 5 Mhz. Deteminae le lunghezze d onda coispondenti ed i peiodi di oscillazione, sapendo che la velocità
Esecizio 9.1 Esecizi con soluzione Te divese onde sonoe hanno fequenza ν ispettivamente 1 Hz, 1 Hz e 5 Mhz. Deteminae le lunghezze d onda coispondenti ed i peiodi di oscillazione, sapendo che la velocità
Integrazione indefinita di funzioni irrazionali
 Esecizi di iepilogo e complemento Integazione indefinita di funzioni iazionali 0.5 setgay0 0.5 setgay Denotiamo con R(,,..., n ) una funzione azionale delle vaiabili indicate. Passiamo in assegna alcuni
Esecizi di iepilogo e complemento Integazione indefinita di funzioni iazionali 0.5 setgay0 0.5 setgay Denotiamo con R(,,..., n ) una funzione azionale delle vaiabili indicate. Passiamo in assegna alcuni
La dinamica dei fluidi
 a dinamica dei fluidi 1 Intoduzione: tii di moto e linee di flusso ibo di testo: a 15.8 Equazione di continuità ibo di testo: a 15.9 3 Equazione di enoulli ibo di testo: a 15.1 Viscosità e moto di un fluido
a dinamica dei fluidi 1 Intoduzione: tii di moto e linee di flusso ibo di testo: a 15.8 Equazione di continuità ibo di testo: a 15.9 3 Equazione di enoulli ibo di testo: a 15.1 Viscosità e moto di un fluido
Geometria analitica in sintesi
 punti distanza ta due punti coodinate del punto medio coodinate del baicento ta due punti di un tiangolo di vetici etta e foma implicita foma esplicita foma segmentaia equazione della etta m è il coefficiente
punti distanza ta due punti coodinate del punto medio coodinate del baicento ta due punti di un tiangolo di vetici etta e foma implicita foma esplicita foma segmentaia equazione della etta m è il coefficiente
Elementi di Dinamica
 Elementi di Dinamica ELEMENTI DI DINAMICA Mente la cinematica si limita allo studio delle possibilità di movimento di un ceto sistema ed alla elativa descizione matematica, la dinamica si occupa delle
Elementi di Dinamica ELEMENTI DI DINAMICA Mente la cinematica si limita allo studio delle possibilità di movimento di un ceto sistema ed alla elativa descizione matematica, la dinamica si occupa delle
La parabola come luogo geometrico
 La paabola come luogo geometico Definizioni e pime popietà Definizioni. Si chiama paabola il luogo ei punti equiistanti a un punto, etto fuoco, e a una etta etta iettice.. Il punto ella paabola che ha
La paabola come luogo geometico Definizioni e pime popietà Definizioni. Si chiama paabola il luogo ei punti equiistanti a un punto, etto fuoco, e a una etta etta iettice.. Il punto ella paabola che ha
Capitolo 7. Costi e minimizzazione dei costi. Soluzioni dei Problemi
 Capitolo 7 Costi e minimizzazione dei costi Soluzioni dei Poblemi 7.1 a) 500 b) 30% di 500, ossia 150 c) Senza idue il pezzo e posto che l impesa non possa vendee alte stampanti, il meglio che essa può
Capitolo 7 Costi e minimizzazione dei costi Soluzioni dei Poblemi 7.1 a) 500 b) 30% di 500, ossia 150 c) Senza idue il pezzo e posto che l impesa non possa vendee alte stampanti, il meglio che essa può
Parte II (Il Condizionamento)
 Pate II (Il Cicuiti di condizionamento dei sensoi esistivi I sensoi basati sulla vaiazione della esistenza sono molto comuni. Ciò è dovuto al fatto che molte gandezze fisiche poducono la vaiazione della
Pate II (Il Cicuiti di condizionamento dei sensoi esistivi I sensoi basati sulla vaiazione della esistenza sono molto comuni. Ciò è dovuto al fatto che molte gandezze fisiche poducono la vaiazione della
1 Definizioni e proprietà
 Definizioni e popietà Retta e ciconfeenza ngoli al cento ed angoli alla ciconfeenza Equazione della ciconfeenza nel piano catesiano 5 Posizioni elative ed asse adicale di due ciconffeenze Definizioni e
Definizioni e popietà Retta e ciconfeenza ngoli al cento ed angoli alla ciconfeenza Equazione della ciconfeenza nel piano catesiano 5 Posizioni elative ed asse adicale di due ciconffeenze Definizioni e
Equilibrio dei corpi rigidi- Statica
 Equilibio dei copi igidi- Statica Ci ifeiamo solo a situazioni paticolai in cui i copi igidi non si muovono in nessun modo: ne taslano ( a 0 ), ne uotano ( 0 ), ossia sono femi in un oppotuno sistema di
Equilibio dei copi igidi- Statica Ci ifeiamo solo a situazioni paticolai in cui i copi igidi non si muovono in nessun modo: ne taslano ( a 0 ), ne uotano ( 0 ), ossia sono femi in un oppotuno sistema di
F 1 F 2 F 3 F 4 F 5 F 6. Cosa è necessario per avere una rotazione?
 Cosa è necessaio pe avee una otazione? Supponiamo di vole uotae il sistema in figua intono al bullone, ovveo intono all asse veticale passante pe, usando foze nel piano oizzontale aventi tutte lo stesso
Cosa è necessaio pe avee una otazione? Supponiamo di vole uotae il sistema in figua intono al bullone, ovveo intono all asse veticale passante pe, usando foze nel piano oizzontale aventi tutte lo stesso
7. Sistemi articolati.
 7. Sistemi aticolati. In questo capitolo sono fonite alcune infomazioni di base sui meccanismi aticolati piani. Si affonteanno essenzialmente poblematiche elative alla analisi di posizione. Vediamo alcuni
7. Sistemi aticolati. In questo capitolo sono fonite alcune infomazioni di base sui meccanismi aticolati piani. Si affonteanno essenzialmente poblematiche elative alla analisi di posizione. Vediamo alcuni
E, ds. - Flusso totale uscente dalla superficie chiusa S: è la somma di tutti i flussi elementari, al tendere a zero delle aree infinitesime: r )
 Flusso del campo elettico e legge di Gauss. - Si definisce supeficie gaussiana una ipotetica supeficie S chiusa, che contiene un volume V. - La legge di Gauss mette in elazione i valoi dei campi elettici
Flusso del campo elettico e legge di Gauss. - Si definisce supeficie gaussiana una ipotetica supeficie S chiusa, che contiene un volume V. - La legge di Gauss mette in elazione i valoi dei campi elettici
Momenti d'inerzia di figure geometriche semplici
 Appofondimento Momenti d'inezia di figue geometice semplici Pidatella, Feai Aggadi, Pidatella, Coso di meccanica, maccine ed enegia Zanicelli 1 Rettangolo Pe un ettangolo di ase e altezza (FGURA 1.a),
Appofondimento Momenti d'inezia di figue geometice semplici Pidatella, Feai Aggadi, Pidatella, Coso di meccanica, maccine ed enegia Zanicelli 1 Rettangolo Pe un ettangolo di ase e altezza (FGURA 1.a),
Gravitazione. Dati due corpi di massa m 1 e m 2, posti ad una distanza r, tra di essi si esercita una forza attrattiva data in modulo da
 Gavitazione Dati due copi di massa m 1 e m 2, posti ad una distanza, ta di essi si esecita una foza attattiva data in modulo da F = G m 1m 2 dove G è una costante univesale, avente lo stesso valoe pe tutte
Gavitazione Dati due copi di massa m 1 e m 2, posti ad una distanza, ta di essi si esecita una foza attattiva data in modulo da F = G m 1m 2 dove G è una costante univesale, avente lo stesso valoe pe tutte
Legge di Ohm. La corrente elettrica dal punto di vista microscopico: modello di Drude
 Legge di Ohm. Obiettivi didattici: Veifica della elazione ta coente e d.d.p. pe un conduttoe metallico. Veifica della elazione ta la esistenza di un conduttoe e le sue dimensioni (lunghezza, sezione) Misua
Legge di Ohm. Obiettivi didattici: Veifica della elazione ta coente e d.d.p. pe un conduttoe metallico. Veifica della elazione ta la esistenza di un conduttoe e le sue dimensioni (lunghezza, sezione) Misua
LIBRO DI TESTO S.Melone, F.Rustichelli Introduzione alla Fisica Biomedica Libreria Scientifica Ragni Ancona, 1998
 LIBRO DI TESTO S.Melone, F.Rustichelli Intoduzione alla Fisica Biomedica Libeia Scientifica Ragni Ancona, 1998 TESTO DI CONSULTAZIONE E WEB F.Bosa, D.Scannicchio Fisica con Applicazioni in Biologia e Medicina
LIBRO DI TESTO S.Melone, F.Rustichelli Intoduzione alla Fisica Biomedica Libeia Scientifica Ragni Ancona, 1998 TESTO DI CONSULTAZIONE E WEB F.Bosa, D.Scannicchio Fisica con Applicazioni in Biologia e Medicina
Potenza in alternata
 otenza in altenata sin t 0 ( ) ω +φ i [ ( )] sin ω t + φ ( ω + φ) 0 0 sin t E significativo consideae la potenza media dissipata sulla esistenza andando a calcolae l integale su un peiodo 1 T T 0 sin sin
otenza in altenata sin t 0 ( ) ω +φ i [ ( )] sin ω t + φ ( ω + φ) 0 0 sin t E significativo consideae la potenza media dissipata sulla esistenza andando a calcolae l integale su un peiodo 1 T T 0 sin sin
SESTA LEZIONE: campo magnetico, forza magnetica, momenti meccanici sui circuiti piani
 A. Chiodoni esecizi di Fisica II SESTA LEZIONE: campo magnetico, foza magnetica, momenti meccanici sui cicuiti piani Esecizio 1 Un potone d enegia cinetica E k 6MeV enta in una egione di spazio in cui
A. Chiodoni esecizi di Fisica II SESTA LEZIONE: campo magnetico, foza magnetica, momenti meccanici sui cicuiti piani Esecizio 1 Un potone d enegia cinetica E k 6MeV enta in una egione di spazio in cui
32. Significato geometrico della derivata. 32. Significato geometrico della derivata.
 32. Significato geometico della deivata. Deivata Definizione deivata di una funzione in un punto (30) Definizione deivata di una funzione (30) Significato della deivata Deivata in un punto (32) Deivata
32. Significato geometico della deivata. Deivata Definizione deivata di una funzione in un punto (30) Definizione deivata di una funzione (30) Significato della deivata Deivata in un punto (32) Deivata
Applicazioni della trigonometria alla geometria
 unti di matematica licazioni della tigonometia alla geometia. ea di un tiangolo, note le misue di due lati e quella dell'angolo da essi comeso. TEOREM L'aea di un qualsiasi tiangolo è eguale al semiodotto
unti di matematica licazioni della tigonometia alla geometia. ea di un tiangolo, note le misue di due lati e quella dell'angolo da essi comeso. TEOREM L'aea di un qualsiasi tiangolo è eguale al semiodotto
4. DINAMICA. I tre principi della dinamica per un corpo puntiforme (detto anche punto materiale o particella) sono:
 4.1 Pincipi della dinamica 4. DINAMICA I te pincipi della dinamica pe un copo puntifome (detto anche punto mateiale o paticella) sono: 1) pincipio di intezia di Galilei; 2) legge dinamica di Newton; 3)
4.1 Pincipi della dinamica 4. DINAMICA I te pincipi della dinamica pe un copo puntifome (detto anche punto mateiale o paticella) sono: 1) pincipio di intezia di Galilei; 2) legge dinamica di Newton; 3)
Esercizio 1. Date le rette
 Date le ette Eseciio y : : y a) Scivee le equaioni paametiche delle ette e. b) Dopo ave veificato che le ette ed sono sghembe, tovae l equaione di un piano σ contenente e paallelo a. c) Deteminae le equaioni
Date le ette Eseciio y : : y a) Scivee le equaioni paametiche delle ette e. b) Dopo ave veificato che le ette ed sono sghembe, tovae l equaione di un piano σ contenente e paallelo a. c) Deteminae le equaioni
IL VOLUME DEI SOLIDI Conoscenze
 IL VOLUME DEI SOLIDI Conoscenze 1. Completa. a. Il peso di un copo dipende dal...e dalla...di cui è costituito b. Ogni sostanza ha il suo peso specifico, che è... di quella sostanza c. Il peso specifico
IL VOLUME DEI SOLIDI Conoscenze 1. Completa. a. Il peso di un copo dipende dal...e dalla...di cui è costituito b. Ogni sostanza ha il suo peso specifico, che è... di quella sostanza c. Il peso specifico
Momenti. Momento di una forza, momento di inerzia, momento angolare
 Momenti Momento di una foza, momento di inezia, momento angolae Momento di una foza Supponiamo di avee una pota vista dall alto e supponiamo che sia incadinata su un lato, diciamo in A. A Se applicassimo
Momenti Momento di una foza, momento di inezia, momento angolae Momento di una foza Supponiamo di avee una pota vista dall alto e supponiamo che sia incadinata su un lato, diciamo in A. A Se applicassimo
Simulazione del fronte di plasticizzazione in un nuovo modello analitico del comportamento elasto-plastico di giunzioni saldate a punti
 P. Fanelli et alii, Poblematiche di Fattua nei Mateiali e l ngegneia, Foni di Soa 7-9 gennaio 21, 84-92 Simulazione del fonte di lasticizzazione in un nuovo modello analitico del comotamento elasto-lastico
P. Fanelli et alii, Poblematiche di Fattua nei Mateiali e l ngegneia, Foni di Soa 7-9 gennaio 21, 84-92 Simulazione del fonte di lasticizzazione in un nuovo modello analitico del comotamento elasto-lastico
DISTRIBUZIONE DELLA CARICA NEI CONDUTTORI
 1 DISTRIBUZIONE DELLA CARICA NEI CONDUTTORI I copi conduttoi sono caatteizzati dal fatto di avee moltissimi elettoni libei di muovesi (elettoni di conduzione). Cosa accade se un copo conduttoe viene caicato
1 DISTRIBUZIONE DELLA CARICA NEI CONDUTTORI I copi conduttoi sono caatteizzati dal fatto di avee moltissimi elettoni libei di muovesi (elettoni di conduzione). Cosa accade se un copo conduttoe viene caicato
( ) ( ) ( ) ( ) Esercizi 2 Legge di Gauss
 Esecizi Legge di Gauss. Un involuco sfeico isolante ha aggi inteno ed esteno a e b, ed e caicato con densita unifome ρ. Disegnae il diagamma di E in funzione di La geometia e mostata nella figua: Usiamo
Esecizi Legge di Gauss. Un involuco sfeico isolante ha aggi inteno ed esteno a e b, ed e caicato con densita unifome ρ. Disegnae il diagamma di E in funzione di La geometia e mostata nella figua: Usiamo
Energia potenziale elettrica
 Enegia potenziale elettica L ultima ossevazione del capitolo pecedente iguadava le analogie e le diffeenze ta il campo elettico e il campo gavitazionale pendendo in esame la foza di Coulomb e la legge
Enegia potenziale elettica L ultima ossevazione del capitolo pecedente iguadava le analogie e le diffeenze ta il campo elettico e il campo gavitazionale pendendo in esame la foza di Coulomb e la legge
ESERCIZI AGGIUNTIVI MODELLO IS/LM IN ECONOMIA CHIUSA
 ESERCIZI AGGIUNTIVI MODELLO IS/ IN ECONOMIA CHIUSA ESERCIZIO 1 Illustate gaficamente ed economicamente quali conseguenze ha sul mecato monetaio la decisione della Banca Centale di aumentae il Tasso Ufficiale
ESERCIZI AGGIUNTIVI MODELLO IS/ IN ECONOMIA CHIUSA ESERCIZIO 1 Illustate gaficamente ed economicamente quali conseguenze ha sul mecato monetaio la decisione della Banca Centale di aumentae il Tasso Ufficiale
TEST PER RECUPERO OFA 25 marzo 2010
 TEST PER RECUPERO OFA mazo 010 A 1. Quale ta i seguenti numei, moltiplicato pe, dà come podotto un numeo azionale? A) 0 B) 1+ C) + D) 1 6 E).. Un esagono egolae è inscitto in una ciconfeenza di aggio.
TEST PER RECUPERO OFA mazo 010 A 1. Quale ta i seguenti numei, moltiplicato pe, dà come podotto un numeo azionale? A) 0 B) 1+ C) + D) 1 6 E).. Un esagono egolae è inscitto in una ciconfeenza di aggio.
ESERCITAZIONE N.2 MODELLO IS/LM IN ECONOMIA CHIUSA
 ESERCITAZIONE N.2 MODELLO IS/LM IN ECONOMIA CHIUSA LEGENDA: H = BM = base monetaia mm = moltiplicatoe monetaio = 1 + c c + (o i) = tasso d inteesse = iseve/depositi c = cicolante /depositi id (D) = tasso
ESERCITAZIONE N.2 MODELLO IS/LM IN ECONOMIA CHIUSA LEGENDA: H = BM = base monetaia mm = moltiplicatoe monetaio = 1 + c c + (o i) = tasso d inteesse = iseve/depositi c = cicolante /depositi id (D) = tasso
IL VOLUME DEI SOLIDI Conoscenze
 IL VOLUME DEI SOLIDI Conoscenze 1. Completa. a. Il peso di un copo dipende dal volume e dalla sostanza di cui è costituito b. Ogni sostanza ha il suo peso specifico, che è il peso dell unità di volume
IL VOLUME DEI SOLIDI Conoscenze 1. Completa. a. Il peso di un copo dipende dal volume e dalla sostanza di cui è costituito b. Ogni sostanza ha il suo peso specifico, che è il peso dell unità di volume
PROBLEMI SULLE FIGURE CIRCOSCRITTE A UN CERCHIO O A UNA SFERA. di Ezio Fornero
 PROBLEMI SULLE FIGURE CIRCOSCRITTE A UN CERCHIO O A UNA SFERA di Ezio Foneo Indice dei poblemi Tiangolo ettangolo cicoscitto a un cechio di aggio assegnato Deteminae le misue dei cateti del tiangolo sapendo
PROBLEMI SULLE FIGURE CIRCOSCRITTE A UN CERCHIO O A UNA SFERA di Ezio Foneo Indice dei poblemi Tiangolo ettangolo cicoscitto a un cechio di aggio assegnato Deteminae le misue dei cateti del tiangolo sapendo
Fondamenti di Gravitazione
 Fondamenti di Gavitazione Intoduzione all Astofisica AA 205/206 Pof. Alessando Maconi Dipatimento di Fisica e Astonomia Univesità di Fienze Dispense e pesentazioni disponibili all indiizzo http://www.aceti.asto.it/
Fondamenti di Gavitazione Intoduzione all Astofisica AA 205/206 Pof. Alessando Maconi Dipatimento di Fisica e Astonomia Univesità di Fienze Dispense e pesentazioni disponibili all indiizzo http://www.aceti.asto.it/
1 Potenziale elettrostatico e seconda equazione di Maxwell per E
 1 Potenziale elettostatico e seconda equazione di Maxwell pe E Consideiamo il campo elettico oiginato da una caica puntifome q che ipotizziamo fissa nell oigine degli assi: E( ) = q ˆ 2 = q 3 (1) Pe definizione,
1 Potenziale elettostatico e seconda equazione di Maxwell pe E Consideiamo il campo elettico oiginato da una caica puntifome q che ipotizziamo fissa nell oigine degli assi: E( ) = q ˆ 2 = q 3 (1) Pe definizione,
Moto su traiettorie curve: il moto circolare
 Moto su taiettoie cuve: il moto cicolae Così come il moto ettilineo è un moto che avviene lungo una linea etta, il moto cicolae è un moto la cui taiettoia è cicolae, cioè un moto che avviene lungo una
Moto su taiettoie cuve: il moto cicolae Così come il moto ettilineo è un moto che avviene lungo una linea etta, il moto cicolae è un moto la cui taiettoia è cicolae, cioè un moto che avviene lungo una
Le equazioni di Maxwell.
 Le equazioni di Maxwell. Campi elettici indotti. Pe la legge di Faady, in una spia conduttice dove c è una vaiazione di Φ concatenato si osseva una coente indotta i. Ricodando che una coente è un flusso
Le equazioni di Maxwell. Campi elettici indotti. Pe la legge di Faady, in una spia conduttice dove c è una vaiazione di Φ concatenato si osseva una coente indotta i. Ricodando che una coente è un flusso
ed è pari a: 683 lumen/watt, pertanto:
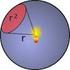 RICIAI GRADEZZE FOTOMETRICHE Fattoe di visibilità (o di sensibilità visiva) K ( λ) : funzione che appesenta la sensibilità media dell occhio umano a adiazioni di diffeente lunghezza d onda ma di eguale
RICIAI GRADEZZE FOTOMETRICHE Fattoe di visibilità (o di sensibilità visiva) K ( λ) : funzione che appesenta la sensibilità media dell occhio umano a adiazioni di diffeente lunghezza d onda ma di eguale
Moto di puro rotolamento
 oto-taslaione di un copo igido di seione cicolae (disco,cilindo,sfea) su di un piano, pe il quale il punto (o i punti) di contatto ta il copo ed il piano è femo ispetto a questo ( non vi è stisciamento
oto-taslaione di un copo igido di seione cicolae (disco,cilindo,sfea) su di un piano, pe il quale il punto (o i punti) di contatto ta il copo ed il piano è femo ispetto a questo ( non vi è stisciamento
Attività didattica Determinazione della massa di Giove tramite le osservazioni dei satelliti galileiani
 Piazza. Ungaetti, 1 81100 Caseta tel. 08/44580 - www.planetaiodicaseta.it, info@planetaiodicaseta.it Attività didattica Deteminazione della massa di iove tamite le ossevazioni dei satelliti galileiani
Piazza. Ungaetti, 1 81100 Caseta tel. 08/44580 - www.planetaiodicaseta.it, info@planetaiodicaseta.it Attività didattica Deteminazione della massa di iove tamite le ossevazioni dei satelliti galileiani
Campi scalari e vettoriali (1)
 ampi scalai e vettoiali (1) 3 e ad ogni punto P = (x, y, z) di una egione di spazio Ω R è associato uno ed uno solo scalae φ diemo che un campo scalae è stato definito in Ω. In alti temini: φ 3 : P R φ(p)
ampi scalai e vettoiali (1) 3 e ad ogni punto P = (x, y, z) di una egione di spazio Ω R è associato uno ed uno solo scalae φ diemo che un campo scalae è stato definito in Ω. In alti temini: φ 3 : P R φ(p)
Lezione 21 - La geometria delle aree. Richiami
 Lezione 1 - La geometia delle aee. Riciami [Ultimaevisione: evisione: gennaio gennaio009] In questa Lezione si iciamano sinteticamente alcune nozioni di geometia delle aee, aicento di una figua piana,
Lezione 1 - La geometia delle aee. Riciami [Ultimaevisione: evisione: gennaio gennaio009] In questa Lezione si iciamano sinteticamente alcune nozioni di geometia delle aee, aicento di una figua piana,
Esistono due tipi di forze di attrito radente: le forze di attrito statico, per cui vale la relazione:
 oze di attito f N P Le foze di attito adente si geneano sulla supeficie di contatto di due copi e hanno la caatteistica di opposi sepe al oto elativo dei due copi. Le foze di attito adente non dipendono,
oze di attito f N P Le foze di attito adente si geneano sulla supeficie di contatto di due copi e hanno la caatteistica di opposi sepe al oto elativo dei due copi. Le foze di attito adente non dipendono,
CAPITOLO 12 GONIOMETRIA
 CAPITOLO 1 GONIOMETRIA 1.01 - Misua degli Angoli e degli Achi 1.01.a) Unità di Misua degli Angoli o degli Achi Dato un angolo, è possibile scegliee come unità di misua un ulteioe (ovviamente) angolo definito
CAPITOLO 1 GONIOMETRIA 1.01 - Misua degli Angoli e degli Achi 1.01.a) Unità di Misua degli Angoli o degli Achi Dato un angolo, è possibile scegliee come unità di misua un ulteioe (ovviamente) angolo definito
di Enzo Zanghì pag 1 applichiamo il teorema di Pitagora e otteniamo:
 m@th_cone di Enzo Zanghì pag Distanza di due punti Pe deteminae la distanza ta i punti ( ; ) ( ; ) applichiamo il teoema di Pitagoa e otteniamo: = ( ) + ( ) Punto medio di un segmento M O M + Osseviamo
m@th_cone di Enzo Zanghì pag Distanza di due punti Pe deteminae la distanza ta i punti ( ; ) ( ; ) applichiamo il teoema di Pitagoa e otteniamo: = ( ) + ( ) Punto medio di un segmento M O M + Osseviamo
Capacità ele+rica. Condensatori
 Capacità ele+ica Condensatoi Condensatoi Il sistema più semplice pe immagazzinae enegia elettostatica è caicae un condensatoe. Genealmente il condensatoe è costituito da due piani metallici sepaati da
Capacità ele+ica Condensatoi Condensatoi Il sistema più semplice pe immagazzinae enegia elettostatica è caicae un condensatoe. Genealmente il condensatoe è costituito da due piani metallici sepaati da
MACCHINA ELEMENTARE A RILUTTANZA
 Sistemi magnetici con moto meccanico MACCHINA ELEMENTARE A RILUTTANZA Consiste in un nucleo magnetico con un avvolgimento a N spie e una pate mobile che uota con spostamento angolae θ e velocità angolae
Sistemi magnetici con moto meccanico MACCHINA ELEMENTARE A RILUTTANZA Consiste in un nucleo magnetico con un avvolgimento a N spie e una pate mobile che uota con spostamento angolae θ e velocità angolae
SPAZIO CARTESIANO E 3 (R) Sia [O,B] un riferimento euclideo nello spazio euclideo E 3 (R). B è una base ortonormale. condizioni di ortogonalità
![SPAZIO CARTESIANO E 3 (R) Sia [O,B] un riferimento euclideo nello spazio euclideo E 3 (R). B è una base ortonormale. condizioni di ortogonalità SPAZIO CARTESIANO E 3 (R) Sia [O,B] un riferimento euclideo nello spazio euclideo E 3 (R). B è una base ortonormale. condizioni di ortogonalità](/thumbs/69/60506168.jpg) SPZIO CRTESINO E (R) Sia [O,B] un ifeimento euclideo nello spaio euclideo E (R). B è una base otonomale. P P e e e P P condiioni di otogonalità ) etta-etta di paameti diettoi [(l,m,n )],[(l,m,n )] (l,m,n
SPZIO CRTESINO E (R) Sia [O,B] un ifeimento euclideo nello spaio euclideo E (R). B è una base otonomale. P P e e e P P condiioni di otogonalità ) etta-etta di paameti diettoi [(l,m,n )],[(l,m,n )] (l,m,n
Unità Didattica N 10 : I momenti delle forze
 Unità didattica N 10 I momenti delle foze 1 Unità Didattica N 10 : I momenti delle foze 01) omento di una foza ispetto ad un punto 02) omento isultante di un sistema di foze 03) omento di una coppia di
Unità didattica N 10 I momenti delle foze 1 Unità Didattica N 10 : I momenti delle foze 01) omento di una foza ispetto ad un punto 02) omento isultante di un sistema di foze 03) omento di una coppia di
Circuiti RLC RIASSUNTO: L(r)C serie: impedenza Z(ω) Q valore risposta in frequenza L(r)C parallelo Circuiti risonanti Circuiti anti-risonanti
 icuiti R RIASSUNTO: () seie: impedenza () valoe isposta in fequenza () paallelo icuiti isonanti icuiti anti-isonanti icuito in seie I cicuiti pesentano caatteistiche inteessanti. Ad esempio, ponendo un
icuiti R RIASSUNTO: () seie: impedenza () valoe isposta in fequenza () paallelo icuiti isonanti icuiti anti-isonanti icuito in seie I cicuiti pesentano caatteistiche inteessanti. Ad esempio, ponendo un
SELEZIONE DI ESERCIZI DI ELETTROSTATICA.
 Fisica geneale II, a.a. 13/14 SELEZIONE DI ESEIZI DI ELETTOSTATIA..1. Un pocesso elettolitico divide 1.3 mg di Nal (massa di una mole = 59 g) in Na + e l. Le caiche positive vengono allontanate da quelle
Fisica geneale II, a.a. 13/14 SELEZIONE DI ESEIZI DI ELETTOSTATIA..1. Un pocesso elettolitico divide 1.3 mg di Nal (massa di una mole = 59 g) in Na + e l. Le caiche positive vengono allontanate da quelle
Vista dall alto. Vista laterale. a n. Centro della traiettoria
 I poblema Un ciclista pedala su una pista cicolae di aggio 5 m alla velocità costante di 3.4 km/h. La massa complessiva del ciclista e della bicicletta è 85.0 kg. Tascuando la esistenza dell aia calcolae
I poblema Un ciclista pedala su una pista cicolae di aggio 5 m alla velocità costante di 3.4 km/h. La massa complessiva del ciclista e della bicicletta è 85.0 kg. Tascuando la esistenza dell aia calcolae
Note del corso di Geometria
 Giuseppe ccascina Valeio Monti Note del coso di Geometia ppendice nno ccademico 2008-2009 ii apitolo 1 Richiami di geometia del piano 1.1 Intoduzione Richiamiamo alcuni agomenti di geometia euclidea del
Giuseppe ccascina Valeio Monti Note del coso di Geometia ppendice nno ccademico 2008-2009 ii apitolo 1 Richiami di geometia del piano 1.1 Intoduzione Richiamiamo alcuni agomenti di geometia euclidea del
SETTIMA-OTTAVA LEZIONE: sorgenti del campo magnetico, legge di Ampere, legge di Biot-Sawart
 . Chiodoni esecizi di Fisica II SETTIM-OTTV LEZIONE: sogenti del campo magnetico, legge di mpee, legge di Biot-Sawat Esecizio 1 Due spie cicolai di aggio 3cm, aventi lo stesso asse, sono poste in piani
. Chiodoni esecizi di Fisica II SETTIM-OTTV LEZIONE: sogenti del campo magnetico, legge di mpee, legge di Biot-Sawat Esecizio 1 Due spie cicolai di aggio 3cm, aventi lo stesso asse, sono poste in piani
Le Galassie. Lezione 4
 Le Galassie Lezione 4 Fotometia delle ellittiche Le galassie ellittiche pesentano isofote ben appossimabili con ellissi. In geneale la fomula di Sesic fonisce un fit miglioe al pofilo di billanza a tutte
Le Galassie Lezione 4 Fotometia delle ellittiche Le galassie ellittiche pesentano isofote ben appossimabili con ellissi. In geneale la fomula di Sesic fonisce un fit miglioe al pofilo di billanza a tutte
Cinematica III. 11) Cinematica Rotazionale
 Cinematica III 11) Cinematica Rotazionale Abbiamo già tattato il moto cicolae unifome come moto piano (pa. 8) intoducendo la velocità lineae v e l acceleazione lineae a, ma se siamo inteessati solo al
Cinematica III 11) Cinematica Rotazionale Abbiamo già tattato il moto cicolae unifome come moto piano (pa. 8) intoducendo la velocità lineae v e l acceleazione lineae a, ma se siamo inteessati solo al
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2009
 ESME DI STT DI LICE SCIENTIFIC CRS DI RDINMENT 009 Il candidato isolva uno dei due poblemi e 5 dei 0 quesiti in cui si aticola il questionaio. PRLEM È assegnato il settoe cicolae di aggio e ampiezza (
ESME DI STT DI LICE SCIENTIFIC CRS DI RDINMENT 009 Il candidato isolva uno dei due poblemi e 5 dei 0 quesiti in cui si aticola il questionaio. PRLEM È assegnato il settoe cicolae di aggio e ampiezza (
Politecnico di Milano Fondamenti di Fisica Sperimentale a.a Facoltà di Ingegneria Industriale - Ind. Aero-Energ-Mecc
 Politecnico di Milano Fondamenti di Fisica Speimentale a.a. 9-1 - Facoltà di Ingegneia Industiale - Ind. Aeo-Eneg-Mecc II pova in itinee - 5/7/1 Giustificae le isposte e scivee in modo chiao e leggibile.
Politecnico di Milano Fondamenti di Fisica Speimentale a.a. 9-1 - Facoltà di Ingegneia Industiale - Ind. Aeo-Eneg-Mecc II pova in itinee - 5/7/1 Giustificae le isposte e scivee in modo chiao e leggibile.
ψ β F ESERCIZIO PIEGAMENTI SULLE BRACCIA
 S ϕ α E h W ψ β ESERCIZIO PIEGMENTI SULLE BRCCI W Un atleta compie una seie di piegamenti sulle baccia, mantenendo il movimento dei segmenti del baccio (omeo ed avambaccio) paalleli al piano sagittale.
S ϕ α E h W ψ β ESERCIZIO PIEGMENTI SULLE BRCCI W Un atleta compie una seie di piegamenti sulle baccia, mantenendo il movimento dei segmenti del baccio (omeo ed avambaccio) paalleli al piano sagittale.
