Capitolo V Applicazioni
|
|
|
- Angelica Roberti
- 6 anni fa
- Visualizzazioni
Transcript
1 Citolo Alizioni. Clolo di sint Pr lolr l sint sritt d fluidi inomrimibili in movimnto sull surfii on ui vngono onttto, si f uso dll quzion di bilnio dll quntità di moto in form globl: I M Π G 0 ( ) Tl quzion dv ssr lit d un oro fluido h ou un volum mtril, oinidnt istntnmnt on il volum di ontrollo su ui vngono lolti i trmini dll (). Tl volum è dlimitto d un surfii, l surfii di ontrollo, ostituit in rt dll surfii su ui si dv lolr l sint in rt d surfii usiliri di form smli. L rt di surfii di ontrollo su ui si dv lolr l sint è imrmbil: u n 0, mntr l rt di surfii di ontrollo usiliri è ostituit d surfii di ingrsso usit dl fluido, su ui u n 0. L iotsi smlifitiv h si dottno usulmnt nl lolo dll sint sono l sgunti:. Il moto è rmnnt;. Il fluido è idl; In virtù dll rim iotsi il rimo trmin rimo mmbro dll () è idntimnt nullo: I0, mntr in virtù dll sond iotsi gli sforzi tngnzili ossono ssr trsurti: dunqu l risultnt dll forz di onttto è dovut l solo sforzo di rssion: Π nd. Pr qunto rigurd il lolo dll forz M, si dv ossrvr h il volum di ontrollo è dlimitto in rt d surfii imrmbili, su ui M0, in rt d surfii usiliri di flusso in, su ui M 0. Su qust ultim si ssum un distribuzion di vloità in ui tutt l lin di flusso sono tr loro rlll, on urvtur null o trsurbil, rttrizzt dll vr dirzion rlll ll norml ll surfii (ntrnt nl volum di ontrollo) vrso risttivmnt onord od oosto tl norml sond h si trtti di surfii di ingrsso o di usit. In ltr rol sino uu n u-u n l distribuzioni di vloità su,, ssndo n,n l normli ll surfii di ingrsso usit, vnti vrso ntrnt nl volum di ontrollo. Il trmin M ssum l srssion: M ( u n) d ρu( u n) d ρu d n ρu d n ρβ n ρβ n ( b) ρu in ui β,β sono i offiinti di rgguglio dll ortt di quntità di moto dfiniti trmit l: u d β ( ) rmttono di srimr gli intgrli nll (b) trmit l vloità mdi sull szion. I offiinti di rgguglio vngono rminti srimntlmnt il loro vlor dind dll ondizioni di moto dll orrnt. Normlmnt l orrnti rs in onsidrzion ni loli tnii si trovno in ondizioni di moto tli d fr ssumr l offiint di rgguglio un vlor
2 rssohé unitrio: β. D or in vnti rtnto, slvo divrsmnt d srssmnt sifito, si ssumrà tl vlor r il offiint unitrio. Dunqu, nll iotsi ost, il flusso dll quntità di moto è un forz il ui vrso è smr onord l vrsor norml ll surfii in su ui gis, vnt vrso ntrnt nl volum di ontrollo. Il unto di lizion dl flusso dll quntità di moto oinid on il ntro di figur dll szion. Si dv inoltr sottolinr h sull szioni di ingrsso usit, vndo ssunto l linrità dll orrnt, stnt l ostnz dll izomtri, l distribuzion dll rssion è di tio idrosttio. Tl ftto smlifi notvolmnt il lolo dll risultnt dll forz di onttto, om si vdrà nll lizioni illustrt di sguito... Sint su l urv. Pl Plton Si un surfii ilindri, rt, l ui dirttri si l urv C, trit sul ino orizzontl (figur.). y i x α i i n i C Figur. Elmnti gomtrii dll l urv Tl surfii si invstit d un gtto libro, ossi d un orrnt linr l ui surfii ltrl si trovi rssion tmosfri, rttrizzto d un vloità ssolut u i, di modulo uniform sull szion, dirtt om l ss x d un szion. Il gtto, doo vr invstito l l, vin dvito d ss in modo tl h l ngolo formto dll ss dl gtto in usit on l dirzion originri si α. L l si inoltr nimt d vloità ssolut i. Pr lolr l sint S sritt dl gtto sull l, ugul in modulo dirzion, oost nl vrso ll sint Π g h l l srit sull rt di gtto onttto on ss, si rnd un volum di ontrollo dlimitto dll surfii in di ingrsso usit dll surfii ltrl dl gtto. Qust ultim, in rt è onttto on l tmosfr in rt è onttto on l l. Di onsgunz l quzion globl fornis: Qust ffrmzion uò ssr giustifit dl ftto h l orrnti rs in onsidrzion normlmnt hnno un rofilo di vloità simmtrio ristto ll ss o ddirittur uniform sull szion.
3 I M G Π 0 I 0 M ρr i ρ R n Π Π g S G ρgk S ρri ρ R n ρgk ( ) Com si vd, l risultnt dll forz di onttto Π sritt sul gtto, oinid on l sint h l l srit sull rt di gtto onttto on ss: Π g. Tutti gli ltri ontributi ll risultnt dll forz di onttto sono nulli, drivndo d surfii immrs in mbint rssion tmosfri: l surfii ltrl dl gtto non onttto on l l l surfii di ingrsso usit, il ui ontorno è rssion tmosfri. I flussi dll quntità di moto sono stti lolti fndo rifrimnto ll vloità rltiv dl gtto ristto ll l: R, R. Alindo il torm di Brnoulli nl sistm di rifrimnto solidl ll l, su un lin di flusso ost sul ino orizzontl z0, tr l szioni di ingrsso di usit si trov h: g R R g () ossi il modulo dll vloità rltiv rst ostnt. Di onsgunz, r l ostnz dll ortt rltiv, nh l szion dl gtto rst ostnt. L roizion dll sint sull dirzion dll ss x è dll: S i ρ ( ) os( ) [ ] ( ) α Si ossrvi h, r απ ossi r un l ftt in modo tl h il gtto bbi vloità rltiv di usit dirtt in snso oosto qull di ntrt (l Plton), si h il mssimo dll sint: S i S x ρ( ) L otnz dut ll l Plton è fornit dll: P S i ρ ( ) ( 5) Inv l otnz originri dl gtto è ri : P g ρ gq ρ g ( 6) Di onsgunz il rndimnto dll l Plton, dfinito om il rorto tr l otnz d ss dut dl gtto l otnz originri di qust ultimo, vl: η ( ) ( 7)
4 L ondizion di ottimo rndimnto l vrir dll vloità dll l, vin ottnut nnullndo l drivt dl rndimnto (7) ristto ll vloità dll l. Si ottngono l du ondizioni:, () 8 L rim orrisond ffttivmnt d un mssimo, mntr l sond l minimo rndimnto ( η 0 ). In orrisondnz dl rimo vlor, l otnz dl gtto, l otnz dut ll l d il rndimnto vlgono risttivmnt: 7 Pg ρ 6 P ρ () 9 6 η Il vlor dl rndimnto ottimo è minor dll unità, ur ssndo stto rivto in ssnz di dissizioni rdit nrgtih, iò si giustifi si on il ftto h llontnndosi l l dll origin dl gtto rt dll otnz originri di qusto dv ssr ss r rggiungr l l, si on il ftto h il gtto ossid ll usit dll l un nrgi inti ssolut divrs d zro. L otnz ss dl gtto r rggiungr l l si uò lolr onsidrndo h durnt un intrvllo di tmo unitrio qust ultim rorr un distnz ri. Di onsgunz l mss di liquido h dv rggiungr l l on vloità, è ri : ρ d ss omt un otnz ri : P 9 ρ ρ ( 0) Si onsidri or h l vloità rltiv di usit vl R ( )i oihé invrt il vrso, m mntin ostnt il modulo. L vloità ssolut di usit vl dunqu, r : ( ) i [ ( )] i ( ) i ( ) Ai R i In onsgunz di tl vlor non nullo dll vloità ssolut di usit, l gtto è ssoito il sgunt vlor dll otnz, lsmnt non utilizzt: P u ( ) A ρ ( ) ρ h dv ssr lolto on l nrgi inti r unità di volum dll vloità ssolut di usit l ortt rltiv dl gtto ristto ll l. In dfinitiv si vd om l somm dll otnz dut ll l, dll otnz di llungmnto (0) di usit () si sttmnt ri ll otnz originri dl gtto. L rirtizion tr l otnz è tl d mssimizzr, nll iotsi ost, l otnz util, ioè qull dut ll l. Tuttvi è intrssnt ossrvr, dll
5 srssion () dll vloità ssolut di usit dl gtto: A, h qust ultim si nnull r. In tli ondizioni si hnno i sgunti vlori dll otnz dl rndimnto: Pg ρ P ρ P ρ Pu 0 η 0. 5 ( ) In tli ondizioni il rndimnto è infrior ristto l so rdnt, m l otnz dl gtto in usit si nnull, l qul os è fvorvol gli fftti dll lizioni rtih, oihé si limin un dll us h gnrno l otnz non utilizzt. Nll rltà inftti l sint rodott d un gtto su un l riurv dl tio sminto vin imigt nll roduzion di nrgi. Pr limitr l ltr us di otnz non utilizzt, l llungmnto dl gtto, si f in modo h il gtto intrtti un sussion di l. Si uò vlutr l umnto di rndimnto dovuto ll sussion di l iotizzndo h, r, nll unità di tmo il gtto si llunghi di un quntità ri φ, ssndo φ un offiint ositivo minor di h tin onto dll rsnz dll moltliità di l. Di onsgunz l otnz nssri ll llungmnto dl gtto è ri : P ρφ ρφ ( ) mntr l otnz originri dl gtto è smr dll (6), on. Sihè l otnz dut ll l è dll diffrnz tr l (6) l (), non vndosi otnz non utilizzt r nrgi inti llo srio: P φ ρ ( 5) Di onsgunz il rndimnto, risult ri : η φ ( 6) Il rndimnto (6) umnt l diminuir di φ, ossi l diminuir dll llungmnto dl gtto. Tl ondizion è soddisftt s si immgin h non n un l si stt invstit dl gtto si omini d llontnr, un nuov l si trovi sotto l zion dl gtto. Ciò è qunto si vrifi nll turbin Plton, ostituit d ruot sull quli sono montt l l in sussion, om in figur.. Pr bilnir l forz gnti sull ruot, l turbin è sottoost ll zion di iù gtti (nh o 5) l l sono doio uhiio. 5
6 Gtto Gtto ist di fino ist dll lto Figur.. L ruot Plton l l doio uhiio.. Sint su un oro invstito d un orrnt Si onsidri un oro di form not, immrso in un orrnt, in quit ristto d ss (figur.). y x n n Si n Figur.. Il oro invstito d un orrnt Si suong h l orrnt si limitt d rti rigid d imrmbili. In figur., il disgno è rifrito l ino orizzontl. L orrnt, di fluido idl in moto rmnnt, doo vr invstito il oro d ssr stt dvit d sso, gnr l si, zon di fluido vll dl oro sd di moti vortiosi, h, nll rltà, si stingu d un rt distnz dl oro. Il moto dll si è strmmnt omlito. Ai fini di un shmtizzzion di rim rossimzion, il fluido nll si uò ssr onsidrto ttto l oro dunqu frmo. In ltr rol, si iotizz h l orrnt h irond l si sorr su qust ultim snz smbir zioni tngnzili h l si si stnd indfinitmnt vll dl oro. Si tng rsnt h nll rltà l mutu zioni tngnzili smbit tr l orrnt l si fnno sì h qust ultim si stingu d un rt distnz vll dl oro, ssndosi omltmnt msolt ll orrnt. 6
7 Allo soo di lolr l sint sritt dll orrnt sul oro, si onsidri il volum di ontrollo dlimitto dll rti imrmbili, dll surfii usiliri in ssnti r l szioni, dll surfii dl oro. L surfii usiliri in ssnt r l szion è ri ll surfii usiliri in ssnt r, diminuit dll surfii ostrior dl oro. L quzion di bilnio dll quntità di moto in form globl, lit l volum di ontrollo dfinito in figur. on l onsut iotsi sull distribuzioni di vloità sull szioni sull linrità dll orrnt nll szioni,, fornis: I 0 M Π G ρgk ρq( ) i ( ) i Π Π S [ ρq( ) ] i ρgk ( 7) In ui Π è l sint h il oro srit sull orrnt, ugul in modulo dirzion, oost nl vrso, ll sint S h l orrnt srit sul oro. I vlori dll rssioni, ssndo onsidrti su un ino orizzontl, sono ostnti su tutt l szion. Il so ontribuis ll sint sul oro on un forz vnt omonnt null ristto ll dirzion dl moto; roittndo l sint su tl dirzion si h: S x ( ) ( ) ρq Avndo srsso:, ossi l surfii usiliri in om diffrnz tr qull in l surfii ostrior dl oro. Pr vr l sint totl h subis il oro in dirzion rlll ll ss x, si dv rò ggiungr ll rdnt srssion l forz sritt dl fluido sull surfii ostrior dl oro: tl forz è rorio ri. Di onsgunz si h: S x ( ) ( ) ( 8) ρq Alindo or il torm di Brnoulli su un dll du lin di flusso, simmtrih ristto l oro, h rtono dll szion rrivno nll, si ottin l diffrnz dll rssioni nll szioni strm in funzion dll vloità: ρg g ρg g ρ ( ) ( 9) Sostitundo infin l diffrnz dll rssioni (9) nll (8) si h: S x ρ ρq ( ) ( ) ( 0) Qust ultim srssion, uò ssr ost in funzion dll vloità di ingrsso, sfruttndo l ostnz dll ortt: 7
8 S C x D ρ C D ρ ( ) L () è l formul dll sint subit d un oro immrso in un orrnt, vlid nll mbito dll iotsi ost. L formul () f rifrimnto, r il lolo dll sint, ll vloità di ingrsso, ll szion di ingrsso dll orrnt ll szion mstr dl oro, ossi ll roizion dll surfii dl oro su un ino rndiolr ll dirzion dl moto. Il offiint di sint C D o drg offiint nll iotsi ost è funzion slusivmnt dll gomtri. Nll rltà dind nh dl moto dll orrnt dll rttristih fisih dl fluido tl dindnz vin solitmnt rttrizzt srimntlmnt. Nl so di un oro immrso in un orrnt non limitt o lontn d rti, l formul () rd vlidità il offiint di drg vin rminto slusivmnt r vi srimntl... Eli Si onsidri un li, ostituit d un rto numro di l h ruotno on vloità ngolr ostnt dsrivnti un r irolr, t diso dll li, in moto di trslzion on vloità ostnt in un fluido in quit. Si vuol lolr l sint h l li il fluido si smbino. A tl soo è oortuno onsidrr iuttosto il fluido in moto di trslzion uniform on vloità di modulo ri vrso oosto qull dll li l li frm, on l l rotnti. L dirzion di si rndiolr l diso dll li. Gli lmnti fluidi h trnsitno r il diso dll li, formno un tubo di flusso (figur.), di szion trsvrsl inizil, vloità rssion risttivmnt ri,, h onvrg vrso il diso dll li, l sur ontinu onvrgr fino d ssumr il vlor., s, Figur.. Rrsntzion shmti dl flusso ttrvrso l li. In orrisondnz dll szion l vloità l rssion dl flusso ssumono risttivmnt i vlori,. Gli ndmnti dll rssion dll vloità, riortti in figur.5 in funzion dll siss s, mostrno om l rssion dll orrnt subis un bruso inrmnto Δ nl ssggio 8
9 ttrvrso il diso dll li, di sguito rurto, mntr l vloità umnt il suo vlor d on ontinuità. s s Δ s Figur.5. Andmnto dll rssion dll vloità. L sint sritt dll li sull orrnt fluid si lol rtnto lindo l quzion di bilnio dll quntità di moto in form intgrl l volum di ontrollo (figur.) omrso tr l szioni, immditmnt rim doo il diso dll li, l surfii ltrl l surfii omlssiv dll l dll li. Si onsidrrà dirttmnt l omonnt slr dll quzion di bilnio dll quntità di moto nll dirzion dl flusso (dirzion onord on s). Dunqu: Π ( ) Π ( ) Δ ( ) 0 Il trmin di inrzi lol I è nullo r l stzionrità dl moto. Il flusso dll quntità di moto M è nullo, oihé dl digrmm dll vloità riortto in figur.5 si ossrv h nll szioni di ingrsso usit i vlori dll vloità si ssumono rtimnt idntii oinidnti on il vlor dll vloità in orrisondnz dl diso dll li:. L Π è l omonnt dll sint sondo l dirzion dl flusso rivut dl fluido d rt dll li h vrso onord on l vloità. Il fluido ioè vin sinto llontnto dl diso dll li. L sint S gnt sull li rtnto h vrso oosto, immginndo l li montt su un mzzo nvl o ro, tndrbb singr il mzzo nll dirzion oost qull dl flusso. Pr srimr l Π in funzion dll quntità not, si dv lir il torm di Brnoulli tr l szioni - -: ρg ρg g g ρg ρg g g ( ) Sottrndo l rim dll sond riordndo h si h: 9
10 ρ Δ ( ) ( ) D ui: Π ρ ( ) ( 5) Si lihi or l quzion di bilnio dll quntità di moto in form intgrl l volum di ontrollo omrso tr l szioni, oinidnt on il tubo di flusso illustrto in figur.. Si h: Π ( ) ρ ρ Π ρq( ) ( 6) 0 In ui si è ftt omrir l ortt in volum, ostnt ttrvrso tutt l szioni onsidrt. Il ontributo dll rssion, onsidrndo h nll szioni ssum lo stsso vlor, è nullo. guglindo l (5) l (6), si uò srimr l vloità di usit dl fluido in funzion dll vloità dl fluido in ingrsso ( ) in orrisondnz dl diso dll li ( ): ρq ρ ( ) ρ ( ) ( ) ( ) ρ ( ) ( ) ( 7) Si, sono not: è in funzion dll rttristih gomtrih dll l dll li dll vloità di rotzion di qust, è l vloità dll orrnt indisturbt, ossi l vloità on ui vnz il diso dll li dunqu il mzzo d ss solidl. Dll sond dll (7) si h dunqu: (8) Di onsgunz, l sint Π rivut dl fluido (ugul oost qull h il fluido imrim sull li), vin srss dll: Π ( ) ( 9) ρ L otnz util ssoit ll sint dll (9) r l vloità : Π rivut dl fluido vin lolt ffttundo il rodotto P f ρ ( ) ( 0) L otnz sorgnt ssoit ll sint rodotto dll (9) r l vloità : Π rivut dl fluido vin lolt ffttundo il P ( ) ( ) ρ Il rorto tr l (0) l (), fornis il rndimnto dll li: 0
11 η intso om il rorto tr l fftto util (l otnz ssoit ll sint) l otnz sorgnt (l otnz lgt l slto di rssion gnrto dll rotzion dll li). Tnto iù il rndimnto è rossimo ll unità tnto iù l li è disgnt in modo ffiint. Si ossrvi rtnto qunto sgu: r umntr il rndimnto si dovrbb fr in modo h i vlori dll vloità, sino il iù ossibil rossimi; in tl modo rò tnto l sint, qunto l otnz motri tndono zro (formul (9) (0)); si uò nsr riò di omnsr l diminuzion dll otnz motri dll sint umntndo l szion dl diso dll li: si hnno rò limiti strutturli us dll forz ntrifugh gnti sull l, sorttutto nll lizioni ronutih. Nll lizioni nvli, l rsr dll dimnsioni dll li, si ggrv il fnomno dll vitzion, lgto ll ssiv diminuzion di rssion subit dll orrnt immditmnt rim di ttrvrsr il diso dll li onsistnt nll gnrzion sussivo rissorbimnto di boll di riform (gs vor). L vitzion è un fnomno ltmnt orrosivo dnnoso r i mtrili.. L quzion di bilnio dll quntità di moto in sistmi non inrzili. Proulsion rzion. Qundo si ffrontno roblmi di dinmi di fluidi in sistmi di rifrimnto in movimnto, è nssrio formulr l quzion di bilnio dll quntità di moto in sistmi non inrzili. Si onsidri rtnto un oro fluido in moto rltivo ristto d un sistm di rifrimnto in moto rigido, on vloità lrzion di trsinmnto risttivmnt d v T, T on vloità di rotzion ngolr d Ω. E noto h l vloità l lrzion di un lmnto fluido v, rtnnt l oro fluido rilvt in un sistm di rifrimnto inrzil sono lgt qull du rilvt nl sistm di rifrimnto in moto u,, dll formul: v v T T Ω r u dω du Ω u Ω Ω r r ( ) in ui r è il vttor distnz dl unto outo dll lmnto fluido dll origin dl sistm di rifrimnto in moto rigido. Si onsidri l quzion di bilnio dll quntità di moto in form globl: d ρv d f d nd μ ( Dn) d ( ) Si uò lir un rtiolr form dl torm dl trsorto, sfruttndo l quzion di bilnio dll mss in form indfinit, l rimo mmbro dll quzion ():
12 d dρv dρ dv ρvd ( v) d v ρdiv( v) d ρ d ρ d ( ) ρvdiv I mmbrodll quzion di ontinuità in form indfinit dv Sussivmnt è ossibil srimr l lrzion ssolut (); dv trmit l sond dll dv ρ d ρ T dω du Ω u Ω Ω r r d ( 5) in modo d srimr l drivt tmorl dll quntità di moto in funzion dll vloità lrzion rltiv, oltrhè dll lrzion di trsinmnto dll vloità di rotzion ngolr. L () si modifi infin nll: du dω ρ d ρ d d d - T Ω u Ω Ω r r f n μdnd ( 6) Al rimo mmbro dll quzion (6) uò or ssr lito il torm dl trsorto sondo l formul (6) dl I itolo. Portndo tutti i trmini sondo mmbro si ottin: t ρud ρu ( u n) d ρ T dω Ω u Ω Ω r r d fd nd - μdnd 0 ( 7) L (7) è l form dll quzion di bilnio dll quntità di moto rt. In rti oinid on l quzion (6) dl I itolo. Si noti rò h: i trmini di inrzi lol di flusso dll quntità di moto sono lolti on l vloità dl fluido rltiv l sistm di rifrimnto non inrzil; omr l intgrl di volum dll forz rnti dovut l moto dl sistm di rifrimnto. L quzion (7) uò ssr lit l lolo dll sint dovut ll rzion di fflusso di roulsori rzion. Si onsidri tl roosito (figur.6) un rzzo, sottoosto ll zion dll forz di grvità, h si sollvi dl suolo on vloità. Dll ugllo osto sul fondo dl rzzo fuoris fluido, risultnt dll ombustion dl rollnt, on vloità rltiv ristto l rzzo ri v, ostnt. Di onsgunz l mss di rollnt ll intrno dl rzzo vri sondo un lgg linr: m f m 0 m& t, ssndo hirmnt m& l ortt in mss usnt dll ugllo. Posto h l fflusso dl fluido vvng rssion, si vuol lolr l sint sritt sul rzzo us dll fflusso dll ugllo. Dll figur.6 si uò vdr om onvng dirttmnt onsidrr l roizion dll quzion globl (7) nll dirzion dll vloità di vnzmnto dl rzzo, individut dl vrsor, omun nh ll dirzion dll vloità rltiv di fflusso dl fluido v. In tl mbito inoltr l vloità è d onsidrrsi om vloità di trsinmnto l su drivt ristto l tmo l lrzion di trsinmnto, di modulo T. olndo or lir l quzion
13 (7) l volum di ontrollo oinidnt on il volum di fluido ontnuto ll intrno dl rzzo, si dv onsidrr qunto sgu: θ -k v Figur.6 Shm dll roulsion rzion su un rzzo il rimo mmbro dll quzion (7) è nullo, in qunto si uò ritnr h l vloità rltiv di fflusso dl fluido ssum, ll intrno dl rzzo, vlori ovunqu trsurbili ristto qullo ssunto in orrisondnz dll szion di fflusso ; il sondo mmbro, vl: ρv m& v, ssndo l uni surfii di flusso; il trzo mmbro, onsidrndo null l omonnti di moto rottorio, vl: d ρ T d m f ; il qurto mmbro, onsidrndo om forz di oro l forz so, vl: f d m g os θ ; f ( ) infin, trsurndo l ultimo mmbro, ossi onsidrndo solo gli sforzi di rssion, si h: n d S, ssndo l rssion di fflusso S l sint rivut dl rzzo d rt dl fluido. In dfinitiv si h: S m g os θ f ( ) m m& v ( 8) f d Com si vd dll (8), rt il trsurbil ontributo o dll rssion di fflusso, l rt util dll sint roulsiv è ffi ll ultimo trmin sondo mmbro dll (8), ossi ll sulsion dll ortt di mss fluid m&. L sint (8) uò ssr insrit nll quzion di quilibrio dinmio dl rzzo, roittt nll dirzion :
14 d d m R mrg os f θ f ( θ ) R m g os( ) m m& v ( 9) in ui m R è l mss dl rzzo R l forz rsistnt l moto. L quzion (9) uò ssr imigt, ssgnt l forz rsistnt l moto, r rminr l ndmnto tmorl dll vloità di vnzmnto dl rzzo. n ultrior lizion dll (7) uò ssr ffttut nl so in ui vi si nl roulsor un szion di ingrsso i, di fluido mbint dnsità ρ, nssrio ll ombustion dl rollnt, vnt dnsità ρ. Tl so si rifris i motori rzion omunmnt imigti ngli ri lo shm di ssi è rrsntto nll figur.7. S - θ -k v Com si vd dll figur.7, il roulsor si muov on vloità in dirzion, in un fluido mbint in quit. L vloità di ingrsso dl fluido mbint, rltiv l roulsor, è dunqu ri. Assumndo un volum di ontrollo oinidnt on qullo dl roulsor, l lizion dll (7), roittt nll dirzion, fornis: t Figur.7 Shm dll roulsion rzion su un romobil ρu ρud 0 ( u n) ρ f d nd -S d ρ v ρ v ρ dω Ω u Ω Ω r r d ( ρ ρ ) g os( θ ) S ρ v ρ v ρ T i ( ρ ρ ) ( ρ ρ ) ( ρ ρ ) g os( θ ) (0) i d d
15 L srssion dll sint mostr om l omonnt util si fornit dll fflusso dll ortt in mss di gs ombusti (rrsntti dll somm dll ortt in mss di rollnt fluido d mbint). Qundo l romobil è in fs di volo di rgim ( 0,os( θ ) 0 ), il trzo qurto trmin dll sint si nnullno qust ultim è dll: S ρ v ρ v ρ. L quzion di bilnio dl momnto dll quntità di moto In luni si, nl lolo dll zioni smbit tr i ori fluidi l mbint strno, è nssrio fr riorso ll quzion di bilnio dl momnto dll quntità di moto in form intgrl. Qust ultim, si ottin imonndo h l vrizion tmorl dl momnto dll quntità di moto di un oro fluido dv guglir il momnto risultnt dll forz di oro dll forz di onttto sritt sul oro ttrvrso l surfii di frontir. Il momnto dll quntità di moto di un oro fluido, h ou il volum mtril, si lol intgrndo sul volum mtril l dnsità di momnto di quntità di moto ρ ( r u) : K ρ ( r u) d ( ) Intndndo di qui in vnti on r, nl lolo dl momnto di un vttor ristto d un olo, il vttor osizion dl unto di lizion dl vttor ristto l olo rslto. L drivt totl dl momnto dll quntità di moto si lol lindo il torm dl trsorto (formul (5), C. I): i dk t ρ ( r u) d ρ ( r u)( u n) d ( ) - in ui è il volum di ontrollo oinidnt istntnmnt on il volum mtril è l surfii di frontir di tl volum. I momnti risultnti dll forz di oro di onttto lit l fluido sono i dll: r f d r ( n μdn) d ( ) Eguglindo l () ll () si rvin ll: t ρ ( r u) d ρ ( r u)( u n) d r f d r ( n μdn) d ( ) - L () è l quzion di bilnio dl momnto dll quntità di moto in form intgrl. Ess si li l oro fluido nllo stsso modo in ui si li l quzion di bilnio dll quntità di moto. A tl soo si uò nh srimr in form omtt om quilibrio di momnti risultnti dll forz di inrzi loli, dl flusso dll quntità di moto, dll forz di oro dll forz di onttto: 5
16 M M M M M I I M G Π M t M ρ r M ρ M ( r u) ( r u)( u n) r f d G Π d ( n μdn) 0 d d ( 5) Si uò inoltr formulr un quzion di bilnio dl momnto dll quntità di moto in form globl nl rifrimnto non inrzil, sgundo un rgionmnto nlogo qullo svolto r ottnr l quzion (7). Snz rirorrr il rgionmnto svolto, si ottin un quzion in form globl in ui il momnto dll forz di inrzi lol dl flusso dll quntità di moto sono lolti on l vloità dl fluido rltiv l rifrimnto in ui omr il momnto dll forz di oro rnti. Ovvimnt tutti i momnti sono lolti ristto d un olo fisso ristto l rifrimnto rltivo. E util mostrr l utilità dll (), lindol l lolo dl momnto risultnt sritto dll zion dl fluido sull ltttur di un mhin idruli rotnt. Qust ultim è rrsntt shmtimnt in figur.6, in ui si rsnt un szion dll mhin on un ino orizzontl. Tl szion mostr un sri di tr di rofili lri, rotnti on vloità ngolr ostnt ω ristto l unto o. L ortt fluid in ntrt ossid un vloità ssolut, v orintt in modo tl d formr un ngolo ri θ on l tngnt ll ironfrnz, di rggio R, irosritt ll l. Tl vloità risult dll omosizion dll vloità rltiv u R dl fluido ristto ll l dll vloità di trsinmnto u T dovut ll rotzion dll l on vloità ngolr ostnt. Il modulo dll vloità ssolut dv ssr rgolto in modo tl h l vloità rltiv dl fluido ristto ll l si tngnt ll l. L rgolzion dll vloità di ingrsso vvin trmit ositi orgni fissi mobili (vlvol di rgolzion, ltttur fiss di invio t.). In usit, l vloità ssolut è orintt in modo tl d formr un ngolo ri θ on l tngnt ll ironfrnz di rggio R. L vloità rltiv srà nlogmnt tngnt ll l. ω u R v θ v u T R o u R θ u T R Figur.6. Rrsntzion shmti di un mhin idruli rotnt. 6
17 Gli ngoli θ,θ, l ortt di fluido in trnsito, l vloità u T, u T (lgt ll vloità ngolr di rotzion ostnt dll mhin) dindono dll gomtri dll dinmi dll mhin. Con tli i si ossono rttrizzr omltmnt i tringoli di vloità di ingrsso usit. Allo soo di lolr il momnto risultnt dll zioni dl fluido sull l, si onsidri il volum di ontrollo dlimitto dll surfii ilindrih irolri trttggit, di rggio R,R dll surfii dll l. L lizion dll quzion di bilnio dll quntità di moto in form globl risult ssi omlit, mntr si rivl rtiolrmnt onvnint l lizion dll quzion di bilnio dl momnto dll quntità di moto. Si ssumrà om olo il ntro di rotzion si suorrnno vrifit l sgunti iotsi:. il moto è rmnnt;. il fluido è idl;. l distribuzioni dll vloità sull ironfrnz di ingrsso usit sono uniformi; Di onsgunz si h, onsidrndo il modulo dll vloità ssolut v l roizioni di vri trmini dll (5) sull ss di rotzion, onsidrto vrtil, rivolto vrso l lto: M M M M I M G Π k 0 k ρ k 0 ( v R os( θ ) v sin( θ ) πr v R os( θ ) v sin( θ ) πr ) k M S k ( 6) Il rimo trmin è nullo r l rmnnz dl moto. Il sondo trmin vin lolto filmnt r l iotsi ost sui mi di vloità in ingrsso in usit. Il trzo trmin è nullo rhé l forz di oro (l forz so) è ovunqu rlll ll ss di rotzion rhé l su risultnt h rtt d zion oinidnt on l ss dll mhin. Infin il qurto trmin oinid dirttmnt, mno dl sgno, on l inognit rt. Inftti l forz dovut ll distribuzion di rssion sull surfii di ingrsso usit hnno dirzion rdil: n onsgu h il loro momnto risultnt, lolto onsidrndo om olo il ntro di rotzion, è nullo. Infin, tnndo onto h l ortt è d: Q v si h, r il modulo dl momnto: ( θ ) πr v sin( θ ) π ( 7) sin R M S ρq ( v R os( θ ) v R os( )) ( 8) θ dirzion vrso oinidono on qull dll ss vrtil, rivolto vrso l lto. L (8) fornis dunqu il modulo dll oi sritt dl fluido sull ltttur dll mhin h rtnto uò ssr misurt sull ss di rotzion. L rltiv otnz si ottin moltilindo l (8) r l vloità ngolr di rotzion dll ss: P S ρqω ( v R os( θ ) v R os( )) ( 9) θ L (9) è un otnz motri s ositiv: in tl so l mhin è un turbin ssorb l otnz (9) dll orrnt h vi trnsit. L (9) è un otnz rsistnt s ngtiv: in tl so l mhin è un om d l otnz (9), fornitl d un motor strno, ll orrnt h vi trnsit. Si dv fr ttnzion l ftto h l otnz (9) è qull dut dll orrnt fluid 7
18 ll mhin, ugul in modulo di sgno oosto qull dut dll mhin ll orrnt fluid. Nll omuni lizioni si f in modo h l omonnt MM ristto ll ss di rotzion si null sull szion di ntrt o di usit, rndndo ssil l dirzion dl flusso in tl szion. (figur.7): v v Pom R R Turbin v v R R Figur.7. Szion di mhin on un ino vrtil. Priò: nll om l ingrsso dll orrnt è ssil nll szion di rggio R ; nll turbin l usit dll orrnt è ssil nll szion di rggio R ; 8
Ellisse. L ellisse è il luogo geometrico dei punti del piano tali che la somma delle distanze da due punti fissi. definizione. P semidistanza focale
 Elliss dfinizion L lliss è il luogo gomtrio di punti dl pino tli h l somm dll distnz d du punti fissi F1 F2 dtti fuohi è ostnt, ioè: smiss mggior smiss minor P smidistnz fol F 2 smidistnz fol F 1 F 2 smiss
Elliss dfinizion L lliss è il luogo gomtrio di punti dl pino tli h l somm dll distnz d du punti fissi F1 F2 dtti fuohi è ostnt, ioè: smiss mggior smiss minor P smidistnz fol F 2 smidistnz fol F 1 F 2 smiss
IL MOTO NELLA ZONA INSATURA
 L ritnzion dll umidità L suprfii d 1 4 rpprsntno l sussiv fsi di drnggio gio dll qu d un mzzo poroso. Al rsr dl drnggio l qu l si ritir ngli spzi intrstizili on suprfii urvtur ur rsnt d umntndo il rio
L ritnzion dll umidità L suprfii d 1 4 rpprsntno l sussiv fsi di drnggio gio dll qu d un mzzo poroso. Al rsr dl drnggio l qu l si ritir ngli spzi intrstizili on suprfii urvtur ur rsnt d umntndo il rio
INTEGRALI. 1. Integrali indefiniti
 INTEGRALI. Intgrli indiniti Si un unzion ontinu in [, ]. Un unzion F dinit ontinu in [, ], drivil in ], [, disi primitiv di in [, ] s F, ], [. Tormi. S F è un primitiv di in [, ] llor nh G F, on R, è un
INTEGRALI. Intgrli indiniti Si un unzion ontinu in [, ]. Un unzion F dinit ontinu in [, ], drivil in ], [, disi primitiv di in [, ] s F, ], [. Tormi. S F è un primitiv di in [, ] llor nh G F, on R, è un
e una funzione g ε S f tali che = sup g : g S f tale che h ε f < ε/2; analogamente, per
 C.13 ntgrl di Rimnn Prmttimo il sgunt risultto. Lmm C.13.1 Si f un funzion limitt su = [, b]. Allor f è intgrbil s solo s pr ogni ε > 0 sistono un funzion h ε S + f un funzion g ε S f tli h h ε g ε < ε.
C.13 ntgrl di Rimnn Prmttimo il sgunt risultto. Lmm C.13.1 Si f un funzion limitt su = [, b]. Allor f è intgrbil s solo s pr ogni ε > 0 sistono un funzion h ε S + f un funzion g ε S f tli h h ε g ε < ε.
Macchine non completamente specificate. Sintesi Sequenziale Sincrona Sintesi Comportamentale di Reti Sequenziali Sincrone
 Mhin non ompltmnt spifit Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spifit Comptiilità Vrsion l 5/12/02 Sono mhin in ui pr lun onfigurzioni
Mhin non ompltmnt spifit Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spifit Comptiilità Vrsion l 5/12/02 Sono mhin in ui pr lun onfigurzioni
Circuiti Sequenziali Macchine Non Completamente Specificate
 CEFRIEL Consorzio pr l Formzion l Rir in Inggnri ll Informzion Politnio i Milno Ciruiti Squnzili Mhin Non Compltmnt Spifit Introuzion Comptiilità Riuzion l numro gli stti Mtoo gnrl FSM non ompltmnt spifit
CEFRIEL Consorzio pr l Formzion l Rir in Inggnri ll Informzion Politnio i Milno Ciruiti Squnzili Mhin Non Compltmnt Spifit Introuzion Comptiilità Riuzion l numro gli stti Mtoo gnrl FSM non ompltmnt spifit
RACCORDI PER APPLICAZIONI SPECIALI GIUNTI ECCENTRICI E CONICI
 RACCORDI PER APPLICAZIONI SPECIALI GIUNTI ECCENTRICI E CONICI 2 L soluzion dimnsionl ottiml pr signz prtiolri Rordi on snz ihir Innsti on snz ihir Clssi sondo nssità Dimtro di usit vriil Collgmnto l fondo
RACCORDI PER APPLICAZIONI SPECIALI GIUNTI ECCENTRICI E CONICI 2 L soluzion dimnsionl ottiml pr signz prtiolri Rordi on snz ihir Innsti on snz ihir Clssi sondo nssità Dimtro di usit vriil Collgmnto l fondo
Matematica 15 settembre 2009
 Nom: Mtriol: Mtmti 5 sttmbr 2009 Non sono mmss loltrii. Pr l domnd rispost multipl, rispondr brrndo o rhindo hirmnt un un sol lttr. Pr l ltr domnd srivr l soluzion on svolgimnto ngli spzi prdisposti..
Nom: Mtriol: Mtmti 5 sttmbr 2009 Non sono mmss loltrii. Pr l domnd rispost multipl, rispondr brrndo o rhindo hirmnt un un sol lttr. Pr l ltr domnd srivr l soluzion on svolgimnto ngli spzi prdisposti..
Elettronica dei Sistemi Digitali Sintesi di porte logiche combinatorie fully CMOS
 Elttroni di Sistmi Digitli Sintsi di port logih omintori full CMOS Vlntino Lirli Diprtimnto di Tnologi dll Informzion Univrsità di Milno, 26013 Crm -mil: lirli@dti.unimi.it http://www.dti.unimi.it/ lirli
Elttroni di Sistmi Digitli Sintsi di port logih omintori full CMOS Vlntino Lirli Diprtimnto di Tnologi dll Informzion Univrsità di Milno, 26013 Crm -mil: lirli@dti.unimi.it http://www.dti.unimi.it/ lirli
Corso di ordinamento - Sessione suppletiva - a.s. 2009-2010
 Corso di ordinmnto - Sssion suppltiv -.s. 9- PROBLEMA ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE SUPPLETIA Tm di: MATEMATICA. s. 9- Dt un circonrnz di cntro O rggio unitrio, si prndno
Corso di ordinmnto - Sssion suppltiv -.s. 9- PROBLEMA ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE SUPPLETIA Tm di: MATEMATICA. s. 9- Dt un circonrnz di cntro O rggio unitrio, si prndno
Studio di funzione. Pertanto nello studio di tali funzioni si esamino:
 Prof. Emnul ANDRISANI Studio di funzion Funzioni rzionli intr n n o... n n Crttristich: sono funzioni continu drivbili in tutto il cmpo rl D R quindi non sistono sintoti vrticli D R quindi non sistono
Prof. Emnul ANDRISANI Studio di funzion Funzioni rzionli intr n n o... n n Crttristich: sono funzioni continu drivbili in tutto il cmpo rl D R quindi non sistono sintoti vrticli D R quindi non sistono
GEODESIA: PROPRIETA GEOMETRICHE DELL ELLISSOIDE
 GEODESIA: PROPRIETA GEOMETRICHE DELL ELLISSOIDE PROPRIETA GEOMETRICHE DELL ELLISSOIDE Al fin di stbilir un gomtri sull llissoid di rotzion è ncssrio non solo dfinir l quzioni dll curv idon d individur
GEODESIA: PROPRIETA GEOMETRICHE DELL ELLISSOIDE PROPRIETA GEOMETRICHE DELL ELLISSOIDE Al fin di stbilir un gomtri sull llissoid di rotzion è ncssrio non solo dfinir l quzioni dll curv idon d individur
Caratterizzazione meccanica dei materiali
 Crttrizzzion mni di mtrili Esist notvol numro di prov mnih tt ll rttrizzzion dl omportmnto strutturl di mtrili /trzion, omprssion, fti, frttur, Lo sopo di isun è dfinir, in isun mito, i limiti di utilizzilità
Crttrizzzion mni di mtrili Esist notvol numro di prov mnih tt ll rttrizzzion dl omportmnto strutturl di mtrili /trzion, omprssion, fti, frttur, Lo sopo di isun è dfinir, in isun mito, i limiti di utilizzilità
6) Nel 1991 Carl Lewis ha stabilito il record del mondo dei 100 m percorrendoli in 9,86 s. Qual è la velocità media in km/h?
 1) L unità l SI pr l tmprtur l mss sono, rispttivmnt gri grmmi klvin kilogrmmi Clsius milligrmmi Clsius kilogrmmi klvin grmmi 2) Qul mtril ffon nll olio ( = 0,94 g/m 3 )? ghiio ( = 0,92 g/m 3 ) sughro
1) L unità l SI pr l tmprtur l mss sono, rispttivmnt gri grmmi klvin kilogrmmi Clsius milligrmmi Clsius kilogrmmi klvin grmmi 2) Qul mtril ffon nll olio ( = 0,94 g/m 3 )? ghiio ( = 0,92 g/m 3 ) sughro
ESERCIZIO 1 Calcolare i raggi di curvatura delle sezioni normali principali nel Polo Nord dell' ellissoide di Hayford.
 CORSO DI OOGRAFIA A - A.A. 006-007 ESERCIAZIOI - 09.05.06 ESERCIZI DI GEODESIA ESERCIZIO 1 Clcolr i rggi di curvtur dll szioni normli principli nl olo ord dll' llissoid di Hyford. 1) Szioni ormli rincipli
CORSO DI OOGRAFIA A - A.A. 006-007 ESERCIAZIOI - 09.05.06 ESERCIZI DI GEODESIA ESERCIZIO 1 Clcolr i rggi di curvtur dll szioni normli principli nl olo ord dll' llissoid di Hyford. 1) Szioni ormli rincipli
( ) ESERCIZI PROPOSTI. y x. cos x y. x y. c cos. xlog. x y. ctg 2. sin 1. x + 1. ctgx. c sin = + ( ) 1 = + ( ) ( )
 ESERCIZI PROPOSTI I) Dtrminar l intgral gnral dll sgunti quazioni diffrnziali linari dl primo ordin (fr..): ) ' ) ' ) ) ' os ' 5) ' 6) 7) tg ' ' 8) ' ( + log ) 9) ' ) ) log sin os [ log ] ' + ' sin ( +
ESERCIZI PROPOSTI I) Dtrminar l intgral gnral dll sgunti quazioni diffrnziali linari dl primo ordin (fr..): ) ' ) ' ) ) ' os ' 5) ' 6) 7) tg ' ' 8) ' ( + log ) 9) ' ) ) log sin os [ log ] ' + ' sin ( +
L ELLISSOIDE TERRESTRE
 L ELLISSOIDE TERRESTRE Fin dll scond mtà dl XVII scolo (su propost di Nwton) l suprfici più dtt ssr ssunt com suprfici di rifrimnto pr l Trr è stt individut in un ELLISSOIDE DI ROTAZIONE. E l suprfici
L ELLISSOIDE TERRESTRE Fin dll scond mtà dl XVII scolo (su propost di Nwton) l suprfici più dtt ssr ssunt com suprfici di rifrimnto pr l Trr è stt individut in un ELLISSOIDE DI ROTAZIONE. E l suprfici
Minimizzazione degli Stati in una macchina a stati finiti
 Rti Loih Sintsi i rti squnzili sinron Minimizzzion li Stti in un mhin stti initi Proimnto: Spiih Dirmm li stti Tll li stti Minimizzzion li stti Coii li stti Tll ll trnsizioni Slt lmnti i mmori Tll ll itzioni
Rti Loih Sintsi i rti squnzili sinron Minimizzzion li Stti in un mhin stti initi Proimnto: Spiih Dirmm li stti Tll li stti Minimizzzion li stti Coii li stti Tll ll trnsizioni Slt lmnti i mmori Tll ll itzioni
Minimizzazione degli Stati in una Rete Sequenziale Sincrona
 Minimizzzion gli Stti in un Rt Squnzil Sinron Murizio Plsi Murizio Plsi 1 Sintsi i Rti Squnzili Sinron Il proimnto gnrl i sintsi si svolg ni sgunti pssi: 1. Rlizzzion l igrmm gli stti prtir ll spifih l
Minimizzzion gli Stti in un Rt Squnzil Sinron Murizio Plsi Murizio Plsi 1 Sintsi i Rti Squnzili Sinron Il proimnto gnrl i sintsi si svolg ni sgunti pssi: 1. Rlizzzion l igrmm gli stti prtir ll spifih l
Trasformazioni geometriche +sometrie Omotetia e similitudine Teoremi di Euclide e teorema di Talete
 Trsormzioni gomtrih +somtri Omotti similituin Tormi i Euli torm i Tlt +somtri Stilisi s l sgunti rmzioni sono vr o ls. SEZ. N g h i l pplino un isomtri un igur, ss si orm. L simmtri ntrl è un prtiolr rotzion.
Trsormzioni gomtrih +somtri Omotti similituin Tormi i Euli torm i Tlt +somtri Stilisi s l sgunti rmzioni sono vr o ls. SEZ. N g h i l pplino un isomtri un igur, ss si orm. L simmtri ntrl è un prtiolr rotzion.
Corso di Fisica Tecnica (ING-IND/11). 1 anno laurea specialistica in architettura: indirizzo città Docente: Antonio Carbonari
 Corso di Fisic cnic (ING-IND/). nno lur spcilistic in rchitttur: indirizzo città Docnt: Antonio Crbonri Cpitolo I Il sistm città l uso pproprito dll nrgi.. Introduzion Un insdimnto urbno è un sistm strmmnt
Corso di Fisic cnic (ING-IND/). nno lur spcilistic in rchitttur: indirizzo città Docnt: Antonio Crbonri Cpitolo I Il sistm città l uso pproprito dll nrgi.. Introduzion Un insdimnto urbno è un sistm strmmnt
Sistemi lineari COGNOME... NOME... Classe... Data...
 Cpitolo Sistmi linri Risoluzion grfi lgri rifi pr l lss prim COGNOME............................... NOME............................. Clss.................................... Dt...............................
Cpitolo Sistmi linri Risoluzion grfi lgri rifi pr l lss prim COGNOME............................... NOME............................. Clss.................................... Dt...............................
CORSO DI TOPOGRAFIA A - A.A. 2006-2007 ESERCITAZIONI - 09.05.07 ALLEGATO al file Esercizi di geodesia. r a. Z c. nella quale
 CORSO DI TOPOGRAFIA A - A.A. 6-7 ESERCITAZIONI - 9.5.7 ALLEGATO l fil Esrcizi di godsi Ellissoid trrstr Fin dll scond mtà dl VII scolo (su propost di Nwton) l suprfici più dtt ssr ssunt com suprfici di
CORSO DI TOPOGRAFIA A - A.A. 6-7 ESERCITAZIONI - 9.5.7 ALLEGATO l fil Esrcizi di godsi Ellissoid trrstr Fin dll scond mtà dl VII scolo (su propost di Nwton) l suprfici più dtt ssr ssunt com suprfici di
tx P ty P 1 + t(z P 1)
 Esrcizi dll dcim sttimn - Soluzioni Indichimo con S R 3 l sfr unitri nll mtric Euclid di R 3, oro S {x, y, z R 3 x + y + z 1}. Indichimo con N S il polo nord il polo sud di S, rispttimnt, oro N,, 1 S,,
Esrcizi dll dcim sttimn - Soluzioni Indichimo con S R 3 l sfr unitri nll mtric Euclid di R 3, oro S {x, y, z R 3 x + y + z 1}. Indichimo con N S il polo nord il polo sud di S, rispttimnt, oro N,, 1 S,,
a b }. L insieme Q è pertanto l insieme delle frazioni.
 I1. Insimisti I1.1 Insimi Il ontto i insim è un ontto primitivo, prtnto non n vin t un finizion rigoros. Si può ir, intuitivmnt, h un insim è un ollzion i oggtti pr ui vlgono lun proprità: Un lmnto i un
I1. Insimisti I1.1 Insimi Il ontto i insim è un ontto primitivo, prtnto non n vin t un finizion rigoros. Si può ir, intuitivmnt, h un insim è un ollzion i oggtti pr ui vlgono lun proprità: Un lmnto i un
Q = Le + U* + Ec + Eg + Ecf. Si ha inoltre:
 Esm d lzon dl mo no dll tmodnm n fom sostnzl Clolo tmtu d so Dtmn l tmtu md T sf d gs st d un moto ltntvo T (vnt szo moto tsubl), not l ondzon d sson tmtu ll'ntno dll m d ombuston l tmn dll fs/os d snson,
Esm d lzon dl mo no dll tmodnm n fom sostnzl Clolo tmtu d so Dtmn l tmtu md T sf d gs st d un moto ltntvo T (vnt szo moto tsubl), not l ondzon d sson tmtu ll'ntno dll m d ombuston l tmn dll fs/os d snson,
Lezioni sull analisi di gusci sottili assialsimmetrici
 Lezioni sull nlisi di gusi sottili ssilsimmetrii Gusi sottili: ori bidimensionli l ui suerfiie medi non è in m si svilu nello szio, on rihi liti si gienti sul ino medio he ortogonli d esso. 1/ Corso di
Lezioni sull nlisi di gusi sottili ssilsimmetrii Gusi sottili: ori bidimensionli l ui suerfiie medi non è in m si svilu nello szio, on rihi liti si gienti sul ino medio he ortogonli d esso. 1/ Corso di
MODELLI DEI SISTEMI ELETTROMECCANICI
 Ing Mrigrzi Dotoli Controlli Autotici NO (9 CFU) Modlli di Sisti Elttroccnici MODELLI DEI SISTEMI ELETTROMECCANICI Nl sguito ci occupio dll odllzion di sisti ibridi ch cobinno sisti lttrici con sisti ccnici,
Ing Mrigrzi Dotoli Controlli Autotici NO (9 CFU) Modlli di Sisti Elttroccnici MODELLI DEI SISTEMI ELETTROMECCANICI Nl sguito ci occupio dll odllzion di sisti ibridi ch cobinno sisti lttrici con sisti ccnici,
j Verso la scuola superiore Geometria euclidea e analitica
 j rso l suol suprior Gomtri uli nliti Ossrv l spzzt stilisi quli ll sgunti rmzioni sono vr quli ls. B D G E B è onsutivo B. DE è onsutivo G. B è onsutivo D. B è int D. B è onsutivo D. E è onsutivo G. Il
j rso l suol suprior Gomtri uli nliti Ossrv l spzzt stilisi quli ll sgunti rmzioni sono vr quli ls. B D G E B è onsutivo B. DE è onsutivo G. B è onsutivo D. B è int D. B è onsutivo D. E è onsutivo G. Il
------------------------------------------------------------------------------------------------
 ------------------------------------------------------------------------------------------------ CAPIOLO 8 ANALISI ERMODINAMICA DEI PROCESSI DI CONVERSIONE ------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------ CAPIOLO 8 ANALISI ERMODINAMICA DEI PROCESSI DI CONVERSIONE ------------------------------------------------------------------------------------------------
MACCHINE TRACCIALINEE ED ACCESSORI
 MHIN TRILIN D SSORI D M PR SGNLTI ORIZZONTL G G N H I L F F ON MISURTOR STRDL INORPORTO FIGUR QT'. 2400MTRMT000 MHIN TRILIN 2400MTRMT0002 MHIN TRILIN 2400MTRMT0003 MHIN TRILIN D 2400MTRPM0005 PISTOL MNUL
MHIN TRILIN D SSORI D M PR SGNLTI ORIZZONTL G G N H I L F F ON MISURTOR STRDL INORPORTO FIGUR QT'. 2400MTRMT000 MHIN TRILIN 2400MTRMT0002 MHIN TRILIN 2400MTRMT0003 MHIN TRILIN D 2400MTRPM0005 PISTOL MNUL
ELABORAZIONE di DATI SPERIMENTALI
 ELABORAZIONE DATI SPERIMENTALI Prof. Giovnn CATANIA Prof. Rit DONATI Dr. Tibrio T DI CORCIA L stribuzion norml o gusn com modlità borzion dti sprimntli qtittivmnt numro I N T R O D U Z I O N E Un Un dll
ELABORAZIONE DATI SPERIMENTALI Prof. Giovnn CATANIA Prof. Rit DONATI Dr. Tibrio T DI CORCIA L stribuzion norml o gusn com modlità borzion dti sprimntli qtittivmnt numro I N T R O D U Z I O N E Un Un dll
Macchine non completamente specificate. Sintesi Sequenziale Sincrona Sintesi Comportamentale di Reti Sequenziali Sincrone
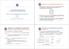 Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spiit Comptiilità Vrsion l 13/01/05 (Frrni( Antol) Mhin non ompltmnt spiit Sono mhin in ui
Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spiit Comptiilità Vrsion l 13/01/05 (Frrni( Antol) Mhin non ompltmnt spiit Sono mhin in ui
+ poligoni e l equivalenza di figure piane + triangoli + quadrilateri
 + poligoni + poligoni l quivlnz i figur pin + tringoli + quriltri + poligoni l quivlnz i figur pin 1 Stilisi s l sgunti ffrmzioni sono vr o fls. SEZ. E In un poligono i lti sono onsutivi u u. L somm gli
+ poligoni + poligoni l quivlnz i figur pin + tringoli + quriltri + poligoni l quivlnz i figur pin 1 Stilisi s l sgunti ffrmzioni sono vr o fls. SEZ. E In un poligono i lti sono onsutivi u u. L somm gli
Teorema (seconda condizione sufficiente per i campi conservativi piani): Sia F ( x, y)
 Campi Vttoriali Form iffrnziali-sconda Part Torma (sconda condizion sufficint pr i campi consrvativi piani): Sia F (, y) un campo vttorial piano dfinito in un aprto A di R, si supponga ultriormnt = y ;
Campi Vttoriali Form iffrnziali-sconda Part Torma (sconda condizion sufficint pr i campi consrvativi piani): Sia F (, y) un campo vttorial piano dfinito in un aprto A di R, si supponga ultriormnt = y ;
1. Condizioni di arbitraggio internazionale delle merci e dei titoli. Le teorie de la Parità dei poteri d acquisto la Parità dei tassi d interesse
 . Condizioni di arbitraggio intrnazional dll rci di titoli L tori d la Parità di otri d acuisto la Parità di tassi d intrss 5_Andic_G.GAROFALO L arbitraggio è un'orazion ch consist nll'acuistar un bn o
. Condizioni di arbitraggio intrnazional dll rci di titoli L tori d la Parità di otri d acuisto la Parità di tassi d intrss 5_Andic_G.GAROFALO L arbitraggio è un'orazion ch consist nll'acuistar un bn o
13. EQUAZIONI ALGEBRICHE
 G. Smmito, A. Bernrdo, Formulrio di mtemti Equzioni lgerihe F. Cimolin, L. Brlett, L. Lussrdi. EQUAZIONI ALGEBRICHE. Prinipi di equivlenz Si die identità un'uguglinz tr due espressioni ontenenti un o più
G. Smmito, A. Bernrdo, Formulrio di mtemti Equzioni lgerihe F. Cimolin, L. Brlett, L. Lussrdi. EQUAZIONI ALGEBRICHE. Prinipi di equivlenz Si die identità un'uguglinz tr due espressioni ontenenti un o più
w(r)=w max (1-r 2 /R 2 ) completamente sviluppato in un tubo circolare è dato da wmax R w max = = max
 16-1 Copyright 009 Th McGraw-Hill Companis srl RISOLUZIONI CAP. 16 16.1 Nl flusso laminar compltamnt sviluppato all intrno di un tubo circolar vin misurata la vlocità a r R/. Si dv dtrminar la vlocità
16-1 Copyright 009 Th McGraw-Hill Companis srl RISOLUZIONI CAP. 16 16.1 Nl flusso laminar compltamnt sviluppato all intrno di un tubo circolar vin misurata la vlocità a r R/. Si dv dtrminar la vlocità
SPECIFICHE DI PROGETTO DI SISTEMI DI CONTROLLO
 CONROLLI DIGIALI Laura Magistral in Inggnria Mccatronica SPECIFICHE DI PROGEO DI SISEMI DI CONROLLO Ing. l. 5 535 -mail: cristian.scchi@unimor.it htt://www.dismi.unimo.it/mmbrs/cscchi Scifich r un Sistma
CONROLLI DIGIALI Laura Magistral in Inggnria Mccatronica SPECIFICHE DI PROGEO DI SISEMI DI CONROLLO Ing. l. 5 535 -mail: cristian.scchi@unimor.it htt://www.dismi.unimo.it/mmbrs/cscchi Scifich r un Sistma
Corso di Analisi: Algebra di Base 5^ Lezione Logaritmi. Proprietà dei logaritmi Equazioni logaritmiche. Disequazioni logaritmiche. Allegato Esercizi.
 Corso di Anlisi: Algbr di Bs ^ Lzion Logritmi. Proprità di ritmi Equzioni ritmih. Disquzioni ritmih. Allgto Esrizi. LOGARITMI : Pr ritmo intndimo un sprssion lttrl indint un vlor numrio. Dfinizion : Si
Corso di Anlisi: Algbr di Bs ^ Lzion Logritmi. Proprità di ritmi Equzioni ritmih. Disquzioni ritmih. Allgto Esrizi. LOGARITMI : Pr ritmo intndimo un sprssion lttrl indint un vlor numrio. Dfinizion : Si
4.2 10/2015. Serbatoi speciali Bollitori / Accumulatori tampone / Accumulatori combinati. caldamente raccomandato
 4.2 10/2015 Srtoi scili ollitori / ccumultori tmon / ccumultori cominti cldmnt rccomndto 4.2 Srtoi scili Srtoi scili Pgin SW ollitor colonn con uno scmitor trmico 3 5 SW ollitor colonn con du scmitori
4.2 10/2015 Srtoi scili ollitori / ccumultori tmon / ccumultori cominti cldmnt rccomndto 4.2 Srtoi scili Srtoi scili Pgin SW ollitor colonn con uno scmitor trmico 3 5 SW ollitor colonn con du scmitori
Corso di Modellistica dei Sistemi Biologici A.A. 2008/09. Cinetiche di Reazione
 Coro di Modlliti di Sitmi Biologii A.A. 8/9 Cintih di Rzion Dont: ing. Crlo Contino Lb. di Biomtroni E-mil: rlo.ontino@uniz.it Tl: 96-69-45 URL: http://bioinggnri.uniz.it http://wpg.unin.it/ron Univrità
Coro di Modlliti di Sitmi Biologii A.A. 8/9 Cintih di Rzion Dont: ing. Crlo Contino Lb. di Biomtroni E-mil: rlo.ontino@uniz.it Tl: 96-69-45 URL: http://bioinggnri.uniz.it http://wpg.unin.it/ron Univrità
Superfici di Riferimento (1/4)
 Superfici di Riferimento (1/4) L definizione di un superficie di riferimento nsce dll necessità di vere un supporto mtemtico su cui sviluppre il rilievo eseguito sull superficie terrestre. Tle superficie
Superfici di Riferimento (1/4) L definizione di un superficie di riferimento nsce dll necessità di vere un supporto mtemtico su cui sviluppre il rilievo eseguito sull superficie terrestre. Tle superficie
Funzione esponenziale e logaritmo. Proprietà di esponenziale e logaritmo.
 Funzion sponnzil ritmo. Proprità di sponnzil ritmo. 6. Funzion sponnzil ritmo. Proprità di sponnzil ritmo. Funzion sponnzil f ( ) fissto f : ( + ) è l bs dll funzion sponnzil d è fisst è l sponnt dll funzion
Funzion sponnzil ritmo. Proprità di sponnzil ritmo. 6. Funzion sponnzil ritmo. Proprità di sponnzil ritmo. Funzion sponnzil f ( ) fissto f : ( + ) è l bs dll funzion sponnzil d è fisst è l sponnt dll funzion
CLIMATIZZAZIONE DI AMBIENTI CONFINATI: FUNZIONE COMPENSATRICE DEGLI IMPIANTI
 Corso di Impinti Tcnici.. 2009/2010 Docnt: Prof. C. Istti CAPITOLO 4 : FUNZIONE COMPENSATRICE DEGLI IMPIANTI 4.1 Gnrlità Col trmin impinto di climtizzzion si intnd un dispositivo cpc di compnsr i flussi
Corso di Impinti Tcnici.. 2009/2010 Docnt: Prof. C. Istti CAPITOLO 4 : FUNZIONE COMPENSATRICE DEGLI IMPIANTI 4.1 Gnrlità Col trmin impinto di climtizzzion si intnd un dispositivo cpc di compnsr i flussi
EQUAZIONI DIFFERENZIALI DEL PRIMO ORDINE EQUAZIONI DIFFERENZIALI DEL SECONDO ORDINE A COEFFICIENTI COSTANTI
 Risoluzion di uazioni diffrnziali a ura dl prof. Massimo Latino EQUZIONI DIFFERENZILI DEL PRIMO ORDINE Dnominazion Com si prsntano Com si risolvono Euazion diffrnzial dl d primo ordin a variaili sparaili
Risoluzion di uazioni diffrnziali a ura dl prof. Massimo Latino EQUZIONI DIFFERENZILI DEL PRIMO ORDINE Dnominazion Com si prsntano Com si risolvono Euazion diffrnzial dl d primo ordin a variaili sparaili
PROGRAMMA DI RIPASSO ESTIVO
 ISTITUTO TECNICO PER IL TURISMO EUROSCUOLA ISTITUTO TECNICO PER GEOMETRI BIANCHI SCUOLE PARITARIE PROGRAMMA DI RIPASSO ESTIVO CLASSI MATERIA PROF. QUARTA TURISMO Matmatica Andra Brnsco Làvor ANNO SCOLASTICO
ISTITUTO TECNICO PER IL TURISMO EUROSCUOLA ISTITUTO TECNICO PER GEOMETRI BIANCHI SCUOLE PARITARIE PROGRAMMA DI RIPASSO ESTIVO CLASSI MATERIA PROF. QUARTA TURISMO Matmatica Andra Brnsco Làvor ANNO SCOLASTICO
1 Integrali doppi di funzioni a scala su rettangoli
 INEGRALI DOPPI L prim motivzione per lo studio degli integrli di funzioni di due vribili è il lolo di volumi, in nlogi on l pplizione degli integrli di funzioni di un vribile l lolo di ree. L proedur di
INEGRALI DOPPI L prim motivzione per lo studio degli integrli di funzioni di due vribili è il lolo di volumi, in nlogi on l pplizione degli integrli di funzioni di un vribile l lolo di ree. L proedur di
Grandezze, funzioni empiriche e matematiche. 1 Stabilisci se le seguenti affermazioni sono vere o false.
 Grnzz unzioni Grnzz, unzioni mpirih mtmtih Grnzz irttmnt invrsmnt proporzionli Applizioni ll proporzionlità Grnzz, unzioni mpirih mtmtih Stilisi s l sunti rmzioni so vr o ls. SZ. I Un rnzz è vriil s ssum
Grnzz unzioni Grnzz, unzioni mpirih mtmtih Grnzz irttmnt invrsmnt proporzionli Applizioni ll proporzionlità Grnzz, unzioni mpirih mtmtih Stilisi s l sunti rmzioni so vr o ls. SZ. I Un rnzz è vriil s ssum
Fisica Generale VI Scheda n. 1 esercizi di riepilogo dei contenuti di base necessari. 1.) Dimostrare le seguenti identità vettoriali:
 Fisica Gnral VI Schda n. 1 srcizi di ripilogo di contnuti di bas ncssari 1.) Dimostrar l sgunti idntità vttoriali:. A (B C) = B (A C) C (A B) (A B) = ( A) B ( B) A ( A) = ( A) 2 A. suggrimnto: è important
Fisica Gnral VI Schda n. 1 srcizi di ripilogo di contnuti di bas ncssari 1.) Dimostrar l sgunti idntità vttoriali:. A (B C) = B (A C) C (A B) (A B) = ( A) B ( B) A ( A) = ( A) 2 A. suggrimnto: è important
PROVINCIA DI TORINO SERVIZIO LOGISTICA PROGETTO DEFINITIVO-ESECUTIVO
 ALLEGATO: N. 1 PROVINCIA DI TORINO SERVIZIO LOGISTICA PROGETTO DEFINITIVO-ESECUTIVO MANUTENZIONE ORDINARIA E RIPARATIVA DEGLI EDIFICI PATRIMONIALI DESTINATI AD UFFICI DELLA PROVINCIA. IMPIANTI ELETTRICI
ALLEGATO: N. 1 PROVINCIA DI TORINO SERVIZIO LOGISTICA PROGETTO DEFINITIVO-ESECUTIVO MANUTENZIONE ORDINARIA E RIPARATIVA DEGLI EDIFICI PATRIMONIALI DESTINATI AD UFFICI DELLA PROVINCIA. IMPIANTI ELETTRICI
1. DESCRIZIONE DEL PRODOTTO
 1. DESCRIZIONE DEL PRODOTTO Gli snodi ngolri sono orgni mccnici pr il collgmnto di du prti prpndicolri tr loro, ch prmttono trsmission di forz ltrnt con movimnti ngolri oscilltori di vlocità modrt. Sono
1. DESCRIZIONE DEL PRODOTTO Gli snodi ngolri sono orgni mccnici pr il collgmnto di du prti prpndicolri tr loro, ch prmttono trsmission di forz ltrnt con movimnti ngolri oscilltori di vlocità modrt. Sono
VERSO L ESAME DI STATO LA DERIVATA DI UNA FUNZIONE
 VERSO L ESAME DI STATO LA DERIVATA DI UNA FUNZIONE Soluzioni di quesiti e prolemi trtti dl Corso Bse Blu di Mtemti volume 5 [] (Es. n. 8 pg. 9 V) Dell prol f ( ) si hnno le seguenti informzioni, tutte
VERSO L ESAME DI STATO LA DERIVATA DI UNA FUNZIONE Soluzioni di quesiti e prolemi trtti dl Corso Bse Blu di Mtemti volume 5 [] (Es. n. 8 pg. 9 V) Dell prol f ( ) si hnno le seguenti informzioni, tutte
Calcolo delle Probabilità e Statistica. Prova scritta del III appello - 7/6/2006
 Corso di Laura in Informatica - a.a. 25/6 Calcolo dll Probabilità Statistica Prova scritta dl III appllo - 7/6/26 Il candidato risolva i problmi proposti, motivando opportunamnt l propri rispost.. Sia
Corso di Laura in Informatica - a.a. 25/6 Calcolo dll Probabilità Statistica Prova scritta dl III appllo - 7/6/26 Il candidato risolva i problmi proposti, motivando opportunamnt l propri rispost.. Sia
Informatica 3. Informatica 3. LEZIONE 25: Algoritmi sui grafi. Lezione 25 - Modulo 1. Problema. Notazioni per il percorso più breve
 Informti Informti LZION : lgoritmi sui grfi Lzion - Moulo Moulo : Prolm l prorso più rv Moulo : Spnning tr osto minimo Prolm l prorso più rv Politnio i Milno - Prof. Sr omi Politnio i Milno - Prof. Sr
Informti Informti LZION : lgoritmi sui grfi Lzion - Moulo Moulo : Prolm l prorso più rv Moulo : Spnning tr osto minimo Prolm l prorso più rv Politnio i Milno - Prof. Sr omi Politnio i Milno - Prof. Sr
SOLUZIONE PROBLEMI Insegnamento di Fisica dell Atmosfera Seconda prova in itinere
 Doente: rof Dino Zri serittore: in lessio Bertò OLUZION PROBLMI Insenento i Fisi ell tosfer eon rov in itinere /3 Vlori elle ostnti Rio terrestre eio: 637 Rio solre eio: 7 5 Distnz ei terr-sole : 9 6 Vlore
Doente: rof Dino Zri serittore: in lessio Bertò OLUZION PROBLMI Insenento i Fisi ell tosfer eon rov in itinere /3 Vlori elle ostnti Rio terrestre eio: 637 Rio solre eio: 7 5 Distnz ei terr-sole : 9 6 Vlore
Soluzione del tema di: ELETTROTECNICA, ELETTRONICA ED APPLICAZIONI anno scolastico
 cur di: R. Giomtti Impinto Soluzion dl tm di: ELETTROTECNICA, ELETTRONICA ED APPLICAZIONI nno scolstico 23 24 L impinto dv ssr rlizzto in funzion di du tipi di crico: - il motor in continu 4, ch può ssr
cur di: R. Giomtti Impinto Soluzion dl tm di: ELETTROTECNICA, ELETTRONICA ED APPLICAZIONI nno scolstico 23 24 L impinto dv ssr rlizzto in funzion di du tipi di crico: - il motor in continu 4, ch può ssr
Compito di Fisica Generale I (Mod. A) Corsi di studio in Fisica ed Astronomia 4 aprile 2011
 Compito di Fisica Gnral I (Mod A) Corsi di studio in Fisica d Astronomia 4 april 2011 Problma 1 Du blocchi A B di massa rispttivamnt m A d m B poggiano su un piano orizzontal scabro sono uniti da un filo
Compito di Fisica Gnral I (Mod A) Corsi di studio in Fisica d Astronomia 4 april 2011 Problma 1 Du blocchi A B di massa rispttivamnt m A d m B poggiano su un piano orizzontal scabro sono uniti da un filo
0.1. CIRCONFERENZA 1. La 0.1.1, espressa mediante la formula per la distanza tra due punti, diviene:
 0.1. CIRCONFERENZA 1 0.1 Circonfrnza Considriamo una circonfrnza di cntro P 0 (x 0, y 0 ) raggio r, cioè il luogo di punti dl piano P (x, y) pr i quali si vrifica la rlazion: 0.1.1. P 0 P = r. La 0.1.1,
0.1. CIRCONFERENZA 1 0.1 Circonfrnza Considriamo una circonfrnza di cntro P 0 (x 0, y 0 ) raggio r, cioè il luogo di punti dl piano P (x, y) pr i quali si vrifica la rlazion: 0.1.1. P 0 P = r. La 0.1.1,
Esercizi di Segnali Aleatori per Telecomunicazioni
 Corso di Lur in Inggnri Inormic corso di Tlcomunicioni (ro. G. Giun) (diing cur dll ing. F. Bndo) srcii di Sgnli Alori r Tlcomunicioni Diniioni di momni sisici (di rimo scondo ordin) di vriili lori: -
Corso di Lur in Inggnri Inormic corso di Tlcomunicioni (ro. G. Giun) (diing cur dll ing. F. Bndo) srcii di Sgnli Alori r Tlcomunicioni Diniioni di momni sisici (di rimo scondo ordin) di vriili lori: -
Svolgimento di alcuni esercizi
 Svolgimnto di alcuni srcizi Si ha ch dal momnto ch / tnd a pr ch tnd a (la frazion formata da un numro, in qusto caso il numro, fratto una quantità ch tnd a ±, in qusto caso, tnd smpr a ) S facciamo tndr
Svolgimnto di alcuni srcizi Si ha ch dal momnto ch / tnd a pr ch tnd a (la frazion formata da un numro, in qusto caso il numro, fratto una quantità ch tnd a ±, in qusto caso, tnd smpr a ) S facciamo tndr
x BP, controllando che risulta :
 Corso sprimntl - Sssion suppltiv -.s. 9- ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE SESSIONE SUPPLETIA Tm di: MATEMATICA. s. 9- PROBLEMA E dt un circonrnz di cntro O dimtro AB. Sul prolungmnto
Corso sprimntl - Sssion suppltiv -.s. 9- ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE SESSIONE SUPPLETIA Tm di: MATEMATICA. s. 9- PROBLEMA E dt un circonrnz di cntro O dimtro AB. Sul prolungmnto
semiconduttori E c E gap E v
 Carattristih a 0K: - banda di valnza opltant oupata - banda di onduzion opltant vuota - piolo gap di nrgi proibit g 1,1 V Si); 0,7 V G); 1,4 V GaAs) a >0K: - un lttron può ssr itato dalla banda di valnza
Carattristih a 0K: - banda di valnza opltant oupata - banda di onduzion opltant vuota - piolo gap di nrgi proibit g 1,1 V Si); 0,7 V G); 1,4 V GaAs) a >0K: - un lttron può ssr itato dalla banda di valnza
Ulteriori esercizi svolti
 Ultriori srcizi svolti Effttuar uno studio qualitativo dll sgunti funzioni ) 4 f ( ) ) ( + ) f ( ) + 3) f ( ) con particolar rifrimnto ai sgunti asptti: a) trova il dominio di f b) indica quali sono gli
Ultriori srcizi svolti Effttuar uno studio qualitativo dll sgunti funzioni ) 4 f ( ) ) ( + ) f ( ) + 3) f ( ) con particolar rifrimnto ai sgunti asptti: a) trova il dominio di f b) indica quali sono gli
Elenco ufficiale delle località con il numero postale d avviamento e il perimetro Informazioni sul prodotto
 Dipartimnto fdral dlla difsa, dlla protzion dlla popolazion dllo sport DDPS Uffiio fdral di topografia swisstopo Elno uffiial dll loalità on il numro postal d avviamnto il primtro Informazioni sul prodotto
Dipartimnto fdral dlla difsa, dlla protzion dlla popolazion dllo sport DDPS Uffiio fdral di topografia swisstopo Elno uffiial dll loalità on il numro postal d avviamnto il primtro Informazioni sul prodotto
Totti, 37 anni da leggenda. Un monumento vivente. Scritto da Redazione Venerdì 27 Settembre 2013 08:39 - VALERIA META
 37 nni d lggnd Un monumnto vivnt Scritto d Rdzion VALERIA META Scrivrlo sull fccit Sn Pitro potv ffttivmnt smbrr irrivrnt pr qunto l omonimo inquino dl Vticno si si mostrto prson ll mno Così gli uguri
37 nni d lggnd Un monumnto vivnt Scritto d Rdzion VALERIA META Scrivrlo sull fccit Sn Pitro potv ffttivmnt smbrr irrivrnt pr qunto l omonimo inquino dl Vticno si si mostrto prson ll mno Così gli uguri
Matematica. Indice lezione. (Esercitazioni) dott. Francesco Giannino dott. Valeria Monetti. Funzione esponenziale
 Mtmtic (Esrcitzioni) Equzioni Disquzioni sponnzili - ritmich dott. Frncsco Ginnino dott. Vlri Montti Indic lzion Funzion sponnzil Equzioni disquzioni sponnzili Funzion ritmo Equzioni disquzioni ritmich
Mtmtic (Esrcitzioni) Equzioni Disquzioni sponnzili - ritmich dott. Frncsco Ginnino dott. Vlri Montti Indic lzion Funzion sponnzil Equzioni disquzioni sponnzili Funzion ritmo Equzioni disquzioni ritmich
ANALISI STRUTTURALE sistema STRUTTURA STRUTTURA. I modelli meccanici possono suddividersi in: MODELLI CONTINUI. STRUTTURA = modello meccanico
 AZIONI ANALISI STRUTTURALE sistma STRUTTURA STATO I modlli mccanici possono suddividrsi in: MODELLI CONTINUI Forz Coazioni STRUTTURA = modllo mccanico IDEALIZZAZIONE DELLA STRUTTURA Posizion Vlocità Acclrazion
AZIONI ANALISI STRUTTURALE sistma STRUTTURA STATO I modlli mccanici possono suddividrsi in: MODELLI CONTINUI Forz Coazioni STRUTTURA = modllo mccanico IDEALIZZAZIONE DELLA STRUTTURA Posizion Vlocità Acclrazion
Algebra + numeri relativi +l calcolo letterale Equazioni, disequazioni, problemi
 Algr + numri rltivi +l lolo lttrl Equzioni, isquzioni, prolmi + numri rltivi Rpprsnt on un numro rltivo l sgunti grnzz. SEZ. O g Altituin i 00 m sul livllo l mr. Trzo pino i un prhggio sottrrno. Prit i
Algr + numri rltivi +l lolo lttrl Equzioni, isquzioni, prolmi + numri rltivi Rpprsnt on un numro rltivo l sgunti grnzz. SEZ. O g Altituin i 00 m sul livllo l mr. Trzo pino i un prhggio sottrrno. Prit i
OPZIONE SPECIFICA FISICA ED APPLICAZIONI DELLA MATEMATICA
 Lico Cantonal Lugano Vial C Cattano 4 CH-6900 Lugano Lugano, giugno 00 ESAME SCRITTO DI MATURITÀ 009/00 OPZIONE SPECIFICA FISICA ED APPLICAZIONI DELLA MATEMATICA Durata dll sam: Tr or (dall 0800 all 00)
Lico Cantonal Lugano Vial C Cattano 4 CH-6900 Lugano Lugano, giugno 00 ESAME SCRITTO DI MATURITÀ 009/00 OPZIONE SPECIFICA FISICA ED APPLICAZIONI DELLA MATEMATICA Durata dll sam: Tr or (dall 0800 all 00)
test Di chimica per l accesso alle Facoltà UNiVersitarie
 tst i himia pr l asso all Faoltà UNiVrsitari il sistma priodio dgli lmnti il sistma priodio dgli lmnti 1. indiar qual di sgunti lmnti NoN è di transizion: a F zn as Cu Cr (Mdiina Chirurgia 2005) 2. indiar
tst i himia pr l asso all Faoltà UNiVrsitari il sistma priodio dgli lmnti il sistma priodio dgli lmnti 1. indiar qual di sgunti lmnti NoN è di transizion: a F zn as Cu Cr (Mdiina Chirurgia 2005) 2. indiar
Analisi dei Sistemi. Soluzione del compito del 26 Giugno ÿ(t) + (t 2 1)y(t) = 6u(t T ). 2 x1 (t) 0 1
 Analisi di Sistmi Soluzion dl compito dl 26 Giugno 23 Esrcizio. Pr i du sistmi dscritti dai modlli sgunti, individuar l proprità strutturali ch li carattrizzano: linar o non linar, stazionario o tmpovariant,
Analisi di Sistmi Soluzion dl compito dl 26 Giugno 23 Esrcizio. Pr i du sistmi dscritti dai modlli sgunti, individuar l proprità strutturali ch li carattrizzano: linar o non linar, stazionario o tmpovariant,
Test di autovalutazione
 Tst i utovlutzion 0 10 20 0 0 0 60 70 80 90 100 n Il mio puntggio, in ntsimi, è n Risponi ogni qusito sgnno un sol ll ltntiv. n Confont l tu ispost on l soluzioni. n Colo, ptno sinist, tnt sll qunt sono
Tst i utovlutzion 0 10 20 0 0 0 60 70 80 90 100 n Il mio puntggio, in ntsimi, è n Risponi ogni qusito sgnno un sol ll ltntiv. n Confont l tu ispost on l soluzioni. n Colo, ptno sinist, tnt sll qunt sono
Distribuzione gaussiana
 Appunti di Misur Elttric Distribuion gaussiana Funion dnsità di probabilità di Gauss... Calcolo dlla distribuion cumulativa pr una variabil di Gauss... Funion dnsità di probabilità congiunta...6 Funion
Appunti di Misur Elttric Distribuion gaussiana Funion dnsità di probabilità di Gauss... Calcolo dlla distribuion cumulativa pr una variabil di Gauss... Funion dnsità di probabilità congiunta...6 Funion
ISTRUZIONI DI MONTAGGIO per controtelai SP
 ISTRUZIONI DI MONTAGGIO pr ontrotli SP 100-125 Controtli vrsion rtonsso INCASTRO NOMENCLATURA: ontrotlio, inrio rrmnt Controtli pr port somprs i m l SET i ALLARGAMENTO pr SP 125 Montnti vrtili ntriori
ISTRUZIONI DI MONTAGGIO pr ontrotli SP 100-125 Controtli vrsion rtonsso INCASTRO NOMENCLATURA: ontrotlio, inrio rrmnt Controtli pr port somprs i m l SET i ALLARGAMENTO pr SP 125 Montnti vrtili ntriori
CHIARA ZUCCHELLI. Florenzi, arriva il premio: contratto fino al 2016 e stipendio aumentato. Scritto da Redazione Giovedì 04 Ottobre 2012 07:31 -
 Flornzi rriv il prmio: contrtto fino l 2016 stipno umntto CHIARA ZUCCHELLI Il prmio più mritto rrivto Com nnuncito si d Sbtini si dl suo gnt Alssndro Lucci rrivto il rinnovo dl contrtto Alssndro Flornzi
Flornzi rriv il prmio: contrtto fino l 2016 stipno umntto CHIARA ZUCCHELLI Il prmio più mritto rrivto Com nnuncito si d Sbtini si dl suo gnt Alssndro Lucci rrivto il rinnovo dl contrtto Alssndro Flornzi
Simulazione Prova Esame di Maturità di Matematica per Liceo Scientifico SIMULAZIONE PROVA ESAME DI MATURITA PER LICEO SCIENTIFICO. Prova di Matematica
 Simulzion Prov Esm di Mturità di Mtmtic pr Lico Scintiico SIMULAZIONE PROVA ESAME DI MATURITA PER LICEO SCIENTIFICO PROBLEMA Prov di Mtmtic Si dt l unzion. Studir l unzion dtrminndo l ntur vntuli punti
Simulzion Prov Esm di Mturità di Mtmtic pr Lico Scintiico SIMULAZIONE PROVA ESAME DI MATURITA PER LICEO SCIENTIFICO PROBLEMA Prov di Mtmtic Si dt l unzion. Studir l unzion dtrminndo l ntur vntuli punti
L offerta della singola impresa: l impresa e la massimizzazione del profitto
 L offert dell singol imres: l imres e l mssimizzzione del rofitto Qundo un imres ot er un ino di roduzione sceglie un certo livello di inut che le grntisc un dto outut L scelt del ino di roduzione h l
L offert dell singol imres: l imres e l mssimizzzione del rofitto Qundo un imres ot er un ino di roduzione sceglie un certo livello di inut che le grntisc un dto outut L scelt del ino di roduzione h l
Aquauno Video 2 Plus
 Collgr il progrmmtor l ruintto. Aquuno Vio 2 Plus Pg. 1 Gui ll utilizzo 3 START STOP RESET CANCEL 3 4 5 6 3 4 5 6 3 4 5 6 lik! Pr Aquuno Vio 2 (o.): 8454-8428 Pr Aquuno Vio 2 Plus (o.): 8412 Aprir il moulo
Collgr il progrmmtor l ruintto. Aquuno Vio 2 Plus Pg. 1 Gui ll utilizzo 3 START STOP RESET CANCEL 3 4 5 6 3 4 5 6 3 4 5 6 lik! Pr Aquuno Vio 2 (o.): 8454-8428 Pr Aquuno Vio 2 Plus (o.): 8412 Aprir il moulo
ESERCIZI PARTE I SOLUZIONI
 UNIVR Facoltà di Economia Corso di Matmatica finanziaria 008/09 ESERCIZI PARTE I SOLUZIONI Domini di funzioni di du variabili Esrcizio a f, = log +. L unica condizion di sistnza è data dalla disquazion
UNIVR Facoltà di Economia Corso di Matmatica finanziaria 008/09 ESERCIZI PARTE I SOLUZIONI Domini di funzioni di du variabili Esrcizio a f, = log +. L unica condizion di sistnza è data dalla disquazion
Soluzione a) La forza esercitata dall acqua varia con la profondita` secondo la legge di Stevino: H H
 eccnic Un bcino d cqu, profondo, e` contenuto d un prti verticle di lunghezz (orizzontle, lungo y) L, vincolt l terreno nel punto B. Per sostenere l prti si usno lcuni pli fissti d un estremit` sull prti,
eccnic Un bcino d cqu, profondo, e` contenuto d un prti verticle di lunghezz (orizzontle, lungo y) L, vincolt l terreno nel punto B. Per sostenere l prti si usno lcuni pli fissti d un estremit` sull prti,
Esercizio 1. Cov(X,Y)=E(X,Y)- E(X)E(Y).
 Esrcizi di conomtria: sri 4 Esrcizio Siano, Z variabili casuali distribuit scondo la lgg multinomial di paramtri n, p, p, p p p.. Calcolar la Covarianza tra l variabili d. Soluzion Dat du variabili dinit
Esrcizi di conomtria: sri 4 Esrcizio Siano, Z variabili casuali distribuit scondo la lgg multinomial di paramtri n, p, p, p p p.. Calcolar la Covarianza tra l variabili d. Soluzion Dat du variabili dinit
Informatica II. Capitolo 5. Alberi. E' una generalizzazione della struttura sequenza
 Alri Informtic II Cpitolo 5 Alri E' un gnrlizzzion dll struttur squnz Si rilss il rquisito di linrità: ogni lmnto (nodo) h un solo prdcssor m può vr più succssori. Il numro di succssori (figli) può ssr
Alri Informtic II Cpitolo 5 Alri E' un gnrlizzzion dll struttur squnz Si rilss il rquisito di linrità: ogni lmnto (nodo) h un solo prdcssor m può vr più succssori. Il numro di succssori (figli) può ssr
PROPORZIONI. Cosa possiamo dire di esse? Che la superficie della figura A sta alla superficie della figura B come 4 sta a 6.
 Corso di laura: BIOLOGIA Tutor: Floris Marta PRECORSI DI MATEMATICA PROPORZIONI Ossrvar l sgunti figur: Cosa possiamo dir di ss? Ch la suprfici dlla figura A sta alla suprfici dlla figura B com sta a 6.
Corso di laura: BIOLOGIA Tutor: Floris Marta PRECORSI DI MATEMATICA PROPORZIONI Ossrvar l sgunti figur: Cosa possiamo dir di ss? Ch la suprfici dlla figura A sta alla suprfici dlla figura B com sta a 6.
Teoria dell integrazione secondo Riemann per funzioni. reali di una variabile reale.
 Capitolo 2 Toria dll intgrazion scondo Rimann pr funzioni rali di una variabil ral Esistono vari tori dll intgrazion; tutt hanno com comun antnato il mtodo di saustion utilizzato dai Grci pr calcolar l
Capitolo 2 Toria dll intgrazion scondo Rimann pr funzioni rali di una variabil ral Esistono vari tori dll intgrazion; tutt hanno com comun antnato il mtodo di saustion utilizzato dai Grci pr calcolar l
Scuole Italiane all'estero ESAMI DI STATO DI LICEO SCIENTIFICO Sessione SECONDA PROVA SCRITTA Tema di Matematica
 Sssion ordinri Estro Scuol Itlin llestro ESAMI DI STATO DI LICEO SCIENTIFICO Sssion SECONDA PROVA SCRITTA Tm di Mtmtic PROBLEMA E ssnto un cilindro quiltro Q il cui rio di bs misur. ) Si dtrmini il cono
Sssion ordinri Estro Scuol Itlin llestro ESAMI DI STATO DI LICEO SCIENTIFICO Sssion SECONDA PROVA SCRITTA Tm di Mtmtic PROBLEMA E ssnto un cilindro quiltro Q il cui rio di bs misur. ) Si dtrmini il cono
ESERCIZI SULLA DEMODULAZIONE INCOERENTE
 Esrcitazioni dl corso di trasmissioni numrich - Lzion 4 6 Fbbraio 8 ESERCIZI SULLA DEMODULAZIONE INCOERENE I du sgnali passa basso di figura sono utilizzati pr la trasmission di simboli binari quiprobabili
Esrcitazioni dl corso di trasmissioni numrich - Lzion 4 6 Fbbraio 8 ESERCIZI SULLA DEMODULAZIONE INCOERENE I du sgnali passa basso di figura sono utilizzati pr la trasmission di simboli binari quiprobabili
Test di autovalutazione
 UNITÀ LE FRAZIONI Tst Tst i utolutzion 0 0 0 0 0 0 0 0 0 0 00 n Il mio puntggio, in ntsimi, è n Risponi ogni qusito sgnno un sol ll ltrnti. n Conront l tu rispost on l soluzioni. n Color, prtno sinistr,
UNITÀ LE FRAZIONI Tst Tst i utolutzion 0 0 0 0 0 0 0 0 0 0 00 n Il mio puntggio, in ntsimi, è n Risponi ogni qusito sgnno un sol ll ltrnti. n Conront l tu rispost on l soluzioni. n Color, prtno sinistr,
Circolare n. 1 Prot. n. 758 Roma 29/01/2015
 Ministro dll Istruzion, dll Univrsità dlla Ricrca Dipartimnto pr il sistma ducativo di istruzion formazion Dirzion Gnral pr gli ordinamnti scolastici la valutazion dl sistma nazional di istruzion Circolar
Ministro dll Istruzion, dll Univrsità dlla Ricrca Dipartimnto pr il sistma ducativo di istruzion formazion Dirzion Gnral pr gli ordinamnti scolastici la valutazion dl sistma nazional di istruzion Circolar
operazioni con vettori
 omposizione e somposizione + = operzioni on vettori = + = + Se un vettore può essere dto dll omposizione di due o più vettori, questi vettori omponenti possono essere selti lungo direzioni ortogonli fr
omposizione e somposizione + = operzioni on vettori = + = + Se un vettore può essere dto dll omposizione di due o più vettori, questi vettori omponenti possono essere selti lungo direzioni ortogonli fr
Capitolo 7 - Predizione lineare
 Appunti di lborzion numric di sgnli Cpitolo 7 - Prdizion linr Introduzion... rror mdio di prvision...3 Ossrvzion: prdizion linr com sbinctor dll squnz di ingrsso 5 Ortogonlità tr dti d rror...6 Vlor minimo
Appunti di lborzion numric di sgnli Cpitolo 7 - Prdizion linr Introduzion... rror mdio di prvision...3 Ossrvzion: prdizion linr com sbinctor dll squnz di ingrsso 5 Ortogonlità tr dti d rror...6 Vlor minimo
DOSSI ARTIFICIALI OMOLOGATI - FIG. 474
 OSSI RTIFIILI OMOLOGTI - FIG. 474 OSSO H M - SU STR ON LIMIT I VLOITÀ 50 KMH QT'. MIN. 10ORV0018 RLLNTTOR I VLOIT' (48x60 M - H M) OMPLTO I N 4 TSSLLI PR L POS IN OPR 0 OSSO H 5 M - SU STR ON LIMIT I VLOITÀ
OSSI RTIFIILI OMOLOGTI - FIG. 474 OSSO H M - SU STR ON LIMIT I VLOITÀ 50 KMH QT'. MIN. 10ORV0018 RLLNTTOR I VLOIT' (48x60 M - H M) OMPLTO I N 4 TSSLLI PR L POS IN OPR 0 OSSO H 5 M - SU STR ON LIMIT I VLOITÀ
METODO DEGLI ELEMENTI FINITI
 Dal libro di tsto Zinkiwicz Taylor, Capitolo 14 pag. 398 Il mtodo dgli lmnti finiti fornisc una soluzion approssimata dl problma lastico; tal approssimazion driva non dall avr discrtizzato il dominio in
Dal libro di tsto Zinkiwicz Taylor, Capitolo 14 pag. 398 Il mtodo dgli lmnti finiti fornisc una soluzion approssimata dl problma lastico; tal approssimazion driva non dall avr discrtizzato il dominio in
Le rette r e s sono dette generatrici del fascio. Lezione 16 - Algebra e Geometria - Anno accademico 2009/10 1
 Fsi di rette Si die fsio imrorio di rette generto d rett r:, di rmetri direttori [(,-)], insieme di tutte e rette ree d r. Te insieme srà quindi ostituito d rette rtterite d equioni de tio:,. Si die fsio
Fsi di rette Si die fsio imrorio di rette generto d rett r:, di rmetri direttori [(,-)], insieme di tutte e rette ree d r. Te insieme srà quindi ostituito d rette rtterite d equioni de tio:,. Si die fsio
SICUREZZA SUL LAVORO SAFETY AT WORK SICUREZZA SUL LAVORO SAFETY AT WORK R 290 31 R 290 31
 SICUREZZA SUL LAVORO SAFETY AT WORK R 290 31 R 290 31 Sgnli i siurzz pr fontnll o i mrgnz pr l ontminzion UNI 7546/3. Symols for sfty signs-ys wshing - mrgny showr. 332 Normtiv in mtri i tutl ll slut siurzz
SICUREZZA SUL LAVORO SAFETY AT WORK R 290 31 R 290 31 Sgnli i siurzz pr fontnll o i mrgnz pr l ontminzion UNI 7546/3. Symols for sfty signs-ys wshing - mrgny showr. 332 Normtiv in mtri i tutl ll slut siurzz
Misura e incertezza METODI DI MISURA
 ppunti di Misur lttrih Misur inrtzz Mtodi di misur...1 Inrtzz di misur... Il risultto di un misur...3 rrori...3 Propgzion dgli rrori nll misur indirtt...4 smpi...6 Propgzion dll inrtzz nll misur indirtt...8
ppunti di Misur lttrih Misur inrtzz Mtodi di misur...1 Inrtzz di misur... Il risultto di un misur...3 rrori...3 Propgzion dgli rrori nll misur indirtt...4 smpi...6 Propgzion dll inrtzz nll misur indirtt...8
CONOSCENZE. 1. La derivata di una funzione y = f (x)
 ESAME D STATO ESEMP D QUEST D MATEMATCA PER LA TERZA PROVA CONOSCENZE. La drivata di una funzion y f (), in un punto intrno al suo dominio, : il it, s sist d è finito, dl rapporto incrmntal pr h, f ( h)
ESAME D STATO ESEMP D QUEST D MATEMATCA PER LA TERZA PROVA CONOSCENZE. La drivata di una funzion y f (), in un punto intrno al suo dominio, : il it, s sist d è finito, dl rapporto incrmntal pr h, f ( h)
I criteri di resistenza (o teorie della rottura) definiscono un legame tra lo stato tensionale e la sua pericolosità.
 6-0 6- I critri di rsistnza (o tori dlla rottura) dfiniscono un lgam tra lo stato tnsional la sua pricolosità. Ogni stato tnsional può ssr rapprsntato da una funzion scalar dll tnsioni principali ch può
6-0 6- I critri di rsistnza (o tori dlla rottura) dfiniscono un lgam tra lo stato tnsional la sua pricolosità. Ogni stato tnsional può ssr rapprsntato da una funzion scalar dll tnsioni principali ch può
La scelta di equilibrio del consumatore. Integrazione del Cap. 21 del testo di Mankiw 1
 M.Blconi e R.Fontn, Disense di conomi: 3) quilirio del consumtore L scelt di equilirio del consumtore ntegrzione del C. 21 del testo di Mnkiw 1 Prte 1 l vincolo di ilncio Suonimo che il reddito di un consumtore
M.Blconi e R.Fontn, Disense di conomi: 3) quilirio del consumtore L scelt di equilirio del consumtore ntegrzione del C. 21 del testo di Mnkiw 1 Prte 1 l vincolo di ilncio Suonimo che il reddito di un consumtore
APPUNTI DI GEOMETRIA ANALITICA
 Prof. Luigi Ci 1 nno solstio 13-14 PPUNTI DI GEOMETRI NLITIC Rett orientt Un rett r si die orientt qundo: 1. È fissto un punto di riferimento, detto origine;. Dei due possiili versi in ui un punto si può
Prof. Luigi Ci 1 nno solstio 13-14 PPUNTI DI GEOMETRI NLITIC Rett orientt Un rett r si die orientt qundo: 1. È fissto un punto di riferimento, detto origine;. Dei due possiili versi in ui un punto si può
