RUOTE DENTATE ELLITTICHE ELLIPTICAL GEARS
|
|
|
- Niccolina Vitale
- 7 anni fa
- Visualizzazioni
Transcript
1 Istituto Tenio Industrile Aldini Vlerini CLASSE 5C MECCANICA A.S. 001/00 Are di progetto: RUOTE DENTATE ELLITTICHE ELLIPTICAL GEARS Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 1
2 Ringrzimenti: A nome di tutti, rgzzi ed insegnnti, è doveroso un sentito ringrzimento ll ditt Nnni Ingrnggi he i h dto l possibilità di visitre i propri loli, ogliendoi on esemplre pzienz e disponibilità, e h donto ll istituto vlido, nonhé ostoso, mterile per il nostro studio. Gli llievi: Brid Mtteo Cevenini Lu Elefnte Giovnni Fenr Filippo Finelli Mtteo Gmberini Federio Grgnelli Mro Gzzillo Frneso Giovnnini Rirdo Gruppi Mro Impstto Dvide Le Alessndro Mestrini Polo Pgni Federio Priori Giomo Provenzni Dniele Red Ernesto Simoni Federio Tibldi Dniele Trebbi Frneso Turrini Simone Zmbelli Andre Gli insegnnti Altvill Cludio Bvieri Giuli Benni Mro Burnelli Andre Cnestri Trotti Pier Antonio Collin Dnilo D Amore Sndr Foresti Cosett Lorenzetti Giorgio Msotti Alessndr Pldino Angiolino Piotrowsk Bozenn Telmon Andre Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe
3 Indie: Introduzione pg. 3 Rihimi di mtemti: gli ngoli, gli rhi e l loro misur. pg. 5 Rihimi di mtemti: relzioni tr gli elementi di un tringolo qulunque pg. 6 Il teorem delle proiezioni ed il teorem del oseno. pg. 7 l ellisse pg. 10 Rihimi di mtemti: definizione di derivt di un funzione di un vribile pg. 15 Alune grndezze fisihe definite ome derivte di ltre pg. 18 Studio inemtio di un oppi di ruote dentte ellittihe pg. 1 Legge rotzioni (spostmenti ngolri dell ruot ondott in funzione dei grdi di rotzione dell ruot onduttrie pg. 1 Grfio rotzioni in grdi dell ruot ondott in funzione dell rotzione dell onduttrie pg. 1 Legge dell veloità ngolre dell ruot ondott in funzione dei grdi di rotzione dell ruot onduttrie pg. 5 Digrmm dell ndmento dell veloità ngolre dell ruot ondott in funzione degli ngoli di rotzione dell ruot onduttrie pg. 5 Legge dell elerzione ngolre dell ruot ondott in funzione dei grdi di rotzione dell ruot onduttrie pg. 7 Digrmm dell ndmento dell elerzione ngolre dell ruot ondott in funzione degli ngoli di rotzione dell ruot onduttrie pg. 7 Commento dei grfii pg. 9 Crtteristihe ostruttive pg. 33 Criteri di selt delle ruote ellitihe pg. 35 Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 3
4 Introduzione: L energi oorrente l funzionmento delle mhine opertrii è fornit, sotto form d energi ineti, d mhine motrii (i motori he l ottengono ome risultto finle dell trsformzione d energi d ltro tipo. Qulunque si il tipo di motore, l potenz he esso fornise è trsmess i vri orgni dell mhin opertrie, on le modifihe rihieste dlle loro speifihe esigenze. Ad esempio, in un tornio il moto deve ndre si l mndrino si l rrello portutensili per relizzre, rispettivmente, il moto di tglio ed il moto d limentzione. Mentre il primo deve muoversi di moto rottorio il seondo è guidto spostrsi di moto rettilineo. Nell mggior prte dei si periò non bst limitrsi trsmettere il moto m bisogn provvedere trsformrlo. Le oppite ruot dentt vite senz fine, rohetto e dentier, biell e mnovell, oppure, per ontinure eentrii, mme e punterie sono tutti menismi di trsformzione del moto. In un nihi di tle ontesto si inserisono gli ingrnggi ellittii, oppie di ruote dentte d intersse ostnte e profilo omplementre venti l rtteristi di trsformre un moto rottorio uniforme in un moto sempre rottorio m on veloità ngolre vribile nello stesso giro. Quindi le suddette onsentono di modulre l veloità ngolre sull sse d usit, restituendo un moto elerto/deelerto. Fino d or l uso degli ingrnggi ellittii è stto poo diffuso, si per l diffioltà nell loro ostruzione, si per l prtiolrità dell trsformzione del moto he relizzno. Esse sono utilizzte d ostruttori di mhine d stmp, tessili ed utomtihe i quli possono vere, ome già ennto, le seguenti esigenze: -vrire l veloità nell ro di un giro di un lm, un sldtore, uno spingitore. Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe
5 -effetture movimenti ilii, posizionmenti rpidi - smorzti, -diltre i tempi utili e ontrrre i tempi morti in ili ripetitivi. Nessun libro di testo di meni e disegno tuttvi trtt tle rgomento in mnier pprofondit. Proprio l mnnz d informzioni rigurdo tli ruote dentte i h spinto seglierle ome tem dell re di progetto. In prti i simo prefissti di rispondere lle stess domnd he sorge spontne nel vedere il tlogo dell ditt Nnni Ingrnggi he le produe e ommerilizz: Come funzionernno?. Noi pensimo di vere risposto in mnier esuriente l suddetto quesito. Buon lettur. Gli llievi e gli insegnnti dell VC meni Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 5
6 Rihimi di mtemti: gli ngoli, gli rhi e l loro misur. Angoli e rhi: Se in un pino si trino due semirette venti l origine in omune il pino diviso in due prti, isun delle quli viene himt ngolo. Le due semirette vengono dette i lti dei due ngoli e l origine omune il loro vertie. Dt un ironferenz vente il entro nel vertie di un ngolo, si him ro irolre quell prte di ironferenz intern ll ngolo e vente per estremi i punti di intersezione on i lti dell ngolo stesso. Misur degli ngoli e degli rhi: Per misurre un grndezz oorre fissre l unità di misur. Le più uste unità di misur degli ngoli sono il grdo ed il rdinte. Si him grdo l 360 prte dell ngolo giro. I suoi multipli sono il minuto primo ( o sempliemente primo, he è 1/60 di grdo, ed il minuto seondo ( o sempliemente seondo he è 1/60 di primo. Si him rdinte l ngolo l entro di un ironferenz, di rggio rbitrrio, he sottende un ro di lunghezz ugule l rggio stesso (si teng presente he se un ngolo l entro di un ironferenz sottende un ro lungo qunto il rggio iò suede per ogni ltr ironferenz onentri on l prim. Ovvimente, se l lunghezz dell ro sotteso è, d esempio, metà di quell del rggio, l ngolo è di mezzo rdinte; se è doppi di quell del rggio, l ngolo è di due rdinti; e osì vi. L ngolo giro, he sottende l inter ironferenz (l ui lunghezz è π volte quell del rggio, è di π rdinti; l ngolo pitto è di π rdinti; l ngolo retto è di π/ rdinti. In generle, l misur in rdinti di un ngolo he sottende un ro irolre di lunghezz l, è l/r essendo r il rggio dell ironferenz di ui l ro è prte. Per qunto onerne l unità di misur degli rhi irolri risult onveniente ssumere ome unità l ro in ui ngolo l entro orrispondente è l unità di misur degli ngoli. Si h osì l ro grdo, he è l ro di ironferenz he orrisponde ll ngolo l entro di un grdo, e l ro rdinte, he è l ro di ironferenz he orrisponde ll ngolo l entro di un rdinte. Seguendo quest onvenzione l misur di un ro di ironferenz e l misur del orrispondente ngolo l entro sono espresse dllo stesso numero. E di importnz prti spere ome si pss dll misur di un ngolo (o di un ro in grdi, ll misur in rdinti dello stesso ngolo ( o ro, e vievers. Dette e le misure, rispettivmente in grdi ed in rdinti, di uno stesso ngolo (o ro si h: D quest proporzione si rivno le due formule: 360:π : / π e /π l prim delle quli dà l misur in rdinti, not quell in grdi, l seond l misur in grdi, not quell in rdinti. Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 6
7 Angoli ed rhi orientti e loro misur: E spesso neessrio ttribuire d un ngolo un orientzione. Un ngolo si die orientto qundo i suoi lti sono onsiderti in un ero ordine, qundo ioè è stbilito qule dei due deve onsiderrsi ome primo. In tl so l ngolo può essere pensto ome generto dll rotzione del primo lto (lto origine verso il seondo (lto termine, fino ll sovrpposizione dei due. Convenendo di onsiderre positiv un rotzione he vviene nel verso ntiorrio e negtiv quell he vviene nel verso orrio, l ngolo dell prim figur viene detto ngolo positivo mentre quello dell seond figur viene detto ngolo negtivo. L misur di un ngolo orientto si ottiene premettendo ll su misur ssolut il segno se l ngolo è positivo, il segno se è negtivo. Qunto si è detto per gli ngoli vle nhe per gli rhi. Rihimi di mtemti: relzioni tr gli elementi di un tringolo qulunque Medinte il teorem dell ord, l ui definizione è he l misur di un ord di un ironferenz è ugule l prodotto tr l misur del dimetro ed il seno di uno qulunque degli ngoli ll ironferenz he insistono su uno dei due rhi sottesi dll ord, si può dimostrre il teorem dei seni (o di Eulero, he stbilise un relzione tr gli elementi di un tringolo. Questo fferm he in un tringolo qulunque è ostnte il rpporto tr l misur di un lto ed il seno dell ngolo opposto; ioè he inditi on A, B, C i tre vertii di un tringolo, α, β, γ i tre ngoli orrispondenti e on, b, le misure dei lti rispettivmente opposti gli ngoli di vertii A, B, C (seguiremo d or in poi quest onvenzione per indire gli elementi di un tringolo si h: b senα senβ senγ Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 7
8 Inftti, se onsiderimo l ironferenz irosritt l tringolo e pplihimo d ogni lto il teorem: e quindi: r senα, b r senβ, r senγ r b r r senα senβ senγ Per l proprietà trnsitiv dell uguglinz si h periò: b senα senβ senγ Il teorem delle proiezioni ed il teorem del oseno. Ci proponimo or di dimostrre he in un qulunque tringolo l misur di un lto è ugule ll somm dei prodotti di quelle degli ltri due lti per il oseno dell ngolo he isuno di questi form on il primo; ioè tr gli elementi di un qulsisi tringolo vlgono le relzioni: b os γ os β b os γ os α os β b os α E questo il teorem delle proiezioni. Per dimostrrlo onsiderimo le figure seguenti. α β γ πγ Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 8
9 α β γ Nell prim l ltezz AH del tringolo ABC de internmente l lto BC; si h pertnto: BH HC osβ b os γ Nell seond l ltezz AH de esternmente l lto BC; in questo so si h pertnto: BH CH osβ b os (π γ osβ b osγ Per il lto vle dunque, in ogni so, il teorem delle proiezioni; in modo nlogo si dimostr he vle nhe per isuno degli ltri lti. Come immedit onseguenz del teorem delle proiezioni si h il seguente teorem, detto del oseno (o di Crnot: in un tringolo qulsisi,il tringolo dell misur di ogni lto è ugule ll somm dei qudrti delle misure degli ltri due, diminuit del doppio prodotto delle misure di questi per il oseno dell ngolo tr essi ompreso; vlgono ioè le relzioni: b b os α b os β b b os γ Lo dimostrimo per un lto, d esempio per. Considerimo le tre uguglinze he esprimono il teorem delle proiezioni per isuno dei lti e, seguendo l ordine nel qule sono stte sritte, moltiplihimo mbo i membri dell prim per, mbo i membri dell seond per b, mbo i membri dell terz per : Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 9
10 b os γ os β -b - b os γ b os α - - os β b os α Sommndo membro membro queste tre uguglinze e riduendo i termini simili, si ottiene: - b - - b os α d ui si riv b - b os α he è qunto volevmo dimostrre. Vle l pen di osservre he il teorem di Pitgor può essere onsiderto un so prtiolre del teorem di Crnot. Inftti, se α 90 è os α 0 e pertnto per il teorem di Crnot si h: b he è ppunto l relzione tr ipotenus e teti espress dl teorem di Pitgor. Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 10
11 Rihimi di mtemti: l ellisse Generlità: Si die ellisse il luogo dei punti del pino per i quli è ostnte l somm delle distnze d due punti fissi, detti fuohi. Indihimo on F 1 ed F i due fuohi, on ( > 0 l loro distnz, on ( > 0 l somm ostnte delle distnze dei punti dell elisse di fuohi; se P è un generio punto del luogo dovrà llor essere ( fig.1 : PF 1 PF Figur 1. L ellisse è il luogo dei punti P per i quli è: PF PF, essendo F1 ed F due punti fissi ( denominti fuohi ed un ostnte. L ondizione ffinhè questo luogo esist è he si: e quindi PF 1 PF > F!F > ossi >. L elisse non può vere punti interni l segmento F 1 F ; per questi punti è inftti l somm delle distnze di fuohi. Semplii onsiderzioni i portno d ffermre he l elisse h due ssi di simmetri : l rett dei fuohi e l rett d ess perpendiolre nel punto medio del segmento F 1 F. Inftti, se il punto P pprtiene l luogo, se ioè vle l relzione PF 1 PF, nlog relzione verrà per i punti P e P, simmetrii di P rispetto lle due rette ( fig.. Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 11
12 Figur. L rett F1F dei fuohi e l rett quest perpendiolre nel punto medio O del segmento F1F sono ssi di simmetri per l elisse. Se P pprtiene ll elisse, pprtengono ll urv nhe P e P. L elisse è pure simmetri rispetto l punto O intersezione dei due ssi di simmetri (fig. 3. Inftti, se per un punto P vle l relzione PF PF, l stess relzione vrrà nhe per il punto P, simmetrio di P rispetto d O. Il punto O viene himto entro dell elisse. Figur 3. L elisse gode di un simmetri entrle rispetto l punto medio O del segmento vente per estremi i fuohi. Se P pprtiene ll elisse, pprtiene ll urv nhe P. Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 1
13 Equzione dell ellisse riferit i suoi ssi: Dt un ellisse di fuohi F 1 ed F e di entro O, fissimo un sistem di riferimento rtesino on l sse delle sisse oinidente on l rett F 1 F e on l origine nel entro O. Indindo on l distnz fole si h: ( 1 ;0 F e F ( ;0 Se è l somm ostnte delle distnze dei punti dell ellisse di fuohi, l ondizione ffinhè un generio punto P(; pprteng l luogo è he si: PF PF 1 Figur : Si vuole trovre l equzione rtesin dell ellisse rispetto d un sistem di riferimento vente per ssi gli ssi di simmetri dell ellisse stess. Clolndo PF1 e PF on l formul dell distnz tr due punti ottenimo: ( ; PF (. PF 1 L ondizione di pprenz di P ll ellisse può llor osì venir sritt: ( ( Quest ultim è l equzione del luogo in esme, m l form in ui si present è poo prti, us dei rdili ontenuti; erhimo pertnto di rendere rzionle l equzione. A tl fine trsportimo uno dei rdili nel membro di destr ed elevimo l qudrto entrmbi i membri: Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 13
14 Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 1 ( ( ; ( (. Svolgendo le operzioni indite e sopprimendo i termini uguli nei due membri ottenimo: ( ; (. Isolimo il rdile rimsto, dividimo i termini dell equzione per ed elevimo nuovmente l qudrto i due membri: ( ( ( [ ] ( ( (. ; ; ; ; Ponimo or b (poihé > è 0 > : b b e dividimo per b i termini dell equzione: 1 b Quest ultim è l equzione dell ellisse riferit i propri ssi (ioè d un sistem di riferimento i ui ssi oinidono on gli ssi di simmetri del luogo stesso; ess prende il nome di equzione noni o normle. I punti d intersezione dell ellisse on l sse delle sisse e on quello delle ordinte si ottengono risolvendo i sistemi: b 1 0 e b 1 0
15 Essi vengono himti i vertii dell ellisse e sono: V 1 (- ; 0 V ( ; 0 V 3 (0 ; b V (0 ; -b Mndndo per questi punti le rette prllele gli ssi rtesini si ottiene un rettngolo entro il qule luogo è tutto ontenuto. L ellisse è tutt ontenut nel rettngolo i ui lti pssno per i suoi quttro vertii e sono prlleli i suoi ssi di simmetri. Inftti, poihé è: b 1 è nhe ertmente 1 e 1 b Di onseguenz srà e b b Ciò signifi he ogni punto dell ellisse h l siss ompres tr ed e l ordint ompres tr b e b. I segmenti V 1 V e V 3 V, di lunghezze rispettivmente e b, vengono himti ssi dell ellisse, sse mggiore il primo, sse minore il seondo ( e b sono quindi i semissi. Il segmento F 1 F, di lunghezz, viene himto sse fole ( è pertnto il semisse fole. Il rpporto viene generlmente indito on e e himto eentriità. Per il numero e vle l relzione 0 e 1 L ellisse è tnto più shiit qunto più il vlore di e è viino d 1. per e 0 si h un erhio; inftti se 0 e di onseguenz b ; l equzione si ridue llor ll form 1 e quindi Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 15
16 Rihimi di mtemti: definizione di derivt di un funzione di un vribile I problemi fondmentli i quli si deve fr rislire l origine del onetto di derivt sono due: quello dell determinzione dell equzione dell tngente d un urv in un suo punto e quello del lolo dell veloità di un orpo in moto. Dremo or un definizione purmente nliti di derivt di un funzione di un vribile e ne illustreremo poi il signifito geometrio (tngente e quello inemtio (veloità ed elerzione. Si f( un funzione definit in un intervllo di estremi e b e sino un punto interno detto intervllo ed il vlore ssunto dll funzione per. Se ll vribile indipendente dimo un inremento (positivo e negtivo, se ioè pssimo dl punto o l punto o, pprentemente nh esso ll intervllo di definizione, nhe l vribile dipendente, ioè l funzione, subirà un vrizione; ess psserà inftti dl vlore f( o l vlore f( o. Chimimo inremento dell funzione, e lo indihimo on i simboli o f(, l differenz f ( 0 f ( 0 (vedi figur; il vlore di tle inremento dipende nturlmente di vlori di o e di e può essere positivo, negtivo o nullo. f( tr l inremento subito dll funzione f( e l inremento dto dll vribile indipendente ; e preismente, rpporto inrementle sinistro quello orrispondente d un <0 e rpporto inrementle destro quello orrispondente d un >0. Il rpporto inrementle dell funzione f(, orrispondente d un determinto vlore dell inremento dell vribile indipendente, è un indie del ome vri l funzione nell intorno del punto o ; esso viene nhe himto l vrizione medi dell funzione orrispondente ll vrizione subit dll vribile indipendente. Un volt fissto o il vlore del rpporto inrementle dipende unimente dl vlore di, è ioè un funzione dell vribile. Proponimoi or di vedere os suede di detto rpporto per 0. Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 16
17 Se ttribuimo vlori sempre più pioli in vlore ssoluto, se ioè fimo tendere 0 (si vlori negtivi he per vlori positivi, l inremento f( tenderà nh esso 0 e se f( è f ( 0 ontinu in o ; il lim si presenterà periò nell form indetermint. 0 0 Null si può pertnto dire in generle del vlore di detto limite; se esso esiste ed è finito viene himto derivt dell funzione f( in o. Diimo dunque he: l derivt dell funzione f( nel punto o è il limite, se esiste ed è finito, del rpporto inrementle f ( f ( 0 f ( 0 l tendere omunque 0 dell inremento dell vribile indipendente (on l prol omunque intendimo dire he v ftto tendere 0 si per vlori positivi he negtivi. L derivt si indi in genere on uno dei seguenti simboli: Sriveremo dunque: ' ' f ( 0 ; ; ( 0 [ Df ( ] 0 f '( 0 f ( 0 f ( 0 lim 0 Alune grndezze fisihe definite ome derivte di ltre Allo sopo di hirire meglio il onetto di derivt, riportimo or luni semplii esempi di grndezze fisihe definite ome derivte di ltre grndezze. A Veloità istntne Si P un punto he si muove di moto vrio su un triettori r (he per sempliità supporemo rettiline, sull qule è fissto un sistem di oordinte sisse di origine 0. L posizione del punto P è individut, istnte per istnte, dll siss s, he risult funzione del tempo t. Si: ss(t l funzione he esprime l dipendenz di s d t, ioè l osì dett legge orri o equzione del moto. All istnte t 0 l siss del punto P srà llor s ( t 0 ed ll istnte t0 t srà s( t 0 t. Lo spzio perorso d P nell intervllo di tempo t è dunque: s( t s( t0 t s( t0 Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 17
18 s( t Mentre il rpporto inrementle t P perorre lo spzio s ; è ioè: è, per definizione, l veloità medi v m on l qule v m s t s( t t t s( t ( 0 0 t Se il moto non è uniforme, l veloità medi per vlori di t sempre più pioli v m vri l vrire di t v vri sempre meno l vrire di t m, m, in generle,. Il vlore ui tende il rpporto inrementle s( t t, l tendere 0 di t, viene himto veloità istntne di P nell istnte t 0 ; indindo on v(t l veloità istntne di P srà llor: s( t0 t s( t0 v( t lim v lim s' ( t 0 0 m t 0 t 0 t L veloità di un punto P in un istnte t 0 è dunque l derivt rispetto l tempo dello spzio s(t. B Aelerzione istntne Ritornimo nor ll esempio del punto P he perorre l triettori rettiline r. Se v t e v( t 0 t sono le veloità di P rispettivmente negli istnti t 0 e t0 t, l vrizione di veloità subit dl punto nell intervllo di tempo t è v t v( t t v( ( 0 ( 0 t0. Com è noto, si definise elerzione medi m, reltiv ll intervllo t, il rpporto tr l vrizione di veloità v e l intervllo t nel qule l vrizione è vvenut: m v t v( t t t v( t ( 0 0 t Il vlore ui tende detto rpporto qundo t 0 viene himto elerzione istntne di P nell istnte t 0. L elerzione ( t 0 in un istnte t 0 è dunque l derivt, rispetto l tempo, dell veloità v(t: v( t0 t v( t0 ( t lim lim v'( t 0 0 m. t 0 t 0 t Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 18
19 ρ ρ Studio inemtio di un oppi di ruote dentte ellittihe: Lo studio inemtio di un oppi di ruote dentte ellittihe denti dritti è ffrontto riferendosi lle ruote di frizione ellittihe primitive dei suddetti ingrnggi. Riero un relzione he leghi l rotzione dell ruot ondott ( vribile dipendente o di usit ll ngolo di rotzione dell ruot onduttrie ( vribile indipendente o di ingresso. ρ ρ π π Osservndo ttentmente l figur si deduono importnti informzioni: - Gli ellissi sono infulrti nei fuohi; - L intersse tr i due lberi durnte il moto rimne nturlmente invrito (F F 1 ost.; - I tringoli F 1 PF ed F 1 PF sono uguli. L ultim onsiderzione è quell più signifitiv. L ngolo di rotzione dell ruot ondott, per l similitudine dei tringoli, è quello desritto di segmenti F 1 P ed F P, vribili on l posizione di P sull ellisse. M tle ngolo pprtenente l tringolo desritto sull ruot ondott lo individuo nhe sul tringolo ostruito sull ellisse motrie, in virtù dell similitudine dei tringoli. Eo he i si liber di un grn frdello! All lue di qunto detto lo studio del moto di un oppi di ruote di frizione ellittihe si riondue ll nlisi del moto di un punto su un ellisse. L rotzione ert v espress in funzione di. Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 19
20 Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 0 I segmenti F 1 P ed F P sono, ome già detto, vribili seond dell posizione oupt d P he dipende, su volt, d. Il tringolo F 1 PF, nel generio istnte di moto, è un tringolo qulsisi e, ome tle, v studito on il Teorem di Crnot. Applio il suddetto l fine di rivre i lti PF 1 e PF in funzione di. os( ( π ρ ρ ρ os ρ ρ ρ ρ os ρ ρ os ( ρ ρ Il legme inognito fr gli ngoli ed è fornito dl Teorem dei seni pplito l tringolo F 1 PF he, riordimo, è generio. E un fse delit, si seglie di ffidrsi l lto in qunto è l unio del tringolo restre immutto poihé rppresent l distnz tr i due fuohi. Applio il teorem dei seni ngolo PF F π π π π ( 1 ( ( sen sen π ρ sen sen sen os ( ( ( π ρ π on sen(π sen sen rsen os on e espressi in rdinti 360 os sen rsen π π π π on e espressi in grdi Con gli ngoli selti in figur si è verifito he i risultti oinidono on quelli del tlogo dell ditt Nnni Ingrnggi m le rotzioni presentno sfsmenti di : iò è imputbile ll differente selt delle posizioni di prtenz dell oppi di ruote.
21 Si orregge immeditmente l disordnz tenedo onto dello sfsmento di nelle rotzioni, iò evit di ridisegnre ompletmente l figur preedente: 360 sen π ( π π rsen π ( os 360 L legge dell veloità ngolre viene rivt sempliemente derivndo rispetto l tempo l espressione ppen determint. Oorre osservre he l ngolo dipende d il qule, su volt, è funzione del tempo ( wt. Pertnto sono in presenz di un relzione del tipo: ((t. Andndo derivre otterò: d dt d d d dt on w d dt poihé l veloità ngolre è l derivt dell ngolo spzzto rispeto l tempo. Per determinre l espressione dell elerzione derivo l veloità ngolre dell ruot ondot rispetto l tempo, rgionndo nlogmente. Le funzioni suddette verrnno riportte più vnti. Tle fse di lolo può essere demndt trnquillmente ll elbortore. I grfii dell relzione sono stti relizzti on l loltrie grfi in dotzione nel sistem opertivo del Mintosh (Grphing Clultor 1.1 m è possibile utilizzre per l mbiente Windows il progrmm Derive 5 dell Softwre House. Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 1
22 Legge rotzioni (spostmenti ngolri dell ruot ondott in funzione dei grdi di rotzione dell ruot onduttrie: 360 π π 360 sin sin π 360 ( π os π 360 ( π Legend: ngolo di rotzione in grdi dell ruot ondott (vribile di usit; ngolo di rotzione in grdi dell ruot onduttrie (vribile di ingresso; semisse mggiore dell ellisse; b semisse minore dell ellisse; metà dell distnz fole. Grfio rotzioni in grdi dell ruot ondott in funzione dell rotzione dell onduttrie: (esempio: ruot ellitti on semisse mggiore 65 mm; semisse minore b 61,83 mm; metà distnz fole 1,6665 mm oppi di ruote ditt Nnni Ingrnggi odie Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe
23 Ingrndendo mggiormente il pino rtesino: Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 3
24 Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe
25 Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 5
26 Legge dell veloità ngolre dell ruot ondott in funzione dei grdi di rotzione dell ruot onduttrie: π ( π os π ( os π ( π ( sin 90 π 90 os ( π π ( sin 1 π ( os π ( os w π Legend: veloità ngolre dell ruot ondott (vribile di usit; ngolo di rotzione in grdi dell ruot onduttrie (vribile di ingresso; semisse mggiore dell ellisse; b semisse minore dell ellisse; metà dell distnz fole; w veloità ngolre dell lbero onduttore. Digrmm dell ndmento dell veloità ngolre dell ruot ondott in funzione degli ngoli di rotzione dell ruot onduttrie: (esempio: ruot ellitti on semisse mggiore 65 mm; semisse minore b 61,83 mm; metà distnz fole 1,6665 mm; w 100 rd/s oppi di ruote ditt Nnni Ingrnggi odie Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 6
27 Con un sl più entut: Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 7
28 π π w π ( sin π ( os 90 π ( π ( sin os π ( os ( π ( sin os π π ( os π π ( os π ( 8100 os sin 3 ( π ( os sin ( 1 π ( os π π ( os 90 π ( os sin ( 1 π π ( os π sin ( π ( 90 os π ( os π ( π sin π ( os 5 π ( os π π ( os π ( 5 os sin 3 ( π ( os π ( sin 1 π ( os π π ( os ( ( sin sin 1 π ( os π ( 90 os Legge dell elerzione ngolre dell ruot ondott in funzione dei grdi di rotzione dell ruot onduttrie: ( π ( π ( 3 π π π ( π ( 3 π 1/ ( π π Legend: Y.. elerzione ngolre dell ruot ondott (vribile di usit; X ngolo di rotzione in grdi dell ruot onduttrie (vribile di ingresso; semisse mggiore dell ellisse; b semisse minore dell ellisse; metà dell distnz fole; w veloità ngolre dell lbero onduttore. Digrmm dell ndmento dell elerzione ngolre dell ruot ondott in funzione degli ngoli di rotzione dell ruot onduttrie: (esempio: ruot ellitti on semisse mggiore 65 mm; semisse minore b 61,83 mm; metà distnz fole 1,6665 mm; w 100 rd/s oppi di ruote ditt Nnni Ingrnggi odie Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 8
29 Con un sl più entut: Premess: tutti i grfii seguenti sono stti ostruiti riferendosi sempre ll oppi di ruote ellittihe prodotte dll ditt Nnni Ingrnggi, odie venti: semisse mggiore 65 mm; semisse minore b 61,83 mm; metà distnz fole 1,6665 mm; intersse 130 mm. Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 9
30 Commento dei grfii: - legge delle rotzioni In verde: rotzione in grdi dell ruot ondott denti dritti ellitti in funzione dell rotzione dell ruot onduttrie; In ros: rotzione in grdi dell ruot ondott denti dritti irolre in funzione dell rotzione dell ruot onduttrie. Se esmino le rotzioni di un oppi di ruote dentte denti dritti irolri venti ugul numero di denti e stesso dimetro primitivo, il grfio srebbe un rett inlint di 5 pssnte per l origine (bisettrie del I e III qudrnte. Nei punti in ui l legge delle rotzioni (verde interse l rett (ros le ruote ellittihe sono nelle posizioni di qudrtur, ioè hnno i semissi mggiori llineti sull medesim rett. fig.1 0, 0. fig.,. E opportuno osservre he l form dell legge delle rotzioni è l seguente: f( rsen(f( Essendo rsen(f( un quntità osillnte si pise perhé il grfio bbi il suddetto ndmento. Ad un giro dell ruot morie orrisponde un giro dell ruot ondott. Il rpporto di trsmissione, vribile istnte per istnte, è nel periodo unitrio. Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 30
31 legge dell veloità ngolre dell ruot ondott: L line orizzontle di olore fusi rppresent l veloità ngolre dell lbero dell ruot motrie, he è ostnte nel tempo e pri nell esempio di figur w 100 rd/s. L line in verde rppresent l veloità ngolre dell lbero su ui è lettt l ruot ondott, vribile nell ro di un giro. Per gli intervlli di nei quli l line verde gie l di sotto dell line ros, l ruot ondott ruot più lentmente dell ruot motrie. Vievers per gli intervlli di nei quli l line verde gie l di sopr dell line ros, l ruot ondott ruot più veloemente dell ruot motrie. D ltronde l funzione degli ingrnggi ellittii è proprio quest, ioè ottenere un veloità ngolre vribile nell ro dello stesso giro, mntenendo un rpporto di trsmissione medio pri d 1:1. L veloità ngolre dell ruot ellitti ondott vri d 50 rd/s 00 rd/s, venendo ioè nell ro di un giro ftt vrire tr w/ e w. L entità dell suddett vrizione dipende dll geometri dell ingrnggio. Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 31
32 - legge dell elerzione ngolre dell ruot ondott: Dove l veloità ngolre dell ruot ondott present vlore minimo ( 0 e 360 l elerzione è null. Ciò è onfermto e giustifito dl ftto he l elerzione ngolre sturise dll derivt prim rispetto l tempo dell veloità ngolre dell ruot ondott. Quest ultim gir periò on veloità ngolre pressohé ostnte eslusivmente negli intorni dei punti 0 e 360. Notre he nell intervllo 0 - l elerzione è positiv, pur se inostnte. Inftti l veloità st umentndo: l ruot onduttrie st elerndo l ruot ellitti ondott. Notre infine he nell intervllo -360 l elerzione è negtiv, pur se inostnte. Inftti l veloità st diminuendo: l ruot onduttrie st rllentndo l ruot ellitti ondott. Lo studio inemtio di un oppi di ruote ellittihe h portto relzioni l ui vlidità è onfermt si di dti del tlogo dell ditt Nnni Ingrnggi si dll simulzione eseguit on il progrmm Autod 000. Un ulteriore onferm si h dl rffronto tr i nostri" grfii on il prospetto he Nnni fornise i suoi Clienti. Se i è permesso vorremmo umilmente sottolinere un inongruenz nei suddetti digrmmi: l elerzione h segno meno qundo l veloità ngolre dell lbero ondotto è resente... e vievers Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 3
33 Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 33
34 Crtteristihe ostruttive: I denti di un ruot dentte ellitti non sono tutti uguli, ome mostrno hirmente le figure seguenti: iò è dovuto l ftto he, durnte l denttur (eseguit on un denttrie tipo Pfuter CNC il retore non ingrn on l ironferenz primitiv bensì on un ellisse primitivo. In tl modo vri il rggio di urvtur dell superfiie su ui rotol il segmento he desrive il profilo d evolvente del fino del dente. Il psso tuttvi deve restre nvrito lungo l ellisse primitivo, ondizione neessri per l ingrnmento. Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 3
35 E fondmentle per il funzionmento dell ingrnggio posizionre i denti ome in figur (notre l presenz dei riferimenti rppresentti di bulini : Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 35
36 Criteri di selt delle ruote ellitihe: Qulittivmente si er di dre un tri per il progettist d seguire per segliere l oppi di ruote ellittihe opportune. Lo sopo è ottenere un erto rpporto tr le veloità ngolri mssime e minime he si verifino nell ro di un rotzione omplet, situzioni, ome già visto, he si hnno nelle posizioni di qudrtur. R R1 R R1 w w1ost w w1ost Ruot ondott 0 Ruot motrie Ruot ondott Ruot motrie Poihé si sono sempre prese ome esempio le ruote ellittihe on semisse mggiore 65 mm; semisse minore b 61,83 mm; metà distnz fole 1,6665 mm dell ditt Nnni Ingrnggi (odie , si ontinu on esse: w m w min 00rd / s 50rd / s Come rrivo tele risultto senz pssre ttrverso l uso dell legge on il rispettivo grfio? Anlizzimo le situzioni delle ruote ellittihe in qudrtur: Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 36
37 R ,6665 3,3335mm R 65 1, ,6665mm w min w ost R 1 R 3,3335mm 86,6665mm 1/ w m w ost R R 1 86,6665mm 3,3335mm periò: R r v w w ost m R 1 w min R w 1 os t quindi R ( R R 1 r v w m w min ( R 1 R (r r Giondo sulle forme delle ruote ellittihe rivo il rpporto tr le veloità desiderto. Il tlogo evit i loli poihé fornise già tli vlori. Istituto Tenio Industrile Aldini Vlerini Bologn Are progetto ruote dentte ellittihe 37
Ellisse ed iperbole. Osservazione. Considereremo sempre ellissi della forma + = 1 le quali hanno tutte centro nell origine degli
 Ellisse ed iperole Ellisse Definizione: si definise ellisse il luogo geometrio dei punti del pino per i quli è ostnte l somm delle distnze d due punti fissi F e F detti fuohi. L equzione noni dell ellisse
Ellisse ed iperole Ellisse Definizione: si definise ellisse il luogo geometrio dei punti del pino per i quli è ostnte l somm delle distnze d due punti fissi F e F detti fuohi. L equzione noni dell ellisse
Verifica di matematica
 Nome Cognome. Clsse D 7 Mrzo Verifi di mtemti ) Dt l equzione: (punti ) k ) Srivi per quli vlori di k rppresent un ellisse, preisndo per quli vlori è un ironferenz b) Srivi per quli vlori di k rppresent
Nome Cognome. Clsse D 7 Mrzo Verifi di mtemti ) Dt l equzione: (punti ) k ) Srivi per quli vlori di k rppresent un ellisse, preisndo per quli vlori è un ironferenz b) Srivi per quli vlori di k rppresent
L IPERBOLE. L iperbole è il luogo geometrico dei punti del piano per i quali è costante la differenza delle distanze da due punti fissi detti fuochi.
 prof.ss Cterin Vespi 1 Appunti di geometri nliti L IPERBOLE L iperole è il luogo geometrio dei punti del pino per i quli è ostnte l differenz delle distnze d due punti fissi detti fuohi. Sino F1 e F i
prof.ss Cterin Vespi 1 Appunti di geometri nliti L IPERBOLE L iperole è il luogo geometrio dei punti del pino per i quli è ostnte l differenz delle distnze d due punti fissi detti fuohi. Sino F1 e F i
Es1 Es2 Es3 Es4 Es5 tot
 Ottore lsse E Verifi sommtiv Cognome Nome rgomenti: onihe, funzione esponenzile e grfii derivti Tempo disposizione: ore Voto Es Es Es Es Es tot.... Considert l ellisse vente ome sse fole l sse, eentriità
Ottore lsse E Verifi sommtiv Cognome Nome rgomenti: onihe, funzione esponenzile e grfii derivti Tempo disposizione: ore Voto Es Es Es Es Es tot.... Considert l ellisse vente ome sse fole l sse, eentriità
APPUNTI DI GEOMETRIA ANALITICA
 Prof. Luigi Ci 1 nno solstio 13-14 PPUNTI DI GEOMETRI NLITIC Rett orientt Un rett r si die orientt qundo: 1. È fissto un punto di riferimento, detto origine;. Dei due possiili versi in ui un punto si può
Prof. Luigi Ci 1 nno solstio 13-14 PPUNTI DI GEOMETRI NLITIC Rett orientt Un rett r si die orientt qundo: 1. È fissto un punto di riferimento, detto origine;. Dei due possiili versi in ui un punto si può
L ELLISSE 1. L'ellisse come luogo geometrico ellisse fuochi. centro
 L ELLISSE 1. L ellisse ome luogo geometrio.. Equzione dell ellisse on i fuohi sull sse. 3. Le proprietà dell ellisse.. Clolo dei semissi, dei vertii, dei fuohi e rppresentzione grfi. 5. Equzione dell ellisse
L ELLISSE 1. L ellisse ome luogo geometrio.. Equzione dell ellisse on i fuohi sull sse. 3. Le proprietà dell ellisse.. Clolo dei semissi, dei vertii, dei fuohi e rppresentzione grfi. 5. Equzione dell ellisse
Ing. Alessandro Pochì
 Dispense di Mtemti lsse terz Prol ed ellisse Quest oper è distriuit on: Lienz Cretive Commons Attriuzione - Non ommerile - Non opere derivte 3.0 Itli Ing. Alessndro Pohì ( Appunti di lezione svolti ll
Dispense di Mtemti lsse terz Prol ed ellisse Quest oper è distriuit on: Lienz Cretive Commons Attriuzione - Non ommerile - Non opere derivte 3.0 Itli Ing. Alessndro Pohì ( Appunti di lezione svolti ll
a b c Triangolo rettangolo In un triangolo rettangolo : un cateto è uguale al prodotto dell ipotenusa per il seno dell angolo opposto al cateto.
 Tringolo rettngolo In un tringolo rettngolo : un teto è ugule l prodotto dell ipotenus per il seno dell ngolo opposto l teto. = sen = sen un teto è ugule l prodotto dell ipotenus per il oseno dell ngolo
Tringolo rettngolo In un tringolo rettngolo : un teto è ugule l prodotto dell ipotenus per il seno dell ngolo opposto l teto. = sen = sen un teto è ugule l prodotto dell ipotenus per il oseno dell ngolo
Geometria analitica +l piano cartesiano Le funzioni retta, parabola, iperbole Le trasformazioni sul piano cartesiano
 Geometri nliti +l pino rtesino Le funzioni rett, prol, iperole Le trsformzioni sul pino rtesino SEZ. P +l pino rtesino Osserv le oorinte ei seguenti punti: (, 0), (, ), C(, +), D + +, E(+, 9)., Che os
Geometri nliti +l pino rtesino Le funzioni rett, prol, iperole Le trsformzioni sul pino rtesino SEZ. P +l pino rtesino Osserv le oorinte ei seguenti punti: (, 0), (, ), C(, +), D + +, E(+, 9)., Che os
Geometria Analitica Domande, Risposte & Esercizi
 Geometri Anliti Domnde, Risposte & Eserizi L ironferenz. Dre l definizione di ironferenz ome luogo di punti. L ironferenz è un luogo di punti, è ioè un insieme di punti del pino le ui distnze d un punto
Geometri Anliti Domnde, Risposte & Eserizi L ironferenz. Dre l definizione di ironferenz ome luogo di punti. L ironferenz è un luogo di punti, è ioè un insieme di punti del pino le ui distnze d un punto
Vettori - Definizione
 Vettori - Definizione z Verso Origine Modulo Direzione V y Form geometri x Form nliti Un vettore è un ente geometrio definito d: - Direzione: rett sull qule gie il vettore, he ne indi l orientmento nello
Vettori - Definizione z Verso Origine Modulo Direzione V y Form geometri x Form nliti Un vettore è un ente geometrio definito d: - Direzione: rett sull qule gie il vettore, he ne indi l orientmento nello
operazioni con vettori
 omposizione e somposizione + = operzioni on vettori = + = + Se un vettore può essere dto dll omposizione di due o più vettori, questi vettori omponenti possono essere selti lungo direzioni ortogonli fr
omposizione e somposizione + = operzioni on vettori = + = + Se un vettore può essere dto dll omposizione di due o più vettori, questi vettori omponenti possono essere selti lungo direzioni ortogonli fr
( ) 1. Scrivi l equazione della parabola ad asse verticale passante per il punto ( ) P e con vertice. Soluzione Dall equazione generica della parabola
 . Srivi l euzione dell prol d sse vertile pssnte per il punto ( ) ; P e on vertie ( ) ; V. Dll euzione generi dell prol e dll onosenze del vertie, le ui oordinte generihe sono V ; possimo srivere sostituendo
. Srivi l euzione dell prol d sse vertile pssnte per il punto ( ) ; P e on vertie ( ) ; V. Dll euzione generi dell prol e dll onosenze del vertie, le ui oordinte generihe sono V ; possimo srivere sostituendo
1) Si ha quindi Un cateto è uguale al prodotto dell ipotenusa per il seno dell angolo opposto.
 Trigonometri prte esy mtemti Elin pgin TRIANGOLO RETTANGOLO Considerimo i tringoli rettngoli OPQ e OP ' Q A γ C Essi sono simili per ui Q P : QP OP : OP Essendo Q ' P ' QP sin OP OP ottenimo : sen : e
Trigonometri prte esy mtemti Elin pgin TRIANGOLO RETTANGOLO Considerimo i tringoli rettngoli OPQ e OP ' Q A γ C Essi sono simili per ui Q P : QP OP : OP Essendo Q ' P ' QP sin OP OP ottenimo : sen : e
] a; b [, esiste almeno un punto x 0
![] a; b [, esiste almeno un punto x 0 ] a; b [, esiste almeno un punto x 0](/thumbs/88/115232227.jpg) Anlisi Limiti notevoli sen lim = ( lim + = e Un funzione si die ontinu in qundo, + lim f( = lim f(. + sintoti vertili: se lim f ( = ± oppure lim f ( = ± sintoti orizzontli: se sintoti oliqui: l'equzione
Anlisi Limiti notevoli sen lim = ( lim + = e Un funzione si die ontinu in qundo, + lim f( = lim f(. + sintoti vertili: se lim f ( = ± oppure lim f ( = ± sintoti orizzontli: se sintoti oliqui: l'equzione
Anno 2. Triangoli rettangoli e teorema delle corde
 Anno Tringoli rettngoli e teorem delle orde 1 Introduzione In quest lezione impreri d pplire i teoremi di Eulide e di Pitgor e sopriri quli prtiolrità nsondono i tringoli rettngoli on ngoli prtiolri. Infine,
Anno Tringoli rettngoli e teorem delle orde 1 Introduzione In quest lezione impreri d pplire i teoremi di Eulide e di Pitgor e sopriri quli prtiolrità nsondono i tringoli rettngoli on ngoli prtiolri. Infine,
01 Matematica Liceo \ Unità Didattica N 6 La retta 1
 Mtemti Lieo \ Unità Didtti N 6 L rett Unità didtti N 6 L rett rtesin ) Equzione vettorile dell rett 2) Equzioni prmetrihe dell rett 3) Equzione dell rett pssnte per due punti 4) Equzione dell rett pssnte
Mtemti Lieo \ Unità Didtti N 6 L rett Unità didtti N 6 L rett rtesin ) Equzione vettorile dell rett 2) Equzioni prmetrihe dell rett 3) Equzione dell rett pssnte per due punti 4) Equzione dell rett pssnte
Geometria Analitica Domande, Risposte & Esercizi
 Geometri Anliti Domnde, Risposte & Eserizi L ellisse. Dre l definizione di ellisse ome luogo di punti. L ellisse è un luogo di punti, è ioè un insieme di punti del pino le ui distnze d due punti fissi
Geometri Anliti Domnde, Risposte & Eserizi L ellisse. Dre l definizione di ellisse ome luogo di punti. L ellisse è un luogo di punti, è ioè un insieme di punti del pino le ui distnze d due punti fissi
Unità Didattica N 08 I sistemi di primo grado a due incognite U.D. N 08 I sistemi di primo grado a due incognite
 66 Unità idtti N 08 I sistemi di primo grdo due inognite U.. N 08 I sistemi di primo grdo due inognite 01) Coordinte rtesine 0) I sistemi di primo grdo due inognite 0) Metodo di sostituzione 04) Metodo
66 Unità idtti N 08 I sistemi di primo grdo due inognite U.. N 08 I sistemi di primo grdo due inognite 01) Coordinte rtesine 0) I sistemi di primo grdo due inognite 0) Metodo di sostituzione 04) Metodo
8. Calcolo integrale.
 Politenio di Milno - Foltà di Arhitettur Corso di Lure in Edilizi Istituzioni di Mtemtihe - Appunti per le lezioni - Anno Ademio 200/20 26 8 Clolo integrle 8 Signifito geometrio dell integrle definito
Politenio di Milno - Foltà di Arhitettur Corso di Lure in Edilizi Istituzioni di Mtemtihe - Appunti per le lezioni - Anno Ademio 200/20 26 8 Clolo integrle 8 Signifito geometrio dell integrle definito
Le equazioni di secondo grado
 Le equzioni di seondo grdo Un equzione è di seondo grdo se, dopo ver pplito i prinipi di equivlenz, si può srivere nell form on 0,, R Not: è nhe detto termine noto. Esempio Sviluppimo l seguente equzione:
Le equzioni di seondo grdo Un equzione è di seondo grdo se, dopo ver pplito i prinipi di equivlenz, si può srivere nell form on 0,, R Not: è nhe detto termine noto. Esempio Sviluppimo l seguente equzione:
Misura degli archi e degli angoli
 Misur degli rhi e degli ngoli. Si definise ome positivo il verso ntiorrio di perorrenz di un ironferenz; ome negtivo il verso orrio.. Fissto su un ironferenz un punto A ome origine e un punto B ome estremo
Misur degli rhi e degli ngoli. Si definise ome positivo il verso ntiorrio di perorrenz di un ironferenz; ome negtivo il verso orrio.. Fissto su un ironferenz un punto A ome origine e un punto B ome estremo
c β Figura F2.1 Angoli e lati in un triangolo rettangolo.
 F. Trigonometri F. Risoluzione dei tringoli rettngoli Risolvere un tringolo rettngolo signifi trovre tutti i suoi lti e tutti i suoi ngoli. Un ngolo lo si onose già ed è l ngolo retto. Le inognite sono
F. Trigonometri F. Risoluzione dei tringoli rettngoli Risolvere un tringolo rettngolo signifi trovre tutti i suoi lti e tutti i suoi ngoli. Un ngolo lo si onose già ed è l ngolo retto. Le inognite sono
Unità Didattica N 11 Le equazioni di secondo grado ad una incognita Unità Didattica N 11 Le equazioni di secondo grado ad una incognita
 86 Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di
86 Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di
Geometria. Domande introduttive
 PT, 695 noio Geometri si di mtemti per l MPT 3 Tringoli L pdronnz delle rtteristihe e delle proprietà dei tringoli è fondmentle per pire il pitolo dell trigonometri, uno dei pitoli di geometri non trttto
PT, 695 noio Geometri si di mtemti per l MPT 3 Tringoli L pdronnz delle rtteristihe e delle proprietà dei tringoli è fondmentle per pire il pitolo dell trigonometri, uno dei pitoli di geometri non trttto
VERSO L ESAME DI STATO LA DERIVATA DI UNA FUNZIONE
 VERSO L ESAME DI STATO LA DERIVATA DI UNA FUNZIONE Soluzioni di quesiti e prolemi trtti dl Corso Bse Blu di Mtemti volume 5 [] (Es. n. 8 pg. 9 V) Dell prol f ( ) si hnno le seguenti informzioni, tutte
VERSO L ESAME DI STATO LA DERIVATA DI UNA FUNZIONE Soluzioni di quesiti e prolemi trtti dl Corso Bse Blu di Mtemti volume 5 [] (Es. n. 8 pg. 9 V) Dell prol f ( ) si hnno le seguenti informzioni, tutte
Corso Integrato: Matematica e Statistica. Corso di Matematica (6 CFU)
 Corso di Lure in Scienze e Tecnologie Agrrie Corso Integrto: Mtemtic e Sttistic Modulo: Mtemtic (6 CFU) (4 CFU Lezioni + CFU Esercitzioni) Corso di Lure in Tutel e Gestione del territorio e del Pesggio
Corso di Lure in Scienze e Tecnologie Agrrie Corso Integrto: Mtemtic e Sttistic Modulo: Mtemtic (6 CFU) (4 CFU Lezioni + CFU Esercitzioni) Corso di Lure in Tutel e Gestione del territorio e del Pesggio
Unità Didattica N 11 Le equazioni di secondo grado ad una incognita
 Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di seondo
Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit ) L definizione di equzione di seondo grdo d un inognit ) L risoluzione delle equzioni di seondo
Relazioni e funzioni. Relazioni
 Relzioni e unzioni Relzioni Deinizione: dti due insiemi A e B, si deinise un relzione R tr A e B un orrispondenz stilit d un proposizione tr un elemento A e B, in tl so si die he è in relzione on e si
Relzioni e unzioni Relzioni Deinizione: dti due insiemi A e B, si deinise un relzione R tr A e B un orrispondenz stilit d un proposizione tr un elemento A e B, in tl so si die he è in relzione on e si
ipotenusa cateto adiacente ad α cateto opposto ad α ipotenusa cateto adiacente ad α ipotenusa cateto adiacente ad α
 Trigonometri I In quest prim prte dell trigonometri denimo le funzioni trigonometriche seno, coseno e tngente e le loro funzioni inverse. Vedremo nche come utilizzrle nell risoluzione dei tringoli. Comincimo
Trigonometri I In quest prim prte dell trigonometri denimo le funzioni trigonometriche seno, coseno e tngente e le loro funzioni inverse. Vedremo nche come utilizzrle nell risoluzione dei tringoli. Comincimo
La parabola. Fuoco. Direttrice y
 L prol Definizione: si definise prol il luogo geometrio dei punti del pino equidistnti d un punto fisso detto fuoo e d un rett fiss dett direttrie. Un rppresentzione grfi inditiv dell prol nel pino rtesino
L prol Definizione: si definise prol il luogo geometrio dei punti del pino equidistnti d un punto fisso detto fuoo e d un rett fiss dett direttrie. Un rppresentzione grfi inditiv dell prol nel pino rtesino
I S I E. Fermi - Lucca Istituto Tecnico settore Tecnologico
 I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
EQUAZIONI DI SECONDO GRADO
 Autore: Enrio Mnfui - 30/04/0 EQUAZIONI DI SECONDO GRADO Le equzioni di seondo grdo in un inognit sono uguglinze di due polinomi di ui lmeno uno è di seondo grdo e l ltro è di grdo minore o ugule due.
Autore: Enrio Mnfui - 30/04/0 EQUAZIONI DI SECONDO GRADO Le equzioni di seondo grdo in un inognit sono uguglinze di due polinomi di ui lmeno uno è di seondo grdo e l ltro è di grdo minore o ugule due.
I S I E. Fermi - Lucca Istituto Tecnico settore Tecnologico
 I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
Argomento 10 Integrali impropri
 Premess Argomento Integrli impropri Nell Arg. 9 è stt introdott l nozione di integrle definito f() d per funzioni ontinue f : [, b] R. Un derog ll ontinuità di f è nhe stt introdott, m solo per onsiderre
Premess Argomento Integrli impropri Nell Arg. 9 è stt introdott l nozione di integrle definito f() d per funzioni ontinue f : [, b] R. Un derog ll ontinuità di f è nhe stt introdott, m solo per onsiderre
TOPOGRAFIA. Prima parte. Prof. Roma Carmelo
 TOPOGRFI Prim prte TOPOGRFI Sommrio onversione tr sistemi di misur ngolri Funzioni goniometrihe tngente e otngente Teorem dei seni (o di Eulero) Teorem di rnot onversione tr sistemi di misur ngolri Sistemi
TOPOGRFI Prim prte TOPOGRFI Sommrio onversione tr sistemi di misur ngolri Funzioni goniometrihe tngente e otngente Teorem dei seni (o di Eulero) Teorem di rnot onversione tr sistemi di misur ngolri Sistemi
Formule di Gauss Green
 Formule di Guss Green In queste lezioni voglimo studire il legme esistente tr integrli in domini bidimensionli ed integrli urvilinei sull frontier di questi. In seguito i ouperemo del problem nlogo nello
Formule di Guss Green In queste lezioni voglimo studire il legme esistente tr integrli in domini bidimensionli ed integrli urvilinei sull frontier di questi. In seguito i ouperemo del problem nlogo nello
Definizione. Si chiama similitudine una corrispondenza biunivoca dal piano in sé tale che,
 CAPITOLO 6 LE SIMILITUDINI 6 Rihimi i teori Definizione Si him similituine un orrisponenz iunivo l pino in sé tle he presi ue punti qulunque A B el pino e etti A B i loro orrisponenti si h he esiste un
CAPITOLO 6 LE SIMILITUDINI 6 Rihimi i teori Definizione Si him similituine un orrisponenz iunivo l pino in sé tle he presi ue punti qulunque A B el pino e etti A B i loro orrisponenti si h he esiste un
Ellisse riferita al centro degli assi
 Appunti delle lezioni tenute in clsse: ellisse e iperole Ellisse riferit l centro degli ssi Dti due punti F ed F detti fuochi, l ellisse è il luogo geometrico dei punti P del pino per cui è costnte l somm
Appunti delle lezioni tenute in clsse: ellisse e iperole Ellisse riferit l centro degli ssi Dti due punti F ed F detti fuochi, l ellisse è il luogo geometrico dei punti P del pino per cui è costnte l somm
4 ; messo in forma = 2. 4 Le tangenti saranno: = x + 8. La circonferenza (Paolo Urbani prima stesura settembre 2002 aggiornamento novembre 2013)
 Fsio iproprio di rette prllele r: ipliit risult q r si h: q ; esso in for. onsiderndo he ( ;) q ( q) q e 8 q q q q 6q 6 q ± 6 q 8; q Le tngenti srnno: 8, ; L ironferenz (Polo Urni pri stesur settere ggiornento
Fsio iproprio di rette prllele r: ipliit risult q r si h: q ; esso in for. onsiderndo he ( ;) q ( q) q e 8 q q q q 6q 6 q ± 6 q 8; q Le tngenti srnno: 8, ; L ironferenz (Polo Urni pri stesur settere ggiornento
FUNZIONI SENO & COSENO TANGENTE & COTANGENTE
 FUNZINI SEN & SEN TNGENTE & TNGENTE DEFINIZINE DI SEN E SEN onsiderndo l ngolo =, trimo un erhio di rggio qulunque R = = e on entro sul vertie dell ngolo. Le intersezioni del erhio on le semirette dell
FUNZINI SEN & SEN TNGENTE & TNGENTE DEFINIZINE DI SEN E SEN onsiderndo l ngolo =, trimo un erhio di rggio qulunque R = = e on entro sul vertie dell ngolo. Le intersezioni del erhio on le semirette dell
Corso multimediale di matematica
 2006 GNIMETRI funzioni goniometriche di ngoli qulsisi rof. Clogero Contrino funzioni goniometriche di ngoli qulsisi er mplire il dominio delle funzioni goniometriche è necessrio che: Si estend il concetto
2006 GNIMETRI funzioni goniometriche di ngoli qulsisi rof. Clogero Contrino funzioni goniometriche di ngoli qulsisi er mplire il dominio delle funzioni goniometriche è necessrio che: Si estend il concetto
Ciro Baratto GONIOMETRIA TRIGONOMETRIA 799 ESERCIZI SVOLTI
 Ciro Brtto GONIOMETRIA TRIGONOMETRIA 99 ESERCIZI SVOLTI INTRODUZIONE Gli eserizi (n. 99) he seguono sono stti svolti per un migliore omprensione dell goniometri e dell trigonometri, erndo, in lrg misur,
Ciro Brtto GONIOMETRIA TRIGONOMETRIA 99 ESERCIZI SVOLTI INTRODUZIONE Gli eserizi (n. 99) he seguono sono stti svolti per un migliore omprensione dell goniometri e dell trigonometri, erndo, in lrg misur,
8 Equazioni parametriche di II grado
 Equzioni prmetrihe di II grdo Un equzione he oltre ll inognit (o lle inognite) ontiene ltre lettere (un o più) si die letterri o prmetri e le lettere sono himte, nhe, prmetri; si suppong he l equzione
Equzioni prmetrihe di II grdo Un equzione he oltre ll inognit (o lle inognite) ontiene ltre lettere (un o più) si die letterri o prmetri e le lettere sono himte, nhe, prmetri; si suppong he l equzione
j Verso la scuola superiore +l calcolo letterale Monomi Polinomi e prodotti notevoli Equazioni
 j Verso l suol superiore +l lolo letterle Monomi Polinomi e prodotti notevoli Equzioni Monomi Il monomio x 4 y è simile : x 4 y 5 +x 4 y x y Due monomi sono simili se hnno l prte letterle ugule e, siome
j Verso l suol superiore +l lolo letterle Monomi Polinomi e prodotti notevoli Equzioni Monomi Il monomio x 4 y è simile : x 4 y 5 +x 4 y x y Due monomi sono simili se hnno l prte letterle ugule e, siome
Maturità scientifica, corso di ordinamento, sessione ordinaria 2000-2001
 Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone Mturità scientific, corso di ordinmento, sessione ordinri 000-001 PROBLEMA 1 Si consideri l seguente relzione tr le vribili reli x, y: 1 1 1 +
Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone Mturità scientific, corso di ordinmento, sessione ordinri 000-001 PROBLEMA 1 Si consideri l seguente relzione tr le vribili reli x, y: 1 1 1 +
Teoremi di geometria piana
 l congruenz teoremi sugli ngoli γ teorem sugli ngoli complementri Se due ngoli sono complementri di uno stesso ngolo α β In generle: Se due ngoli sono complementri di due ngoli congruenti α γ β teorem
l congruenz teoremi sugli ngoli γ teorem sugli ngoli complementri Se due ngoli sono complementri di uno stesso ngolo α β In generle: Se due ngoli sono complementri di due ngoli congruenti α γ β teorem
Algebra Condizioni di Esistenza Equazioni di secondo grado Scomposizione di un trinomio di secondo grado Definizione di valore assoluto
 Alger Condizioni di Esistenz n N x D x A(x) on n pri D x 0 A x 0 tn f(x) f x + k se f(x) f x + k log A x B(x) A x > 0 A x B x > 0 f x α f x 0 on α > 0 irrz. f x α f x > 0 on α < 0 irrz. f x g x f x > 0
Alger Condizioni di Esistenz n N x D x A(x) on n pri D x 0 A x 0 tn f(x) f x + k se f(x) f x + k log A x B(x) A x > 0 A x B x > 0 f x α f x 0 on α > 0 irrz. f x α f x > 0 on α < 0 irrz. f x g x f x > 0
Area di una superficie piana o gobba 1. Area di una superficie piana. f x dx 0 e quindi :
 Are di un superficie pin o go Are di un superficie pin L're dell superficie del trpezoide si B ottiene pplicndo l seguente formul: f d [] A T e risult 0 [, ] è f f d 0 e quindi : [] f d f d f d f d c Nel
Are di un superficie pin o go Are di un superficie pin L're dell superficie del trpezoide si B ottiene pplicndo l seguente formul: f d [] A T e risult 0 [, ] è f f d 0 e quindi : [] f d f d f d f d c Nel
L IPERBOLE. x si sviluppano i prodotti notevoli; 25 y 8 si porta un radicale al 2 membro; 25 y si elevano i due membri al quadrato;
 L IPERBOLE L'IPERBOLE COME LUOGO GEOMETRICO L iperole è il luogo geometrio dei punti P del pino rtesino per i quli è ostnte l differenz delle distnze d due punti fissi, F ed F, detti fuohi. Il punto medio
L IPERBOLE L'IPERBOLE COME LUOGO GEOMETRICO L iperole è il luogo geometrio dei punti P del pino rtesino per i quli è ostnte l differenz delle distnze d due punti fissi, F ed F, detti fuohi. Il punto medio
corrispondenza dal piano in sé, che ad ogni punto P del piano fa corrispondere il punto P' in
 Cpitolo 5 Le omotetie 5. Richimi di teori Definizione Sino fissti un punto C del pino ed un numero rele. Si chim omoteti di centro C e rpporto ( che si indic con il simolo O, ) l corrispondenz dl pino
Cpitolo 5 Le omotetie 5. Richimi di teori Definizione Sino fissti un punto C del pino ed un numero rele. Si chim omoteti di centro C e rpporto ( che si indic con il simolo O, ) l corrispondenz dl pino
Circonferenza e cerchio La circonferenza e il cerchio Poligoni inscritti e circoscritti a una circonferenza
 ironferenz e erhio L ironferenz e il erhio Poligoni insritti e irosritti un ironferenz L ironferenz e il erhio Stilisi se le seguenti ffermzioni sono vere o flse. SEZ. M e f g h Il rpporto tr l lunghezz
ironferenz e erhio L ironferenz e il erhio Poligoni insritti e irosritti un ironferenz L ironferenz e il erhio Stilisi se le seguenti ffermzioni sono vere o flse. SEZ. M e f g h Il rpporto tr l lunghezz
LICEO SCIENTIFICO CLASSICO SCIENZE UMANE MARCONI DELPINO
 LICEO SCIENTIFICO CLASSICO SCIENZE UMANE MARCONI DELPINO RECUPERO ESTIVO PER LE CLASSI ^D- E SCIENTIFICO Argomenti d rivedere: I QUADRIMESTRE: ) Equzioni di secondo grdo e relzioni tr coefficienti e rdici
LICEO SCIENTIFICO CLASSICO SCIENZE UMANE MARCONI DELPINO RECUPERO ESTIVO PER LE CLASSI ^D- E SCIENTIFICO Argomenti d rivedere: I QUADRIMESTRE: ) Equzioni di secondo grdo e relzioni tr coefficienti e rdici
Lezione 7: Rette e piani nello spazio
 Lezione 7: Rette e pini nello spzio In quest lezione i metteremo in un riferimento rtesino ortonormle dello spzio. I primi oggetti geometrii he individuimo sono le rette e i pini. Per qunto rigurd le rette
Lezione 7: Rette e pini nello spzio In quest lezione i metteremo in un riferimento rtesino ortonormle dello spzio. I primi oggetti geometrii he individuimo sono le rette e i pini. Per qunto rigurd le rette
FUNZIONI MATEMATICHE. Una funzione lineare è del tipo:
 FUNZIONI MATEMATICHE Le relzioni mtemtihe utilizzte per desrivere fenomeni nturli, in iologi ome in ltre sienze, possono ovvimente essere le più svrite. Per lo più si trtt di equzioni lineri, qudrtihe,
FUNZIONI MATEMATICHE Le relzioni mtemtihe utilizzte per desrivere fenomeni nturli, in iologi ome in ltre sienze, possono ovvimente essere le più svrite. Per lo più si trtt di equzioni lineri, qudrtihe,
Grafici elementari 1 - geometria analitica
 Grfii elementri - geometri nliti Un equzione rppresent un funzione se è possiile metterl in form espliit (rivre l y) ottenendo un sol espressione. Un urv rppresent un funzione se, preso un qulsisi punto
Grfii elementri - geometri nliti Un equzione rppresent un funzione se è possiile metterl in form espliit (rivre l y) ottenendo un sol espressione. Un urv rppresent un funzione se, preso un qulsisi punto
Cinematica rotazionale. 28 febbraio 2009 PIACENTINO - PREITE (Fisica per Scienze Motorie)
 Cinemti rotzionle 8 febbrio 009 PIACENTINO - PEITE (Fisi per Sienze Motorie) 1 Moto Cirolre Uniforme Un oggetto he si muove su un ironferenz on un veloità ostntev, ompie unmotoirolreuniforme. Il modulo
Cinemti rotzionle 8 febbrio 009 PIACENTINO - PEITE (Fisi per Sienze Motorie) 1 Moto Cirolre Uniforme Un oggetto he si muove su un ironferenz on un veloità ostntev, ompie unmotoirolreuniforme. Il modulo
Si noti che da questa definizione segue che il punto C è il punto medio del segmento PP'. Figura 1
 APITOLO 3 LE SIMMETRIE 3. Richimi di teori Definizione. Si dto un punto del pino; si chim simmetri centrle di centro (che si indic con il simbolo s ) l corrispondenz dl pino in sé che d ogni punto P del
APITOLO 3 LE SIMMETRIE 3. Richimi di teori Definizione. Si dto un punto del pino; si chim simmetri centrle di centro (che si indic con il simbolo s ) l corrispondenz dl pino in sé che d ogni punto P del
1. Determinare e rappresentare nel piano cartesiano il luogo dei vertici delle parabole della famiglia.
 . Dt l'equzione: rppresentt in un sistem di oordinte rtesine ortogonli d prbole on sse prllelo ll'sse, determinre -in funzione del oeffiiente - i oeffiienti b e he individuno l fmigli delle prbole pssnti
. Dt l'equzione: rppresentt in un sistem di oordinte rtesine ortogonli d prbole on sse prllelo ll'sse, determinre -in funzione del oeffiiente - i oeffiienti b e he individuno l fmigli delle prbole pssnti
I.S.I. E. Fermi - Lucca Istituto Tecnico settore Tecnologico
 Anno scolstico / Progrmm di MATEMATICA Clsse : B Insegnnte : Ghilrducci Pol I.S.I. E. Fermi - Lucc Istituto Tecnico settore Tecnologico Equzioni e disequzioni di primo grdo : Equzioni intere frtte e letterli
Anno scolstico / Progrmm di MATEMATICA Clsse : B Insegnnte : Ghilrducci Pol I.S.I. E. Fermi - Lucc Istituto Tecnico settore Tecnologico Equzioni e disequzioni di primo grdo : Equzioni intere frtte e letterli
LAVORO PER IL RECUPERO DEL DEBITO MATEMATICA CLASSI 3 S.M. DA CONSEGNARE IL PRIMO GIORNO DI ATTIVITA DI SPORTELLO
 LAVORO PER IL RECUPERO DEL DEBITO MATEMATICA CLAI.M. DA CONEGNARE IL PRIMO GIORNO DI ATTIVITA DI PORTELLO DEVI RIOLVERE PRIMA DI TUTTO I PROBLEMI E GLI EERCIZI QUI ELENCATI. TERMINATI QUETI, RIOLVI ALCUNI
LAVORO PER IL RECUPERO DEL DEBITO MATEMATICA CLAI.M. DA CONEGNARE IL PRIMO GIORNO DI ATTIVITA DI PORTELLO DEVI RIOLVERE PRIMA DI TUTTO I PROBLEMI E GLI EERCIZI QUI ELENCATI. TERMINATI QUETI, RIOLVI ALCUNI
L IPERBOLE. x y 0 x 5 + y 0 = si sviluppano i prodotti notevoli; Cioè ( ) ( ) ( ) ( ) y = 8 si porta un radicale al 2 membro;
 L IPERBOLE L'IPERBOLE COME LUOGO GEOMETRICO L iperole è il luogo geometrio dei punti P del pino rtesino per i quli è ostnte l differenz delle distnze d due punti fissi, F ed F, detti fuohi. Il punto medio
L IPERBOLE L'IPERBOLE COME LUOGO GEOMETRICO L iperole è il luogo geometrio dei punti P del pino rtesino per i quli è ostnte l differenz delle distnze d due punti fissi, F ed F, detti fuohi. Il punto medio
Facoltà di Scienze della Formazione Corso di Laurea in Politica del Territorio. Dispense del Corso di GEOMETRIA
 Foltà di Sienze dell Formzione Corso di Lure in oliti del Territorio Dispense del Corso di GEOMETRIA (Dott. Ing. iemonte Andre) Assiom: proprietà ssunt ome ver e fondmentle Teorem: proprietà verifite on
Foltà di Sienze dell Formzione Corso di Lure in oliti del Territorio Dispense del Corso di GEOMETRIA (Dott. Ing. iemonte Andre) Assiom: proprietà ssunt ome ver e fondmentle Teorem: proprietà verifite on
1 Integrali doppi di funzioni a scala su rettangoli
 INEGRALI DOPPI L prim motivzione per lo studio degli integrli di funzioni di due vribili è il lolo di volumi, in nlogi on l pplizione degli integrli di funzioni di un vribile l lolo di ree. L proedur di
INEGRALI DOPPI L prim motivzione per lo studio degli integrli di funzioni di due vribili è il lolo di volumi, in nlogi on l pplizione degli integrli di funzioni di un vribile l lolo di ree. L proedur di
MATRICI E DETERMINANTI
 MTRICI E DETERMINNTI di vinenzo sudero 1 DEFINIZIONI Per mtrie si intende un tell di elementi ordinti per righe e per olonne Di un mtrie oorre speifire il numero di righe, di olonne e l insieme ui pprtengono
MTRICI E DETERMINNTI di vinenzo sudero 1 DEFINIZIONI Per mtrie si intende un tell di elementi ordinti per righe e per olonne Di un mtrie oorre speifire il numero di righe, di olonne e l insieme ui pprtengono
Test di autovalutazione
 UNITÀ ELEMENTI DI CALCOLO ALGEBRICO Test di utovlutzione 0 0 0 0 0 0 60 0 80 90 00 n Il mio punteggio, in entesimi, è n Rispondi ogni quesito segnndo un sol delle lterntive. n Confront le tue risposte
UNITÀ ELEMENTI DI CALCOLO ALGEBRICO Test di utovlutzione 0 0 0 0 0 0 60 0 80 90 00 n Il mio punteggio, in entesimi, è n Rispondi ogni quesito segnndo un sol delle lterntive. n Confront le tue risposte
Compito di matematica Classe III ASA 26 marzo 2015
 Compito di mtemtic Clsse III ASA 6 mrzo 05 Quesiti. Per quli vlori di l espressione può rppresentre l eccentricità di un ellisse? Dovrà risultre 0 < e
Compito di mtemtic Clsse III ASA 6 mrzo 05 Quesiti. Per quli vlori di l espressione può rppresentre l eccentricità di un ellisse? Dovrà risultre 0 < e
MATEMATICA Classe Prima
 Liceo Clssico di Treiscce Esercizi per le vcnze estive 0 MATEMATICA Clsse Prim Cpitolo Numeri nturli Primi ogni pgin del cpitolo Cpitolo Numeri nturli Primi ogni pgin del cpitolo Per gli llievi promossi
Liceo Clssico di Treiscce Esercizi per le vcnze estive 0 MATEMATICA Clsse Prim Cpitolo Numeri nturli Primi ogni pgin del cpitolo Cpitolo Numeri nturli Primi ogni pgin del cpitolo Per gli llievi promossi
ISTITUTO TECNICO INDUSTRIALE "E. Fermi" LUCCA Anno Scolastico 2017/2018 Programma di MATEMATICA classe prima Sez. G Insegnante: MUSUMECI LUCIANA
 ISTITUTO TENIO INDUSTILE "E. Fermi" LU nno Solstio / Progrmm di MTEMTI lsse prim Sez. G Insegnnte MUSUMEI LUIN Gli insiemi ppresentzione di un insieme. I sottoinsiemi. Le operzioni on gli insiemi unione
ISTITUTO TENIO INDUSTILE "E. Fermi" LU nno Solstio / Progrmm di MTEMTI lsse prim Sez. G Insegnnte MUSUMEI LUIN Gli insiemi ppresentzione di un insieme. I sottoinsiemi. Le operzioni on gli insiemi unione
Soluzione. Studiamo la funzione. Dominio: la funzione è definita in tutto R; Intersezione asse ascisse: ( x)
 Sessione ordinri LS_ORD Soluzione di De Ros Niol Soluzione Studimo l unzione Dominio: l unzione è deinit in tutto R; ; Intersezione sse sisse: Intersezioni sse delle ordinte: y ; Prità o disprità: l unzione
Sessione ordinri LS_ORD Soluzione di De Ros Niol Soluzione Studimo l unzione Dominio: l unzione è deinit in tutto R; ; Intersezione sse sisse: Intersezioni sse delle ordinte: y ; Prità o disprità: l unzione
Esercizi della 8 lezione sulla Geomeria Linere ESERCIZI SULLA CIRCONFERENZA ESERCIZI SULLA PARABOLA ESERCIZI SULL' ELLISSE ERCIZI SULL' IPERBOLE
 Eserizi dell lezione sull Geomeri Linere ESERCIZI SULLA CIRCONFERENZA ESERCIZI SULLA PARABOLA ESERCIZI SULL' ELLISSE ES ERCIZI SULL' IPERBOLE ESERCIZI SULLA CIRCONFERENZA. Determinre l equzione dell ironferenz
Eserizi dell lezione sull Geomeri Linere ESERCIZI SULLA CIRCONFERENZA ESERCIZI SULLA PARABOLA ESERCIZI SULL' ELLISSE ES ERCIZI SULL' IPERBOLE ESERCIZI SULLA CIRCONFERENZA. Determinre l equzione dell ironferenz
dr Valerio Curcio Le affinità omologiche Le affinità omologiche
 1 Le ffinità omologiche 2 Tringoli omologici: Due tringoli si dicono omologici se le rette congiungenti i punti omologhi dei due tringoli si incontrno in un medesimo punto. Principio dei tringoli omologici
1 Le ffinità omologiche 2 Tringoli omologici: Due tringoli si dicono omologici se le rette congiungenti i punti omologhi dei due tringoli si incontrno in un medesimo punto. Principio dei tringoli omologici
Unità Didattica N 11 Le equazioni di secondo grado ad una incognita
 Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit 0) L definizione di equzione di seondo grdo d un inognit 0) L risoluzione delle equzioni di
Unità Didtti N Le equzioni di seondo grdo d un inognit Unità Didtti N Le equzioni di seondo grdo d un inognit 0) L definizione di equzione di seondo grdo d un inognit 0) L risoluzione delle equzioni di
1. In un piano, riferito ad un sistema di assi cartesiani ortogonali (Oxy), sono assegnate le curve di equazione: y ax x b = + +
 . In un pino, riferito d un sistem di ssi crtesini ortogonli (O), sono ssegnte le curve di equzione:, dove, sono prmetri reli con. ) Determinre i vlori di per i quli queste curve hnno un punto di mssimo
. In un pino, riferito d un sistem di ssi crtesini ortogonli (O), sono ssegnte le curve di equzione:, dove, sono prmetri reli con. ) Determinre i vlori di per i quli queste curve hnno un punto di mssimo
UTILIA SULL INTEGRALE MULTIPLO SECONDO RIEMANN
 UTILIA SULL INTGRAL MULTIPLO SCONDO RIMANN Avvertenz: tutto iò detto nel seguito vle in R n e non solo in R 2. 1. INTGRAL DI RIMANN SU RTTANGOLI Un insieme R 2 si die essere un rettngolo (hiuso) se = [,b]
UTILIA SULL INTGRAL MULTIPLO SCONDO RIMANN Avvertenz: tutto iò detto nel seguito vle in R n e non solo in R 2. 1. INTGRAL DI RIMANN SU RTTANGOLI Un insieme R 2 si die essere un rettngolo (hiuso) se = [,b]
quattro trasformazioni
 ilo di rnot e un ilo termio ostituito d quttro trsformzioni p() reversibili di un gs perfetto : un espnsione isoterm d tempertur un espnsione dibti d un ompressione isoterm d tempertur un ompressione dibti
ilo di rnot e un ilo termio ostituito d quttro trsformzioni p() reversibili di un gs perfetto : un espnsione isoterm d tempertur un espnsione dibti d un ompressione isoterm d tempertur un ompressione dibti
Problema: Calcolo dell'area di una superficie piana
 Corso di Lure in Disegno Industrile Corso di Metodi Numerii per il Design Lezione 7 Novemre 00 Integrle definito F. Cliò Prolem: Clolo dell're di un superfiie pin Metodi Numerii per il Design - Lezione
Corso di Lure in Disegno Industrile Corso di Metodi Numerii per il Design Lezione 7 Novemre 00 Integrle definito F. Cliò Prolem: Clolo dell're di un superfiie pin Metodi Numerii per il Design - Lezione
1. Integrali impropri (o generalizzati)
 Corso di Lure in Ingegneri delle Teleomunizioni - A.A.- Tri del orso di Anlisi Mtemti L-B. Integrli impropri (o generlizzti) Riferimenti. Brozzi: PCAM, pr..8; Minnj: Mtemti Due, pr.. http://eulero.ing.unibo.it/~brozzi/scam/scam-tr.pdf.
Corso di Lure in Ingegneri delle Teleomunizioni - A.A.- Tri del orso di Anlisi Mtemti L-B. Integrli impropri (o generlizzti) Riferimenti. Brozzi: PCAM, pr..8; Minnj: Mtemti Due, pr.. http://eulero.ing.unibo.it/~brozzi/scam/scam-tr.pdf.
RECUPERO EQUAZIONI E DISEQUAZIONI CON COEFFICIENTI IRRAZIONALI
 I NUMERI REALI E I RADICALI Recupero RECUPERO EQUAZIONI E DISEQUAZIONI CON COEFFICIENTI IRRAZIONALI COMPLETA Risolvi l disequzione ( ). ( ) ( ) ( ) Elimin le prentesi clcolndo il prodotto. Applic l regol
I NUMERI REALI E I RADICALI Recupero RECUPERO EQUAZIONI E DISEQUAZIONI CON COEFFICIENTI IRRAZIONALI COMPLETA Risolvi l disequzione ( ). ( ) ( ) ( ) Elimin le prentesi clcolndo il prodotto. Applic l regol
a è detta PARTE LETTERALE
 I MONOMI Si die MONOMIO un espressione letterle in ui le unihe operzioni presenti sino il prodotto e l divisione. Esempio è detto COEFFICIENTE del monomio e è dett PARTE LETTERALE Un monomio si die ridotto
I MONOMI Si die MONOMIO un espressione letterle in ui le unihe operzioni presenti sino il prodotto e l divisione. Esempio è detto COEFFICIENTE del monomio e è dett PARTE LETTERALE Un monomio si die ridotto
Il moto rettilineo uniformemente accelerato è un moto che avviene su una retta con accelerazione costante. a = costante
 Prof.. Di Muro Moto rettilineo uniformemente ccelerto ( m.r.u.. ) Il moto rettilineo uniformemente ccelerto è un moto che iene su un rett con ccelerzione costnte. Dll definizione di ccelerzione t t t t
Prof.. Di Muro Moto rettilineo uniformemente ccelerto ( m.r.u.. ) Il moto rettilineo uniformemente ccelerto è un moto che iene su un rett con ccelerzione costnte. Dll definizione di ccelerzione t t t t
= det b, a, b, c R 3. In quest ottica, il determinante del terzo ordine e caratterizzato dalle seguenti proprieta : a a. c c
 Determinnti n = 3. Propriet Possimo rigurdre il determinnte di un mtrie del terzo ordine ome un funzione delle sue olonne: det b = det [, b,,, b, R 3. In quest otti, il determinnte del terzo ordine e rtterizzto
Determinnti n = 3. Propriet Possimo rigurdre il determinnte di un mtrie del terzo ordine ome un funzione delle sue olonne: det b = det [, b,,, b, R 3. In quest otti, il determinnte del terzo ordine e rtterizzto
(somma inferiore n esima), (somma superiore n esima).
 Clcolo integrle Appunti integrtivi lle dispense di Mtemtic ssistit rgomento 9 (Integrli definiti) e rgomento (Integrli impropri) cur di C.Znco (Il contenuto di questi ppunti f prte del progrmm d esme)
Clcolo integrle Appunti integrtivi lle dispense di Mtemtic ssistit rgomento 9 (Integrli definiti) e rgomento (Integrli impropri) cur di C.Znco (Il contenuto di questi ppunti f prte del progrmm d esme)
Geometria Analitica Domande, Risposte & Esercizi
 Geometri Anlitic Domnde, Risposte & Esercizi. Dre l definizione di iperole come luogo di punti. L iperole è un luogo di punti, è cioè un insieme di punti del pino le cui distnze d due punti fissi F e F
Geometri Anlitic Domnde, Risposte & Esercizi. Dre l definizione di iperole come luogo di punti. L iperole è un luogo di punti, è cioè un insieme di punti del pino le cui distnze d due punti fissi F e F
, x 2. , x 3. è un equazione nella quale le incognite appaiono solo con esponente 1, ossia del tipo:
 Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
INSIEMI, RETTA REALE E PIANO CARTESIANO
 INSIEMI, ETTA EALE E PIANO CATESIANO ICHIAMI DI TEOIA SUGLI INSIEMI Un insieme E è definito ssegnndo i suoi elementi, tutti distinti tr loro: se x è un elemento di E scrivimo x E, mentre, se non lo è,
INSIEMI, ETTA EALE E PIANO CATESIANO ICHIAMI DI TEOIA SUGLI INSIEMI Un insieme E è definito ssegnndo i suoi elementi, tutti distinti tr loro: se x è un elemento di E scrivimo x E, mentre, se non lo è,
Appunti di Matematica Computazionale Lezione 1. Equazioni non lineari. Consideriamo il problema della determinazione delle radici dell equazione
 Appunti di Mtemti Computzionle Lezione Equzioni non lineri Considerimo il prolem dell determinzione delle rdii dell equzione dove è un funzione definit in [,]. Teorem: Zeri di unzioni Continue Si un funzione
Appunti di Mtemti Computzionle Lezione Equzioni non lineri Considerimo il prolem dell determinzione delle rdii dell equzione dove è un funzione definit in [,]. Teorem: Zeri di unzioni Continue Si un funzione
Equazioni di secondo grado Capitolo
 Equzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Equzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
7 Simulazione di prova d Esame di Stato
 7 Simulzione di prov d Esme di Stto Problem 1 Risolvi uno dei due problemi e 5 dei 10 quesiti in cui si rticol il questionrio Si consideri l fmigli di funzioni definite d { f n () = n (1 ln ) se 0,n N
7 Simulzione di prov d Esme di Stto Problem 1 Risolvi uno dei due problemi e 5 dei 10 quesiti in cui si rticol il questionrio Si consideri l fmigli di funzioni definite d { f n () = n (1 ln ) se 0,n N
Capitolo 2. Il problema del calcolo delle aree
 Cpitolo 2 Il prolem del clcolo delle ree Introduzione Il prolem del clcolo delle ree nsce più di 2000 nni f qundo i greci tentrono di clcolre le ree con un metodo detto di esustione. Tle metodo può essere
Cpitolo 2 Il prolem del clcolo delle ree Introduzione Il prolem del clcolo delle ree nsce più di 2000 nni f qundo i greci tentrono di clcolre le ree con un metodo detto di esustione. Tle metodo può essere
Angoli e funzioni goniometriche
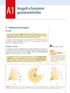 ngoli e funzioni goniometrihe. Definizioni di ngolo ngolo L geometri definise ngolo isun delle prti del pino in ui esso è diviso d due semirette usenti d uno stesso punto ; il punto si die vertie dell
ngoli e funzioni goniometrihe. Definizioni di ngolo ngolo L geometri definise ngolo isun delle prti del pino in ui esso è diviso d due semirette usenti d uno stesso punto ; il punto si die vertie dell
Il problema delle aree. Metodo di esaustione.
 INTEGRALE DEFINITO. DEFINIZIONE E SIGNIFICATO GEOMETRICO. PROPRIETA DELL INTEGRALE DEFINITO. FUNZIONE INTEGRALE. TEOREMA DELLA MEDIA. TEOREMA FONDAMENTALE DEL CALCOLO INTEGRALE. FORMULA DI LEIBNITZ NEWTON.
INTEGRALE DEFINITO. DEFINIZIONE E SIGNIFICATO GEOMETRICO. PROPRIETA DELL INTEGRALE DEFINITO. FUNZIONE INTEGRALE. TEOREMA DELLA MEDIA. TEOREMA FONDAMENTALE DEL CALCOLO INTEGRALE. FORMULA DI LEIBNITZ NEWTON.
). Poiché tale funzione è una parabola, il suo
 PROBLEMA ) Il rggio dell circonferenz di centro B vri tr i vlori: x b) ( x x ) ( PQCR) = ( ABC) ( APR) ( BPQ) = ( x) x = + 8 6 8 I vlori di x che rendono minim o mssim l funzione rendono, rispettivmente,
PROBLEMA ) Il rggio dell circonferenz di centro B vri tr i vlori: x b) ( x x ) ( PQCR) = ( ABC) ( APR) ( BPQ) = ( x) x = + 8 6 8 I vlori di x che rendono minim o mssim l funzione rendono, rispettivmente,
c a (seno di alfa); (coseno di alfa); (tangente di alfa).
 Sito Personle di Ettore Limoli Lezioni di Mtemtic Prof. Ettore Limoli Sommrio Elementi di trigonometri... 1 Angoli e loro misur... Funzioni e loro grfici... 4 Usre i grfici... 5 Funzioni inverse delle
Sito Personle di Ettore Limoli Lezioni di Mtemtic Prof. Ettore Limoli Sommrio Elementi di trigonometri... 1 Angoli e loro misur... Funzioni e loro grfici... 4 Usre i grfici... 5 Funzioni inverse delle
Disequazioni irrazionali n a( x)
 Formulrio RICHIAMI DI ALGERA... I rdili... Il vlore ssoluto... Le equzioni di seondo grdo... Regole di somposizione dei polinomi... RICHIAMI DI GEMETRIA EUCLIDEA...4 Perimetri ed ree e di lune figure pine...5
Formulrio RICHIAMI DI ALGERA... I rdili... Il vlore ssoluto... Le equzioni di seondo grdo... Regole di somposizione dei polinomi... RICHIAMI DI GEMETRIA EUCLIDEA...4 Perimetri ed ree e di lune figure pine...5
CALCOLARE L AREA DI UNA REGIONE PIANA
 INTEGRALI Integrle definito e re con segno Primitiv di un funzione e integrle indefinito Teorem fondmentle del clcolo integrle Clcolo di ree Metodi di integrzione: per prti e per sostituzione CALCOLARE
INTEGRALI Integrle definito e re con segno Primitiv di un funzione e integrle indefinito Teorem fondmentle del clcolo integrle Clcolo di ree Metodi di integrzione: per prti e per sostituzione CALCOLARE
Risolvere gli esercizi proposti e rispondere a 4 quesiti scelti all interno del questionario. sin = x
 Risolvere gli esercizi proposti e rispondere quesiti scelti ll interno del questionrio Clcolre l derivt delle seguenti unzioni cos cos sin sin ( cos ) cos ( cos )( sin ) sin sin cos sin cos ( cos ) ( cos
Risolvere gli esercizi proposti e rispondere quesiti scelti ll interno del questionrio Clcolre l derivt delle seguenti unzioni cos cos sin sin ( cos ) cos ( cos )( sin ) sin sin cos sin cos ( cos ) ( cos
Equazioni parametriche di primo grado
 Polo Sivigli Equzioni prmetriche di primo grdo Premess Come si s dll lgebr elementre, si chim equzione un uguglinz fr due espressioni letterli che si verific soltnto ttribuendo prticolri vlori lle lettere,
Polo Sivigli Equzioni prmetriche di primo grdo Premess Come si s dll lgebr elementre, si chim equzione un uguglinz fr due espressioni letterli che si verific soltnto ttribuendo prticolri vlori lle lettere,
Geometria solida Rette e piani nello spazio + poliedri + solidi di rotazione
 Geometri solid ette e pini nello spzio + poliedri + solidi di rotzione ette e pini nello spzio tilisi se le seguenti ffermzioni sono vere o flse. EZ. d e e tre rette nello spzio sono tr loro prllele, llor
Geometri solid ette e pini nello spzio + poliedri + solidi di rotzione ette e pini nello spzio tilisi se le seguenti ffermzioni sono vere o flse. EZ. d e e tre rette nello spzio sono tr loro prllele, llor
Calcolo integrale per funzioni di una variabile
 Clolo integrle per unzioni di un vriile Clolo integrle Integrle deinito Si :[,] R, limitt ξ ξ ξ ξ 4 ξ 5 = 4 5 = Costruimo l somm di Cuhy-Riemnn n n S n j j j j j n j Dove l suddivisione dell intervllo
Clolo integrle per unzioni di un vriile Clolo integrle Integrle deinito Si :[,] R, limitt ξ ξ ξ ξ 4 ξ 5 = 4 5 = Costruimo l somm di Cuhy-Riemnn n n S n j j j j j n j Dove l suddivisione dell intervllo
