b a J(y) = y (x) 2 dx.
|
|
|
- Isabella Carrara
- 7 anni fa
- Visualizzazioni
Transcript
1 1. Il clcolo delle vrizioni Per illustrre lcuni concetti di questo importnte settore dell nlisi e dell mtemtic pplict prtimo d un esempio molto semplice. Considerimo l clsse di funzioni A = {y(x) C 1 [, b]; y() = y, y(b) = y b } e l ppliczione J : A IR 1 definit trmite y (x) 2 dx. Ci chiedimo se esiste in A il minimo ssoluto di J(y) e cioè un funzione ȳ A tle che J(y) J(ȳ) per ogni y A. Per il teorem fondmentle del clcolo bbimo, utilizzndo l diseguglinz di Cuchy Schwrtz, y b y = Ne segue ( /2 b y (x)dx y (x) dx) 2 (b ) 1/2. (y b y ) 2 b y (x) 2 dx per tutte le funzioni dell clsse mmissibile. D ltr prte, se ȳ(x) = y(b) y() (x ) + y(), b bbimo subito J(ȳ) = (y b y ) 2 b. Quindi ȳ(x) relizz il minimo ssoluto del funzionle nell clsse indict. Possimo nche ffrontre il problem in modo diverso e più costruttivo. Si ȳ(x) un funzione di clsse C 2 [, b] pprtenente ll clsse delle mmissibili e h(x) un funzione di clsse C 1 [, b] tle che h() =, h(b) =. È immedito verificre che l funzione ȳ(x) + h(x) descrive, l vrire di h(x), l clsse delle mmissibili. Considerimo l incremento del funzionle J(ȳ + h) J(ȳ) = 2 ȳ h dx + h 2 dx = (integrndo per prti e tenendo conto che h() = h(b) = ) = 2 ȳ hdx + 1 h 2 dx.
2 D ltr prte, se sceglimo ȳ in modo d essere l soluzione (unic) del problem ȳ = y() = y y(b) = y b, bbimo J(ȳ + h) J(ȳ) = Quindi ȳ(x) è il minimo ssoluto cercto. h 2 dx. Esercizio. Provre che esiste il minimo ssoluto del funzionle y (x) p dx nell clsse A = {y(x) C 1 [, b] ; y() = y, y(b) = y b } qundo 1 p <. Si consigli di utilizzre l diseguglinz di Hölder. Esercizio. Esiste il minimo ssoluto del funzionle dell esercizio precedente nell clsse A qundo < p < 1? Esercizio. Fr tutte le curve del pino che congiungono i punti (, y ), (b, y b ) e che sono dei grfici di funzioni C 1 [, b] trovre quell di lunghezz minim e provre che è unic. Si trtt evidentemente di cercre il minimo del funzionle 1 + y (x) 2 dx nell solit clsse A. Si consigli di pplicre il teorem fondmentle del clcolo ll funzione g(t) = (b )(t ) + (y b y b )(y(t) y ). 2. Alcuni problemi storici Dopo questi esempi elementri vle l pen di prire un piccol prentesi storic. Forse il più fmoso problem di clcolo delle vrizioni è quello dell brchistocron proposto nel 1696 d Giovnni Bernoulli i mtemtici d Europ e risolto d I. Newton. Considerimo in un pino verticle con sse Oy verticle e orientto verso il bsso due punti P 1 = (x 1, y 1 ) e P 2 = (x 2, y 2 ) con x 2 > x 1, y 1 > y 2 e si y(x) C 1 [x 1, x 2 ] un ssegnt funzione tle che y(x 1 ) = y 1, y(x 2 ) = y 2, y(x) > y 1 per x (x 1, x 2 ]. 2
3 Un punto P di mss m è libero di muoversi senz ttrito sul grfico dell y(x) sotto l zione dell sol forz peso. Scrivendo l integrle dell energi e seprndo le vribili è fcile clcolre il tempo di cdut che il punto impieg per ndre d P 1 P 2. Si trov T = 1 x2 1 + y (x) 2 2g y(x) y1 + α x 1 dove α = 1 2g v o 2. Ad ogni funzione dell clsse delle mmissibili il funzionle J(y) ssoci il tempo di cdut. Ci chiedimo se esist un tempo minimo di cdut. Il problem dell superficie di rotzione di re lterle minim Fcendo ruotre il grfico di un funzione y(x) C 1 [, b] positiv ttorno ll sse x si gener un superficie di rotzione l cui re lterle è dt, come è noto, d L clsse delle mmissibili è ncor Are Lterle = 2π y 1 + y (x) 2 dx. A = {y(x) C 1 [, b] ; y() = y, y(b) = y b, y(x) > }. È intuitivmente chiro che in certi csi l soluzione (non più pprtenente ll clsse delle mmissibili) del problem di minimo srà dt d due cerchi prlleli di rggi y() e y(b). Il problem del solido di rotzione di minim resistenz Si cerc il solido di rivoluzione che incontr l minim resistenz qundo si muove di moto uniforme in un mezzo resistente come l ri. L formulzione dt d Newton questo problem comport l minimizzzione del funzionle nell clsse x 1 + y (x) 2 A = {y(x) C 1 [, b] ; y() = y, y(b) = y b, y(x) }. Il problem, oltre l vlore storico, è interessnte perché mette in luce un difficoltà tipic: è inftti privo si di minimo che di mssimo ssoluto nell clsse A, che quindi deve essere opportunmente ristrett. 3
4 Il problem di Didone Nell clsse B di tutte le curve pine, semplici, rettificbili, chiuse di dt lunghezz L, trovre quell che rcchiude l porzione di pino di re A mssim. Il problem differisce di precedenti poiché l clsse delle mmissibili non è compost d grfici e per l condizione ggiuntiv dell lunghezz prescritt. Se ccettimo (vedi l dimostrzione più vnti) l vlidità dell diseguglinz isoperimetric (1) L 2 4π A l soluzione del problem è immedit. Possimo inftti definire il funzionle J(C) = A C B. Per l (1) bbimo J(C) L2 4π per ogni C B. D ltr prte se C = C, dove C è il cerchio di rggio R = L/2π, ottenimo J C = L2 4π e quindi C è l soluzione del problem. Possimo formulre il problem di Didone nche nell mbito dei grfici cercndo il mssimo del funzionle nell clsse di mmissibili y(x)dx A = {y(x) C 1 [, ], y( ) = y() =, 1 + y (x) 2 dx = L} con l condizione L 2. Si trov ovvimente un settore circolre. Esempio. Qule esempio di problem isoperimetrico elementrmente risolubile cerchimo il minimo del funzionle J(q) = nell clsse di mmissibili q (t) 2 dt A = {q(t) C 1 [, 1], q() = 1, q(1) = 6, q(t)dt = 3}. Si q(t) un funzione mmissibile di clsse C 2 [, 1] e considerimo un funzione h(t) C 1 [, 1] tle che h() = h(1) = 4 h(t)dt =.
5 Al vrire di h(t) l funzione q(t) + h(t) gener l clsse delle mmissibili. Abbimo, integrndo per prti, J( q + h) J( q) = 2 q h dt + h 2 dt = 2 q hdt + h 2 dt. Poiché h(t)dt = il termine 2 q hdt è nullo se prendimo q = C 1. Integrndo bbimo q(t) = 2 t2 + bt + c. Le costnti, b, c si clcolno con le condizioni q() = 1, q(1) = 6, q(t)dt = 3 e si trov q(t) = 3t2 + 2t + 1 che dà il minimo ssoluto. È fcile vedere che le funzioni C 1 sono indegute nche per trttre situzioni molto semplici. Cerchimo, per esempio, il minimo ssoluto del funzionle J(q) = 2 q 2 (1 q ) 2 dt con le condizioni q() = q(2) = 1. È evidente che tutte le spezzte di estremi (, ) e (2, 1) e lti prlleli o ll sse t o ll rett q = t rendono nullo il funzionle, d ltr prte J(q). Ognun di queste spezzte fornisce quindi un minimo ssoluto che non è C 1. Per formulre problemi di questo tipo dobbimo definire nuove clssi di funzioni. 3. Funzioni continue trtti e funzioni C 1 trtti Indicheremo con D [, b] l totlità delle funzioni continue in [, b] eccetto, l più, un numero finito di punti in ciscuno dei quli esistono finiti i limiti destro e sinistro dell funzione. D 1 [, b] srà l clsse delle funzioni continue in [, b], derivbili con derivt continu eccetto, l più, un numero finito di vlori in ciscuno dei quli esistono finiti i limiti destro e sinistro dell derivt. Questo, come subito segue dl teorem di Lgrnge, implic che in ciscuno dei punti di discontinuità dell derivt esiste l derivt destr e sinistr. Se q(t) D [, b] bbimo φ(t) = t q(z)dz D 1 [, b]. Inoltre φ (t) = q(t) eccetto gli eventuli punti di discontinuità di q(t) (e.e.p.d.d.). Come è noto, se u(t), v(t) D 1 [, b], vle l formul di integrzione per prti (1) u(t)v (t)dt = u (t)v(t)dt + [u(t)v(t)] b. 5
6 Un clsse di mmissibili rgionevole per l esempio precedente è quindi A = {y(x) D 1 [, b]; y() = y, y(b) = y b }. In certi csi nche le funzioni C 1 trtti sono indegute. Si consideri per esempio il funzionle x 2/3 y 2 dx con le condizioni y() =, y(1) = 1. È fcile vedere che ỹ(x) = x 1/3 fornisce il minimo ssoluto di J(y), m evidentemente ỹ(x) non pprtiene ll clsse D 1 [, b]. Esiste nche un motivo più profondo per llrgre ulteriormente l clsse delle mmissibili ed è l qusi impossibilità di dimostrre teoremi di esistenz del minimo nell clsse D 1 [, b]. Conviene, per questi motivi, introdurre un ulteriore clsse di funzioni. Le funzioni ssolutmente continue Un funzione q(t) si dice ssolutmente continu se per ogni ɛ > esiste δ(ɛ) tle che per ogni sistem finito {(α k, β k )} di sottointervlli perti e disgiunti di [, b] tli che si h N β k α k < δ(ɛ) k=1 N q(β k ) q(α k ) < ɛ. k=1 Indicheremo l totlità delle funzioni ssolutmente continue con AC[, b]. Le funzioni di D 1 [, b] sono ssolutmente continue. Se un funzione f(t) è integrbile secondo Lebesgue, e cioè f(t) L 1 (, b), l funzione q(t) = t f(z)dz è ssolutmente continu, come subito segue dll ssolut continuità dell integrle di Lebesgue. Vicevers, se φ(t) AC[, b], l derivt φ (t) di φ(t) (limite del rpporto incrementle) esiste qusi ovunque, eccetto in punti di un insieme di misur null, e inoltre φ (t) L 1 (, b), mentre vle l formul fondmentle del clcolo φ(t) = φ() + 6 t φ (z)dz.
7 Per le funzioni ssolutmente continue, vle ncor l formul di integrzione per prti (2). 4. Il problem semplice del clcolo delle vrizioni Dt un funzione L(t, q, z) C 1 ([, b] R R), che chimeremo funzione lgrngin, considerimo il funzionle (1) J(q) = definito in un delle seguenti clssi L(t, q(t), q (y))dt A 1 = {q(t) D 1 [, b], q() = q, q(b) = q b } (problem con estremi fissti) A 2 = {q(t) D 1 [, b], q() = q } (problem con un estremo libero) A 3 = {q(t) D 1 [, b]} (problem con estremi liberi). lsci come esercizio Useremo i seguenti lemmi, l cui dimostrzione si Lemm 1. Se f(t) D [, b] tle che f(t) e f(t)dt =, llor f(t) = eccetto gli eventuli punti di discontinuità. Lemm 2. Se f(t) L 1 [, b] tle che f(t) e f(t)dt =, llor f(t) = qusi ovunque. 7
8 5. Funzionli inferiormente limitti, m privi di minimo ssoluto Il seguente esempio è stto proposto d Weierstrss in relzione l principio di Dirichlet. Considerimo il funzionle J(q) = 1 t 2 q 2 dt nell clsse A = {q(t) D 1 [, b]; q( 1) = 1 q(1) = 1}. Provimo intnto che l estremo inferiore del funzionle nell clsse A è zero. Evidentemente J(q). D ltr prte per l successione di funzioni mmissibili q n (t) = 1 nt se 1 t 1 n se 1 n < t < 1 n 1 se 1 n < t < 1 bbimo Ne segue che lim J(q n) =. n inf{j(q); q A} =. Supponimo per ssurdo che esist il minimo ssoluto q(t) A del funzionle. Può solo essere J( q) = e cioè 1 t 2 q 2 (t)dt =. D ltr prte l funzione t 2 q 2 (t) è continu trtti e non negtiv, per cui eccetto gli eventuli punti di discontinuità si h q (t) =. Tenendo conto che q(t) è un funzione continu, vremo che q(t) è costnte, ftto questo incomptibile con le condizioni per t = 1 e t = 1. Il funzionle è quindi privo di minimo ssoluto. Il rgionmento può essere fcilmente dttto l cso in cui l clsse delle funzioni mmissibili é:. A = {q(t) C 1 [, b]; q( 1) = 1 q(1) = 1}. 8
9 Come secondo esempio considerimo il funzionle J(q) = [ (q 2 1) 2 + q 2] dt nell clsse A = {q(t) D 1 [, b]; q() =, q(1) = }. Anche questo funzionle è privo di minimo ssoluto in A. Inftti inf{j(q); q A} =. Bst osservre che J(q) e considerre l successione di funzioni mmissibili q n (t) = t sign sin 2π2 n 1 τdτ i cui grfici sono riportti nell figur per n = 1, 2, 3, 4. Abbimo q 2 n (t) = 1, per cui J(q n ) 1 n 2. Ne segue inf{j(q); q A} =. Supponimo per ssurdo che esist il minimo ssoluto q(t) del funzionle. Deve essere J( q) = e cioè [ ( q 2 1) 2 + q 2] dt =. Come ulteriore esempio esminimo il funzionle J(q) = q2 + q 2 dt e provimo che è privo di minimo ssoluto nell clsse A 1 = {q(t) D 1 [, 1], q() =, q(1) = 1}. Inftti J(q) q (t)dt = 1 per ogni q(t) A 1. 9
10 M l successione di funzioni q k (t) = se t 1 1/k, q k (t) = 1 k(t 1) se 1 1/k < t 1, è tle che J(q k ) se k. Quindi inf{j(q); q A 1 } = 1. Se, per ssurdo, esistesse un minimo ssoluto q(t) del funzionle, vremmo [ q(t)2 + q (t) 2 q (t)] dt = d cui segue q(t) 2 + q (t) 2 q (t) = e nche q(t) 2 =. Questo è incomptibile con le condizioni per t = e t = 1. Esercizio. Provre che il funzionle y 2 dx è privo di minimo ssoluto nell clsse A 1 = {y(x) D 1 [, 1], y() =, y(1) = 1}. Esercizio. Provre che il funzionle 2 (y 4 6y 2 dx) h minimi ssoluti nell clsse A 1 = {y(x) D 1 [, 2], ȳ() = y(2) = }. Trovrli e trovre il vlore numerico di tle minimo. Riprendimo in esme il funzionle che interviene nel problem del solido di rotzione di minim resistenz e cioè x dx 1 + y 2 (x) nell clsse A 1 = {y(x) D 1 [, ], y(x), y() =, y() = b}. Provimo che J(y) è privo di minimo ssoluto. Abbimo intnto J(y) per ogni y A 1. Inoltre, se considerimo l successione di funzioni mmissibili y n (x) = 2nx/ qundo x /2, y n (x) = 2(b n)x/ se /2 < x, trovimo subito J(y n ) per n. Quindi inf{j(y), y A 1 } =. Se per ssurdo esiste ȳ(x) A 1 tle che J(ȳ) =, si h nche x/(1 + ȳ 2 ) =, e questo non può essere. Occorre, per 1
11 dre senso l problem, restringere l clsse delle funzioni mmissibili ggiungendo l condizione y (x). Esercizio. Mostrre che il funzionle J(y) è nche privo di mssimo ssoluto. 6. Mssimi e minimi reltivi deboli e forti Oltre i minimi e mssimi ssoluti per il problem semplice del clcolo delle vrizioni si pongono nche le seguenti definizioni: q(t) A k è un minimo reltivo forte per J(y) nell clsse A k, (k = 1, 2, 3, ) se esiste ρ > tle che per ogni q(t) N ρ () ( q) A k si h J(q) J( q), dove N () ρ ( q) = {q(t) D 1 [, b]; q(t) q(t) < ρ}. Diremo che q(t) è un minimo reltivo debole per J(q) in un delle clssi A k se esiste ρ > tle che per ogni q(t) N ρ (1) ( q) A k si h J(q) J( q), dove N (1) ρ ( q) = {q(t) D 1 [, b]; q(t) q(t) < ρ, q (t) q (t) < ρ}. Anloghe definizioni si dnno per i mssimi reltivi deboli e forti. È evidente che un minimo (mssimo) reltivo forte è nche un minimo (mssimo) reltivo debole, m non vicevers, come mostr il seguente Esempio. J(q) = (q 2 + q 3 )dt nell clsse A 1 = {q(t) D 1 [1, ], q() =, q(1) = }. È immedito verificre che q(t) = per ogni t [, 1] è un minimo reltivo debole per J(y). Bst inftti prendere ρ = 1/2 nell definizione. D ltr prte q(t) non è un minimo reltivo forte. Per dimostrre questo ftto occorre provre che per ogni ρ > esiste q(t) N ρ () ( q) tle che J(q) < J( q). Considerimo tl fine l successione di funzioni mmissibili: q ɛ (t) = ɛt/(1 ɛ 2 ) se t 1 ɛ 2, q ɛ (t) = (1 t)/ɛ se 1 ɛ 2 t 1. Trovimo subito J(q ɛ ) qundo ɛ +. Poiché q ɛ (t) se ɛ +, concludimo che q(t) non è un minimo reltivo forte. 7. Condizione necessri perché un funzione mmissibile si un minimo reltivo debole in un delle clssi A 1, A 2 o A 3 11
12 Supponimo che q(t) A 1 si un minimo reltivo debole di J(q) = L(t, q, q )dt nell clsse A 1. Se fissimo un funzione η(t) D 1 [, b] tle che η() = e η(b) =, l funzione q(t)+ɛη(t) pprtiene per ogni ɛ d A 1. Ricordndo l definizione di minimo reltivo debole esiste, ɛ > tle che se ɛ ɛ, llor q(t)+ɛη(t) N ρ (1) ( q) A 1, dove ρ è l costnte di cui si prl nell definizione di minimo reltivo debole. L funzione dell vribile rele g(ɛ) = J( q + ɛη) h per ɛ = un minimo reltivo. D ltr prte, per il teorem di derivzione, sotto il segno di integrle g () esiste e si h g () =. Il clcolo di g () mostr che si h g () = J 1 ( q, η) = dove bbimo posto per comodità [ˆLq (t)η(t) + ˆL q (t)η (t)] dt ˆL q (t) = L q (t, q(t), q (t)) ˆLq (t) = L q (t, q(t), q (t)). Concludimo con il seguente Lemm. Condizione necessri perché q(t) si un minimo (o mssimo) reltivo debole del funzionle J(q) nell clsse A 1 è che si bbi (I) J 1 ( q, η) = per ogni η(t) D 1 [, b] tle che η() =, η(b) =. In modo nlogo bbimo il Lemm. Condizione necessri perché q(t) si un minimo (o mssimo) reltivo debole del funzionle J(q) nell clse A 2 è che vlg (II) J 1 ( q, η) = per ogni η(t) D 1 [, b] tle che η() =. Infine vle il Lemm. Condizione necessri perché q(t) si un minimo (o mssimo) reltivo debole del funzionle J(q) nell clse A 3 è che si bbi (III) J 1 ( q, η) = per ogni η(t) D 1 [, b]. L espressione J 1 ( q, η) si chim vrizione prim del funzionle e i lemmi precedenti sono l nlogo del teorem di Fermt per le funzioni di vribile rele. 12
13 Utilizzndo i due lemmi che seguono ricveremo dlle condizioni (I), (II) e (III) ulteriori condizioni necessrie. Lemm (Fondmentle del clcolo delle vrizioni). Se f(t) C [, b] soddisf l condizione (1) f(t)η(t)dt = per ogni funzione η(t) D 1 [, b] tle che η() =, η(b) =, si h f(t) = in [, b]. Dim. Supponimo che esist t (, b) tle che f( t), per esempio f( t) >. Per l permnenz del segno delle funzioni continue esiste un intervllo (ξ, ξ 1 ) contenente t tle che f(t) > in (ξ, ξ 1 ). Sceglimo nell (1) un funzione η 1 (t) così definit: η 1 (t) = in [, b]\(ξ, ξ 1 ) e η 1 (t) = (t ξ ) 2m (t ξ 1 ) 2m per t (ξ, ξ 1 ) con m 1. Evidentemente η 1 (t) D 1 [, b] e η 1 () = η 1 (b) =. D ltr prte (2) in contrsto con (1). f(t)η 1 (t)dt > Lemm (Du Boys Reymond). Se f(t) D [, b] è tle che (3) f(t)η (t)dt = per ogni η(t) D 1 [, b], η() = η(b) = l funzione f(t) è costnte eccetto gli eventuli punti di discontinuità che sono quindi punti di discontinuità eliminbile. Dim. Definimo C = (b ) 1 η(t) = f(t)dt e considerimo l funzione (f(τ) C)dt. Abbimo η(t) D 1 [, b] e nche η() = η(b) =, η (t) = f(t) C. Per l (3) vle = quindi f(t) = C e.e.p.d.d. f(t)(f(t) C)dt = (f(t) C) 2 dt + C (f(t) C + C)(f(t) C)dt = (f(t) C)dt = 13 (f(t) C) 2 dt
14 8. Prim form integrle dell equzione di Eulero Teorem Si L(t, q, q ) C 1 [, b] R 1 R 1 ), q(t) D 1 [, b] e vlg (I) J 1 ( q, η) = per ogni η(t) D 1 [, b] tle che η() =, η(b) = esiste un costnte C tle che (1) ˆLq (t) = t ˆL q (τ)dτ + C C = ˆL q () e.e.p.d.d. di q (t) ˆL q (t) = L q (t, q(t), q (t)) ˆLq (t) = L q (t, q(t), q (t)). Dim. 1) Considerimo preliminrmente il teorem in ipotesi più restrittive e precismente L(t, q, q ) C 2 ([, b] R 1 R 1 ), q(t) C 2 [, b]. Si trtt di ipotesi innturli (specilmente l second), m legittime. Possimo integrre per prti nel secondo termine dell relzione [ˆLq (t)η(t) + ˆL q (t)η (t)] dt per ogni η(t) D 1 [, b] tle che η() =, η(b) = e ottenere [ ˆL q (t) d ] dt ˆL q (t) η (t)dt = per ogni η(t) D 1 [, b] tle che η() =, η(b) =. Per il lemm fondmentle del clcolo delle vrizioni bbimo (2) ˆLq (t) d dt ˆL q (t) =. Pensndo l (2) come un equzione del secondo ordine in q(t), ess coincide con l equzione di Lgrnge dei sistemi con un sol grdo di libertà. Integrndo l (2) fr e t ottenimo l (1). L integrzione per prti è res lecit dll ipotesi q(t) C 2 [, b]. Se supponimo semplicemente q(t) D 1 [, b] occorre procedere nel modo seguente: definimo l funzione Φ(t) = ˆL q (τ)dτ. Poiché ˆL q (t) D [, b] si h Φ(t) D 1 [, b] e nche Φ (t) = ˆL q (t), eccetto gli eventuli punti di discontinuità di q (t). Abbimo [ Φ (t)η(t) + ˆL ] q (t)η (t) dt = per ogni η(t) D 1 [, b] tle che η() =, η(b) =. L integrzione per prti nel primo termine è or lecit. Ottenimo, tenendo conto che η() =, η(b) =, [ Φ(t) + ˆL ] q (t) η (t)dt = per ogni η(t) D 1 [, b] tle che η() =, η(b) =. Dl lemm di Du Boys Reymond segue l tesi (1). 14
15 Esercizio. Provre che il funzionle 1 + x + x2 y 2 dx h minimo ssoluto nell clsse A 1 = {y(x) D 1 [, b], y() = 1, y(1) = } e trovrlo. Vedimo quli conseguenze possimo vere dll (III). Teorem 2. Si L(t, q, q ) C 1 ([, b] R 1 R 1 ) e q(t) D 1 [, b] tle che J 1 ( q, η) = per ogni η(t) D 1 [, b]. Provimo che si h (3) ˆLq (t) = t ˆL q (τ)dτ (4) ˆLq () = ˆLq (b) =. Dim. Anche in questo cso, se supponimo q(t) C 2 [, b], L C 2, possimo procedere ll Eulero e integrre per prti nel secondo termine di [ˆLq (t)η(t) + ˆL q (t)η (t)] dt = grzie l ftto che ˆL q (t) C 1 [, b]. Ottenimo (5) [ ˆL q (t) d ] dt ˆL q (t) η (t)dt + ˆL q (b)η(b) ˆL q ()η() = per ogni η(t) D 1 [, b]. In prticolre l (5) vle per ogni η(t) D 1 [, b] tle che η() =, η(b) =. In questo cso dl lemm fondmentle bbimo (6) ˆLq (t) d dt ˆL q (t) =. Tenendo conto dell (6), l (5) diviene (7) ˆLq (b)η(b) ˆL q ()η() = per ogni η(t) D 1 [, b] 15
16 d cui segue subito l (4). Se ci limitimo supporre L(t, q, q ) C 1 ([, b] R 1 R 1 ) e q(t) D 1 [, b] occorre utilizzre il lemm di Du Boys Reymond. Definimo Φ(t) = ˆL q (τ)dτ. Come nel teorem precedente ottenimo, trmite integrzione per prti, (8) [ Φ(t)η (t) + ˆL ] q (t)η (t) dt + Φ(b)η(b) = per ogni η(t) D 1 [, b]. In prticolre, se nell (8) sceglimo η(b) = η() = ottenimo (9) [ Φ(t)η (t) + ˆL ] q (t)η (t) dt = per ogni η(t) D 1 [, b] η(b) =, η() = e, per il lemm di Du Boys Reymond, bbimo (1) Φ(t) + ˆL q (t) = ˆL q (). Sostituendo in (8) concludimo che (11) ˆLq ()η(b) ˆL q ()η() + Φ(b)η(b) = per ogni η(t) D 1 [, b]. Scegliendo in (1) η(b) = e η() ottenimo (12) ˆLq () =. L (11) diviene llor Φ(b)η(b) = per ogni η(t) D 1 [, b] per cui Φ(b) =. D ltr prte dll (1) e (12) segue Φ(b) = ˆL q (). Esercizio. Dimostrre l seguente vrinte dei teoremi 1 e 2. Si L(t, q, q ) C 1 ([, b] R 1 R 1 ) e q(t) D 1 [, b] tle che Provre che (13) ˆLq (t) = J 1 ( q, η) = per ogni η(t) D 1 [, b] η() =. t ˆL q (τ)dτ + ˆL q () 16
17 (14) ˆLq (b) =. Not. Condizioni come le (4) si chimno condizioni nturli. Trimo lcune importnti conclusioni dll prim form integrle dell equzione di Eulero. Se un funzione q(t) D 1 [, b] soddisf l (15) ˆLq (t) = t ˆL q (τ)dτ + ˆL q () e t = c è un punto di discontinuità per q (t), vle dire p = lim t c q (t) lim t c+ q (t) = r, t = c è un punto di discontinuità eliminbile per ˆL q (t) che è quindi più regolre di q (t). Questo ftto è immedit conseguenz dell (15), poiché membro destro bbimo un funzione continu. Ottenimo in definitiv l prim equzione di Erdmnn Weierstrss (16) L q (c, q(c), p) = L q (c, q(c), r). Esempio. Per il funzionle J(q) = 1 q 2 (t q) 2 dt definito nell clsse A 1 = {q(t) D 1 [ 1, 1], q( 1) =, q(1) = 1} l funzione q(t) = per t [ 1, ], q(t) = t qundo t (, 1] fornisce il minimo ssoluto di J(q) in A 1. Per t = l derivt prim di q(t) è discontinu, d ltr prte ˆL q (t) = per ogni t [ 1, 1]\{}. L discontinuità di ˆL q (t) = è quindi eliminbile. Se q(t) C 1 [, b] bbimo ˆL q (t) C [, b]. Per l (15) ˆL q (t) è derivbile e vle (17) d dt ˆL q (t) = ˆL q (t) in [, b]. Qundo q(t) h discontinuità nell derivt prim l (17) continu vlere negli intervlli di continuità di q (t). 17
18 Not. Può esistere d dt ˆL q (t) senz che esist q (t), come mostr il funzionle J(q) = 1 q 2 (q t 2 ) 2 dt definito nell clsse di funzioni A 1 = {q(t) D 1 [ 1, 1], q( 1) =, q(1) = 1}. Inftti l funzione q(t) = per t [ 1, ], q(t) = t se t (, 1] fornisce il minimo ssoluto di J(q) in A 1. Or q () non esiste, m ˆL q (t) = per ogni t [ 1, 1]\{} ed è quindi, postoˆl q () =, ottenimo un funzione derivbile. Notimo infine che se q(t) C 2 [, b] e L C 2 è possibile scrivere l equzione (16) nell form (18). L q q q + L q qq + L q t = L q Se poi L q q è possibile ricvre l q dll (17). Esempio. i) Considerimo il funzionle L (y 2 + y 2 )dx nell clsse A 1 = {y(x) D 1 [, L]; y() = y, y(l) = y L }. L equzione di Eulero è y y = il cui integrle generle è, come è noto, y(x)c 1 e x + c 2 e x. Clcolimo le costnti c 1 e c 2 trmite le condizioni y() = y, y(l) = y L. Si trov fcilmente che esiste per ogni L > un e un sol soluzione ȳ(x). ii) Anlogmente il funzionle si può pensre definito nell clsse A 1 = {y(x) D 1 [, L]; y() = y }. In questo cso oltre ll condizione impost bbimo l condizione nturle y (L) =. Si lsci come esercizio di provre che esiste un e un sol soluzione dell equzione di Eulero che soddisf l condizione impost e quell nturle. iii) Un terz possibile scelt è di considerre il funzionle A 3 = D 1 [, L]. In questo cso bbimo due condizioni nturli y () =, y (L) =. L unic soluzione dell equzione di Eulero che soddisf queste due condizioni è l soluzione null. iv) Provre che nei tre csi i), ii) e iii) gli estremli trovti sono minimi ssoluti. Osservimo che questo modo di procedere può, per su ntur, fornire solo degli estremli C 2 [, L], privi quindi di discontinuità nell derivt prim. 18
19 Esercizio. Considerre il funzionle (y 2 + y 2 + e x y)dx nelle clssi A 1, A 2 e A 3 dell esempio precedente. Provre che in ciscun di esse esiste uno ed un sol minimo ssoluto. Trovrlo tle minimo. Esercizio. Trovre gli estremli C 2 del funzionle L (y 2 + y 2 + f(x)y)dx dove f(x) è un rbitrri funzione continu (pplicre il metodo dell vrizione delle costnti rbitrrie). Provre che per ogni L > esiste uno ed un solo minimo ssoluto di J(y) nelle clssi A 1, A 2 e A 3 dell esempio precedente. 9. Second form integrle dell equzione di Eulero Teorem. Se q(t) D 1 [, b] è un minimo (mssimo) reltivo debole del funzionle J(q) = L(t, q, q )dt in un delle clssi A 1, A 2, A 3 llor esiste un costnte C tle d versi (1) L(t, q(t), q (t)) q (t)l q (t, q(t), q (t)) = t L t (τ, q(τ), q (τ))dτ + C per ogni t [, b], eccetto gli eventuli punti di discontinuità di q (t). Dim. Possimo supporre che J(q) minimizzi nell clsse A 1. Inftti se J(q) minimizz in A 2 o A 3, minimizz nche nell clsse A = {q(t) D 1 [, b], q() = q(), q(b) = q(b)} e quindi ci riducimo l cso dell clsse A 1. Per l dimostrzione immergimo q(t) in un fmigli un prmetro ϕ(t, ɛ) di funzioni mmissibili definit nel modo seguente. Si h(t) D 1 [, b] tle che h() = h(b) = un funzione fisst. Considerimo l fmigli di curve K ɛ del pino (t, q) dt prmetricmente dlle equzioni (2) t = τ + ɛh(τ) τ [, b] 19
20 (3) q = q(τ). Prendendo ɛ < ɛ con ɛ sufficientemente piccolo, le K ɛ srnno dei grfici. Bst inftti scegliere ɛ tle che ɛ sup h (τ) = 1/2 perché l (1) si risolubile rispetto τ nell form (4) τ = F (t, ɛ). Abbimo F (t, ) = t, F (, ɛ) =, F (b, ɛ) = b per ogni ɛ( ɛ < ɛ ) e inoltre df dt (t, ɛ) = ɛh (F (t, ɛ)). Le K ɛ si possono esprimere come grfici nell form K ɛ : q = ϕ(t, ɛ) = q(f (t, ɛ)). Abbimo ϕ(t, ) = q(t), ϕ(, ɛ) = q(), ϕ(b, ɛ) = q(b) per cui ϕ(t, ɛ) A 1. Inoltre Definimo l funzione g(ɛ) = J(ϕ(t.ɛ)) = dϕ q (t, ɛ) = dt Con il cmbimento di vribile d integrzione bbimo (5) g(ɛ) = (F (t, ɛ)) 1 + ɛh (F (t, ɛ)). L(t, ϕ(t, ɛ), dϕ (t, ɛ))dt = dt ( q (F (t, ɛ)) L t, q(f (t, ɛ)), 1 + ɛh (F (t, ɛ)) t = τ + ɛh(τ) τ = F (t, ɛ) ) dt. ( q (τ) ) L τ + ɛh(τ), q(τ), 1 + ɛh (τ) (1 + ɛh (τ)) dτ. Poiché q(t) è minimo reltivo debole esiste ρ > tle che per ogni q(t) N 1 ρ ( q) vle J(q) J( q). Quindi esiste < ɛ 1 ɛ tle che ϕ(t, ɛ) N 1 ρ ( q) se ɛ ɛ 1. Ne segue che 2
21 ɛ = é un minimo reltivo per g(ɛ) e bbimo g () =. Derivndo l (5) rispetto ɛ ottenimo [L(τ, q(τ), q (τ))h (τ) + L t (τ, q(τ), q (τ))h(τ) L q (τ, q(τ), q (τ))q (τ)h (τ)] dτ =. Definimo Φ(τ) = τ L t (ζ, q(ζ), q (ζ))dζ. Ottenimo integrndo per prti, cos lecit poiché Φ(τ) D 1 [, b], (6) [L(τ, q(τ), q (τ)) L q (τ, q(τ), q (τ))q (τ) Φ(τ)] h (τ)dτ = per ogni h(τ) D 1 [, b], h() = h(b) =. L tesi segue dl lemm di Du Boys Reymond. Come nel cso dell prim form integrle dell equzione di Eulero l (1) h interesse in sé. 1. Conseguenze dell second form integrle dell equzione di Eulero Se t = c è un punto di discontinuità di q (t), e vle l (1) bbimo, posto p = q (c + ) e r = q (c ), (1) L(c, q(c), p) pl q (c, q(c), p) = L(c, q(c), r) rl q (c, q(c), r). L (1) è l second equzione di Erdmnn Weierstrss ed è conseguenz immedit del ftto che nell (9.1) il membro destro è un funzione continu. Se q(t) C 1 [, b] e soddisf l (9.1) bbimo che ˆL(t) q (t)ˆl q, (t) è un funzione derivbile e vle (2) d dt (ˆL(t) q (t)ˆl q (t)) = ˆL t (t). Se infine q(t) C 2 [, b] e soddisf l (9.1), mentre L C 2, possimo sviluppre i clcoli nell (2); trovimo L t + L q q + L q q q L q q d dt (L q ) = L t 21
22 per cui (3) q [ L q d dt (L q ) ] =. Quindi se q (t), q(t) è soluzione dell equzione di Eulero. Ne segue che tutte le soluzioni regolri dell (8.13) sono nche soluzioni dell (9.1), m non vicevers: le constnti sono soluzioni di (9.1), m non necessrimente di (8.13). Conviene porre l seguente Definizione. Dt l lgrngin L(t, q, q ) C 1 ([, b] R 1 R 1 ), un funzione q(t) D 1 [, b] si dice estremle spezzto se soddisf simultnemente ll prim e second form integrle dell equzione di Eulero e cioè (8.13) e (9.1). In prticolre, nei punti di discontinuità dell derivt prim di un estremle spezzto sono verificte si l prim che l second equzione di Erdmnn Weierstrss. Definizione. Chimeremo estremli le soluzioni di clsse C 1 dell equzione di Eulero. 11. Regolrizzzione degli estremli Si present come molto nturle il problem di dre delle condizioni sufficienti perché un estremle spezzto, priori soltnto di clsse D 1, si di clsse C 1 o ddirittur di clsse C 2. Utile questo rigurdo è il seguente Lemm Se q(t) è un estremle spezzto e t = c un punto di discontinuità di q (t), l funzione g(z) = L q (c, q(c), z) ssume lmeno tre volte lo stesso vlore. Dim. Si p = q (c ), r = q (c + ). Per ipotesi p r. Dlle equzioni di Erdmnn Weierstrss ottenimo (1) L q (c, q(c), p) = L q (c, q(c), r) (2) L(c, q(c), p) L(c, q(c), r) = (p r)l q (c, q(c), r). D ltr prte, per il teorem di Lgrnge, bbimo (3) L(c, q(c), p) L(c, q(c), r) = (p r)l q (c, q(c), ξ) 22
23 dove ξ p, ξ r. Dlle (2) e (3) per differenz ottenimo (4) (p r) [L q (c, q(c), r) Lq (c, q(c), ξ)] = e poiché p r, in definitiv, si ottiene (5) L q (c, q(c), p) = L q (c, q(c), r) = L q (c, q(c), ξ). Corollrio. Se L(t, q, q ) C 2 ([, b] R 1 R 1 ) e t = c è punto di discontinuità per l derivt dell estremle spezzto q(t), l funzione di z : L q q (c, q(c), z) si nnull lmeno due volte. È conseguenz immedit del lemm precedente e del teorem di Rolle. In prticolre se L q q (t, q, z) per ogni (t, q, z) [, b] R1 R 1 ogni estremle è di clsse C 1 [, b]. Per esempio, tutti gli estremli dei funzionli J(q) = sono di clsse C q2 q 2 dt J(q) = 1 + t + t2 q 2 dt Esercizio. Esistono estremli spezzti del funzionle e y2 y 3 dx? Teorem (Regolrità C 2 degli estremli). Si L(t, q, q ) C 2 ([, b] R 1 R 1 ), e q(t) C 1 [, b] un estremle tle che (6) L q q (t, q(t), q (t)) per ogni t [, b]. In queste ipotesi q(t) C 2 [, b]. Dim. Poiché q(t) è un estremle, bbimo (7) L q (t, q(t), q (t)) = t L q (τ, q(τ), q (τ))dτ + C. 23
24 Fissimo t (, b) e considerimo l funzione (8) F (t, z) = L q (t, q(t), z) t L q (τ, q(τ), q (τ))dτ C. Se z = q (t ), bbimo F (t, z ) =. Poiché F z (t, z ) = L q q (t, q(t ), q (t )), possimo pplicre il teorem di Dini sulle funzioni implicite ll equzione F (t, z) =. Poiché F (t, z) C 1, esiste un e un sol funzione z = Ψ(t) di clsse C 1 definit loclmente in un opportuno intorno (t δ, t + δ) tle che z = Ψ(t ) e inoltre F (t, Ψ(t)) = per ogni t (t δ, t + δ). Poiché si h nche F (t, q (t)) = concludimo che q (t) = Ψ(t) per cui q (t) C 1 e quindi q(t) C 2. Tenendo conto che t è un punto rbitrrio di (, b) ottenimo l tesi. Per induzione si prov poi che se L(t, q, q ) C k ([, b] R 1 R 1 ), e q(t) C 1 [, b] un estremle tle che L q q (t, q(t), q (t)) per ogni t [, b] llor q(t) C k [, b]. Si noti che pplicndo l formul che dà l derivt di Ψ(t), e cioè si trov l rppresentzione dell Ψ (t ) = F t(t, z ) F z (t, z ), q (t ) = L q(t, q(t ), q (t )) L qt (t, q(t ), q (t )) q (t )L q q(t, q(t ), q (t )) L q q (t, q(t ), q (t )) che coincide con quell che segue ricvndo q (t) dll L q d dt (L q ). Si noti che il teorem mostr che, se L q q (t, q(t), q (t)) per ogni t [, b] e q(t) C 1 [, b], l regolrità dell estremle dipende solo dll regolrità di L(t, q, q ). Esempio. Considerimo il funzionle J(q) = (q 2 1) 2 dt con q(t) D 1 [, b] e q( 1) = 1, q(1) = 1. L funzione q(t) = t è un estremle spezzto nell clsse indict. Inoltre L q q (q ) = 4(q 2 1) + 8q 2. 24
25 Per cui L q q ( q (t)) = 8. D ltr prte q(t) non è di clsse C 2. L ipotesi che l estremle si di clsse C 1 è essenzile. 12. Csi di integrbilità elementre dell equzione di Eulero Considerimo i funzionle del tipo (1) J(q) = dove f(z) C 2 (R 1 ). Se si suppone f(q )dt (2) f (z) per ogni z R ogni estremle è di clsse C 1 [, b] per il lemm precedente; d ltr prte, per il teorem gli estremli sono nche di clsse C 2 [, b]. L equzione di Eulero Lgrnge si scrive llor f (q )q =, d cui segue q =. Gli estremli sono tutte e solo funzioni dell form q(t) = mt + n. Se f (z) = h un sol rdice in R possimo nuovmente escludere l esistenz di estremli spezzti. Ogni estremle è C 1 [, b]. Se q(t) è un estremle bbimo per l prim form integrle dell equzione di Eulero (3) f(q (t)) = C 1 per ogni t [, b] ; q (t) può essere solo un costnte. Inftti se esistono due vlori t 1 e t 2 (, b) t 1 t 2 tli che q (t 1 ) q (t 2 ), q (t) ssume tutti i vlori compresi fr q (t 1 ), q (t 2 ) per cui, in prticolre, bbimo f (q (t 1 )) = f(q (t 2 )) = f (q (t 3 )) e questo non può essere poiché f (z) = h un sol rdice. Esempio. L = q 3 + q 2 + q. Poiché L q q = 6q + 2 non vi sono estremli spezzti. Esempio. L = q. Ogni funzione pprtenente ll clsse A 1 = {q(t) D 1 [, b], q() = q, q(b) = q b } è estremle del funzionle J(q) = q dt. L figurtrice Per l ricerc degli estremli spezzti del funzionle dell form (1) è utile studire il grfico dell funzione f(z), z R. Supponimo che q(t) si un estremle spezzto e che t = c si un punto di discontinuità di q (t). Ponimo p = q (c + ) q (c ) = r. 25
26 Per l prim equzione di Erdmnn Weierstrss bbimo (4) f (p) = f (q). Il significto geometrico dell (4) è evidente: nei punti z = p e z = r le tngenti l grfico dell figurtrice v = f(z) sono prllele. D ltr prte, l tngente l grfico dell figurtrice in z = p è dt d (5) v = f (p)(z p) + f(p). Or l rett (5) pss per il punto (r, f(r)), inftti l condizione f(r) = f (p)(r p) + f(p) ltro non è che l second equzione di Erdmnn Weierstrss. Quindi le tngenti ll figurtrice in z = p e z = r coincidono. Vicevers, se due tngenti ll figurtrice in punti distinti coincidono, il funzionle h estremli spezzti. Esempio. Considerimo il funzionle 2 ( 18q q ) 6 dt 6 q nell clsse A 1 = {q(t) D 1 [, 2]; q() =, q(2) = }. L figurtrice è l funzione f(z) = 18z z z6. Il grfico è quello dell figur. Abbimo due clssi di estremli spezzti: i) le spezzte di estremi (,) e (2,) i cui lti hnno pendenz 2 e 2, ii) le spezzte di estremi (,) e (2,) i cui lti hnno pendenz 3 e 3. Vi è inoltre l estremle q(t) = per t [, 2]. Come subito si verific, quest ultimo estremle è un minimo ssoluto. Esercizio. Trovre gli estremli spezzti del funzionle J(q) = 2 (q 4 6q 2 )dt 26
27 nell clsse q(t) D 1 [, 2], q() =, q(2) =. Provre che si trtt di minimi ssoluti. 2.Funzionli dell form (6) J(q) = f(t, q )dt. Dll prim form integrle dell equzione di Eulero bbimo che lungo gli estremli spezzti e quelli regolri si h (7) f q (t, q ) = C 1. Nei csi in cui l (7) può essere risolt rispetto q può essere possibile ridurre il problem dell ricerc degli estremli lle qudrture. Esempio. Riprendimo il funzionle di Weierstrss 1 x 2 y 2 dx nell clsse A 1 = {y(x) C 1 [ 1, 1]; y( 1) = 1, y(1) = 1}. Non vi sono estremli spezzti. Inoltre vle l (7) che si scrive x 2 y = C. Ottenimo y = C x 2 d cui segue y(x) = C x + C 1. Quest funzione pprtiene ll clsse A 1 solo se C =. È quindi impossibile soddisfre entrmbe le condizioni l bordo. Esercizio. Trovre l estremle del funzionle 3 2 (x 2 1)y 2 dx che soddisf le condizioni y(2) =, y(3) = 1. Provre che si trtt di un minimo ssoluto. 3. Funzionli che non dipendono d x. Per i funzionli dell form (8) 27 f(y, y )dx.
28 vle l integrle primo dell energi (9) f(y, y ) y f y (y, y ) = C Se l (9) è risolubile rispetto y può essere possibile trovre l integrle generle dell equzione di Eulero per seprzione di vribili. Esempio. Il problem dell ricerc delle superfici di rotzione di re minim si trduce nell ricerc degli estremli del funzionle 2π y 1 + y 2 )dx nell clsse delle funzioni y(x) D 1 [, b] tli che y() = y, y(b) = y b. Dll (9) ottenimo y 1 + y 2 = α con α. Per seprzione di vribili trovimo l integrle generle dell equzione di Eulero del funzionle nell form y(x, α, β) = α cos h x β α. Si trtt di un fmigli di ctenrie. È importnte notre che dti due punti (, y ), (b, y b ) non sempre esiste un estremle che li congiunge. A titolo di esempio prendimo =, y = 1. Dll condizione y() = 1 ottenimo, posto λ = β α, y(x, λ) = cos h(x cos hλ λ) cos hλ Imponendo l ltr condizione l bordo, e cioè y(b, λ) = y, si h D ltr prte, y b = cos h(b cos hλ λ) cos hλ dove λ = Quindi se sceglimo b cos hλ λ cos hλ λ cos hλ λ cos hλ y b < b λ cos hλ 28. b λ cos hλ.
29 non esiste lcun estremle che soddisfi entrmbe le condizioni l bordo. Esercizio. Trovre gli estremli del funzionle e y y 2 dx che soddisfno le condizioni y() = e y(1) = log Funzionli dell form (1) [M(x, y) + N(x, y)y ]dx. Supponimo che le funzioni M(x, y) e N(x, y) sino di clsse C 1 (S) nell strisci S = {(x, y); x b, < y < }. L equzione di Eulero del funzionle è (11) N x (x, y) = M y (x, y). Nell (11) non intervengono derivte e srà in generle impossibile trovre estremli che soddisfno condizioni gli estremi. Un cso prticolrmente significtivo si h qundo (12) N x (x, y) = M y (x, y) per ogni (x, y) S. Come è noto dll nlisi, l (12) grntisce l esistenz di un funzione U(x, y) C 2 (S) tle che M(x, y) = U x (x, y), N(x, y) = U y (x, y). Se il funzionle è definito nell clsse A 1 = {y(x) D 1 [, b]; y(x ) = y, y(x b ) = y b } e vle l (12) bbimo du dx (x, y(x))dx = U(b, y b) U(, y ) per ogni funzione di A 1. Il funzionle è quindi costnte in A 1 coerentemente con il ftto che l equzione di Eulero è identicmente verifict. Esempio. Il funzionle (y 2 + 2xyy )dx rientr nell clsse (1). L condizione (12) è verifict e J(y) è quindi costnte nell clsse A 1. 29
30 Esercizio. Considerre il funzionle y 3 dx nell clsse A 1 = {y(x) D 1 [, ]; y() =, y() = b}. Provre che: i) non vi sono estremli spezzti. ii) Il funzionle non h né minimo né mssimo ssoluto. iii) Gli estremli sono minimi reltivi deboli se b > e mssimi reltivi deboli se b <. iv) Se b = l estremle non è né mssimo né minimo reltivo debole. Esercizio. Il funzionle /2 y 2 dx + 2 ydx non rientr in quelli studiti finor. Se definimo l funzione f(x) = 1 se x < 1/2 e f(x) = se 1/2 < x 1, possimo nche scrivere (y 2 + 2f(x)y)dx m l lgrngin F (x, y, y ) = y 2 + 2f(x)y non è di clsse C 1. Provre che J(y) h minimo ssoluto nell clsse A 1 = {y(x) D 1 [, 1]; y() =, y(1) = }. Esercizio. Definimo l funzione (x) = 1 se 1 x <, (x) = 5 se x < 1. Considerimo il funzionle 1 (x)y 2 dx = 1 y 2 dx + 5y 2 dx. L lgrngin F (x, y, y ) = (x)y 2 non è di clsse C 1. Provre che il funzionle h minimo ssoluto nell clsse A 1 = {y(x) D 1 [ 1, 1]; y( 1) = 1, y(1) = 3}. 13. Il cso vettorile Per le lgrngine dell form L(t, q, z) C 1 ([, b] R n R n ) dove q e z R n, l condizione necessri di Eulero Lgrnge si ricv in modo simile l cso sclre. Considerimo, per esempio, il funzionle (1) J(q) = L(t, q(t), q (t))dt 3
31 nell clsse A 1 = {q(t) D 1 [, b], q() = q, q(b) = q b } e, per fissre le idee, supponimo che q(t) A 1 si il minimo ssoluto del funzionle nell clsse indict. Immergimo q(t) nell fmigli di funzioni mmissibili q(t) + ɛη(t) A 1 dove η(t) D 1 [, b] e inoltre η() = η(b) =. Posto g(ɛ) = J( q + ɛη) definimo l vrizione prim del funzionle (2) J 1 ( q, η) = g () = n i=1 [ˆLqi (t)η i (t) + ˆL ] q (t)η i i(t) dt dove ˆL qi (t) = L qi (t, q i (t), q i (t)), ˆL q i (t) = ˆL q i (t, q i (t), q i (t)). Poiché q(t) è il minimo ssoluto bbimo (3) J 1 ( q, η) = per ogni η(t) D 1 [, b] tle che η() = η(b) =. Sceglimo η i (t) = qundo i j, e ponimo L (3) diviene Φ j (t) = t ˆL qi (t)dt. (4) ] [ˆLq (t) Φ j(t) η i j(t)dt = per ogni η(t) D 1 [, b], η j () = η j (b) =. Dll (4) seguono le equzioni di Eulero Lgrnge in form integrle (5) ˆLq i (t) = t ˆL qi (τ)dτ + C j j = 1, 2,..., n. Sussiste nche l nlogo vettorile dell condizione necessri (#) e cioè il Teorem. Se L(t, q, z) C 1 ([, b] R n R n ) e q(t) è minimo ssoluto del funzionle J(q) vle n (6) ˆL(t) q i(t)ˆl q i (t) = i=1 t ˆL q i (τ)dτ + C. Come nel cso sclre, le condizioni (5) hnno interesse in sé e ciò prescindere dl ftto che q(t) si minimo ssoluto. 31
32 Definizione. Chimeremo estremle spezzto un funzione q(t) D 1 [, b] con discontinuità nell derivt prim e che soddisf le (5) e (6). In un punto di discontinuità t = c dell derivt prim q (t) di un estremle spezzto q(t) vlgono le equzioni di Erdmnn Weierstrss L q i (c, q(c), q (c + )) = ˆL q i (c, q(c), q (c )) i = 1, 2,..., n L(c, q(c), q (c + )) L(c, q(c), q (c )) n q i(c + )L q i (c, q(c), q (c + )) = i=1 n q i(c )L q i (c, q(c), q (c )). Se un soluzione delle (5) è di clsse C 1 [, b] dlle (5) segue (7) i=1 d dt L q i = L q i. Chimeremo estremli le soluzioni di clsse C 1 [, b] delle equzioni (7). Se poi q(t) è di clsse C 2 [, b] e inoltre L(t, q, z) C 2 ([, b] R n R n ), possimo sviluppre i clcoli nell (7), che si scrivono nell form (8) n L q i q q k k = G i(t, q, q ) i = 1, 2,..., n. k=1 Se q(t) è un soluzione delle (8) e inoltre per ogni t [, b] vle [ ] (9) det L q i q (t, q(t)q (t)), k è possibile ricvre le q k dlle (8). Vicevers vle il seguente risultto di esistenz dell derivt second e delle derivte superiori: Teorem. Supponimo che (1) L(t, q, z) C m ([, b] R n R n ) m 2 (11) q(t) C 1 [, b] (12) q(t) soddisf ˆL q i (t) = t ˆL qi (τ)dτ + C j j = 1, 2,..., n. 32
33 [ ] (13) det L q i q (t, q(t)q (t)). k In queste ipotesi q(t) è di clsse C m [, b]. L dimostrzione è simile quell del cso n = 1 e l si lsci come esercizio. Esempio. x = x(u, v), y = y(u, v), z = z(u, v) sono le equzioni di un crt locle di un superficie di R 3 e P, P 1 due punti dell superficie corrispondenti i vlori (u, v ), (u 1, v 1 ). Specifichimo sull superficie un curv congiungente i punti P e P 1 trmite le u = u(t), v = v(t) soddisfcenti lle condizioni u(t ) = u, v(t ) = v, u(t 1 ) = u 1, v(t 1 ) = v 1. L lunghezz di quest curv è dt dl funzionle J(u, v) = t1 t Eu 2 + 2F u v + Gv 2 dt dove E = x 2 u + y 2 u + z 2 u, f = x u x v + y u y v + z u z v, E = x 2 v + y 2 v + z 2 v sono i coefficienti dell prim form qudrtic fondmentle. Le soluzioni delle equzioni di Eulero reltive l funzionle J(u, v) sono le curve geodetiche dell superficie. Not. Evidentemente il funzionle (1) può essere definito nche in ltre clssi di funzioni in cui solo lcune delle componenti di q(t) sono prefisste per t = e per t = b. Il consueto procedimento eulerino permette nche in questo cso di trovre le condizioni nturli che vnno ggiunte lle condizioni imposte priori. 14. Funzionli dipendenti d derivte di ordine superiore Si f(x, y, y, y,..., y (n) C n+1 ([, b] R n+1 ) e considerimo il funzionle (1) f(x, y, y, y,..., y (n) )dx che, per fissre le idee, supponimo definito nell clsse A = {y(x) D n [, b], y() = y, y () = y,..., y (n 1) () = y (n 1), y(b) = y b, y (b) = y b,... y (n 1) (b) = y (n 1) b }. Si ȳ(x) C 2n [, b] il minimo ssoluto di J(y) in A che immergimo nell fmigli di funzioni mmissibili ȳ(x) + ɛη(x) dove η(x) D n [, b] e verific η() = η () = 33
34 ... η n 1 () =, η(b) = η (b) =... η n 1 (b) =. Posto, come l solito, g(ɛ) = J(ȳ + ɛη), bbimo g () =, condizione che si scrive (2) [ ˆfy (x)η(x) + ˆf y (x)η (x) ˆf y ( n)(x)η (n) (x)] dx = per tutte le funzioni η(x) D n [, b] tli che η() = η () =... η n 1 () =, η(b) = η (b) =... η n 1 (b) =. Nell (2) bbimo posto ˆf y (x) = f y (x, ȳ(x), ȳ (x),..., ȳ (n) (x)) ecc. L ipotesi ȳ(x) C 2n [, b] permette di integrre per prti nell (2) scricndo successivmente le derivte di η(t). Poiché tutti i termini di frontier sono nulli, ottenimo (4) [ ˆf y d ] dx ( ˆf y (x)) + d2 dx 2 ( ˆf y (x)) ( 1) n dn dx n ( ˆf y (n)(x)) ηdx = per tutte le η specificte in precedenz. Dl lemm fondmentle del clcolo delle vrizioni ottenimo l condizione necessri di Eulero per questo tipo di problem e cioè: (5) f y d dx (f d2 y ) + dx 2 (f dn y ) ( 1)n dx n (f y (n)) =. Per clssi di funzioni mmissibili in cui i vlori di y, y,..., y (n 1) in x = e x = b sino imposti solo przilmente, procedendo in modo simile si ottiene ncor l (5) come condizione necessri e inoltre vrie condizioni nturli che si clcolno dll nlisi dei termini di frontier non nulli che si generno nelle successive integrzioni per prti. È nche possibile, prezzo di qulche compliczione formle, evitre l ipotesi ȳ(x) C 2n [, b], supporre semplicemente ȳ(x) A e procedere come nel cso n = 1. Esercizio Clcolre l equzione di Eulero e le condizioni nturli del funzionle (y 2 + 2xy)dx definito in A = {y(x) C 2 [, 1], y() = 1, y () = 2}. Trovre l soluzione dell equzione di Eulero che soddisf le condizioni nturli e quelle imposte. Provre che si trtt di un minimo ssoluto. 34
35 Esempio. Considerimo un st elstic unidimensionle rettiline e di lunghezz L (qundo non soggett crichi) che può deformrsi solo in un pino verticle xy (l sse y è vertic scendente). Supponimo che l st, uniforme e di densità ρ, si soggett solo l proprio peso. Indichimo con y(x) l deflessione dell sbrr in equilibrio. Ci proponimo di determinre quest configurzione di equilibrio come minimo del funzionle dell energi dell st, somm dell energi potenzile elstic e dell energi potenzile grvitzionle. L energi potenzile elstic è proporzionle ll integrle sull lunghezz del qudrto dell curvtur che pprossimimo con l derivt second. Tenendo conto che l energi potenzile grvitzionle è dt d L ρgy(x)dx ottenimo, per il funzionle dell energi, l espressione (6) L L equzione di Eulero del funzionle è µ 2 y 2 (x) + ρgy(x)dx µ >. (7) y IV + ρg µ =. Se l sbrr è incstrt in entrmbi gli estremi imporremo le condizioni: (8) y() = y, y(l) = y L, y () = y, y (L) = y L. Risolvendo l (7) con le condizioni (8) si trov l configurzione d equilibrio. Si lsci come esercizio di provre che si trtt di un minimo ssoluto del funzionle (6) nell clsse (8). È fisicmente chiro che sono possibili nche ltre condizioni l bordo: l sbrr può essere incstrt per x =, il che comport le condizioni (9) y() = y, y () = y, e semplicemente ppoggit per x = L, vle dire (1) y(l) = y L. Con le tre condizioni (9) e (1) l soluzione di (7) è indetermint. Cerchimo l condizione nturle corrispondente ll clsse di funzioni mmissibili determint 35
36 dlle (9) e (1). Per restre nell clsse delle funzioni mmissibili considerimo vrizioni dell form y(x) + ɛη(x), dove η(x) D 2 [, L] e inoltre η() =, η () =, η(l) =. Derivndo l funzione g(ɛ) = J(y + ɛη) e procedendo nel modo solito, trovimo l condizione nturle (11) y (L) =. Trovre, per esercizio, l soluzione di (7) determint dlle condizioni (9), (1) e (11). Esercizio. Trovre l configurzione di equilibrio di un sbrr omogene qundo l sbrr è incstrt in x = e liber in x = L. 15. Condizione necessri per il problem isoperimetrico Le funzioni f(x, y, y ) g(x, y, y ) pprtengono entrmbe ll clsse C 1 ([, b] R 1 R 1 ). Considerimo i funzionli (1) f(x, y, y )dx (2) I(y) = g(x, y, y )dx. Il funzionle J(y) si suppone definito nell clsse A = {y(x) D 1 [, b], y() = y, y(b) = y b, I(y) = L}. Problemi di questo tipo si chimno isoperimetrici. Esempio tipico è il problem di Didone visto pgin 4. Teorem. Se y = ϕ(x) A è un minimo reltivo debole, per il funzionle J(y) nell clsse A esistono due numeri λ e λ 1 non entrmbi nulli per cui y = ϕ(x) nnull l vrizione prim del funzionle usilirio H(y) = λ J(y) + λ 1 I(y) 36
37 nell clsse B = {y(x) D 1 [, b], y() = y, y(b) = y b } che non contiene il vincolo integrle. Si h cioè (3) H 1 (ϕ, h) = λ J 1 (ϕ, h) + λ 1 I 1 (ϕ, h) per ogni h(x) D 1 [, b] tle che h() =, h(b) =. Dim. Se vle (4) I 1 (ϕ, h) = per ogni h(x) D 1 [, b] tle che h() =, h(b) = e cioè se ϕ(x) è un estremle del funzionle I(y), possimo prendere λ = e λ 1 non nullo e rbitrrio e il teorem è dimostrto. Supponimo, vicevers, che esist un funzione ĥ(x) D1 [, b] con ĥ() = ĥ(b) = e inoltre (5) I 1 (ϕ, ĥ). Considerimo poi un rbitrri funzione h(x) D 1 [, b] tle che h() =, h(b) =. Definimo l funzione Φ(α, β) C 1 (R 2 ) nel modo che segue Φ(α, β) = g(x, ϕ + αh + βĥ, ϕ + αh + βĥ )dx L. Abbimo Φ(, ) = g(x, ϕ, ϕ )dx L = poiché ϕ A. Inoltre Φ β (, ) = I 1 (ϕ, ĥ). Per il teorem delle funzioni implicite è possibile risolvere l equzione Φ(α, β) = rispetto β e trovre un funzione β = β(α) di clsse C 1 ( δ, δ) tle che β() = e Φ(α, β(α)) = e inoltre (6) β () = Φ α(, ) Φ β (, ) = I 1(ϕ, h) I 1 (ϕ, ĥ). Immergimo ϕ(x) nell fmigli di funzioni ϕ(x) + αh(x) + β(α)ĥ(x). Per l scelt di β(α) bbimo ϕ(x) + αh(x) + β(α)ĥ(x) A, tenendo nche conto del ftto che ϕ(x) + αh(x) + β(α)ĥ() = y ϕ(b) + αh(b) + β(α)ĥ(b) = y b Si ρ > l costnte che interviene nell definizione di minimo reltivo debole. Poiché β(α) è un funzione continu, esiste α 1 > tle che αh(x) + β(α)ĥ(x) < ρ αh (x) + β(α)ĥ (x) < ρ qundo α < α 1 37
38 (1) per cui ϕ(x) + αh(x) + β(α)ĥ(x) N ρ (ϕ). Ne segue che, posto g(α) = J(ϕ + αh + β(α)ĥ), si h g () = J 1 (ϕ, h) + β ()J 1 (ϕ, ĥ) =. Tenendo conto delle (6) ottenimo (7) I 1 (ϕ, ĥ)j 1(ϕ, h) J 1 (ϕ, ĥ)i 1(ϕ, h) = per ogni h(x) D 1 [, b] tle che h() =, h(b) =. Segue l tesi con λ = I 1 (ϕ, ĥ), λ 1 = J 1 (ϕ, ĥ). Il teorem fornisce un lgoritmo per trovre gli estremli del problem isoperimetrico. Esempio. Considerimo il funzionle y 2 dx nell clsse A = { } y(x) D 1 [, 1], y() = 1, y(1) = 6, y(x)dx = 3. Il funzionle usilirio di cui occorre cercre gli estremli è H(y) = (y 2 + λy)dx. Si trov y(x) = λ 4 x2 + c 1 x + c 2. Le costnti λ, c 1 e c 2 si clcolno imponendo le condizioni y() = 1, y(1) = 6, y(x)dx = 3. Si trov y(x) = 3x 2 + 2x + 1. Come già sppimo si trtt di un minimo ssoluto. Esempio. Nel cso del problem di Didone dobbimo cercre il mssimo del funzionle y(x)dx 38
39 con le condizioni Considerimo il funzionle y( ) =, y() =, I(y) = H(y) = 1 + y 2 dx = L. ( y + λ ) 1 + y 2 dx. Scrivendo l equzione di Eulero e integrndo un volt, trovimo y 2 = Integrndo nuovmente ottenimo (x + c 1 ) 2 [λ 2 (x + c 1 ) 2 ]. y(x) = ± λ 2 (x + c 1 ) 2 + c 2. Dlle condizioni y( ) =, y() = segue ( y + λ 2 2 ) 2 + x 2 = λ 2. Si trtt di cerchi di rggio λ e centro (, λ 2 2). Clcolimo λ con l condizione 1 + y 2 dx = L. Si trov l equzione rcsin λ = L 2λ per cui se < L < 2 non vi è nessun soluzione, se 2 < L < π bbimo due soluzioni; per L = π gli estremli sono i semicerchi y(x) = ± 2 x 2, mentre qundo L > π non vi sono estremli. Si noti che questo procedimento non fornisce lcun informzione sull ntur degli estremli trovti, nche se è intuitivmente chiro che si trtt di un minimo e di un mssimo ssoluto. 16. Un importnte funzionle specile Considerimo il funzionle (1) L (y 2 y 2 )dx L > 39
40 nell clsse delle funzioni mmissibili A 1 = {y(x) D 1 [, L], y() =, y(l) = }. È subito visto che non vi sono estremli spezzti. Cerchimo le soluzioni dell equzione di Eulero (2) y + y = che soddisfno le condizioni l bordo. L integrle generle dell equzione di Eulero è y(x) = C 1 sin x + C 2 cos x per cui occorre risolvere il sistem (3) C 2 =, C 1 sin L + C 2 cos L = che h un sol soluzione qundo L kπ k = 1, 2, 3,..., mentre qundo L = kπ h infinite soluzioni. Quindi nel primo cso vi è solo l estremle ȳ(x) =, mentre nel secondo vi sono infiniti estremli dti d ȳ(x) = C sin x con C un costnte rbitrri. Supponimo che < L < π e mostrimo che ȳ(x) = fornisce il minimo ssoluto. Considerimo l funzione w(x) = cotn ( x + π L ) 2 che nell intervllo [, L] è di clsse C 1. Se y(x) è un generic funzione mmissibile bbimo, poiché y() = y(l) =, L (y 2 w) dx =. Quindi per ogni funzione y(x) A 1 ottenimo (4) L [ y 2 y 2 (y 2 w) ] dx = L (y yw) 2 dx. Ne segue che ȳ(x) = è minimo ssoluto del funzionle nell clsse indict. Il cso in cui L = π richiede qulche osservzione ulteriore. Come sppimo, in questo cso vi sono infiniti estremli dti d ȳ(x) = C sin x. Provimo che si trtt di minimi ssoluti. Si w(x) = cotn x, x [, π] e y(x) un generic funzione di A 1. Tenendo 4
Integrale Improprio. f(x) dx =: Osserviamo che questa definizione ha senso dal momento che per ogni y è ben definito l integrale b
 Integrle Improprio In queste lezioni riprendimo l teori dell integrzione in un vribile, l ide è di estendere l integrle definito nche in csi in cui l funzione integrnd o l intervllo di integrzione non
Integrle Improprio In queste lezioni riprendimo l teori dell integrzione in un vribile, l ide è di estendere l integrle definito nche in csi in cui l funzione integrnd o l intervllo di integrzione non
1 Integrale delle funzioni a scala
 INTEGRALE DELLE FUNZIONI DI UNA VARIABILE Teori di Riemnn 1 Integrle delle funzioni scl (1.1) Definizione Si dice suddivisione di un intervllo chiuso e limitto [, b] un sottoinsieme {,..., n } di [, b]
INTEGRALE DELLE FUNZIONI DI UNA VARIABILE Teori di Riemnn 1 Integrle delle funzioni scl (1.1) Definizione Si dice suddivisione di un intervllo chiuso e limitto [, b] un sottoinsieme {,..., n } di [, b]
Integrali dipendenti da un parametro e derivazione sotto il segno di integrale.
 1 Integrli dipendenti d un prmetro e derivzione sotto il segno di integrle. Considerimo l funzione f(x, t) : A [, b] R definit nel rettngolo A [, b], essendo A un sottoinsieme perto di R e [, b] un intervllo
1 Integrli dipendenti d un prmetro e derivzione sotto il segno di integrle. Considerimo l funzione f(x, t) : A [, b] R definit nel rettngolo A [, b], essendo A un sottoinsieme perto di R e [, b] un intervllo
Il lemma di ricoprimento di Vitali
 Il lemm di ricoprimento di Vitli Si I = {I} un fmigli di intervlli ciusi contenuti in R. Diremo ce l fmigli I ricopre l insieme E nel senso di Vitli (oppure ce I è un ricoprimento di Vitli di E) se per
Il lemm di ricoprimento di Vitli Si I = {I} un fmigli di intervlli ciusi contenuti in R. Diremo ce l fmigli I ricopre l insieme E nel senso di Vitli (oppure ce I è un ricoprimento di Vitli di E) se per
Osserviamo che per trovare le costanti A e B possiamo anche ragionare così: se moltiplichiamo l equazione x + 1 (x + 2)(x + 3) = A.
 88 Roberto Turso - Anlisi 2 Osservimo che per trovre le costnti A e B possimo nche rgionre così: se moltiplichimo l equzione + ( + 2)( + 3) = A + 2 + B + 3 per + 2, dopo ver semplificto, ottenimo + + 3
88 Roberto Turso - Anlisi 2 Osservimo che per trovre le costnti A e B possimo nche rgionre così: se moltiplichimo l equzione + ( + 2)( + 3) = A + 2 + B + 3 per + 2, dopo ver semplificto, ottenimo + + 3
ANALISI REALE E COMPLESSA a.a. 2007-2008
 ANALISI REALE E COMPLESSA.. 2007-2008 1 Successioni e serie di funzioni 1.1 Introduzione In questo cpitolo studimo l convergenz di successioni del tipo n f n, dove le f n sono tutte funzioni vlori reli
ANALISI REALE E COMPLESSA.. 2007-2008 1 Successioni e serie di funzioni 1.1 Introduzione In questo cpitolo studimo l convergenz di successioni del tipo n f n, dove le f n sono tutte funzioni vlori reli
1 b a. f(x) dx. Osservazione 1.2. Se indichiamo con µ il valore medio di f su [a, b], abbiamo che. f(x) dx = µ(b a) =
![1 b a. f(x) dx. Osservazione 1.2. Se indichiamo con µ il valore medio di f su [a, b], abbiamo che. f(x) dx = µ(b a) = 1 b a. f(x) dx. Osservazione 1.2. Se indichiamo con µ il valore medio di f su [a, b], abbiamo che. f(x) dx = µ(b a) =](/thumbs/19/319521.jpg) Note ed esercizi di Anlisi Mtemtic - (Fosci) Ingegneri dell Informzione - 28-29. Lezione del 7 novembre 28. Questi esercizi sono reperibili dll pgin web del corso ttp://utenti.unife.it/dmino.fosci/didttic/mii89.tml
Note ed esercizi di Anlisi Mtemtic - (Fosci) Ingegneri dell Informzione - 28-29. Lezione del 7 novembre 28. Questi esercizi sono reperibili dll pgin web del corso ttp://utenti.unife.it/dmino.fosci/didttic/mii89.tml
x = x(t) y = y(t) t [a, b]
![x = x(t) y = y(t) t [a, b] x = x(t) y = y(t) t [a, b]](/thumbs/50/26298328.jpg) Dt un curv continu. Curve ed integrli di line : t [, b] i punti () = (x(), y()) e (b) = (x(b), y(b)) si chimno primo e secondo estremo dell curv, rispettivmente. L curv si dice chius se () = (b). L curv
Dt un curv continu. Curve ed integrli di line : t [, b] i punti () = (x(), y()) e (b) = (x(b), y(b)) si chimno primo e secondo estremo dell curv, rispettivmente. L curv si dice chius se () = (b). L curv
Anno 5. Applicazione del calcolo degli integrali definiti
 Anno 5 Appliczione del clcolo degli integrli definiti 1 Introduzione In quest lezione vedremo come pplicre il clcolo dell integrle definito per determinre le ree di prticolri figure pine, i volumi dei
Anno 5 Appliczione del clcolo degli integrli definiti 1 Introduzione In quest lezione vedremo come pplicre il clcolo dell integrle definito per determinre le ree di prticolri figure pine, i volumi dei
, x 2. , x 3. è un equazione nella quale le incognite appaiono solo con esponente 1, ossia del tipo:
 Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
1 Il problema del calcolo dell area di una regione piana limitata
 Anlisi Mtemtic 2 1 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 1 INTEGRALI DI FUNZIONI DI UNA VARIABILE REALE 1 Il problem del clcolo dell re di un regione pin limitt Se si consider un
Anlisi Mtemtic 2 1 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 1 INTEGRALI DI FUNZIONI DI UNA VARIABILE REALE 1 Il problem del clcolo dell re di un regione pin limitt Se si consider un
FUNZIONI CONTINUE A TRATTI E LORO INTEGRALI
 FUNZIONI CONTINUE A TRATTI E LORO INTEGRALI Considerimo un funzione f : I R, dove I è un intervllo di R. Si c un punto interno I in cui f è discontinu. Diremo che c è un punto di discontinuità di prim
FUNZIONI CONTINUE A TRATTI E LORO INTEGRALI Considerimo un funzione f : I R, dove I è un intervllo di R. Si c un punto interno I in cui f è discontinu. Diremo che c è un punto di discontinuità di prim
Integrali de niti. Il problema del calcolo di aree ci porterà alla de nizione di integrale de nito.
 Integrli de niti. Il problem di clcolre l re di un regione pin delimitt d gr ci di funzioni si può risolvere usndo l integrle de nito. L integrle de nito st l problem del clcolo di ree come l equzione
Integrli de niti. Il problem di clcolre l re di un regione pin delimitt d gr ci di funzioni si può risolvere usndo l integrle de nito. L integrle de nito st l problem del clcolo di ree come l equzione
INTEGRALI IMPROPRI. f(x) dx. e la funzione f(x) si dice integrabile in senso improprio su (a, b]. Se tale limite esiste ma
![INTEGRALI IMPROPRI. f(x) dx. e la funzione f(x) si dice integrabile in senso improprio su (a, b]. Se tale limite esiste ma INTEGRALI IMPROPRI. f(x) dx. e la funzione f(x) si dice integrabile in senso improprio su (a, b]. Se tale limite esiste ma](/thumbs/17/120065.jpg) INTEGRALI IMPROPRI. Integrli impropri su intervlli itti Dt un funzione f() continu in [, b), ponimo ε f() = f() ε + qundo il ite esiste. Se tle ite esiste finito, l integrle improprio si dice convergente
INTEGRALI IMPROPRI. Integrli impropri su intervlli itti Dt un funzione f() continu in [, b), ponimo ε f() = f() ε + qundo il ite esiste. Se tle ite esiste finito, l integrle improprio si dice convergente
POTENZA CON ESPONENTE REALE
 PRECORSO DI MATEMATICA VIII Lezione ESPONENZIALI E LOGARITMI E. Modic mtemtic@blogscuol.it www.mtemtic.blogscuol.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero rele > 0 ed un numero rele qulunque,
PRECORSO DI MATEMATICA VIII Lezione ESPONENZIALI E LOGARITMI E. Modic mtemtic@blogscuol.it www.mtemtic.blogscuol.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero rele > 0 ed un numero rele qulunque,
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA ESPONENZIALI E LOGARITMI Dr. Ersmo Modic ersmo@glois.it www.glois.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA ESPONENZIALI E LOGARITMI Dr. Ersmo Modic ersmo@glois.it www.glois.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero
Esercizi svolti Limiti. Prof. Chirizzi Marco.
 Cpitolo II Limiti delle funzioni di un vribile Esercizi svolti Limiti Prof. Chirizzi rco www.elettrone.ltervist.org 1) Verificre che risult: = Dobbimo provre che per ogni ε positivo, rbitrrimente piccolo,
Cpitolo II Limiti delle funzioni di un vribile Esercizi svolti Limiti Prof. Chirizzi rco www.elettrone.ltervist.org 1) Verificre che risult: = Dobbimo provre che per ogni ε positivo, rbitrrimente piccolo,
DISPENSE DI ANALISI MATEMATICA. Indice
 DISPENSE DI ANALISI MATEMATICA ANNAMARIA MONTANARI Indice. Integrle di Riemnn.. Proprietà elementri dell integrle di Riemnn 5.2. Teorem fondmentle del clcolo integrle. Primitive 6.3. Integrle generlizzto
DISPENSE DI ANALISI MATEMATICA ANNAMARIA MONTANARI Indice. Integrle di Riemnn.. Proprietà elementri dell integrle di Riemnn 5.2. Teorem fondmentle del clcolo integrle. Primitive 6.3. Integrle generlizzto
Serie di Potenze. Introduciamo il concetto di convergenza puntuale ed uniforme per successioni. { 0 se 1 < x < 1
 Serie di Potenze Introducimo il concetto di convergenz puntule ed uniforme per successioni di funzioni. Definizione 1 Si I un intervllo di R. Si dt l vrire di n N l funzione f n : I R. Dicimo che l successione
Serie di Potenze Introducimo il concetto di convergenz puntule ed uniforme per successioni di funzioni. Definizione 1 Si I un intervllo di R. Si dt l vrire di n N l funzione f n : I R. Dicimo che l successione
FUNZIONI IPERBOLICHE
 FUNZIONI IPERBOLICHE Umberto Mrconi Diprtimento di Mtemtic Pur e Applict Pdov Premess Si [, [, fissto. Voglimo cpire cos signific: w dw perché l funzione integrnd è illimitt. Se considerimo, per b [, [,
FUNZIONI IPERBOLICHE Umberto Mrconi Diprtimento di Mtemtic Pur e Applict Pdov Premess Si [, [, fissto. Voglimo cpire cos signific: w dw perché l funzione integrnd è illimitt. Se considerimo, per b [, [,
Equivalenza tra equazioni di Lagrange e problemi variazionali
 Equivlenz tr equzioni di Lgrnge e problemi AM Cherubini 20 Aprile 2007 1 / 21 Problemi Mostrimo or come si possono ricvre sistemi di equzioni con struttur lgrngin in un mbito diverso: prim si er crtterizzt
Equivlenz tr equzioni di Lgrnge e problemi AM Cherubini 20 Aprile 2007 1 / 21 Problemi Mostrimo or come si possono ricvre sistemi di equzioni con struttur lgrngin in un mbito diverso: prim si er crtterizzt
Pietro Baldi Successioni e serie di funzioni. 1 Convergenza puntuale
 Pietro Bldi Successioni e serie di funzioni Testi di riferimento: W. Rudin, Principi di Anlisi Mtemtic, McGrw-Hill Libri Itli; N. Fusco, P. Mrcellini, C. Sbordone, Anlisi Mtemtic Due, Liguori Editore;
Pietro Bldi Successioni e serie di funzioni Testi di riferimento: W. Rudin, Principi di Anlisi Mtemtic, McGrw-Hill Libri Itli; N. Fusco, P. Mrcellini, C. Sbordone, Anlisi Mtemtic Due, Liguori Editore;
Il problema delle aree. Metodo di esaustione.
 INTEGRALE DEFINITO. DEFINIZIONE E SIGNIFICATO GEOMETRICO. PROPRIETA DELL INTEGRALE DEFINITO. FUNZIONE INTEGRALE. TEOREMA DELLA MEDIA. TEOREMA FONDAMENTALE DEL CALCOLO INTEGRALE. FORMULA DI LEIBNITZ NEWTON.
INTEGRALE DEFINITO. DEFINIZIONE E SIGNIFICATO GEOMETRICO. PROPRIETA DELL INTEGRALE DEFINITO. FUNZIONE INTEGRALE. TEOREMA DELLA MEDIA. TEOREMA FONDAMENTALE DEL CALCOLO INTEGRALE. FORMULA DI LEIBNITZ NEWTON.
Corso di Analisi Matematica. Calcolo integrale
 .. 2011/12 Lure triennle in Informtic Corso di Anlisi Mtemtic Clcolo integrle Avvertenz Questi sono ppunti informli delle lezioni, che vengono resi disponibili per comodità degli studenti. Prte del mterile
.. 2011/12 Lure triennle in Informtic Corso di Anlisi Mtemtic Clcolo integrle Avvertenz Questi sono ppunti informli delle lezioni, che vengono resi disponibili per comodità degli studenti. Prte del mterile
I Teoremi di Green, della divergenza (o di Gauss) e di Stokes
 I Teoremi di Green, dell divergenz o di Guss e di Stokes In R Si un sottoinsieme limitto di R semplice rispetto d entrmbi gli ssi crtesini con costituit dll unione di un numero finito di sostegni di curve
I Teoremi di Green, dell divergenz o di Guss e di Stokes In R Si un sottoinsieme limitto di R semplice rispetto d entrmbi gli ssi crtesini con costituit dll unione di un numero finito di sostegni di curve
TEORIA ELEMENTARE DEL PROBLEMA DI CAUCHY
 TEORIA ELEMENTARE DEL PROBLEMA DI CAUCHY DANIELE ANDREUCCI DIP. METODI E MODELLI, UNIVERSITÀ LA SAPIENZA VIA A.SCARPA 16, 00161 ROMA, ITALY ndreucci@dmmm.unirom1.it 1. Notzione fondmentle e prime definizioni
TEORIA ELEMENTARE DEL PROBLEMA DI CAUCHY DANIELE ANDREUCCI DIP. METODI E MODELLI, UNIVERSITÀ LA SAPIENZA VIA A.SCARPA 16, 00161 ROMA, ITALY ndreucci@dmmm.unirom1.it 1. Notzione fondmentle e prime definizioni
Esponenziali e logaritmi
 Esponenzili e ritmi ESPONENZIALI Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z Sono definite: ( ) ( ) ( ) 7 7 Non sono definite:
Esponenzili e ritmi ESPONENZIALI Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z Sono definite: ( ) ( ) ( ) 7 7 Non sono definite:
INTEGRAZIONE NUMERICA
 INTEGRAZIONE NUMERICA Frncesc Pelosi Diprtimento di Mtemtic, Università di Rom Tor Vergt CALCOLO NUMERICO.. 008 009 http://www.mt.unirom.it/ pelosi/ INTEGRAZIONE NUMERICA p.1/0 INTEGRAZIONE NUMERICA Dt
INTEGRAZIONE NUMERICA Frncesc Pelosi Diprtimento di Mtemtic, Università di Rom Tor Vergt CALCOLO NUMERICO.. 008 009 http://www.mt.unirom.it/ pelosi/ INTEGRAZIONE NUMERICA p.1/0 INTEGRAZIONE NUMERICA Dt
Maturità scientifica, corso di ordinamento, sessione ordinaria 2000-2001
 Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone Mturità scientific, corso di ordinmento, sessione ordinri 000-001 PROBLEMA 1 Si consideri l seguente relzione tr le vribili reli x, y: 1 1 1 +
Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone Mturità scientific, corso di ordinmento, sessione ordinri 000-001 PROBLEMA 1 Si consideri l seguente relzione tr le vribili reli x, y: 1 1 1 +
Esercizi su spazi ed operatori lineari
 Esercizi su spzi ed opertori lineri Corso di Fisic Mtemtic 2,.. 2013-2014 Diprtimento di Mtemtic, Università di Milno 23 Ottobre 2013 1 Spzio L 2 Esercizio 1. Per = 0, b = 1, dire quli delle seguenti funzioni
Esercizi su spzi ed opertori lineri Corso di Fisic Mtemtic 2,.. 2013-2014 Diprtimento di Mtemtic, Università di Milno 23 Ottobre 2013 1 Spzio L 2 Esercizio 1. Per = 0, b = 1, dire quli delle seguenti funzioni
B8. Equazioni di secondo grado
 B8. Equzioni di secondo grdo B8.1 Legge di nnullmento del prodotto Spendo che b0 si può dedurre che 0 oppure b0. Quest è l legge di nnullmento del prodotto. Pertnto spendo che (-1) (+)0 llor dovrà vlere
B8. Equzioni di secondo grdo B8.1 Legge di nnullmento del prodotto Spendo che b0 si può dedurre che 0 oppure b0. Quest è l legge di nnullmento del prodotto. Pertnto spendo che (-1) (+)0 llor dovrà vlere
2. Teoremi per eseguire operazioni con i limiti in forma determinata
 . Teoremi per eseguire operzioni con i iti in form determint Vedimo dunque i teoremi che consentono il clcolo dei iti, ttrverso i quli si riconducono le situzioni rticolte semplici operzioni lgebriche
. Teoremi per eseguire operzioni con i iti in form determint Vedimo dunque i teoremi che consentono il clcolo dei iti, ttrverso i quli si riconducono le situzioni rticolte semplici operzioni lgebriche
26/03/2012. Integrale Definito. Calcolo delle Aree. Appunti di analisi matematica: Il concetto d integrale nasce per risolvere due classi di problemi:
 ppunti di nlisi mtemtic: Integrle efinito Il concetto d integrle nsce per risolvere due clssi di prolemi: Integrle efinito lcolo delle ree di fig. delimitte d curve clcolo di volumi clcolo del lvoro di
ppunti di nlisi mtemtic: Integrle efinito Il concetto d integrle nsce per risolvere due clssi di prolemi: Integrle efinito lcolo delle ree di fig. delimitte d curve clcolo di volumi clcolo del lvoro di
8. Prodotto scalare, Spazi Euclidei.
 8. Prodotto sclre, Spzi Euclidei. Ricordimo l definizione di prodotto sclre di due vettori del pino VO 2 (vle in modo del tutto nlogo nche in VO 3 ). Definizione: Sino v, w VO 2 e si θ l ngolo convesso
8. Prodotto sclre, Spzi Euclidei. Ricordimo l definizione di prodotto sclre di due vettori del pino VO 2 (vle in modo del tutto nlogo nche in VO 3 ). Definizione: Sino v, w VO 2 e si θ l ngolo convesso
Siano α(x), β(x) due funzioni continue in un intervallo [a, b] IR tali che. α(x) β(x).
![Siano α(x), β(x) due funzioni continue in un intervallo [a, b] IR tali che. α(x) β(x). Siano α(x), β(x) due funzioni continue in un intervallo [a, b] IR tali che. α(x) β(x).](/thumbs/22/1643654.jpg) OMINI NORMALI. efinizione Sino α(), β() due funzioni continue in un intervllo [, b] IR tli che L insieme del pino (figur 5. pg. ) α() β(). = {(, ) [, b] IR : α() β()} si chim dominio normle rispetto ll
OMINI NORMALI. efinizione Sino α(), β() due funzioni continue in un intervllo [, b] IR tli che L insieme del pino (figur 5. pg. ) α() β(). = {(, ) [, b] IR : α() β()} si chim dominio normle rispetto ll
Integrali. all integrale definito all integrale indefinito. Integrali: riepilogo
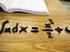 Integrli ll integrle deinito ll integrle indeinito Indice dell lezione Integrle Deinito Rettngoloide Integrle deinito come re del rettngoloide Esempi e propriet Primitiv Teorem ondmentle del clcolo integrle
Integrli ll integrle deinito ll integrle indeinito Indice dell lezione Integrle Deinito Rettngoloide Integrle deinito come re del rettngoloide Esempi e propriet Primitiv Teorem ondmentle del clcolo integrle
b a 2. Il candidato spieghi, avvalendosi di un esempio, il teorema del valor medio.
 Domnde preprzione terz prov. Considert, come esempio, l funzione nell intervllo [,], il cndidto illustri il concetto di integrle definito. INTEGRALE DEFINITO, prendendo in esme un generic funzione f()
Domnde preprzione terz prov. Considert, come esempio, l funzione nell intervllo [,], il cndidto illustri il concetto di integrle definito. INTEGRALE DEFINITO, prendendo in esme un generic funzione f()
2 x = 64 (1) L esponente (x) a cui elevare la base (2) per ottenere il numero 64 è detto logaritmo (logaritmo in base 2 di 64), indicato così:
 Considerimo il seguente problem: si vuole trovre il numero rele tle che: = () L esponente () cui elevre l bse () per ottenere il numero è detto ritmo (ritmo in bse di ), indicto così: In prticolre in questo
Considerimo il seguente problem: si vuole trovre il numero rele tle che: = () L esponente () cui elevre l bse () per ottenere il numero è detto ritmo (ritmo in bse di ), indicto così: In prticolre in questo
1 Integrali generalizzati su intervalli illimitati
 Lezioni per il corso di Anlisi 2, AA 07-08. Dott.ss Sndr Lucente Argomento: Integrli generlizzti 1 1 Integrli generlizzti su intervlli ilitti Definizione 1.1. Si f : [,[ R un funzione continu. Se esiste
Lezioni per il corso di Anlisi 2, AA 07-08. Dott.ss Sndr Lucente Argomento: Integrli generlizzti 1 1 Integrli generlizzti su intervlli ilitti Definizione 1.1. Si f : [,[ R un funzione continu. Se esiste
" Osservazione. 6.1 Integrale indefinito. R Definizione (Primitiva) E Esempio 6.1 CAPITOLO 6
 CAPITOLO 6 Clcolo integrle 6. Integrle indefinito L nozione fondmentle del clcolo integrle è quell di funzione primitiv di un funzione f (). Tle nozione è in qulche modo speculre ll nozione di funzione
CAPITOLO 6 Clcolo integrle 6. Integrle indefinito L nozione fondmentle del clcolo integrle è quell di funzione primitiv di un funzione f (). Tle nozione è in qulche modo speculre ll nozione di funzione
si definisce Funzione Integrale; si chiama funzione integrale in quanto il suo * x
 Appunti elorti dll prof.ss Biondin Gldi Funzione integrle Si y = f() un funzione continu in un intervllo [; ] e si 0 [; ]; l integrle 0 f()d si definisce Funzione Integrle; si chim funzione integrle in
Appunti elorti dll prof.ss Biondin Gldi Funzione integrle Si y = f() un funzione continu in un intervllo [; ] e si 0 [; ]; l integrle 0 f()d si definisce Funzione Integrle; si chim funzione integrle in
1. Elementi di analisi funzionale Esercizi
 . Elementi di nlisi funzionle Esercizi http://www.cirm.unibo.it/~brozzi/mi/pdf/mi-cp.-ese.pdf.. Spzi vettorili.. Spzi vettorili normti.-. Dimostrre l diseguglinz tringolre in C n reltivmente ll norm (
. Elementi di nlisi funzionle Esercizi http://www.cirm.unibo.it/~brozzi/mi/pdf/mi-cp.-ese.pdf.. Spzi vettorili.. Spzi vettorili normti.-. Dimostrre l diseguglinz tringolre in C n reltivmente ll norm (
Appunti di Analisi Matematica 1
 Appunti di Anlisi Mtemtic 1 MASTER IN ECONOMIA DIGITALE & e-business Centro per lo studio dei sistemi complessi Università di Sien Mrzo 2005 Prof. Polo Nistri Un funzione (o ppliczione) tr due insiemi
Appunti di Anlisi Mtemtic 1 MASTER IN ECONOMIA DIGITALE & e-business Centro per lo studio dei sistemi complessi Università di Sien Mrzo 2005 Prof. Polo Nistri Un funzione (o ppliczione) tr due insiemi
LEZIONE 20. è lineare. Per la commutatività del prodotto scalare segue anche la linearità dell applicazione
 LEZIONE 20 20.1. Prodotti sclri. Definizione 20.1.1. Si V uno spzio vettorile su R. Un prodotto sclre su V è un ppliczione tle che:, : V V R (v 1, v 2 ) v 1, v 2 (PS1) per ogni v 1, v 2 V si h v 1, v 2
LEZIONE 20 20.1. Prodotti sclri. Definizione 20.1.1. Si V uno spzio vettorile su R. Un prodotto sclre su V è un ppliczione tle che:, : V V R (v 1, v 2 ) v 1, v 2 (PS1) per ogni v 1, v 2 V si h v 1, v 2
TEST DI MATEMATICA. Funzioni in una, Funzioni in due variabili Integrali Equazioni differenziali. 1) Il valore del limite seguente. e e. e 1.
 TEST DI MATEMATICA Funzioni in un, Funzioni in due vriili Integrli Equzioni differenzili ) Il vlore del limite seguente e e e lim è ) Il vlore del limite seguente 5 lim 5 è : ) L derivt prim dell funzione
TEST DI MATEMATICA Funzioni in un, Funzioni in due vriili Integrli Equzioni differenzili ) Il vlore del limite seguente e e e lim è ) Il vlore del limite seguente 5 lim 5 è : ) L derivt prim dell funzione
Calcolo integrale per funzioni di una variabile
 Cpitolo 10 Clcolo integrle per funzioni di un vribile 10.1 Funzioni primitive Abbimo studito il problem di dedurre d un dt funzione l su derivt. Voglimo or occuprci del problem inverso: dt un funzione
Cpitolo 10 Clcolo integrle per funzioni di un vribile 10.1 Funzioni primitive Abbimo studito il problem di dedurre d un dt funzione l su derivt. Voglimo or occuprci del problem inverso: dt un funzione
SUGLI INSIEMI. 1.Insiemi e operazioni su di essi
 SUGLI INSIEMI 1.Insiemi e operzioni su di essi Il concetto di insieme è primitivo ed è sinonimo di clsse, totlità. Si A un insieme di elementi qulunque. Per indicre che è un elemento di A scriveremo A.
SUGLI INSIEMI 1.Insiemi e operzioni su di essi Il concetto di insieme è primitivo ed è sinonimo di clsse, totlità. Si A un insieme di elementi qulunque. Per indicre che è un elemento di A scriveremo A.
Equazioni di 2 grado. Definizioni Equazioni incomplete Equazione completa Relazioni tra i coefficienti della equazione e le sue soluzioni Esercizi
 Equzioni di grdo Definizioni Equzioni incomplete Equzione complet Relzioni tr i coefficienti dell equzione e le sue soluzioni Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Un equzione è: Un uguglinz
Equzioni di grdo Definizioni Equzioni incomplete Equzione complet Relzioni tr i coefficienti dell equzione e le sue soluzioni Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Un equzione è: Un uguglinz
Scheda Sei ESPONENZIALI E LOGARITMI. 0,+. Inoltre valgono le
 Sched Sei ESPONENZIALI E LOGARITMI L funzione esponenzile Assegnto un numero rele >0, si dice funzione esponenzile in bse l funzione Grfici dell funzione esponenzile Se = l funzione esponenzile è costnte:
Sched Sei ESPONENZIALI E LOGARITMI L funzione esponenzile Assegnto un numero rele >0, si dice funzione esponenzile in bse l funzione Grfici dell funzione esponenzile Se = l funzione esponenzile è costnte:
INTEGRALI IMPROPRI. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Integrali impropri cap10.pdf 1
 INTEGRALI IMPROPRI c Pol Gervsio - Anlisi Mtemtic - A.A. 6/7 Integrli impropri cp.pdf Abbimo visto che l integrle di Riemnn è definito per funzioni limitte e su intervlli limitti. Si or I R un intervllo
INTEGRALI IMPROPRI c Pol Gervsio - Anlisi Mtemtic - A.A. 6/7 Integrli impropri cp.pdf Abbimo visto che l integrle di Riemnn è definito per funzioni limitte e su intervlli limitti. Si or I R un intervllo
Lezione 14. Risoluzione delle equazioni algebriche.
 Lezione Prerequisiti: Lezioni 8,. Risoluzione delle equzioni lgebriche. Si F un cmpo, e si K un chiusur lgebric di F. Si f ( ) F[ ] non costnte. Studimo i metodi di risoluzione per l equzione f ( ) = 0,
Lezione Prerequisiti: Lezioni 8,. Risoluzione delle equzioni lgebriche. Si F un cmpo, e si K un chiusur lgebric di F. Si f ( ) F[ ] non costnte. Studimo i metodi di risoluzione per l equzione f ( ) = 0,
dr Valerio Curcio Le affinità omologiche Le affinità omologiche
 1 Le ffinità omologiche 2 Tringoli omologici: Due tringoli si dicono omologici se le rette congiungenti i punti omologhi dei due tringoli si incontrno in un medesimo punto. Principio dei tringoli omologici
1 Le ffinità omologiche 2 Tringoli omologici: Due tringoli si dicono omologici se le rette congiungenti i punti omologhi dei due tringoli si incontrno in un medesimo punto. Principio dei tringoli omologici
Esercizio 1. Dimostrare che se (X, d) è uno spazio metrico anche (X, d ) lo è, dove d =
 I seguenti esercizi sono stti proposti, e qusi tutti risolti, ttrverso l miling list del corso di Geometri IV durnte l nno ccdemico 2004/2005. Esercizio 1. Dimostrre che se (X, d) è uno spzio metrico nche
I seguenti esercizi sono stti proposti, e qusi tutti risolti, ttrverso l miling list del corso di Geometri IV durnte l nno ccdemico 2004/2005. Esercizio 1. Dimostrre che se (X, d) è uno spzio metrico nche
Analisi e Geometria 1
 Anlisi e Geometri Esercizi sugli integrli Integrli propri. Clcolre i seguenti integrli immediti: I = I = I 5 = ln e e d I = e + e + 6e + e d I = rtg ln ( + ln ) d I 6 = e e + d d rtg + ( + ) ( + ( + )
Anlisi e Geometri Esercizi sugli integrli Integrli propri. Clcolre i seguenti integrli immediti: I = I = I 5 = ln e e d I = e + e + 6e + e d I = rtg ln ( + ln ) d I 6 = e e + d d rtg + ( + ) ( + ( + )
INTERVALLI NELL INSIEME R
 INTEVALLI NELL INSIEME Lo studio dell topologi (1) (dl greco "nlysis situs" ossi "studio del luogo") dell'insieme è di fondmentle importnz per gli rgomenti e i prolemi di nlisi infinitesimle. Il "luogo"
INTEVALLI NELL INSIEME Lo studio dell topologi (1) (dl greco "nlysis situs" ossi "studio del luogo") dell'insieme è di fondmentle importnz per gli rgomenti e i prolemi di nlisi infinitesimle. Il "luogo"
Lezione 16 Derivate ed Integrali
 Lezione 16 Derivte ed Integrli Frnk Sullivn 1 Dicembre 11 1 Prim Or Compiti di letture ed esercizi per 3 Dicembre Durnte l lezione di oggi pplicheremo le regole per differenzire funzioni l clcolo di integrli.
Lezione 16 Derivte ed Integrli Frnk Sullivn 1 Dicembre 11 1 Prim Or Compiti di letture ed esercizi per 3 Dicembre Durnte l lezione di oggi pplicheremo le regole per differenzire funzioni l clcolo di integrli.
Corso di Analisi Matematica Calcolo integrale per funzioni di una variabile
 Corso di Anlisi Mtemtic Clcolo integrle per funzioni di un vribile Lure in Informtic e Comuniczione Digitle A.A. 2013/2014 Università di Bri ICD (Bri) Anlisi Mtemtic 1 / 40 1 L integrle come limite di
Corso di Anlisi Mtemtic Clcolo integrle per funzioni di un vribile Lure in Informtic e Comuniczione Digitle A.A. 2013/2014 Università di Bri ICD (Bri) Anlisi Mtemtic 1 / 40 1 L integrle come limite di
Calcolo Integrale. F (x) = f(x)?
 3 Clcolo Integrle Nello studio del clcolo differenzile si è visto come si può ssocire d un funzione l su derivt. Il clcolo integrle si occup del problem inverso: dt un funzione f è possibile determinre
3 Clcolo Integrle Nello studio del clcolo differenzile si è visto come si può ssocire d un funzione l su derivt. Il clcolo integrle si occup del problem inverso: dt un funzione f è possibile determinre
ELEMENTI DI TEORIA DEI NUMERI
 ELEMENTI DI TEORIA DEI NUMERI 1. Richimi di teori Con Z indichimo l insieme dei numeri reltivi. Comincimo con il ricordre l definizione di quoziente e resto dell divisione di due numeri in Z. Definizione
ELEMENTI DI TEORIA DEI NUMERI 1. Richimi di teori Con Z indichimo l insieme dei numeri reltivi. Comincimo con il ricordre l definizione di quoziente e resto dell divisione di due numeri in Z. Definizione
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2002 Sessione ordinaria
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO Sessione ordinri Il cndidto risolv uno dei due problemi e 5 dei quesiti in cui si rticol il questionrio. PROBLEMA In un pino, riferito d un sistem
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO Sessione ordinri Il cndidto risolv uno dei due problemi e 5 dei quesiti in cui si rticol il questionrio. PROBLEMA In un pino, riferito d un sistem
Differenziale. Consideriamo la variazione finita, x della variabile indipendente a cui corrisponde una variazione finita della funzione f x, f x y
 Differenzile Considerimo l vrizione finit, dell vriile indipendente cui corrisponde un vrizione finit dell funzione f, f y Δf 1 Δ 2 L vrizione dell vriile dipendente puo' essere molto piccol, infinitesim
Differenzile Considerimo l vrizione finit, dell vriile indipendente cui corrisponde un vrizione finit dell funzione f, f y Δf 1 Δ 2 L vrizione dell vriile dipendente puo' essere molto piccol, infinitesim
Il calcolo integrale
 CAPITOLO 4 Il clcolo integrle Il problem che ffrontimo in questo cpitolo è il clcolo di ree di lcune regioni del pino. Inizimo il cpitolo spiegndo quli regioni pine simo interessti. Questi rgomenti sono
CAPITOLO 4 Il clcolo integrle Il problem che ffrontimo in questo cpitolo è il clcolo di ree di lcune regioni del pino. Inizimo il cpitolo spiegndo quli regioni pine simo interessti. Questi rgomenti sono
Nome.Cognome classe 5D 18 Marzo 2014. Verifica di matematica
 Nome Cognome cls 5D 18 Mrzo 01 Problem Verific di mtemtic In un sistem di riferimento crtesino Oy, si consideri l funzione: ln f ( > 0 0 e si determini il vlore del prmetro rele in modo tle che l funzione
Nome Cognome cls 5D 18 Mrzo 01 Problem Verific di mtemtic In un sistem di riferimento crtesino Oy, si consideri l funzione: ln f ( > 0 0 e si determini il vlore del prmetro rele in modo tle che l funzione
II-8 Integrale di Riemann
 II-8 INTEGRALE DI RIEMANN DEFINIZIONE DI INTEGRALE DI RIEMANN II-8 Integrle di Riemnn Indice Definizione di integrle di Riemnn Condizioni di esistenz dell integrle di Riemnn 3 3 Proprietà dell integrle
II-8 INTEGRALE DI RIEMANN DEFINIZIONE DI INTEGRALE DI RIEMANN II-8 Integrle di Riemnn Indice Definizione di integrle di Riemnn Condizioni di esistenz dell integrle di Riemnn 3 3 Proprietà dell integrle
1 Definizione di integrale di Riemann 1. 2 Condizioni di esistenza dell integrale di Riemann 3. 3 Proprietà dell integrale di Riemann 4
 DEFINIZIONE DI INTEGRALE DI RIEMANN Integrle di Riemnn Indice Definizione di integrle di Riemnn Condizioni di esistenz dell integrle di Riemnn 3 3 Proprietà dell integrle di Riemnn 4 4 Clcolo dell integrle
DEFINIZIONE DI INTEGRALE DI RIEMANN Integrle di Riemnn Indice Definizione di integrle di Riemnn Condizioni di esistenz dell integrle di Riemnn 3 3 Proprietà dell integrle di Riemnn 4 4 Clcolo dell integrle
AUTOVALORI ED AUTOVETTORI. Sia V uno spazio vettoriale di dimensione finita n.
 AUTOVALORI ED AUTOVETTORI Si V uno spzio vettorile di dimensione finit n. Dicesi endomorfismo di V ogni ppliczione linere f : V V dello spzio vettorile in sé. Se f è un endomorfismo di V in V, considert
AUTOVALORI ED AUTOVETTORI Si V uno spzio vettorile di dimensione finit n. Dicesi endomorfismo di V ogni ppliczione linere f : V V dello spzio vettorile in sé. Se f è un endomorfismo di V in V, considert
Erasmo Modica. : K K K
 L insieme dei numeri reli L INSIEME DEI NUMERI REALI Ersmo Modic helthinsurnce@tin.it www.glois.it Per introdurre l insieme dei numeri reli si hnno disposizione diversi modi. Generlmente l iennio si preferisce
L insieme dei numeri reli L INSIEME DEI NUMERI REALI Ersmo Modic helthinsurnce@tin.it www.glois.it Per introdurre l insieme dei numeri reli si hnno disposizione diversi modi. Generlmente l iennio si preferisce
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2002 Sessione straordinaria
 ESAME DI STAT DI LICE SCIENTIFIC CRS DI RDINAMENT 00 Sessione strordinri Il cndidto risolv uno dei due problemi e 5 dei 0 quesiti in cui si rticol il questionrio. PRBLEMA Con riferimento un sistem monometrico
ESAME DI STAT DI LICE SCIENTIFIC CRS DI RDINAMENT 00 Sessione strordinri Il cndidto risolv uno dei due problemi e 5 dei 0 quesiti in cui si rticol il questionrio. PRBLEMA Con riferimento un sistem monometrico
Integrazione numerica. I(f) := Non sempre si riesce a trovare la forma esplicita della primitiva.
 Approssimzione numeric di: Motivzioni. Integrzione numeric I(f) = f(x)dx. Non sempre si riesce trovre l form esplicit dell primitiv. Vlutzione costos dell primitiv. L funzione d integrre può essere dt
Approssimzione numeric di: Motivzioni. Integrzione numeric I(f) = f(x)dx. Non sempre si riesce trovre l form esplicit dell primitiv. Vlutzione costos dell primitiv. L funzione d integrre può essere dt
Seconda prova maturita 2016 soluzione secondo problema di matematica scientifico
 Second prov mturit 06 soluzione secondo problem di mtemtic scientifico Skuol.net June, 06 Primo Problem Le tre funzioni proposte sono f () ( ) k f () 6 + 9k + f () cos( π k ). Punto Affinche l funzione
Second prov mturit 06 soluzione secondo problem di mtemtic scientifico Skuol.net June, 06 Primo Problem Le tre funzioni proposte sono f () ( ) k f () 6 + 9k + f () cos( π k ). Punto Affinche l funzione
Proiettività della Retta e del Piano.
 Introduzione. In queste note proponimo l clssificzione delle proiettività per l rett proiettiv ed il pino proiettivo su un corpo lgebricmente chiuso. Nel cso dell rett studieremo nche il cso del corpo
Introduzione. In queste note proponimo l clssificzione delle proiettività per l rett proiettiv ed il pino proiettivo su un corpo lgebricmente chiuso. Nel cso dell rett studieremo nche il cso del corpo
1 Integrali impropri di funzioni continue
 ntegrli impropri di funzioni continue. ntegrli impropri su intervlli semiperti Definizione Dt un funzione continu f : [, b) R, con b +, si dice che f è integrbile se esiste finito il t b f(x) dx ed in
ntegrli impropri di funzioni continue. ntegrli impropri su intervlli semiperti Definizione Dt un funzione continu f : [, b) R, con b +, si dice che f è integrbile se esiste finito il t b f(x) dx ed in
Teoremi sulle funzioni derivabili
 Teoremi sulle unzioni derivili Inizimo con l deinizione di punto di mssimo o minimo reltivo di un unzione. Deinizione: D è un punto di mssimo reltivo se esiste un intorno I tle che : I Deinizione: D è
Teoremi sulle unzioni derivili Inizimo con l deinizione di punto di mssimo o minimo reltivo di un unzione. Deinizione: D è un punto di mssimo reltivo se esiste un intorno I tle che : I Deinizione: D è
Teorema della Divergenza (di Gauss)
 eorem dell ivergenz (di Guss) i un dominio tridimensionle regolre, l cui frontier è un superficie chius orientt con cmpo normle unitrionˆ uscente d. e F(,,z) F (,,z) i F (,,z) j F (,,z) k è un cmpo vettorile
eorem dell ivergenz (di Guss) i un dominio tridimensionle regolre, l cui frontier è un superficie chius orientt con cmpo normle unitrionˆ uscente d. e F(,,z) F (,,z) i F (,,z) j F (,,z) k è un cmpo vettorile
Funzioni a variazione limitata
 Cpitolo 1 Funzioni vrizione limitt 1.1 Il problem delle primitive di funzioni L 1 Il problem dell ricerc delle primitive di un ssegnt funzione f : I R con I = [, b] intervllo limitto, cioè le soluzioni
Cpitolo 1 Funzioni vrizione limitt 1.1 Il problem delle primitive di funzioni L 1 Il problem dell ricerc delle primitive di un ssegnt funzione f : I R con I = [, b] intervllo limitto, cioè le soluzioni
Integrale Definito. Appunti di analisi matematica: Il concetto d integrale nasce per risolvere due classi di problemi: Integrale Definito
 Appunti di nlisi mtemtic: Integrle Deinito Il concetto d integrle nsce per risolvere due clssi di prolemi: Integrle Deinito Clcolo delle ree di ig. delimitte d curve clcolo di volumi clcolo del lvoro di
Appunti di nlisi mtemtic: Integrle Deinito Il concetto d integrle nsce per risolvere due clssi di prolemi: Integrle Deinito Clcolo delle ree di ig. delimitte d curve clcolo di volumi clcolo del lvoro di
Nome.Cognome. 18 Dicembre 2008 Classe 4G. VERIFICA di MATEMATICA
 Nome.Cognome. 8 Dicembre 008 Clsse G VERIFICA di MATEMATICA A) Risolvi le seguenti disequzioni goniometriche sin ) sin + ) 0 6 tn cos + sin ) 0 (punti:0,5) ) tn + tn > 0 sin 5) sin > cos (punti: ) 6) sin
Nome.Cognome. 8 Dicembre 008 Clsse G VERIFICA di MATEMATICA A) Risolvi le seguenti disequzioni goniometriche sin ) sin + ) 0 6 tn cos + sin ) 0 (punti:0,5) ) tn + tn > 0 sin 5) sin > cos (punti: ) 6) sin
13. Metodi Hilbertiani per la soluzione di problemi ai limiti
 13. Metodi Hilbertini per l soluzione di problemi i limiti Nell Sezione precedente bbimo sviluppto, nche se in form estremmente concis, lcuni spetti dell teori degli opertori lineri fr spzi normti, soffermndoci
13. Metodi Hilbertini per l soluzione di problemi i limiti Nell Sezione precedente bbimo sviluppto, nche se in form estremmente concis, lcuni spetti dell teori degli opertori lineri fr spzi normti, soffermndoci
ESPONENZIALI E LOGARITMI
 Esponenzili e logritmi ESPONENZIALI E LOGARITMI Potenze Fino d or si sono definite le potenze d esponenete intero e rzionle (si positivi che negtivi). Ripssimo le definizioni e i concetti che li rigurdno:
Esponenzili e logritmi ESPONENZIALI E LOGARITMI Potenze Fino d or si sono definite le potenze d esponenete intero e rzionle (si positivi che negtivi). Ripssimo le definizioni e i concetti che li rigurdno:
Ellisse riferita al centro degli assi
 Appunti delle lezioni tenute in clsse: ellisse e iperole Ellisse riferit l centro degli ssi Dti due punti F ed F detti fuochi, l ellisse è il luogo geometrico dei punti P del pino per cui è costnte l somm
Appunti delle lezioni tenute in clsse: ellisse e iperole Ellisse riferit l centro degli ssi Dti due punti F ed F detti fuochi, l ellisse è il luogo geometrico dei punti P del pino per cui è costnte l somm
acuradi Luca Cabibbo e Walter Didimo Esercizi di Informatica teorica - Luca Cabibbo e Walter Didimo 1
 curdi Luc Cio e Wlter Didimo Esercizi di Informtic teoric - Luc Cio e Wlter Didimo 1 espressioni regolri e grmmtiche regolri proprietà decidiili dei linguggi regolri teorem di Myhill-Nerode notzioni sul
curdi Luc Cio e Wlter Didimo Esercizi di Informtic teoric - Luc Cio e Wlter Didimo 1 espressioni regolri e grmmtiche regolri proprietà decidiili dei linguggi regolri teorem di Myhill-Nerode notzioni sul
Equazioni 1 grado. Definizioni Classificazione Risoluzione Esercizi
 Equzioni grdo Definizioni Clssificzione Risoluzione Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Prendimo in esme le due espressioni numeriche 8 entrmbe sono uguli 7, e l scrittur si chim uguglinz
Equzioni grdo Definizioni Clssificzione Risoluzione Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Prendimo in esme le due espressioni numeriche 8 entrmbe sono uguli 7, e l scrittur si chim uguglinz
LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13)
 LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13) DISPENSA N. 9 Sommrio. Crtterizzimo l equivlenz elementre in termini di sistemi di isomorfismi przili e di giochi di Ehrenfeucht-Frïssé. 1. Giochi di Ehrenfeucht-Frïssé
LOGICA MATEMATICA PER INFORMATICA (A.A. 12/13) DISPENSA N. 9 Sommrio. Crtterizzimo l equivlenz elementre in termini di sistemi di isomorfismi przili e di giochi di Ehrenfeucht-Frïssé. 1. Giochi di Ehrenfeucht-Frïssé
Capitolo 7. Integrali doppi. 7.1 Motivazioni
 Cpitolo 7 Integrli doppi In questo cpitolo studieremo gli integrli per funzioni di più vribili: più precismente ci occuperemo degli integrli di funzioni di due vribili (dunque integrli doppi), m piccole
Cpitolo 7 Integrli doppi In questo cpitolo studieremo gli integrli per funzioni di più vribili: più precismente ci occuperemo degli integrli di funzioni di due vribili (dunque integrli doppi), m piccole
Integrale definito. Introduzione: il problema delle aree
 Integrle definito Introduzione: il prolem delle ree Il prolem delle ree è uno dei tre grndi prolemi che ci sono stti trmndti dgli ntichi, che lo definivno come il prolem dell qudrtur del cerchio: trovre,
Integrle definito Introduzione: il prolem delle ree Il prolem delle ree è uno dei tre grndi prolemi che ci sono stti trmndti dgli ntichi, che lo definivno come il prolem dell qudrtur del cerchio: trovre,
Il volume del cilindro è dato dal prodotto della superficie di base per l altezza, quindi
 Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone 3 Questionrio Quesito 1 Provre che un sfer è equivlente i /3 del cilindro circoscritto. r 4 3 Il volume dell sfer è 3 r Il volume del cilindro
Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone 3 Questionrio Quesito 1 Provre che un sfer è equivlente i /3 del cilindro circoscritto. r 4 3 Il volume dell sfer è 3 r Il volume del cilindro
Successioni di funzioni
 Successioni di funzioni 3.1 Introduzione Considerimo l successione (x n ) n0,icuiterminisono 1, x,x 2,x 3,..., x n,... Si trtt dell progressione geometric di termine inizile 1 e rgione x, che bbimo già
Successioni di funzioni 3.1 Introduzione Considerimo l successione (x n ) n0,icuiterminisono 1, x,x 2,x 3,..., x n,... Si trtt dell progressione geometric di termine inizile 1 e rgione x, che bbimo già
Integrazione Numerica
 Integrzione Numeric Si f un funzione integrbile sull intervllo [, b]. Il suo integrle I (f ) = b f (x) dx può essere difficile d clcolre (può nche non essere vlutbile in form esplicit). Un formul esplicit
Integrzione Numeric Si f un funzione integrbile sull intervllo [, b]. Il suo integrle I (f ) = b f (x) dx può essere difficile d clcolre (può nche non essere vlutbile in form esplicit). Un formul esplicit
( x) a) La simmetrica della parabola rispetto all origine è tale che: La parabola di equazione y = x + ax a ha vertice V = = mentre la parabola y S
 Sessione ordinri 996 Liceo di ordinmento Soluzione di De Ros Nicol ) In un pino, riferito d un sistem di ssi crtesini ortogonli (O), sono ssegnte le prbole di equzione:, dove è un numero rele positivo.
Sessione ordinri 996 Liceo di ordinmento Soluzione di De Ros Nicol ) In un pino, riferito d un sistem di ssi crtesini ortogonli (O), sono ssegnte le prbole di equzione:, dove è un numero rele positivo.
E U Q A U Z A I Z O I N O I N DI SE S C E O C N O DO
 EQUAZIONI DI ECONDO GRADO Riepilogo delle soluzioni in bse l segno di < φ : b > : b b Prof I voi, EQUAZIONI DI ECONDO GRADO EQUAZIONI PURE DI ECONDO GRADO : EEMPI ) ) ) 7 7 ) > φ (impossibile) ) impossibil
EQUAZIONI DI ECONDO GRADO Riepilogo delle soluzioni in bse l segno di < φ : b > : b b Prof I voi, EQUAZIONI DI ECONDO GRADO EQUAZIONI PURE DI ECONDO GRADO : EEMPI ) ) ) 7 7 ) > φ (impossibile) ) impossibil
Esponenziali e logaritmi
 Teori in sintesi ESPONENZIALI Potenze con esponente rele Esponenzili e ritmi L potenz è definit: se, per ogni R se, per tutti e soli gli R se, per tutti e soli gli Z. Sono definite: 7 7. Non sono definite:.
Teori in sintesi ESPONENZIALI Potenze con esponente rele Esponenzili e ritmi L potenz è definit: se, per ogni R se, per tutti e soli gli R se, per tutti e soli gli Z. Sono definite: 7 7. Non sono definite:.
fattibile con le tecniche elementari che imparerai in seguito. Ad esempio il polinomio
 Scomposizione di un polinomio in fttori Scomporre in fttori primi un polinomio signific esprimerlo come il prodotto di due più polinomi non più scomponibili Ad esempio 9 = ( 3) fttore 1 ( + 3) fttore +
Scomposizione di un polinomio in fttori Scomporre in fttori primi un polinomio signific esprimerlo come il prodotto di due più polinomi non più scomponibili Ad esempio 9 = ( 3) fttore 1 ( + 3) fttore +
Ing. Alessandro Pochì
 Dispense di Mtemtic clsse quint -Gli integrli Quest oper è distriuit con: Licenz Cretive Commons Attriuzione - Non commercile - Non opere derivte. Itli Ing. Alessndro Pochì Appunti di lezione svolti ll
Dispense di Mtemtic clsse quint -Gli integrli Quest oper è distriuit con: Licenz Cretive Commons Attriuzione - Non commercile - Non opere derivte. Itli Ing. Alessndro Pochì Appunti di lezione svolti ll
Esponenziali e logaritmi
 Prof Emnuele ANDRISANI Teori in sintesi ESPONENZIALI Potenze con esponente rele L potenz è definit: se 0, per ogni R se 0, per tutti e soli gli R se 0, per tutti e soli gli Z Esponenzili e ritmi Sono definite:
Prof Emnuele ANDRISANI Teori in sintesi ESPONENZIALI Potenze con esponente rele L potenz è definit: se 0, per ogni R se 0, per tutti e soli gli R se 0, per tutti e soli gli Z Esponenzili e ritmi Sono definite:
ESPONENZIALI E LOGARITMI
 ESPONENZIALI E LOGARITMI RICHIAMI DI TEORIA dom f Im f grfico Funzioni esponenzili y=^ con > Funzioni esponenzili y=^ con
ESPONENZIALI E LOGARITMI RICHIAMI DI TEORIA dom f Im f grfico Funzioni esponenzili y=^ con > Funzioni esponenzili y=^ con
7.5. BARICENTRI 99. Esempio 7.18 (Baricentro di una lamina ellissoidale omogenea). Consideriamo la lamina ellissoidale omogenea in figura.
 7.5. BAICENTI 99 P J Q Gli ssi HJ e PQ (che isecno i lti opposti del rettngolo) sono ssi di simmetri mterile. il ricentro dell lmin coincide con l intersezione dei due ssi: G, G H Esempio 7.18 (Bricentro
7.5. BAICENTI 99 P J Q Gli ssi HJ e PQ (che isecno i lti opposti del rettngolo) sono ssi di simmetri mterile. il ricentro dell lmin coincide con l intersezione dei due ssi: G, G H Esempio 7.18 (Bricentro
Esercitazione di Matematica sulle equazioni di secondo grado (o ad esse riconducibili) nel campo reale
 Esercitzione di Mtemtic sulle equzioni di secondo grdo (o d esse riconducibili) nel cmpo rele 1. Risolvere, nel cmpo rele, le seguenti equzioni di secondo grdo: () 81x 0; (b) (x 1) 7x ; (c) 7x x 0; (d)
Esercitzione di Mtemtic sulle equzioni di secondo grdo (o d esse riconducibili) nel cmpo rele 1. Risolvere, nel cmpo rele, le seguenti equzioni di secondo grdo: () 81x 0; (b) (x 1) 7x ; (c) 7x x 0; (d)
Superfici di Riferimento (1/4)
 Superfici di Riferimento (1/4) L definizione di un superficie di riferimento nsce dll necessità di vere un supporto mtemtico su cui sviluppre il rilievo eseguito sull superficie terrestre. Tle superficie
Superfici di Riferimento (1/4) L definizione di un superficie di riferimento nsce dll necessità di vere un supporto mtemtico su cui sviluppre il rilievo eseguito sull superficie terrestre. Tle superficie
{ 3 x y=4. { x=2. Sistemi di equazioni
 Sistemi di equzioni Definizione Un sistem è un insieme di equzioni che devono essere verificte contempornemente, cioè devono vere contempornemente le stesse soluzioni. Definimo grdo di un sistem il prodotto
Sistemi di equzioni Definizione Un sistem è un insieme di equzioni che devono essere verificte contempornemente, cioè devono vere contempornemente le stesse soluzioni. Definimo grdo di un sistem il prodotto
Il dominio della funzione, cioè l'insieme dei valori che si possono attribuire a x è tutto R ;
 CAPITOLO ESPONENZIALI E LOGARITMI ESPONENZIALI Teori in sintesi Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z. + Sono definite:
CAPITOLO ESPONENZIALI E LOGARITMI ESPONENZIALI Teori in sintesi Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z. + Sono definite:
