CALCOLO DIFFERENZIALE INTEGRALE a.a
|
|
|
- Fabiola Alberti
- 6 anni fa
- Visualizzazioni
Transcript
1 CALCOLO DIFFERENZIALE INTEGRALE ELENA MUSELLI Dispense per il corso di lure in Informtic dell.. 0/0
2 CAPITOLO. - Simboli e notzioni signific esiste/ono ; st per non esiste/ono ; signific per ogni, per tutti ; := signific ugule per definizione (è usto per introdurre notzioni). = e si leggono rispettivmente implic e se e solo se. Sino φ e ψ due ffermzioni: φ = ψ signific che se è ver φ llor è ver nche ψ φ ψ vuol dire che φ è ver se e solo è ver ψ Prodotto crtesino A B di due insiemi A, B è l insieme delle coppie ordinte (, b) di un elemento di A e di un elemento di B ossi A B := {(, b) : A, b B}.. - Insiemi numerici L insieme dei numeri nturli si denot con N, ossi N + := {,, 3,...} i numeri nturli positivi. Prticolri sottoinsiemi di N sono: N:={0,,, 3,...} ; denotimo con i numeri pri: {n N : n =m, m N + } i numeri dipri: {n N : n =m +,m N} Si denot con Z l insieme dei numeri interi e con Q l insieme dei numeri rzionli: Z:={..., 3,,, 0,,, 3,...} Q:={ p m : p Z, m N+ }. NUMERI REALI: costituiscono un insieme di numeri, che denotimo con R, nei quli sono definite un somm, un prodotto ed un relzione d ordine (<), che soddisfno le usuli regole lgebriche. Il sottoinsieme di R costituito d R\Q è detto insieme dei numeri irrzionli. Denoteremo R + := {x R : x>0} R := {x R : x<0}. Ricordimo lcune proprietà di R ; dti x,y,z,w R, si h: ) x<y, z w = x + z<y+ w ; ) x<y, z>0 = xz <yz ; ) x<y, z<0 = xz >yz. 3) 0 x<y, 0 z<w = xz <yw ; 4) p, q Q, x R\Q tle che p<x<q. 5) x, y R\Q, q Q tle che x<q<y. 6) Dto x R, unico un elemento m Z tle che m x<m+. Tle numero m è detto prte inter di x e si denot m =[x]. Notzioni: b = +( b), se b 0, b = b.
3 Rppresentzione grfic di R. Fissto su di un rett r un punto o, detto origine, e l unità di lunghezz, si f corrispondere d ogni numero rele x>0 il punto dell rett r, destr dell origine, l cui distnz d o misuri x. Ad un numero x<0 ssocimo il punto sinistr dell origine vente distnz x d o. Vicevers, d ogni punto destr dell origine corrisponde un numero > 0 dto dll distnz del punto d o, mentre d ogni punto sinistr dell origine corrisponde un numero < 0 dto dll opposto del vlore dell distnz del punto d o. Rppresentzione grfic di R = R R. Considerimo due rette ortogonli tr loro (un orizzontle e un verticle) dette ssi crtesini ortogonli, denotimo con (0, 0) il punto intersezione, detto origine degli ssi, e su ognun delle due rette rppresentimo R. L sse orizzontle è detto sse delle scisse l ltro sse delle ordinte. Associmo ll coppi (, b) R il punto intersezione dell rett ll sse delle scisse nel punto con l rett ll sse delle ordinte nel punto b. Denoteremo tle punto con P(, b); i vlori e b sono le coordinte di P: rispettivmente sciss ed ordint. L bisettrice del primo e terzo qudrnte è il sottoinsieme: {(x, y) :y = x, x R} = {(x, x) : x R}. Simmetrie. Dt un coppi (, b) R si hnno le seguenti simmetrie (vedi figure seguenti): il punto (, b) è il simmetrico di (, b) rispetto ll sse delle ordinte; il punto (, b) è il simmetrico di (, b) rispetto ll sse delle scisse; il punto (, b) è il simmetrico di (, b) rispetto ll origine; il punto (b, ) è il simmetrico di (, b) rispetto ll bisettrice del primo e terzo qudrnte. 3
4 .3 - Intervlli, intorni Dti, b R, < b ricordimo che, si definiscono intervlli gli insiemi seguenti: (, b) ={x R: <x<b} [, b] ={x R: x b} [, b) ={x R: x<b} (, b] ={x R: <x b} (, + ) ={x R: <x}, [, + ) ={x R: x}, (,)={x R: x<}, (,]={x R: x }. Gli intervlli (, b), (, + ), (,) sono detti perti, gli intervlli [, b], [, + ), (,] sono detti chiusi. Dto un punto x 0 R diremo intorno di x 0 di rggio r l intervllo perto (x 0 r, x 0 + r). Diremo, rispettivmente, intorno destro e intorno sinistro di x 0 di rggio r gli intervlli perti (x 0,x 0 + r) (x 0 r, x 0 )..4 - Vlore ssoluto Definizione. Il vlore ssoluto o modulo di un numero x R, che denotimo x, è definito d { x se x 0 x = x se x<0 Le seguenti proprietà discendono direttmente dll definizione precedente: ) x 0 x R; 4) x x x x R; ) x =0 x = 0; 5) xy = x y x, y R ; 3) x = x x R; 6) x y = x y x R, y R\{0}. Teorem. - Dti x,y, z R vlgono le seguenti relzioni: 7) Dto 0 si h: x x e x {x } {x }. 7 ) Dto >0 si h: x < <x< e x > {x< } {x>}. 8) y + z y + z e y z y + z (diseguglinz tringolre); 9) y ± z y z ed nche y ± z z y ; 0 ) y z y z. Dimostrzione. - Verifichimo soltnto l 7). Dll definizione di x, l relzione x si riscrive come { x 0 x { x<0 x ; il primo sistem equivle d 0 x, mentre dl secondo si h x<0 ; unendo i due risultti si ottiene l prim prte dell 7). L second prte si dimostr in modo nlogo. 4
5 Esempi - Dll definizione di vlore ssoluto si ottiene: { 3 x se 3 x 0 { 3 x se x 3 ) 3 x = (3 x) se 3 x<0 e d 3 x 0 x 3 si h 3 x = 3+x se x>3. { x x se x x 0 ) x x = (x x ) se x x < 0 { x x se 0 x x x = x + x se x<0 e x> e d x x 0 0 x si h. Osservzione. - Con dimostrzione nlog quell vist per l 7) si ottengono le relzioni che sono utili per risolvere le disequzioni con i vlori ssoluti: P (x) Q(x) () P (x) (<) Q(x) (<) P (x) Q(x) (>) () P (x) Q(x) {P (x) Q(x)} (>) (>) {P (x) Q(x)} (<) Esempi - Risolvimo le disequzioni seguenti pplicndo le relzioni dell Osservzione.: ) x 0 x (dll () Oss..) {x } {x } 3 (, ] [, 3 ] [, + ). ) x x x > x x x < x x (dll () Oss..) { x 3x <0 x>0 (0, 3 ). { x x<x x x x> (x x ) 3) x x + x > 0 x >x x (dll () Oss..) { x>x x } { x< x + x } R. Osservzione. - Poichè l distnz tr due punti distinti x, y di R è dt d y x se y > x e d x y se x > y, utilizzndo l definizione di vlore ssoluto vremo: y x è l distnz tr x ed y ; x è l distnz del punto x d o. Ne segue che l intorno di x 0 di rggio r si può scrivere nei due modi equivlenti (x 0 r, x 0 + r) x x 0 <r. 5
6 .5 - Mssimo e minimo di sottoinsiemi di R Definizioni. Si A R,A. ) Se esiste α A t.c. x α x A llor α è detto il mssimo di A e si denot α = mx A. Si può verificre che se il mssimo esiste è unico. ) Se esiste β A t.c. β x x A llor β è detto il minimo di A e si denot β = min A. Si può verificre che se il minimo esiste è unico. Esempi ) Si A =[, 3) ; si h: x x A e A quindi = min A. Poichè 3 A, si può verificre che: non esiste un elemento di A che si di tutti gli ltri, quindi mx A. ) Si B =(, ] ; con considerzioni simili quelle viste per l insieme A si h min B e mx B =..6 - Mggiornti, minornti, estremo superiore (sup), estremo inferiore (inf) Definizioni. Si A R,A. ) Un numero k R t.c. x k x A è detto mggiornte di A. Denotimo M(A) l insieme dei mggiornti di A. Se M(A) si può verificre che esiste sempre il minimo di M(A) detto estremo superiore di A che si denot sup A. ) Un numero h R t.c. h x x A è detto minornte di A. Denotimo m(a) l insieme dei minornti di A. Se m(a) si può verificre che esiste sempre il mssimo di m(a) detto estremo inferiore di A che si denot inf A. Notzioni. Se M(A) = cioè sea non h mggiornti si denot, per convenzione, sup A =+. Se m(a) = cioè sea non h minornti si denot, per convenzione, inf A =. Proposizione. - Si A R,A, si h: Se sup A A llor mx A e si h mx A = sup A; se sup A A llor mx A. Se inf A A llor min A e si h min A = inf A; se inf A A llor min A. 6
7 Esempi ) Si A =[, 3) si h M(A) =[3, + ) = sup A =3 A = mx A m(a) =(, ] = inf A = A = min A =. ) Si C =(, 0] (, + ) si h M(C) = = sup C =+ = mx C m(c) =(, ] = inf C = C = min C..7 - Insiemi itti. Definizioni. Si A R. ) A è detto superiormente itto se K R t.c. x K x A ; ) A è detto inferiormente itto se N R t.c. N x x A ; 3) A è detto itto se lo è si sup.te che inf.te, cioè se K,N R t.c. N x K x A o equivlentemente M > 0 t.c. x M x A. 7
8 CAPITOLO. - Definizione di funzione e notzioni. Dti due insiemi A e B non vuoti, un funzione d A in B è un legge che d ogni elemento di A ssoci un solo elemento di B ed usimo l notzione: f : A B x f(x) dove A è i l dominio o insieme di definizione di f, B è i l codominio di f x è dett vribile, f(x) è dett immgine di x. L insieme Imf = f(a) :={f(x) :x A} è detto immgine o rngo di f. Se D A, l insieme f(d) :={f(x) :x D} è detto immgine di D ( secondo f ). Si definisce grfico di f il sottoinsieme di A B dto d G f := {(x, f(x)) : x A}.. - Prolungmenti e restrizioni. Definizione. - Si f : A B ; ) se C è un insieme t.c. A C, con A C ; un qulunque funzione g : C E t.c. g(x) =f(x) x A. è dett prolungmento di f C; ) se D A, D A, definimo restrizione di f D, con notzione f /D, l funzione f /D : D B t.c. f /D (x) =f(x) x D..3 - Iniettività, surgettività, bigettività. Definizioni. - Un f : A B è dett ) iniettiv se x x = f(x ) f(x ) (o equiv. f(x )=f(x ) = x = x ) ossi punti distinti hnno immgini distinte; ) surgettiv se y B, x A t.c. y = f(x) ossi ogni elemento del codominio B è immgine di qulche punto di A; 3) bigettiv se è si iniettiv che surgettiv. Osservzione. - Dll definizione di f(a) si h: f : A B iniettiv = f : A f(a) bigettiv. Nel seguito considereremo solo funzioni reli (cioè B R )di vribile rele (cioè A R). 8
9 .4 - Funzioni itte. Definizione. - Un f : A R è ) superiormente itt se K R t.c. f(x) K x A ; cioè se l insieme Imf è sup.te itto; ) inferiormente itt se N R t.c. N f(x) x A ; cioè se l insieme Imf è inf.te itto; 3) itt se N, K R t.c. N f(x) K x A o equiv.te M>0 t.c. f(x) M x A cioè se l insieme Imf è itto..5 - Punti di mssimo e punti di minimo (ssoluti e reltivi). Estremi ssoluti e/o reltivi. Definizione. - Si f : A R ed x 0 A; ) il punto x 0 è detto di mssimo (ssoluto) se: f(x 0 ) f(x) x A cioè f(x 0 ) = mx f(a), f(x 0 ) è detto vlore mssimo; ) il punto x 0 è detto di mssimo reltivo se: δ>0 t.c. f(x 0 ) f(x) x A (x 0 δ, x 0 + δ); 3) il punto x 0 è detto di minimo (ssoluto) se: f(x 0 ) f(x) x A cioè f(x 0 )=minf(a), f(x 0 ) è detto vlore minimo; 4) il punto x 0 è detto di minimo reltivo se: δ>0 t.c. f(x 0 ) f(x) x A (x 0 δ, x 0 + δ). I punti di mssimo e di minimo ssoluto (reltivo) sono detti estremi ssoluti (reltivi). Esempio - Dto il seguente grfico di un funzione f con dominio [, + ), bbimo: tre estremi reltivi ed un estremo ssoluto, inftti 9
10 x = è p.to di mssimo ssoluto perchè f( ) f(x) x dom f; x = è p.to di mssimo reltivo perchè f() f(x) x (0, ); x = è p.to di minimo reltivo perchè f( ) f(x) x [, ) = ( 3, ) dom f; x =0 è p.to di minimo reltivo perchè f(0) f(x) x (, )..6 - Funzioni pri e funzioni dispri. Definizioni. - Si f : A R, con A t.c. x A = x A. ) f è dett pri se f( x) =f(x) x A. Dll definizione di funzione pri, segue che x A si h: ) (x, f(x)) G f = (x, f(x)) G f e ( x, f(x)) G f ; ( x, f( x)) G f quindi, se f è pri, il suo G f è simmetrico rispetto ll sse delle ordinte. ) f è dett dispri se f( x) = f(x) x A. Dll definizione di funzione dispri, segue che x A si h: ) (x, f(x)) G f = (x, f(x)) e ( x, f(x)) G f ; ( x, f( x)) G f llor, se f è dispri, il suo G f è simmetrico rispetto ll origine..7 - Funzioni monotone. Definizioni. - Un funzione f : A R è dett ) crescente se x,x A, x <x = f(x ) f(x ); ) strettmente crescente se x,x A, x <x = f(x ) <f(x ); 3) decrescente se x,x A, x <x = f(x ) f(x ); 4) strett.te decrescente se x,x A, x <x = f(x ) >f(x ); 5) monoton se verific uno dei quttro csi precedenti..8 - Funzione compost. Definizione. - Sino f : A R e g : D R. Se f(a) D l funzione denott con g f e definit su A come: (g f)(x) =g(f(x)) x A è dett funzione compost di g con f. Se f(a) D m f(a) D, l funzione compost g f vrà come dominio l insieme dom (g f) ={x A : f(x) D}. 0
11 .9 - Funzione invers e sue proprietà. Osservimo che, se f : A R è iniettiv llor f : A f(a) è bigettiv e quindi y f(a) un solo x A t.c. y = f(x). L unicità di tle x è dt dll iniettività dell f. Si può, llor, definire su f(a) un funzione, dett funzione invers di f, nel modo seguente: Definizione. - Un funzione f : A R iniettiv è dett invertibile. L funzione f : f(a) A che d ogni y f(a) ssoci l unico elemento x A t.c. y = f(x) è dett funzione invers di f. Osservzione. - Ovvimente, se f è invertibile nche f è iniettiv e quindi invertibile e si h (f ) = f. Teorem.. - Si f : A R invertibile e si f l su invers; si h: ) dom f = f(a); ) y = f(x) x = f (y); 3) (f f)(x) =x, x A e (f f )(y) =y, y f(a); 4) G f e G f sono simmetrici rispetto ll bisettrice del I o e III o qudrnte. Dimostrzione. - Le prime tre discendono (in modo immedito) dll definizione. Verifichimo l proprietà 4). Si (x, y) G f. Dll definizione di G f si h y = f(x) d cui, per l ), ottenimo (x, y) =(f (y),y) che è il punto simmetrico, rispetto ll bisettrice del I o e III o qudrnte (vedi pg.3), di (y, f (y)) G f. Il teorem seguente dimostr come l strett monotoni si un condizione sufficiente per l invertibilità dell funzione. Teorem. - Si f : A R str.te monoton. Allor f è invertibile ed f h l stess monotoni dell f. Dimostrzione. - Supponimo che f si str.te crescente (nel cso str.te decrescente si procede nello stesso modo). Sino x,x A, x x.sex <x, dll strett crescenz di f,sih f(x ) <f(x ) quindi f(x ) f(x ); l stess conclusione si ottiene se x >x e quindi f risult iniettiv cioè invertibile. Considerimo, or, y,y f(a), y <y ed osservimo che dll iniettività di f si h f (y ) f (y ). Se fosse f (y ) >f (y ) si vrebbe, per l strett crescenz di f, f(f (y )) >f(f (y )) cioè y >y che contrddice l scelt di y ed y. Allor si h f (y ) <f (y ) cioè l strett crescenz di f. Osservzione.3 - L esempio seguente dimostr che: ci sono funzioni invertibili non str.te monotone.
12 Esempio - Considerimo l funzione f(x) = x. l iperbole in figur Si h domf = {x 0} ed il suo grfico, come noto, è Dl G f si deduce l iniettività di f : inftti, le rette orizzontli, che intersecno il G f, hnno un sol intersezione. Allor, ogni elemento di Imf è immgine di un solo elemento del dom f. L funzione f è quindi invertibile m non è str.te monoton. Inftti, mentre f /(0,+ ) (o f /(,0) ) è str.te decrescente, dll diseguglinz f( ) <f() si deduce che l funzione non è str.te decrescente sul dominio. Osservndo, inoltre, che il G f è simmetrico rispetto ll bisettrice del I o e III o qudrnte si ottiene che G f = G f e quindi l invers è dt d f (y) = y.0 - Funzioni elementri. Funzioni lineri, funzione modulo e funzione prte inter ) - f(x) =mx+ q, m, q R, m 0; dom f = R. Sono dette funzioni lineri. I loro grfici sono rette pssnti per i punti (0,q)e( q, 0). L ngolo che tli rette formno con l sse delle m scisse è: cuto se m>0, ottuso se m<0. m è detto coefficiente ngolre dell rett: se m>0 l funzione è str.te crescente, se invece m<0l funzione è str.te decrescente (vedi figur seguente): m>0 f str.te crescente m<0 f str.te decrescente
13 ) - f(x) = x ; dom f = R. { x x 0 Dll definizione di x = x x < 0 si ottiene il grfico f /(,0) è str.te decrescente f /(0,+ ) è str.te crescente f(x) = x è pri : f( x) = x = x = f(x), x R. 3) - f(x) =[x] ; dom f = R. Dll definizione di [x] (prte inter di x pg. ), si ottiene: Imf = Z ed il grfico Ne segue che f(x) =[x] è costnte trtti e crescente. Funzioni potenze intere e rdici n-esime 4) - f(x) =x n, n N + ; dom f = R, f(0) = 0. Le proprietà dipendono d n, in prticolre: n dispri: f(x) > 0 se x>0 e f(x) < 0 se x<0; f è dispri f( x) =( x) n = x n = f(x) e G f è simmetrico rispetto ll origine; f è str.te crescente su R. Inftti, se 0 <x <x moltiplicndo membro membro n-volte si h (x ) n < (x ) n ; inoltre, se x <x < 0 si h x > x > 0 = ( x ) n > ( x ) n = (x ) n < (x ) n ; infine, osservimo che x < 0 <x = (x ) n < 0 < (x ) n. n pri: f(x) 0 x R; f è pri f( x) =( x) n = x n = f(x) e G f è simmetrico rispetto ll sse delle ordinte; f è str.te crescente su [0, + ) f è str.te decrescente su (, 0]. L strett monotoni su [0, + ) e su (, 0] si verific in modo nlogo qunto visto per n dispri. 3
14 n dispri n pri Osservzione.4 - D qunto visto, se n è dispri l funzione f(x) =x n è invertibile su R mentre se n è pri considerimo l restrizione, invertibile, f /[0,+ ). n Le due inverse sono dette rdici n-esime di x e sono indicte, in entrmbi i csi, con l notzione x = x n. 5) - f(x) = n x = x n, n N + ; dom f dipende d n. n dispri: dom f = R, f str.te crescente n pri: dom f =[0, + ), f str.te crescente I grfici, ottenuti per simmetri d quelli delle funzioni potenze n-esime, sono: Osservzione.5 - Dll proprietà 3) del Teorem. (pg ) si h ( x) = x x [0, + ) mentre x = x x R, inftti { x = x se x 0 x = ( x) = x se x<0.. - Funzioni esponenzili e logritmiche. Osservzione.6 - Dto >0 e q Q,q= p m, bbimo visto che q = m p. Definizione. - Sino > e x R; definimo x = sup{ q : q Q, q x} (se 0<< x = ( ). )x L uguglinz precedente, per l unicità dell estremo superiore, definisce un funzione su R dett funzione esponenzile di bse. Poichè x = x R, trtteremo solo funzioni esponenzili di bse >0,. 4
15 6) - Funzioni esponenzili di bse >0,. Si f(x) = x con >0, si h: dom f = R, f(0) =, Imf =(0, + ); L monotoni dipende invece dll bse : x è str.te crescente se > x è str.te decrescente se 0 <<. I grfici nei due csi sono: Notzione - L funzione f(x) = x si indic nche con exp (x). Un cso importnte si h qundo l bse è ugule l numero di Nepero, un numero irrzionle che si indic con l letter e. Un pprossimzione di tle numero è: e L funzione f(x) =e x si indic nche con exp(x) ed ovvimente risult str.te crescente. Proprietà - Dti, b>0,,b, ricordimo le proprietà delle potenze:. x y = x+y x y = x y. (b) x = x b x ( b ) x = x b x x,y R x R 3. ( x ) y = xy x,y R. Osservzione.7 - Le funzioni esponenzili f(x) = x con >0, sono invertibili. Le funzioni inverse, definite su Imf =(0, + ) e dette funzioni logritmiche, sono denotte log x e le proprietà si ottengono dlle proprietà delle funzioni inverse. 5
16 7) - Funzioni logritmiche di bse >0,. Si f(x) = log x con >0, si h: dom f =(0, + ), Imf = R; I grfici, ottenuti per simmetri d quelli delle funzioni esponenzili, sono: L monotoni dipende dll bse : log x è str.te crescente se > log x è str.te decrescente se 0 <<. I grfici, ottenuti per simmetri d quelli delle funzioni esponenzili, sono: Notzione - Per il logritmo in bse nturle e si usno le notzioni: log e x, log x, ln x Proprietà - Dlle proprietà delle funzioni inverse (Teorem., pg ), se >0,, si h:. log x = x, x>0 log ( x )=x, x R dll. si ottiene. log = 0 log = log ( )= >0, le seguenti proprietà discendono dlle proprietà delle potenze (verrà verifict solo l 3. titolo esplictivo). Sino, b>0,,b : 3. log (xy) = log x + log y x, y >0 4. log ( x y ) = log x log y x, y >0 5. log (x) y = y log x x>0,y R 6. log b x = log x log b x>0 (cmbimento di bse) d cui log x = log x x>0 [Per verificre l 3., ponimo: z = log (xy) m = log x s = log y. Poichè log è l invers dell funzione esponenzile si h: z = log (xy) = xy nlogmente m = x s = y; ne segue che z = xy = m s = m+s e, per l iniettività dell funzione esponenzile, si h z = m + s cioè l tesi.] 6
17 . - Funzioni trigonometriche. Definizione. Un funzione f : R R è dett periodic di periodo T > 0 se f(x + T )=f(x) x R Osservzione.8 - L definizione di funzione periodic di periodo T>0 implic che i vlori dell funzione si ripetono dopo intervlli di mpiezz T. Allor, per conoscere le proprietà di un funzione periodic f, bst conoscere le proprietà di f ristrett d un intervllo di lunghezz ugule l periodo T. Per trccirne il grfico, bst trccire il grfico di f ristrett d un intervllo di mpiezz T e poi ripeterlo trslndolo orizzontlmente. Possimo osservre che, dti x R e n N +, dll definizione di funzione periodic si h f(x) =f(x + T )=f((x + T )+T )=f(x +T )=f((x +T )+T )=f(x +3T )= = f(x + nt)) ed nlogmente f(x) =f((x T )+T )=f(x T )=f((x T )+T )=f(x T )=f((x 3 T )+T )=f(x 3 T ) = f(x nt)) che si possono rissumere nell formul f(x) =f(x + kt) k Z. Esempio - Disegnre il grfico dell funzione periodic di periodo T = spendo che f(x) =x se x (0, ]. Trccimo prim il grfico di f /(0,] (fig.) e poi estendimo con periodicità (cioè ripetendo il grfico in intervlli di mpiezz ) tutto R (fig.b) fig. fig. b Funzioni seno e coseno. Si γ un circonferenz di rggio ; sppimo che lunghezz(γ)= π. Nel pino di γ considerimo un sistem di ssi crtesini con origine nel centro di γ: l circinferenz γ con tle sistem di ssi è dett circonferenz goniometric (vedi fig. pgin seguente). Si A il punto di intersezione di γ con l semirett positiv delle scisse. Dto x [0, π) possimo considerre P x l unico punto di γ t.c. l rco rco(ap x ), con primo estremo A e secondo estremo P x, percorso in senso ntiorrio bbi lunghezz x. Se x ( π, 0], considerimo P x l unico punto di γ t.c. l rco rco(ap x ) percorso in senso orrio bbi lunghezz x. 7
18 Definizione. Sino x [0, π) e P x l unico punto di γ t.c. l rco rco(ap x ) percorso in senso ntiorrio bbi lunghezz x. Si definisce sen x := ordint di P x cos x := sciss di P x D semplici considerzioni geometriche si h, per x [0, π): sen x + cos x = (teorem di Pitgor) ed nche sen 0 = 0 sen π = sen π = 0 sen 3 π = cos 0 = cos π = 0 cos π = cos 3 π =0 sen x cos x sen ( x) = sen x cos ( x) = cos x sen /[0, π e ] è str. cresc. sen sen /[ π /[ 3 π, π), 3 π] è str. decresc. cos /[0,π] è str. decresc. cos /[π, π) è str. cresc. Definimo or le funzioni sen : R [, ] e cos : R [, ] estendendo per periodicità tutto R i vlori sen x e cos x determinti nell intervllo [0, π). Le funzioni seno e coseno srnno quindi periodiche di periodo T = π: sen (x) = sen (x +kπ) e cos(x) = cos(x +kπ) x R k Z ; ricordimo, inoltre, l relzione fondmentle sen x + cos x = x R. I grfici sono rispettivmente 8
19 Ricordimo inoltre lcuni vlori e proprietà sen π 6 = cos π 6 = 3 ; sen π 4 = cos π 4 = ; sen π 3 = 3 cos π 3 = ; seno e coseno sono funzioni itte: sen x cos x x R; seno è funzione dispri: sen ( x) = sen x x R; coseno è funzione pri: cos ( x) =cosx x R. Formule trigonometriche Ricordimo solo lcune tr le formule trigonometriche; ll pgin web del corso è disponibile un formulrio completo. L notzione inglese sin è ust l posto di seno. Le prime si possono dedurre d considerzioni geometriche, delle ltre omettimo l dimostrzione. sin( π x) = cos x sin( π + x) =cosx sin(π x) = sin x sin(π + x) = sin x cos( π x) = sin x cos( π + x) = sin x cos(π x) = cos x cos(π + x) = cos x Formule di dupliczione: sin( x) = sin x cos x cos( x) = cos x sin x = sin x = cos x dll second si ricv: sin x = cos( x) cos +cos( x) x = Formule di prostferesi ( solo di 4): sin x sin y = sin( x y x+y ) cos( ) cos x cos y = sin( x y x+y ) sin( ) 9
20 Funzione tngente. È definit come rpporto tr seno e coseno: tn x = sin x cos x dom tn = {x π + kπ, k Z}. (L notz. inglese tn è ust l posto di tng). Con considerzioni sui tringoli simili H0P x e A0Q x nel pino dell circonferenz γ (su cui sono stti definiti sin x e cos x ) si ottiene che tn x è l ordint del punto Q x. Il grfico dell funzione tn : {x π + kπ, k Z} R è trccito di seguito: Proprietà - Dlle proprietà del seno e del coseno si ricvno le proprietà delle tngente: tn 0 = 0 tn π 6 = 3 3 tn π 4 = tn π 3 = 3 tn(π x) = tn x; tngente è periodic di periodo T = π: tn(x) = tn(x + kπ) k Z x dom tn; tngente è funzione dispri: tn( x) = tn x x π + kπ, k Z; Teorem.3 - L funzione seno verific l seguente disuguglinz sin x x x R. Dimostrzione.. - Si x [0, π ]. Dll relzione tr corde ed rchi di un circonferenz e dll definizione di sin x, si ottiene 0 sin x x 0 sin x x x [0, π ]. Se x [ π, 0], utilizzndo l precedente relzione per rchi positivi e le proprietà del modulo, si h 0 sin( x) x 0 sin( x) x 0 sin x x 0 sin x x. Concludimo osservndo che, se x (, π ) ( π, + ) cioè x > π si h: sin x < π < x. 0
21 .3 - Trigonometri pplict ll geometri. Seno, coseno e tngente di ngoli. Sppimo che, in un circonferenz C r di rggio r, l ngolo l centro sotteso d un rco di lunghezz r misur rdinte. Avremo: sin(90 ) = sin π = sin(80 )=sinπ = 0 sin(70 ) = sin 3 π = cos(90 ) = cos π = 0 cos(80 ) = cos π = cos(70 ) = cos 3 π =0 sin(30 ) = sin π 6 = sin(45 ) = sin π 4 = sin(60 )=sin π 3 = 3 cos(30 ) = cos π 6 = 3 cos(45 ) = cos π 4 = cos(60 )=cos π 3 = Per il seno e coseno di ngoli complementri, supplementri etc. si usno le regole viste per le funzioni sin e cos. L tngente di ngoli è ncor definit come il rpporto tr seno e coseno. Trigonimetri pplict i tringoli rettngoli. - Dto un tringolo rettngolo: si h: BA : PH = CB : CP b : sen(α) = : d cui b = sin(α). Anlogmente si ottiene: c = cos(α) e b c = tn(α).
22 .4 - Funzioni: rcseno, rccoseno, rctngente. Le funzioni seno, coseno e tngente non sono iniettive sul loro dominio. Se considerimo le tre restrizioni sin /[ π, π ] cos /[0,π] tn /( π, π ) esse risultno str.te monotone e quindi invertibili; d tli restrizioni deducimo: dominio, monotoni e grfico dell invers. Tli inverse, dette rispettivmente rcseno, rccoseno e rctngente, hnno quindi le seguenti proprietà: Osservzione.9 - Osservimo che d tn x = x = π 4 + kπ, k Z non segue che rctn = π 4 + kπ m rctn = π 4 perchè l immgine dell funzione rctn è ( π, π ).
23 .5 - Simmetrie, trslzioni, compressioni e diltzioni di grfici. Dto il grfico di un funzione f, possimo ricvre il grfico delle funzioni: f(x), f( x), f(x), f( x ), f(x)+c, f(x + c), f(cx),c>0,c. Riportimo di seguito i grfici nei vri csi ed un confronto con il grfico dell funzione originri f. Si f un funzione con grfico: si h - f(x) ssume i vlori di segno opposto quelli dell f; il grfico è quindi simmetrico quello dell f rispetto ll sse delle scisse f(-x) in (0, + ) quest funzione ssume i vlori che l f vev in (, 0); il grfico è quindi simmetrico quello dell f rispetto ll sse delle ordinte 3
24 f(x) L prte positiv del grfico di f rest invrit, l prte negtiv si simmetrizz rispetto ll sse delle scisse f( x ) è funzione pri e coincide con f in (0, + ); il grfico è poi simmetrizzto rispetto ll sse delle ordinte f(x)+c se c>0 il grfico si ottiene trslndo verso l lto di un quot c il grfico di f ; se c<0 l trslzione srà verso il bsso 4
25 f(x + c) se c>0 il grfico si ottiene trslndo verso sinistr di un intervllo di mpiezz c il grfico di f ; se c<0 l trslzione srà verso destr f(cx), c > 0,c se c> il grfico è un compressione del grfico di f ; se 0 <c< il grfico è un diltzione del grfico di f 5
26 CAPITOLO Limiti di funzioni. Definizioni. - Diremo () intorno bucto di x 0 un intorno di x 0 privto di x 0 : (x 0 r, x 0 + r) \{x 0 } con r>0 (b) intorno destro di x 0 un intervllo (x 0,x 0 + r) con r>0 (c) intorno sinistro di x 0 un intervllo (x 0 r, x 0 ) con r>0 (d) intorno di + un intervllo (b, + ) con b R (e) intorno di un intervllo (,b) con b R Notzione. - Nel seguito, denoteremo R = R {± } e, dto x 0 R, il simbolo I x0 denoterà gli intorni definiti in (), (d) ed (e) nei rispettivi csi: x 0 R,x 0 =+ e x 0 =. Limiti l finito. Considerimo i grfici delle funzioni: { { x + x x x f(x) =x +, g(x) = x =, h(x) = x + x> Osservimo che f(x 0 ) g(x 0 ) m il comportmento di f e g in un intorno bucto di x 0 è lo stesso perchè sono uguli. Vogo crtterizzre il comportmento di un funzione nell intorno bucto di un punto indipendentemente dl vlore che tle funzione potrebbe vere nel punto. Se, nel grfico di g, si consider un intorno di l = di rggio vribile (che indicheremo con l letter ε ) si riesce determinre un intorno di x 0 =, che denotimo I x0 =( δ, +δ), tle che (vedi figur seguente) g(i x0 \{x 0 }) ( ε, +ε). Nel grfico di h, invece, se si consider ε = si trov soltnto un intorno destro che verific l inclusione precedente. 6
27 Sull rig dei rgionmenti ftti grficmente, per descrivere rigorosmente il comportmento di un funzione f vicino d un punto x 0 R si us l nozione di ite. Introduzione ll definizione e notzione di ite. Se, dto l R, per ogni intorno V di l esiste un intorno U di x 0 tle che si bbi f(u\{x 0 }) V diremo che f(x) tende d l qundo x tende d x 0. Per sintetizzre tle concetto utilizzeremo l notzione f(x) =l che leggeremo il ite di f(x), per x che tende x 0, è ugule d l, o nche f(x) tende l per x che tende x 0. Un notzione nlog è dt d f(x) l per x x 0. Denotimo l intorno V di l come (l ε, l + ε) e l intorno U\{x 0 } con (x 0 δ, x 0 + δ)\{x 0 }. È ovvio che per ottenere tutti gli intorni di l dovremo fr vrire l mpiezz ε>0 dell intorno. Scrivendo gli intorni V ed U come indicto vremo, nel cso x 0 ed l reli, l seguente definizione di ite: Definizione. - Sino f : A R, x 0 R t.c. (x 0 r, x 0 + r)\{x 0 } A per qulche r>0. Diremo che f(x) =l R ε>0 δ>0 t.c. x (x 0 δ, x 0 + δ)\{x 0 } si h f(x) l <ε. Ricordimo che f(x) l <ε l ε<f(x) <l+ ε f(x) (l ε, l + ε). Considerimo desso i grfici delle funzioni: f (x) = x ; g (x) = x +; h (x) = x. Possimo crtterizzre il comportmento delle f e g vicino d x 0 =, osservndo che: per ogni quot M>0 esiste un intorno I x0 =( δ, +δ) (come si vede nelle prime due fig.) t.c. f (x) >M g (x) < M x I x0 \{}. Il comportmento di h, invece, è diverso second che considerimo un intorno destro o un intorno sinistro di x 0 =. 7
28 In nlogi qunto visto nel cso l R, se per ogni intorno V di + (opp. ) esiste un intorno U di x 0 tle che si bbi f(u\{x 0 }) V diremo che f(x) tende d + ( ) qundo x tende d x 0 e useremo l notzione f(x) =+ ( ). Dto M > 0, denotndo l intorno V di + come (M, + ) e l intorno V di come (, M) vremo le seguenti definizioni di ite: Definizioni. - Sino f : A R, x 0 R t.c. (x 0 r, x 0 + r)\{x 0 } A per qulche r>0. Diremo che f(x) =+ M>0 δ>0 t.c. x (x 0 δ, x 0 + δ)\{x 0 } si h f(x) >M f(x) = M>0 δ>0 t.c. x (x 0 δ, x 0 + δ)\{x 0 } si h f(x) < M Notzione. - Possimo considerre l notzione f(x) =l R. Ess rppresent tutte e tre le definizioni precedenti, cioè si h: f(x) =l R con l R ε>0 δ>0 t.c. x (x 0 δ, x 0 + δ)\{x 0 } si h f(x) l <ε l =+ M>0 δ>0 t.c. x (x 0 δ, x 0 + δ)\{x 0 } si h f(x) >M l = M>0 δ>0 t.c. x (x 0 δ, x 0 + δ)\{x 0 } si h f(x) < M. Volendo crtterizzre il comportmento di un funzione in un intorno destro o in un intorno sinistro di un punto, vremo invece le seguenti definizioni: Definizioni di ite destro. - Sino f : A R, x 0 R t.c. (x 0,x 0 + r) A per qulche r>0. Definimo f(x) =l R x x + 0 se l R ε>0 δ>0 t.c. x (x 0,x 0 + δ) si h f(x) l <ε se l =+ M>0 δ>0 t.c. x (x 0,x 0 + δ) si h f(x) >M se l = M>0 δ>0 t.c. x (x 0,x 0 + δ) si h f(x) < M. Definizioni di ite sinistro. - Sino f : A R, x 0 R t.c. (x 0 r, x 0 ) A per qulche r>0. Definimo f(x) =l R x x 0 se l R ε>0 δ>0 t.c. x (x 0 δ, x 0 ) si h f(x) l <ε se l =+ M>0 δ>0 t.c. x (x 0 δ, x 0 ) si h f(x) >M se l = M>0 δ>0 t.c. x (x 0 δ, x 0 ) si h f(x) < M. Vedremo nel prgrfo successivo il teorem che leg l esistenz di un ite per x x 0 R ll esistenz ed uguglinz del ite destro e ite sinistro 8
29 Limiti ll infinito. Se il dominio di un funzione f non è itto superiormente ( inferiormente ) vogo crtterizzre il comportmento dell funzione in un intorno di + ( ) o, come si dice usulmente, qundo x tende + ( tende ). I seguenti grfici descrivono tre comportmenti diversi. Ricordndo che un intervllo (b, + ) è un intorno di +, se riproducimo grficmente le crtterizzzioni viste nel cso x 0 R, possimo osservre che si ripresentno le stesse situzioni dove l posto dell intorno di x 0 trovimo un intorno di + ( ). Notndo che x (b, + ) x>b, in nlogi qunto descritto nel cso x 0 R, vremo le seguenti definizioni: Definizioni. - Si f : A R con (d, + ) A per qulche d. Definimo f(x) =l R x + se l R ε>0 b>0 t.c. x>b si h f(x) l <ε se l =+ M>0 b>0 t.c. x>b si h f(x) >M se l = M>0 b>0 t.c. x>b si h f(x) < M. Anlogmente definimo i iti per x. Definizioni. - Si f : A R con (,d) A per qulche d. Definimo f(x) =l R x se l R ε>0 b<0 t.c. x<b si h f(x) l <ε se l =+ M>0 b<0 t.c. x<b si h f(x) >M se l = M>0 b<0 t.c. x<b si h f(x) < M. Possimo utilizzre un notzione che rcchiud tutti i nove iti visti in questo prgrfo. Notzione. - L notzione di ite viste in precedenz. f(x) =l R, con x 0 R rppresent, cso per cso, tutte le definizioni Esempi. - Utilizzre l definizione di ite per verificre che i) c = c x 0 R ii) x = x0 iii) x = ± iv) R x ± x x =+ 9
30 ii) Lscimo l lettore l verific di i) e iii). x = R x0. Considerimo f(x) =x. Si x 0 R si h: dto ε>0 poichè f(x) x 0 <ε x x 0 <ε se considerimo d es. δ = ε (o δ < ε) l definizione di ite è verifict. iv) x x =+. Considerimo f(x) =x. Si x 0 = si h: dto M>0, si h f(x) >M x >M (, M) ( M,+ ) se considerimo d es. b = M (o b< M ) l definizione di ite è verifict. Osservzione 3. - Sino x 0 R ed f definit in un intorno bucto I x0. Si h: f(x) =l R ( f(x) l )=0. (Scrivere le due def.ni di ite ed osservre che sono uguli.) Definizione di sintoto.. Se f(x) =+ ( ) l rett x = x 0 è dett sintoto verticle (Anlog def.ne per x x x x + 0 ); 0. Se f(x) =l R l rett y = l è dett sintoto orizzontle (Anlog def.ne per x ). x Teoremi sui iti di funzioni. Teorem 3.(unicità del ite) - Si x 0 R. Se f(x) esiste llor è unico. Teorem 3.(legme tr ite, ite destro e ite sinistro) - Si x 0 R ed l R. Si h: f(x) =l f(x) = f(x) =l. x x + 0 x x 0 Proposizione 3. - Sino x 0,l R ed f definit in un intorno bucto I x0. Si h ) f(x) =0 f(x) =0. b) f(x) =l = f(x) = l. Dimostrzione.. - Considerimo il cso x 0 R. Per verificre l ), bst osservre che: f(x) =0 ε>0 δ>0 t.c. x (x 0 δ, x 0 + δ)\{x 0 } si h f(x) <ε f(x) =0 perchè f(x) = f(x). Dimostrimo l b) solo nel cso l R. Avremo f(x) =l R ε>0 δ>0 t.c. x (x 0 δ, x 0 + δ)\{x 0 } si h f(x) l <ε e dll relzione 9) del Teor.. pg. 4 segue che d cui l tesi. f(x) l f(x) l <ε x (x 0 δ, x 0 + δ)\{x 0 } 30
31 Nei csi x 0 = ± i rgionmenti sono nloghi; lscimo l lettore di scrivere l dimostrzione in questi csi. Per verificre, invece, che in b) l impliczione oppost è fls, bst considerre il controesempio seguente: { x x f(x) = x x < : si h f(x) = m x f(x) = e x + f(x) = quindi f(x). x x Teorem 3.3 (permnenz del segno) - Si x 0 R. Se f(x) =l R\{0} bucto I x0 in cui f h lo stesso segno di l. llor esiste un intorno Dimostrzione.. - Dimo l dimostrzione solo nel cso x 0 R ed l R\{0}. Se l>0 considerimo ε = l ; dll definizione di ite vremo che δ>0 t.c. x (x 0 δ, x 0 + δ)\{x 0 } si h f(x) l < l l l <f(x) <l+ l 0 < l <f(x) < 3 l d cui l tesi nel cso l>0. Se l<0 considerimo ε = l e, come prim, dll definizione di ite ottenimo, in un intorno bucto, f(x) l < l l + l <f(x) <l l 3 l <f(x) < l < 0. Eventuli relzioni tr funzioni permettono di ottenere relzioni tr i iti, qundo questi esistono, come risult di teoremi seguenti: Se Teorem 3.4 (del confronto) - Sino x 0 R e f,g funzioni t.c. f(x) g(x) x I x0 f(x) =l R e g(x) =m R llor si h l m. intorno bucto. Dimostrzione. - Dimo l dimostrzione nel cso in cui x 0, l, m R, osservndo che negli ltri csi si procede in modo nlogo. Si I x0 =(x 0 r, x 0 + r)\{x 0 } e supponimo, per ssurdo, che si l>m. Considerndo g(x) =m ε = l m vremo ( = ll metà dell distnz tr l ed m ), dlle definizioni di f(x) =l δ > 0 t.c. x (x 0 δ,x 0 + δ )\{x 0 } si h l l m δ > 0 t.c. x (x 0 δ,x 0 + δ )\{x 0 } si h m l m <f(x) <l+ l m <g(x) <m+ l m. Se prendimo δ<min{δ,δ,r}, llor, per ogni x (x 0 δ, x 0 + δ)\{x 0 } vlgono entrmbe le relzioni, d cui edi g(x) <m+ l m = l + m = l l m <f(x) che contrddice l ipotesi. 3
32 Teorem 3.5 (del confronto biltero o dei crbinieri) - Sino x 0 R e f,g,h funzioni t.c. h(x) f(x) g(x) x I x0 intorno bucto. Se h(x) = g(x) =l R llor si h f(x) =l. Dimostrzione. - Si x 0 R ed I x0 =(x 0 r, x 0 + r)\{x 0 }. Dlle definizioni di h(x) = l = g(x), l R, ottenimo che: dto ε>0 δ > 0 t.c. x (x 0 δ,x 0 + δ )\{x 0 } si h l ε<h(x) <l+ ε δ > 0 t.c. x (x 0 δ,x 0 + δ )\{x 0 } si h l ε<g(x) <l+ ε. Se prendimo δ<min{δ,δ,r}, llor, per ogni x (x 0 δ, x 0 + δ)\{x 0 } vlgono entrmbe le relzioni ed, in prticolre, utilizzndo l ipotesi vremo l ε<h(x) f(x) g(x) <l+ ε d cui l tesi. Se x 0 = ± si rgion in modo nlogo; si lsci l lettore il compito di scrivere l dimostrzione in questi csi. Teorem Sino x 0 R e f,g funzioni t.c. f(x) g(x) x I x0 intorno bucto. Si h ) f(x) =+ = g(x) =+ b) g(x) = = f(x) = Dimostrzione. - Si x 0 R ed I x0 =(x 0 r, x 0 + r)\{x 0 }. Per verificre l ), bst osservre che dll definizione del ite di f vremo M>0 δ>0 t.c. x (x 0 δ, x 0 + δ)\{x 0 } si h f(x) >M dove, con considerzioni viste nei teoremi precedenti, possimo prendere δ<r. Quindi, utilizzndo l ipotesi, vremo M<f(x) g(x) d cui g(x) >M cioè l tesi. Anlogmente per l b); dll definizione del ite di g ed f(x) g(x) ottenimo M>0 δ>0,δ<r, t.c. x (x 0 δ, x 0 + δ)\{x 0 } si h f(x) g(x) < M. Se x 0 = ± si rgion in modo nlogo; si lsci l lettore il compito di scrivere l dimostrzione in questi csi. Estensione clcolo in R. - Per comodità di clcolo definimo +(± ) =± R (+ ) (+ ) =+ (+ )+(+ ) =+ ( ) ( ) =+ ( ) +( ) = { ( ) (+ ) = ± se >0 0, (± ) = =0 ± =+ se <0 ± Le forme +, 0 ±, ± ±, 0 0 sono dette forme indeterminte. Dlle definizioni di ite e di teoremi precedenti uniti d lcune tecniche di clcolo, si ottiene il seguente teorem di cui dimostrimo solo il primo punto: 3
33 Teorem 3.7 (operzioni con i iti) - Si x 0 R, f(x) =l R, g(x) =m R. Si h: ) ( f(x) +g(x)) =l + m trnne forme indet +, + ) ( f(x) g(x)) =l m trnne forme indet. 0 ±, ± 0 3) se m 0 : f(x) g(x) = l m trnne f orme indet. ± ± f(x) 4) se m =0 e g(x) h segno costnte in I x0 : g(x) = 5) n dispri n f(x) = n pri ( f(x) 0 in I x0 ) n f(x) = { ± se l = ± n l { l (+ ) g(x) > 0 l ( ) g(x) < 0 se l R { + se l =+ n l se l 0. trnne f. i. 0 0 Dimostrzione. - Dimo soltnto l dimostrzione di ) nel cso in cui x 0,l,m R. Dto ε>0, considerimo ε = ε ; dlle definizioni di f(x) =l e di δ > 0 t.c. l ε <f(x) <l+ ε x (x 0 δ,x 0 + δ )\{x 0 } g(x) =m bbimo δ > 0 t.c. m ε <g(x) <m+ ε x (x 0 δ,x 0 + δ )\{x 0 }. Se prendimo δ<min{δ,δ }, per ogni x (x 0 δ, x 0 + δ)\{x 0 } vlgono entrmbe le relzioni l ε <f(x) <l+ ε m ε <g(x) <m+ ε che sommte membro membro dnno l + m ε = l + m ε <f(x)+g(x) <l+ m +ε = l + m + ε cioè l tesi. Notzioni. i) In bibliogrfi si trov l notzione f(x) =. Tle simbolo equivle f(x) =+. Notimo che esistono funzioni per le quli si h: f(x) = m f(x) come si verific fcilmente per l funzione f(x) = x ; inftti x 0 =+ m x x 0 x = =+ quindi x 0 + x x 0 x. ii) Se f(x) 0 (opp. f(x) 0 ) in un intorno bucto I x0 e f(x) = 0, può essere utile l notzione f(x) =0 + (0 ). Teorem Sino x 0 R, f e g definite in I x0 intorno bucto con f itt in I x0. Allor ) g(x) =0 = ( f(x) g(x)) =0 b) g(x) = + ( ) = ( f(x)+g(x)) = + ( ) 33
34 Dimostrzione.. - Per verificre l ) dimostrimo che f(x) g(x) = 0 ( vedi prop.3. )). Poichè f è itt, M>0 t.c. f(x) M per ogni x I x0 (vedi def. pg.9). Allor 0 f(x) g(x) = f(x) g(x) M g(x) con M g(x) 0 per x x 0 ; dl Teor.3.5 ottenimo l ). Per l b), poichè d f itt si h N f(x) K per ogni x I x0 dove N,K R (vedi def. pg.9) d cui di Teor.3.7 punto ) e Teor.3.6 vremo N + g(x) f(x)+g(x) K + g(x); g(x) =+ = (N + g(x)) = + = (f(x)+g(x)) = + g(x) = = (K + g(x)) = = (f(x)+g(x)) = Per clcolre iti di funzioni composte si utilizz il seguente teorem di cui è omess l dimostrzione Teorem 3.9 (cmbimento di vribile) - Sino f : A R,g: B R con f(a) B t.c. f(x) =l R e g(y) =m R. R y l Allor, se l B si h g( f(x)) =m. Osservzione L tesi del teor. precedente è equivlente g( f(x) ) = g(y). y l D qui l denominzione cmbimento di vribile ; inftti, il ite viene clcolto utilizzndo un nuov vribile y legt ll x dll relzione y = f(x) ed osservndo che se x x 0 llor y l. Il teorem seguente leg l monotoni delle funzioni ll esistenz dei iti. L dimostrzione è omess. Teorem 3.0 (iti di funzioni monotone) - Sino, b R, <b ed f monoton in (, b); llor f(x) =l R f(x) =m R. x + x b Inoltre, se l ed m R, si h l f(x) m x (, b) se f crescente m f(x) l x (, b) se f decrescente Clcolo dei iti di lcune funzioni. Si α 0ex 0 > 0. x α = x α 0 ; x α = x 0 + { 0 α>0 + α<0; x + xα = { + α>0 0 α<0. sin x = sin x 0 x 0 R ; x ± sin x. Verific: se x 0 R, per l prop.3. ), bst verificre che sin x sin x 0 = 0. Dlle formule di prostferesi ( pg.9 ), dl Teor..3 pg. 0 e dll ittezz del coseno ( cos( x+x 0 ) ) si ottiene: 0 sin x sin x 0 = sin( x x 0 ) cos( x+x 0 ) x x 0 = x x 0 e per il teorem del confronto biltero si h l tesi. 34
35 Omettimo l verific del ite ± l cui non esistenz dipende dll periodicità dell funzione seno. In modo del tutto nlogo si ottiene: cos x = cos x 0 x 0 R ; x ± cos x. tn x = tn x 0 x 0 dom tn ; x ( π +kπ) tn x =+ Verific: bst osservre che tn x = sin x cos x ed pplicre il Teor.3.7 punti 3) e 4). Dei seguenti iti ne omettimo l verific: tn x =. x ( π +kπ)+ rcsin x = rcsin x 0 x 0 [, ]; rccos x = rccos x 0 x 0 [, ]; rctn x = rctn x 0 x 0 R; x rctn x = π ; rctn x = π x +. x = x0 x 0 R; x x = { { 0 > + > + 0 << ; x + x = 0 0<<. { { > + > log x x x = log x 0 x 0 > 0; log x = 0 x < < ; log x = x + 0 << Limiti notevoli. sin x x 0 x = ; tn x x 0 x =; x 0 sin n x x n =, n N +. il secondo ite si ottiene dl primo osservndo che sin x mentre per il terzo si h n volte. sin n x x n = sin x x x x 0 tn x x = x 0 sin x x cos x = ; x 0 cos x x =. Verific: x 0 cos x x = x 0 cos x x +cos x +cos x = x 0 sin x x +cos x =. 35
36 x 0 rctn x x = ; x 0 rcsin x x =. Verific: omess. ( + x = e ; x ± x) ( + x) x = e. Verific omess. x 0 x 0 log ( + x) x = log e ; x log x x = log e ; >0,. Verific: x 0 x log ( + x) = x 0 log ( + x) x = log e perchè (+x) x e per x 0. log Il secondo si ottiene con il cmb.to di vr.le y = x : (x) log x x = (+y) y 0 y = log e. x 0 x x =ln ; >0,. Verific: si ottiene con il cmb. di vr. y = x, d cui x = log (y +) e x y x 0 x = y 0 log (y+) = log e =ln (perchè log e log e = vedi proprietà 6. pg 6). L verific dei iti seguenti è omess. Se > ed α>0 si h: x + x =+ e xα x ( x)α x =0 log x Se >0, ed α>0 si h: =0 e (x) α log x + x α x =0. x Esempi. Clcolre, se esistono, i iti delle seguenti forme indeterminte: x 3. f.i. x x x 0 0. x 3 x 3 + = x x x x x x x ( x)( + x) x ( x)(+ x 3) = x x 3 + x 3 = x +x x ( + x 3) = x +3 ( x x )(+ x 3) = x 4 x x ( x)(+ x 3) = x 3. x x x f.i Osservimo che il binomio x x è positivo per 0 <x<; ne segue che x x cmbi segno in un intorno del punto x 0 = e quindi per esplicitre il modulo dobbimo dividere il ite in ite destro e ite sinistro e si h: x 3 x + x x x 3 x + = x 3 + x 3 = x + x x + x + x + x 3 = x +3 x + ( x + x )(+ x 3) = = x + ( x)( + x) x (x ) ( + x 3) = ( + x) x + x ( + x 3) = ; inoltre, per il ite sinistro, con conti nloghi i precedenti si ottiene x 3 x 3 = = = x x x x x x x 3 Si conclude che x x x perchè il ite destro è diverso dl ite sinistro. 36
37 3. ( x x 4 x 3) f.i. +. x + ( x x 4 x 3) = x ( ( x ) ) x (4 ( 3 x + x + x ) = x x 4 3x =+ ( ) = x + 4. x + ( x x x 3) f.i. +. Poichè, con pssggi nloghi ll es 3, procedimo nel modo seguente: ( x x x 3) = x + = x + x x ( + 3 ) x ) = ( x + 3 x ( x x x 3) x + x + perchè x = x in un intorno opportuno di +. x ( x x x 3) = x x + x + x x + x 3 x x + x 3 = x ( + 3 ) x ) = ( x + 3 x x + x + ( x 3x ) + 3 x x + 3 x x x x +3 x x + x 3 = = f.i. + 0, 5. x 0 sin(x + x) x f.i. 0 sin y. Cerchimo di utilizzre il ite notevole = : 0 y 0 y sin(x + x) sin(x + x) = x 0 x x 0 x + x x + x x = x 0 sin(x + x) x + x x + = = inftti, posto y = x + x si h y 0 per x 0 e quindi dl Teorem 3.9 del cmbimento di vribile si ottiene sin(x +x) x +x per x 0 perchè sin y y per y x 0 + log( x ) e x f.i. 0. Come nel ite precedente, cerchimo di ricondurci iti notevoli: 0 log( x ) log( x ) x 0 + e x = ( x ) x 0 + x inftti: x e x x = x 0 + log( x ) x x e x ( x x)= 0=0 posto y = x 0 per x 0 si ottiene log( x ) x dl ite notevole log(+y) y per y 0 posto t = x 0 per x 0 + si ottiene x e x t dl ite notevole per t 0. e t Funzioni h(x) =f(x) g(x) e forme indeterminte:, 0 0, + 0. Definimo dom h := {x dom g t.c. f(x) > 0}. Ovvimente si h h(x) > 0 x dom h. Possimo riscrivere h nell form h(x) =e ln( h(x)) = e ln( f(x))g(x) = e g(x) ln( f(x)). Allor, per clcolre R f(x) g(x) bst sper clcolre R g(x) ln( f(x) ) e poi si conclude utilizzndo i iti dell funzione esponenzile. Diremo che R f(x) g(x) è form indetermint se lo è il R g(x) ln( f(x)). Avremo quindi che è form indet.; inftti se f(x) e g(x) bbimo g(x) ln( f(x) ) f.i è form indet.; inftti se f(x) 0 e g(x) 0 bbimo g(x) ln( f(x) ) f.i. 0 ( ) + 0 è form indet.; inftti se f(x) + e g(x) 0 bbimo g(x) ln( f(x) ) f.i. 0 (+ ). 37
38 CAPITOLO Successioni: definizioni e prime proprietà. Definizione. - Un funzione f : N R è dett successione. Denotimo n := f(n) termine n-esimo dell successione n è detto indice f(n) :={ n : n N} = { 0,,, 3,, n, } l immgine dell successione. Esempi. - Esempi di successioni sono: n = n + {,, 3,, n +, }; n = n {0,,, 3,, n, }; n = n n + {0,, 5,, n n +, }; n =+( )n n + {,, 4 3,, + ( )n n +, }. Osservzione 4. - Prleremo ncor di successione nche nel cso in cui non sino definiti i termini n per un numero finito di indici. Esempi. - Sono successioni nche le seguenti: n = n, n N\{}, {,,, 3,, n, }; n = n 7, n N n 7, {0,,, 3,, n 7, }; Osservzione 4. - Alcune successioni sono restrizioni d N (o sottoinsiemi di N ) di funzioni di vribile rele, d esempio: n = n può essere considert come l restrizione f /N + di f(x) = x ; n = n 7 può essere considert come l restrizione f /{n N : n 7} di f(x) = x 7. Ci sono, però, successioni nelle quli non si può sostituire l posto dell vribile n N un vribile x R ;d esempio: n = n! ( dove n! :=n (n ) (n ) 3 ); n =( ) n. Se dt un successione { n } ne scego (estrimo) infiniti termini ottenimo ncor un successione. Se l scelt è ftt in modo str. crescente rispetto ll indice, bbimo l seguente definizione. Definizione. - Se d un successione { n } estrimo infiniti termini in modo str. crescente rispetto ll indice l successione ottenut è dett estrtt o sottosuccessione di { n }. [ Notimo che: estrrre i termini in modo str. crescente rispetto ll indice equivle scegliere ogni termine tr i "successivi" di quelli già scelti.] Esempio. - Dt l successione { n} considerimo le due successioni: { 3,, 7, 5,, 9, 5, 3, } {, 4, 9, 6,, n, } solo l second è sottosuccessione di { n}. Due sottosuccessioni importnti sono: { 0,, 4,, n, } estrtt pri {, 3, 5,, n+, } estrtt dispri. 38
39 Esempio. - Se n =( ) n 3 n si h: n =3 n estrtt pri e n+ = 3 n+ estrtt dispri. Definizioni. - Dt un successione { n } diremo che:. - { n } verific un proprietà P se n verific P per ogni n N ; es. n = n : n 0 n N;. - { n } verific definitivmente un proprietà P se n (indice) t.c. n verific P per ogni n> n ; cioè i termini sottolineti { 0,,,, n, n+,, n, } verificno P; es. n = n 50 : n > 0 definitivmente, perchè n > 0 n 8 ( n =7). Poichè le successioni sono funzioni (definite su N ), le definizioni e le proprietà viste per le funzioni vlgono, quindi, per le successioni. L prticolrità del dominio può semplificre, volte, le definizioni viste. Riscrivimo le definizioni di ittezz e di monotoni nel cso di un successione. Tli definizioni, utilizzndo l prticolrità del dominio, diventno: Definizioni. - Dt un successione { n } si h:. - { n } è itt se N, K R t.c. N n K n N o equiv.te se M>0 t.c. n M n N.. - { n } è crescente ( str. crescente ) se n n+ n N ( n < n+ n N ) { n } è decrescente ( str. decrescente ) se n n+ n N ( n > n+ n N ). Esempi. - Dt l prticolrità del dominio, può essere semplice verificre l monotoni di lcune successioni pplicndo l definizione precedente. Determinre se n = n + n + è monoton. Osservndo che il denomintore cresce in modo più rpido del numertore, provimo verificre se n è decrescente; vremo n n+ n + (n +)+ n + (n +) + (n +)(n +n +) (n +)(n +n +) (n +)(n +) (n +)(n +n +) (essendo i denomintori > 0) (n +)(n +n +) (n +)(n +) n +3n 0 che è sempre verifict n N. Quindi n è decrescente. Determinre se n = n n + è monoton. Provndo verificre se l succ.ne è decrescente, vremo n n+ n n + n + n ++ n ( n ++) n +( n +) ( n +)( n ++) ( n +)( n ++) (essendo i denom. > 0) n n + n n + mi verifict. Quindi n < n+ n N d cui n è str. crescente. 39
40 4. - Successioni: iti e proprietà. Essendo { n } un funzione con dominio N, vedimo quli definizioni di ite, viste per le funzioni, hnno senso ed in tl cso come si possono riscrivere utilizzndo le prticolrità del dominio, cioè le prticolrità di N. Osservimo, innnzi tutto, che preso un punto n 0 del dominio N, nell intorno bucto (n 0,n 0 + )\{n 0} non ci sono punti del domino N e quindi non h senso clcolre n con n 0 N. n n 0 Considerimo intorno di + in N l insieme (b, + ) N, b > 0; vremo che dto b>0 n N t.c. (b, + ) N = {n N : n> n}. Definimo llor: intorno di + in N un insieme del tipo {n N : n > n}. L unico ite che si può, quindi, clcolre per un successione è il n. n + In nlogi lle definizioni di f(x) =l R, tenendo conto dell nozione di intorno precedente, ottenimo x + le definizioni seguenti. Definizione. - Dt { n } successione definimo: n = l R n + se l R ε>0 n N t.c. n> n si h n l <ε se l =+ M>0 n N t.c. n> n si h n >M se l = M>0 n N t.c. n> n si h n < M. I due teoremi seguenti, di cui omettimo l dimostrzione, mettono in relzione il ite di un successione con i iti delle sue estrtte. Teorem 4. - Se n = l R, ogni sottosuccessione di { n } h ite ugule d l. n + Teorem 4. - Sino n e n+ l estrtt pri e l estrtt dispri di un successione n.se n l R e n+ m R, llor n + n m = l e si h n + n = l. Il seguente teorem indic come utilizzre iti di funzioni con vribile in R per clcolre iti di successioni. L dimostrzione, che discende in modo ovvio dlle definizioni di ite, è omess. Teorem Si f : A R con N A t.c. f(x) =l R.Se n = f(n) si h x + n + n = l R. Esempi. Clcolre, se esistono, i seguenti iti di successioni: ) ( n. + n ) = ( n ( n n + n ) ( n ) n + n + = n + n ( n + n n ) =.. n + n sin( n ) = dl ite sin( ) n n + n sin( n n = ) n n =+ n + n sin y y per y 0 e cmbimento di vribile y = n 0 per n +. 40
41 3. n + ( )n n + n : n pri n dispri n + = n + n n + = n + n quindi n + ( )n n + n. ( )n 4. ( + n + n ) : n pri n dispri n + ( + n )= ( n + n )= llor ( )n ( + n + n )=. 5. n + n e n =0 (dl ite pg 36 si ottiene x + (x) e x =0 e si conclude per il Teor.4.3) Limiti notevoli di successioni. n! = + Verific: d n! n si conclude per il Teor.3.6 pg 3. n + n + n n = Verific: si h n n = n n = e n ln n e 0 = (d x + ln x x = 0 e Teor.4.3). n + n n n + n! =+ >eα>0 (Verific:dllo stesso ite con vribile x R). nα =0 > (Verific omess) n! n + n =0 n (Verific omess) Proprietà legte iti di successioni. Osservzione Poichè le successioni sono funzioni, vlgono ncor tutti i teoremi sui iti visti per le funzioni. A titolo d esempio riscrivimo il teorem dell permnenz del segno utilizzndo le proprietà del dominio N. Teorem 4.4 (dell permnenz del segno) - Se stesso segno di l n> n. n = l R \{0}, llor n N t.c. n h lo n + [cioè n h definitivmente il segno di l.] I teoremi seguenti rigurdno l ittezz di successioni. L dimostrzione del secondo è omess. Teorem Se un successione { n } mmette ite rele llor tle successione è itt. Non è vero il vicevers. Dimostrzione. - Si ε =. Dll definizione di l < n <l+ n = l R, esiste n N t.c. n + n> n. Allor, se N = min{ 0,,,, n,l } e K = mx{ 0,,,, n,l+} si h Quindi { n } è itt. N n K n N 4
Integrale Improprio. f(x) dx =: Osserviamo che questa definizione ha senso dal momento che per ogni y è ben definito l integrale b
 Integrle Improprio In queste lezioni riprendimo l teori dell integrzione in un vribile, l ide è di estendere l integrle definito nche in csi in cui l funzione integrnd o l intervllo di integrzione non
Integrle Improprio In queste lezioni riprendimo l teori dell integrzione in un vribile, l ide è di estendere l integrle definito nche in csi in cui l funzione integrnd o l intervllo di integrzione non
Esercizi svolti Limiti. Prof. Chirizzi Marco.
 Cpitolo II Limiti delle funzioni di un vribile Esercizi svolti Limiti Prof. Chirizzi rco www.elettrone.ltervist.org 1) Verificre che risult: = Dobbimo provre che per ogni ε positivo, rbitrrimente piccolo,
Cpitolo II Limiti delle funzioni di un vribile Esercizi svolti Limiti Prof. Chirizzi rco www.elettrone.ltervist.org 1) Verificre che risult: = Dobbimo provre che per ogni ε positivo, rbitrrimente piccolo,
SUGLI INSIEMI. 1.Insiemi e operazioni su di essi
 SUGLI INSIEMI 1.Insiemi e operzioni su di essi Il concetto di insieme è primitivo ed è sinonimo di clsse, totlità. Si A un insieme di elementi qulunque. Per indicre che è un elemento di A scriveremo A.
SUGLI INSIEMI 1.Insiemi e operzioni su di essi Il concetto di insieme è primitivo ed è sinonimo di clsse, totlità. Si A un insieme di elementi qulunque. Per indicre che è un elemento di A scriveremo A.
POTENZA CON ESPONENTE REALE
 PRECORSO DI MATEMATICA VIII Lezione ESPONENZIALI E LOGARITMI E. Modic mtemtic@blogscuol.it www.mtemtic.blogscuol.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero rele > 0 ed un numero rele qulunque,
PRECORSO DI MATEMATICA VIII Lezione ESPONENZIALI E LOGARITMI E. Modic mtemtic@blogscuol.it www.mtemtic.blogscuol.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero rele > 0 ed un numero rele qulunque,
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA ESPONENZIALI E LOGARITMI Dr. Ersmo Modic ersmo@glois.it www.glois.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA ESPONENZIALI E LOGARITMI Dr. Ersmo Modic ersmo@glois.it www.glois.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero
Scheda Sei ESPONENZIALI E LOGARITMI. 0,+. Inoltre valgono le
 Sched Sei ESPONENZIALI E LOGARITMI L funzione esponenzile Assegnto un numero rele >0, si dice funzione esponenzile in bse l funzione Grfici dell funzione esponenzile Se = l funzione esponenzile è costnte:
Sched Sei ESPONENZIALI E LOGARITMI L funzione esponenzile Assegnto un numero rele >0, si dice funzione esponenzile in bse l funzione Grfici dell funzione esponenzile Se = l funzione esponenzile è costnte:
, x 2. , x 3. è un equazione nella quale le incognite appaiono solo con esponente 1, ossia del tipo:
 Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
Funzioni 1. 3) una legge che ad un elemento x di X associa al più un unico elemento ( x)
 Funzioni Un funzione f d X in Y è costituit d un tern di elementi ) un insieme X, detto dominio di f 2) un insiemey, detto codominio di f f di Y. Nel cso, in cui X,Y sino sottinsiemi di R, generlmente
Funzioni Un funzione f d X in Y è costituit d un tern di elementi ) un insieme X, detto dominio di f 2) un insiemey, detto codominio di f f di Y. Nel cso, in cui X,Y sino sottinsiemi di R, generlmente
5. Funzioni elementari trascendenti
 ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA 5. Funzioni elementri trscendenti A. A. 2013-2014 1 FUNZIONI ESPONENZIALI Le più semplici funzioni esponenzili sono le funzioni f: R R definite
ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA 5. Funzioni elementri trscendenti A. A. 2013-2014 1 FUNZIONI ESPONENZIALI Le più semplici funzioni esponenzili sono le funzioni f: R R definite
Nome.Cognome. 18 Dicembre 2008 Classe 4G. VERIFICA di MATEMATICA
 Nome.Cognome. 8 Dicembre 008 Clsse G VERIFICA di MATEMATICA A) Risolvi le seguenti disequzioni goniometriche sin ) sin + ) 0 6 tn cos + sin ) 0 (punti:0,5) ) tn + tn > 0 sin 5) sin > cos (punti: ) 6) sin
Nome.Cognome. 8 Dicembre 008 Clsse G VERIFICA di MATEMATICA A) Risolvi le seguenti disequzioni goniometriche sin ) sin + ) 0 6 tn cos + sin ) 0 (punti:0,5) ) tn + tn > 0 sin 5) sin > cos (punti: ) 6) sin
Esponenziali e logaritmi
 Esponenzili e ritmi ESPONENZIALI Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z Sono definite: ( ) ( ) ( ) 7 7 Non sono definite:
Esponenzili e ritmi ESPONENZIALI Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z Sono definite: ( ) ( ) ( ) 7 7 Non sono definite:
1 Integrale delle funzioni a scala
 INTEGRALE DELLE FUNZIONI DI UNA VARIABILE Teori di Riemnn 1 Integrle delle funzioni scl (1.1) Definizione Si dice suddivisione di un intervllo chiuso e limitto [, b] un sottoinsieme {,..., n } di [, b]
INTEGRALE DELLE FUNZIONI DI UNA VARIABILE Teori di Riemnn 1 Integrle delle funzioni scl (1.1) Definizione Si dice suddivisione di un intervllo chiuso e limitto [, b] un sottoinsieme {,..., n } di [, b]
INTEGRALI IMPROPRI. f(x) dx. e la funzione f(x) si dice integrabile in senso improprio su (a, b]. Se tale limite esiste ma
![INTEGRALI IMPROPRI. f(x) dx. e la funzione f(x) si dice integrabile in senso improprio su (a, b]. Se tale limite esiste ma INTEGRALI IMPROPRI. f(x) dx. e la funzione f(x) si dice integrabile in senso improprio su (a, b]. Se tale limite esiste ma](/thumbs/17/120065.jpg) INTEGRALI IMPROPRI. Integrli impropri su intervlli itti Dt un funzione f() continu in [, b), ponimo ε f() = f() ε + qundo il ite esiste. Se tle ite esiste finito, l integrle improprio si dice convergente
INTEGRALI IMPROPRI. Integrli impropri su intervlli itti Dt un funzione f() continu in [, b), ponimo ε f() = f() ε + qundo il ite esiste. Se tle ite esiste finito, l integrle improprio si dice convergente
y = Funzioni Lineari : Funzione quadrato: Modulo Funzione omografica (iperbole): Funzioni Potenza: Funzione Esponenziale Funzione Logaritmica
 Funzioni Lineri : Funzione qudrto: Modulo Funzione omogrfic (iperbole: Funzioni Elementri 1/ y m + q y + b + y y c + + b d c Funzioni Potenz: y Funzione Esponenzile Funzione Logritmic y y log ( Funzioni
Funzioni Lineri : Funzione qudrto: Modulo Funzione omogrfic (iperbole: Funzioni Elementri 1/ y m + q y + b + y y c + + b d c Funzioni Potenz: y Funzione Esponenzile Funzione Logritmic y y log ( Funzioni
Equazioni parametriche di primo grado
 Polo Sivigli Equzioni prmetriche di primo grdo Premess Come si s dll lgebr elementre, si chim equzione un uguglinz fr due espressioni letterli che si verific soltnto ttribuendo prticolri vlori lle lettere,
Polo Sivigli Equzioni prmetriche di primo grdo Premess Come si s dll lgebr elementre, si chim equzione un uguglinz fr due espressioni letterli che si verific soltnto ttribuendo prticolri vlori lle lettere,
ESPONENZIALI E LOGARITMI
 ESPONENZIALI E LOGARITMI RICHIAMI DI TEORIA dom f Im f grfico Funzioni esponenzili y=^ con > Funzioni esponenzili y=^ con
ESPONENZIALI E LOGARITMI RICHIAMI DI TEORIA dom f Im f grfico Funzioni esponenzili y=^ con > Funzioni esponenzili y=^ con
FUNZIONI IPERBOLICHE
 FUNZIONI IPERBOLICHE Umberto Mrconi Diprtimento di Mtemtic Pur e Applict Pdov Premess Si [, [, fissto. Voglimo cpire cos signific: w dw perché l funzione integrnd è illimitt. Se considerimo, per b [, [,
FUNZIONI IPERBOLICHE Umberto Mrconi Diprtimento di Mtemtic Pur e Applict Pdov Premess Si [, [, fissto. Voglimo cpire cos signific: w dw perché l funzione integrnd è illimitt. Se considerimo, per b [, [,
Integrali dipendenti da un parametro e derivazione sotto il segno di integrale.
 1 Integrli dipendenti d un prmetro e derivzione sotto il segno di integrle. Considerimo l funzione f(x, t) : A [, b] R definit nel rettngolo A [, b], essendo A un sottoinsieme perto di R e [, b] un intervllo
1 Integrli dipendenti d un prmetro e derivzione sotto il segno di integrle. Considerimo l funzione f(x, t) : A [, b] R definit nel rettngolo A [, b], essendo A un sottoinsieme perto di R e [, b] un intervllo
INTEGRALI IMPROPRI. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Integrali impropri cap10.pdf 1
 INTEGRALI IMPROPRI c Pol Gervsio - Anlisi Mtemtic - A.A. 6/7 Integrli impropri cp.pdf Abbimo visto che l integrle di Riemnn è definito per funzioni limitte e su intervlli limitti. Si or I R un intervllo
INTEGRALI IMPROPRI c Pol Gervsio - Anlisi Mtemtic - A.A. 6/7 Integrli impropri cp.pdf Abbimo visto che l integrle di Riemnn è definito per funzioni limitte e su intervlli limitti. Si or I R un intervllo
Ellisse riferita al centro degli assi
 Appunti delle lezioni tenute in clsse: ellisse e iperole Ellisse riferit l centro degli ssi Dti due punti F ed F detti fuochi, l ellisse è il luogo geometrico dei punti P del pino per cui è costnte l somm
Appunti delle lezioni tenute in clsse: ellisse e iperole Ellisse riferit l centro degli ssi Dti due punti F ed F detti fuochi, l ellisse è il luogo geometrico dei punti P del pino per cui è costnte l somm
{ } 3 [ ] [ ] [ ] [ ] Esercizi per il precorso ( )( ) Prof. Margherita Fochi. 1.- Esercizi sui polinomi. + x. x R. ( )( ) + R. ( )( )( ) a.
![{ } 3 [ ] [ ] [ ] [ ] Esercizi per il precorso ( )( ) Prof. Margherita Fochi. 1.- Esercizi sui polinomi. + x. x R. ( )( ) + R. ( )( )( ) a. { } 3 [ ] [ ] [ ] [ ] Esercizi per il precorso ( )( ) Prof. Margherita Fochi. 1.- Esercizi sui polinomi. + x. x R. ( )( ) + R. ( )( )( ) a.](/thumbs/59/42788277.jpg) Prof. Mrgherit Fochi Esercizi per il precorso.- Esercizi sui polinomi Semplificre le seguenti espressioni utilizzndo i prodotti notevoli:. ) ) ) ) ) 8 [ ] 8. ) ) ) ) ] [. ) ) ) [ ] { } y y y y y [ ] 8
Prof. Mrgherit Fochi Esercizi per il precorso.- Esercizi sui polinomi Semplificre le seguenti espressioni utilizzndo i prodotti notevoli:. ) ) ) ) ) 8 [ ] 8. ) ) ) ) ] [. ) ) ) [ ] { } y y y y y [ ] 8
Anno 5. Applicazione del calcolo degli integrali definiti
 Anno 5 Appliczione del clcolo degli integrli definiti 1 Introduzione In quest lezione vedremo come pplicre il clcolo dell integrle definito per determinre le ree di prticolri figure pine, i volumi dei
Anno 5 Appliczione del clcolo degli integrli definiti 1 Introduzione In quest lezione vedremo come pplicre il clcolo dell integrle definito per determinre le ree di prticolri figure pine, i volumi dei
Osserviamo che per trovare le costanti A e B possiamo anche ragionare così: se moltiplichiamo l equazione x + 1 (x + 2)(x + 3) = A.
 88 Roberto Turso - Anlisi 2 Osservimo che per trovre le costnti A e B possimo nche rgionre così: se moltiplichimo l equzione + ( + 2)( + 3) = A + 2 + B + 3 per + 2, dopo ver semplificto, ottenimo + + 3
88 Roberto Turso - Anlisi 2 Osservimo che per trovre le costnti A e B possimo nche rgionre così: se moltiplichimo l equzione + ( + 2)( + 3) = A + 2 + B + 3 per + 2, dopo ver semplificto, ottenimo + + 3
2 x = 64 (1) L esponente (x) a cui elevare la base (2) per ottenere il numero 64 è detto logaritmo (logaritmo in base 2 di 64), indicato così:
 Considerimo il seguente problem: si vuole trovre il numero rele tle che: = () L esponente () cui elevre l bse () per ottenere il numero è detto ritmo (ritmo in bse di ), indicto così: In prticolre in questo
Considerimo il seguente problem: si vuole trovre il numero rele tle che: = () L esponente () cui elevre l bse () per ottenere il numero è detto ritmo (ritmo in bse di ), indicto così: In prticolre in questo
Integrali de niti. Il problema del calcolo di aree ci porterà alla de nizione di integrale de nito.
 Integrli de niti. Il problem di clcolre l re di un regione pin delimitt d gr ci di funzioni si può risolvere usndo l integrle de nito. L integrle de nito st l problem del clcolo di ree come l equzione
Integrli de niti. Il problem di clcolre l re di un regione pin delimitt d gr ci di funzioni si può risolvere usndo l integrle de nito. L integrle de nito st l problem del clcolo di ree come l equzione
Esponenziali e logaritmi
 Teori in sintesi ESPONENZIALI Potenze con esponente rele Esponenzili e ritmi L potenz è definit: se, per ogni R se, per tutti e soli gli R se, per tutti e soli gli Z. Sono definite: 7 7. Non sono definite:.
Teori in sintesi ESPONENZIALI Potenze con esponente rele Esponenzili e ritmi L potenz è definit: se, per ogni R se, per tutti e soli gli R se, per tutti e soli gli Z. Sono definite: 7 7. Non sono definite:.
FUNZIONI CONTINUE A TRATTI E LORO INTEGRALI
 FUNZIONI CONTINUE A TRATTI E LORO INTEGRALI Considerimo un funzione f : I R, dove I è un intervllo di R. Si c un punto interno I in cui f è discontinu. Diremo che c è un punto di discontinuità di prim
FUNZIONI CONTINUE A TRATTI E LORO INTEGRALI Considerimo un funzione f : I R, dove I è un intervllo di R. Si c un punto interno I in cui f è discontinu. Diremo che c è un punto di discontinuità di prim
2. Teoremi per eseguire operazioni con i limiti in forma determinata
 . Teoremi per eseguire operzioni con i iti in form determint Vedimo dunque i teoremi che consentono il clcolo dei iti, ttrverso i quli si riconducono le situzioni rticolte semplici operzioni lgebriche
. Teoremi per eseguire operzioni con i iti in form determint Vedimo dunque i teoremi che consentono il clcolo dei iti, ttrverso i quli si riconducono le situzioni rticolte semplici operzioni lgebriche
Integrali. Il concetto di integrale nasce per risolvere due classi di problemi:
 Integrli Il concetto di integrle nsce per risolvere due clssi di problemi: clcolo delle ree di figure delimitte d curve, clcolo di volumi, clcolo del lvoro di un forz, clcolo dello spzio percorso,... integrle
Integrli Il concetto di integrle nsce per risolvere due clssi di problemi: clcolo delle ree di figure delimitte d curve, clcolo di volumi, clcolo del lvoro di un forz, clcolo dello spzio percorso,... integrle
Erasmo Modica. : K K K
 L insieme dei numeri reli L INSIEME DEI NUMERI REALI Ersmo Modic helthinsurnce@tin.it www.glois.it Per introdurre l insieme dei numeri reli si hnno disposizione diversi modi. Generlmente l iennio si preferisce
L insieme dei numeri reli L INSIEME DEI NUMERI REALI Ersmo Modic helthinsurnce@tin.it www.glois.it Per introdurre l insieme dei numeri reli si hnno disposizione diversi modi. Generlmente l iennio si preferisce
Teoria in pillole: logaritmi
 Teori in pillole: logritmi EQUAZIONI ESPONENZIALI Un'equzione si dice esponenzile qundo l'incognit compre soltnto nell'esponente di un o più potenze. L'equzione esponenzile più semplice (elementre) è del
Teori in pillole: logritmi EQUAZIONI ESPONENZIALI Un'equzione si dice esponenzile qundo l'incognit compre soltnto nell'esponente di un o più potenze. L'equzione esponenzile più semplice (elementre) è del
INTERVALLI NELL INSIEME R
 INTEVALLI NELL INSIEME Lo studio dell topologi (1) (dl greco "nlysis situs" ossi "studio del luogo") dell'insieme è di fondmentle importnz per gli rgomenti e i prolemi di nlisi infinitesimle. Il "luogo"
INTEVALLI NELL INSIEME Lo studio dell topologi (1) (dl greco "nlysis situs" ossi "studio del luogo") dell'insieme è di fondmentle importnz per gli rgomenti e i prolemi di nlisi infinitesimle. Il "luogo"
Il dominio della funzione, cioè l'insieme dei valori che si possono attribuire a x è tutto R ;
 CAPITOLO ESPONENZIALI E LOGARITMI ESPONENZIALI Teori in sintesi Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z. + Sono definite:
CAPITOLO ESPONENZIALI E LOGARITMI ESPONENZIALI Teori in sintesi Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z. + Sono definite:
Esponenziali e logaritmi
 Prof Emnuele ANDRISANI Teori in sintesi ESPONENZIALI Potenze con esponente rele L potenz è definit: se 0, per ogni R se 0, per tutti e soli gli R se 0, per tutti e soli gli Z Esponenzili e ritmi Sono definite:
Prof Emnuele ANDRISANI Teori in sintesi ESPONENZIALI Potenze con esponente rele L potenz è definit: se 0, per ogni R se 0, per tutti e soli gli R se 0, per tutti e soli gli Z Esponenzili e ritmi Sono definite:
Appunti di Analisi Matematica 1
 Appunti di Anlisi Mtemtic 1 MASTER IN ECONOMIA DIGITALE & e-business Centro per lo studio dei sistemi complessi Università di Sien Mrzo 2005 Prof. Polo Nistri Un funzione (o ppliczione) tr due insiemi
Appunti di Anlisi Mtemtic 1 MASTER IN ECONOMIA DIGITALE & e-business Centro per lo studio dei sistemi complessi Università di Sien Mrzo 2005 Prof. Polo Nistri Un funzione (o ppliczione) tr due insiemi
Funzioni Elementari 1/2
 Funzioni Lineri : Funzione qudrto: Modulo Funzione omogric iperbole: Funzioni Elementri / y m q y y y c b c b d Funzioni Potenz: Funzione Esponenzile Funzione Logritmic y y y log Funzioni trigonometriche
Funzioni Lineri : Funzione qudrto: Modulo Funzione omogric iperbole: Funzioni Elementri / y m q y y y c b c b d Funzioni Potenz: Funzione Esponenzile Funzione Logritmic y y y log Funzioni trigonometriche
Il lemma di ricoprimento di Vitali
 Il lemm di ricoprimento di Vitli Si I = {I} un fmigli di intervlli ciusi contenuti in R. Diremo ce l fmigli I ricopre l insieme E nel senso di Vitli (oppure ce I è un ricoprimento di Vitli di E) se per
Il lemm di ricoprimento di Vitli Si I = {I} un fmigli di intervlli ciusi contenuti in R. Diremo ce l fmigli I ricopre l insieme E nel senso di Vitli (oppure ce I è un ricoprimento di Vitli di E) se per
CORSO ANALISI MATEMATICA 1 A.A. 2015/2016. Testo consigliato
 Università degli studi di Cgliri CORSO ANALISI MATEMATICA 1 A.A. 2015/2016 Docente: Monic Mrrs 1 Anlisi Mtemtic 1 Testo consiglito con elementi di geometri e lgebr linere. M. Brmnti, C.D. Pgni, S. Sls
Università degli studi di Cgliri CORSO ANALISI MATEMATICA 1 A.A. 2015/2016 Docente: Monic Mrrs 1 Anlisi Mtemtic 1 Testo consiglito con elementi di geometri e lgebr linere. M. Brmnti, C.D. Pgni, S. Sls
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2002 Sessione straordinaria
 ESAME DI STAT DI LICE SCIENTIFIC CRS DI RDINAMENT 00 Sessione strordinri Il cndidto risolv uno dei due problemi e 5 dei 0 quesiti in cui si rticol il questionrio. PRBLEMA Con riferimento un sistem monometrico
ESAME DI STAT DI LICE SCIENTIFIC CRS DI RDINAMENT 00 Sessione strordinri Il cndidto risolv uno dei due problemi e 5 dei 0 quesiti in cui si rticol il questionrio. PRBLEMA Con riferimento un sistem monometrico
Maturità scientifica, corso di ordinamento, sessione ordinaria 2000-2001
 Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone Mturità scientific, corso di ordinmento, sessione ordinri 000-001 PROBLEMA 1 Si consideri l seguente relzione tr le vribili reli x, y: 1 1 1 +
Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone Mturità scientific, corso di ordinmento, sessione ordinri 000-001 PROBLEMA 1 Si consideri l seguente relzione tr le vribili reli x, y: 1 1 1 +
Equazioni di 2 grado. Definizioni Equazioni incomplete Equazione completa Relazioni tra i coefficienti della equazione e le sue soluzioni Esercizi
 Equzioni di grdo Definizioni Equzioni incomplete Equzione complet Relzioni tr i coefficienti dell equzione e le sue soluzioni Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Un equzione è: Un uguglinz
Equzioni di grdo Definizioni Equzioni incomplete Equzione complet Relzioni tr i coefficienti dell equzione e le sue soluzioni Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Un equzione è: Un uguglinz
Nome..Cognome.classe 4C 7 Maggio Verifica di Matematica
 Noe..Cognoe.clsse 4C 7 Mggio Verific di Mtetic PROBLEMA ( punti In un tringolo ABC il lto BC isur e l ngolo opposto è di. Deterinre in funzione dell piezz di ABC ˆ CH l ndento di f ( essendo CH e bisettrici
Noe..Cognoe.clsse 4C 7 Mggio Verific di Mtetic PROBLEMA ( punti In un tringolo ABC il lto BC isur e l ngolo opposto è di. Deterinre in funzione dell piezz di ABC ˆ CH l ndento di f ( essendo CH e bisettrici
TEST DI MATEMATICA. Funzioni in una, Funzioni in due variabili Integrali Equazioni differenziali. 1) Il valore del limite seguente. e e. e 1.
 TEST DI MATEMATICA Funzioni in un, Funzioni in due vriili Integrli Equzioni differenzili ) Il vlore del limite seguente e e e lim è ) Il vlore del limite seguente 5 lim 5 è : ) L derivt prim dell funzione
TEST DI MATEMATICA Funzioni in un, Funzioni in due vriili Integrli Equzioni differenzili ) Il vlore del limite seguente e e e lim è ) Il vlore del limite seguente 5 lim 5 è : ) L derivt prim dell funzione
FUNZIONI LOGARITMICHE
 FUNZIONI LOGARITMICHE Voglimo vedere come dl grfico δ di un funzione y=f(x) si può pssre l grfico δ dell funzione y = f (x). Dobbimo vere ben presente il grfico dell funzione y = x con x R + e con >0,
FUNZIONI LOGARITMICHE Voglimo vedere come dl grfico δ di un funzione y=f(x) si può pssre l grfico δ dell funzione y = f (x). Dobbimo vere ben presente il grfico dell funzione y = x con x R + e con >0,
1 Integrali generalizzati su intervalli illimitati
 Lezioni per il corso di Anlisi 2, AA 07-08. Dott.ss Sndr Lucente Argomento: Integrli generlizzti 1 1 Integrli generlizzti su intervlli ilitti Definizione 1.1. Si f : [,[ R un funzione continu. Se esiste
Lezioni per il corso di Anlisi 2, AA 07-08. Dott.ss Sndr Lucente Argomento: Integrli generlizzti 1 1 Integrli generlizzti su intervlli ilitti Definizione 1.1. Si f : [,[ R un funzione continu. Se esiste
lim lim lim + Nome.Cognome Classe 4D 7 Aprile 2011 Verifica di matematica Problema (punti 3) Sono date le funzioni: f ( x)
 Nome.Cognome Clsse D 7 Aprile 0 Verific di mtemtic Problem (punti ) Sono dte le funzioni: f ( ) =, g ( ) = ( ) ) determinre il dominio di f() e di g() b) determinre, senz l uso dell clcoltrice f ( ) c)
Nome.Cognome Clsse D 7 Aprile 0 Verific di mtemtic Problem (punti ) Sono dte le funzioni: f ( ) =, g ( ) = ( ) ) determinre il dominio di f() e di g() b) determinre, senz l uso dell clcoltrice f ( ) c)
1 Il problema del calcolo dell area di una regione piana limitata
 Anlisi Mtemtic 2 1 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 1 INTEGRALI DI FUNZIONI DI UNA VARIABILE REALE 1 Il problem del clcolo dell re di un regione pin limitt Se si consider un
Anlisi Mtemtic 2 1 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 1 INTEGRALI DI FUNZIONI DI UNA VARIABILE REALE 1 Il problem del clcolo dell re di un regione pin limitt Se si consider un
Serie di Potenze. Introduciamo il concetto di convergenza puntuale ed uniforme per successioni. { 0 se 1 < x < 1
 Serie di Potenze Introducimo il concetto di convergenz puntule ed uniforme per successioni di funzioni. Definizione 1 Si I un intervllo di R. Si dt l vrire di n N l funzione f n : I R. Dicimo che l successione
Serie di Potenze Introducimo il concetto di convergenz puntule ed uniforme per successioni di funzioni. Definizione 1 Si I un intervllo di R. Si dt l vrire di n N l funzione f n : I R. Dicimo che l successione
1 COORDINATE CARTESIANE
 1 COORDINATE CARTESIANE In un sistem di ssi crtesini (,) un punto P è identificto dll su sciss e dll su ordint : Asciss : distnz di P dll sse delle ordinte Ordint :distnz di P dll sse delle scisse P(-4,4)
1 COORDINATE CARTESIANE In un sistem di ssi crtesini (,) un punto P è identificto dll su sciss e dll su ordint : Asciss : distnz di P dll sse delle ordinte Ordint :distnz di P dll sse delle scisse P(-4,4)
8. Prodotto scalare, Spazi Euclidei.
 8. Prodotto sclre, Spzi Euclidei. Ricordimo l definizione di prodotto sclre di due vettori del pino VO 2 (vle in modo del tutto nlogo nche in VO 3 ). Definizione: Sino v, w VO 2 e si θ l ngolo convesso
8. Prodotto sclre, Spzi Euclidei. Ricordimo l definizione di prodotto sclre di due vettori del pino VO 2 (vle in modo del tutto nlogo nche in VO 3 ). Definizione: Sino v, w VO 2 e si θ l ngolo convesso
Nome.Cognome classe 5D 18 Marzo 2014. Verifica di matematica
 Nome Cognome cls 5D 18 Mrzo 01 Problem Verific di mtemtic In un sistem di riferimento crtesino Oy, si consideri l funzione: ln f ( > 0 0 e si determini il vlore del prmetro rele in modo tle che l funzione
Nome Cognome cls 5D 18 Mrzo 01 Problem Verific di mtemtic In un sistem di riferimento crtesino Oy, si consideri l funzione: ln f ( > 0 0 e si determini il vlore del prmetro rele in modo tle che l funzione
Il problema delle aree. Metodo di esaustione.
 INTEGRALE DEFINITO. DEFINIZIONE E SIGNIFICATO GEOMETRICO. PROPRIETA DELL INTEGRALE DEFINITO. FUNZIONE INTEGRALE. TEOREMA DELLA MEDIA. TEOREMA FONDAMENTALE DEL CALCOLO INTEGRALE. FORMULA DI LEIBNITZ NEWTON.
INTEGRALE DEFINITO. DEFINIZIONE E SIGNIFICATO GEOMETRICO. PROPRIETA DELL INTEGRALE DEFINITO. FUNZIONE INTEGRALE. TEOREMA DELLA MEDIA. TEOREMA FONDAMENTALE DEL CALCOLO INTEGRALE. FORMULA DI LEIBNITZ NEWTON.
Equazioni 1 grado. Definizioni Classificazione Risoluzione Esercizi
 Equzioni grdo Definizioni Clssificzione Risoluzione Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Prendimo in esme le due espressioni numeriche 8 entrmbe sono uguli 7, e l scrittur si chim uguglinz
Equzioni grdo Definizioni Clssificzione Risoluzione Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Prendimo in esme le due espressioni numeriche 8 entrmbe sono uguli 7, e l scrittur si chim uguglinz
AUTOVALORI ED AUTOVETTORI. Sia V uno spazio vettoriale di dimensione finita n.
 AUTOVALORI ED AUTOVETTORI Si V uno spzio vettorile di dimensione finit n. Dicesi endomorfismo di V ogni ppliczione linere f : V V dello spzio vettorile in sé. Se f è un endomorfismo di V in V, considert
AUTOVALORI ED AUTOVETTORI Si V uno spzio vettorile di dimensione finit n. Dicesi endomorfismo di V ogni ppliczione linere f : V V dello spzio vettorile in sé. Se f è un endomorfismo di V in V, considert
26/03/2012. Integrale Definito. Calcolo delle Aree. Appunti di analisi matematica: Il concetto d integrale nasce per risolvere due classi di problemi:
 ppunti di nlisi mtemtic: Integrle efinito Il concetto d integrle nsce per risolvere due clssi di prolemi: Integrle efinito lcolo delle ree di fig. delimitte d curve clcolo di volumi clcolo del lvoro di
ppunti di nlisi mtemtic: Integrle efinito Il concetto d integrle nsce per risolvere due clssi di prolemi: Integrle efinito lcolo delle ree di fig. delimitte d curve clcolo di volumi clcolo del lvoro di
dr Valerio Curcio Le affinità omologiche Le affinità omologiche
 1 Le ffinità omologiche 2 Tringoli omologici: Due tringoli si dicono omologici se le rette congiungenti i punti omologhi dei due tringoli si incontrno in un medesimo punto. Principio dei tringoli omologici
1 Le ffinità omologiche 2 Tringoli omologici: Due tringoli si dicono omologici se le rette congiungenti i punti omologhi dei due tringoli si incontrno in un medesimo punto. Principio dei tringoli omologici
Siano A e B due insiemi non vuoti. Una funzione f da A a B è un assegnamento di esattamente un elemento di B ad ogni elemento di A
 Funzioni Definizione di funzione: Sino A e B due insiemi non vuoti. Un funzione f d A B è un ssegnmento di esttmente un elemento di B d ogni elemento di A Scrivimo f() = b se b è l unico elemento dell
Funzioni Definizione di funzione: Sino A e B due insiemi non vuoti. Un funzione f d A B è un ssegnmento di esttmente un elemento di B d ogni elemento di A Scrivimo f() = b se b è l unico elemento dell
Sezione Esercizi ; ; ; 1 4. f ) 13 + g ) , 100, 125; f ) 216; 8 27 ; ; e ) g ) 0; h )
 Sezione Esercizi Esercizi Esercizi dei singoli prgrfi - Rdici Determin le seguenti rdici qudrte rzionli (qundo è possiile clcolrle) 00 l ) m ) n ) o ) 0,0 0,0 0,000 0, Determin le seguenti rdici qudrte
Sezione Esercizi Esercizi Esercizi dei singoli prgrfi - Rdici Determin le seguenti rdici qudrte rzionli (qundo è possiile clcolrle) 00 l ) m ) n ) o ) 0,0 0,0 0,000 0, Determin le seguenti rdici qudrte
ESPONENZIALI E LOGARITMI
 Esponenzili e logritmi ESPONENZIALI E LOGARITMI Potenze Fino d or si sono definite le potenze d esponenete intero e rzionle (si positivi che negtivi). Ripssimo le definizioni e i concetti che li rigurdno:
Esponenzili e logritmi ESPONENZIALI E LOGARITMI Potenze Fino d or si sono definite le potenze d esponenete intero e rzionle (si positivi che negtivi). Ripssimo le definizioni e i concetti che li rigurdno:
1 Integrali impropri di funzioni continue
 ntegrli impropri di funzioni continue. ntegrli impropri su intervlli semiperti Definizione Dt un funzione continu f : [, b) R, con b +, si dice che f è integrbile se esiste finito il t b f(x) dx ed in
ntegrli impropri di funzioni continue. ntegrli impropri su intervlli semiperti Definizione Dt un funzione continu f : [, b) R, con b +, si dice che f è integrbile se esiste finito il t b f(x) dx ed in
Corso di Analisi Matematica Calcolo integrale per funzioni di una variabile
 Corso di Anlisi Mtemtic Clcolo integrle per funzioni di un vribile Lure in Informtic e Comuniczione Digitle A.A. 2013/2014 Università di Bri ICD (Bri) Anlisi Mtemtic 1 / 40 1 L integrle come limite di
Corso di Anlisi Mtemtic Clcolo integrle per funzioni di un vribile Lure in Informtic e Comuniczione Digitle A.A. 2013/2014 Università di Bri ICD (Bri) Anlisi Mtemtic 1 / 40 1 L integrle come limite di
Lezione 14. Risoluzione delle equazioni algebriche.
 Lezione Prerequisiti: Lezioni 8,. Risoluzione delle equzioni lgebriche. Si F un cmpo, e si K un chiusur lgebric di F. Si f ( ) F[ ] non costnte. Studimo i metodi di risoluzione per l equzione f ( ) = 0,
Lezione Prerequisiti: Lezioni 8,. Risoluzione delle equzioni lgebriche. Si F un cmpo, e si K un chiusur lgebric di F. Si f ( ) F[ ] non costnte. Studimo i metodi di risoluzione per l equzione f ( ) = 0,
Appunti di Analisi Matematica
 Appunti di Anlisi Mtemtic Stefno Med e Alberto Peretti Appunti per il corso di Mtemtic I I semestre,.. 2001/2002 Fcoltà di Scienze Sttistiche Università di Milno-Bicocc c Stefno Med e Alberto Peretti,
Appunti di Anlisi Mtemtic Stefno Med e Alberto Peretti Appunti per il corso di Mtemtic I I semestre,.. 2001/2002 Fcoltà di Scienze Sttistiche Università di Milno-Bicocc c Stefno Med e Alberto Peretti,
Esercizio 1. Dimostrare che se (X, d) è uno spazio metrico anche (X, d ) lo è, dove d =
 I seguenti esercizi sono stti proposti, e qusi tutti risolti, ttrverso l miling list del corso di Geometri IV durnte l nno ccdemico 2004/2005. Esercizio 1. Dimostrre che se (X, d) è uno spzio metrico nche
I seguenti esercizi sono stti proposti, e qusi tutti risolti, ttrverso l miling list del corso di Geometri IV durnte l nno ccdemico 2004/2005. Esercizio 1. Dimostrre che se (X, d) è uno spzio metrico nche
1 Funzioni continue: definizioni e prime proprietà. 2 Continuità delle funzioni elementari 2
 FUNZIONI CONTINUE FUNZIONI CONTINUE: DEFINIZIONI E PRIME PROPRIETÀ Funzioni continue Indice Funzioni continue: definizioni e prime proprietà 2 Continuità delle funzioni elementri 2 3 Funzioni continue
FUNZIONI CONTINUE FUNZIONI CONTINUE: DEFINIZIONI E PRIME PROPRIETÀ Funzioni continue Indice Funzioni continue: definizioni e prime proprietà 2 Continuità delle funzioni elementri 2 3 Funzioni continue
La parabola con asse parallelo all ady
 L prbol con sse prllelo ll dy I Prbol con vertice nell origine degli ssi crtesini I disegni degli esercizi dll 1 l 3 dell sched di lbortorio, sono i seguenti: Quindi il segno del coefficiente di x determin
L prbol con sse prllelo ll dy I Prbol con vertice nell origine degli ssi crtesini I disegni degli esercizi dll 1 l 3 dell sched di lbortorio, sono i seguenti: Quindi il segno del coefficiente di x determin
FORMULARIO GENERALE DEI CORSI DI ISTITUZIONI DI MATEMATICHE
 FORMULARIO GENERALE DEI CORSI DI ISTITUZIONI DI MATEMATICHE ALGEBRA LINEARE Operzioni tr mtrici Sino A = { ij } e B = {b ij } venti l stess imensione. L loro somm è l mtrice C i cui elementi sono {c ij
FORMULARIO GENERALE DEI CORSI DI ISTITUZIONI DI MATEMATICHE ALGEBRA LINEARE Operzioni tr mtrici Sino A = { ij } e B = {b ij } venti l stess imensione. L loro somm è l mtrice C i cui elementi sono {c ij
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2002 Sessione ordinaria
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO Sessione ordinri Il cndidto risolv uno dei due problemi e 5 dei quesiti in cui si rticol il questionrio. PROBLEMA In un pino, riferito d un sistem
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO Sessione ordinri Il cndidto risolv uno dei due problemi e 5 dei quesiti in cui si rticol il questionrio. PROBLEMA In un pino, riferito d un sistem
DISPENSE DI ANALISI MATEMATICA. Indice
 DISPENSE DI ANALISI MATEMATICA ANNAMARIA MONTANARI Indice. Integrle di Riemnn.. Proprietà elementri dell integrle di Riemnn 5.2. Teorem fondmentle del clcolo integrle. Primitive 6.3. Integrle generlizzto
DISPENSE DI ANALISI MATEMATICA ANNAMARIA MONTANARI Indice. Integrle di Riemnn.. Proprietà elementri dell integrle di Riemnn 5.2. Teorem fondmentle del clcolo integrle. Primitive 6.3. Integrle generlizzto
Geometria analitica. punti, rette, circonferenza, ellisse, iperbole, parabola. ITIS Feltrinelli anno scolastico Il piano cartesiano
 Geometri nlitic punti, rette, circonferenz, ellisse, iperbole, prbol ITIS Feltrinelli nno scolstico 007-008 Il pino crtesino Si dice pino crtesino un sistem formto d due rette perpendicolri che si intersecno
Geometri nlitic punti, rette, circonferenz, ellisse, iperbole, prbol ITIS Feltrinelli nno scolstico 007-008 Il pino crtesino Si dice pino crtesino un sistem formto d due rette perpendicolri che si intersecno
INTRODUZIONE ALLA TRIGONOMETRIA
 INTRODUZIONE ALLA TRIGONOMETRIA L trigonometri: come e perché. L prol trigonometri signific misur degli elementi di un tringolo; prolem primrio di questo cpitolo dell mtemtic è quello di determinre l misur
INTRODUZIONE ALLA TRIGONOMETRIA L trigonometri: come e perché. L prol trigonometri signific misur degli elementi di un tringolo; prolem primrio di questo cpitolo dell mtemtic è quello di determinre l misur
{ 3 x y=4. { x=2. Sistemi di equazioni
 Sistemi di equzioni Definizione Un sistem è un insieme di equzioni che devono essere verificte contempornemente, cioè devono vere contempornemente le stesse soluzioni. Definimo grdo di un sistem il prodotto
Sistemi di equzioni Definizione Un sistem è un insieme di equzioni che devono essere verificte contempornemente, cioè devono vere contempornemente le stesse soluzioni. Definimo grdo di un sistem il prodotto
( x) a) La simmetrica della parabola rispetto all origine è tale che: La parabola di equazione y = x + ax a ha vertice V = = mentre la parabola y S
 Sessione ordinri 996 Liceo di ordinmento Soluzione di De Ros Nicol ) In un pino, riferito d un sistem di ssi crtesini ortogonli (O), sono ssegnte le prbole di equzione:, dove è un numero rele positivo.
Sessione ordinri 996 Liceo di ordinmento Soluzione di De Ros Nicol ) In un pino, riferito d un sistem di ssi crtesini ortogonli (O), sono ssegnte le prbole di equzione:, dove è un numero rele positivo.
Esercizi sulle serie di Fourier
 Esercizi sulle serie di Fourier Corso di Fisic Mtemtic,.. 3- Diprtimento di Mtemtic, Università di Milno Novembre 3 Sviluppo in serie di Fourier (esponenzile) In questi esercizi, si richiede di sviluppre
Esercizi sulle serie di Fourier Corso di Fisic Mtemtic,.. 3- Diprtimento di Mtemtic, Università di Milno Novembre 3 Sviluppo in serie di Fourier (esponenzile) In questi esercizi, si richiede di sviluppre
Differenziale. Consideriamo la variazione finita, x della variabile indipendente a cui corrisponde una variazione finita della funzione f x, f x y
 Differenzile Considerimo l vrizione finit, dell vriile indipendente cui corrisponde un vrizione finit dell funzione f, f y Δf 1 Δ 2 L vrizione dell vriile dipendente puo' essere molto piccol, infinitesim
Differenzile Considerimo l vrizione finit, dell vriile indipendente cui corrisponde un vrizione finit dell funzione f, f y Δf 1 Δ 2 L vrizione dell vriile dipendente puo' essere molto piccol, infinitesim
Corso di Analisi Matematica. Calcolo integrale
 .. 2011/12 Lure triennle in Informtic Corso di Anlisi Mtemtic Clcolo integrle Avvertenz Questi sono ppunti informli delle lezioni, che vengono resi disponibili per comodità degli studenti. Prte del mterile
.. 2011/12 Lure triennle in Informtic Corso di Anlisi Mtemtic Clcolo integrle Avvertenz Questi sono ppunti informli delle lezioni, che vengono resi disponibili per comodità degli studenti. Prte del mterile
ESPONENZIALI E LOGARITMI
 ESPONENZIALI E LOGARITMI 1 se 0, per ogni R ; Teori in sintesi ESPONENZIALI Potenze con esponente rele L potenz è definit: se >0: Sono definite: se >0: Non sono definite: Csi prticolri: Le proprietà delle
ESPONENZIALI E LOGARITMI 1 se 0, per ogni R ; Teori in sintesi ESPONENZIALI Potenze con esponente rele L potenz è definit: se >0: Sono definite: se >0: Non sono definite: Csi prticolri: Le proprietà delle
Integrali. all integrale definito all integrale indefinito. Integrali: riepilogo
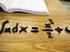 Integrli ll integrle deinito ll integrle indeinito Indice dell lezione Integrle Deinito Rettngoloide Integrle deinito come re del rettngoloide Esempi e propriet Primitiv Teorem ondmentle del clcolo integrle
Integrli ll integrle deinito ll integrle indeinito Indice dell lezione Integrle Deinito Rettngoloide Integrle deinito come re del rettngoloide Esempi e propriet Primitiv Teorem ondmentle del clcolo integrle
Antonella Greco, Rosangela Mapelli. E-Matematica. E-Book di Matematica per il triennio. Volume 1
 Antonell Greco, Rosngel Mpelli E-Mtemtic E-Book di Mtemtic per il triennio Volume COPIA SAGGIO Cmpione grtuito fuori commercio d esclusivo uso dei docenti Grmond 009 Tutti i diritti riservti Vi Tevere,
Antonell Greco, Rosngel Mpelli E-Mtemtic E-Book di Mtemtic per il triennio Volume COPIA SAGGIO Cmpione grtuito fuori commercio d esclusivo uso dei docenti Grmond 009 Tutti i diritti riservti Vi Tevere,
Integrale Definito. Appunti di analisi matematica: Il concetto d integrale nasce per risolvere due classi di problemi: Integrale Definito
 Appunti di nlisi mtemtic: Integrle Deinito Il concetto d integrle nsce per risolvere due clssi di prolemi: Integrle Deinito Clcolo delle ree di ig. delimitte d curve clcolo di volumi clcolo del lvoro di
Appunti di nlisi mtemtic: Integrle Deinito Il concetto d integrle nsce per risolvere due clssi di prolemi: Integrle Deinito Clcolo delle ree di ig. delimitte d curve clcolo di volumi clcolo del lvoro di
1 b a. f(x) dx. Osservazione 1.2. Se indichiamo con µ il valore medio di f su [a, b], abbiamo che. f(x) dx = µ(b a) =
![1 b a. f(x) dx. Osservazione 1.2. Se indichiamo con µ il valore medio di f su [a, b], abbiamo che. f(x) dx = µ(b a) = 1 b a. f(x) dx. Osservazione 1.2. Se indichiamo con µ il valore medio di f su [a, b], abbiamo che. f(x) dx = µ(b a) =](/thumbs/19/319521.jpg) Note ed esercizi di Anlisi Mtemtic - (Fosci) Ingegneri dell Informzione - 28-29. Lezione del 7 novembre 28. Questi esercizi sono reperibili dll pgin web del corso ttp://utenti.unife.it/dmino.fosci/didttic/mii89.tml
Note ed esercizi di Anlisi Mtemtic - (Fosci) Ingegneri dell Informzione - 28-29. Lezione del 7 novembre 28. Questi esercizi sono reperibili dll pgin web del corso ttp://utenti.unife.it/dmino.fosci/didttic/mii89.tml
Seconda prova maturita 2016 soluzione secondo problema di matematica scientifico
 Second prov mturit 06 soluzione secondo problem di mtemtic scientifico Skuol.net June, 06 Primo Problem Le tre funzioni proposte sono f () ( ) k f () 6 + 9k + f () cos( π k ). Punto Affinche l funzione
Second prov mturit 06 soluzione secondo problem di mtemtic scientifico Skuol.net June, 06 Primo Problem Le tre funzioni proposte sono f () ( ) k f () 6 + 9k + f () cos( π k ). Punto Affinche l funzione
Strumenti Matematici per la Fisica
 Strumenti Mtemtici per l Fisic Strumenti Mtemtici per l Fisic Approssimzioni Notzione scientific (o esponenzile) Ordine di Grndezz Sistem Metrico Decimle Equivlenze Proporzioni e Percentuli Relzioni fr
Strumenti Mtemtici per l Fisic Strumenti Mtemtici per l Fisic Approssimzioni Notzione scientific (o esponenzile) Ordine di Grndezz Sistem Metrico Decimle Equivlenze Proporzioni e Percentuli Relzioni fr
Esercizi su spazi ed operatori lineari
 Esercizi su spzi ed opertori lineri Corso di Fisic Mtemtic 2,.. 2013-2014 Diprtimento di Mtemtic, Università di Milno 23 Ottobre 2013 1 Spzio L 2 Esercizio 1. Per = 0, b = 1, dire quli delle seguenti funzioni
Esercizi su spzi ed opertori lineri Corso di Fisic Mtemtic 2,.. 2013-2014 Diprtimento di Mtemtic, Università di Milno 23 Ottobre 2013 1 Spzio L 2 Esercizio 1. Per = 0, b = 1, dire quli delle seguenti funzioni
PROGRAMMA SVOLTO A. S. 2014/ 2015
 A. S. 4/ Nome docente Borgn Giorgio Mteri insegnt Mtemtic Clsse Previsione numero ore di insegnmento IV G mnutenzione e ssistenz tecnic ore complessive di insegnmento settimne X 4 ore = ore Nome Ins. Tecn.
A. S. 4/ Nome docente Borgn Giorgio Mteri insegnt Mtemtic Clsse Previsione numero ore di insegnmento IV G mnutenzione e ssistenz tecnic ore complessive di insegnmento settimne X 4 ore = ore Nome Ins. Tecn.
Cap. 4 - Algebra vettoriale
 Mssimo Bnfi Cp. 4 - Algebr vettorile Cpitolo 4 Algebr vettorile 4.1. Grndezze sclri Si definiscono sclri quelle grndezze fisiche che sono descritte in modo completo d un numero con l reltiv unità di misur.
Mssimo Bnfi Cp. 4 - Algebr vettorile Cpitolo 4 Algebr vettorile 4.1. Grndezze sclri Si definiscono sclri quelle grndezze fisiche che sono descritte in modo completo d un numero con l reltiv unità di misur.
Elementi grafici per Matematica
 Elementi grfici per Mtemtic Sommrio: Sistemi di coordinte crtesine... Grfici di funzioni... 4. Definizione... 4. Esempi... 5.3 Verificre iniettività e suriettività dl grfico... 8.4 L rett... 9.5 Esempi
Elementi grfici per Mtemtic Sommrio: Sistemi di coordinte crtesine... Grfici di funzioni... 4. Definizione... 4. Esempi... 5.3 Verificre iniettività e suriettività dl grfico... 8.4 L rett... 9.5 Esempi
1) Si ha quindi Un cateto è uguale al prodotto dell ipotenusa per il seno dell angolo opposto.
 Trigonometri prte esy mtemti Elin pgin TRIANGOLO RETTANGOLO Considerimo i tringoli rettngoli OPQ e OP ' Q A γ C Essi sono simili per ui Q P : QP OP : OP Essendo Q ' P ' QP sin OP OP ottenimo : sen : e
Trigonometri prte esy mtemti Elin pgin TRIANGOLO RETTANGOLO Considerimo i tringoli rettngoli OPQ e OP ' Q A γ C Essi sono simili per ui Q P : QP OP : OP Essendo Q ' P ' QP sin OP OP ottenimo : sen : e
LEZIONE 20. è lineare. Per la commutatività del prodotto scalare segue anche la linearità dell applicazione
 LEZIONE 20 20.1. Prodotti sclri. Definizione 20.1.1. Si V uno spzio vettorile su R. Un prodotto sclre su V è un ppliczione tle che:, : V V R (v 1, v 2 ) v 1, v 2 (PS1) per ogni v 1, v 2 V si h v 1, v 2
LEZIONE 20 20.1. Prodotti sclri. Definizione 20.1.1. Si V uno spzio vettorile su R. Un prodotto sclre su V è un ppliczione tle che:, : V V R (v 1, v 2 ) v 1, v 2 (PS1) per ogni v 1, v 2 V si h v 1, v 2
ANALISI REALE E COMPLESSA a.a. 2007-2008
 ANALISI REALE E COMPLESSA.. 2007-2008 1 Successioni e serie di funzioni 1.1 Introduzione In questo cpitolo studimo l convergenz di successioni del tipo n f n, dove le f n sono tutte funzioni vlori reli
ANALISI REALE E COMPLESSA.. 2007-2008 1 Successioni e serie di funzioni 1.1 Introduzione In questo cpitolo studimo l convergenz di successioni del tipo n f n, dove le f n sono tutte funzioni vlori reli
COGNOME..NOME CLASSE.DATA
 COGNOME..NOME CLASSE.DATA FUNZIONE ESPONENZIALE - VERIFICA OBIETTIVI Sper definire un funzione esponenzile. Sper rppresentre un funzione esponenzile. Sper individure le crtteristiche del grfico di un funzione
COGNOME..NOME CLASSE.DATA FUNZIONE ESPONENZIALE - VERIFICA OBIETTIVI Sper definire un funzione esponenzile. Sper rppresentre un funzione esponenzile. Sper individure le crtteristiche del grfico di un funzione
Lezione 1 Insiemi e numeri
 Lezione Insiemi e numeri. Nozione di insieme, sottoinsieme, pprtenenz Con l prol insieme intendimo un collezione di oggetti detti suoi elementi. Ogni insieme è denotto con lettere miuscole e i suoi elementi
Lezione Insiemi e numeri. Nozione di insieme, sottoinsieme, pprtenenz Con l prol insieme intendimo un collezione di oggetti detti suoi elementi. Ogni insieme è denotto con lettere miuscole e i suoi elementi
{ 1, 2,3, 4,5,6,7,8,9,10,11,12, }
 Lezione 01 Aritmetic Pgin 1 di 1 I numeri nturli I numeri nturli sono: 0,1,,,4,5,6,7,8,,10,11,1, L insieme dei numeri nturli viene indicto col simbolo. } { 0,1,,, 4,5,6,7,8,,10,11,1, } L insieme dei numeri
Lezione 01 Aritmetic Pgin 1 di 1 I numeri nturli I numeri nturli sono: 0,1,,,4,5,6,7,8,,10,11,1, L insieme dei numeri nturli viene indicto col simbolo. } { 0,1,,, 4,5,6,7,8,,10,11,1, } L insieme dei numeri
Appunti di matematica 3 Indice
 Appunti di mtemtic Indice. Ripsso di lgebr e geometri del biennio. Geometri nlitic Il pino crtesino Rett Circonferenz Prbol Ellisse Iperbole Complementi di geometri nlitic. Successioni numeriche. Funzione
Appunti di mtemtic Indice. Ripsso di lgebr e geometri del biennio. Geometri nlitic Il pino crtesino Rett Circonferenz Prbol Ellisse Iperbole Complementi di geometri nlitic. Successioni numeriche. Funzione
x = x(t) y = y(t) t [a, b]
![x = x(t) y = y(t) t [a, b] x = x(t) y = y(t) t [a, b]](/thumbs/50/26298328.jpg) Dt un curv continu. Curve ed integrli di line : t [, b] i punti () = (x(), y()) e (b) = (x(b), y(b)) si chimno primo e secondo estremo dell curv, rispettivmente. L curv si dice chius se () = (b). L curv
Dt un curv continu. Curve ed integrli di line : t [, b] i punti () = (x(), y()) e (b) = (x(b), y(b)) si chimno primo e secondo estremo dell curv, rispettivmente. L curv si dice chius se () = (b). L curv
Anno 1. Numeri reali: proprietà e applicazioni di uso comune
 Anno Numeri reli: proprietà e ppliczioni di uso comune Introduzione L insieme dei numeri rzionli è composto d numeri che si ottengono dl rpporto tr due numeri interi. Tle rpporto, o frzione, è sempre ssociile
Anno Numeri reli: proprietà e ppliczioni di uso comune Introduzione L insieme dei numeri rzionli è composto d numeri che si ottengono dl rpporto tr due numeri interi. Tle rpporto, o frzione, è sempre ssociile
ELEMENTI DI TEORIA DEI NUMERI
 ELEMENTI DI TEORIA DEI NUMERI 1. Richimi di teori Con Z indichimo l insieme dei numeri reltivi. Comincimo con il ricordre l definizione di quoziente e resto dell divisione di due numeri in Z. Definizione
ELEMENTI DI TEORIA DEI NUMERI 1. Richimi di teori Con Z indichimo l insieme dei numeri reltivi. Comincimo con il ricordre l definizione di quoziente e resto dell divisione di due numeri in Z. Definizione
MATEMATICA Classe Prima
 Liceo Clssico di Treiscce Esercizi per le vcnze estive 0 MATEMATICA Clsse Prim Cpitolo Numeri nturli Primi ogni pgin del cpitolo Cpitolo Numeri nturli Primi ogni pgin del cpitolo Per gli llievi promossi
Liceo Clssico di Treiscce Esercizi per le vcnze estive 0 MATEMATICA Clsse Prim Cpitolo Numeri nturli Primi ogni pgin del cpitolo Cpitolo Numeri nturli Primi ogni pgin del cpitolo Per gli llievi promossi
Equazioni e disequazioni
 Cpitolo Equzioni e disequzioni.1 Princìpi di equivlenz 1. Sommndo o sottrendo l stess quntità d entrmbi i membri di un equzione o di un disequzione ess non cmbi, ovvero: A(x) B(x) A(x) k(x) B(x) k(x).
Cpitolo Equzioni e disequzioni.1 Princìpi di equivlenz 1. Sommndo o sottrendo l stess quntità d entrmbi i membri di un equzione o di un disequzione ess non cmbi, ovvero: A(x) B(x) A(x) k(x) B(x) k(x).
3. Funzioni iniettive, suriettive e biiettive (Ref p.14)
 . Funzioni iniettive, suriettive e iiettive (Ref p.4) Dll definizione di funzione si ricv che, not un funzione y f( ), comunque preso un vlore di pprtenente l dominio di f( ) esiste un solo vlore di y
. Funzioni iniettive, suriettive e iiettive (Ref p.4) Dll definizione di funzione si ricv che, not un funzione y f( ), comunque preso un vlore di pprtenente l dominio di f( ) esiste un solo vlore di y
